
Modeling of Two Sub-reach Water Systems: Application to Navigation
Canals in the North of France
Pau Segovia
1,2
, Klaudia Horv
´
ath
3
, Lala Rajaoarisoa
1
, Fatiha Nejjari
2
, Vicenc¸ Puig
2
and Eric Duviella
1
1
Unit
´
e de Recherche en Informatique et Automatique, IMT Lille Douai, Lille, France
2
Automatic Control Department, Universitat Polit
`
ecnica de Catalunya, Terrassa, Spain
3
Department of Mechanical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands
Keywords:
Large-scale Systems, Water Systems, Saint-Venant Equations, Modeling, IDZ Models.
Abstract:
Inland navigation networks are large-scale systems that can be described by using the nonlinear Saint-Venant
partial differential equations. However, as there is no analytical solution for them, simplified models are used
instead for modeling purposes. This work addresses the modeling of two sub-reach systems by means of the
well-known Integrator Delay Zero model. Two main scenarios are considered: in the first one, the two partial
models are independently computed one from each other; the second one uses previous knowledge of the
whole two sub-reach system in order to ensure the flow consistency along the system. The application of these
two methodologies to a part of the navigation network in the north of France serves as the case study for this
work.
1 INTRODUCTION
Inland navigation networks cover more than 38000
km in Europe and are used principally for trans-
port. The navigation transport takes part in the
Trans-European network program (TEN-T
1
), which
promotes the development of transport infrastructure
policies to close the gaps between Member States’
transport networks and to guarantee seamless trans-
port chains for passengers and freight. In France, an
intensification in the use of inland waterways is ex-
pected in the near future. The gauge of the allowed
boats and the navigation schedule will be risen up.
Hence, constraints on the inland waterway manage-
ment will be more severe.
The accommodation of navigation requires the
control of the water levels in each part of the navi-
gation network, which is composed of several inter-
connected reaches that represent portions of a water
stream between at least two hydraulic structures such
as locks. These reaches are large-scale, free-surface
systems that exhibit large delays between the genera-
tion of an upstream input and its measurement along
the water course and at the downstream end of the
reach. Some perturbations can travel back and forth,
1
http://ec.europa.eu/transport/themes/infrastructure/ten-t-
guidelines/index en.htm
resulting in resonance phenomena. The dynamics of
the reach can be accurately described by the Saint-
Venant’s partial differential equations (Chow, 1959).
However, as there is no known analytical solution for
these equations, simplified models such as transfer
functions (Litrico and Georges, 1999) or the Integra-
tor Delay (ID) model (Schuurmans et al., 1999) are
used instead. These models are designed by consider-
ing some assumptions on the linearity of the reach dy-
namics. The ID model was improved by considering
an additional zero that allows taking into account high
frequency phenomena. The obtained Integrator De-
lay Zero model (IDZ) was tested and compared with
the ID model on several canals (Litrico and Fromion,
2004). More recently, an Integrator Resonance model
(IR) has been proposed (van Overloop et al., 2010),
(Horv
´
ath et al., 2014b) and (van Overloop et al.,
2014) to reproduce the resonance phenomena. Gray-
box models can be used when lacking prior knowl-
edge of the physical characteristics of canals, such as
dimensions or the Manning-Strickler coefficient (Du-
viella et al., 2013) and (Horv
´
ath et al., 2014a). Fi-
nally, approaches based on linear parameter-varying
models or multi-models that enable to take into ac-
count the nonlinearities due to the consideration of
large operating ranges were proposed (Duviella et al.,
2007), (Duviella et al., 2010), (Bolea et al., 2014) and
(Bolea and Puig, 2016).
Segovia, P., Horváth, K., Rajaoarisoa, L., Nejjari, F., Puig, V. and Duviella, E.
Modeling of Two Sub-reach Water Systems: Application to Navigation Canals in the North of France.
DOI: 10.5220/0006418604590467
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 459-467
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
459

Many man-made, hydraulic structures such as
gates can be located along the navigation reaches,
as well as secondary inputs. Therefore, they can-
not be considered as a single reach with only two
controlled points, the upstream and the downstream
ends. This particularity demands a decomposition of
the reaches in several sub-reaches according to the
hydraulic structures and secondary inputs that affect
the water stream. The models that represent the in-
fluence of the discharges on the water levels for each
sub-reach have to be computed. The next step is to
interconnect these partial models to reproduce the be-
havior of the whole canal. In this work, this modeling
step is based on IDZ models. However, this model-
ing procedure might cause the flow profiles for each
of these partial models to be not consistent with the
flow profiles of the adjacent sub-reaches. This means
that the interconnected model will most probably not
reproduce adequately the real dynamics of the whole
reach. This work aims to develop a modeling ap-
proach in which the prior knowledge of the whole
system dynamics are taken into account when each
of these sub-reaches is modeled.
The content of this paper is structured as follows:
Section 2 is dedicated to the description of the IDZ
model. Section 3 addresses the modeling step of two
sub-reach systems introducing some considerations
as well as the interconnection method. In Section
4, the proposed approach is used by considering a
real navigation reach located in the north of France,
the Cuinchy-Fontinettes reach. The comparison of
the interconnection approaches with and without prior
knowledge of the whole system with a reference
model is performed. This reference model is provided
by an hydraulic simulation software that solves nu-
merically the Saint-Venant equations. Finally, conclu-
sions about the performed work are drawn in Section
5.
2 SELECTING A MODEL TO
DESCRIBE A REACH
As already mentioned, the Saint-Venant differential
equations accurately describe the real dynamics of
the system. However, since no analytical solution is
known for these equations, as well as being extremely
sensitive to errors in the geometry and other unmod-
eled dynamics, simplified models are needed. Among
all the existing possibilities, the IDZ model (Litrico
and Fromion, 2004) is used in this paper. It results
from the linearization of the Saint-Venant’s differen-
tial equations around an operating point q
op
, and con-
stitutes a simple yet efficient option to accurately de-
scribe a canal in high and low regimes.
The IDZ model, as its name implies, consists of an
integrator, a delay and a zero: the two first terms cap-
ture the low frequencies tank-like behavior, whereas
the zero accounts for the high frequencies. In Laplace
form, its structure is as follows:
p
i j
(s) =
α
i j
s + 1
A
i j
s
e
−τ
i j
s
, (1)
where α
i j
represents the inverse of the zero, A
i j
the in-
tegrator gain and τ
i j
the propagation time delay. The
exact values of these parameters cannot be computed,
but an accurate approximation can be used instead
(Litrico and Fromion, 2004). Since the used parame-
ters are an approximation of the theoretical ones, the
notation ˆp
i j
(s) replaces p
i j
(s) hereinafter.
The integrator gain illustrates how the volume
changes according to the variation of the water level.
This parameter is also known as the equivalent back-
water area due to its dimensions. The time delay rep-
resents the minimum required time for a perturbation
to travel from its origin to the measurement points.
The zero approximates through a constant gain the os-
cillatory phenomena that occurs in high frequencies.
The model representing the influence of the dis-
charges on the water levels at the boundaries is given
by:
y(0,s)
y(L,s)
=
ˆp
11
(s) ˆp
12
(s)
ˆp
21
(s) ˆp
22
(s)
| {z }
P(s)
q(0,s)
q(L,s)
, (2)
where 0 and L are the abscissas for the initial and final
ends of the reach; ˆp
i j
(s), the IDZ model that links the
i
th
water level and the j
th
discharge and follows the
structure given in (1); y(0,s) and y(L,s), the upstream
and downstream water levels, respectively; q(0,s) and
q(L,s), the upstream and downstream discharges, re-
spectively.
In order to compute α
i j
, A
i j
and τ
i j
(with i, j =
1,2), it is necessary to know where the transition be-
tween the upstream uniform and downstream backwa-
ter flows occurs. The value of this abscissa is named
x
1
and can be obtained as follows:
x
1
=
(
max
n
L −
y
L
−y
n
s
L
,0
o
i f s
L
6= 0
L i f s
L
= 0
, (3)
with y
L
[m] the downstream boundary condition, y
n
[m] the normal depth and s
L
(dimensionless) the de-
viation from bed slope of the line tangent to the water
curve at the downstream end of the pool. The reader
is referred to (Litrico and Fromion, 2004) for further
details about the computation of these magnitudes.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
460
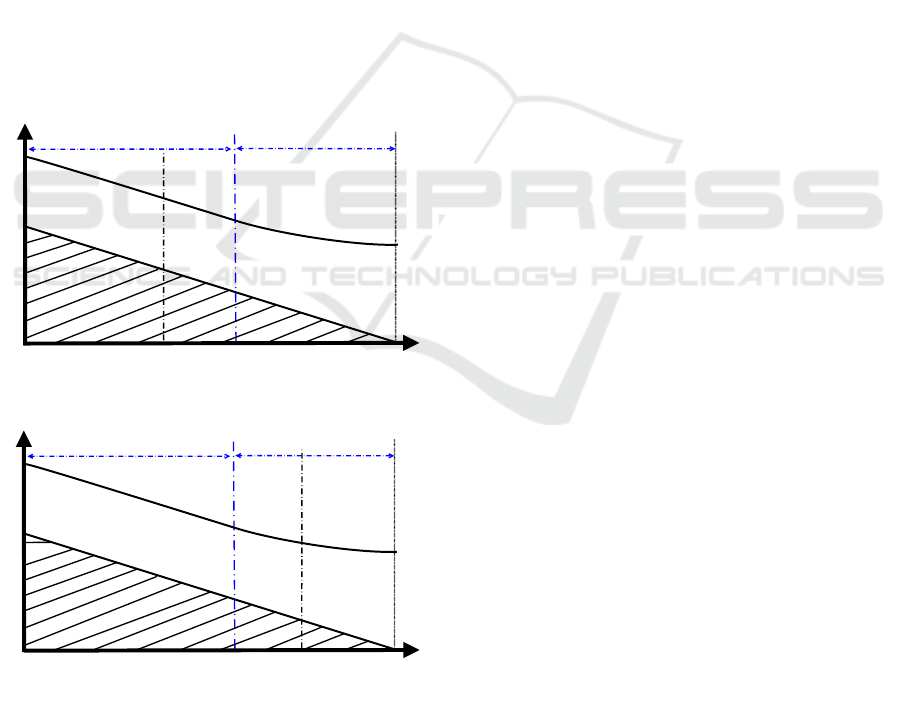
According to (3), x
1
can either be 0, L or take
an intermediate value between 0 and L. The reach
is completely under backwater flow if x
1
= 0, com-
pletely under uniform flow if x
1
= L or present both
kinds of flow if 0 < x
1
< L. In particular, the interval
(0,x
1
) is under uniform flow whereas the interval (x
1
,
L) is under backwater flow. This is an important fact
for the computation of the parameters α
i j
, A
i j
and τ
i j
,
as they have to be computed for each kind of flow that
is present in the reach. The same formulas are applied
for the uniform and backwater parts but are evaluated
according to the length of each of these parts. The
partial uniform and backwater parameters are merged
into the so-called equivalent parameters, which rep-
resent the whole pool. In the event that x
1
= 0 or
x
1
= L, they will only have to be computed once, for
the whole length of the reach.
Finally, the following consideration serves to in-
troduce the problem that is studied in this work, which
is no other than the presence of secondary inputs in a
canal; in particular, the relative position of x
1
and the
abscissa in which the inflow takes place (x
in f low
here-
inafter). The two possibilities are depicted in Fig. 1.
(a)
0
B
x
1
U
x
inflow
L
(b)
0
B
x
1
U
x
inflow
L
Figure 1: (a) Water profile for x
1
> x
in f low
. (b) Water profile
for x
1
< x
in f low
.
The same water profile is obtained for both cases
as the upstream and downstream boundary conditions
are the same. The difference, however, appears when
the whole reach is regarded as the interconnection of
two sub-reaches due to the presence of the inflow. Fig.
1(a) is composed of a first sub-reach which is only un-
der uniform flow and a second sub-reach under uni-
form flow in the interval (x
in f low
, x
1
) and backwater
flow in the interval (x
1
, L). On the other hand, Fig.
1(b) shows that the first sub-reach is under uniform
flow in the interval (0, x
1
) and under backwater flow
in the interval (x
1
, x
in f low
) whereas the second sub-
reach is only under backwater flow.
The objective, therefore, is to compute the IDZ
model as an interconnection of two sub-reaches di-
vided by a secondary inflow within the ends of the
reach.
3 MODELING A TWO
SUB-REACH SYSTEM
In this section, the general formulation of intercon-
nected sub-reaches (Litrico and Fromion, 2004) is
given. It is then extended by considering different
criteria regarding the use of the previous knowledge
of the global dynamics. Two different interconnected
models are proposed and discussed.
3.1 Formulation of the Interconnected
IDZ Model
One possible approach to model the systems that were
presented in Fig. 1 is to consider two different sub-
reaches. This division of a reach into sub-reaches is
always done when there is an hydraulic structure that
physically divides the reach, but also under other cir-
cumstances, i.e. the presence of a secondary input or
a change in the cross section of the the water stream.
Moreover, since there is no such hydraulic structure,
this situation is hereinafter referred to as simple in-
terconnection. Fig. 2 (where big-sized markers at
sections 0 and L denote the presence of an hydraulic
structure) illustrates this situation. For the sake of
convenience, 0, x
in f low
and L denote the initial, inter-
mediate (where the inflow takes place) and final ab-
scissas of the reach, respectively.
From relation (2), and according to Fig. 2, the
following set of equations can be considered. SR
1
and
SR
2
denote sub-reaches 1 and 2, respectively.
SR
1
:
y(0,s)
y(x
in f low
,s)
=
"
ˆp
(1)
11
(s) ˆp
(1)
12
(s)
ˆp
(1)
21
(s) ˆp
(1)
22
(s)
#
q(0,s)
q(x
in f low
,s)
(4)
Modeling of Two Sub-reach Water Systems: Application to Navigation Canals in the North of France
461

Figure 2: Water inflow flowing into a canal, leading to a
simple interconnection structure.
SR
2
:
y(x
in f low
,s)
y(L,s)
=
"
ˆp
(2)
11
(s) ˆp
(2)
12
(s)
ˆp
(2)
21
(s) ˆp
(2)
22
(s)
#
q(x
in f low
,s)
q(L,s)
(5)
This paper studies the particular case in which
q(x
in f low
) = 0, which can occur, for instance, when
a lateral hydraulic device such as a controlled valve is
closed and does not let the water flow into the main
stream. The more general case q(x
in f low
) 6= 0, i.e.
when the controlled valve is open, will be addressed
in the future.
For the case q(x
in f low
) = 0, the final model that
represents the interconnection is obtained by impos-
ing the following conditions at the interconnection
node (Litrico and Fromion, 2004):
y
(1)
(x
in f low
,s) = y
(2)
(x
in f low
,s) (6a)
q
(1)
(x
in f low
,s) = q
(2)
(x
in f low
,s) (6b)
These two equations express the continuity con-
ditions that hold true at the interconnection abscissa
x
in f low
. In particular, Eq. (6a) ensures that no sudden
change in the water depth occurs, whereas Eq. (6b)
guarantees the flow consistency in the abscissa x
in f low
and is a direct consequence of q(x
in f low
) = 0.
Therefore, the final model (2) that represents the
two interconnected sub-reaches is given by:
y(0,s)
y(L,s)
=
"
ˆp
(G)
11
(s) ˆp
(G)
12
(s)
ˆp
(G)
21
(s) ˆp
(G)
22
(s)
#
q(0,s)
q(L,s)
(7)
where ˆp
(G)
i j
represent the interconnecting transfer
functions. Their expressions are:
ˆp
(G)
11
= ˆp
(1)
11
+
ˆp
(1)
12
ˆp
(1)
21
ˆp
(2)
11
− ˆp
(1)
22
(8a)
ˆp
(G)
12
= −
ˆp
(1)
12
ˆp
(2)
12
ˆp
(2)
11
− ˆp
(1)
22
(8b)
ˆp
(G)
21
=
ˆp
(1)
21
ˆp
(2)
21
ˆp
(2)
11
− ˆp
(1)
22
(8c)
ˆp
(G)
22
= ˆp
(2)
22
−
ˆp
(2)
12
ˆp
(2)
21
ˆp
(2)
11
− ˆp
(1)
22
(8d)
Note: the Laplace variable s has been omitted for
readability in all ˆp
(k)
i j
terms.
In order to obtain the global model for the two
sub-reach system, it seems it might be enough to com-
pute a separate model for each sub-reach and then use
(8a)–(8d) to obtain the interconnected model. The
model obtained by means of this procedure is here-
inafter referred to as a two sub-reach system with in-
dependent flow profiles.
However, as the two sub-reaches are not divided
by any hydraulic structure, it does not seem correct to
treat them independently. Instead, since q(x
in f low
) =
0 in this paper, it is possible to obtain the value of
x
1
for the whole canal and use this information when
modeling each of the two sub-reaches. The model that
is obtained by using this information about the global
dynamics is hereinafter referred to as a two sub-reach
system with consistent flow profile.
3.2 Two Sub-reach Systems with
Independent Flow Profiles
The first and simplest option is to compute the model
for each sub-reach separately according to the pro-
cedure described in Section 2 and then interconnect
them. However, since there is no hydraulic struc-
ture dividing the two sub-reaches, a consistent flow
profile is not obtained, which does not seem logical.
This is caused by the need to compute x
1
for each
sub-reach, which will probably result in obtaining a
different flow profile with a completely different dy-
namic response. This idea is depicted in Fig. 3(a) and
4(a): a value of x
1
is computed for each sub-reach
(blue dash-dot lines), which results in a completely
different profile than the real one, shown in Fig. 1.
3.3 Two Sub-reach Systems with
Consistent Flow Profiles
In this approach, the value of x
1
computed for the
reach is used to build the interconnected two sub-
reach system model afterward. The first sub-reach is
forced to change from uniform to backwater flow in
x
1
when x
1
< x
in f low
, whereas in the situation x
1
>
x
in f low
the second sub-reach is forced from uniform
to backwater flow in x
1
. This behavior is shown in
Fig. 3(b) and 4(b), which results in the same curves
as those depicted in Fig. 1.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
462

(a)
0
B
x
1
U
B
U
x
inflow
x
L
inflow
(b)
0
B
x
1
U
B
x x
L
inflow inflow
Figure 3: Flow profiles for a two-reach system when x
1
<
x
in f low
. (a) Independent flow profile. (b) Consistent flow
profile.
4 APPLICATION
The aim is to verify which of the two approaches pre-
sented in Section 3 leads to a better model, even if one
has the intuition that taking into account the previous
knowledge of the system to ensure the flow continu-
ity should yield better results than treating them as
two sub-reaches with independent flow profiles. In
order to compare them, both models are computed
for a real system and then compared with the results
provided by SICˆ2
2
(Malaterre et al., 2014), an hy-
draulic simulation software. Since it solves numer-
ically the Saint-Venant equations without simplifica-
tions, the obtained results with this software will be
used as the basis to compare the accuracy of both ap-
proaches.
The chosen two sub-reach system is the Cuinchy-
Fontinettes reach (CFr), which belongs to the inland
navigation network in the north of France and is il-
lustrated in Fig. 5. This reach is bounded both up-
stream and downstream by the locks of Cuinchy and
Fontinettes, respectively. The gate Port de Garde,
which is located within both ends and placed outside
of the CFr, can be used to regulate the amount of water
that is sent to Aire. According to the current manage-
2
http://sic.g-eau.net/
(a)
0
x
U
B
x
UB
1
inflow
x
L
inflow
(b)
0
x
U
B
x
1
U
x
L
inflow
inflow
Figure 4: Flow profiles for a two-reach system when x
1
>
x
in f low
. (a) Independent flow profile. (b) Consistent flow
profile.
ment strategy, this gate is generally closed, which is
the reason why this value is considered to be equal to
0 in this work. The discharges in the locks of Cuinchy
and Fontinettes are considered as the inputs of the
IDZ model given by (2). On the other hand, they are
modeled as discharge boundary conditions in SICˆ2.
Figure 5: Schematic view of the CFr.
Table 1 sums up the physical and geometrical
data used to model the CFr: n
r
[s/m
1/3
] is the Man-
ning’s roughness coefficient, m (dimensionless) is the
side slope of the cross section (m = 0 for rectangular
shape), B
w
[m] is the bottom width of the reach, q
op
Modeling of Two Sub-reach Water Systems: Application to Navigation Canals in the North of France
463

[m
3
/s] is the considered flow for the linearization of
the Saint-Venant equations, L [m] is the length and y
x
[m] is the downstream water depth. Besides, the bot-
tom slope s
b
is equal to 10
−4
for both reaches. On
the other side, C, A and F stand for Cuinchy, Aire and
Fontinettes, respectively.
Table 1: Physical data for CFr.
n
r
m B
w
q
op
L y
x
C-A 0.035 0 52 0.6 28700 2.44
A-F 0.035 0 52 0.6 13600 3.8
C-F 0.035 0 52 0.6 42300 3.8
Two real scenarios are considered: the first one
presents the operation of the Cuinchy lock; the sec-
ond one, the operation of the Fontinettes lock. Table
2 contains the details of these lock operations. A pos-
itive sign for the dispatched water volume means that
the water volume is flowing into the system, whereas
a negative sign means that it is leaving the system.
Table 2: Considered scenarios.
Scenario Volume [m
3
] Duration [min]
1 3000 15
2 -23000 20
The following fit coefficients are computed (be-
tween the reference and each of the proposed models)
for a quantitative comparison of the accuracy of the
results:
• Pearson product-moment correlation coefficient,
which measures the linear dependance between
two variables. It is defined in the following way:
r =
T
∑
t=1
Y
o
(t) −Y
o
Y
m
(t) −Y
m
s
T
∑
t=1
Y
o
(t) −Y
o
2
s
T
∑
t=1
Y
m
(t) −Y
m
2
(9)
with T the horizon for which the data have been
acquired, Y
o
(t) the observed water depth at time
t, Y
m
(t) the predicted water depth at time t and Y
o
and Y
m
the mean value of observed and modeled
water depths, respectively.
This coefficient is bounded between +1 (total pos-
itive linear correlation) and -1 (total negative lin-
ear correlation), and 0 means that there is no linear
correlation.
• Nash-Sutcliffe model efficiency coefficient, which
is used to assess the predictive power of hydrolog-
ical models as follows (Nash and Sutcliffe, 1970):
E = 1 −
T
∑
t=1
(Y
o
(t) −Y
m
(t))
2
T
∑
t=1
Y
o
(t) −Y
o
2
(10)
E can range from 1 to −∞, where 1 indicates a
perfect match of modeled and observed values, 0
corresponds to the case in which the model pre-
dictions are as accurate as the mean of observed
data and E < 0 means that the model predictions
are less accurate than the mean of observed data.
• Maximum difference between the modeled and ob-
served data as a measure of the magnitude of the
maximum error. It is computed as:
∆ = max
1≤t≤T
|Y
o
(t) −Y
m
(t)| (11)
The results for both scenarios are presented below.
For each of them, the previous fit coefficients between
the reference (SICˆ2) and the three different modeling
approaches (model of the reach, two sub-reaches with
independent and consistent flow profiles) are summa-
rized in Tables 3 and 4. In addition, the simulation re-
sults for Y
C
and Y
F
are presented for the four models.
Each figure is zoomed in the area of interest; how-
ever, the same simulation time has been used for both
scenarios.
Remark: the computation of the IDZ model for the
reach results in x
1
= 5760 m, which indicates that the
present case study falls under the situation described
by Fig. 3 as x
in f low
= 28700 m. This means that the
C-A reach is under both uniform and backwater flow
(with flow transition at x = x
1
) and that A-F is under
backwater flow only. On the other hand, the obtained
profile for the two-reach model with independent flow
profile is only backwater for both of them: when the
IDZ model is computed for each sub-reach, a value of
x
1
= 0 is obtained for both sub-reaches, which means
that they are both under backwater.
4.1 Scenario 1
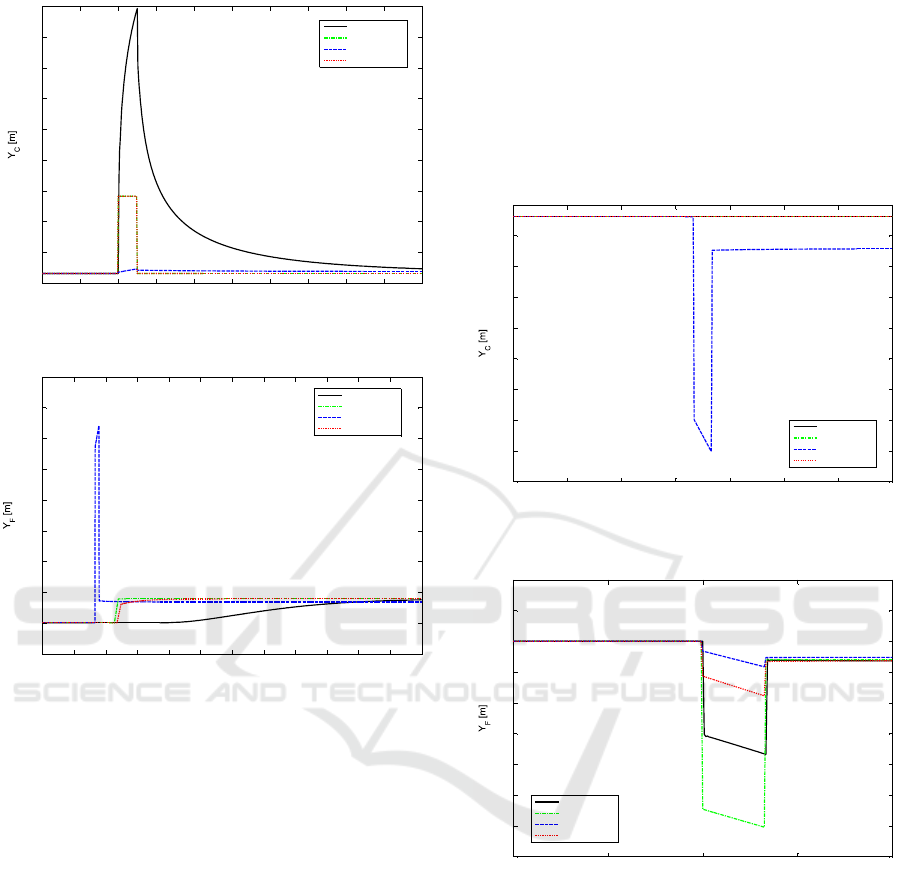
Figures 6 and 7 and Table 3 summarize the results
obtained for the Cuinchy lock operation.
Table 3: Fit coefficients for an upstream lock operation.
Reach Indep. flow Cont. flow
C
E
C
0.2831 -0.0193 0.2831
r
C
0.7311 0.4328 0.7312
∆
C
[m] 0.1225 0.1703 0.1272
F
E
F
-1.2637 -5.3193 -1.0506
r
F
0.5110 0.0641 0.5613
∆
F
[m] 0.0016 0.0128 0.0015
None of the three models is capable of represent-
ing the observed peak in Y
C
with satisfying accuracy,
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
464
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0.16
0.18
0.2
0.22
0.24
0.26
0.28
0.3
0.32
Time [h]
SIC
Reach
Indep. flow
Cont. flow
Figure 6: Upstream water levels for an upstream lock oper-
ation.
0 2 4 6 8 10 12 14 16 18 20 22 24
3.798
3.8
3.802
3.804
3.806
3.808
3.81
3.812
3.814
3.816
Time [h]
SIC
Reach
Indep. flow
Cont. flow
Figure 7: Downstream water levels for an upstream lock
operation.
even if the equilibrium value is well fitted. Never-
theless, the consistent flow profile model, which is
overlapped with the reach model, offers a better peak
response than the two sub-reach model with indepen-
dent flow profile.
Moreover, the two sub-reach model with indepen-
dent flow profile clearly predicts a much worse re-
sponse for Y
F
than the other two models, represented
by the nonexistent predicted peak according to the
reference. The appearance of this peak is physically
justified by the fact that the computation of the flow
profile for the two sub-reach system with independent
flow yields backwater flow only. The systems that ex-
hibit this kind of flow profile are more sensitive to res-
onance phenomena. An example of this behavior was
obtained in a work with flat systems (Segovia et al.,
2017).
It is also worth noting that both the reach model
and the consistent flow profile model predict a much
faster response than it is actually observed, which
causes the Nash-Sutcliffe indicators to be negative for
Y
F
. Nevertheless, when the consistent flow model is
considered, the maximum difference is lower and the
dynamics are better reproduced, as shown by the com-
puted correlation coefficients.
4.2 Scenario 2
In this case, Figures 8 and 9 and Table 4 summarize
the results for the Fontinettes lock operation.
0 1 2 3 4 5 6 7
0.06
0.07
0.08
0.09
0.1
0.11
0.12
0.13
0.14
0.15
Time [h]
SIC
Reach
Indep. flow
Cont. flow
Figure 8: Upstream water levels for a downstream lock op-
eration.
0 0.5 1 1.5 2
3.66
3.68
3.7
3.72
3.74
3.76
3.78
3.8
3.82
3.84
Time [h]
SIC
Reach
Indep. flow
Cont. flow
Figure 9: Downstream water levels for a downstream lock
operation.
For the upstream level Y
C
, the flat signal cor-
responds to the overlapping of the observed water
depths and the predicted responses with the reach
model and the consistent flow model. This fact is
shown by the maximum difference indicator in Ta-
ble 4, which prevents the computation of the Nash-
Sutcliffe indicators for these two models. The two
sub-reach model with independent flow profile pre-
dicts a very different response from the observed data.
Indeed, a peak is predicted in the response of the
two sub-reach system with independent flow profile,
whose justification is the same as given for Y
F
in Sec-
tion 4.1. The Nash-Sutcliffe indicator takes an ex-
Modeling of Two Sub-reach Water Systems: Application to Navigation Canals in the North of France
465

Table 4: Fit coefficients for a downstream lock operation.
Reach Indep. flow Cont. flow
C
E
C
— -3.38 ·10
9
—
r
C
0.3894 0.2388 0.3785
∆
C
[m] 0 0.0764 0
F
E
F
0.2394 0.0444 0.5671
r
F
0.9549 0.4370 0.8607
∆
F
[m] 0.0471 0.0630 0.0383
tremely large, negative value, showing the deviation
between this model and the observed values.
With regard to Y
F
, the predicted dynamics for the
three models are similar, albeit the reach model and
the consistent flow profile models offer a better pre-
diction than the other model.
A conclusion for both scenarios is that an oper-
ation performed at one end of the system does not
have a major impact at the other end, which is due
to the large dimension of the system. Another fac-
tor that might play a role in this behavior is the fact
that a bed slope equal to 10
−4
is considered, which
results in different values for the upstream and down-
stream bottom elevation. For the second scenario, a
large volume of water is dispatched outside the sys-
tem, and the observed data show that the water level
remains (almost) constant upstream. The final water
level variation is due to the mass balance along the
system.
Another conclusion that can be drawn for both
scenarios is that the two sub-reach model with inde-
pendent flow profile predicts significant peaks in Y
F
for the upstream action and in Y
C
for the downstream
action results from considering two backwater flow
dynamics. If a system has to be modeled as the inter-
connection of two sub-reaches, the best choice seems
to consider the consistent flow profile model.
5 CONCLUSIONS AND FUTURE
WORK
This work presented the study of a two sub-reach sys-
tem based on IDZ models. Some considerations that
need to be taken into account in order to ensure the
flow consistency of the system were addressed, and
those steps were illustrated by means of a case study
based on a real system in the north of France. Ac-
cording to the obtained results, it is possible to state,
as one could previously anticipate, that the accuracy
with respect to the reference is greater if the previous
knowledge of the system (namely x
1
) is considered to
ensure the continuity of the flow.
In the light of the outcome, although the IDZ
model yields acceptable results, other aspects may
need to be considered to possibly come up with some
rules about its applicability. Further work includes ad-
dressing the general case q(x
in f low
) 6= 0. In this case,
the structure of the global model (2) will be different,
but the modeling approach will be similar. In addi-
tion, canals characterized by a different topography
such as tributaries and distributaries will be consid-
ered. The obtained models are expected to be used in
fault detection and isolation (FDI) and fault-tolerant
control (FTC).
REFERENCES
Bolea, Y. and Puig, V. (2016). Gain-scheduling multivari-
able LPV control of an irrigation canal system. ISA
Transactions, 63:274–280.
Bolea, Y., Puig, V., and Blesa, J. (2014). Linear parame-
ter varying modeling and identification for real-time
control of open-flow irrigation canals. Environmental
modelling & software, 53:87–97.
Chow, V. T. (1959). Open-channel hydraulics. McGraw-
Hill. New York.
Duviella, E., Bako, L., and Charbonnaud, P. (2007). Gaus-
sian and boolean weighted models to represent vari-
able dynamics of open channel systems. Conference
on Decision and Control, New Orleans, USA, Decem-
ber 12-14.
Duviella, E., Bako, L., Sayed-Mouchaweh, M., Blesa, J.,
Bolea, Y., Puig, V., and Chuquet, K. (2013). In-
land navigation channel model: Application to the
Cuinchy-Fontinettes reach. In Networking, Sensing
and Control (ICNSC), 2013 10th IEEE International
Conference on, pages 164–169. IEEE.
Duviella, E., Puig, V., Charbonnaud, P., Escobet, T., Car-
rillo, F., and Quevedo, J. (2010). Supervised gain-
scheduling multimodel versus linear parameter vary-
ing internal model control of open-channel systems
for large operating conditions. Journal of Irrigation
and Drainage Engineering, 136(8):543–552.
Horv
´
ath, K., Duviella, E., Blesa, J., Rajaoarisoa, L., Bolea,
Y., Puig, V., and Chuquet, K. (2014a). Gray-box
model of inland navigation channel: application to the
Cuinchy-Fontinettes reach. Journal of Intelligent Sys-
tems, 23(2):183–199.
Horv
´
ath, K., Duviella, E., Petreczky, M., Rajaoarisoa, L.,
and Chuquet, K. (2014b). Model predictive control
of water levels in a navigation canal affected by reso-
nance waves. HIC 2014, New York, USA, 17-21 Au-
gust.
Litrico, X. and Fromion, V. (2004). Simplified modeling
of irrigation canals for controller design. Journal of
Irrigation and Drainage Engineering, pages 373–383.
Litrico, X. and Georges, D. (1999). Robust continuous-
time and discrete-time flow control of a dam–river
system. (I) Modelling. Applied mathematical mod-
elling, 23(11):809–827.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
466

Malaterre, P.-O., Baume, J.-P., and Dorchies, D. (2014).
Simulation and integration of control for canals soft-
ware (sic 2), for the design and verification of manual
or automatic controllers for irrigation canals. In US-
CID Conference on Planning, Operation and Automa-
tion of Irrigation Delivery Systems, pages 377–382.
Nash, J. E. and Sutcliffe, J. V. (1970). River flow forecast-
ing through conceptual models part I: a discussion of
principles. Journal of hydrology, 10(3):282–290.
Schuurmans, J., Clemmens, A., Dijkstra, S., Hof, A., and
Brouwer, R. (1999). Modeling of irrigation and
drainage canals for controller design. Journal of Irri-
gation and Drainage Engineering, December, 125(6).
Segovia, P., Blesa, J., Horv
´
ath, K., Rajaoarisoa, L., Nejjari,
F., Puig, V., and Duviella, E. (2017). Fault detection
and isolation in flat navigation canals. 4
th
Interna-
tional Conference on Control, Decision and Informa-
tion Technologies, April 5–7, Barcelona, Spain.
van Overloop, P., Horv
´
ath, K., and Aydin, B. E. (2014).
Model predictive control based on an integrator res-
onance model applied to an open water channel. Con-
trol Engineering Practice, 27:54–60.
van Overloop, P., Miltenburg, I., Bombois, X., Clemmens,
A., Strand, R., van de Giesen, N., and Hut, R. (2010).
Identification of resonance waves in open water chan-
nels. Control Engineering Practice, Volume 18, Issue
8, August, pages 863–872.
Modeling of Two Sub-reach Water Systems: Application to Navigation Canals in the North of France
467
