A Fuzzy Logic-based Approach for Assessing the Quality of Business

Process Models

Fadwa Yahya

, Khouloud Boukadi

, Han

ene Ben Abdallah

1,2

and Zakaria Maamar

University of Sfax, Mir@cl Laboratory, Sfax, Tunisia

King Abdulaziz University, Jeddah, K.S.A.

Zayed University, Dubai, U.A.E.

Keywords:

Business Process, BPMN, Model Quality, Quality Metrics and Fuzzy Logic.

Abstract:

Similar to software products, the quality of a Business Process model is vital to the success of all the phases of

its lifecycle. Indeed, a high quality BP model paves the way to the successful implementation, execution and

performance of the business process. In the literature, the quality of a BP model has been assessed through

either the application of formal veriﬁcation, or most often the evaluation of quality metrics calculated in the

static and/or simulated model. Each of these assessment means addresses different quality characteristics and

meets particular analysis needs. In this paper, we adopt metrics-based assessment to evaluate the quality of

business process models, modeled with Business Process Modeling and Notation (BPMN), in terms of their

comprehensibility and modiﬁability. We propose a fuzzy logic-based approach that uses existing quality met-

rics for assessing the attainment level of these two quality characteristics. By analyzing the static model, the

proposed approach is easy and fast to apply. In addition, it overcomes the threshold determination problem

by mining a repository of BPMN models. Furthermore, by relying on fuzzy logic, it resembles human rea-

soning during the evaluation of the quality of business process models. We illustrate the approach through a

case study and its tool support system developed under the eclipse framework. The preliminary experimental

evaluation of the proposed system shows encouraging results.

1 INTRODUCTION

A Business Process (BP) model covers different di-

mensions of an enterprise, mainly functional, organi-

zational, behavioral, and informational (Curtis et al.,

1992). Integrating all these dimensions into one high-

quality model is vital to the persistence of the enter-

prise (S

anchez-Gonz

alez et al., 2010) and (de Oca

et al., 2015). Indeed, such a model will surely fa-

cilitate various tasks related to its implementation,

deployment, execution, and continuous improvement

in short, the BP lifecycle (Weske, 2010). A high-

quality BP model will also guarantee its acceptance

by end users and thus prevent common BP problems

like model reality divide where the modeled and exe-

cuted processes are not aligned (Schmidt and Nurcan,

2009).

In the literature, BP model quality assessment has

been dealt with two main approaches: the application

of formal veriﬁcation methods (Watahiki et al., 2011)

and (Morimoto, 2008), or the evaluation of a set of

quality metrics calculated on the BP model (S

anchez-

Gonz

alez et al., 2010), (Mendling et al., 2012), and

(de Oca et al., 2015). Formal methods (e.g., model

checking and theorem proving) provide for the veriﬁ-

cation of behavioral quality properties like progress

and deadlock freedom. While they offer objective

analysis results that inspire high conﬁdence, their ap-

plication remains hindered by their complexity. In

addition, they do not provide for a qualitative analy-

sis of the model like its complexity, comprehensibility

and modiﬁability; these quality characteristics impact

both various tasks of the BP lifecycle and the perfor-

mance of the enacted BP.

Adopting a qualitative assessment of BP models,

researchers proposed to calculate a set of metrics ei-

ther on the static BP model (e.g. (S

anchez-Gonz

alez

et al., 2010), (Mendling et al., 2012), and (de Oca

et al., 2015)), or the simulated BP model (e.g. (Hein-

rich, 2013)). In these works, several quality metrics

were used either to assess certain quality character-

istics of the BP model itself (case of static model

assessment of, for instance, the model complexity,

maintainability, Integrity, etc. (Mendling et al., 2012),

Yahya, F., Boukadi, K., Ben-Abdallah, H. and Maamar, Z.

A Fuzzy Logic-based Approach for Assessing the Quality of Business Process Models.

DOI: 10.5220/0006419500610072

In Proceedings of the 12th International Conference on Software Technologies (ICSOFT 2017), pages 61-72

ISBN: 978-989-758-262-2

(Makni et al., 2010), and (Sadowska, 2015)) or to pre-

dict the BP performance (case of simulated model as-

sessment of, for instance, the mutual impact between

the BP and its underlying information system (Hein-

rich, 2013)). The main challenges in metric-based as-

sessment are: what are the quality characteristics of a

BP model, how to relate the metrics to quality char-

acteristics, and how to interpret the values of the met-

rics.

There is no consensus on the quality character-

istics of BP models. Several researchers explored

the similarities between processes and software prod-

ucts to adopt the quality characteristics of the latter

for business processes. In particular, they adopted

the eight model quality characteristics deﬁned in the

ISO/IEC 25010 (ISO, 2011) standard quality model,

e.g. (S

anchez-Gonz

aLez et al., 2013) and (Sadowska,

2015). Because the ISO/IEC 25010 quality model

does not deﬁne any technique for the evaluation of the

characteristics, different studies recommended vari-

ous metrics for assessing the quality of BP models

in terms of the proposed characteristics, e.g. (Van-

derfeesten et al., 2007a), (Vanderfeesten et al., 2008),

(Cardoso et al., 2010), (S

anchez-Gonz

aLez et al.,

2013), and (Sadowska, 2015). In addition, based

on the recommended metrics, some researchers pro-

posed the development of an automated framework to

evaluate BP model quality, e.g. (S

anchez-Gonz

alez

et al., 2010), (S

anchez-Gonz

alez et al., 2011) and

(Mendling et al., 2012). The common barrier hinder-

ing the development of such a framework is the lack

of a consensus about threshold values of the quality

metrics, which are required to interpret/evaluate a BP

model’s quality (S

anchez-Gonz

alez et al., 2010) and

(de Oca et al., 2015). This paper addresses this prob-

lem through a fuzzy logic-based approach for evalu-

ating the quality of BP models with an emphasis on

the comprehensibility and modiﬁability characteris-

tics. The choice of these two quality characteristics

is justiﬁed by their importance to guarantee that a BP

model can be easily implemented, deployed, and exe-

cuted. These characteristics are also important when

dealing with the continuous improvement of a BP.

The herein proposed approach consists of two es-

sential phases: threshold determination and fuzzy

logic application. The ﬁrst phase applies data min-

ing, speciﬁcally decision trees, to determine approxi-

mate thresholds for each quality metric. These thresh-

olds will be used for interpreting the comprehen-

sibility or modiﬁability levels of BP models, mod-

eled in BPMN (ISO, 2013). To this end, we used a

BP repository, called “SOA-based Business Process

Database”

, built within our laboratory. This repos-

https://sites.google.com/site/bposcteam2015/ressources

itory contains 1000 business processes of organiza-

tions operating in different sectors. The second phase

uses the approximate thresholds identiﬁed in the ﬁrst

phase along with fuzzy logic (Zadeh, 1965) to assess

the quality of a BPMN model. The use of fuzzy logic

aims at dealing with the approximate and imprecise

nature of the obtained thresholds. Indeed, according

to Zadeh, fuzzy logic operates perfectly in an environ-

ment of “imperfect information” (Zadeh, 2008).

The proposed approach is implemented in a sys-

tem that allows the qualitative assessment of BPMN

models in terms of comprehensibility and modiﬁabil-

ity. To prove the performance of the proposed system,

we conducted two types of experiments. The former

is done through the proposed system while the second

is accomplished in conjunction with students from our

college. These preliminary experimental evaluations

of the proposed system show encouraging results.

To recapitulate, this paper has a three-fold con-

tributions: (i) identiﬁcation of approximate thresh-

olds for the different quality metrics to be used for

assessing the quality of BP models in terms of com-

prehensibility and modiﬁability; (ii) management of

the approximate and imprecise nature of the identi-

ﬁed thresholds using fuzzy logic; and (iii) proposition

of a system that supports the proposed approach.

The remainder of this paper is organized as fol-

lows: Section 2 summarizes existing works on the

adoption of quality metrics and the deﬁnition of their

thresholds for the assessment of the comprehensibil-

ity and modiﬁability of BP models. Section 3 presents

the proposed approach mining metrics’ thresholds.

Section 4 shows how we use fuzzy logic to support

the approximate and imprecise nature of the deﬁned

thresholds. Section 5 illustrates the developed sys-

tem of BP model quality assessment. Section 6 evalu-

ates the proposed system through two types of exper-

iments. Finally, section 7 summarizes the paper and

gives some directions for future work.

2 RELATED WORKS

We ﬁrst overview the quality metrics used in the liter-

ature to assess the comprehensibility and modiﬁabil-

ity of BP models. Second, we discuss works on BP

model quality assessment.

2.1 Quality Metrics

Different research initiatives adopt quality metrics

from the software engineering to assess the quality

of BP models. They consider that business processes

ICSOFT 2017 - 12th International Conference on Software Technologies

are a kind of software systems (Reijers and Vander-

feesten, 2004), (Guceglioglu and Demirors, 2005),

(Cardoso et al., 2006), and (S

anchez-Gonz

aLez et al.,

2013). The adopted quality metrics are used to as-

sess BP models quality in terms of different charac-

teristics among those deﬁned in the ISO/IEC 25010

quality model (ISO, 2011). In this paper, we use ex-

isting metrics to put in place an approach as well as a

support system for BP models quality assessment.

To this end, we have conducted a literature review

on existing quality metrics for assessing the compre-

hensibility and modiﬁability levels of BP models. To

shortlist the relevant metrics, we raised the following

questions:

1. Is the metric validated either theoretically or em-

pirically?

2. Is there a method for calculating the metric?

3. Is it possible to calculate the metric for BP mod-

eled in BPMN?

4. Is the metric used to evaluate the comprehensibil-

ity and/or the modiﬁability of BP models?

At the end of this study, only a few number metrics

were retained. The metrics were eliminated essen-

tially by the ﬁrst question; indeed, several metrics

are adopted from the software engineering domain but

they are not validated in the BP domain neither theo-

retically nor empirically (Muketha et al., 2010). In ad-

dition, some metrics were excluded through the third

criteria, i.e., they are not adopted for BPMN (Sad-

owska, 2015). The retained metrics are listed below:

• Control Flow Complexity (CFC) was deﬁned by

Cardoso et al. (Cardoso et al., 2006) to mea-

sure the complexity introduced by XOR, OR, and

AND split constructs.

CFC(p) =

∑

a∈P∧a∈XOR−Split

CFC

XOR

(a) +

∑

a∈P∧a∈OR−Split

CFC

(a) +

∑

a∈P∧a∈AND−Split

CFC

AND

(a)

(1)

where: CFC

XOR

(a) = n; CFC

(a) = 2

− 1;

CFC

AND

(a) = 1; n=number of outgoing arcs.

• Halstead-based Process Complexity (HPC) was

adapted by Cardoso et al. (Cardoso et al., 2006)

to estimate the length N, the volume V , and the

difﬁculty D of a process as follows:

N = n

∗ log

) + n

∗ log

) (2)

V = (N

+ N

) ∗ log

+ n

) (3)

D = (

) ∗ (

) (4)

where: n

is the number of activities, splits and

joins, and control-ﬂow elements of a BP. n

is the

number of data variables manipulated by the BP

and its activities. N

and N

are respectively the

total number of elements and data occurrences.

• Interface Complexity (IC) was adapted from in-

formation ﬂow metric (Henry and Kafura, 1981)

by Cardoso et al. (Cardoso et al., 2006). IC mea-

sures the complexity of a process as follows:

IC = length ∗ (NbO f Inputs ∗ NbO f Out puts)

(5)

• Number of Activities (NOA) was deﬁned by Car-

doso et al. (Cardoso et al., 2006) to measure the

number of activities (task and sub-process) of a

business process.

• Number of Activities, Joins and Splits (NOAJS)

was deﬁned by Cardoso et al. (Cardoso et al.,

2006) to measure number of activities, joins and

splits of a business process.

• Coefﬁcient of Network Complexity (CNC) was

deﬁned by Cardoso et al. (Cardoso et al., 2006).

The CNC metric is the ratio of the total number

of arcs in a process model to its total number of

nodes.

• Cross Connectivity (CC) was deﬁned by Van-

derfeesten et al. (Vanderfeesten et al., 2008) to

measure the strength of the arcs between process

model nodes. The cross connectivity metric ex-

presses the sum of the connectivity between all

pairs of nodes in a process model, relative to the

theoretical maximum number of paths between all

nodes.

• Coupling metric (CP) was deﬁned by Vander-

feesten et al. (Vanderfeesten et al., 2007b) to cal-

culate the coupling degree of a process. This cou-

pling degree depends on the complexity of con-

nections between the tasks and the type of these

connections (i.e., AND, OR, XOR).

• Density (D) was deﬁned by Mendling (Mendling,

2006). The density metric is the ratio of the total

number of arcs to the maximum number of arcs.

Following software engineering, these metrics are

used to measure either comprehensibility or modiﬁa-

bility or both of them. Table 1 shows the usability of

these metrics to measure either comprehensibility or

modiﬁability as deﬁned in the literature.

2.2 Work on Thresholds for Business

Process Evaluation

Despite the importance of BP model to enterprises,

there is a serious lack of an effective approach and

A Fuzzy Logic-based Approach for Assessing the Quality of Business Process Models

Table 1: Identiﬁed quality metrics for assessing comprehen-

sibility and modiﬁability.

Quality met-

rics

Comprehensibility Modiﬁability

CFC ? ?

HPC ?

IC ?

NOA ? ?

NOAJS ? ?

CNC ? ?

CC ?

CP ? ?

D ? ?

?: The metric is used to assess the comprehensibility or the

modiﬁability.

support systems for BP models quality assessment

anchez-Gonz

aLez et al., 2013) and (Sadowska,

2015). Our literature review revealed that ISO stan-

dards for quality assessment and quality metrics are

the basis of the different propositions. However, the

common problem addressed by the existing works is

the lack of thresholds for the deﬁned quality metrics

to be used during BP models quality assessment.

Makni et al. in (Makni et al., 2010) proposed a

tool for evaluating the quality of BP models using

existing complexity, coupling, and cohesion quality

metrics. However, the authors did not focus on the

identiﬁcation of thresholds as the proposed tools en-

sure the evaluation based on thresholds introduced by

the user for the different metrics.

In (S

anchez-Gonz

alez et al., 2010), the authors

use the Bender method (Bender, 1999) to identify

thresholds for some quality metrics. The method al-

lows quantitative risk assessment in epidemiological

studies based on the logistic regression model. This

method has two major limitations: (i) logistic regres-

sion model requires a binary variable, and (ii) ne-

cessity to arbitrarily deﬁne P0 probability, which is

used to calculate the Value of an Acceptable Risk

Level (VARL). The Bender method was also used

in (S

anchez-Gonz

alez et al., 2011), to deﬁne thresh-

old for the CFC metric. In (S

anchez-Gonz

alez et al.,

2012) the authors conducted an experiment to deter-

mine threshold values for gateway complexity metrics

to be used for the evaluation of the understandabil-

ity and modiﬁability of BP models. The authors also

propose a Gateway Complexity Indicator (GCI) de-

ﬁned based on the identiﬁed threshold values for the

selected gateway complexity measures.

Mendling et al. proposed an approach for predict-

ing errors in BP model (Mendling et al., 2012). The

approach is based on a set of quality metrics used in

the literature for evaluating the quality of BP models.

The author use logistic regression (Bender, 1999) and

ROC curves (Hanley and McNeil, 1982) to determine

thresholds for the used metrics.

In (Sadowska, 2015) Sadowska proposed a meta-

model for assessing the quality of BPMN 2.0 process

models. This meta-model is built upon the ISO/IEC

25010 standard (ISO, 2011). To evaluate the different

quality characteristics, the author used a set of quality

metrics deﬁned in the literature. In addition, they used

a BP repository of 57 BPs modeled with BPMN along

with K-means to classify the possible values of qual-

ity metrics into 4 clusters. Based on the used quality

metrics and the deﬁned clusters the author proposed

a system that supports the evaluation of BP models

quality.

Our literature review revealed the lack of a con-

sensus concerning thresholds values for BP models

quality assessment. This is one of the important ob-

stacles hindering the development of an effective sys-

tem supporting qualitative assessment of BP models.

3 THRESHOLD

DETERMINATION

We detail our approach for determining approximate

thresholds for BP quality metrics in order to evaluate

BP model quality in terms of modiﬁability and com-

prehensibility.

Our approach is based on data mining techniques;

namely decision tree. Thus, four steps are required:

data collection to build a repository of business pro-

cesses, data preparation to create the learning and test

datasets, data mining to build a decision tree, and val-

idation to assess the performance of the resulted deci-

sion tree.

3.1 Data Collection

We created the “SOA-Based Business Process

Database” by collecting a set of business processes

that belong to different organizations to guarantee

that our approach is generic (e.g., academic institu-

tions, commercial enterprises, healthcare centers, and

banks). Furthermore, from each type of organiza-

tion, we examined different business processes; for

example, from academic institutions, we considered,

among others, student registration, exam preparation,

timetable creation, jury thesis defenses allocation, etc.

All of these business processes are modeled using

BPMN 2.0. The total number of the collected busi-

ness processes is 1000.

After the model collection, we examined the pro-

cesses in conjunction with design instructors from the

ICSOFT 2017 - 12th International Conference on Software Technologies

IT department of our university (considered as ex-

perts). The goal is to classify these processes accord-

ing to the level of their comprehensibility and modiﬁ-

ability easiness. To this end, we organized ourselves

into four groups. Each group examined 250 pro-

cesses. Afterward, we conducted a cross-validation

process among the different groups. Finally, we orga-

nized the business processes of the “SOA-Based Busi-

ness Process Database” into three levels of compre-

hensibility (easy to understand, moderately difﬁcult to

understand, and difﬁcult to understand) and three lev-

els of modiﬁability (easy to modify, moderately difﬁ-

cult to modify, and difﬁcult to modify).

3.2 Data Preparation

To prepare the data for the next phases, we built two

matrices based on the database “SOA-Based Business

Process Database”. The ﬁrst is devoted to the com-

prehensibility data, while the second is dedicated to

the modiﬁability data. Each row in a matrix repre-

sents a BP from the “SOA-Based Business Process

Database” and each column represents a quality met-

ric among the identiﬁed quality metrics to measure

comprehensibility and modiﬁability (cf. section 2.1).

The last column of each matrix represents the level

of comprehensibility (i.e., easy to understand, moder-

ately difﬁcult to understand, or difﬁcult to understand)

or modiﬁability (easy to modify, moderately difﬁcult

to modify, or difﬁcult to modify).

In our case, we used these matrices to create

two sub-databases from each matrix: one for learn-

ing “training database” and one for testing “test

database”. The “training database” includes 70% of

the “SOA-Based Business Process Database”, and the

“test database” comprises the rest.

3.3 Data Mining: Decision Trees

At this stage, we used decision trees to extract thresh-

olds for quality metrics from the “SOA-Based Busi-

ness Process Database”. A decision tree consists of

a root node and several intermediate and leave nodes.

The transitions from the root node to a leaf node are

based on the values of the criteria, quality metrics in

our case. At each node, the criterion that maximizes

the homogeneity of child nodes is chosen. Homo-

geneity of a node is reached when all the BPs of this

node belong to the same class (e.g., all the BP of a

node are easy to understand, in the case of compre-

hensibility). A homogeneous node is usually a leaf

node as it cannot be divided. A leaf node corresponds

to the class, which is in our case the level of compre-

hensibility or the level of modiﬁability.

To create the required two decision trees (one for

the comprehensibility and one for the modiﬁability),

we used WEKA system, which is recognized as a

landmark system in data mining and machine learn-

ing (Hall et al., 2009). WEKA supports several algo-

rithms for the construction of decision trees like for

example J48, ADTree, and REPTree. In this work,

we ﬁrst used all of the provided algorithms, and then

we have chosen the best one (i.e., the one that have a

lower error rate) based on the validation stage (cf. sub-

section 3.4).

3.4 Validation

The literature proposes several possible ratios for as-

sessing the quality of a prediction model. In our work,

we use: precision (6), recall (7), f-measure (8), and

global error rate (9). In the following, we discuss only

the three best algorithms (based on the values of the

used ratios), namely are J48, ADTree, and REPTree.

Precision =

CorrectEntitiesFound

TotalEntitiesFound

(6)

Recall =

CorrectEntitiesFound

TotalCorrectEntities

(7)

F − measure = 2 ∗

Precision ∗ Recall

Precision + Recall

(8)

GlobalErrorRate = 1 −

CorrectEntitiesFound

TotalEntities

(9)

3.4.1 Training Database based Validation

First, we calculate these ratios after testing the result-

ing decision trees (i.e., comprehensibility and modi-

ﬁability trees) on the training database. Table 2 and

3 show, respectively, the values of the different ratios

for the three algorithms per decision tree. These ta-

bles depict that J48 algorithm gives the best values of

precision, recall, F-mesure, and global error rates for

both comprehensibility and modiﬁability.

Table 2 shows that we achieved very acceptable

results with J48, for assessing the BP model compre-

henisibility: the values of precision, recall, and F-

measure are of 97.3% and the global error rate is of

2.7%. Similarly, Table 3 shows that J48 can also be

used for assessing the modiﬁability of BP model as

the values of precision, recall, and F-measure are of

96.1% while the global error rate is of 3.8%. How-

ever, to prove the effectiveness of the proposed de-

cision trees, we need to use another database, “test

database”.

A Fuzzy Logic-based Approach for Assessing the Quality of Business Process Models

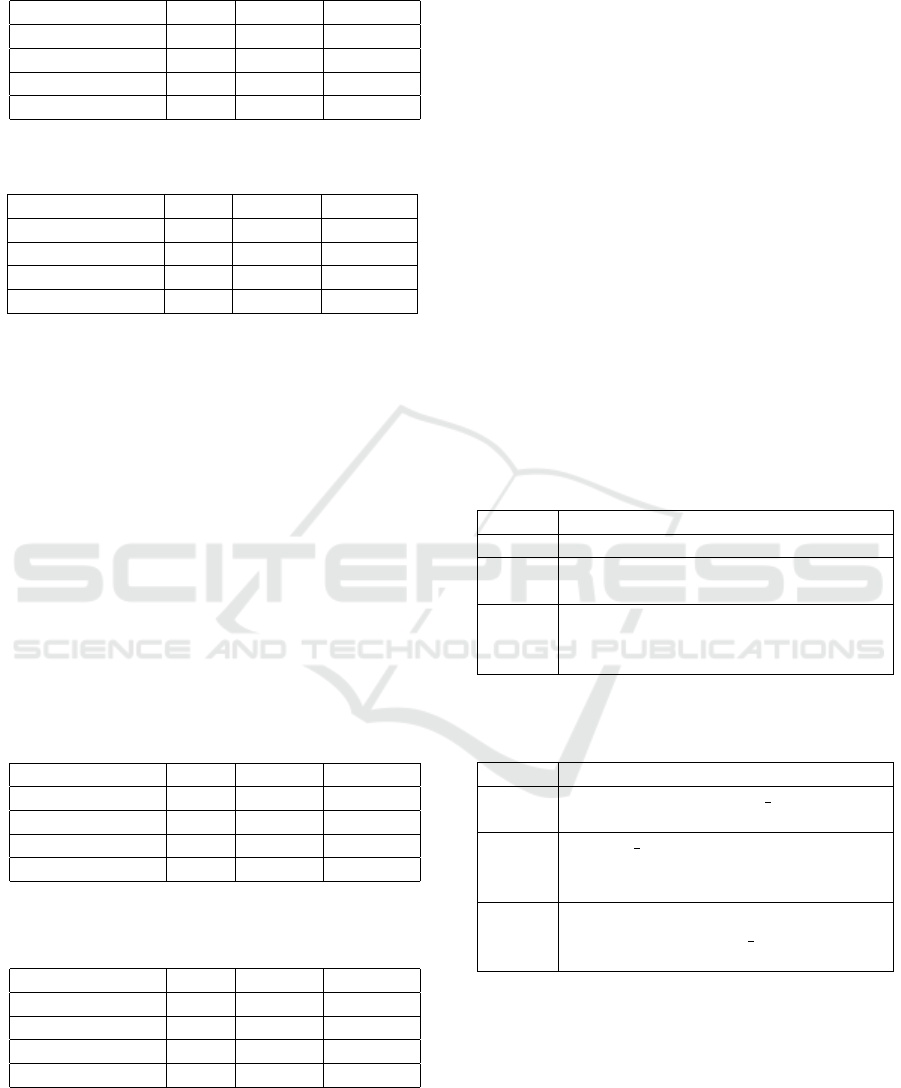
Table 2: J48 vs ADTree vs REPTree for decision tree of

comprehensibility.

J48 ADTree REPTree

Precision 0.973 0.961 0.942

Recall 0.973 0.96 0.94

F-Measure 0.973 0.96 0.941

Global error rate 0.027 0.04 0.06

Table 3: J48 vs ADTree vs REPTree for decision tree of

modiﬁability.

J48 ADTree REPTree

Precision 0.961 0.92 0.925

Recall 0.961 0.92 0.924

F-Measure 0.961 0.92 0.924

Global error rate 0.038 0.08 0.075

3.4.2 Test Database based Validation

To assess the performance of the proposed decision

trees and choose the most suitable algorithm among

those provided by WEKA, we evaluated the obtained

trees using the “test database”, which is extracted

from the “SOA-Based Business Process Database”.

At this stage, we apply each decision tree to all BPs

of the “test database” to assess the comprehensibil-

ity and modiﬁability levels of each process. This as-

sessment is performed independently of the assess-

ments already done by experts. The goal is to com-

pare the experts’ judgement with the obtained trees

assessments and hence, to identify the error rate of

our decision trees.

Table 4: J48 vs ADTree vs REPTree for decision tree of

comprehensibility.

J48 ADTree REPTree

Precision 0.969 0.971 0.962

Recall 0.967 0.967 0.953

F-Measure 0.967 0.968 0.955

Global error rate 0.033 0.033 0.046

Table 5: J48 vs ADTree vs REPTree for decision tree of

modiﬁability.

J48 ADTree REPTree

Precision 0.943 0.875 0.92

Recall 0.94 0.87 0.897

F-Measure 0.94 0.869 0.899

Global error rate 0.06 0.13 0.103

Tables 4 and 5 list the values of the four used ratios

for evaluating the performance of the proposed com-

prehensibility and modiﬁability decision trees. These

tables show that we achieved very acceptable results

using the “test database” using J48. Indeed, the values

of precision are: 96.9% for the comprehensibility tree

and 94.3% for the modiﬁability tree. The values of

recall and f-measure are 96.7% for the comprehensi-

bility tree, and 94% for the modiﬁability tree. Finally,

the global error rate is of 3.3% for the comprehensi-

bility tree and 6% for the modiﬁability tree.

3.5 Discussion

Decision tree is used to classify the BP of the “SOA-

Based Business Process Database” according to their

level of comprehensibility (ﬁrst decision tree) and

modiﬁability (second decision tree) based on the val-

ues of the used quality metrics. Based on these de-

cision trees, we deﬁned a set of decision rules along

with the thresholds of the different quality metrics for

evaluating both comprehensibility and modiﬁability

of a BP model. Tables 6 and 7, respectively, depict

an extract of the deﬁned decision rules for compre-

hensibility and modiﬁability.

Table 6: Excerpt of decision rules to assess the level of com-

prehensibility.

Decision rules

R1 If IC <= 12 Then Easy to understand

R2 If IC <= 17 and IC > 12 and CNC <=

1.26 Then Easy to understand

R3 If IC <= 17 and IC > 12 and CNC >

1.26 and CFC <= 3 Then Moderately

difﬁcult to understand

Table 7: Excerpt of decision rules to assess the level of mod-

iﬁability.

Decision rules

R1 If CFC <= 9 and HPC V <= 53 and

NOA <= 6 Then Easy to modify

R2 If HPC V <= 53 and NOA > 6 and

CFC <= 3 and NOA <= 12 and

CP <= 0.077 Then Easy to modify

R3 If NOA <= 26 and CFC > 3 and

NOA > 12 and HPC V <= 14 Then

Moderately difﬁcult to modify

Table 8 shows the identiﬁed thresholds for each

quality metric. However, the identiﬁed thresholds re-

main usually approximate and imprecise due to the

fact that they depend on the expert judgments during

the ﬁrst phase, “data collection” (cf. subsection 3.1).

In the next section, we detail the use of fuzzy logic to

manage these approximate and imprecise thresholds.

ICSOFT 2017 - 12th International Conference on Software Technologies

Table 8: Obtained thresholds values of quality metrics.

Quality

met-

rics

Comprehensibility Modiﬁability

IC IC < 12

12 <= IC < 17

17 < IC <= 59

IC > 59

CNC CNC <= 1.26

1.26 < CNC <=

1.65

CNC > 1.65

CNC <= 1.30

1.30 < CNC <=

1.54

1.54 < CNC <=

1.61

1.61 < CNC <=

1.85

CNC > 1.85

CFC CFC <= 3

3 < CFC <= 9

9 < CFC <= 18

CFC > 18

CFC <= 3

3 < CFC <= 9

CFC > 9

NOAJS NOAJS <= 39

39 < NOAJS <=

NOAJS > 55

NOAJS <= 7

7 < NOAJS <= 17

17 < NOAJS <=

33 < NOAJS <=

NOAJS > 55

D D <= 0.043

D > 0.043

D <= 0.043

D > 0.043

NOA NOA <= 14

14 < NOA <= 26

NOA > 26

NOA <= 6

6 < NOA <= 12

12 < NOA <= 26

26 < NOA <= 44

NOA > 44

CP CP <= 0.031

CP > 0.031

CP <= 0.032

0.032 < CP <=

0.077

0.077 < CP <=

0.09

CP > 0.09

HPC V - HPC V <= 14

14 < HPC V <=

HPC V > 53

HPC D - HPC D <= 5.25

HPC D > 5.25

4 FUZZY LOGIC FOR BUSINESS

PROCESS QUALITY

ASSESSMENT

According to his founder, fuzzy logic is a precise

logic that supports imprecision and approximate rea-

soning (Zadeh, 2008). In this paper, we use fuzzy

logic to manage the approximate and imprecise na-

ture of the identiﬁed thresholds for the different qual-

ity metrics. Indeed, the use of fuzzy logic adjusts a

bit the identiﬁed thresholds to be more general. This

happens through the ﬁrst step called fuzziﬁcation. At

this step, the thresholds, which are crisp values, are

transformed into linguistic values (e.g., low, medium,

high) known as fuzzy sets. The second step is the in-

ference, which is based on a set of fuzzy rules. In

our case, we deduce these fuzzy rules from the rules

obtained in Section 3.5. Finally, the last step is the

defuzziﬁcation, which produces a quantiﬁable (crisp

value) result. In the remainder of this section, we de-

tail the use of fuzzy logic to assess the quality of BP

models

4.1 Fuzziﬁcation

Fuzziﬁcation converts crisp values of input variables

(i.e., quality metrics) into fuzzy sets (i.e., linguistic

values). This conversion is ensured thanks to a set

of membership functions that we deﬁned based on

the identiﬁed approximate thresholds (cf. section 3.5).

We deﬁned one membership function for each possi-

ble fuzzy set per quality metric (cf. section 3.5).

In the ﬁrst part of Fig.1 (i.e., without fuzziﬁca-

tion), a and b values represent the approximate thresh-

olds determined through the use of decision trees and

fuzzy sets associated with the different intervals ﬁxed

by experts (i.e., low, moderate, and high). In this ﬁg-

ure, each value of a quality metric can belong only to

a single fuzzy set with a membership degree equals to

1. This case is true when the ﬁxed thresholds are ex-

act and precise. However, because it is not the case of

the thresholds deﬁned in this paper, we use the mem-

bership function depicted in the second part of Fig.1

(i.e., with fuzziﬁcation). The values of a’, a”, b’,

and b” are deﬁned by experts for each quality met-

ric. Each value within the intervals [ a’, a” ] and

[ b’, b” ] belong to two fuzzy sets with different

membership degrees. For example, the value “x” be-

longs to the two fuzzy sets “low” and “moderate” with

membership degree of “x1” and “x2” respectively.

4.2 Inference

Inference is the second step in the decision making

process using fuzzy logic. It is based on a set of fuzzy

rules deﬁned in a natural language. Fuzzy logic im-

poses that fuzzy rules are written according to a spe-

ciﬁc syntax “if X is A and/or Y is B then Z is C”,

where X and Y are input variables, Z is output vari-

able, and A, B, C are their corresponding linguistic

A Fuzzy Logic-based Approach for Assessing the Quality of Business Process Models

Figure 1: Membership function deﬁnition.

values. These rules are essential to any system built

upon fuzzy logic as they are used to determine the val-

ues of the output variables based on the input values.

In our work, we deﬁned rules to determine the

level of comprehensibility and modiﬁability of a BP

model based on the set of quality metrics. We used the

set of rules obtained from the decision tree (cf. sec-

tion 3.5): We replaced the crisp values with their cor-

responding linguistic values and rewrote the rules ac-

cording to the syntax required by fuzzy logic. The

total number of deﬁned fuzzy rules is of 210 rules

for the comprehensibility and 260 for the modiﬁabil-

ity. Tables 9 and 10, respectively, depict an extract of

the deﬁned fuzzy decision rules for comprehensibility

and modiﬁability.

4.3 Defuzziﬁcation

Defuzziﬁcation is the process which converts the

fuzzy value of the output variable, obtained by the in-

ference engine, into a crisp value. To do so, it aggre-

gates the fuzzy outputs for all the activated rules to a

one fuzzy set, which will be transformed into a crisp

value.

In the literature, there are several defuzziﬁcation

techniques like: center of gravity, center average, and

maximum. We used the well-used defuzziﬁcation

method: the center of gravity. The crisp value of the

output variable is calculated using the following for-

mula:

y* =

y ∗ µ(y) dy

µ(y)dy

(10)

where µ is the universe of discourse that considers all

the output values according to the activated rules.

Defuzziﬁcation determines the level of compre-

hensibility or modiﬁability of a BP model as well as

the degree of certainty of this level. For example, a BP

model can be estimated as easy to understand with a

certainty degree of 70%.

5 SYSTEM DEVELOPMENT:

BP-FUZZQUAL

We developed a system; BP-FuzzQual, which sup-

ports our fuzzy-based approach for assessing the qual-

ity of BP models. It is developed in Java with

Jdom and JFuzzyLogic libraries and under the Eclipse

framework. The functional architecture of this system

is shown in Fig.2. A complete video demonstrating

the different steps of the BP quality assessment using

our system is available at: https://youtu.be/qaCDjd–

54.

Figure 2: Functional architecture of BP-FuzzQual.

The following are the list of modules within BP-

FuzzQual:

• Parser module: takes as input a BP model mod-

eled in BPMN 2.0 and determines the crisp values

of each used quality metric.

• Fuzzy Control module is implemented in Fuzzy

Control Language (FCL) which follows the

IEC1131 standard, the ﬁrst international standard

for process control software. FCL includes four

components: function block interface, fuzziﬁca-

tion, rule block, and defuzziﬁcation. FCL also

allows deﬁning a ﬁfth optional component called

optional parameters. The use of the four required

components is detailed in the following:

– Function block interface deﬁnes the set of in-

put and output parameters as well as local vari-

ables, if required.

– Fuzziﬁcation component deﬁnes a set of mem-

bership functions for each quality metric.

Based on these membership functions, it con-

verts the crisp values of the quality metric into

linguistic values that will be used by the infer-

ence engine.

– Rule block includes the set of linguistic rules

that are used to estimate the quality of the BP

model. These rules are deﬁned following the

syntax imposed by fuzzy logic.

– Defuzziﬁcation component converts the lin-

guistic value of the output variable “compre-

hensibility and modiﬁability levels” into crisp

values. This conversation is based on a deﬁned

ICSOFT 2017 - 12th International Conference on Software Technologies

Table 9: Excerpt of decision rules to assess the level of comprehensibility.

Fuzzy decision rules

FR1 IF IC IS Low THEN ComprehensibilityLevel IS ComprehensibilityLevel IS EasyToUnderstand

FR2 IF IC IS Moderate AND CNC IS Low THEN ComprehensibilityLevel IS EasyToUnderstand

FR3 IF IC IS Moderate AND CNC IS Moderate AND CFC IS Low THEN ComprehensibilityLevel IS Moder-

atelyDifﬁcultToUnderstand

Table 10: Excerpt of decision rules to assess the level of modiﬁability.

Fuzzy decision rules

FR1 IF CFC IS Moderate AND HPC V IS Moderate AND NOA IS VeryLow THEN ModiﬁabilityLevel IS

EasyToModify

FR2 IF HPC V IS Moderate AND NOA IS VeryLow AND CFC IS Low AND CP IS Moderate THEN Modiﬁa-

bilityLevel IS EasyToModify

FR3 IF HPC V IS High AND CFC IS Low AND NOA IS Low AND CP IS Moderate THEN ModiﬁabilityLevel

IS ModeratelyDifﬁcultToModify

technique (e.g., center of gravity, center aver-

age, and maximum). As per section 4.3 the

proposed system uses the center of gravity tech-

nique.

• Decision maker module runs the FCL code in or-

der to estimate the quality of the BP model. This

module takes as input the crisp values produced

by the parser module and communicates these val-

ues to the fuzzy control module. The decision

maker module is developed using java language.

6 EXPERIMENTS

For validating the approach and the system, we

carried out two types of experiments. The ﬁrst was

done using our system, BP-FuzzQual, and the second

involved anonymous students from our college. In

both experiments the business process model of

Fig. 3 was used. In this model, we use abstract labels

in tasks and pools in order to bypass the complexity

that could be caused by the business domain.

Experiment 1: consists of modeling a BP using

BPMN2 modeler, for example. Then if the BP engi-

neer selects “Quality assessment” menu and then “As-

sess BP model comprehensibility”, the system dis-

plays the crisp and fuzzy values of the different qual-

ity metrics used for assessing comprehensibility. It

also displays the estimated level of comprehensibility.

For instance, the estimated comprehensibility level of

the BP model of Fig. 3 is “Moderately difﬁcult to

understand with a certainty degree of 63%”. Fig. 4

shows the interface for comprehensibility assessment.

In addition, if the BP engineer selects “Quality

assessment” menu and then “Assess BP model

modiﬁability”, the system displays the crisp and

fuzzy values of the different quality metrics used for

Figure 3: Example of BP model modeled with BPMN.

assessing modiﬁability. It also displays the estimated

level of modiﬁability. For instance, the estimated

modiﬁability level of the BP model of Fig. 3 is “Mod-

erately difﬁcult to modify with a certainty degree

of 100%”. Fig. 5 shows the interface dedicated for

modiﬁability assessment.

Experiment 2: uses the BP model of Fig. 3 and

two sets of exercises (available at: https://sites.

google.com/site/bposcteam2015/ressources). In the

ﬁrst exercise, 60 undergraduate students from our

College were asked some multi-choice questions to

assess their understanding of the BP model. In the

second exercise, the same students were invited to

make some changes in the BP model. Fig. 6 rep-

resents the number of correct and incorrect answers

for the ﬁrst exercise. In this ﬁgure, 78% of the re-

sponses are correct showing that the majority of stu-

dents understood the BP model. This is also con-

ﬁrmed through their responses to the last question of

the ﬁrst exercise, which is about their ability to un-

derstand the BP model. Indeed, as depicted in Fig. 7

76% of students considered the BP model as moder-

ately difﬁcult to understand, 14% as easy to under-

A Fuzzy Logic-based Approach for Assessing the Quality of Business Process Models

Figure 4: Comprehensibility assessment interface.

Figure 5: Modiﬁability assessment interface.

Figure 6: Correct and incorrect answers for comprehensi-

bility assessment.

Figure 7: Students’ judgments about the BP model compre-

hensibility level.

stand, and 10% as difﬁcult to understand.

Fig. 8 represents the number of correct and incor-

rect answers for the second exercise. In this ﬁgure,

69% of the responses are correct showing that a good

number of students have correctly modiﬁed the BP

model. In addition, as depicted in Fig. 9 53% of stu-

dents considered the BP model as moderately difﬁcult

to modify, 33% as difﬁcult to modify, and 14% as easy

to modify.

Figure 8: Correct and incorrect answers for modiﬁability

assessment.

To sum up, the experiment shows that the students

considered the BP model as moderately difﬁcult to

understand; this is proved by their responses to the

comprehensibility questions. This is in line with the

ICSOFT 2017 - 12th International Conference on Software Technologies

Figure 9: Students judgment about the BP model modiﬁa-

bility level.

evaluation done by FuzzQual, which considers the BP

model as moderately difﬁcult to understand. Simi-

larly, when dealing with modiﬁability, the students

consider the BP model as around moderately difﬁ-

cult to modify and difﬁcult to modify while FuzzQual

considers that the BP model is moderately difﬁcult

to modify. Overall, these comforming results show

that our approach produces encouraging results that

should be proved through additional experiments.

7 CONCLUSION

BP modeling is important for enterprises that wish

to remain competitive. However, this task, which is

usual manual, can result into a BP model of a poor

quality. Such a model could affect the remainder BP

lifecycle phases (Weske, 2010). To overcome this

challenge, Mendling et al. proposed seven guide-

lines that can assist BP engineers develop a BP model

of a high quality (Mendling et al., 2010). Other re-

search initiatives focus on the use of quality metrics

used in the ﬁeld of software engineering to assess the

quality of BP models (Vanderfeesten et al., 2007b),

(Mendling et al., 2012), and (de Oca et al., 2015).

However, to date, there is no consistent framework

for assessing BP models quality. The lack of such

a framework is due to different challenges like the

lack consensus about the used metrics, their thresh-

olds, etc.

To tackle these challenges, we proposed, in this

paper, a fuzzy-based approach for assessing the qual-

ity of BP models modeled in BPMN 2.0 in terms of

comprehensibility and modiﬁability. The proposed

approach is based on the ISO/IEC 25010 standard as

along with a set of quality metrics used in the liter-

ature to assess BP models quality. It consists of two

essential phases: threshold determination and fuzzy

logic application. The ﬁrst phase applies data mining

techniques, speciﬁcally decision tree, to determine

approximate thresholds for each used quality metric

to assess the quality of BP models, modeled using

BPMN language, in terms of comprehensibility or

modiﬁability. This phase used the “SOA-based Busi-

ness Process Database”, which is built within our lab-

oratory. The second phase of the proposed approach

uses the approximate thresholds identiﬁed in the ﬁrst

phase along with fuzzy logic (Zadeh, 1965) to assess

the quality of BP models. The use of fuzzy logic

aims at dealing with the approximate and imprecise

nature of the obtained thresholds. To automate BP

models quality assessment we developed FuzzQual,

which is a system supporting the proposed approach.

This system is developed in Java language and un-

der eclipse framework. To prove the performance of

the proposed system, we conduct two types of exper-

iments. The former is done through the proposed sys-

tem while the second is accomplished in conjunction

with students from our college. These preliminary ex-

perimental evaluations of the proposed system show

encouraging results.

As a future endeavor, we plan to validate the

proposed fuzzy approach for BP quality assessment

through some real case studies and in conjunction

with enterprises’ experts. In addition, we plan to as-

sess the quality of BP models in terms of other quality

characteristics among those presented in the ISO/IEC

25010 quality model. We, also, intent to put in place

an approach and its support system that could help

enterprises improve the quality of their BPs.

REFERENCES

Bender, R. (1999). Quantitative risk assessment in epidemi-

ological studies investigating threshold effects. Bio-

metrical Journal, 41(3):305–319.

Cardoso, J., Mendling, J., Neumann, G., and Reijers, H. A.

(2006). A discourse on complexity of process mod-

els. In International Conference on Business Process

Management, pages 117–128. Springer.

Cardoso, J., Vanderfeesten, I., and Reijers, H. A. (2010).

Computing coupling for business process mod-

els. available from Internet¡ http://eden. dei.

uc. pt/˜ jcardoso/Research/Papers/Old% 20pa-

per% 20format/Caise-19th-Coupling-Cardoso-

Vanderfeesten. pdf¿(20 September 2012).

Curtis, B., Kellner, M. I., and Over, J. (1992). Process mod-

eling. Communications of the ACM, 35(9):75–90.

de Oca, I. M.-M., Snoeck, M., Reijers, H. A., and

Rodr

ıguez-Morfﬁ, A. (2015). A systematic literature

review of studies on business process modeling qual-

ity. Information and Software Technology, 58:187–

205.

Guceglioglu, A. S. and Demirors, O. (2005). Using soft-

ware quality characteristics to measure business pro-

cess quality. In International Conference on Business

Process Management, pages 374–379. Springer.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

A Fuzzy Logic-based Approach for Assessing the Quality of Business Process Models

ing software: an update. ACM SIGKDD explorations

newsletter, 11(1):10–18.

Hanley, J. A. and McNeil, B. J. (1982). The meaning and

use of the area under a receiver operating characteris-

tic (roc) curve. Radiology, 143(1):29–36.

Heinrich, R. (2013). Aligning Business Process Quality and

Information System Quality. PhD thesis.

Henry, S. and Kafura, D. (1981). Software structure met-

rics based on information ﬂow. IEEE transactions on

Software Engineering, (5):510–518.

ISO (2011). Iso/iec 25010:2011 - systems and software en-

gineering – systems and software quality requirements

and evaluation (square) – system and software qual-

ity models. https://www.iso.org/standard/35733.html.

(Accessed on 12/08/2016).

ISO (2013). Iso/iec 19510:2013 - information technology

– object management group business process model

and notation. http://www.iso.org/iso/catalogue detail.

htm?csnumber=62652. (Accessed on 10/17/2016).

Makni, L., Khlif, W., Haddar, N. Z., and Ben-Abdallah, H.

(2010). A tool for evaluationg the quality of business

process models. In ISSS/BPSC, pages 230–242. Cite-

seer.

Mendling, J. (2006). Testing density as a complexity met-

ric for epcs. In German EPC workshop on density of

process models.

Mendling, J., Reijers, H. A., and van der Aalst, W. M.

(2010). Seven process modeling guidelines (7pmg).

Information and Software Technology, 52(2):127–

136.

Mendling, J., S

anchez-Gonz

alez, L., Garcia, F., and

La Rosa, M. (2012). Thresholds for error probabil-

ity measures of business process models. Journal of

Systems and Software, 85(5):1188–1197.

Morimoto, S. (2008). A survey of formal veriﬁcation for

business process modeling. In International Con-

ference on Computational Science, pages 514–522.

Springer.

Muketha, G., Ghani, A., Selamat, M., and Atan, R. (2010).

A survey of business process complexity metrics. In-

formation Technology Journal, 9(7):1336–1344.

Reijers, H. A. and Vanderfeesten, I. T. (2004). Cohesion

and coupling metrics for workﬂow process design. In

International Conference on Business Process Man-

agement, pages 290–305. Springer.

Sadowska, M. (2015). An approach to assessing the qual-

ity of business process models expressed in bpmn. e-

Informatica Software Engineering Journal, 9(1).

anchez-Gonz

alez, L., Garc

ıa, F., Mendling, J., and Ruiz, F.

(2010). Quality assessment of business process mod-

els based on thresholds. In OTM Confederated Inter-

national Conferences” On the Move to Meaningful In-

ternet Systems”, pages 78–95. Springer.

anchez-Gonz

alez, L., Garc

ıa, F., Ruiz, F., and Mendling, J.

(2012). Quality indicators for business process models

from a gateway complexity perspective. Information

and Software Technology, 54(11):1159–1174.

anchez-Gonz

aLez, L., Garc

ıA, F., Ruiz, F., and Piattini,

M. (2013). Toward a quality framework for business

process models. International Journal of Cooperative

Information Systems, 22(01):1350003.

anchez-Gonz

alez, L., Ruiz, F., Garc

ıa, F., and Cardoso, J.

(2011). Towards thresholds of control ﬂow complex-

ity measures for bpmn models. In Proceedings of the

2011 ACM symposium on Applied computing, pages

1445–1450. ACM.

Schmidt, R. and Nurcan, S. (2009). Augmenting bpm with

social software. In International Conference on Busi-

ness Process Management, pages 201–206. Springer.

Van Der Aalst, W. M., Ter Hofstede, A. H., and Weske, M.

(2003). Business process management: A survey. In

International conference on business process manage-

ment, pages 1–12. Springer.

Vanderfeesten, I., Cardoso, J., Mendling, J., Reijers, H. A.,

and van der Aalst, W. M. (2007a). Quality metrics for

business process models. BPM and Workﬂow hand-

book, 144:179–190.

Vanderfeesten, I., Reijers, H. A., Mendling, J., van der

Aalst, W. M., and Cardoso, J. (2008). On a quest for

good process models: the cross-connectivity metric.

In International Conference on Advanced Information

Systems Engineering, pages 480–494. Springer.

Vanderfeesten, I. T., Cardoso, J., and Reijers, H. A. (2007b).

A weighted coupling metric for business process mod-

els. In CAiSE Forum, volume 247.

Watahiki, K., Ishikawa, F., and Hiraishi, K. (2011). Formal

veriﬁcation of business processes with temporal and

resource constraints. In Systems, Man, and Cybernet-

ics (SMC), 2011 IEEE International Conference on,

pages 1173–1180. IEEE.

Weske, M. (2010). Business process management: con-

cepts, languages, architectures. Springer Publishing

Company, Incorporated.

Zadeh, L. A. (1965). Fuzzy sets. Information and control,

8(3):338–353.

Zadeh, L. A. (2008). Is there a need for fuzzy logic? Infor-

mation sciences, 178(13):2751–2779.

ICSOFT 2017 - 12th International Conference on Software Technologies