Developing a Mathematical Model of Oil Production in a Well That

Uses an Electric Submersible Pumping System

María Hallo

, Byron Jaramillo

, José Aguilar

1,3

, Hector Lozada

3,4

and Edgar Camargo

Escuela Politécnica Nacional, Quito, Ecuador

NOUX C.A., Quito, Ecuador

CEMISID, Dpto. Computación, Universidad de los Andes, 5101, Mérida, Venezuela

PDVSA, Línea de Servicio AIT, Maracaibo, Venezuela

Keywords: Genetic Programming, Electro Submersible Pump Efficiency, Identification Problem, Well Production.

Abstract: This paper presents an approach to get a mathematical model for describing the production of an Electro

Submersible Oil Pumping System (ESP). The determination of this mathematical model considering the

variables of the process, is a very hard task. In this case, we propose the determination of this model using a

data approach, in order to exploit the large quantity of data about the process obtained from its sensors. Our

approach based on data uses the genetic programming techniques for the identification of the mathematical

model, which follows an evolutionary process to solve the problem. Our approach has been implemented

using an extension of R program. The training data were collected from an oil well. This paper presents the

results of the training phase and of the generated models after several iterations. Additionally, the paper

analyses the differences between the generated models, according to the number of variables considered, the

complexity of the expressions, and the error.

1 INTRODUCTION

Due to the demands of productivity, safety and

profitability in the industry, process automation

demands sophisticated and complex Information

Communication and Automation Technology

(ICATs), which must operate on different platforms

and exploit diverse data and information sources.

Thus, the number, complexity, and variety of ICAT

applications for process automation continue to grow.

In previous works, we have proposed a

mechanism for integrating the different intelligent

techniques, to conform what we have called an

Intelligent Autonomous System for Petroleum

Processes (SAi2P, for its acronym in Spanish

"Sistema Autonómico Inteligente para Procesos

Petroleros"), which has the abilities to adapt to new

situations, and possesses attributes of reasoning to

generalize and discover knowledge from the data,

among other things, to make decisions about the

processes (Lozada et al., 2017). In this way, SAi2P

involves concepts, paradigms and adaptive

algorithms, which allow to generate appropriate

actions in complex and changing environments.

Specifically, one of the tasks of SAi2P is the

optimization of operational performance, and in order

to perform this task, it is necessary to determine the

mathematical expression that calculates the

efficiency of the production process of a well, based

on the process variables. This mathematical function

allows several things, from predicting the behavior of

the well, until detecting possible problems in the

production process.

SAi2P has been instanced in an oil production

process based on the Electric Submersible Pumping

system (ESP) (Ronning, 2011), which is an

economical and efficient method of artificial crude

lifting, capable of handling large volumes of fluids.

In this paper, we propose an approach to define the

mathematical model of the efficiency of the

production of a well, which uses an Electro

Submersible Pumping System, based on genetic

programming.

The genetic programming has been used to solve

problems of system identification, based on the data

about the system in study. Genetic programming

follows an evolutionary process of the species, and

uses a population of solutions (in our case,

mathematical models) in order to search the best one,

according to the goals of the problem to reach (in our

230

Hallo, M., Jaramillo, B., Aguilar, J., Lozada, H. and Camargo, E.

Developing a Mathematical Model of Oil Production in a Well That Uses an Electric Submersible Pumping System.

DOI: 10.5220/0006421202300237

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 230-237

ISBN: 978-989-758-263-9

case, to follow the behavior of the production).

We consider a real case of oil production. The

application range of this lifting method is between

300 and 80,000 Barrels by day (BPD) for a variety of

operating conditions, in oil crudes ranging from 8.5

to 40° API and viscosities of up to 5000 cp

(centipoise). Additionally, the depths are between

1000 and 14,000 feet with bottom temperatures up to

350° F.

In general, the cost for installing an ESP system is

high, so it requires an adequate operational

management if its useful life is to be extended. That

is why keeping this system within its operational

parameters is the main task of real-time supervising

systems. However, getting an optimal set point of

operation is usually based on the experience of the

field operator. On the other hand, a lot of data from

these systems are being stored in the operational

databases of real-time monitoring systems. This

situation represents a great opportunity for the

development of mathematical models, to describe the

efficiency of the pump of an ESP system, according

to its operational parameters, with the aim of

maximizing production. (Bermúdez, 2015), (Osman

et al., 2005).

In this paper, we propose an approach to

determine the mathematical model that describes the

efficiency of the pump of an ESP system, using the

data stored in the operational databases. Our approach

is based on the genetic programming, and it is able to

determine the mathematical model of the efficiency

of the pump in function of its operational parameters,

with the final objective of optimizing the production

of the system.

Also, this paper presents the theoretical

framework to develop the model, and the parameters

considered as well as the procedure for the creation of

the model. Finally, it presents several operational

scenarios, as well as the results and their analysis.

2 CONTEXT

2.1 Well Problem

This article focuses on the development of a

mathematical model, which describes the efficiency

of a ESP, using its operational variables, such as

(Pwf) flowing pressure of the well, (Php) Pressure in

the Production Head, (Thp) Temperature in the

Production Head, and Produced Flow (Qprod), which

are captured in the field by temperature and pressure

sensors, and are integrated to control devices, and

then transmitted wirelessly to the control rooms,

where production operators adjust the values. The

behaviour of the ESP system can be described by a

serie of characteristic curves, such as load vs flow,

efficiency vs flow, power vs flow, supplied by the

system manufacturer taking into account its model,

engine frequency, speed of rotation, and the specific

gravity (Ramírez, 2004).

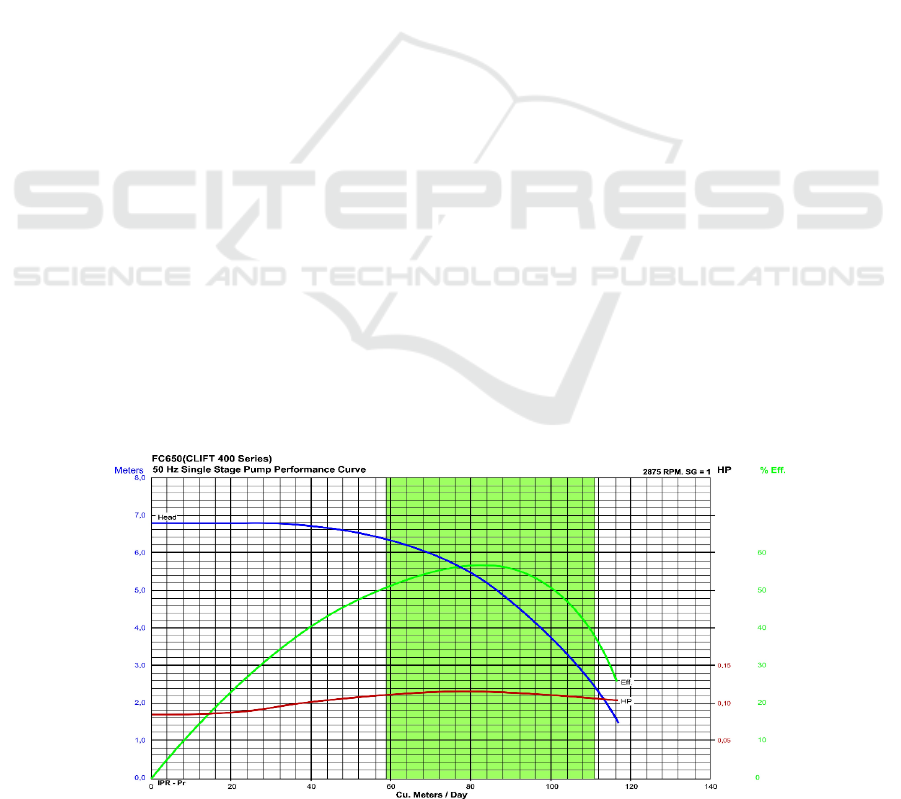
Determining the point of operation of the pump

will be a task where factors such as the total system

load and the load vs. flow curve will play a

fundamental role, and the intersection of each curve

marks the point of operation of the system (See Figure

1), (Baieli et al., 2006). The Figure 1 also shows the

curves of the operational parameters of the system,

and the green zone determines the most efficient

region of operation of a well based on an ESP system.

In general, the flow regulation in this type of

system is performed by adjusting the motor rotation

speed, this results in a change in the flow rate, and this

change causes a new point of operation of the system.

Figure 1: ESP characteristic curves.

Developing a Mathematical Model of Oil Production in a Well That Uses an Electric Submersible Pumping System

231

Likewise, the changes in the physical conditions of

the fluid in which the system works bring as a

consequence a change in the curves, and therefore,

another point of operation of the system.

Keeping the system at an optimum efficiency

point is a task that must be constantly carried out

whenever there are changes in the operating

conditions of the system. In order to achieve this, it is

necessary to have a mathematical model that

describes the efficiency behaviour, in function of the

operational variables of the system.

2.2 SAi2P

In previous works, we have proposed an Intelligent

Autonomous System for Petroleum Processes called

SAi2P, which can generate and discover knowledge

from the data in the process, to make decisions about

it (Lozada et al., 2017). SAi2P uses a set of concepts,

paradigms and adaptive algorithms, which allow to

generate appropriate actions in complex and changing

environments.

SAi2P is defined by a closed loop of data

analytical tasks, which allow exploiting the data

about the oil process, in order to carry out an

intelligent supervision of it (Camargo et al., 2014). In

general, an "Autonomic Cycle of Data Analysis"

defines a set of tasks of data analysis, whose common

goal is to achieve an improvement in the process

under study (Aguilar et al., 2016). They interact with

each other, and have different roles: observe the

process, analyze and interpret what happens in it, or

make decisions in order to improve the process. The

integration of data analytics tasks allows solving

complex problems that have far been impossible to

study by the amount of knowledge required for

resolution.

Particularly, in this paper, we consider SAi2P, an

autonomic cycle of data analytical tasks for oil

production. The autonomous cycle defines a closed

loop of tasks of analysis of data, which supervises

permanently the oil process. It is a supervision cycle

of processes based on LA tasks, in order to

permanently improve them. Specifically, the data

analysis tasks in the autonomous cycle are:

 Monitoring of events affecting the world oil

market.

 Identification of production cost.

 Monitoring of the trends of variables.

 Identification of patterns of oil prices.

 Economic profitability assessment.

 Recognition of fault patterns.

 Diagnosis of the operational problems.

 Optimization of the operational performance.

 Maximization of the production at the lowest cost.

Specifically, in this paper, we are interested in the

“optimization of the operational performance” task of

SAi2. In order to perform this task, it is necessary to

determine the mathematical expression that

calculates the efficiency of the production process of

a well, based on the process variables. This paper

proposes an approach for that.

2.3 Genetic Programming

Genetic Programming is a technique that

automatically solves problems, without requiring the

user to know the structure of the solution in advance

(Aguilar et al., 2001); (Langdon et al., 2013).

Fig. 2 is a flowchart that shows how the

evolutionary process works. The initial step is to

create a population of program trees that are

randomly assembled from the available inputs. This

allows a broad sampling of possible inputs, and

begins the search for productive combinations.

Figure 2: Control Flow for Genetic Programming.

The initial population will probably have a poor

performance overall, some individuals will perform

better than others because of their features, or the way

how they have combined the parameters. It is

improved in the next generations, using an

evolutionary process, where the best individuals are

selected to generate new individuals, which must be

better with respect to the individuals of the previous

generations.

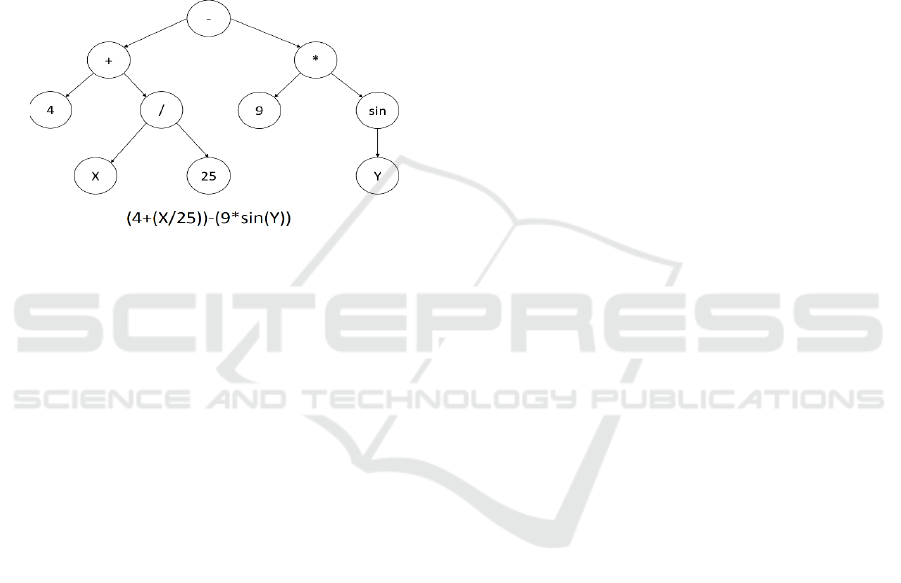
In the Genetic Programming, the programs are

usually expressed as syntax trees. The variables and

constants in the program are leaves of the tree. The

arithmetic operations (+,*, etc.) are internal nodes

called functions.

The steps of the Genetic Programming are:

 Initialization. The individuals in the initial

population are typically randomly generated.

 Selection. Genetic operators are applied to

individuals that are probabilistically selected

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

232

based on their ﬁtness. That is, better individuals

are more likely to have more kids than inferior

individuals.

 Apply genetic operators. The genetic operations

that are used to create new programs from existing

ones are:

o Crossover: The creation of a child by

combining randomly chosen parts from two

selected parent program.

o Mutation: The creation of a new child by

randomly altering a randomly chosen part of a

selected parent program.

Figure 3: Genetic Programming syntax tree representing a

mathematical expression.

2.4 Genetic Program in System

Identification

There are some works about the application of genetic

programing in the identification problem.

(Iba et al., 1995) presents a genetic programming,

which integrates a local parameter tuning mechanism

employing statistical search, for the system

identification. More precisely, they integrate the

structural search of traditional genetic programing

with a multiple regression analysis method to

establish an adaptive program, called

STROGANOFF (STructured Representation On

Genetic Algorithms for NOn-linear Function Fitting).

The fitness evaluation is based on a minimum

description length (MDL) criterion, which effectively

controls the tree growth in GP.

In (Witczak et al., 2002) it is provided a system

identification framework based on genetic

programming technique. Moreover, a fault diagnosis

scheme for non-linear systems is proposed. In

particular, they show how to use the genetic

programming technique to increase the convergence

rate of the observer. (Patelli, 2011) approaches the

nonlinear system identification problem, by

suggesting several original genetic programming

based algorithms enhanced with various mechanisms

designed to increase run time performance.

(Kötzing et al., 2011) analyses the Genetic

Programming in the well-known PAC learning

framework and point out how it can observe quality

changes in the evolution of functions by random

sampling. This leads to computational complexity

bounds for a linear genetic programming algorithm

for perfectly learning any member of a simple class

of linear pseudo-Boolean functions. Finally, (Madar,

2005) proposes a method for the structure selection of

Linear-in-parameters models, which uses genetic

programming to generate nonlinear input−output

models of dynamical systems that are represented in

a tree structure. The main idea of the paper is to apply

the orthogonal least squares (OLS) algorithm to

estimate the contribution of the branches of the tree

to the accuracy of the model.

Our approach presents an innovative application

of genetic programming in the field of continuous

processes, in particular, the identification of systems

in petroleum processes using data stream. To our

knowledge, there are no such applications in this

field.

3 SYSTEM IDENTIFICATION

BASED ON GENETIC

PROGRAMMING

In this section, we present our approach for the

determination of the mathematical expression that

calculates the efficiency of the production process of

a well, based on the process variables. The steps of

our approach, based on genetic programming are:

1. Definition of the parameters of the problem.

2. Determination of the quality of the data.

3. Implementation of the Genetic Programming

model.

4. Test and validation of the results

3.1 Definition of the Parameters of the

Problem

The operational parameters used to develop the

mathematical model for describing the EPS system

used in the oil production are:

 Pwf (psi): Background Fluent pressure (referring

to the vertical midpoint of the perforations).

 Php (psi): Pressure in the Production Head.

 Frec (hz): Frequency of pump rotation.

 Thp (psi): Oil temperature on the Production

Head.

 Qprod (barrels/day): Oil production.

Developing a Mathematical Model of Oil Production in a Well That Uses an Electric Submersible Pumping System

233

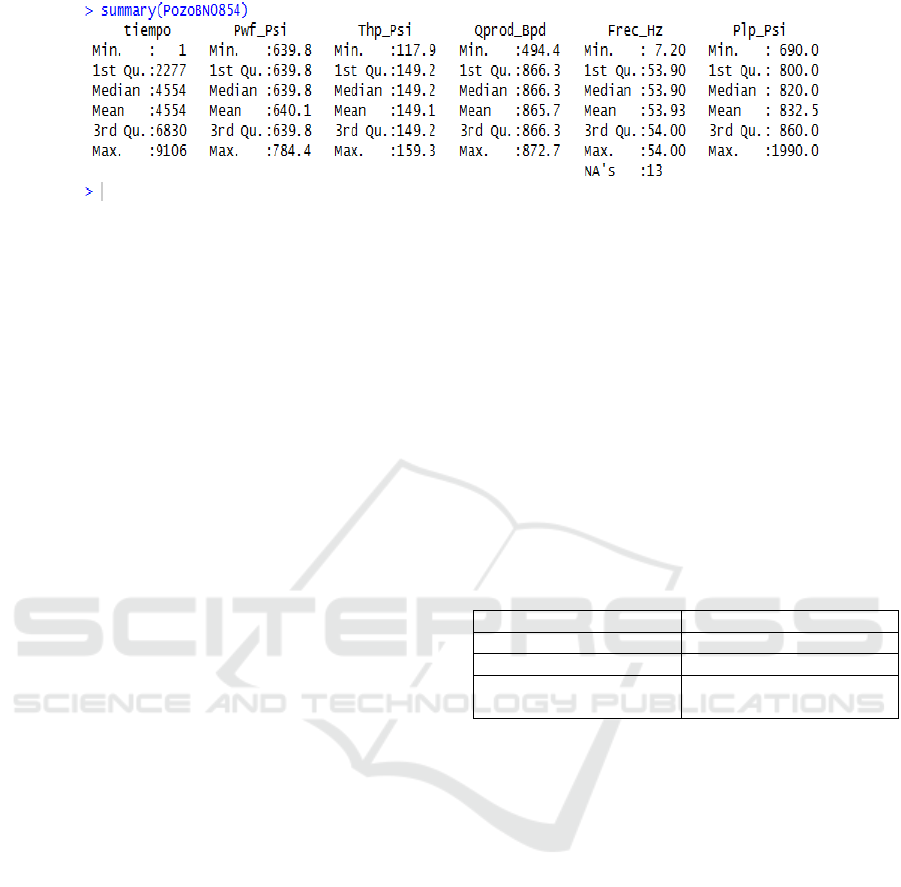
Figure 4: Initial data analysis.

Data were collected from an oil well. The number

of measures were 9107.

3.2 Determination of the Quality of the

Data

The quality of the Data were determined applying

basic statistics to find anomalies.

Figure 4 shows the results of the data analysis

with maximum and minimal values for each variable.

3.3 Implementation of the Genetic

Programming Model

To apply the Genetic Programming to a problem, we

need preparatory steps, in which are defined the set of

parameters of the genetic programming:

 The terminal set, composed of variables,

functions with no arguments and /or constants

(specified or randomly generated).

 The function set (arithmetic, mathematical or

Boolean functions)

 The fitness measure (error between the individual

output and the desire output)

 The parameters that control the run (probabilities

of the genetic operators, etc.)

 The termination criterion (e.g. maximum number

of generations).

3.4 Tests and Validation of the Results

The details of this phase are shown in Section 4.

4 EXPERIMENTATION

For the implementation of our approach, we have

used the software RGP based on the R environment.

This software support Symbolic Regression using

Genetic Programming, and provides a basic set of

genetic operators: mutation, crossover and selection

(Flasch et al., 2010).

In table 1, we show the mean errors of the models

generated in a different set of experiments. In the first

experiment, we use a source of data that has

anomalous data, which represent failures in the

system. The second set of experiments uses a source

of data where have been filtered the anomalous data.

In the third set of experiments we use only correct

data, and the concept of individuals’ elite. We find the

best models in the third set of experiments, with the

lowest mean errors (0.26%), but the models found are

complexes and have only one variable (see next

Tables).

Table 1: Quality of the RGP Models generated by the

different experiments.

Conditions

Mean errors

Without filter

0,6%

With filter

0.29%

With filter and Elite

individuals

0.26%

In table 2, we present some of the mathematical

models generated by the first experiment, where we

have not filtered the data, with the corresponding

errors. We obtain very complex individuals, and the

error is due to that the mathematical equations

generated in this case, consider conditions when the

system has failed. That means, the genetic

programming tries to generate a model that considers

the normal and abnormal behavior.

Table 3 shows the best results of the second

experiment. In this case, we improve the quality of

the error due to that we only consider data without

anomalous data, that means, data that do not represent

situations with faults. Again, we obtain very complex

individuals, but these mathematical equations can be

simplified, because there are constants that can be

eliminated.

Table 4 shows the best mathematical equations

generated in the third experiment, where we reduce

the error in one important level, but the number of

variables considered in the equations are very limited.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

234

To determine the best mathematical equation, we

need to combine several criteria, such as the error,

number of variables and complexity of the

expression. We like a mathematical equation with

little error because we need to follow the system, with

low complexity because the mathematical equation

must be easy to interpret, and which considers the

largest number of variables in the modeling system.

Table 5 shows these results from the different

experiments according to these criteria. The first row

is from the first experiment, and we see that this

individual is very good, but the expression is very

complex and consider only one variable. The second

equation is from the second experiment, and this

equation is very interesting because the error is

not high, it considers three variables of the process,

and the final equation is very simple.

One important remark is that the mathematical

models generated by the second and third

experiments can be used in the context of the

detection of failures in our system (Araujo et al.,

2003). These mathematical equations follow the

normal behaviour of the system, and can predict its

future behaviour. However, when the behaviour of

the real system is different to the estimated by our

models it is because the real system has an abnormal

behaviour. This can be due to failure in the system.

Table 2: RGP Models without filters, ranked by error values.

Mathematical Model

Error

exp(exp(exp(-1.45805039908737 - Frec_Hz)/(Plp_Psi * Pwf_Psi - ln(Thp_Psi)) - (exp(exp(-2.08472784608603)) - (Thp_Psi

+ 4.06191883143038)/(Pwf_Psi + Thp_Psi)) + exp(exp(ln(8.86126783676445/8.49407647270709))))) *

exp(sqrt(sqrt((sqrt(exp(-5.91158133465797)) - (-1.11350659746677 - -

1.72236355952919)/ln(Pwf_Psi))/((2.87925401702523 * 7.04056354705244 - exp(-4.26327155902982))/(-

8.26513446867466/Frec_Hz/(-3.26833550352603 * -2.56143803242594))))))

0.6%

sqrt(Frec_Hz * sqrt(Thp_Psi * ln(7.85157934296876))) + sqrt(Thp_Psi * Thp_Psi * ln(7.6389035070315)) *

ln(sqrt(exp(7.85157934296876)))

0,86%

sin(Thp_Psi) + (-8.43441986013204 + exp(6.77450031973422))

1.42%

sqrt(exp(sqrt(Thp_Psi) + ln(3.46520180348307))) + exp(3.46520180348307)

1.16%

Table 3: RGP Models with filters and without elite individuals, ranked by error values.

RGP Mathematical models

Error <1%

Variables number

Complexity of the

structure

sqrt(Pwf_Psi) + Thp_Psi + Pwf_Psi + Frec_Hz

0,36%

Frec_Hz + (Thp_Psi + Pwf_Psi + sqrt(Pwf_Psi))

0,36%

sqrt(Pwf_Psi) + (Frec_Hz + (Pwf_Psi + Thp_Psi))

0,36%

Pwf_Psi + 4.17186871170998 * Frec_Hz

0,26%

sqrt((Thp_Psi + (Thp_Psi + Pwf_Psi)) * (Thp_Psi + Pwf_Psi)) +

5.222307164222

0,29%

Table 4: RGP Models with filter and elite individuals, ranked by error values.

RGP Mathematical models

Error <1%

Variables number

Complexity of the

structure

exp(sqrt(sqrt(5.1154277799651 * sqrt(exp(5.1154277799651 +

6.8138162791729) + (5.1154277799651 * sqrt(exp(5.1154277799651 +

6.8138162791729)) + (Frec_Hz + exp(6.59457715693861) +

exp(6.59457715693861))))))) + Frec_Hz

0,15%

exp(6.75399861298501) + sqrt(Frec_Hz)

0,22%

5.8022110722959 * Thp_Psi

0,46%

Pwf_Psi * 1.35906734503806

0,46%

9.91066501475871 + sqrt(sqrt(sqrt(exp(Frec_Hz)))) +

9.91066501475871

0,63%

Developing a Mathematical Model of Oil Production in a Well That Uses an Electric Submersible Pumping System

235

Table 5: Best mathematical models, based on the error, number of variables and complexity.

RGP Mathematical models

Error

Complexity of the structure

Variables

exp(sqrt(sqrt(5.1154277799651 * sqrt(exp(5.1154277799651 +

6.8138162791729) + (5.1154277799651 * sqrt(exp(5.1154277799651 +

6.8138162791729)) + (Frec_Hz + exp(6.59457715693861) +

exp(6.59457715693861))))))) + Frec_Hz

0.15%

High

Frec

Frec_Hz + (Thp_Psi + Pwf_Psi + sqrt(Pwf_Psi))

0.36%

Low

Frec, Thp, Pwf

5 CONCLUSIONS

SAi2P is a closed loop of data analytical tasks, which

allow integrating different analytical tasks in order to

give an intelligent supervision of an oil process. This

framework requires of complex data analytical task in

order to improve the production process. In this

paper, we have studied one of them, to determine the

model of production of a well, in order to define the

model of optimization of its production.

Genetic Programming has been the intelligent

technique used, and it has been an appropriated

approach to get the mathematical model from data of

the process. We have carried out different tests, with

different data, in order to analyse different criteria

about the mathematical equations obtained. These

criteria were the error, number of variables and

complexity of the expression.

The mathematical models obtained are very

interesting, because their quality are very different,

according to the criteria used. Additionally, some of

the models obtained can be used in the context of fault

detection, because they can follow the normal

behaviour of our system. When the real system

change its behaviour due to a failure, a detection

system based on our mathematical equations can

detect it (Araujo et al. 2003).

With respect to previous works, in the literature

(Patelli, 2011), (Cerrada et al., 2001) have been

proposed several approaches for the identification

problem using genetic programming. The main

differences with our approach, it is that our approach

can be used in real time, and it forms part of SAi2P,

an autonomic loop of data analytical tasks that allows

the intelligent supervision of an oil process.

ACKNOWLEDGMENT

Dr. Aguilar has been partially supported by the

Prometeo Project of the Ministry of Higher

Education, Science, Technology and Innovation

(SENESCYT) of the Republic of Ecuador.

REFERENCES

Aguilar, J. and Rivas, F. (2001) Introducción a las Técnicas

de Computación Inteligente, Meritec.

Aguilar J. Buendia O., Moreno K., Mosquera D. (2016)

Autonomous Cycle of Data Analysis Tasks for Learning

Processes, Technologies and Innovation (R. Valencia-

García, et al., Eds.), Communications Computer and

Information Science Series, Vol. 658, Springer, pp.

187-202.

Araujo, M. Aponte, H. and Aguilar J. (2003) “Fault

Detection System in Gas Lift Well based on Artificial

Immune System”. Proceeding of the International Joint

Conference on Neural Networks, pp. 1673-1677.

Baieli, L. Daparo, D. and Pereyra, M (2006) “Experiencia

con bombas electro sumergibles de bajo caudal”, Wood

Group ESP. Argentina.

Bermúdez, F. Carvajal, G Moricca, G. Dhar, J. and Adam

F. (2014) “Fuzzy Logic Applications to Monitor and

Predict Unexpected Behavior in Electric Submersible

Pump. Society Petroleum Engineers”. SPE-167820-

MS.

Camargo, E. and Aguilar, J. (2014) “Advanced Supervision

of Oil Wells based on soft computing Techniques”,

Journal of Artificial Intelligence and soft computing

research, Vol 4. Number 3, 215-225.

Camargo, E. and Aguilar, J. (2014) “Hybrid Intelligent

Supervision Model of Oil Wells”, Proceedings of the

IEEE World Congress on Computational Intelligence

(IEEE WCCI), pp. 934 – 939.

Cerrada M., and Aguilar, J. (2001) “Genetic Programming-

Based Approach for System Identification”, Advances

in Fuzzy Systems and Evolutionary Computation,

Artificial Intelligence (Ed. N. Mastorakis), World

Scientific and Engineering Society Press, pp. 329-334.

Flasch, O., Mersmann, O.,and Bartz-Beielstein, T. (2010).

“RGP: An open source genetic programming system for

the R environment”, In Proceedings of the 12th annual

conference companion on Genetic and evolutionary

computation (pp. 2071-2072). ACM.

Iba H., deGaris H., Sato M., (1995). A Numerical Approach

to Genetic Programming for System Identification.

Evolutionary Computation, 3 (4): 417-452.

Kötzing T., Neumann F., Spöhel R. (2011). PAC Learning

and Genetic Programming, Genetic and Evolutionary

Computation Conference.

Langdon, W. B., and Poli, R. (2013). Foundations of

genetic programming. Springer Science & Business

Media.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

236

Lozada H., Aguilar J., Camargo E. (2017) “Sistema

Autonómico Inteligente Para Procesos Petroleros

(SAi2P)”, submitted to publication, Latin American

Journal of Computing.

Madar J., Abonyi J., Szeifert F., (2005). Genetic

Programming for the Identification of Nonlinear Input-

Output, Industrial & Engineering Chemistry Research,

44 (9), 3178–3186.

Osman, O. Shalaby, S. Elayouty. E. and Soleiman, M.

(2005) “Production Data Analysis for Electric

Submersible Pumping (ESP) well” In Proceedings of

Offshore Mediterranean Conference.

Patelli A. (2011). Genetic Programming Techniques for

Nonlinear Systems Identification, Ed. Politehnium.

Poli, R. (2010). “Genetic programming theory”.

In Proceedings of the 12th annual conference

companion on Genetic and evolutionary

computation (pp. 2473-2502). ACM.

Ramírez, M. (2004) “Bombeo Electrosumergible: Análisis,

Diseño, Optimización y Trouble Shooting. Technical

Report”, ESP OIL Maturín. Monagas.Venezuela.

Ronning, R (2011) “Automatic Start-up and Control of

Artificially Lifted Wells, Technical Report”,

Norwegian University of Science and Technology.

Department of Engineering Cybernetics.

Witczak M., Obuchowicz A. KorbiczWitczak J. (2002).

Genetic programming based approaches to

identification and fault diagnosis of non-linear dynamic

systems. International Journal of Control 75(13): 1012-

1031.

Developing a Mathematical Model of Oil Production in a Well That Uses an Electric Submersible Pumping System

237