Blind Decision Feedback Equalizer for Holographic Versatile Disc

Kyuhwan Kim, Seung Hun Kim, Gyogwon Koo, Min Seok Seo and Sang Woo Kim

Department of Electrical Engineering, Pohang University of Science and Technology, 77 Cheongam-Ro, Pohang, Korea

Keywords:

Holographic Data Storage (HDS), Holographic Versatile Disc (HVD), European Standard, Blind Equalizer,

Decision Feedback Equalizer (DFE).

Abstract:

As the amount of data increases, holographic data storage (HDS) is considered as a next generation storage

medium. Since HDS uses two-dimensional (2D) data, it causes intersymbol interference (ISI) between adja-

cent pixels not only in the horizontal direction but also in the vertical direction. Thus, studies have been car-

ried out to reduce such 2D ISI, and especially many researches using the partial response maximum likelihood

(PRML) method have been carried out. These PRML methods have good bit-error-rate (BER) performance,

but also have various disadvantages. Therefore, we propose a simple blind decision feedback equalizer (blind

DFE) that does not use soft output Viterbi algorithm (SOVA) for application to European standard holographic

versatile disc (HVD). First, we propose a blind equalizer using simle theshold method to get information that

the equalizer can refer to. In order to make it work well in any environment, the threshold value is adaptively

determined using the statistical characteristics of the received image. And, in order to reduce errors due to the

data that cannot be distinguished only by the blind equalizer, we add a decision feedback loop after the blind

equalizer. Finally, various simulations were conducted to conﬁrm the performance of blind DFE for HVD.

1 INTRODUCTION

As the amount of data increases, holographic data

storage (HDS) is considered as a next generation stor-

age medium. Unlike other optical disks, HDS uses

holographic images to store two-dimensional (2D)

data pages on a holographic versatile disc (HVD). The

European standard for HVD was proposed in 2007

(ECMA, 2007a; ECMA, 2007b).

Since HDS uses 2D data, it causes intersymbol in-

terference (ISI) between adjacent pixels not only in

the horizontal direction but also in the vertical direc-

tion. This 2D ISI has a lot of impact on the perfor-

mance of HDS, and many studies are going on to re-

duce it. The most studied methods to reduce 2D ISI

in HDS is the partial response maximum likelihood

(PRML) method using soft output Viterbi algorithm

(SOVA) (Kim and Lee, 2009; Koo et al., 2012; Koo

et al., 2013; Koo et al., 2014). These PRML methods

have good bit-error-rate (BER) performance, but also

have various disadvantages.

There are a few problems that arise from the use

of SOVA. In order to improve BER performance, the

PRML methods use SOVA (Hagenauer and Hoeher,

1989) based on Viterbi decoder (Viterbi, 1967) as

maximum likelihood (ML) method. The ﬁrst problem

is that this Viterbi algorithm requires a lot of com-

putation because all Viterbi paths need to be investi-

gated. Especially, since the Viterbi algorithm needs

to be applied in two dimensions in order to apply it to

the HDS, much more computational complexity is re-

quired than the Viterbi decoder used in the ﬁeld of

communications. In (Koo et al., 2012; Koo et al.,

2013; Koo et al., 2014), many studies have been done

to reduce the computational complexity of 2D SOVA

while improving performance, but it is still a problem

to have a large amount of computation as SOVA is

used.

The second problem that arises from using 2D

SOVA is that it does not work with European standard

code. In the European standard, in order to reduce the

error rate of a symbol, if a certain pixel has a value of

1, the adjacent pixels can not have a value of 1 in a 4-

by-4 (4 ×4) symbol. That is, only three pixels of the

sixteen pixels have a value of one and the remaining

pixels have a zero value. However, the Viterbi de-

coder basically assumes that all messages are equally

probable (Viterbi, 1967). Therefore, if the European

standard code is used, SOVA will not work properly

because the probability of 0 and 1 is different.

The last problem with using the PRML method is

that a training sequence is necessary. Using training

468

Kim, K., Kim, S., Koo, G., Seo, M. and Kim, S.

Blind Decision Feedback Equalizer for Holographic Versatile Disc.

DOI: 10.5220/0006425004680473

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 468-473

ISBN: 978-989-758-263-9

sequences can not make use of that much data, and

because the equlizer is trained to a speciﬁc environ-

ment, performance degrades when the environment

changes. Therefore, in order to increase the data rate

and robustness to various environments, blind equal-

izer that do not require training sequences have to be

developed and used as in the ﬁeld of communications.

However, since the PRML method uses a training

equalizer that requires a training sequence, the data

rate is lowered, and when the channel environment is

changed, the performance may be degraded.

Therefore, we propose a simple blind equalizer

that does not use SOVA for application to European

standard HVD. The remaining paper is organized as

follows. Section 2 explains the background HVD

channel model, and a simple form of blind eualizer

is proposed in Section 3. In order to compensate

for the performance of the blind equalizer, Section 4

describes a decision feedback equalizer (DFE), and

several simulation results will be represented in Sec-

tion 5. Finally, we will conclude and discuss the re-

sults in Section 6.

2 HVD CHANNEL MODEL

In HVD, using spatial light modulator (SLM), the in-

put data page, d[x, y], is encoded to the holographic

medium along the reference laser beam (Vadde and

Kumar, 1999). When reading the stored data page,

the data page is displayed in the form of a hologram

using the same reference beam and read by a charge-

coupled device (CCD). In this process, the data page

suffers blur effect (2D ISI), noise and misalignment.

In this channel environment, blur effect and misalign-

ment are modelled as point spread function (PSF) and

noise is modelled as additive white Gaussian noise

(AWGN) (Vadde and Kumar, 1999; Keskinoz and Ku-

mar, 2000).

The continuous PSF is expressed by

h(x, y) =

sinc



x −m

y −m



(1)

where A is the signal ampliﬁer, σ

is the blur grade,

and m

are the misalignments in the horizontal

and vertical directions, respectively. In this paper A is

set to

√

2. And the discrete PSF is given by

h[x, y] =

y−

x−

h(x

, y

)dx

(2)

where α(0 < α ≤ 1) is a linear ﬁll factor of the CCD

pixels. In this paper, we used 1 as α.

As mentioned earlier, channel noise n[x, y] is mod-

elled as AWGN. And the channel signal-to-noise ratio

(SNR) is deﬁned as follows:

SNR = 10log





(3)

where σ

is the AWGN power.

Therefore, the image detected by the CCD sensor

r[x , y] is obtained as follows:

r[x , y] = d[x,y] ⊗h[x, y] + n[x, y] (4)

where ⊗is a 2D convolution operator. Figure 1 shows

the block diagram of this channel model.

Figure 1: Block diagram of channel model.

3 BLIND EQUALIZER

The image obtained by the CCD sensor passes

through a 2D equalizer to eliminate the 2D ISI, and

the equalizer output z[x, y] is as follows:

z[x, y] = r[x, y]⊗C[x, y] (5)

where C[x, y] is the array of equalizer coefﬁcient

which are adaptively updated using the error.

Figure 2 represents the structure of a conventional

2D training equalizer. When the training sequence

is used in the PRML method, the sequence passes

through partial response (PR) target to perform en-

coding for the ML scheme.

Figure 2: Structure of conventional 2D equalizer.

As mentioned earlier, the use of training equalizer re-

duces the data rate because it requires a training se-

quence, and because it is trained to a speciﬁc environ-

ment, it becomes vulnerable to various environmental

changes. Thus, it is necessary to develop and use a

blind equalizer. However, the blind equalizers used in

the ﬁeld of communications, such as constant modu-

lus algorithm (CMA) (Sato, 1975) and multi-modulus

algorithm (Yang et al., 2002), are not applicable to

Blind Decision Feedback Equalizer for Holographic Versatile Disc

469

HVD. This is because the blind equalizers in the ﬁeld

of communications match the norm of complex sym-

bol to a speciﬁc value, but the data of HVD is com-

posed of binary pixel arrays. Therefore, we propose a

simple blind equalizer for HVD which has a different

mechanism from that in the ﬁeld of communications.

Although it is not possible to match the equalizer

output to a speciﬁc value as in the ﬁeld of communi-

cations, some information from the received image is

necessary to update the equalizer. So we used simple

threshold method to get information that the equalizer

can refer to. Figure 3 depicts the structure of proposed

blind equalizer.

Figure 3: Structure of proposed blind equalizer.

To make the threshold method work well, it is impor-

tant to set the threshold value well. Thus, in order

to make it work well in any environment, the thresh-

old value is adaptively determined using the statistical

characteristics of the received image, not simply using

the mean value.

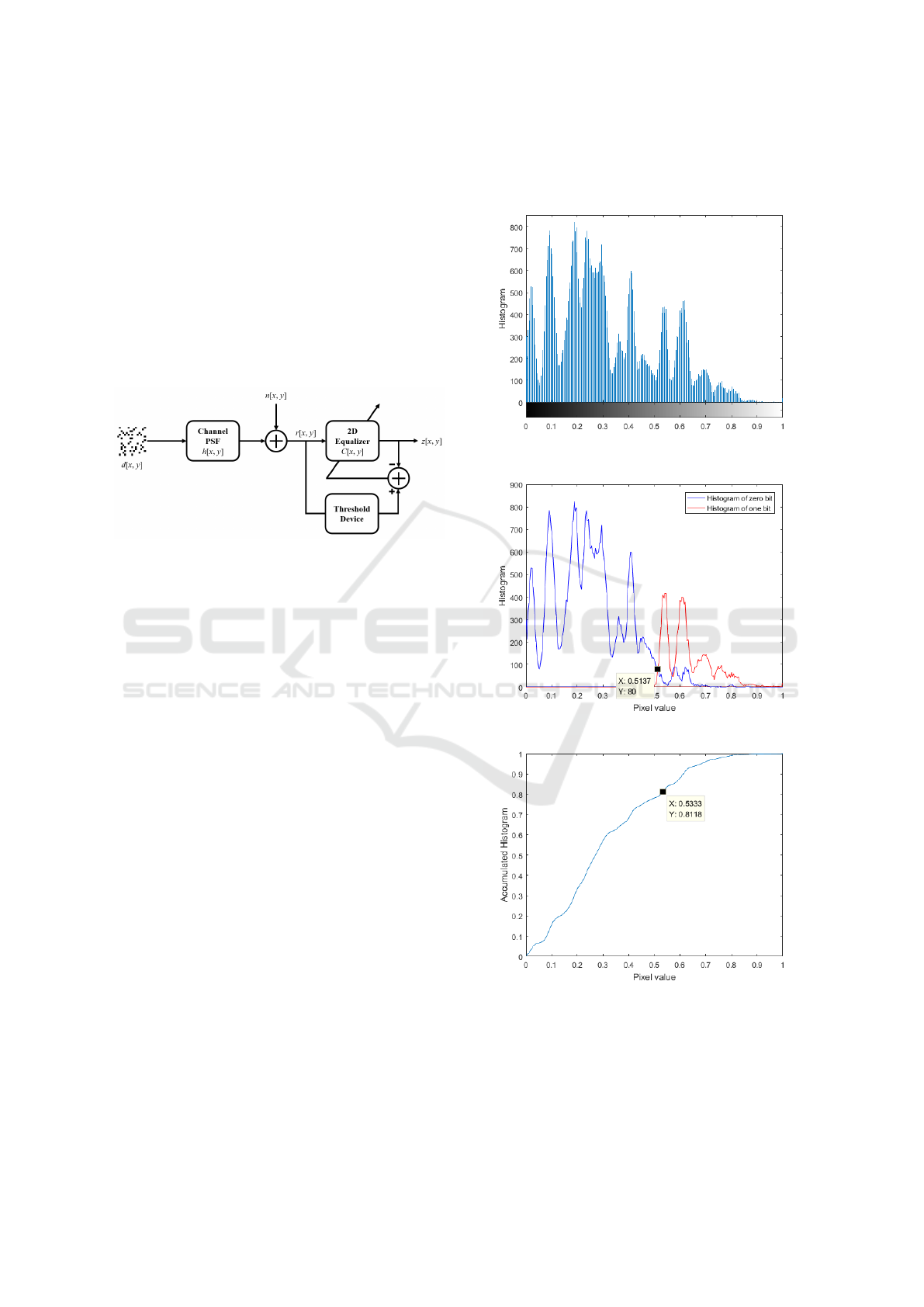
Figure 4 shows the statistical characteristics of the

received images when using the European standard.

Figure 4 (a) represents the histogram of total received

image, and dividing this into a 0-bit histogram and 1-

bit histogram, the results graph is shown in Figure 4

(b). From this graph, we can determine which value

should be set to the threshold value to distinguish be-

tween 0 and 1 well. (In this case, the pixel value of

0.5137 is set as the threshold value because it can

distinguish between 0 and 1 well.) Figure 4 (c) de-

picts accumulative histogram of total received image.

In the European standard, since there are 13 zeros in

one symbol, it can be seen that 0 and 1 can be dis-

tinguished by setting the pixel value having the value

corresponding to 13/16 in the accumulative histogram

as the threshold value. In this case, the pixel value

of 0.5333 having the accumulative histogram value

of 0.8118 closest to 0.8125 corresponding to 13/16

in the accumulative histogram is set as the threshold

value. This threshold value is good enough to dis-

tinguish between 0 and 1 in the present environment.

Using this scheme, it is possible to ﬁnd the optimal

threshold value to distinguish between 0 and 1, even

if the statistical characteristics of the received image

change due to environmental changes. And the out-

put from the proposed equalizer is ﬁnally determined

to be 0 or 1.

(a)

(b)

(c)

Figure 4: (a) Histogram of total received image, (b) his-

togram of zero bit and one bit , (c) accumulative histogram

of total received image.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

470

4 BLIND DECISION FEEDBACK

EQUALIZER

We have previously proposed a simple and efﬁcient

blind equalizer for HVD. However, as shown in Fig-

ure 4 (b), there is a little probability of error occur-

rence when only the blind equalizer using this thresh-

old method is used. Thus, in order to reduce errors

due to the data that cannot be distinguished only by

the blind equalizer, we propose a blind decision feed-

back equalizer (blind DFE) by adding a decision feed-

back loop after the blind equalizer.

The DFE has also been proposed in the ﬁeld of

communications (George et al., 1971). Assuming that

previously determined values are correct, the DFE

basically attempts to obtain a more accurate output

by eliminating the inﬂuence of previously determined

values on later values, i.e. ISI. Figure 5 shows the

structure of the DFE. As shown in the ﬁgure, the DFE

in the ﬁeld of communications updates both feedfor-

ward ﬁlter (FFF), which acts as the equalizer, and

feedback ﬁlter (FBF) in the feedback loop using the

difference between

d[x] and d[x].

Figure 5: Structure of DFE.

This DFE has the advantage of obtaining accurate out-

put on the assumption that the decisions are correct,

but it is difﬁcult to apply to HVD. In the ﬁeld of com-

munications, DFE effectively eliminates ISI by using

1D FBF for 1D FFF. However, in HVD, when using

2D FBF for 2D equalizer, it is ambiguous to accu-

rately deﬁne and use the inﬂuence of the previously

determined value. Thus, a simple form of DFE with-

out FBF for HDS has been proposed (Marrow and

Wolf, 2003). This simple DFE uses decision feedback

in the row or column direction instead of using the 2D

FBF. It also implies that when the detection process

proceeds in the lower right direction, the pixel to be

detected is much affected by the upper pixel and the

left pixel.

Considering these characteristics, we propose a

blind DFE for HVD. Figure 6 represents the structure

of the blind DFE. In the feedback loop, z

−1

and z

−1

are unit delay operator in the horizontal and vertical

directions, respectively, and K is the scalar multiply-

ing operator.

This blind DFE can be divided into two parts. The

front part is the blind equalizer part and the rear part

Figure 6: Structure of proposed blind DFE.

is the decision feedback part. As explained in the pre-

vious section, in the blind equalizer part, the equalizer

is updated by comparing the reference data created by

the threshold method with the output of the equalizer,

not with the result obtained by subtracting the deci-

sion feedback like the DFE in the ﬁeld of communi-

cations. In the decision feedback part, the ISI due to

the already determined symbol is removed by feed-

ing back the value obtained by multiplying the deter-

mined upper or left pixel values and an appropriate

scalar.

In contrast to the conventional DFE, in which

the equalizer part and the decision feedback part are

coupled together to improve the performance of the

equalizer, the blind DFE for HVD is divided into

the equalizer part and the decision feedback part,

and each part performs their respective roles. In the

equalizer part, even if there is some error due to ISI,

the data page is roughly restored using the threshold

method. In the latter part of the decision feedback,

it helps to get more accurate results before the ﬁnal

decision by eliminating the errors due to ISI, that are

missed by the blind equalizer.

5 SIMULATION RESULTS

5.1 Simulation Setting

Various BER simulations were conducted to conﬁrm

the performance of blind DFE for HVD, because the

data rate and robustness increase with increasing BER

in the HDS. In all simulations performed in this paper,

we simulated 256 ×256 data pages which have simi-

lar size to the European standard. And all data pages

are encoded according to European standard codes

(ECMA, 2007a; ECMA, 2007b). The HVD channel

model is assumed to be a discrete PSF of size 5 ×5,

and thus an equalizer with a 5 ×5 size coefﬁcient is

used. The step size used for updating the equalizer is

set to a value of 0.01. The value of scalar K multi-

plied when the decision feedback was used as 0.1 to

reﬂect the ISI phenomenon of HVD. All BER values

resulting from the simulation are the ensemble aver-

ages of simulated results of 100 data pages in each

environment.

Blind Decision Feedback Equalizer for Holographic Versatile Disc

471

5.2 SNR Simulation

First, we simulated the performance of the blind

equalizer for noise. Simulations were performed for

various SNRs in an environment with a blur grade of

1.8 and a misalignment of 5 % in the channel model.

Figure 7 shows the BER performance to the noise. As

can be easily expected, when SNR becomes larger,

BER becomes smaller, and the blind DFE has better

performance than the blind equalizer. But, the inﬂu-

ence of the SNR on the HVD channel model is rela-

tively small, so that the BER variation due to the SNR

change is not so severe. In the case of the blind equal-

izer, when the SNR is 20 or more, the BER is smaller

than 10

−3

, so the data page can be perfectly recon-

structed using an error correction code (ECC). On the

other hand, when the SNR is less than 20, the BER is

larger than 10

−3

, so there is a possibility that the re-

construction rate will fall. However, in the case of the

blind DFE, the BER is much smaller than the blind

equalizer. And, as long as the SNR is not too small,

the BER is less than 10

−3

, which makes it possible to

restore the data page completely using ECC.

Figure 7: BER performance to the noise.

5.3 Blur Grade Simulation

Secondly, we simulated the performance of a blind

equalizer for blur grade. Simulations were performed

for varying blur grade in an environment with a SNR

of 20 dB and a misalignment of 5 %. Figure 8 rep-

resents the BER performance to the blur grade. As

can be easily expected, the BER increases as the blur

grade increases, and the performance of the blind

DFE is better than the blind equalizer. Also, since

the blur grade has a large inﬂuence on the HVD chan-

nel model, it can be seen that the change of blur grade

make the BER change a lot. Thus, if the blur grade

becomes smaller than 1.7 for the blind equalizer and

1.8 for the blind DFE, the equalizer will restore the

data page completely and the number of errors will be

zero. Conversely, if the blur grade increases to about

2, the BER may become larger than 10

−3

, which may

result in a decrease in the reconstruction rate of the

data page.

Figure 8: BER performance to the blur grade.

5.4 Misalignment Simulation

Finally, we simulated the performance of a blind

equalizer for misalignment. Simulations were per-

formed for various misalignments in an environment

with a SNR of 20 dB and a blur grade of 1.8. Fig-

ure 9 depicts the BER performance to the misalign-

ment. Also, if the misalignment increases, the BER

increases too, and the blind DFE has better perfor-

mance than the blind equalizer. Similar to the blur

grade, larger misalignment can have a catastrophic ef-

fect on the performance of the blind equalizer, but

there is little chance of misalignment greater than

10 % in the HVD due to sync patterns. Thus, un-

der the assumption that the misalignment is less than

10 %, it is not easy to have a fatal impact on the BER

performance.

6 CONCLUSIONS

In this paper, we propose the blind DFE for HVD. The

development of the blind DFE has proceeded in two

stages.

The ﬁrst approach was to develop a blind equal-

izer for HVD. Because HVD data is structurally difﬁ-

cult to match the norm value of a symbol to a speciﬁc

value, as in the ﬁeld of communications, it was nec-

essary to design a blind equalizer in a different way

from the ﬁeld of communications. However, since it

is necessary to have information that can be referred

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

472

Figure 9: BER performance to the misalignment.

to by the equalizer, a simple threshold method is used

to generate information to be referred to by the equal-

izer, and the equalizer is updated using the informa-

tion. In addition, the threshold value is determined by

analysing the statistical characteristics of the received

image, rather than simply using the average value, and

thus the same performance can be maintained even

when the environment is changed.

The second step is to add a decision feedback loop

behind the equalizer in order to compensate for the

blind equalizer that may cause errors. In the ﬁeld of

communications, the DFE updated both the equalizer,

which act as FFF, and the FBF by comparing the value

obtained by subtracting the decision feedback from

the equalizer output to the training sequence. How-

ever, since it is structurally difﬁcult to implement a 2D

FBF in HVD, a decision feedback loop is constructed

by multiplying the upper and left pixel values, which

have the greatest effect on the current pixel, by an ap-

propriate scalar value.

Although the blind DFE which consists of two

parts does not perform the entire equalization process

at the same time as the DFE in the ﬁeld of communi-

cations, the data page is roughly restored in the equal-

izer part even if there is a slight error caused by the

ISI, and the effects of errors due to ISI are eliminated

in the decision feedback part. As a result, the two

parts combine to create the blind DFE for HVD, that

effectively removes ISI and performs well.

ACKNOWLEDGEMENTS

This research was supported by Basic Science

Research Program through the National Research

Foundation of Korea (NRF) funded by the Min-

istry of Education, Science and Technology (NRF-

2015R1D1A1A09059377).

REFERENCES

ECMA (2007a). Information Interchange on Holographic

Versatile Disc (HVD) Recordable Cartridges Capac-

ity: 200 Gbytes per Cartridge. ECMA International,

Geneva, 1st edition.

ECMA (2007b). Information Interchange on Read-Only

Memory Holographic Versatile Disc (HVD-ROM)

Capacity: 100 Gbytes per disk. ECMA International,

Geneva, 1st edition.

George, D. A., Bowen, R. R., and Storey, J. R. (1971). An

adaptive decision feedback equalizer. IEEE Transac-

tions on Communication Technology, COM-19.

Hagenauer, J. and Hoeher, P. (1989). A viterbi algorithm

with soft-decision outputs and its applications. In

Global Telecommunications Conference and Exhibi-

tion ’Communications Technology for the 1990s and

Beyond’ (GLOBECOM). IEEE.

Keskinoz, M. and Kumar, B. V. K. V. (2000). Efﬁcient mod-

eling of volume holographic storage channels (vhsc).

In Optical Data Storage. IEEE.

Kim, J. and Lee, J. (2009). Partial response maximum like-

lihood detections using two-dimensional soft output

viterbi algorithm with two-dimensional equalizer for

holographic data storage. Japanese Journal of Applied

Physics, 48.

Koo, K., Kim, S., Jeong, J., and Kim, S. (2013). Two-

dimensional soft output viterbi algorithm with a vari-

able reliability factor for holographic data storage.

Japanese Journal of Applied Physics, 52.

Koo, K., Kim, S., Jeong, J., and Kim, S. (2014). Data page

reconstruction method based on two-dimensional soft

output viterbi algorithm with self reference for holo-

graphic data storage. Optical Review, 21.

Koo, K., Kim, S., and Kim, S. (2012). Modiﬁed two-

dimensional soft output viterbi algorithm with two-

dimensional partial response target for holographic

data storage. Japanese Journal of Applied Physics,

51.

Marrow, M. and Wolf, J. K. (2003). Iterative detection of

2-dimensional isi channels. In Information Theory

Workshop. IEEE.

Sato, Y. (1975). A method of self-recovering equalization

for multilevel amplitude-modulation systems. IEEE

Transactions on Communications, 23.

Vadde, V. and Kumar, B. V. K. V. (1999). Channel model-

ing and estimation for intrapage equalization in pixel-

matched volume holographic data storage. Applied

Optics, 38.

Viterbi, A. J. (1967). Error bounds for convolutional codes

and an asymptotically optimum decoding algorithm.

IEEE Transactions on Information Theory, IT-13.

Yang, J., Werner, J. J., and Dumont, G. A. (2002). The

multimodulus blind equalization and its generalized

algorithms. IEEE Journal on Selected Areas in Com-

munications, 20.

Blind Decision Feedback Equalizer for Holographic Versatile Disc

473