
A Sliding-Mode Controller from a Reduced System Model: Ball and
Plate System Experimental Application
Luis Morales, Oscar Camacho, Paulo Leica and Danilo Chávez
Departamento de Automatización y Control Industrial, Escuela Politécnica Nacional Ladrón de Guevara,
E11-253, Quito, Ecuador
Keywords: Ball-Plate System, Sliding-Mode Control, PID Controller, Stabilization, Reduced System Model.
Abstract: The purpose of this work is to design a Sliding-Mode Control from a reduced system model using a PID as
sliding surface. The controller is applied to a Ball and Plate system which has extremely non-linear
characteristics and therefore does not have a unique solution in terms of ball stabilization control. The results
are obtained by simulations and with real experiments in the implemented system. A comparative performance
analysis is done between the proposed approach and a PID controller to stabilize the ball at fixed points of the
plate.
1 INTRODUCTION
The Ball and Plate system is an extension of the ball-
beam system, which has 2 degrees of freedom and
due to its non-linear characteristics has generated
interest in the study and analysis of classic, modern
and non-linear controllers that respond adequately to
the dynamics of the system, which is extremely
unstable since, in open loop small plate inclinations
cause indefinite displacement of the ball.
The system has two actuators that allow to vary
the inclination of the plate to stabilize the ball or to
track paths. Stabilization means keeping the ball in a
desired position and following path demands making
the ball follow a geometric pattern regardless of time.
The system modeling is obtained easily (Nokhbeh
and Khashabi, 2011), therefore, different works has
focused on analyzing the response of controllers in
order to stabilize the ball on the platform (Bay and
Rasmussen, 2016); the high nonlinearity of the
system implies that there is no a unique satisfactory
solution.
Several experiments have been developed in order
to control the system; The typical experiment is with
the classic PID controller. (Ali and Aphiratsakun,
2016), whose parameters tuning is done through
methods such as Ziegler-Nichols, Tyreus-Luyben and
heuristic (Aphiratsakun and Otaryan, 2015). It is not
necessary to know the mathematical model of the
plant to determine best controller tunings Kp, Ki and
Kd, to stabilize the ball on the plate in the shortest
time as possible, and reducing oscillations. In
(Knuplei et al., 2003), a lead controller is proposed,
however, the controller does not present good results
since there is a considerable error in steady state.
Nonlinear controllers based on Lyapunov´s stability
(Wang et al., 2008) have been tested in the platform
with different frictions and it is evidenced that this
parameter affects the performance of the controller
considerably.
Fuzzy controllers are applied in (Fan et al., 2004),
with the purpose of moving the ball through the track
of a path, taking the ball from point A to point B
without crashing obstacles on the plate.
Sliding-Mode Control (SMC) is also used for
stabilization control, the results of (Debono and
Bugeja, 2015) evidence an improvement in the
system response, however the controller employs
complex trigonometric calculations (Valadez et al.,
2014).
Due to robustness of SMC, it can attenuate the
uncertainty in the measurement of the ball’s position,
and it allows to stabilize the ball in less time and with
fewer oscillations. Previous works have shown an
important amount of results in stabilization tasks for
the ball and plate system using PID and SMC
controllers. Different to those papers, the purpose of
this work is to design a Sliding-Mode Control from a
reduced system model using a PID as sliding surface.
The resulting controller is simple and robust
without complex calculations reducing computational
590
Morales, L., Camacho, O., Leica, P. and Chávez, D.
A Sliding-Mode Controller from a Reduced System Model: Ball and Plate System Experimental Application.
DOI: 10.5220/0006425905900597
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 590-597
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

cost and easy implementation (Camacho and Smith,
2000). The results are obtained by simulations and
with real experiments in the implemented system. A
comparative performance analysis is done between
the proposed approach and a PID controller to
stabilize the ball at some fixed points of the plate.
This paper is organized as follows. Section 2
briefly presents the mathematical model of the plant.
Section 3, presents some basic concepts of the SMC
method and its design. Section 4, the simulation and
experimental tests are presented and a comparison is
made between the performance of the conventional
PID and the SMC with the PID sliding surface.
Section 5, presents the conclusions of the work.
2 MATHEMATICAL MODEL
2.1 Ball and Plate System
The ball and plate system consists of a rigid platform,
in which the ball rolls, two servo motors (actuators)
that allow to vary the inclination angles, a camera that
allows feedback the system with the position of the
ball in the X and Y axes, and the control system as
shown in Figure 1.
Figure 1: Schematic diagram of the ball and plate system.
In Figure 1, α is the angle of the plate in X-axis, β
is the angle of Y-axis, u
x
and u
y
are control actions
applied to actuators for X-axis and Y-axis
respectively.
The plant has been designed, built and
implemented in the Laboratory of Automatic Control
at Escuela Politécnica Nacional. The platform has a
glass surface to minimize friction and to be able to
despise the frictional forces and simplify model
calculation and is controlled by two servo motors to
adjust the inclination of the X-axis and the Y-axis.
The plant has a camera with a resolution of 640x640
pixels that acquires images at a 30 fps to determine
the position of the ball and feedback the control loop
(Figure 2). Image processing has algorithms for ball
detection, and has implemented a Kalman Filter for
noise elimination (Cedeño and Gordón, 2016).
Figure 2: Experimental Ball and Plate System.
2.2 Mathematical Model
The mathematical model of the plant shown in
Figure.2., neglecting the surface friction and applying
the Lagrange method (Fan et al., 2004) is:
0
(1)
0
(2)
Table 1, presents the description of the parameters
of equations (1) and (2).
Table 1: Parameters of the mathematical model.
Parameters of Ball and Plate S
y
stem
Symbol Units Description
kg Mass of the ball
kg cm
2
Moment of inertia of the ball
cm Radius of the ball
cm Position of the ball in the X-axis
cm Position of the ball in the Y-axis
ra
d
Angle of the plate from X-axis
ra
d
Angle of the plate from Y-axis
kg m/s
2
Acceleration due to gravity
A Sliding-Mode Controller from a Reduced System Model: Ball and Plate System Experimental Application
591

2.3 Reduced System Model
Considering small angle of inclination of the plate
(±8° = ±0.139 rad), this movement is slow to stabilize
the ball on the plate, therefore: ≅0,
≅0
(Nokhbeh and Khashabi, 2011), thus is obtained:
(3)
(4)
2.3.1 Linearized Model
Linearizing equations (3) and (4) by Taylor Series at
the operating point 0,
̅
0 when the platform
is in horizontal position and keeps the ball in
equilibrium, the following equations were obtained:
(5)
(6)
Considering the gravity 980
, and
moment of inertia of a solid ball
:
700
(7)
700 (8)
Plate´s angles and actuators’ rotation angles are
related by the following equations:
10
(9)
10
(10)
Where:
,
are the rotation angles of the
servomotors. Substituting (9) and (10) in (7) and (8)
respectively gives:
70
(11)
70
(12)
Laplace transform of the model is calculated:
70
(13)
70
(14)
Where:
, are the positions of the ball in the
X-axis and Y-axis respectively, and
,
are
the rotation angles of servo motors of the plant.
3 CONTROLLER’S DESIGN
This work proposes two methods to stabilize the ball
on a desired position of the plate: the PID controller
and the SMC method with sliding surface PID, to
finally compare its performance.
3.1 PID Controller
To stabilize the ball on a plate position two
independent controllers have been designed, one for
X-axis and another for Y-axis of similar
characteristics due to the symmetry of the system.
Heuristically calibrates the parameters of the
controller in the real plant starting from the values
given by the auto-tuning method of a computational
software until obtaining the lowest ISE, index used to
measure the performance of controllers (Kealy and
O’dwyer, 2003) and defined for a period of time as
shown in (15).
(15)
Where: 20 (time of the experiment),
, is
the error between reference and output in the X-axis,
establishing the constant values for the controllers of
the X-axis and Y-axis 0.035, 0.018,
0.0001,
0.073.
3.2 Sliding-Mode Control
Sliding-Mode Control (SMC) is based off the idea of
variable structure control. One of the main
applications of the SMC method is non-linear systems
since robustness to uncertainty is indispensable in the
field of control systems. This method proposes to
define a surface along which the process can slide
until reaching a final value. Control law of SMC is:
(16)
U
c
is the continuous part of the control that allows to
stay on the sliding surface, and U
d
is the
discontinuous part of the control that allows to reach
the sliding surface. (Slotine and Li, 1991) proposes
the surface shows in (17):
(17)
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
592

Where: is the sliding surface, is the sliding
surface order and is the error.
3.3 SMC Method Design
The following procedure has been presented by
(Camacho and Smith, 2000), in which the
mathematical model of a PID controller is taken as
the sliding surface. The design of the controller for
the X-axis is presented, since the Y-axis has the same
characteristics due to the symmetry of the system.
The PID controller for X-axis is:
(18)
Comparing (17) for 2, with (18):
(19)
2
Then, is considered the PID as a sliding surface since
they have the same mathematical form.
(20)
Controller (16), for X-axis is:
(21)
is computed considering
0,
0:
0
(22)
Deriving error in X-axis the following is obtained:
(23)
Substituting (23) in (22), gives:
0
(24)
Substituting the model of the plant in X-axis (11) in
(24),
is computed:
70
(25)
Substituting (25) in (21), gives:
70
(26)
For the calculation of discontinues part
, is
analyzed Lyapunov´s stability.
Considering a Lyapunov function:
/2
(27)
Stability condition denotes that:
0
(28)
Substituting (24) in (28), gives:
70
0
(29)
Substituting (26) in (29) and simplifying, gives:
70
0
(30)
To perform the condition of (30) is proposed:
(31)
Discontinues part
incorporates a nonlinear
element that includes the switching element of the
control law. This part of the controller is
discontinuous across the sliding surface. (Camacho
and Smith, 2000), propose:
|
|
∴
0
(32)
Substituting (32) in (26), the control law is:
70
|
|
(33)
In (Camacho, 1996), is shown the derivatives of the
reference value can be discarded, without any effect
on the control performance, resulting a simpler
controller for X and Y axis:
70
|
|
(34)
70
(35)
Based on the Lyapunov’s stability analysis, these
controllers guaranteed
→0,
→0 when →∞.
Calibrating values
to obtain the lowest
index, experimentally is determined
0.93,
and 0.75 observing that this value eliminates the
chattering and produces an adequate response of the
system. These values were obtained for a step
A Sliding-Mode Controller from a Reduced System Model: Ball and Plate System Experimental Application
593

reference obtaining
0.065. The designed
controller scheme is shown in Figure. 4.
Figure 4: Proposed control scheme.
This section presents the comparison between
both controllers, first, by simulation, and finally the
experimental results are presented in the laboratory
plant shown in Figure. 2. To analyze the performance
of the controllers, measurement indexes are used.
4 RESULTS
4.1 Simulation Results
First, the ball stabilization test is performed at the
plate’s central point whose coordinate is (23 [cm], 23
[cm]), starting from the initial position (0 [cm], 0
[cm]). Figure 5, illustrates how perform each
controller. It shows the ball position on the X-axis vs.
time, the response on the Y-axis does not presented
since it is similar, in simulation cases.
Figure 5: Simulated ball position on the X-axis.
Results obtained for reaching a sequence of points
corresponding to the vertices of a square 20 [cm] per
side, are presented in Figures 6, 7 and 8, starting from
plate’s central point. Figure 6 and 7, show ball’s
position on X and Y-axis vs. time and Figure 8.,
shows the ball’s movement on the plate.
Figure 6: Simulated ball position on the X-axis.
Figure 7: Simulated ball position on the Y-axis.
Figure 8: Simulated movement of the ball on the plate to
reach the four square vertices.
SMC method allows to reach the desired position
smoother, faster and with lower overshot, since the
control action is not as abrupt as in PID controller.
Performance by index of the two controllers is
shown in Table 2. Settling time has been measured
once the system response is within a band of 5% of
the reference value.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
594

Table 2: Simulation controller’s comparison using
measurement parameters.
PERFORMANCE COMPARISON
INDEXES
ISE
Settling
time (s)
Overshoot
(%)
POINT
PID 0.041 4.0 25.3
SMC 0.036 3.2 18.0
Δ% 12.9% 22.2% 33.7%
SQUARE
VERTICES
PID 0.044 4.7 26.5
SMC 0.041 3.5 19.1
Δ% 7.0% 29.2% 32.4%
There is a considerable difference between the
measured indicators, the most representative is the
settling time and overshot, showing that designed
SMC allows to obtain better results than PID
controller for ball’s stabilizing.
4.2 Experimental Results
Experimental results are obtained using the real plant.
The ball stabilization test is performed at the central
point of the implemented system whose coordinate is
(23 [cm], 23 [cm]), from the position (0 [cm], 0 [cm]),
this is done for the X and Y-axis. Ball’s position is
shown in Figure. 9 and 10. In Figure. 11., ball’s
movement on the plate is shown.
Figure 9: Experimental ball position on the X-axis.
Figure 10: Experimental ball position on the Y-axis.
Figure 11: Experimental movement of the ball on the plate
to stabilize the ball at point (23 [cm], 23 [cm]).
Results obtained for reaching four vertices of a
square 20 [cm] starting from position (23 [cm], 23
[cm]) are presented in Figures. 12, 13 and 14.
SMC method reaches the reference points with a
better performance since its control action is less
abrupt as shown in Figure 15.
Figure 12: Experimental ball position on the X-axis.
Figure 13: Experimental ball position on the Y-axis.
The vibrations in the response of the system are
due to mechanical limitations since the plate is placed
on a central pivot axis.
A Sliding-Mode Controller from a Reduced System Model: Ball and Plate System Experimental Application
595
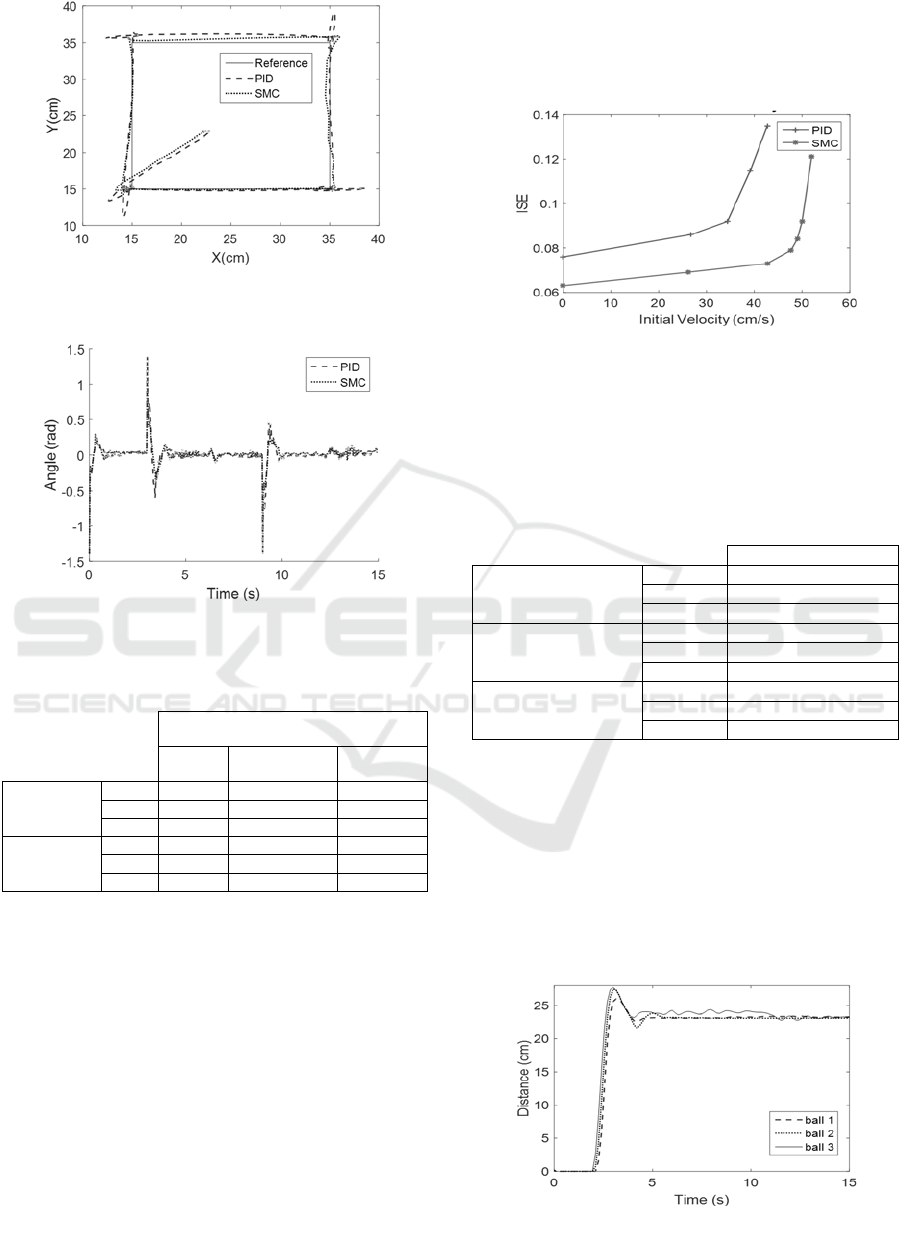
Figure 14: Experimental movement of the ball on the plate
to reach the four square vertices.
Figure 15: Control Action for X-axis.
Table 3: Experimental controller’s comparison using
measurement parameters.
PERFORMANCE COMPARISON
INDEXES
ISE
Settling time
(s)
Overshoot
(%)
POINT
PID 0.073 2.7 20.8
SMC 0.065 1.2 5.2
Δ% 11.6% 76.9% 120%
SQUARE
VERTICES
PID 0.096 2.3 23.7
SMC 0.082 1.1 9.5
Δ% 15.7% 70.5% 85.5%
The most representative values are the settling
time and the overshot, demonstrating that the SMC
approach allows to obtain better results in this system
in a high variation. It is also observed in the graphs
there is a delay in the action of the actuators of 0.4 [s]
which could be reduced with a dead time scheme
controller that improves the system response.
4.3 Robustness Analysis
The first robustness analysis of both controllers is
shown in Figure. 16., in which the ISE value can be
calculated by testing the ball stabilization at different
initial velocities before a step input. The maximum
initial velocity of the ball in the case of the PID is 42
[cm/s], a greater one becomes the system unstable,
while the SMC allows to reach the maximum velocity
of the ball of 52 [cm/s]. It is evident that the ISE is
lower for all cases with SMC method.
Figure 16: Robustness comparison between both
controllers.
Second robustness analysis was performed with
balls of different mass and radius determining the
of each controller as shown in the Table 4.
Table 4: Experimental controller’s comparison using
measurement parameters for different balls.
ISE
Ball 1
Mass = 129[g]
Radius = 17 [mm]
PID 0.074
SMC 0.064
Δ% 14.1%
BALL 2
Mass = 20 [g]
Radius = 13 [mm]
PID 0.063
SMC 0.052
Δ% 19.1%
BALL 3
Mass = 5 [g]
Radius = 8 [mm]
PID 0.082
SMC 0.070
Δ% 15.7%
Figures 17 and 18, show the behavior of the balls
in the X-axis with the PID controller and the SMC
approach respectively, evidencing that the proposal of
this work improves its stabilization in the best of
cases up to 19%. Balls 1 and 2, are easy to stabilize
due to their weight and size, however ball 3 being
lighter before a small vibration, its position changes
in a more sensitive way, SMC presents a minor error
in steady state.
Figure 17: Experimental ball position on the X-axis for 3
balls stabilizing by PID controller.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
596

Figure 18: Experimental ball position on the X-axis for 3
balls stabilizing by SMC proposed approach.
5 CONCLUSIONS
The results obtained through simulation are similar to
those obtained experimentally, which demonstrate
that the performance of the SMC method is better
than PID, since it allows to stabilize the ball in a
shorter time decreasing the considerably the overshot.
The methodology proposed in this work allows
the design of controllers based on Sliding-Mode
through a PID sliding surface, controllers that in most
applications present excellent results, and whose
performance can be improved by applying this
technique providing robustness to the control system
without complex calculations. To design this
controller, it is indispensable to know the
mathematical model of the plant, and its constants
must be calibrated adequately.
ACKNOWLEDGEMENTS
Oscar Camacho thanks PROMETEO project of
SENESCYT, Republic of Ecuador, for its
sponsorship for the realization of this work. Authors
thank to PIJ-15-17 Project of Escuela Politécnica
Nacional for its sponsorship for the realization of this
work.
REFERENCES
Ali, E., & Aphiratsakun, N. (2016). AU ball on plate
balancing robot. 2015 IEEE International Conference
on Robotics and Biomimetics, IEEE-ROBIO 2015,
2031–2034. https://doi.org/10.1109/ROBIO.2015.7419
072
Aphiratsakun, N., & Otaryan, N. (2015). Ball On The Plate
Model Based on PID Tuning Methods * A. AU Ball On
The Plate Balancing Robot, (1), 3–6.
Bay, C., & Rasmussen, B. (2016). Exploring Controls
Education: A Re-Configurable Ball and Plate Platform
Kit. Retrieved from http://oaktrust.library.tamu.edu/
handle/1969.1/156115
Camacho, O. (1996). A New Approach to Design and Tune
Sliding Mode Controllers for Chemical Processes, PhD
dissertation. University of South Florida, Tampa,
Florida.
Camacho, O., & Smith, C. (2000). Sliding mode control: an
approach to regulate nonlinear chemical processes. ISA
Transactions, 39(2), 205–18. https://doi.org/10.1016/
S0019-0578(99)00043-9
Cedeño, A., & Gordón, M. (2016). Implementación de una
plataforma de estabilización para control de posición y
seguimiento de camino de una esfera. Final Career
Project. Escuela Politécnica Nacional, Quito-Ecuador.
Retrieved from http://bibdigital.epn.edu.ec/handle/
15000/16909
Debono, D., & Bugeja, M. (2015). Application of Sliding
Mode Control to the Ball and Plate Problem. 12th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO), 412–419.
Fan, X., Zhang, N., & Teng, S. (2004). Trajectory planning
and tracking of ball and plate system using hierarchical
fuzzy control scheme. Fuzzy Sets and Systems, 144(2),
297–312. https://doi.org/10.1016/S0165-0114(03)
00135-0
Kealy, T., & O ’dwyer, A. (2003). Analytical ISE
Calculation And Optimum Control System Design.
_Issc. Retrieved from http://arrow.dit.ie/engscheleart
Knuplei, A., Chowdhury, A., & Sveeko, R. (2003).
Modelling and Control design for the ball and plate
system. 2003 IEEE International Conference on
Industrial Technology, 1064–1067. https://doi.org/
10.1109/ICIT.2003.1290810
Nokhbeh, M., & Khashabi, D. (2011). Modelling and
Control of Ball-Plate System Final Project Report.
Slotine, J., & Li, W. (1991). Applied Nonlinear Control.
Prentice Hall, New Jersey.
Valadez, H., Loukianov, A., Castillo, B., & Bayro-
Corrochano, E. (2014). Sliding control variation for
ball-plate system stabilization. 13th International
Workshop on Variable Structure Systems (VSS).
Wang, H., Tian, Y., Fu, S., & Sui, Z. (2008). Nonlinear
control for output regulation of ball and plate system.
Proceedings of the 27th Chinese Control Conference,
CCC, 382–387. https://doi.org/10.1109/CHICC.2008.
4605473
A Sliding-Mode Controller from a Reduced System Model: Ball and Plate System Experimental Application
597
