Automatic Acquisition and Update of a Causal Temporal Signatures

Base- for Faults Diagnosis in Automated Production Systems

Nourhène Ben Rabah

1,2

, Ramla Saddem

, Faten Ben Hmida

, Véronique Carre-Menetrier

and Moncef Tagina

Centre de Recherche en STIC (CReSTIC), URCA, Reims, France

National School of Computer Sciences, University of Manouba, 2010, Tunisia

Keywords: Discrete Event Systems, Automated Production System, Causal Temporal Signatures, Simulation, Faults

Diagnosis, Learning, Similarity.

Abstract: Causal Temporal Signatures (CTS) is an efficient formalism for behaviors description and recognition of fault

diagnosis in Discrete Event Systems (DES). The main advantages of this formalism are the readability and

the expressivity. Indeed, it is able to describe clearly all desired behaviors and it is understandable and

readable by an expert in the field. However, it raises the problem of acquisition and updating of expert

knowledge stored in a CTS base. In this paper, we suggest an incremental learning approach based on the

simulation to acquire and update automatically a consistent CTS base. The proposed approach is illustrated

with an example applied to the turntable helps to understand the different modules of the method.

1 INTRODUCTION

Over the recent decades, the automation of industrial

systems has aimed at increasing the production

performance, enhancing product quality, reducing its

cost and making its equipments more available in the

market. Indeed, the Automated Production Systems

(APS) can be considered from three different views

depending on their dynamics: Continuous Systems,

Discrete-Event Systems (DES) and Hybrid Systems.

In this context, on-line diagnosis systems are

necessary to detect, locate, and identify as soon as

possible the potential failure at the system on run. In

this paper, we are interested in an online diagnosis of

APS considered as DES.

In fact, when the system is running, a large

number of observations come forward regularly and

should be considered. These amounts of data cannot

be processed online by a human operator due to their

complexity and / or their large number. From this

observation, the need for proposing specific support

tools used to analyze and process these data has

emerged in order to recognize both normal and faulty

behaviors. These tools are able to first describe and

represent the possible evolutions of the systems in

form of rules or predicates and secondly to recognize

these behaviors in a flow of events.

The literature distinguishes several description

and recognition tools, such as chronicles with

different definitions (Dousson et al., 1993), (Boufaied

et al., 2002), (Bertrand et al., 2007), (Carle et al.,

2011), (Subias et al., 2014), (Cram et al, 2012) and

Causal Temporal Signatures (CTS) (Toguteni et al.,

1991), (Saddem et al., 2011), (Saddem et al., 2014),

etc. The main advantage of these tools is their high

efficiency due to the symptom to fault knowledge

they rely on (Cordier et al., 2000). However, the

common problem is the difficulty of acquiring and

updating this expert knowledge. The literature shows

two types of approaches on this problem: model

based approaches (Guerraz and Dousson, 2004)

(Saddem and Philippot, 2014) and data-based

approaches (Dousson and duong, 1999) (Cordier and

Dousson, 2000) (Cram et al., 2012), (Subias et al.,

2014). A key limitation of data-based approaches is

the need of human expert (analyst) intervention.

Indeed, they require its presence either for the

qualification of the chronicles (Dousson and duong,

1999) (Cordier and Dousson, 2000) or for the

definition of constraints to guide the algorithm of the

discovery of the chronicles of interests (Cram et al.,

2012), (Subias et al., 2014). This article offers a

solution for CTS formalism that is very close to

chronicle formalism. It presents a new approach

based on past experiences and couples simulation

with learning to automatic acquisition and updating

of a CTS base. The coupling between simulation and

learning (AI technique) is a promising solution where

262

Rabah, N., Saddem, R., Hmida, F., Carre-Menetrier, V. and Tagina, M.

Automatic Acquisition and Update of a Causal Temporal Signatures Base- for Faults Diagnosis in Automated Production Systems.

DOI: 10.5220/0006430102620269

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 262-269

ISBN: 978-989-758-263-9

simulation is used as a technique for generating

empirical knowledge for learning. On the one hand

we propose a Representation of Observations in form

of CTS Algorithm (ROCTSA) which describes the

possible evolutions of the system to diagnose as a set

of CTS. The algorithm allows to model normal

behavior of the system as normal CTS and faulty

behavior as abnormal CTS. This set constitutes the

learning base. On the other hand, an incremental

learning module is introduced to learn new CTS and

to update the CTS base based on past experiences.

The remainder of this paper is organized as follows.

In section 2, problem background, definitions and

concepts of CTS are detailed. In section 3, we

describe an example of APS on which we will rely to

illustrate our approach. Section 4 is devoted to present

our proposed method. In section 5, we present the

results of applying our approach to the described

example. A conclusion and a perspective for future

works are presented in section 6.

2 PROBLEM BACKGROUND,

DEFINITIONS AND CONCEPTS

We begin this section by presenting a short state of

the art on knowledge building approaches for

chronicle and CTS formalisms and providing

concepts and definitions that explain CTS formalism.

2.1 State of the Art on Knowledge

Building Approaches for

Chronicles and CTS

In the literature, several approaches have been

suggested for acquiring and updating chronicles or

CTS base either from models or data.

 Model based approaches:

Are problem solving techniques based on models

representing either the system to diagnose or the

faults that may exist in the system.

For example,

(Guerraz and Dousson, 2004) developed a petri nets

based method for the generation of chronicles

necessary for diagnosis from the fault model of the

system to diagnose. The proposal does not require

knowledge of the global behavior of the system.

Another solution is described in (Saddem and

Philippot, 2014) to translate

a timed Atomaton model

of a diagnoser into CTS. The method ensures the

completeness of the CTS data base but it is done

manually.

 Data based approaches:

They rely on historical data by extracting significant

features using temporal data mining techniques. One

of the first examples is suggested in (Dousson and

Duong 1999), (Cordier and Dousson, 2000). It

introduced FACE (Frequency Analyzer for Chronicle

Extraction) which is a technique for analyzing log

files of alarms (i.e. events) inspired from data mining

techniques. It allows analyzing log files of alarms in

order to determine the most frequent alarms and to

reduce their number displayed to the operator. The

negative point of FACE is that during the generation

of chronicles (candidates), there is only one time

constraint that is taken into account.

To fill this limit, (Cram et al., 2012) proposed a

process of discovering chronicles from a trace (i.e.

temporal sequence). The learning process is based on

two steps:

(i) Construction of a database of time constraints. It

allows to associate for each pair of events, a set of

temporal constraints represented in a graph called

constraint graph. The graph is constructed through

the Complete Constraint-Database Construction

(CCDC) algorithm

(ii) A Heuristic Chronicle Discovery Algorithm

(HCDA) that generates a set of chronicles

(candidates) from a set of chronicles that are

frequent and uses the temporal constraint database

to explore the chronicle space.

The latest solution is described in (Subias et al.,

2014). It improved the proposal of (Cram et al., 2012)

to learn frequent chronicles for several temporal

sequences (not only one temporal sequence) in order

to represent variants of a single situation.

The intervention of human experts (i.e. analysts)

represents a major drawback to these data-based

methods. Indeed, they require their presence either for

the qualification of chronicles (Dousson and Duong,

1999), (Cordier and Dousson, 2000) or for the

definition of constraints to guide the algorithm of

discovery of chronicles of interests (Cram et al .

2012), (Subias et al., 2014).

In this work, we present a new approach based on

past experiences to automatic acquisition and

updating of a CTS base. Construction and CTS

labeling are purely automatic (they don’t require a

human expert). The following section details the

basic concepts of CTS formalism.

2.2 Definitions and Concepts

CTS were proposed in the early 90s by (Toguyeni et

al., 1991). Then, they were improved by (Saddem et

al., 2011). Like chronicles, a CTS is a formalism for

Automatic Acquisition and Update of a Causal Temporal Signatures Base- for Faults Diagnosis in Automated Production Systems

263

the description and recognition of behaviors applied

to the DES diagnosis. It was defined in the work of

Saddem (Saddem et al., 2011) as "a subset of

partially-ordered observable events that

characterizes the system faulty behavior" and as "the

description of a temporal pattern defining a partial

order on events determined by their type and date of

occurrence".

Diagnosis based on CTS consists in interpreting

online the event occurrence to instantiate the pattern

to be recognized. In fact, a CTS is recognized when

all its events occur while respecting their temporal

constraints. This determines if the system is operating

normally or not. The literature shows a variety of

algorithms for chronicle and CTS recognition

(Dousson et al., 1993), (Bertrand et al., 2007),

(Saddem and Phillippot, 2014). In this paper, we are

interested in the acquisition and the update of a set of

CTS (CTS base) that will be the input of recognition

algorithm. We present (in the rest of the section) the

basic concepts of CTS formalism in the rest of the

section.

Definition 1 (Event)

Let EN be a finite set whose elements are called by

the observable events names. Let E be a finite set

whose elements are observable events. A naming

function is a total function H: E -> EN that assigns a

name to each observable event.

Definition 2 (Occurrence of an event)

E is a finite set whose elements are observable events.

Let F be a set of times corresponding to the times of

events production. An occurrence function is a

function O: E-> F that associates to each observable

event a time at which it occurs.

Definition 3 (CTS triplet)

Let

be a CTS triplet defined by: (

)

where

is the name of a reference observable event,

is the name of an observable constrained event

expected compared to

, and

is a temporal

constraint.

Definition 4 (Temporal constraint)

Let

be a temporal constraint which corresponds to

a relative time separating the occurrence of an event

having

reference and an expected one

. The time

constraint can be a date, a period or a duration.

 Date constraint:

A date constraint (figure 1) allows modeling the exact

time separating the occurrence of two events. It is

defined by:

() ()Oe Oe t





(1)

Figure 1: Date constraint.

 Period constraint:

A period constraint (figure 2) allows the modeling,

with uncertainty degree, of the time between the

occurrence of two events. It expresses that

must

occur after

in a time interval [α, β] where α and β

∈Q

() ()Oe Oe









(2)

Figure 2: Period constraint.

 Duration constraint

A duration constraint is generally used to characterize

an event which persists in time. It shows that an event

occurs for the date



to the date

t

Note 1:

In order to describe the dynamics of DES that we are

studying, we consider time as a set of discrete

linearly-ordered instants and we use only the period

constraint in our examples.

Definition 5 (CTS)

Let T be a countable set whose elements are triplets

of CTS. Indeed, a CTS represents a rule that can be

formally defined as follows:

XY

(3)

 X consists of a sequence of a subset of triplets TR

included in T where

describes the

recognition of triplet

followed by that of triplet

 Y represents the state of the system following this

signature (normal or faulty behavior).

 We choose to identify each CTS by a unique

identifier which is an integer.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

264

Definition 6 (Normal CTS)

It is a CTS that describes a normal behavior in the

system. It is defined by:

XN

(4)

N denotes a normal behavior in the system.

Definition 7 (Abnormal CTS)

It is a CTS that describes a faulty behavior in the

system. It is defined by:

XFi

(5)

Fi presents a system failure.

We note that APS study is carried out from the point

of view of the operative part (OP). That’s why we

only treat internal failures, those caused by the OP,

such as the stuck-off to 1 or 0 of a sensor or an

actuator.

Example 1:













, , * , , 1, 2 * , , 3, 4 1InAnct AB t t AD t t F

(6)

In is the name of an observable event that is always

occurring. It is used as the reference of events that are

not constrained. nct: implies the absence of time

constraint. The rule (6) implies that if event A (not

limited by any temporal constraint) occurs followed

by the occurrence of event B satisfying the period

constraint [t1, t2] with respect to A and the occurrence

of event D satisfying the period constraint [t3, t4]

with respect to A, then we can deduce the system is

faulty and F1 is the fault.

3 STUDY FRAMEWORK

In this section, we describe an example of APS which

we will rely on to illustrate our approach presented

later. We chose the sorting system which brings boxes

of entry conveyor to exit conveyor by sorting them

according to their size. The system has 11 sensors to

determine boxes size (small or large) and the box

entry or exit in different conveyors (feeding,

intermediate, and evacuation) or turntable. It also has

7 actuators to activate the various conveyors and the

turntable. In our case, we only present our results for

the turntable, a component of the sorting system. It

has 2 sensors (c4, c5) and 1 actuator (S4). The

specifications retained are presented through a state

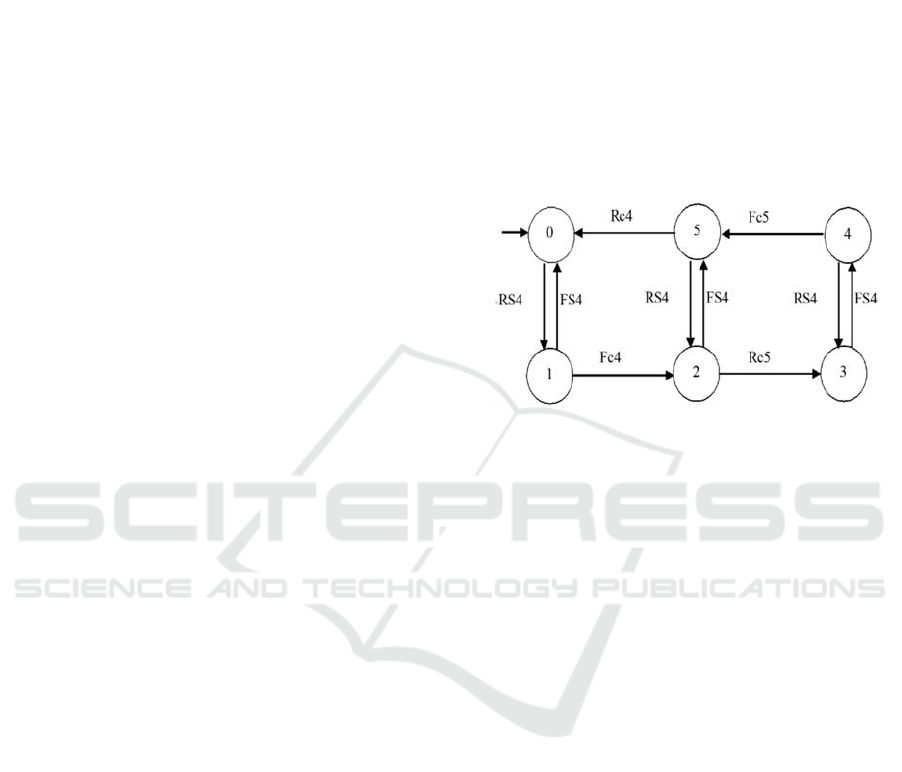
automaton with 6 states and 10 transitions (figure 3).

Normal behavior of the component can be described

through two paths:

Path A: State 0 -> State 1 -> State 2 -> State 3

-> State 4 -> State 5 -> State 0

From the initial state '0', the turntable is in the c4

loading position. If the S4 actuator is activated, the

turntable is moving and sensor c4 is deactivated

(transition from state "1" to "2"). From there, if the

command is still active, the turntable returns to the

unloading position (transition from state "2" to "3").

Disabling the S4 actuators allows returning to the

original position (states "4" after "5" then "0").

Path B: State 0 -> State 1 -> State 2 -> State 5

-> State 0

From state '2', during the movement, and if the S4

actuator is deactivated, the turntable returns directly

to state '0'.

c4: Detector of the turntable loading position

c5: Detector of the turntable unloading position

S4: Turntable

Figure 3: Model of turntable.

An expert work allowed to obtain the following

internal failures that may occur in the turntable: F1:

c4 stuck at 0, F2: c4 stuck at 1, F3: c5 stuck at 0, F4:

c5 stuck at 1, F5: S4 stuck at 0, F6: S4 stuck at 1, F7:

unexpected passage of c4 from 0 to 1, F8: unexpected

passage of c4 from 1 to 0, F9: unexpected passage of

c5 from 0 to 1, F10: unexpected passage of c5 from 1

to 0.

In the following sections, we will try to formulate

automatically CTS which are able to describe these

normal and faulty behaviors of the turntable. Our

approach is presented in the next section.

4 PROPOSED APPROACH

The main idea of our approach (figure 4) is to couple

simulation with learning (AI technique) (Monostori et

al., 2000), (Belisario et al., 2015). The simulation

describes the evolution of the studied model over time

in order to provide useful information on its dynamic

behavior in different situations (including situations

of dysfunctioning). This information can be exploited

by an expert system or a decision maker (Pierreval

and Ralambondrainy, 1992).

Automatic Acquisition and Update of a Causal Temporal Signatures Base- for Faults Diagnosis in Automated Production Systems

265

In our proposal, this information (i.e. signals of

sensors and actuators) is the input of the proposed

Representation of Observations in form of CTS

Algorithm (ROCTSA) which allows to model the

normal behavior of the system as a set of normal CTS

and the faulty behavior as a set of abnormal CTS.

From these CTS examples (i.e learning base), an

incremental learning is introduced to learn new CTS

and to update the CTS base based on past

experiences.

Figure 4: Proposed approach.

4.1 Simulation

Simulation is a necessary module to generate

examples of CTS from which it will be possible to

learn new knowledge and update the knowledge base.

It consists in:

a) Operating the model of the real system in a normal

mode (absence of failures) and abnormal mode

(triggering failures).

b) Collecting for each mode the relevant information

(values of the sensors +actuators+ dates) from the

model.

c) Generating from these information causal

temporal signatures through the proposed

Representation of Observations in form of CTS

Algorithm (ROCTSA) which will be presented in

the following paragraph.

4.1.1 Principle of ROCTSA

For each PLC cycle (T), the algorithm constructs a

triplet (

) from a binary signature which

represents the signals of sensors and actuators of the

system to be diagnosed and from a binary signature

which represents the signals during the previous PLC

cycle (T-1). A CTS is the concatenation of at least

two triplets.

The proposed algorithm can be illustrated through

these steps:

 Step 1: Group the signals of the sensors and

actuators of the system to be diagnosed during the

PLC cycle (T) in order to construct a binary

signature and associate a cycle time to it. (Note:

tampon is the binary signature of the previous

PLC cycle (T-1) and PreviouscycleTime is its

cycle time).

 Step 2: Formulate the reference event (

): If this

is the first PLC cycle executed then er <- "IN"

otherwise the constrained event of the previous

PLC cycle (T-1) becomes the reference event of

the PLC cycle T.

 Step 3: Formulate the constrained event (

Each element of the binary signature is

transformed into an event that can be either the

rising edge (denoted by R) or the falling edge

(denoted by F) of a sensor or actuator. This event

is defined as a constrained event.

 Step 4: Formulate the temporal constraint

(temporalC): If the referent event(er) is equal to

IN then absence of the temporal constraint (nct)

otherwise the temporal constraint is constructed

from two times [DateMin, DateMax].

DateMin<- CurrentcycleTime- PreviouscycleTime

DateMax<- DateMin +d

with "d" is the duration of the PLC cycle,

DateMin is the lower bound of the period

constaint and DateMax is the upper bound of the

period constraint.

 Step 5: Group the result of the 3 previous steps to

construct a triplet of the CTS.

The complexity of the algorithm is a linear

complexity with respect to the size of the binary

signature: O (K (n + m)) where K is the number of

PLC cycles performed by the automated production

system, n is the number of sensors and m is the

number of actuators.

4.1.2 Labeling of CTS

The operation of the model in a normal mode and

abnormal mode (triggering failures) allows the

labeling of each instance of CTS automatically

without the need for an expert accompanying the data

formatting process and it does not need to give advice

(normal or faulty behavior). The normal functioning

of the model is represented as a set of normal CTS,

while the faulty one is defined as a set of abnormal

CTS. Both types of CTS are stored in a CTS Base.

This base is the learning base.

4.2 Learning Module

For new CTS learning, we rely on the learning data

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

266

stored in the CTS base obtained during the simulation

module. Each new observation is transformed into a

new CTS (nCTS) through ROCTSA. The principle

of this module consists in extracting, for each nCTS,

the similar or nearest CTS from the CTS Base. The

research is based on the use of a similarity metrics that

calculates the degree of similarity between the new

CTS and the past CTS.

For this reason, we use a similarity calculator that

has as input a nCTS and the CTS base. Its outputs are

the similarity values between the nCTS and all the

past CTS (pCTS) stored in the base. Then, the new

CTS will inherit the result of the CTS having the

greatest similarity and will be stored in CTS Base.

4.2.1 Similarity Calculator

Let S be the similarity relation defined by:

S= CTS × CTS -> [0, 1]

-If

CTS

and CTS

are equal, then S (

CTS

, CTS

) =1

-If

CTS

and CTS

are not equal, then S (

CTS

, CTS

)

Calculate the similarity between two CTS is to

calculate the distance:

(, )1(, )D CTS CTS S CTS CTS

ij ij



(7)

To calculate the distance between two CTS, we must

compute the distance separating its triplets. The

triplets consist of different types of elements (event

of chain type, time constraint of interval type), which

makes the distance calculating a difficult step.

To solve this problem, we propose to discretize

the values of the triplets’ elements as follows:

 To events, we assign the value 1 if Val

()

= Val

()

and the value 0 if Val

()

≠ Val

()

where Val is the value of the event,

()

denotes

an event of a triplet

of a

CTS

and

()

represents an event of a triplet

CTS

 To temporal constraints of interval type, we assign

the value 1 if Val (lower bound

(

)

) >= Val

(lower bound

(

)

) and Val (upper bound

(

)

) <

= Val (upper bound

(

)

), otherwise 0, where

Val is the value of the lower or upper bound of the

temporal constraint,

(

)

is a time constraint of

a triplet

of a

CTS

and

(

)

is a time constraint

of a triplet

of a

CTS

. Thus, the value of a triplet

of a

CTS

(

)

is calculated by the aggregation

of values of its events and its temporal constraint.

4.2.2 Distance Metric

The choice of distance metric depends on data type to

compare (nominal, ordinal, continuous or binary).

Indeed, values of triplets are numerical. Therefore we

choose the Manhattan distance (Stahl, 2003) to

calculate the distance between two CTS.

(, )

DCTS CTS

Vt Vt

ik jk



 



(8)

Where TR is the set of triplets representing a CTS

defined by

123

{ , , ,..., }

TR ttt t

, m is the triplets

number of a CTS, m>=2 and

are the triplet

values.

5 EXPERIMENTATION

To validate our proposal, we exploit the Interactive

Training System for PLC (ITS PLC) proposed by the

Portuguese company Real Games

(www.realgames.pt). ITS PLC is an education and

training tool dedicated to programming the PLC and

validating the control algorithm through a real time

interactive experience (Riera et al., 2010). It offers 3D

simulations of Operative Parts (OP) of 5 industrial

systems (sorting, batching, palletizer, pick and place

and automatic warehouse).

Each system a graphical

simulation of an operative part including its sensors

and its actuators and allowing a PLC to control it.

We use the beta version of ITS PLC in this study

which allows: (a) using scripts in IronPyton

(http://ironpython.net) to write its own controllers in

a language close to the ST (Structured Text). (b)

accessing to an Interactive IronPython Interpreter

allowing the user to interact with each simulated

system by accessing for example to its inputs / outputs

through the IO object. IO.Actuators and IO.Sensors

respectively return the actuators and sensors signals.

proposal was led through the development of 2

scripts:

 The first one allows controlling the sorting system

without the need for a real API

 The second one allows access to the inputs /

outputs of the simulated system each the 16ms

(ITSPLC cycle duration), to implement the

Automatic Acquisition and Update of a Causal Temporal Signatures Base- for Faults Diagnosis in Automated Production Systems

267

ROCTSA (simulation module) and the similarity

calculator (learning module).

Note: we chose the duration of a temporal constraint

of period type (d) is 5ms.

During the simulation module, the set of normal

and abnormal CTS are recorded in the CTS base to

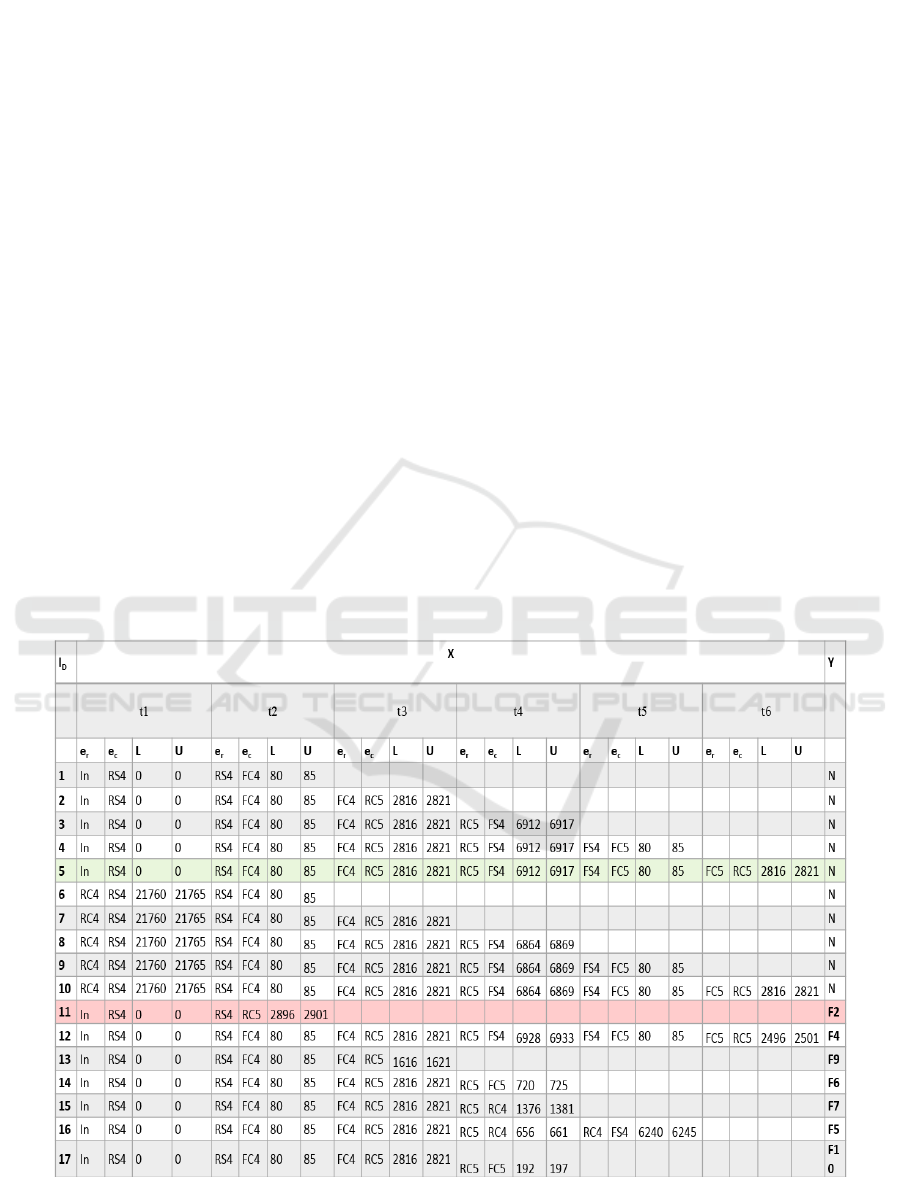
form the learning base. Figure 5 shows various

examples of CTS instances with the different

attributes of the learning base. It describes 10

instances labeled as normal behaviors of the turntable

and 7 instances labeled by the various failures as

previously described.

Instance 5 of the learning base is a normal CTS which

corresponds to this rule:

(In, ↑S4, nct)* (↑S4, ↓c4, [80, 85])* (↓c4, ↑c5,

[2816, 2821])* (↑c5, ↓S4, [6912, 6917])* (↓S4, ↓c5,

[80, 85])* (↓c5, ↑c4, [2816, 2821]) -> N

This signature describes the passage through the

different states of path A (introduced above). It

implies that if the rising edge of the S4 actuator (↑S4)

occurs followed by the occurrence of the falling edge

of sensor c4 (↓c4) satisfying the time constraint [80,

85] with respect to ↑S4, the occurrence of the rising

edge of the sensor c5 (↑c5) satisfying the constraint

[2816, 2821] with respect to ↓c4, the occurrence of

the falling edge of the S4 actuator (↓S4) satisfying the

constraint [6912, 6917] with respect to ↑c5 of the

falling edge of the sensor (↓c5) satisfying the

constraint [80, 85] with respect to ↓S4 and the rising

edge of sensor c4 (↑c4) satisfying the constraint

[2816, 2821] with respect to ↓c5, then we

the normal behavior of the system.

Instance 11 of the learning base is an abnormal

CTS which corresponds to this rule:

(In, ↑S4, nct)*(↑S4, ↑c5, [2896, 2901])-> F2

It implies that if the rising edge of the S4 actuator

(↑S4) occurs followed by the occurrence of the rising

edge of sensor c5 (↑c5) satisfying the time constraint

[2896, 2901], then we can deduce the faulty behavior

F2. The learning module uses these past experiences

to add new CTS to the CTS base (to promote

learning).

Example: We propose to add an nCTS and search the

most similar using our similarity calculator.

ROCTSA starts generating an nCTS:

nCTS: (↑c4, ↑S4, [65664,65669])* (↑S4, ↓c4, [80,

85])-> ?

It does not exist in the CTS base. Consequently,

the similarity calculator can be launched. The nCTS

inherits the (normal or faulty) behavior of the CTS

which has the minimum distance and will be stored in

the CTS Base. In this example, CTS 6 has the

minimum distance (D=0.166). Therefore, the nCTS

inherits the normal behavior of CTS 6 and is stored in

the CTS Base

6 CONCLUSIONS

In the context of diagnoses, we suggest a new

approach based on past experiences which couples a

simulation with learning for automatic acquisition

and update of a set of CTS. We present ROCTSA

algorithm allowing to model the normal behavior of

the system to diagnose as a set of normal CTS and the

faulty behavior as a set of abnormal CTS. A learning

module is introduced to learn new CTS and to update

the CTS base. The proposed approach has many

advantages: (i) An easy update for the CTS Base.

Indeed, when a new behavior occurs in the APS, a

new CTS will be added to the CTS base that models

this new behavior. (ii) It is a generic approach that can

be applied to any APS. (iii) It does not require the

presence of an expert who might be reluctant to

acquire a CTS base. As a prospect, to improve the

expressiveness of ROCRSA, we will express the

absence of events (negation operators). Then, we will

use this work to introduce a distributed approach for

complex system diagnoses. It will be based on a

multi-agent architecture which decomposes the

system to be diagnosed into subsystems. Each

subsystem will be supervised through an agent which

is responsible for the acquisition of its CTS Base and

its local diagnosis.

REFERENCES

Belisário, L. S., and Pierreval, H. (2015). Using genetic

programming and simulation to learn how to

dynamically adapt the number of cards in reactive pull

systems. Expert Systems with Applications, 42(6),

3129-3141.

Boufaied, A., Subias, A., and Combacau, M. (2002).

Chronicle modeling by Petri nets for distributed

detection of process failures. In Systems, Man and

Cybernetics, 2002 IEEE International Conference

on (Vol. 4, pp. 6-pp). IEEE.

Bertrand, O., Carle, P., and Choppy, C. (2007). Chronicle

modelling using automata and colored Petri nets. In

DX-07 18th International Workshop on Principles of

Diagnosis, (pp. 229-234), USA.

Cram, D., Mathern, B., and Mille, A. (2012). A complete

chronicle discovery approach: application to activity

analysis. Expert Systems, 29(4), 321-346.

Cordier, M. O., and Dousson, C. (2000). Alarm driven

monitoring based on chronicles. In Proceedings of

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

268

Safeprocess (pp. 286-291).

Carle, P., Choppy, C., and Kervarc, R. (2011). Behaviour

recognition using chronicles. In Theoretical Aspects of

Software Engineering (TASE), Fifth International

Symposium on (pp. 100-107). IEEE.

Dousson, C., and Duong, T. V. (1999). Discovering

Chronicles with Numerical Time Constraints from

Alarm Logs for Monitoring Dynamic Systems.

In IJCAI (Vol. 99, pp. 620-626).

Guerraz, B., and Dousson, C. (2004). Chronicles

construction starting from the fault model of the system

to diagnose. In International Workshop on Principles of

Diagnosis (DX04), 51-56.

Monostori, L., Kädär, B., Viharos, Z. J., Mezgär, I., &

Stefán, P. (2000). Combined Use of Simulation and

ΑΙ/Machine Learning Techniques In Designing and

Manufacturing Processes and Systems. Journal for

Manufacturing Science and Production, 3(2-4), 111-

118.

Pierreval, H., and Ralambondrainy, H. (1992). A simulation

and learning technique for generating knowledge about

manufacturing systems behavior. In Artificial

Intelligence in Operational Research (pp. 239-252).

Macmillan Education UK.

Riera, B., Marangé, P., Gellot, F., Nocent, O., Magalhaes,

A., and Vigario, B. (2010). Complementary usage of

real and virtual manufacturing systems for safe PLC

training. IFAC Proceedings Volumes, 42(24), 89-94.

Stahl, A. (2003). Learning of Knowledge-Intensive

Similarity Measures in Case-Based Reasoning. PhD

thesis, University of Kaiserslautern.

Saddem, R., Toguyeni, A., and Tagina, M. (2011). A

model-checking approach for checking the Consistency

of a set of Causal Temporal Signatures. In 9th European

Workshop on Advanced Control and Diagnosis (pp. 1-

6).

Saddem, R., and Philippot, A. (2014). Causal Temporal

Signature from diagnoser model for online diagnosis of

iscrete Event Systems, In Control, Decision and

Information Technologies (CoDIT), International

Conference on (pp.551-556). IEEE.

Subias, A., Travé-Massuyès, L., and Le Corronc, E. (2014).

Learning chronicles signing multiple scenario

instances. IFAC Proceedings Volumes, 47(3), 10397-

10402.

Toguyeni, A.K.A., CRaye, E., and Gentina, J.C. (1991). A

method of Temporal Analysis to perform on-line

Diagnosis. In Industrial Electronics Society

(IECON’91), the context of Flexible Manufacturing

System, California, USA.

Toguyeni, A. K. A., Craye, E., and Gentina, J. C. (1997).

Time and reasoning for on-line diagnosis of failures in

flexible manufacturing systems. In Proceedings of the

15th IMACS world congress on scientific computation,

modeling, and applied mathematics (Vol. 6, pp. 709-

714).

Ye, X., and Mathon, A. (1992). Manufacturing

Management System Simulation an Object-oriented

Approach. In 2nd International Conference on System

Simulation and Scientific Computing (pp. 30-34).

ID : identifier of the instance, X: sequence of triplets, Y: state of the system, ti : CTS triplet,

er: reference event, ec: constrained event, L: lower bound of the period constraint, U: upper bound of the period constraint.

Figure 5: Learning base.

Automatic Acquisition and Update of a Causal Temporal Signatures Base- for Faults Diagnosis in Automated Production Systems

269