Multi-objective Order Reduction Problem Solving with Restart

Meta-heuristic Implementation

Ivan Ryzhikov, Christina Brester and Eugene Semenkin

Institute of Computer Sciences and Telecommunication, Siberian State Aerospace University, Krasnoyarsk, Russia

Keywords: Linear Time Invariant Systems, System Identification, Order Reduction, Multi-objective Optimization,

Evolution-based Algorithms, Meta-heuristic, Restart Operator.

Abstract: An order reduction problem for linear time invariant models brought to the multi-objective optimization

problem is considered. Each criterion is multi-extremum and complex, requires an efficient tool for estimating

the parameters of the lower order system and characterizes the model adequacy for the unit-step and Dirac

function inputs. A common problem definition is to estimate the lower order model coefficients by minimizing

the distance between the output of this model and the initial one. We propose an evolution-based multi-

objective stochastic optimization algorithm with a restart operator implemented. The algorithm performance

was estimated on two order reduction problems for a single input-single output system and a multiple input-

multiple output one. The effectiveness of the algorithm increased sufficiently after implementing a meta-

heuristic restart operator. It is shown that the proposed approach is comparable to other approaches, but allows

a Pareto-front approximation to be found and not just a single solution.

1 INTRODUCTION

The idea of reducing an identification problem to a

black-box optimization problem (BBOP) is

considered in this study. The initial identification

problem is to estimate the parameters of the linear

time-invariant (LTI) system of the lower order with

the aim of making its behaviour close to the behaviour

of the higher order model. In many different studies

(Narwal et al., 2016), (Desai et al., 2014) and

(Ramesh et al., 2011) the approaches and therefore

the models are compared by several criteria, but the

model parameters were identified by one of them and

so the others are indicative. Commonly, these criteria

are based on the sum of the output errors, where the

output is a reaction on the unit-step or Dirac function

input. Generally, these criteria form a non-dominated

set of the identification problem solutions, and that is

why the estimation of the lower order parameters

leads to a multi-objective (MO) optimization

problem. In this case, the proposed problem definition

is a generalization of the LTI identification problem.

The BBOP appearing in system identification is a

complex multimodal problem. Recent works on the

LTI order reduction problem are based on a

combination of stochastic nature-inspired

optimization algorithms and methods of providing

stability, i.e. (Chen et al., 1979), and its first

combination with an optimization technique was

initially given in (Parmar et al., 2007). Nature-

inspired stochastic optimization algorithms are used

to solve reduced optimization problems: a genetic

algorithm (Ramesh et al., 2011), Big Bang Big

Crunch (Desai et al., 2014) and Cuckoo Search

Optimization (Narwal et al., 2016). The comparison

made in these works proves that heuristic

optimization is an efficient tool for solving an

extremum seeking problem of this class. Solving the

described MO optimization problem also requires an

efficient tool, which is used to estimate not only the

best solution by each of the criteria, thus dealing with

multimodality and complexity, but also the Pareto set.

As the main optimization algorithm, PICEA-g

was used. This algorithm was improved by

implementing a meta-heuristic, the aim of which is to

avoid stagnation areas and improve the search by

controlling the initial generation randomization. The

main idea of the restart operator is given and

developed in studies (Fukunaga, 1998) and

(Beligiannis et. al., 2004), but was sufficiently

modified in (Ryzhikov and Semenkin, 2017), where

it was applied for a single-criterion optimization

problem and in the current study it was modified for

270

Ryzhikov, I., Brester, C. and Semenkin, E.

Multi-objective Order Reduction Problem Solving with Restart Meta-heuristic Implementation.

DOI: 10.5220/0006431002700278

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 270-278

ISBN: 978-989-758-263-9

solving MO problems. For this purpose, the main

restart criteria were modified and the process of

gathering information for the optimization problem is

related to other statistics. This data is used to improve

the efficiency of the Pareto estimation algorithm and

to perform the final Pareto set estimation.

The proposed approach is based on asymptotic

equivalence (Ryzhikov et al., 2017), so the lower

order model output integral square errors are always

convergent. The stability of the dynamical system

model is provided by including a penalty function in

the criteria. Determining the solution in this way

increases the dimension of the search variable space

by one for each system output. This approach was

compared to other approaches on the same problem

set and with the same number of objective function

evaluations for solving the LTI order reduction

problem for single-input single-output (SISO)

systems and multiple-input multiple-output (MIMO)

systems.

The rest of the paper is organized as follows: in

Section II the order reduction problem is presented.

The restart meta-heuristic and MO evolution-based

algorithm are introduced in Section III. The

experiments conducted and the results obtained are

included in Section IV. The conclusions are presented

in Section V.

2 ORDER REDUCTION

PROBLEM STATEMENT

The SISO LTI system model is determined by the

following linear differential equation



ax t bu t







(1)

where

,1,

aRi n

and

,1,

bRi m

are the

model parameters,

:nn m

is the equation order,





0,t 

is the time variable,









is the i -th

derivative of the output,









is the

-th derivative

of the control input.

In this study we consider the case









0xt



, so

after using the Laplace transformation, the model can

be represented with a transfer function



Gs b s a s



 



(2)

The MIMO LTI system is determined by the

following matrix equations,

  

tAXtBUt

 













Yt CXt DUt 

(3)

where









Yt R R





is the output function,

is the number of outputs,









Ut R R





is the input function,

is the number of inputs,









tR R





is the space variable, the

system matrix





, the control matrix





, the output matrix





and the

feed-forward matrix





In this paper, we consider the MIMO system with

two inputs and two outputs, thus, its transient

function, which is determined by the equation

  

Ws CsI A BD





 

can be represented

with the expression







 

1,1 1,2

2,1 2,2

WsW s

WsWs









(4)

where













,,,ij ij ij

WsDsNs

, and

ij ij

DN,

,1,2ij , are the denominator and nominator,

respectively. Factoring out the denominator gives











 

1,1 1,2

2,1 2,2

Ns Ns

NsNs

















sDs















,, ,

pq pq i j

ipjq

NsNs Ds







(5)

To provide the convergence of integral errors, the

asymptotical equivalence approach is used (hidden

reference 2), where the higher and lower order model

output equivalence is guaranteed by the limit

equivalence of the fraction of parameters



lim

axt





(6)

where the coefficients

and

are given in (1) and

known. This means that the first one could calculate

the initial model (system) output asymptote

, and

on the basis of this determinate the parameters of the

lower order model using the formula (6).

Since our aim is to approximate the initial model

with the lower order model, we need to estimate the

parameters of the 2

order model which is

determined by the following transfer function

Multi-objective Order Reduction Problem Solving with Restart Meta-heuristic Implementation

271



psa p

Gsp

ps p

 





(7)

for the SISO systems and



1,1 1,2

2,1 2,2

Gsp













Dsp s psp





 

12 1 2 1

ij s

ij ij

Nspp sa p

     



(8)

for the MIMO systems.

Now to provide the 2

order model stability we

require the following condition

00pp ,

(9)

where the parameter comes from (7) or (8).

We want the model with the reduced order to be

an adequate estimation of the LTI system, so its

response needs to be close to the response of the

model with the higher order on the same control input





. The response is a function on a time domain

and for both models it can be found by solving the

Cauchy problem for (2) and (7) or (4) and (8). Since

we consider the unit-step and the Dirac functions as

inputs, the output can be expressed via the inverse

Laplace transformation:

















(, ) ,

tp L G sp Lut





















()

tLGsLut





(10)

for the SISO LTI systems and



 







NspLut

xtp L

Dsp

























NsLut

xt L













(11)

for the MIMO LTI systems. Using expressions (10)

and (11) to calculate the responses of the models on

different input functions, one can identify parameters

as the solution of the extremum problem



  



siso u i u i

C p xt xtp











min

siso





(12)

for the SISO system or



  



uijij

mimo u k u k

ijk

Cp xtxtp







(13)





min

mimo







for the MIMO system. In criteria (12) and (13) the

values

,1,

tTiNi N  are the time points,

the final time and

is the number of points.

In this study, a penalty function is used to

implement the stability condition (9) into the criteria

(12) and (13). The modified criteria are as follows,









min

siso siso

CpC с Pp



 



(14)











min ,

mimo mimo

CpCpс Pp









(15)

where









:0PRR





is a static penalty

function



0, 0













and

0с 

is a

coefficient.

To analyse the solution adequacy on the whole

time domain three more criteria are used. These

criteria are involved in comparing the efficiency of

the approaches. Let







txtpxt

 



be the

solutions of (10) or (11), the input is the unit-step

function









ut t





and





arg min

siso











arg min

mimo

pCp







, depending on the problem.

The first criterion we want to calculate is the integral

square error



() ()Ixtxtdt









(16)

Its estimation was used to identify the parameters via

solving problems (14) or (15). The integral (16) is

divergent if









lim lim

txt



 



, and for this

reason the function (6) is implemented and the

stability condition is required.

The next criteria concern the relative integral

square error; they are given in (Parmar and Prasad,

2007) and are proposed in order to check the accuracy

of the model. Both criteria are expressed with by

fraction:

 



  



txtdt

tx dt

















(17)

and the second is for the input









ut t

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

272

 



txtdt

xt dt















(18)

The result of the inverse Laplace transformation (10)

and (11) can be found symbolically for the current

problems, where the initial and reduced order models

are linear.

3 RESTART META-HEURISTIC

AND PICEA-G

The optimization problem considered in this study

can be represented in a following way:









:,dim

Ca A C R A n 

















...

Ca С a С a extrem





(19)

where

is a space of alternatives with dimension

is a subspace of some Euclidean vector space









1, : : ,

iAjA

imС AC R С AC 



are

the unknown mappings. After the problem

formulation and the determination of the

identification parameters, we can use a bijection

between alternatives and binary strings, so every

alternative can be determined with a real value vector

and thus a binary string. Generally, the criteria (19)

are computable functions or mappings with unknown

properties and unknown symbolic form.

For solving MO BBOP we propose using the

PICEA-G algorithm, which is population-based.

Each population is a set of different solutions – a set

of alternatives and our aim is to approximate the

Pareto front. In this case, there is a contradiction

between the need for an in depth search to improve

current solutions and for a search in breadth to

approximate the whole front.

To resolve this contradiction we put forward a

hypothesis that restarting the Pareto front estimation

algorithm improves the population-based

optimization algorithm efficiency. This is why an

independent restarting operator meta-heuristic was

designed and implemented. The proposed meta-

heuristic estimates if the stagnation condition is met

and evaluates the parameters for the randomized

performing of the initial generation. The stagnation

estimation is based on the distances between the

Pareto front estimations, which are taken at the

current generation and the previous one and consist

only of non-dominated individuals. If the distance

does not change for a given number of generations,

the MO optimization algorithm restarts. A more

detailed explanation is given below.

Let the population in the

i -th generation be noted

P . For each algorithm generation a set



 





:, : ,

ij kj k

jk jk

SaAkijkSaaa S  





and a set









ijji

Ca a S

are formed. These sets

are the Pareto set and front estimations at the

-th

generation, respectively. It is easy to see that

1ii i

iS S P







, so the distance









between

two different sets

and



is calculated for the

non-dominated solutions found in the current

generation. Let

be a set of any limited cardinality





,1,

fRi F 

, then









,: 0,

FF F F R







 





,min

ab a b

FF F F





 



(20)

where











is a norm on the

vector space.

The decision of whether to perform a restart or not

is made on the basis of the specific variable value.

This variable is the diameter of a set, which is a queue

that consists of the metric values of the previous

iterations. Let the number of iterations be noted as

tail

l , then the set is determined in the following way











i tail j j tail

Tail l F F i l j i







(21)

and the meta-heuristic performs the restart if the

following condition

















max min

tail

i i tail

Tail j Tail j







(22)

is met. As can be seen from equations (21) and (22),

two different operator settings are used: the tail length

tail

l controls the size of the observation period and

tail



is a threshold level.

Now, if the restart takes place, we collect the

current algorithm run data and put it into the sets to

gather information about the MO optimization

problem and algorithm’s behaviour to provide its

control with the meta-heuristic. In this case, we need

the estimations of the Pareto front and Pareto set, the

last generation population and its criteria values.

These sets are used for performing the final solution

Multi-objective Order Reduction Problem Solving with Restart Meta-heuristic Implementation

273

and initial generation population of the next algorithm

run:



SSi

emory Memory S







emory Memory F





emory Memory P







CCi

emory Memory C





where











:,1,

ijji i

CFcc Pj P



The generation of the initial population is an

important feature of the meta-heuristic and it directly

influences the algorithm’s performance. This

generation is controlled by two parameters: the

probability of each individual in this initial population

being randomly generated -



, and the probability of

each gene of the individual being changed to the

opposite -



, in the case of the individual not being

randomly generated. Each

-th individual can be

generated by one of the proposed schemes and it

means that its

-th gene in the initial population is

generated in one of the following ways:















0,, ,

,0 1

jk jk jk

P r Pr Pr,

(23)

with the probability



and with the probability











cSjk

PfMemoryr









(24)

where

is the index of a gene,



fvp















is a special function and

are the random

values:







1...

jjS

Pr Pr Memory 







1 ...

jjS

Pr Pr Memory 









01 1

jk jk

Pr Pr 

By varying parameters

 and



we control the initial

population generation. If we want the initial

population to be completely randomized, we set



1, and if we want it to be in a some sense near to some

previously estimated Pareto set solutions, we set it

closer to 0 and



closer to 0 too, where



represents

the closeness of the new individual to a found one.

In our study, the restart meta-heuristic is

incorporated into the Preference-inspired Co-

evolutionary Algorithm using goal vectors (PICEA-

g) proposed by Wang in 2013 (Wang, 2013). This

algorithm relates to a class of preference-inspired co-

evolutionary algorithms (PICEAs) which are based

on the concept of co-evolving the population with

decision-maker preferences.

PICEA-g includes the following steps:

Generate an initial population and evaluate

objective values for individuals. Find non-

dominated candidate solutions in the population

and copy them into the archive. Determine the set

of goal vectors as a number of targets randomly

generated within the goal vector bounds.

Produce the offspring solutions with genetic

operators: selection, crossover and mutation.

Evaluate objective values for new generated

individuals.

Pool together parents and children; compile the

common set of objective values.

Append to the set of goal vectors the additional

targets generated within the determined bounds.

Assign fitness values for goal vectors and for

individuals in the united population.

Form the new population and the set of goal

vectors based on their fitness.

Update the archive with new non-dominated

solutions.

Check the stopping criterion: if it is satisfied then

finish the search with the archive set, otherwise

proceed with the second step.

In Steps 1 and 4 decision-maker preferences are

incorporated into the algorithm by using goal vectors.

They represent points generated in the criteria search

space within bounds determined according to the rule:

,)min(

),min()max(

),min(

max

min

BestFg

BestF

BestFF

BestFg







(25)

where

min

g is the lower bound and

max

g is the

upper one for the i-th goal vector component,

BestF

is the best value of the i-th objective function amid

solutions in the archive,

,,1 Mi 

is the number of

criteria. The recommended value of the

 parameter

is 1.2.

4 PERFORMANCE

INVESTIGATION

Since we propose the multi-objective optimization

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

274

problem, and using the proposed approach results in

receiving an estimation of a Pareto set and not a single

solution, for each problem we should present the best

solution by the first criterion and the best one by the

second criterion. As in similar investigations, we

assign a limit to the maximum number of fitness

function evaluation as being equal to 2500. To tune

the restart meta-heuristic parameters we performed

additional experiments for the same MO optimization

problems, where the values of the restart operator

parameters were varied. According to the results of

these experiments the following parameters were

chosen: α=0.9, β=0.7, l

tail

=5, δ

tail

=0.0005.

The first problem we consider is the SISO system,

which is determined by the equation



432

72424

10 35 50 24

ss s

sss

  





(26)

and for which we received models: the best one by the

first criterion value



0.7696275 1.621897

2.522232 1.621897









and the best

one by the second criterion value



0.86107 0.679314

1.568184 0.679314









, after 25

independent launches of the proposed PICEA-g with

the restart meta-heuristic.

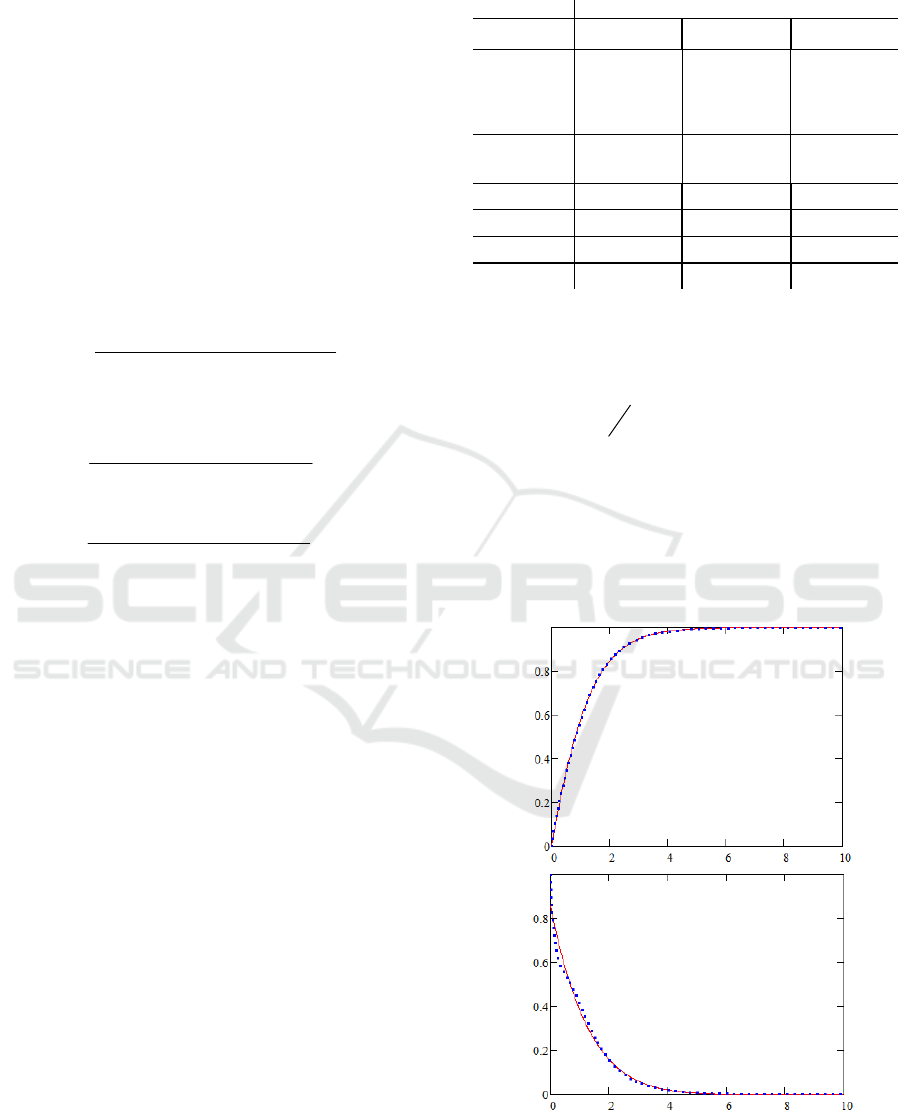
The initial model and reduced model outputs are

given in Figure 1, where the dotted line is the initial

model output and the solid line is the output of the

reduced model. The numeric adequacy estimation is

given in Table 1, where the results of the proposed

approach are compared with the results received in

different studies using other approaches and

optimization tools, including the PICEA-g algorithm

without the restart meta-heuristic. Knowing the

model parameters makes it possible to calculate

criteria and compare approaches. Here we use the

following notation: with “the proposed approach” we

mean the solutions found by PICEA-g with the restart

meta-heuristic, 1 – is the same approach, but without

restarting, 2 – COBRA optimization tool and

asymptotical equivalence (Ryzhikov et al., 2017), 3 –

(Desai, Prasad, 2013), 4 – (Parmar el. al., 2007) and

5 – (Narwal, Prasad, 2016).

Table 1: SISO problem (26): performance of approaches.

Criterion

Approach

Proposed



7.48510

-5

1.31310

-4

 6.51510

-3



Proposed



4.20510

-4

7.37310

-4

 6.04710

-3





7.56410

-5

1.32610

-4

 6.55010

-3





1.13410

-3

1.98910

-3

 6.19810

-3



7.458 10





1.308 10





6.901 10





2.841 10







4.982 10







5.236 10







2.394 10







4.197 10







0.018



1.986 10







3.483 10







7.612 10







The approximations of the Pareto front, which

were made during every algorithm launch and the

randomly chosen single Pareto front estimation, are

given in Figure 2, where the criteria are represented

with a mapping

1 C



, where C is a criterion, and

this mapping was maximized by the searching

algorithm. As can be seen, there is not such a solution

that would bring the maximum of two of these criteria

representations at the same time. This is why it is

necessary to solve the multi-objective optimization

problem if the model must satisfy more than one

criterion.

Figure 1: Initial model (dotted line) and lower order model

(solid line) outputs for the – a) - unit-step input function and

– b) – Dirac input function.

Multi-objective Order Reduction Problem Solving with Restart Meta-heuristic Implementation

275

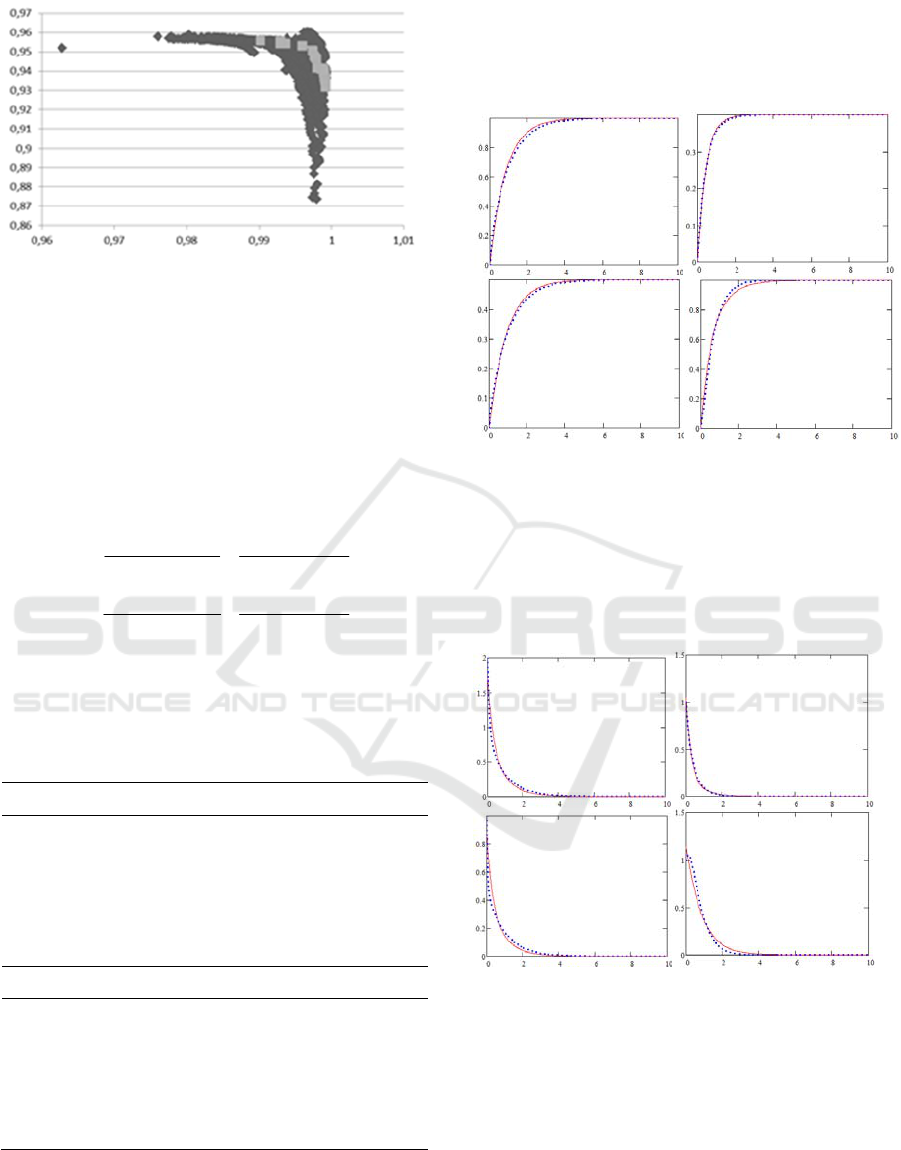
Figure 2: Pareto front estimation in all of the runs (black)

and a single front estimation (grey).

Although the PICEA-g with the restart meta-

heuristic is a multi-objective optimization tool and it

is efficient in solving the problem with two criteria,

solutions with maximum criterion values outperform

most of the solutions obtained by the optimization

algorithms solving a single criterion problem.

A similar problem was considered for the MIMO

system order reduction problem



 



 

110 2 5

10 6

120 23

ss s s









  











  



(27)

for the same computational resources and algorithm

runs we received the set of models with the highest

criteria values given in Table 2.

Table 2: MIMO problem (27): solution found.







3.145035 2.168462,

Ds s s 



*1,1

1.206913 2.168462,

Ns s



*1,2

0.927334 0.867384,

Ns s



*2,1

0.515576 1.084231,

Ns s



*2,2

1.581389 2.168462,

Ns s







4.989368 4.344733,

Ds s s 



*1,1

1.7814044 4.344733,

Ns s



*1,2

1.028391 1.737893,

Ns s



*2,1

0.792901 2.172366,

Ns s



*2,2

1.088212 4.344733,

Ns s

As for the SISO problem, the outputs for unit-step

and Dirac function inputs are given in Figures 3 and

4, respectively. In these figures a) represents the

outputs of (1,1) model components, b) represents the

outputs of (1,2) components, c) represents the outputs

of (2,1) components, and d) represents the outputs of

(2,2).

Figure 3: Initial model (dotted line) and lower order model

(solid line) outputs for the unit-step function.

Similar experimental results are compared in

Table 3, but there criteria are summarized by all the

model components.

Also, the Pareto front estimations are given in

Figure 5.

Figure 4: Initial model (dotted line) and lower order model

(solid line) outputs for the Dirac function.

Here we use the following notation:

“the proposed

approach”

is PICEA with the restart meta-heuristic, 1

– is the same, but without the restart, 2 – COBRA

optimization tool and asymptotical equivalence

(Ryzhikov et al., 2017), 3 – (Desai, Prasad, 2013) and

4 – (Narwal, Prasad, 2016).

0,86

0,88

0,9

0,92

0,94

0,96

0,98

0,96 0,97 0,98 0,99 1 1,01

a) b)

c) d)

a) b)

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

276

Table 3: MIMO problem (27): performance of approaches.

Criterion

Approach



Proposed



5.00410

-3

0.022 0.128

Proposed



0.028 0.103 0.095



6.67010

-3

0.022 0.140



0.025 0.970 0.102

3.323 10





0.027

0.136

0.02



0.325



0.218



0.045



0.372



0.409



Figure 5: Pareto front estimation in all of the runs (black)

and a single front estimation (grey).

To summarize, all the figures and examination

results prove that the proposed approach and the

optimization algorithm are a reliable combination of

techniques for solving the order reduction problems.

5 CONCLUSIONS

It is widely known that solving the order reduction

problem for LTI systems requires a powerful and

reliable global optimization tool for black-box

problems. Many researchers, according to other

studies on this topic, are using heuristic optimization

techniques, which allow them to achieve satisfying

results. However, for some problems there is an aim

not just to identify the parameters by some criterion,

but to identify the parameters which would fit two or

more criteria.

In order to solve the multi-objective problem, it is

necessary to use the MO optimization algorithm

because the Pareto front is not just a single point in a

vector space and, generally, it cannot be determined

with additive or multiplicative combination of the

criteria. Figures 3 and 5 prove this hypothesis for the

considered problems. It can be seen that the Pareto

front is a curve, so the best solution for the unit-step

function would not prove that this model is the best

for another input. Results received in a single run,

which are marked in these figures in grey, prove that

we receive an acceptable approximation of the Pareto

front. As was shown in this study, a meta-heuristic

can be used to sufficiently improve the multi-

objective optimization algorithm performance with

the same computational resources.

This is one more class of optimization problem for

which the algorithm efficiency and performance

improve after implementing the proposed restart

operator. The results of this work demonstrate that

this algorithm is not only good at estimating the

Pareto front, but can also find good solutions, which

are close or even outperform the best solutions found

by the single criterion optimization tools using the

same resources.

Further work is related to improving the quality of

the estimation of the Pareto front in the case of a

higher criterion number as well as to developing a

meta-heuristic to improve the proposed restart

operator and the performance of different multi-

objective algorithms. The other aspect of further work

is related to using a modified optimization tool to

solve MIMO order reduction problems in which each

output is characterized by its own criteria.

ACKNOWLEDGEMENTS

This research is supported by the Russian Foundation

for Basic Research within project No 16-01-00767.

REFERENCES

Beligiannis, G.N., Tsirogiannis, G.A., and Pintelas, P.E.,

2004. Restartings: a technique to improve classic

genetic algorithms’ performance. International Journal

of Computational Intelligence, vol. 1, pp. 112–115.

Chen, T. C., Chang, C. Y., Han, K. W., 1979. Reduction of

transfer functions by the stability equation method.

Journal of Franklin Inst, vol. 308, no. 4: pp. 389-404.

Desai, S., Prasad, R., 2013. A novel order diminution of LTI

systems using Big Bang Big Crunch optimization and

Routh approximation. Appl. Math. Model, vol. 37: pp.

8016-8028.

Fukunaga, A.S., 1998. Restart scheduling for genetic

algorithms. In: Eiben A.E., Bäck T., Schoenauer M.,

Schwefel HP. (eds) Parallel Problem Solving from

Nature – PPSN V. PPSN 1998. Lecture Notes in

Computer Science, vol 1498. Springer, Berlin,

Heidelberg.

Narwal, A., Prasad, B. R., 2016. A Novel Order Reduction

Approach for LTI Systems Using Cuckoo Search

Optimization and Stability Equation. IETE Journal of

Research, 62(2): pp. 154-163.

0,2

0,4

0,6

0,8

0 0,2 0,4 0,6 0,8 1

Multi-objective Order Reduction Problem Solving with Restart Meta-heuristic Implementation

277

Parmar, G., Prasad, R., Mukherjee, S., 2007. Order

reduction of linear dynamic systems using stability

equation method and GA. International Journal of

computer and Infornation Engeneering, 1(1): pp. 26-

32.

Ramesh, K., Nirmalkumar, A., Gurusamy, G., 2011. Order

Reduction of LTIV continuous MIMO system using

Stability Preserving approximation method.

International Journal of Computer Applications, vol.

36, no. 8: pp. 1-8.

Ryzhikov, I., Semenkin, E., Akhmedova, Sh., 2017. LTI

system order reduction approach based on asymptotical

equivalence and the Co-operation of biology-related

algorithms. IOP Conference Series: Materials Science

and Engineering, vol. 173, 2017.

Ryzhikov, I., Semenkin, E., 2017. Restart operator meta-

heuristics for a problem-oriented evolutionary

strategies algorithm in inverse mathematical miso

modelling problem solving. IOP Conference Series:

Materials Science and Engineering, vol. 173, 2017.

Wang, R., 2013. Preference-Inspired Co-evolutionary

Algorithms. A thesis submitted in partial fulfillment for

the degree of the Doctor of Philosophy, University of

Sheffield: p. 231.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

278