
SLAP: Secure Lightweight Authentication Protocol for
Resource-constrained Devices
Giulio Aliberti
1
, Roberto Di Pietro
2,3
and Stefano Guarino
4
1
Department of Mathematics and Physics, Roma Tre University, Rome, Italy
2
Cyber Security Research Department, Nokia Bell Labs, Paris, France
3
Department of Mathematics, University of Padova, Padua, Italy
4
Istituto per le Applicazioni del Calcolo, Consiglio Nazionale delle Ricerche, Rome, Italy
Keywords:
Light-weight Authentication, IoT, Probabilistic Security.
Abstract:
Motivated by the upcoming Internet of Things, designing light-weight authentication protocols for resource
constrained devices is among the main research directions of the last decade. Current solutions in the literature
attempt either to improve the computational efficiency of cryptographic authentication schemes, or to build a
provably-secure scheme relying on the hardness of a specific mathematical problem. In line with the principles
of information-theoretic security, in this paper we present a novel challenge-response protocol, named SLAP,
whose authentication tokens only leak limited information about the secret key, while being very efficient to
be generated. We do support our proposal with formal combinatorial arguments, further sustained by numeric
evaluations, that clarify the impact of system parameters on the security of the protocol, yielding evidence that
SLAP allows performing a reasonable number of secure authentication rounds with the same secret key.
1 INTRODUCTION
The advent of the Internet of Things (IoT) (Atzori
et al., 2010) is leading to a scenario where a multi-
tude of objects with constrained computational capa-
bilities, such as RFID tags (Vogt, 2002) or wireless
sensors (Gubbi et al., 2013), are necessarily equipped
with identification systems. Additionally, low-end
hardware authentication tokens (Weir et al., 2009)
and, more generally, RSA SecurID tokens (RSA, The
Security Division of EMC, 2015) are increasingly
used to realize two-factor authentication, e.g., for e-
banking services. In this context, light-weight authen-
tication protocols can be used to protect data from
unauthorized and potentially harmful access, while
minimizing computational burden, time delay, and
energy consumption.
Most authentication protocols rely on a challenge-
response mechanism, in which valid responses can
be produced based on a secret key s shared between
client and server. A secure scheme must ensure that, if
s is unknown, producinga valid response is infeasible,
either computationally of probabilistically. However,
the only scheme that guarantees perfect secrecy is
based on the well-knownOne-Time Pad (OTP) (Shan-
non, 1949): an n-bit symmetric secret key s is split
into N sub-keys s
1
,...,s
N
of length n/ N, providing
N authentication rounds each with security parame-
ter ε = 2
−n/N
. To mimic the security of OTP-based
schemes, RSA SecurID tokens (RSA, The Security
Division of EMC, 2015) replace the initial secret key
with a short seed and sub-secret keys (e.g., authenti-
cation codes) are generated from the seed using AES-
based cryptography. RSA SecurID tokens offerstrong
security properties relying on computational security
(i.e., the security of the key derivation mechanism).
Recent research efforts aiming at developing light-
weight and practical authentication protocols mostly
resorted to extensions and variants of the Hopper-
Blum (HB) protocol (Hopper and Blum, 2001). HB
is a challenge-response authentication protocol based
on linear coding: the n-bit symmetric key is “en-
coded” through a set of n-bit challenges playing the
role of parity equations; the obtained “codeword” is
then bitwise xored with some pseudo-random noise
to produce the response. To pass the authentica-
tion test, at least some fixed fraction (e.g., the ma-
jority) of the response bits must be correct, i.e., noise-
less. Despite their simplicity, the security of all HB-
based schemes is again based on computational se-
curity, specifically on the assumption that decoding
linear codes is computationally hard in the presence
Aliberti, G., Pietro, R. and Guarino, S.
SLAP: Secure Lightweight Authentication Protocol for Resource-constrained Devices.
DOI: 10.5220/0006431101630174
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 163-174
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
163

of noise, a problem known as Learning Parity with
Noise (LPN) (Pietrzak, 2012).
In this paper, we introduce SLAP, a novel
light-weight solution that combines ideas from the
aforementioned classes of protocols: inspired by
OTP-based authentication, SLAP trades memory
for achieving security, neither involving CPU-heavy
computations nor relying on computational limita-
tions of the adversary
1
; similarly to HB, SLAP’s sys-
tem parameters are tuned so as to make legitimate
responses discernible from random ones, while con-
currently guaranteeing that challenge-response pairs
leak very limited information about the key. With
respect to OTP-based authentication, SLAP benefits
from each key bit having a positive probability of be-
ing involved in each authentication attempt, thus of-
fering increased flexibility and resilience to common
side channel and physical attacks. As a counterpoint,
to obtain the desired level of security SLAP relies
on multiple challenges per authentication round, with
consequent communication/computation overhead.
Albeit all building blocks of SLAP are extremely
efficient, a direct comparison with previous solutions
in terms of resource consumption, useful to clarify
SLAP’s most suitable application setting, would re-
quire a detailed analysis of memory/cpu/energy foot-
prints that lies beyond the scope of the present paper
and is left to future work. Yet, in this paper we care-
fully assess the relation binding security and system
parameters, to provide clear evidence, both theoreti-
cally and experimentally, that SLAP permits a num-
ber N of secure authentications, where N depends on
system and security parameters. Although our pro-
tocol does not guarantee perfect secrecy, because the
entropy of the key slowly decreases with the number
of intercepted challenge-responsepairs, we do present
combinatorial arguments in support of the soundness
of SLAP. Significantly, numerical evaluations of our
analytical findings allow identifying a few concrete
use cases in which the performance of SLAP is com-
parable to OTP-based authentication, in terms of vol-
ume of secure authentication rounds per key.
Roadmap: related work is reviewed in Section 2;
SLAP is presented in Section 3 and analysed in Sec-
tion 4; Section 5 reports numerical evaluations that
enable tuning all system parameters; finally, Section 6
concludes the paper.
1
Except obvious ones, such as assuming that a brute force
attack is unfeasible.
2 RELATED WORK
In the last few years, the need for light-weight proto-
cols arose from both the growing need to minimize
the power consumption of electronic devices (Pat-
ton and McGuinness, 2014; Chabarek et al., 2008)
and the severe constrains imposed by the upcoming
Internet of Things (Gubbi et al., 2013; Raza et al.,
2013; Sehgal et al., 2012). Several light-weight cryp-
tographic protocols for resources constrained devices
have been proposed (Alippi et al., 2014), aiming at
enabling encryption, signature or hashing (Oder et al.,
2014; Aumasson et al., 2010; Engels et al., 2010). A
few protocols, similarly to our SLAP, are designed
explicitly with authentication in mind, and mostly
based on a challenge-response mechanism. When
symmetric encryption is an option, an extremely fast
and communication-efficient solution consists in us-
ing block ciphers (e.g., AES (Feldhofer et al., 2005)
or HUMMINGBIRD (Engels et al., 2011)) to produce
a valid response based on the challenge and the se-
cret key. However, specific scenarios exist where non-
cryptographic authentication is required/preferred, ei-
ther because of resource limitations (e.g., in RFID
tags or IoT scenarios), or because authentication is
the unique security requirement (e.g., in physical ac-
cess control (Kao et al., 2011)). A possible non-
cryptographic approach, based on the LPN assump-
tion, has its roots in the HB protocol (Hopper and
Blum, 2001). Several variants of HB have been pro-
posed, with HB
+
(Juels and Weis, 2005) and HB
#
(Gilbert et al., 2008) being among the most rele-
vant. However, these computationally efficient HB-
based protocols have high communication complexity
and are, thus, not suitable is many practical applica-
tions. More recently, the Lapin protocol (Heyse et al.,
2012), relying on a variation of LPN, has been pro-
posed to overcome communication issues but its va-
lidity was soon questioned (Gaspar et al., 2014; Bern-
stein and Lange, 2012). In (Armknecht et al., 2014)
it is argued that the design of an LPN-based protocol
for low-cost RFID tags is still an open problem. To
the best of our knowledge, SLAP is the first attempt
to obtain a novel light-weight authentication protocol
based on neither the hardness of a mathematical prob-
lem nor cryptography.
The main drawback of SLAP is the limited num-
ber of authentication rounds allowed with a single
key. However, many attacks are currently able to
compromise the lifetime of a key: side channels can
be used to bypass logical layer protections via, for
instance, timing analysis (Kocher, 1996) or differ-
ential power analysis (Kocher et al., 1999), and re-
source constrained low-cost devices may be exposed
SECRYPT 2017 - 14th International Conference on Security and Cryptography
164

to physical attacks, that undermine the security of the
key. Key rotation or updating techniques, already ap-
plied to resource constrained devices (Bowers et al.,
2013) to defend against key compromise, are a pos-
sible solution to extend the usability of SLAP, al-
though the actual feasibility of a similar approach de-
pends on the specific application setting. Interest-
ingly, SLAP leverages the whole key for each authen-
tication round, so that partial knowledge of the key,
although helping, is not enough to permit a success-
ful authentication.
3 PROTOCOL DESCRIPTION
In this section we present SLAP, an authentication
protocol designed for deviceswith constrained energy
and computational capabilities. From a general stand-
point, SLAP is a challenge-response protocol whose
actors are a client that wants to be authenticated and a
server that manages the authentication request.
Notation. Let us first briefly recap the notation used
in the reminder of this paper: if n ∈N, [n] = {1, . . . , n}
is the set of the first n positive integers; the cardinal-
ity of a set A is |A| ∈ N; F
n
2
denotes the set of all
n-bit vectors x = (x
1
,...,x
n
), x
i
∈ F
2
; if x,y ∈ F
n
2
,
H
n
(x,y) denotes their Hamming distance; finally, if
A = {i
1
,...,i
m
} ⊂ [n], π
A
denotes the projection of n-
bit vectors into the m coordinates identified by A, i.e.:
π
A
: F
n
2
−→ F
m
2
, x 7→ π
A
(x) = (x
i
1
,...,x
i
m
).
Protocol. Now, let us describe SLAP, with the help
of its pseudo-code reported in Protocol 1. The pa-
rameters of the protocol are four non-negative inte-
gers (n,m,k,δ) that satisfy the condition n ≥ m ≥
k ≥ δ. Client and server are assumed to initially
agree on a secret key s ∈ F
n
2
, chosen uniformly at
random, and the server has access to a storage de-
vice D used to keep track of already used challenge-
response pairs. The protocol starts when a new au-
thentication request is sent by the client to the server
(Line 1 and Line 16). The authentication server elab-
orates the request generating uniformly at random a
challenge c ∈ F
n
2
(Line 3), satisfying two conditions:
(i) H
n
(s,c) ∈ [k + δ, n −m + k −δ], and (ii) no pre-
vious challenge-response pair (c
i
,R
i
) exists such that
H
m
(π
R
i
(c),π
R
i
(c
i
)) < k.
2
Then the server sends the
challenge c to the client (Line 5), asking (Line 6) and
2
This check is de facto the only difference between the per-
formance of SLAP at the client and server sides. The
storage and computational overhead scale linearly with the
number of allowed pairs N.
waiting (Line 7) for a response. The client, that was
waiting for a challenge (Line 17), receives c and gen-
erates a valid response R for it (Line 18). A valid
response R must satisfy: (i) R ⊂ [n], (ii) |R| = m, and
(iii) H
m
(π
R
(s),π
R
(c)) ∈ [k −δ, k + δ]. The client then
sends R to the server (Line 19) and waits to receive
an acknowledgement (Line 20). When the server re-
ceives the response R, based on its validity (Line 8),
it accepts (Line 9) or denies (Line 13) the authentica-
tion, sending the appropriate acknowledgement to the
client (Lines 10 and 14). In the former case, it writes
the new pair (c,R) in D (Line 11).
Protocol 1: SLAP authentication protocol.
Parameters: non-negative integers n,m,k,δ such that n ≥m ≥k ≥δ.
Initialization: server and client agree on a secret key s ∈F
n
2
; the
server has access to a storage device D, initially empty.
Server side
1
wait
to receive an authentication request from the client;
2 do
3
generate
uniformly at random a challenge c ∈ F
\
∈
;
4 while H
n
(s,c) /∈ [k + δ,n−m+ k −δ]
OR
∃(c
i
,R
i
) ∈ D : H
m
(π
R
i
(c),π
R
i
(c
i
)) < k;
5
send
c to the client;
6
ask
to the client for a response R ⊂ [n] with |R| = m;
7
wait
to receive the response R from the client;
8 if H
m
(π
R
(s),π
R
(c)) ∈[k−δ,k+ δ] then
9
authentication succeeded
;
10
send
an authentication success acknowledgement to the
client;
11
write
(c,R) in the storage device D;
12 else
13
authentication failed
;
14
send
an authentication failure acknowledgement to the client;
15 end
Client side
16
send
an authentication request to the server;
17
wait
to receive a challenge c ∈C from the server;
18
generate
uniformly at random a valid response R ⊂[n] with
|R|= m;
19
send
R to the server;
20
wait
to receive an authentication acknowledgement from the server;
Comments. Defining a lightweight authentication
protocol that does not rely on cryptography presents
us with two conflictual requirements: to make it dif-
ficult to guess R when s is unknown, and where s, c
and R need to be correlated; yet, if challenge-response
pairs can be easily eavesdropped, the conditional en-
tropy of s given c and R must be large. To solve
this dilemma, we defined a challenge-response mech-
anism that depends on four parameters, with the un-
derlying idea that m, k and δ can be tailored to the
eavesdropping ability of the adversary, while increas-
ing n provides the ultimate defence against brute-
force response-guessing attacks.
SLAP: Secure Lightweight Authentication Protocol for Resource-constrained Devices
165

Informally, a valid response is a set of m indices
such that the challenge and the secret key differ on
a number k ±δ of such indices, and coincide on the
others. Eavesdropping on a successful authentication
round only opens a window on a portion of the key,
and the relative size of m with respect to n allows
tuning the size of this window to deal with different
adversary models. m defines both the amount of in-
formation leaked by overheard traffic, and the amount
of information needed to forge a response, and it can
be neither too small nor too close to n (e.g., m = 1
makes random responses valid with probability 1/2,
while m = n forces R = [n]). In any case, snoop-
ing through the window opened by a response R only
gives a blurred view of the corresponding portion of
the key, with k and δ determining how blurred. k and δ
indeed define mean and variance of H
m
(π
R
(s),π
R
(c))
for a valid R, thus k should be kept close to m/2
and δ should be large to limit information leakage.
However, guessing a valid R is easier if k ≈ m/2 (for
a randomly chosen R, H
m
(π
R
(s),π
R
(c)) ≈ m/2) and
if δ is large (e.g., δ = k = m/2 means all responses
are valid). Luckily, all these apparent contradictions
can be solved by increasing n enough to make brute-
force response-guessing attacks infeasible, even once
the relative size of m, k and δ is fixed to limit eaves-
dropper adversaries. Details on the impact of the four
parameters on the security of SLAP will be provided
in Section 4, together with a motivation for condition
(ii) for the choice of a valid challenge. Condition (i)
is only aimed to make sure that the chosen c does not
condition the admitted range for H
m
(π
R
(s),π
R
(c)), as
stated in Theorem 1.
Finally, to support the efficiency of SLAP, let us
suggest a possible algorithm to generate uniformly at
random a valid response: (i) compute y = s ⊕c; (ii)
apply a random permutation ϕ to y; (iii) randomly
select j ∈ [k −δ,k + δ]; (iv) select the first j indices
{a
1
,...,a
j
} such that y
a
l
= 1 and the first m − j in-
dices {b
1
,...,b
m−j
} such that y
b
l
= 0; (v) define R =
{ϕ
−1
(a
1
),...,ϕ
−1
(a
j
)}∪{ϕ
−1
(b
1
),... , ϕ
−1
(b
m−j
)}.
4 SECURITY ANALYSIS
In this section, we analyse the security of SLAP
considering first an oblivious attacker, who tries to
get authenticated without any prior knowledge of
the key, and later on an eavesdropper attacker, who
tries to take advantage of previously intercepted valid
challenge-response pairs to forge a correct response to
a newly issued challenge. For the sake of readability,
all proofs are deferred to the Appendix.
4.1 Oblivious Adversary Model
We here analyse the security of SLAP in the oblivious
adversary model, a scenario where the attacker has no
information about the secret key whatsoever. A sim-
ilar attacker cannot do anything better than randomly
guessing a valid response for the issued challenge
(guessing the key would be even harder). The follow-
ing results determine how hard a response-guessing
attack is, as a function of system parameters. First,
we find the number of valid challenges.
Theorem 1. For any secret key s ∈ F
n
2
and for any
challenge c ∈ F
n
2
, if the condition
k+ δ ≤ H
n
(s,c) ≤ n −m+ k−δ (1)
is satisfied, then for each j ∈ [k −δ,k + δ] the chal-
lenge c admits (at least) a valid response R such that
H
m
(π
R
(s),π
R
(c)) = j. The cardinality of the set of
challenges C = C (n,m,k,δ) satisfying (1) is
|C | =
n−m+k−δ
∑
i=k+δ
n
i
. (2)
Next, we determine the number of valid responses.
Theorem 2. For any secret key s ∈ F
n
2
, let c ∈ C be
such that H
n
(s,c) = i. The number of valid responses
to c is
R(i) =
k+δ
∑
j=k−δ
i
j
n−i
m− j
. (3)
In particular, if P denotes the set of all valid
challenge-response authentication pairs, it holds
|P | = |P (n,m,k, δ)| =
n−m+k−δ
∑
i=k+δ
R(i)
n
i
. (4)
Now, let Aut denote the event of being authen-
ticated when the secret key s and a challenge c are
chosen as prescribed by Protocol 1, and when the re-
sponse R is chosen uniformly at random among all
subsets R ⊂ [n] such that |R| = m. The following re-
sults define the security of SLAP under the oblivious
adversary model.
Lemma 1. In the oblivious adversary model, let s
(0)
and c
(0)
be such that H
n
(s
(0)
,c
(0)
) = j. It holds
P
Aut | {s = s
(0)
,c = c
(0)
}
=
R( j)
n
m
(5)
Theorem 3. In the oblivious adversary model, the
success probability of a response-guessing attack is
P(Aut) =
1
|C |
n
m
n−m+k−δ
∑
j=k+δ
n
j
R( j) (6)
The closed expression (6) is analysed in Section 5
for different choices of parameters n, m, k, and δ.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
166

4.2 Eavesdropper Adversary Model
In this section we analyse the security of SLAP in
the eavesdropper adversary model, i.e., against an at-
tacker able to eavesdrop the communicationsbetween
client and server to earn information about the key.
We aim at estimating the probability ε of guessing a
valid response for a newly issued challenge after the
attacker eavesdropped on N > 0 challenge-response
cycles. At a high level, we will proceed as follows:
• we find suitable conditions to ensure that the en-
tropy of the key is large enough to avoid key-
guessing attacks (Theorem 4);
• we exhibit sample attack scenarios showing that
focusing on the overall entropy of the key (i.e.,
the key pool size) is not sufficient, and that further
attention has to be pointed towards the entropy of
each individual key bit;
• we identify suitable and general conditions to
prevent the adversary from earning a dangerous
amount of information about (portions of) the key,
also showing how these conditions can be en-
forced by a proper tuning of system parameters.
Numerical evaluations of our findings are later dis-
cussed in Section 5.
4.2.1 Number of Compatible Keys
To ease exposition, let us denote
I
N
=
(c
1
,R
1
),...,(c
N
,R
N
)
∈ P
N
a set of N valid challenge-response pairs, and
S
N
=
v ∈F
n
2
:H
m
(π
R
(v),π
R
(c)) = k±δ,∀(c,R) ∈I
N
the restricted key pool induced by eavesdropping I
N
,
i.e., the set of all keys that are compatible with the N
challenge-response pairs in I
N
. The size of S
N
, de-
noted by Y
N
, is a random variable that depends on
the specific choice of I
N
. Y
N
thus gives a first mea-
sure of the security of SLAP against an eavesdrop-
per adversary, by quantifying her uncertainty on the
key (i.e., the entropy of the key) after discarding non-
compatible candidate keys.
Theorem 4. In the eavesdropper adversary model,
after N valid challenge-response pair has been inter-
cepted, the expected size of the key pool is
E[Y
N
] = 2
n
ρ
N
, where ρ = 2
−m
k+δ
∑
j=k−δ
m
j
(7)
Theorem 4 estimates how many vectors of F
n
2
, on
average, are compatible with N randomly selected au-
thentication pairs. The more N increases, the lower is
the number of these vectors. We observe that, for any
fixed N, m6∼n is enough to guarantee that E[Y
N
] tends
to infinity as n grows. Conversely, when all parame-
ters are fixed, as N grows E[Y
N
] tends to zero, i.e.,
sooner or later the key needs to be updated.
4.2.2 Potential Threats
As mentioned before, the fact that a response only in-
volves m < n indices makes it possible for the adver-
sary to exploit significant information earned about a
subset of key bits, even if she has no information at all
about the others. To better explain this, we describe
two sample attack scenarios.
Generalized Replay Attack. If a client is authen-
ticated through a valid pair (c,R), and a challenge
c
(0)
such that π
R
(c) = π
R
(c
(0)
) is subsequently gen-
erated, the authentication system becomes vulnerable
to a replay attack since R would also be a valid re-
sponse to c
(0)
. Precisely, there are exactly 2
n−m
valid
challenges for which the above condition is satisfied,
and the attacker can easily detect this vulnerability by
simply computing H
m
(π
R
(c),π
R
(c
(0)
)). More gener-
ally, if R
′
⊂ R is such that π
R
′
(c) = π
R
′
(c
(0)
), it is
possible for the adversary to define a new response
R
′′
by simply adding m −|R
′
| random indices to R
′
.
Using R
′′
to respond to c
(0)
results in an attack that
succeeds with significantly higher probability than a
standard response-guessing attack. To contrast sim-
ilar generalized replay attacks, in Protocol 1 we as-
sumed that the server uses a storage device D for log-
ging authentication pairs, discarding a newly gener-
ated challenge c
(0)
if there exists (c,R) ∈ D such that
H
m
(π
R
(c),π
R
(c
(0)
)) < k. This condition, in fact, to-
gether with k ∼ m, guarantees that the success prob-
ability of generalized replay attacks is comparable
to that of a standard attack, i.e., that replay-like at-
tacks give the adversary no significant advantage. Let
us notice that the practical relevance of replay at-
tacks can be limited by making |C | large (e.g., choos-
ing n ≫ m). In fact, a large |C | guarantees that
H
m
(π
R
(c),π
R
(c
(0)
)) is large with high probability for
randomly chosen R. Additionally, the δ-tolerance pre-
scribed by SLAP makes even harder to forge valid re-
sponses based on previous ones.
Correlation-like Attack. Let us introduce a toy
example in order to underline what information an
eavesdropper adversary can obtain at single-bit level,
and how this information can be exploited. We con-
sider the following N authentication pairs based on
parameters n = 5, m = 3, k = 1, δ = 0, where re-
SLAP: Secure Lightweight Authentication Protocol for Resource-constrained Devices
167

sponses have been represented using red boxes:
s =
1 0 0 1 0
c
1
=
1 1 0 1 0
c
2
=
1 1 0 1 1
c
3
=
1 0 1 0 0
.
.
.
c
N
=
1 1 1 0 0
Since the distance between each challenge and the
key must be k = 1, and since each response has
m = 3 components, the probability that a challenge
and the key coincide at position i ∈ R is (m−k)/m =
2/3. This means that the adversary can mount a
correlation-like attack to guess key bits, and the suc-
cess rate of the attack grows with the number N of
eavesdropped authentication pairs. In the example,
the leftmost bit of each challenge is 1 and all (shown)
responses include index 0, thus suggesting to the at-
tacker that the first key bit is also 1 (which is indeed
true). Significantly less information is revealed about
other indices. In general, this can happen either be-
cause an index has been used too rarely, so that the
statistical sample is inadequate, or because the cor-
responding bit is (almost) equally often 0 or 1 in the
available challenges. As a consequence, a similar at-
tack can be prevented either (again) imposing a mini-
mal distance among challenges over response indices,
or setting k = m/2 (as we always do in Section 5).
4.2.3 Securing SLAP
Although we suggested specific countermeasures to
the two threats presented in Section 4.2.2, we need to
identify the common traits of eavesdropping attacks,
and to identify a likewise general defence mecha-
nism. The examples show that an eavesdropper ad-
versary can succeed at exploiting the correlation be-
tween multiple sequences of indices that appear to-
gether in different valid responses. As a consequence,
not only the overall entropy of the key, but also the
single-bit level entropy must be kept large. This goal
is achieved by imposing parameter conditions that
aim at limiting superimpositions between different re-
sponses during the protocol execution. In particular,
we estimate the number of repetitions of a given se-
quence of h bits in different responses, and we use this
instrument to identify a choice of system parameters
that make harder to exploit the correlation among bits
of the eavesdropped authentication pairs.
Let {i
1
,...,i
h
} ⊆ [n] be a set of h indices. We de-
fine the random variableC
i
1
,...,i
h
=
∑
N
j=1
D
( j)
i
1
,...,i
h
where
D
( j)
i
1
,...,i
h
=
(
1, if i
1
,...,i
h
⊆ R
j
0, otherwise
(8)
C
i
1
,...,i
h
counts the number of times indices i
1
,...,i
h
∈
[n] appear simultaneously in the valid responses
R
1
,...,R
N
. We can estimate this variable as follows.
Theorem 5. In the eavesdropper adversary model, it
holds
E[C
i
1
,...,i
h
] =
N
|C |
n−m+k−δ
∑
i=k+δ
n
i
p
i
(9)
where
p
i
≤
min
∑
k+δ
j=k−δ
i−l
j−l
n−i−(h−l)
m−j− (h−l)
: l = 0, . . . h
∑
k+δ
j=k−δ
i
j
n−i
m−j
.
(10)
5 PERFORMANCE EVALUATION
The main purpose of this section is to numerically
evaluate the theoretical results from Section 4, in or-
der to show that SLAP is secure against unauthorized
authentication attempts.
5.1 Experimental Results
We set m = 2k and n ≫m, accordingly to our security
analysis (see Section 4.2.2), describing three main in-
stances: i) the logarithmic case m,k ∈ Θ(log
2
n), ii)
the polynomial case m, k ∈ Θ(
√
n), and iii) the linear
case m,k ∈Θ(n). We also evaluate the impact of little
variations of δ.
Number of Challenges. Theorem 1 gives the num-
ber of challenges. Since m = 2k, we can simplify for
easy evaluations
|C | =
n−(m−(k−δ))
∑
i=k+δ
n
i
=
n−(k+δ)
∑
i=k+δ
n
i
Due to binomial coefficient properties, we obtain
|C | ≥
n−(k+δ)
∑
i=k+δ
n
k+ δ
≥
n
k+ δ
k+δ
and, for δ = 0, we have the rough but simple lower-
bound
|C | ≥
n
k
k
(11)
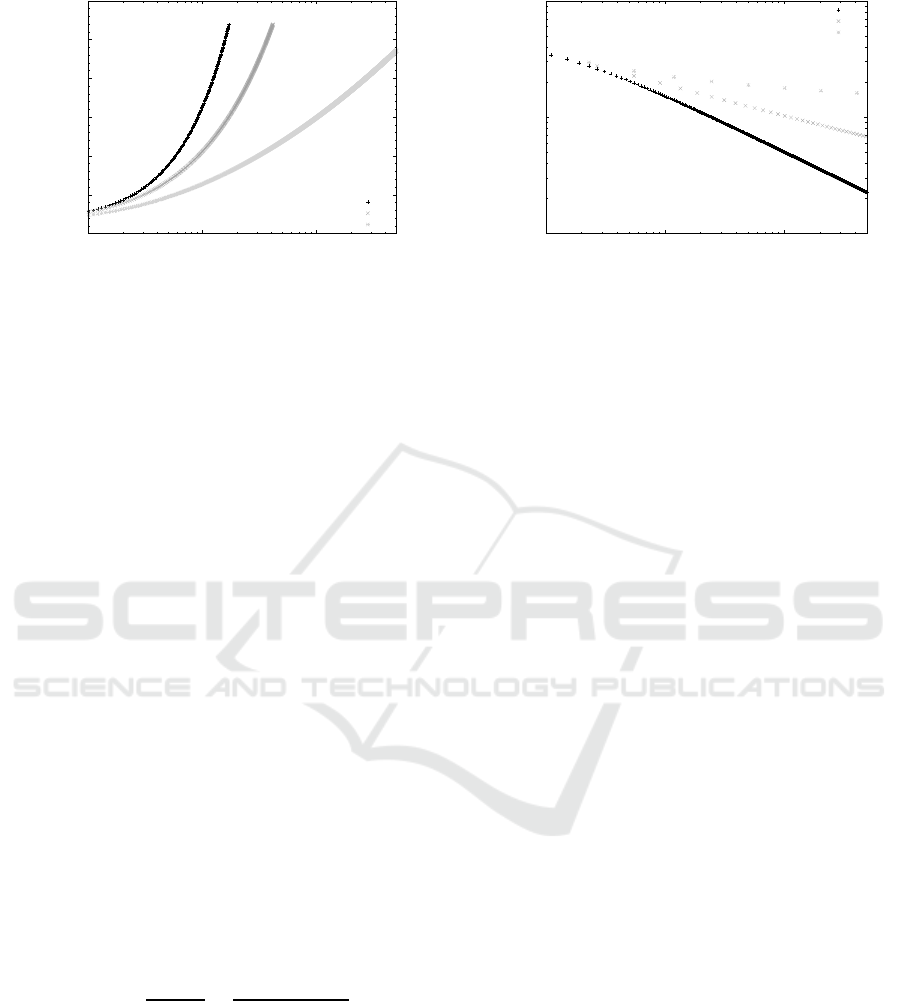
This bound suffices to show that the number of chal-
lenges is large enough, as illustrated in Figure 1 that
comprises cases where n grows exponentially, poly-
nomially or linearly faster than k.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
168
1
100000
1e+10
1e+15
1e+20
1e+25
1e+30
10 100 1000
number of challenges
parameter n
linear case: k=n/4
polynomial case: k=sqrt(n)
logarithmic case: k=log(n)
Figure 1: Number of challenges, accordingly to (11).
Number of Valid Responses. Theorem 2 gives the
number of valid responses. In particular, (3) gives the
number of valid responses for a fixed distance i be-
tween challenge and secret key. To easy computa-
tions, we derive the following upper bound for R(i)
by applying binomial coefficient properties:
R(i) ≤
k+δ
∑
j=k−δ
n/2
j
n/2
2k− j
≤ (2δ+ 1)
n/2
k
2
(12)
Equation (12) shows that the number of valid re-
sponses is relatively high and, consequently, that the
probability of guessing a valid response is a threat
to consider. This motivates the adoption of several
challenge-response cycles per authentication, as ex-
plained later in this section.
Oblivious Adversary Model. Theorem 3, espe-
cially (6), estimates the probability of randomly
guessing a valid response. The estimation is evalu-
ated through the following bound (note that R(i) is
maximized by choosing i = n/2, for m = 2k):
P(A) ≤
R(n/2)
n
2k
≤
(2δ+ 1)
n/2
k
2
n
2k
(13)
where we used (12) in the last passage. Figure 2
illustrates the upper bound in (13) in the linear, poly-
nomial and logarithmic cases when δ = 0. The con-
vergence to zero is rather slow in each case, and
this is mainly due to the high number of valid re-
sponses, as already advanced by (12). To overcome
this issue, the server can ask the client to provide
an answer to a number h > 1 of challenges for each
0.01
0.1
1
10 100 1000
upper bound of probability
parameter n
linear case: k=n/4
polynomial case: k=sqrt(n)
logarithmic case: k=log(n)
Figure 2: Probabilities of guessing a valid response in the
oblivious adversary model, accordingly to (13).
authentication. If P(A) is the probability of guess-
ing a valid response for determinate parameters, then
P(A)
h
< P(A) becomes the probability of guessing h
challenges. This techniques helps at making arbitrar-
ily harder for the attacker to obtain an unauthorized
access through response-guessing attacks. The trade-
off is that the parameter N, used in Section 4 to rep-
resent the number of authentications must be divided
by h. Thus, reducing the total number of secure au-
thentications.
Eavesdropper Adversary Model. Theorem 4 and
Theorem 5 estimate the number of keys compatible
with N authentication pairs and the repetitions of in-
dices over N responses, respectively. The number of
compatible keys, given by (7), after N = 100 is illus-
trated in Figure 3, that focuses on highlighting differ-
ences in linear, polynomial and logarithmic cases, and
in Figure 4, that focuses on the parameter δ. In partic-
ular, we observe that the larger n is with respect to k
(e.g. logarithmic and polynomial cases), the larger is
the number of compatible keys; further, as n overtakes
N, the number of compatible keys begins to grow ex-
ponentially faster, and δ fluctuations positively impact
this growth.
For any sequence of indices i
1
,...,i
h
, Theorem 5,
especially (9), estimates its number of occurrences in
valid responses after N authentications. The lower
this estimated value is, the more unlikely it is that the
attacker deploys a correlation attack. Since for h ≥ 2
we have E[C
i
1
,i
2
] ≤ E[C
i
1
,...,i
h
], we can limit ourself to
analyse the case h = 2. We computed the upper bound
derivable from (10) for δ = 0,1, 5,15, N = 100, con-
sidering the linear case in Figure 5, and the polyno-
mial case in Figure 6. We observe that the parameter
δ does not affect significantly the value, and that the
number of repetitions is overall low with an evident
advantage in the polynomial case.
SLAP: Secure Lightweight Authentication Protocol for Resource-constrained Devices
169

1e-100
1e-50
1
1e+50
1e+100
1e+150
1e+200
1e+250
1e+300
inf
10 100 1000
compatible keys
parameter n
linear case: k=n/4
polynomial case: k=sqrt(n)
logarithmic case: k=log(n)
Figure 3: Number of compatible keys in the eavesdropper
adversary model, accordingly to (7): δ = 0, N = 100, linear,
polynomial and logarithmic cases.
1e-100
1e-50
1
1e+50
1e+100
1e+150
1e+200
1e+250
1e+300
inf
100 1000
compatible keys
parameter n
linear case: k=n/4, delta=15
linear case: k=n/4, delta=5
linear case: k=n/4, delta=1
linear case: k=n/4, delta=0
Figure 4: Number of compatible keys in the eavesdropper
adversary model, accordingly to (7): δ = 0,1,5,15, N =
100, linear case.
5.2 Use Cases
We provide practical examples for specific protocol
parameters, comparing results with the one-time pad
based authentication scheme.
One-time Pad Based Scheme. We assume that the
secret key has length n = 1024 and that ε = 2
−64
is the
security parameter. The one-time pad based scheme
can guarantee N = 1024/64 = 16 secure authentica-
tions, i.e. 64 bits per authentication.
SLAP: Linear Case. We make the above assump-
tions n = 1024 and ε = 2
−64
, and we fix the param-
eters (n,m,k, δ) = (1024, 512,256,2). The number
of challenges is |C | ≈ 1.8×10
308
and the probability
of randomly guessing a valid response without eaves-
dropping the communication is P(A) ≈0.174. We can
impose 26 challenge-response cycles as requirement,
obtaining the wanted security: P(A)
26
≈ε. After N =
14 ×26 = 364 challenge-response cycles, the proba-
bility of guessing the secret key in the eavesdropper
5
10
15
20
25
30
35
40
45
50
100 1000
expected number of repetitions
parameter n
linear case: k=n/4, delta=15
linear case: k=n/4, delta=5
linear case: k=n/4, delta=1
linear case: k=n/4, delta=0
Figure 5: Repetitions of index pairs in the eavesdropper
adversary model, accordingly to Theorem 5: N = 100,
δ = 0,1,5, 15, linear case.
2
4
6
8
10
12
14
100 1000
expected number of repetitions
parameter n
polyomial case: k=sqrt(n), delta=15
polyomial case: k=sqrt(n), delta=5
polyomial case: k=sqrt(n), delta=1
polyomial case: k=sqrt(n), delta=0
Figure 6: Repetitions of index pairs in the eavesdropper
adversary model, accordingly to Theorem 5: N = 100,
δ = 0,1,5, 15, polynomial case.
model is 1/E[Y
416
] < ε. For N = 15 ×26 = 390 the
probability is higher than ε; thus, a total of 15 authen-
tications can be performed with security ε achieving a
performance comparable with the one-time pad based
authentication scheme.
SLAP: Polynomial Case. We change the parame-
ters to (n, m, k,δ) = (1024,62, 32,1). The number of
challenges is still approximated by |C | ≈ 1.8×10
308
and P(A) ≈ 0.292. Thus, 36 challenges for authenti-
cation are required to obtain P(A)
36
≈ ε. We obtain
that N = 15 ×36 = 540 authentication pairs can be
generated without compromising the security of the
system, namely 1/E[Y
540
] ≈ε. After the 16-th authen-
tication, we obtain that 1/E[Y
576
] ≈ 0.46. This means
that after 16 authentications the security of the system
is compromised, as in the one-time pad based authen-
tication. The advantage of the polynomial case over
the linear case of SLAP is that repetitions of indices
are less frequent (see Figure 6).
SECRYPT 2017 - 14th International Conference on Security and Cryptography
170

SLAP: Logarithimc Case. We change the param-
eters to (n,m,k, δ) = (1024,10,5,1). The number of
challenges is still not varying, while P(A) ≈ 0.656.
Thus, about 105 challenges are required to obtain
P(A)
105
≈ ε. The system starts to be compromised
after N = 16×105 authentications, similarly to other
cases and repetitions of indices are even less frequent
than the polynomial case.
5.3 Discussion
The security guaranteed by our scheme is close to
the theoretical limit achievable since it trades memory
requirements with security properties at almost the
same rate of the one-time pad based scheme. How-
ever, there a few significant differences that makes
SLAP preferable for some applications. The main
one is that, at each authentication, the one-time pad
based scheme uses −log
2
(ε) bits of the secret key
while SLAP spreads the information required to be
authenticated over all the n bits of the secret key. This
property makes SLAP more resistant against leakages
of the secret key. In fact, let us assume that the at-
tacker breaches in the authentication server and suc-
cessfully recovers few bits, i.e. −log
2
(ε), of the se-
cret key. If the server implements the one-time pad
based scheme, then the attacker can leak the bits re-
quired for the next authentication gaining access to
the system. If the server implements SLAP, the at-
tacker has not earned enough information to generate
valid responses. In fact, to generate a response for a
given challenge, the attacker must know at least k±δ
bits of the secret key where the challenge differs and
m−(k ±δ) where it coincides. Hence, at least m bits
of the secret key must be leaked by the attacker to
generate a valid response to one challenge (and it is
still not enough to be authenticated). This property
makes SLAP more resistant than the one-time based
scheme against leakages of the secret key.
Another difference is that SLAP is more resistant
against successful impersonation attacks. In fact, let
us assume that a malicious server (i.e. an attacker per-
sonifying the server) collects answers from a client
that wants to be authenticated. If the one-time pad
based scheme is the algorithm of choice, then the an-
swers generated by the client are the bits of the secret
key; thus, the malicious server gains access to the sys-
tem by using these bits. Instead, with SLAP, the an-
swers generated by the client are valid responses for
particular challenges. This means that the malicious
server has to ask for a challenge to the real server,
and forward it to the client; this step introduces a de-
tectable delay in the process since multiple challenge-
response pairs are required for one authentication.
The last difference is the flexibility offered by
SLAP. Adopting the SLAP protocol, the server has
the capability of varying the number of challenges re-
quired to be authenticated in the system during the ex-
ecution of the protocol – i.e. increasing or decreasing
the number of possible secure authentications. For
instance, it might be the case that a server features
different services but that not all of them needs to
be protected with the highest level of security. Using
SLAP, the server has the flexibility of setting differ-
ent security requirements for each of these services
by simply defining, for each of them, the number of
challenges that need to be answered. The server can
also change these values at any time during the exe-
cution of the protocol without acknowledging clients;
indeed, clients do not necessarily need to know how
many answers they must provide for gaining the ac-
cess to a particular service. In the one-time pad based
scheme it is certainly possible to subdivide the se-
cret key to achieve the same goal, but clients must be
aware of this subdivision as well and the management
effort of the server becomes more complicated.
6 CONCLUSION
In this paper we have introduced SLAP, a light-
weight authentication protocol that guarantees a pre-
dictable number of secure authentications. The num-
ber of authentication rounds is proportional to the
length of the secret key shared between server and
client, and thus it is customizable. Differently from
prior work, the proposed protocol is only based on
information-theoretic security methods, thus attack-
ers with strong computational capabilities have no ad-
vantages. The simplicity of the SLAP scheme makes
it an ideal authentication protocol to be implemented
in RFID tags, IoT scenarios, or other contexts where
light-weight protocols are required.
The thorough mathematical analysis of SLAP’s
features has been supported by an extensive experi-
mental campaign – run with real world system param-
eters. Achieved results show the efficacy and practi-
cality of the proposed solution. To further assess the
concrete impact of SLAP, in the next future we plan
to both pinpoint SLAP’s theoretical implant, and care-
fully assess its resource footprint.
REFERENCES
Alippi, C., Bogdanov, A., and Regazzoni, F. (2014).
Lightweight cryptography for constrained devices. In
SLAP: Secure Lightweight Authentication Protocol for Resource-constrained Devices
171

Integrated Circuits (ISIC), 2014 14th International
Symposium on, pages 144–147.
Armknecht, F., Hamann, M., and Mikhalev, V. (2014).
Lightweight authentication protocols on ultra-
constrained rfids - myths and facts. In Radio
Frequency Identification: Security and Privacy Issues
- 10th International Workshop, RFIDSec 2014, Ox-
ford, UK, July 21-23, 2014, Revised Selected Papers,
pages 1–18.
Atzori, L., Iera, A., and Morabito, G. (2010). The In-
ternet of Things: A survey. Computer Networks,
54(15):2787–2805.
Aumasson, J.-P., Henzen, L., Meier, W., and Naya-
Plasencia, M. (2010). Quark: A lightweight hash.
In CHES, volume 6225 of Lecture Notes in Computer
Science, pages 1–15. Springer.
Bernstein, D. J. and Lange, T. (2012). Never trust a
bunny. In Hoepman, J.-H. and Verbauwhede, I., edi-
tors, RFIDSec, volume 7739 of Lecture Notes in Com-
puter Science, pages 137–148. Springer.
Bowers, K. D., Juels, A., Rivest, R. L., and Shen, E.
(2013). Drifting keys: Impersonation detection for
constrained devices. In INFOCOM, pages 1025–1033.
IEEE.
Chabarek, J., Sommers, J., Barford, P., Estan, C., Tsiang,
D., and Wright, S. J. (2008). Power awareness in net-
work design and routing. In INFOCOM, pages 457–
465. IEEE.
Engels, D. W., Fan, X., Gong, G., Hu, H., and Smith,
E. M. (2010). Hummingbird: Ultra-lightweight cryp-
tography for resource-constrained devices. In Finan-
cial Cryptography Workshops, volume 6054 of Lec-
ture Notesin Computer Science, pages 3–18. Springer.
Engels, D. W., Saarinen, M.-J. O., Schweitzer, P., and
Smith, E. M. (2011). The hummingbird-2 lightweight
authenticated encryption algorithm. IACR Cryptology
ePrint Archive, 2011:126.
Feldhofer, M., Wolkerstorfer, J., and Rijmen, V. (2005). Aes
implementation on a grain of sand. IEE Proceedings-
Information Security, 152(1):13–20.
Gaspar, L., Leurent, G., and Standaert, F. (2014). Hardware
implementation and side-channel analysis of lapin. In
Topics in Cryptology - CT-RSA 2014 - The Cryptogra-
pher’s Track at the RSA Conference 2014, San Fran-
cisco, CA, USA, February 25-28, 2014. Proceedings,
pages 206–226.
Gilbert, H., Robshaw, M. J. B., and Seurin, Y. (2008).
Hb#: Increasing the security and efficiency of hb+.
In Smart, N. P., editor, EUROCRYPT, volume 4965 of
Lecture Notes in Computer Science, pages 361–378.
Springer.
Gubbi, J., Buyya, R., Marusic, S., and Palaniswami, M.
(2013). Internet of things (iot): A vision, architec-
tural elements, and future directions. Future genera-
tion computer systems, 29(7):1645–1660.
Heyse, S., Kiltz, E., Lyubashevsky, V., Paar, C., and
Pietrzak, K. (2012). Lapin: An efficient authentica-
tion protocol based on ring-lpn. In Canteaut, A., edi-
tor, FSE, volume 7549 of Lecture Notes in Computer
Science, pages 346–365. Springer.
Hopper, N. J. and Blum, M. (2001). Secure human identi-
fication protocols. In Boyd, C., editor, ASIACRYPT,
volume 2248 of Lecture Notes in Computer Science,
pages 52–66. Springer.
Juels, A. and Weis, S. A. (2005). Authenticating perva-
sive devices with human protocols. In CRYPTO, pages
293–308.
Kao, Y.-W., Luo, G.-H., Lin, H.-T., Huang, Y.-K., and
Yuan, S.-M. (2011). Physical access control based
on qr code. In Cyber-enabled distributed comput-
ing and knowledge discovery (CyberC), 2011 Inter-
national Conference on, pages 285–288. IEEE.
Kocher, P., Jaffe, J., and Jun, B. (1999). Differential
power analysis. Lecture Notes in Computer Science,
1666:388–397.
Kocher, P. C. (1996). Timing attacks on implementations of
diffie-hellman, rsa, dss, and other systems. In Koblitz,
N., editor, CRYPTO, volume 1109 of Lecture Notes in
Computer Science, pages 104–113. Springer.
Oder, T., P¨oppelmann, T., and G¨uneysu, T. (2014). Beyond
ECDSA and RSA: lattice-based digital signatures on
constrained devices. In The 51st Annual Design Au-
tomation Conference 2014, DAC ’14, San Francisco,
CA, USA, June 1-5, 2014, pages 1–6.
Patton, E. W. and McGuinness, D. L. (2014). A power con-
sumption benchmark for reasoners on mobile devices.
In The Semantic Web - ISWC 2014 - 13th International
Semantic Web Conference, Riva del Garda, Italy, Oc-
tober 19-23, 2014. Proceedings, Part I, pages 409–
424.
Pietrzak, K. (2012). Cryptography from learning parity with
noise. In SOFSEM, volume 7147 of Lecture Notes in
Computer Science, pages 99–114. Springer.
Raza, S., Shafagh, H., Hewage, K., Hummen, R., and
Voigt, T. (2013). Lithe: Lightweight Secure CoAP
for the Internet of Things. Sensors Journal, IEEE,
13(10):3711–3720.
RSA, The Security Division of EMC (2015). RSA SecureId
token. Available on line.
Sehgal, A., Perelman, V., Kuryla, S., and Sch¨onw¨alder, J.
(2012). Management of resource constrained devices
in the internet of things. IEEE Communications Mag-
azine, 50(12):144–149.
Shannon, C. (1949). Communication theory of secrecy sys-
tems. Bell System Technical Journal, Vol 28, pp. 656-
715.
Vogt, H. (2002). Efficient object identification with passive
RFID tags. In Proceedings of the First International
Conference on Pervasive Computing, volume 2414 of
Lecture Notes in Computer Science, pages 98–113,
Zurich. Springer-Verlag.
Weir, C. S., Douglas, G., Carruthers, M., and Jack, M. A.
(2009). User perceptions of security, convenience and
usability for ebanking authentication tokens. Comput-
ers & Security, 28(1-2):47–62.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
172

APPENDIX
Let R = {R⊂[n],|R|= m}be the set of formally valid
responses. Our envisaged adversaries can be mod-
elled as follows.
Definition 1 (Oblivious Adversary Model). We define
the discrete probability space (Ω,F ,P) where
i) The sample space is
Ω =
(s,c,R) ∈ F
n
2
×C ×R
;
ii) F = 2
Ω
is the set of events (each event is a subset
of outcomes);
iii) P : Ω → [0,1], E ⊆ Ω 7→
|E|
Ω
is the probability
mass function that assigns events to probabilities.
Definition 2 (Eavesdropper Adversary Model). We
define the discrete probability space (Ω,F ,P) where
i) the sample space is
Ω =
n
{s,(c
1
,R
1
),...,(c
N
,R
N
)} ∈ F
N
2
×(C ×R )
N
s.t.
H
m
(π
R
i
(s),π
R
i
(c
i
)) ∈ [k−δ,k + δ],∀i = 1, . . . , N
o
;
ii) F = 2
Ω
is the set of events;
iii) P : Ω → [0,1], E ⊆ Ω 7→
|E|
Ω
is the probability
mass function that assigns events to probabilities.
Proof of Theorem 1. Given a challenge c ∈ C , a valid
response for c is a subset R ⊂ [n] of m indices such
that H
m
(π
R
(s),π
R
(c)) ∈ [k −δ,k+ δ], where s ∈ F
n
2
is
the secret key selected by the protocol. To generate
a valid response, the secret key s and the challenge c
must differ in, at least, j ∈ [k −δ,k+ δ] of their com-
ponents, while coinciding in m− j components. This
is equivalent to
∃j ∈[k−δ, k+ δ] : j ≤H
n
(s,c) ≤ n−(m− j). (14)
When Eq. (1) is satisfied, then also Eq. (14) is sat-
isfied by all j ∈ [k −δ, k + δ]. Hence, for all values
of j in this range, the challenge c admits a valid re-
sponse R such that H
m
(π
R
(s),π
R
(c)) = j. Then, for
any distance i ∈ {k + δ, . . . ,n −(m −(k−δ))}, there
are
n
i
combinations where exactly i components of
s are left unchanged. Summing over i, we obtain the
cardinality of C and Eq. (2).
Proof of Theorem 2. For a fixed Hamming distance i,
to generate a valid response for c, the client chooses
any number j ∈ [k −δ,k + δ], j out of i components
where s and c differ, and m− j out of n−(m− j) com-
ponents where they coincide. Summing all the com-
binations over j, we obtain Eq. (3). Due to Eq. (1), the
admitted values of the Hamming distance between s
and c are {k+ δ, . . .,n−(m−(k−δ))}. Thus, Eq. (4)
is obtained by summing the number of valid responses
for any admitted value of distance.
Proof of Lemma 1. By definition of conditional prob-
ability, we have
P
A | {s = s
(0)
,c = c
(0)
}
=
=
P
A ∩ {s = s
(0)
} ∩ {c = c
(0)
}
P
{s = s
(0)
} ∩ {c = c
(0)
}
.
Due to Eq. (3) of Theorem 2 and iii) of Definition 1,
the numerator is
R
H
n
(s
(0)
,c
(0)
)
|Ω|
=
R( j)
|Ω|
since this ratio coincides with the number of
favourable outcomes divided by the total number of
outcomes. Instead, the denominator is
n
m
/|Ω| since
there are
n
m
(i.e. number of possible responses)
favourable outcomes. Assembling together numera-
tor and denominator, we conclude the proof.
Proof of Theorem 3. P(Aut | {s = s
(0)
}) by definition
of conditional probability is equivalent to
∑
c
(0)
∈C
P(Aut | {s = s
(0)
,c = c
(0)
})P({c = c
(0)
}).
Due to Eq. (5), the sum can be rewritten as
∑
c
(0)
∈C
R(H
n
(s
(0)
,c
(0)
))
n
m
1
|C |
=
1
|C |
n
m
∑
c
(0)
∈C
R(H
n
(s
(0)
,c
(0)
)).
Thus, by rearranging terms in the sum, we obtain
P(Aut | {s = s
(0)
}) =
1
|C |
n
m
n−(m−(k−δ))
∑
j=k+δ
n
j
R( j).
(15)
To compute P(Aut), we use again the definition of
conditional probability to conclude the proof
P(Aut) =
∑
s
(0)
∈F
n
2
P(Aut | {s = s
(0)
})P({s = s
(0)
}) =
=
∑
s
(0)
∈F
n
2
P(Aut | {s = s
(0)
})2
−n
=
= P(Aut | {s = s
(0)
}).
Proof of Theorem 4. We start by enumerating each
vector of n components, namely by writing F
n
2
=
{v
(i)
, ∀i = 1,...,2
n
}. This allows us to introduce the
random variables
X
(i)
N
: Ω −→ N, ω 7→
(
1, if v
(i)
∈ S
N
(ω)
0, otherwise
SLAP: Secure Lightweight Authentication Protocol for Resource-constrained Devices
173

and to write Y
N
as a sum of them, namely
Y
N
=
2
n
∑
i=1
X
(i)
N
. (16)
Due to the linearity of the expected value, we have
E[Y
N
] =
2
n
∑
i=1
E[X
(i)
N
]. (17)
Proving the following three facts will conclude the
proof:
i) E[X
(i)
N
] = E[X
( j)
N
],∀i, j;
ii) E[X
(i)
N
] = E[X
(i)
1
]
N
;
iii) E[X
(i)
1
] = ρ = 2
−m
∑
k+δ
j=k−δ
m
j
.
Claim i) means that, from the attacker perspec-
tive, each vector in F
n
2
is equally likely to belong to
S
N
. This is true because, even if a vector v
(i)
is more
likely to belong to S
N
for a particular outcome ω
i
,
the sample space Ω allows both the secret key s and
the set I
N
to vary among all possible combinations
in Ω; thus, any other vector v
( j)
would also be more
likely to belong to S
N
for the appropriate outcome
ω
j
. Differently said, the symmetries in the probabilis-
tic model imply that, on average, all the vectors are
equally likely of being in S
N
.
To prove claim ii), we start writing the event { ω ∈
Ω : v
(i)
∈S
N
(ω)}as intersection of the sets A
j
= {ω ∈
Ω :H
m
(π
R
j
(v
(i)
),π
R
(c
j
)) ∈[k−δ,k+δ]}representing
the outcomes in which v
(i)
is compatible with the j-th
authentication pair. Hence, we have
E[X
(i)
N
] = P
{ω ∈ Ω : v
(i)
∈ S
N
(ω)}
= P
N
\
j=1
A
j
.
Since the authentication pairs (c
j
,R
j
) are uniformly
at random chosen by the protocol, the events A
j
are
independent from each other and we can write
E[X
(i)
N
] = P
N
\
j=1
A
j
=
N
∏
j=1
P(A
j
) =
N
∏
j=1
E[X
(i)
1
] = E[X
(i)
1
]
N
.
Claim iii) follows from next considerations. For
any secret key s and for any N, when the authenti-
cation pair (c, R) is used for an authentication, the
attacker acquires the information that a number j ∈
[k−δ,k+ δ] of bits of the challenge c, among those m
indexed by R, differ from bits of s. These j bits can
be combined in
m
j
different ways, and j can be any
value in [k−δ, k + δ]. We notice also that the attacker
is not earning information on the remaining n−m bits
of s. Thus, by eavesdropping a single authentication
pair, the attacker is equally uncertain on a total of
2
n−m
k+δ
∑
j=k−δ
m
j
possible secret keys, that is the cardinality of S
1
. In
particular, we have,
E[X
(i)
1
] = P
{v
(i)
∈S
1
}
=
2
n−m
∑
k+δ
j=k−δ
m
j
2
n
= ρ.
Proof of Theorem 5. Since challenges and responses
are independently at random chosen,
E[C
i
1
,...,i
h
] =
N
∑
j=1
E[D
( j)
i
1
,...,i
h
] = NE[D
( j)
i
1
,...,i
h
],
where the last passage is justified by the fact that chal-
lenges and responses are also identically distributed.
For a given challenge c at distance i from the se-
cret key, accordingly to Eq. (3), there is a number
R(i) =
k+δ
∑
j=k−δ
i
j
n−i
m− j
of valid responses but only a fraction R(i,h) of them
contains the sequence i
1
,...,i
h
. Since the sequence
i
1
,...,i
h
is fixed, we can define l ∈ {0, . . . , h} as the
number of indices in {i
1
,...,i
h
} where c differs from
the secret key. In this way, R(i, h) can be written in
function of l:
R(i,h) = R(i,h,l) =
k+δ
∑
j=k−δ
i−l
j −l
n−i−(h−l)
m− j −(h−l)
.
In particular, we have the inequality
R(i,h) ≤ min{R(i,h,l) : l = 0,...h} .
Hence, for a challenge at distance i from the secret
key, the probability that indices i
1
,...,i
h
appear to-
gether in a valid response is bounded by
p
i
=
R(i,h)
R(i)
≤
min{R(i,h,l) : l ∈ {0, . . . , h}}
R(i)
.
The probability that a uniformly at random selected
challenge has distance i from the secret key is
n
i
/|C |. Thus,
E[D
( j)
i
1
,...,i
h
] =
n−(m−(k−δ))
∑
i=k+δ
n
i
|C |
p
i
and, multiplying this value by N, we conclude the
proof.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
174
