
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
Dmitry Popov, Alexandr Klimchik and Ilya Afanasyev
Institute of Robotics, Innopolis University, Universitetskaya Str. 1, Innopolis, Russia
Keywords:
Stiffness Modeling, Human Mechatronics, Motion Control Systems, Robot Kinematics.
Abstract:
This paper presents a low-cost anthropomorphic robot, considering its design, simulation, manufacturing and
experiments. The robot design was inspired by open source Poppy Humanoid project and enhanced up to
12 DoF lower limb structure, providing additional capability to develop more natural, fast and stable biped
robot walking. The current robot design has a non-spherical hip joint, that does not allow to use an analytical
solution for the inverse kinematics, therefore another hybrid solution was presented. Problem of robot joint’s
compliance was addressed using virtual joint method for stiffness modeling with further compensation of elas-
tic deflections caused by the robot links weight. Finally, we modeled robot’s lower-part in V-REP simulator,
manufactured its prototype using 3D printing technology, and implemented ZMP preview control, providing
experiments with demonstration of stable biped locomotion.
1 INTRODUCTION
The progress in creation of highly specialized robotic
systems contributes to automation of different every-
day life aspects that can partially or fully replace hu-
mans in the future in some routine activities. The
development of androids is one of the most relevant
solution for successful robot operations in human en-
vironment with enhanced functionality. These robots
usually resemble human beings in appearance and/or
internal construction, having the similar body shape
structure and walking principles. One of the most im-
portant part of an anthropomorphic robot is a pelvis
with the lower limbs, which form the lower-part body.
During last decades, robotics community has pro-
posed some successful models of biped robots with
similar lower limb structure with 6 Degree of Free-
dom (DoF) per leg, having 3 DoF hip, 1 DoF knee,
and 2 DoF ankle. Thus, there are some well-known
human-size androids like Honda ASIMO (Sakagami
et al., 2002), WABIAN from Waseda University (Ya-
maguchi et al., 1999), Boston Dynamics Atlas (not a
commercially available model), Pal Robotics Reem-
C (Ferro and Marchionni, 2014), Android Technics
AR-600 (Khusainov et al., 2015), etc. But for small-
size robots the most popular models are ROBOTIS
Darwin (Ha et al., 2011), Aldebaran Robotics Nao
(Gouaillier et al., 2009) and Poppy Humanoid
1
with
1
Open source Poppy Humanoid project, www.poppy-
project.org
5 DoF leg (Lapeyre et al., 2013b).
Stiffness modeling in robotics is considered for in-
dustrial manipulators, where problem of end-effector
precise positioning under external and internal load
are critical (Pashkevich et al., 2011). In humanoid
robots accurate positioning is not always necessary,
but with high compliance in links or joints, deflections
caused by payload or link weights can affect robot sta-
bility. Therefore those deflections should be consid-
ered and compensated as possible.
Our goals in this paper are:
1. Adapt Poppy-like robot to new mechanical struc-
ture with 6 DoF lower limbs, which are able
to support robot’s upper-part (including a torso,
hands, a head, sensors and a possible payload).
2. Implement stiffness model of the robot.
3. Develop software for fast, stable robot walking
that also considers robot joints compliances and
successfully eliminates them.
4. Reduce the robot production cost using hobby ser-
vomotors, inexpensive fabrication methods and
cost-efficient electronics components.
The rest of the paper is organized as follows. Sec-
tion 2 presents the robot design. Section 3 consid-
ers robot lower body’s kinematics analysis includ-
ing forward, inverse kinematic problem and robot
workspace. Section 4 describes stiffness model. Sec-
tion 5 includes trajectory planning and compensation.
66
Popov, D., Klimchik, A. and Afanasyev, I.
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid.
DOI: 10.5220/0006432000660078
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 66-78
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Finally, we conclude in section 6 with discussion on
future work.
2 ROBOT DESIGN
The main feature of two-legged robot platform is the
ability to walk. Therefore, the human body has been
taken as a reference of the most advanced two-legged
mechanism. In general human leg has dozen of DoF,
but in case of bipedal walking, leg motions can be ap-
proximated with 6 DoF, three in the sagittal plane (an-
kle, knee, hip), one in the horizontal plane (hip) and
two in the frontal plane (hip, ankle). Existing open
source project Poppy has only 5 DoF per leg, 3 DoF
in hip, 1 DoF in knee, and 1 DoF in ankle. In order
to use standard 6 DoF approximation, addition DoF
was added in the ankle. Usage of expensive Robo-
tis Dynamixel MX-28, MX-64 is another problem of
Poppy. To reduce overall cost of the robot, we pro-
pose to use more cheaper SpringRC SR-518 servo-
motors with 2 Nm torque and RS485 bus connection.
Mounting places were also altered in order to fit this
new motors.
Since human thigh bones are inclined by 6-7 de-
grees, it was also implemented by (Lapeyre et al.,
2013a) in Poppy robot and our robot limb design. It
allows to reduce falling speed and decrease the lateral
motion of torso for single support phase and double
support phase respectively. In order to make robot
construction lighter and stiffer, we used mesh struc-
ture for thigh and shin.
Usually, most biped robots have unproportionally
big foot. It is required in order to increase pas-
sive stability with increased support polygon. In our
project, the foot size is proportional to human foot,
thus providing additional difficulties to stabilization
algorithms, but at the same time increasing robot mo-
bility (Lapeyre et al., 2014).
(a) 3D printed prototype. (b) Model in V-REP.
Figure 1: Bipedal robot.
Table 1: Robot model joint range of motion.
Joint
Human (deg.) Robot (deg.)
Hip Y
-30 to 45 -25 to 45
Hip Z
-45 to 50 -40 to 60
Hip X
-15 to 130 -60 to 100
Knee X
-10 to 155 -6 to 112
Ankle X
-20 to 50 -35 to 30
Ankle Y
-30 to 60 -35 to 35
Table 2: Robot model mass parameters.
Name Mass (kg) Mass Poppy (kg)
Thigh 0.226 0.239
Shin 0.124 0.108
Foot 0.116 0.047
Total 1.21 1.14
Table 3: Robot model size parameters.
Name Size (mm) Size Poppy (mm)
Thigh 181 181
Shin 178 177
Foot 129 x 63 145 x 50
Total 129 x 200 x 500 145 x 187 x 495
According to Table 1, robot leg’s motion range is
close to human, excepting joints with rotation around
X axis. Their range is enough for walking, but can
limit robot maneuverability for other activities. The
limitations on joint motion range will be considered
in Section 5.
In order to specify requirements to the robot
hardware part, the combination of Dassault Systmes
SolidWorks CAD tool and robot simulator Coppelia
Robotics V-REP were used (Rohmer et al., 2013).
Robot prototype was manufactured using Fused
Deposition Modeling (FDM) technique with Acry-
lonitrile butadiene styrene (ABS) polymer. It allows
to reproduce robot mechanical part on every low-cost
3D printer.
Manufactured prototype and robot model in sim-
ulation environment are shown in Figure 1a and 1b
correspondingly. Table 2 and 3 shows proposed robot
mass and size parameters in comparison with lower
half of Poppy robot. Total mass and size parame-
ters remains the same, despite additional servomotor
in ankle joint (6th DoF).
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
67
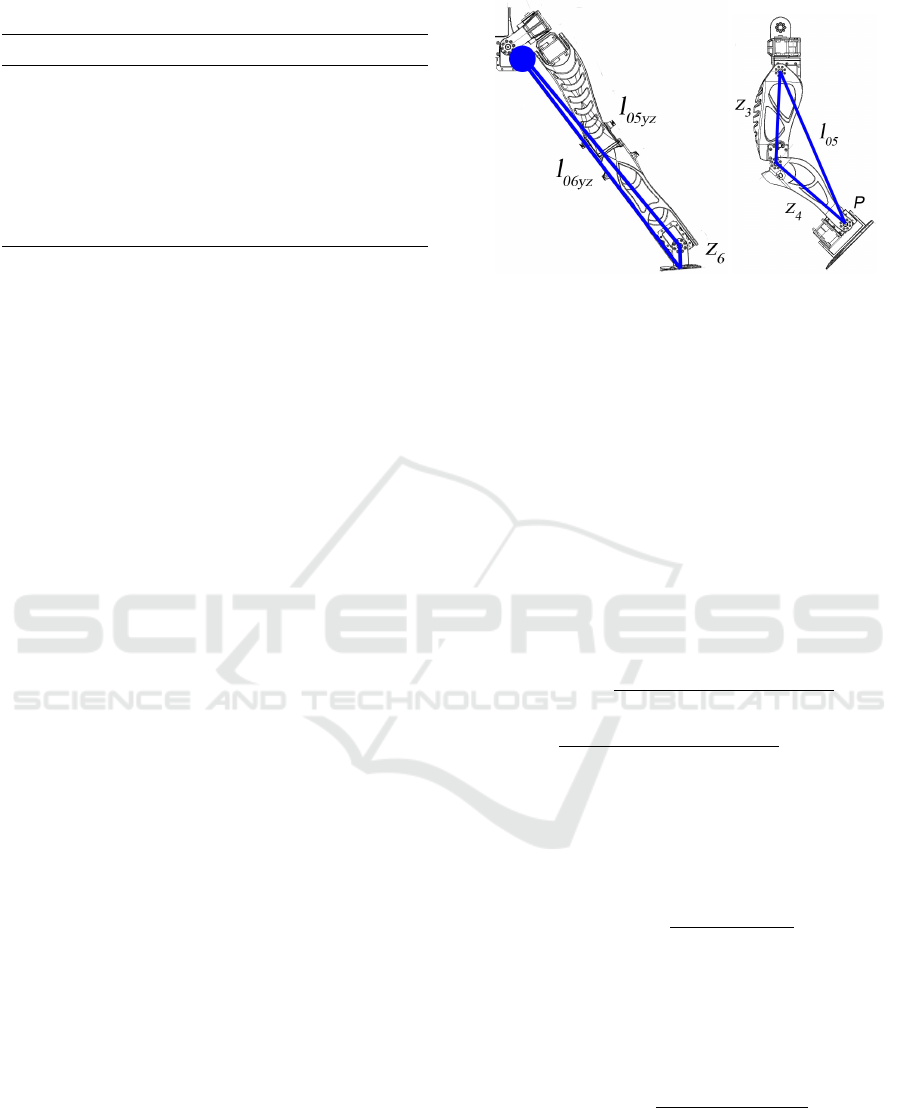
Table 4: Robot model mDH parameters.
θ
n
d
n
, mm a
n−1
, mm α
n−1
, rad Offset
q1 0 19 (y0) π/2 0
q2 47 (z2) 52 (y1) π/2 π/2
q3 0 0 π/2 π/2
q4 -23 (-y3) 181 (z3) 0 0
q5 0 178 (z4) 0 0
q6 0 0 π/2 0
3 KINEMATICS MODELING
3.1 Forward Kinematics
Forward or direct kinematics is the task of determin-
ing the position and orientation of the end-effector by
giving configuration of the robot. The robot can be
modeled as a kinematic chain of 7 links connected
by 6 joints. The base frame of the robot located in
the center of the waist. The local frames are assigned
to joints, according to modified Denavit-Hartenberg
(mDH) convention presented in (Craig, 2005). Ta-
ble 4 shows robot mDH parameters. Since the right
and left leg are identical, kinematics only for one leg
will be considered.
T F = T 0 ∗T1 ∗ T 2 ∗ T 3 ∗ T 4 ∗ T 5 ∗ T 6 ∗ T 7 =
=
r11 r12 r13 T x
r21 r22 r23 Ty
r31 r32 r33 T z
0 0 0 1
(1)
Final transformation matrix T F from the base to the
end-effector can be obtained by multiplying transfor-
mational matrices of all joints (1).
3.2 Inverse Kinematics Problem
The purpose of solving the inverse kinematics (IK) is
to find the angle of each joint for a known foot posi-
tion and orientation. IK can be solved in two different
ways: analytically and numerically. Analytical solu-
tion for 6 DoF serial manipulator can be hard to obtain
directly or geometrically like in chapter 1 (Siciliano
and Khatib, 2008), so different advanced techniques
like Pieper method are usually used.
3.2.1 Analytical Solution
For solving IK with (Peiper, 1968) method serial ma-
nipulator should have 3 joints with consecutive axes
(a) Frontal plane. (b) Sagittal plane.
Figure 2: Robot leg.
intersecting at one point. Its not possible to use it for
the considered robot. Therefore, let us consider an-
other, similar modification, with spherical joint in the
hip.
In order to simplify inverse kinematics, it is pos-
sible to find a geometrical solution for frontal (Fig-
ure 2a) and sagittal (Figure 2b) planes separately. In-
termediate steps of finding inverse kinematics solu-
tion can be found in appendix of this paper.
q1 = sin
−1
(r32 · cos(q6) − r33 · sin(q6)) (2)
q2 = atan2
r12 · cos(q6) − r13 · sin(q6)
−cos (q1)
,
r22 · cos(q6) − r23 · sin(q6)
cos(q1)
(3)
q3 = atan2(−z4 · sin(q4) · A+
(z3 + z4 · cos(q4)) · B,
z4 · sin(q4) · B + (z3 + z4 · cos(q4)) · A)
(4)
q4 = cos
−1
l
05
2
− z3
2
− z4
2
2 · z3 · z4
(5)
q5 = atan2 (−r11 · sin(q1)sin (q2)+
r21 · cos(q2)sin (q1) −r31 · cos(q1),
r11 · cos(q2) + r21 · sin (q2)) −q3 − q4
(6)
q6 = cos
−1
l
06yz
2
− l
05yz
2
− z6
2
2·l
05yz
· z6
!
(7)
Equations (2-7) shows solutions for inverse kinemat-
ics problem for 6 DoF robot with spherical hip.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
68

3.2.2 Numerical Solution
The inverse kinematics problem in the general case
is the searching for the solution of a set of nonlin-
ear algebraic equations. Most popular methods are
the iterative ones. The most common method is the
Newton-Raphson method, that can be found in (Jazar,
2010).
Before solving inverse kinematics with numerical
method it necessary to find Jacobian of the robot.
The time derivative of the kinematics equations
yields the robot Jacobian, which defines the joint con-
tribution to the linear and angular velocity of the end-
effector. Jacobian matrix has the size of 6xN, where
N number of DoF. It consists of two parts: Transla-
tional and Rotational. Jacobian for left leg:
J
ee
(q) =
J
ν
(q)
J
ω
(q)
(8)
where J
ν
(q) – translational part; J
ω
(q) – rotational
part.
Jacobian can be computed as the time derivative
of forward kinematics equations, with skew theory,
or as numerical derivatives. In this work, numerical
derivatives were used.
T F = T 0 ∗ [T (k − 1)(q,π) ∗ H(π
k
)∗
T (k + 1)(q,π)] ∗ T 7
(9)
T
0
k
= T 0 ∗ [T (k − 1)(q,π) ∗ H
0
(π
k
)∗
T (k + 1)(q,π)] ∗ T 7
(10)
where T (q,π) - the transformation matrices on the left
and right sides of the currently considered parameter
π
k
, H
0
(π
k
) is the differential transformation matrix.
Elements of Jacobian will be equal to:
J
π,k
=
T
0
k, (1,4)
T
0
k, (2,4)
T
0
k, (3,4)
[T
0
k
∗ T F
−1
]
(3,2)
[T
0
k
∗ T F
−1
]
(1,3)
[T
0
k
∗ T F
−1
]
(2,1)
(11)
There are numerous ways how to use Jacobian,
but one of the most popular ones are pseudoinverse
method and damped least square (DLS) method. The
pseudoinverse method is widely discussed in the lit-
erature, but it often performs poorly because of in-
stability near singularities. The damped least square
method has better performance (Buss, 2004). Both of
these methods were implemented and compared.
3.2.3 Hybrid Solution
In the proposed robot configuration hip joint is not
spherical since the first three axes do not intersect at
one point that means that previously described analyt-
ical solution cannot be used. Thus, numerical solution
in this case shows non constant efficiency.
In order to improve numerical method efficiency
a hybrid approach from (Cisneros Lim
´
on et al., 2013)
is used. It consists of two phases. Phase one is
to obtain approximate solution, since similar robot
configuration with spherical hip joint is very close
to our robot configuration. Phase two – use this
approximate solution as initial for numerical method.
It allows to greatly reduce the number of iterations.
The hybrid algorithm of inverse kinematics:
1. Set the initial counter i = 0.
2. Find q(0) by using analytical solution of similar
robot.
3. Calculate the residue δT (q(i)) = J(q(i))δq(i). If
every element of T (q(i)) or its norm ||T (q(i))|| is
less than a tolerance, ||T (q(i))|| < ε then termi-
nate the iteration. The q(i) is the desired solution.
4. Calculate q(i + 1) with pseudoinverse or DLS or
any other technique.
5. Set i = i + 1 and return to step 3.
The performance of the hybrid and numerical al-
gorithm was compared in order to evaluate its effi-
ciency. The main evaluation parameters are (1) the
number of iterations, which is needed to find a de-
sired precision and orientation, and (2) the mean time
required for computing this solution.
This evaluation was carried out over a data set
consisting of 750 points along gait trajectory. Desired
accuracy for numerical algorithm is equal to 10
−6
m.
Desired end effector position in X, Y, Z coordinates
is shown in Figure 9a - 9c, whereas achieved joint
angles is shown in Figure 9d. The results of the eval-
uation are shown in Table 5.
Table 5: Performance comparison of inverse kinematics al-
gorithms.
Indicator
Iterations,
ms
Execution
time, ms
Analytical 1 0.04
Hybrid DLS 4 0.24
Numerical
DLS
104 4.46
Numerical
pseudoinverse
205 14.24
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
69

Hybrid solution is up to 20x faster than numeri-
cal DLS. It also has 100% cover rate, which means
that all points of the test set (inside workspace) were
reached. This algorithm allows real-time calculation
with 50 Hz control loop, which is maximum for used
robot.
3.3 Workspace Analysis
The workspace of a manipulator is defined as the vol-
ume of space, which the end-effector can reach. Two
different definitions of workspace are usually used. A
reachable workspace is the volume of space within
which every point can be reached by the end effec-
tor in at least one orientation. A dexterous workspace
is the volume of space within which every point can
be reached by the end effector in all possible orienta-
tions. The dexterous workspace is a subset of reach-
able workspace (Jazar, 2010; Siciliano and Khatib,
2008).
According to robot task - forward walking on the
flat surface, only inclusive orientation workspace is
needed. In this case end-effector orientation locked
to 0 deg. in roll, pitch and yaw. The workspace
was calculated for different left foot positions rela-
tive to the torso coordinate Z: 0.325, 0.35, 0.375, and
0.43 meters (Figure 3). As a performance index for
workspace Jacobean condition number was chosen.
Condition number shows general accuracy, dexterity
of the robot, closeness to singularity.
Since the robot configuration is a 6R serial chain
for one leg, workspace is limited by serial singular-
ity and mechanical joint limits. Serial singularity
can be identified by low condition number near it.
The mechanical joints limit appears as an unreach-
able area near the Y axis zero position (Hip joint lim-
its) see Figure 4a, 4b, 4c and as an ellipse inside the
workspace at small torso height (Knee joint limit) see
Figure 4a, 4b.
Figure 3: Foot positions relative to the torso coordinate Z.
(a) Distance between foot and the torso Z=325 mm.
(b) Distance between foot and the torso Z=350 mm.
(c) Distance between foot and the torso Z=375 mm.
(d) Distance between foot and the torso Z=430 mm.
Figure 4: Achievable foot location and condition number
with example configuration.
4 STIFFNESS ANALYSIS
In real life robot mechanical components (both joints
and links) are not perfectly rigid, so the foot and
torso position can differ from the expected one un-
der the load induced my robot link weights. So if we
need an accurate robot location and stable locomo-
tion, we need to calculate these deflections and pos-
sibly to compensate them. This can be done by de-
veloping and analyzing robot stiffness model. This
stiffness model can be obtained using Virtual Joint
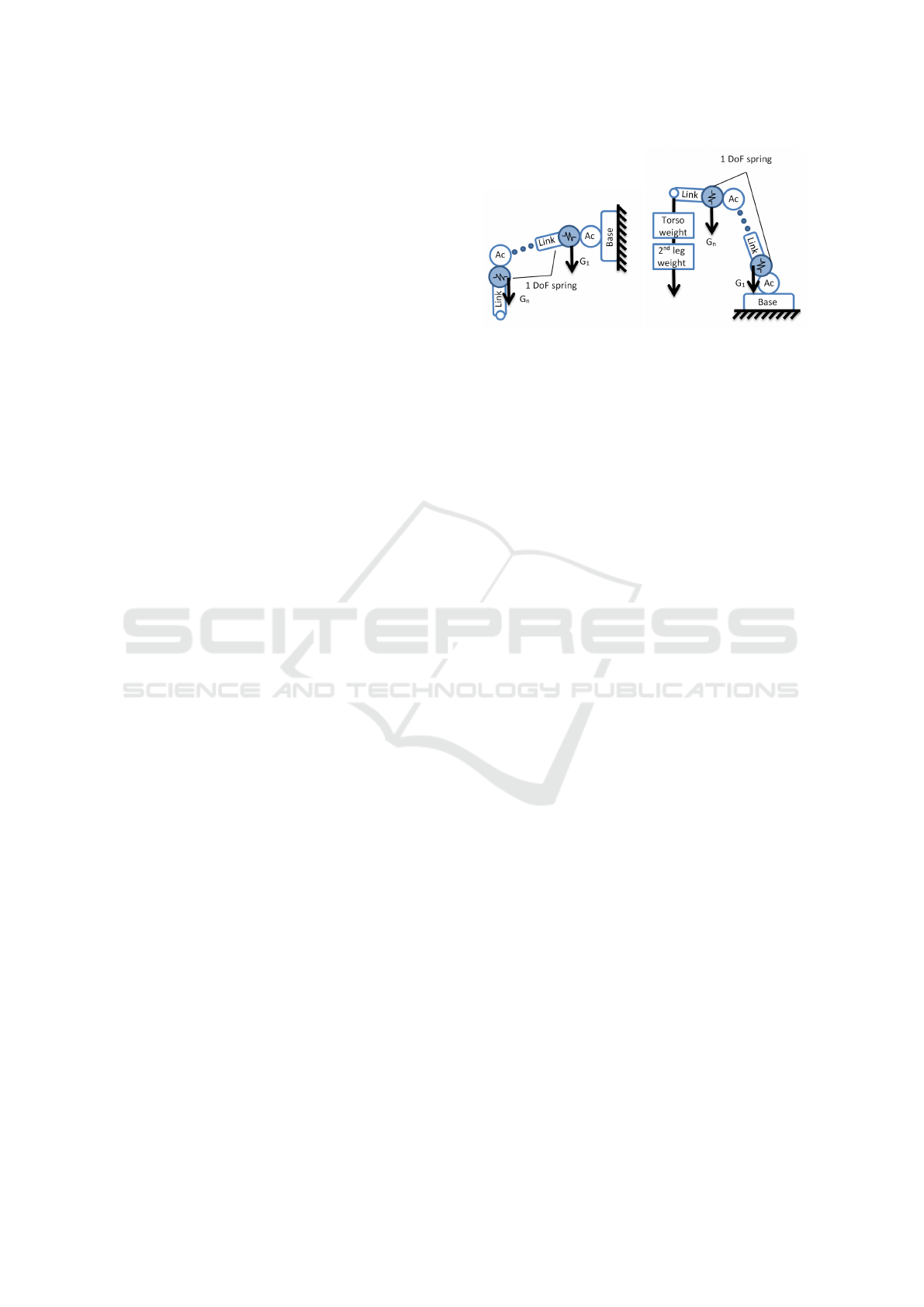
Method (VJM) (Pashkevich et al., 2011). According
to this method non-rigid manipulator links can be rep-
resented as pair of rigid link and 6 DoF virtual spring
and non-rigid actuators as perfect actuator and 1 DoF
virtual spring describing its elasticity.
In practice, the end-effector position (foot or/and
torso position) can be found from the extended geo-
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
70
metric model as
t = g(q,θ) (12)
where q is the vector of actuator coordinates q =
(q
1
,q
2
,...,q
n
)
T
and θ the vector of virtual joint co-
ordinates θ = (θ
1
,θ
2
,...,θ
m
)
T
. Since the link weights
are the main source of deflections in anthropomorphic
robots, it should be also considered in the model. Ex-
ternal load caused by weight of the links can be repre-
sented as forces acting in the node-points correspond-
ing to virtual spring locations. In the simplified model
used in this paper these virtual springs take into ac-
count both link and actuator compliances. By apply-
ing principle of virtual work, the static equilibrium of
corresponding static system can be founded as (Klim-
chik et al., 2014)
J
(G)T
θ
· G + J
(F)T
θ
· F = K
θ
· θ (13)
where the matrix J
(G)
θ
=
h
J
(1)T
θ
,..,J
(n)T
θ
i
T
aggregates
partial Jacobians from the robot base to correspond-
ing node point with gravity load, J
(F)
θ
is the Jaco-
bian from base of the robot to end-effector with ex-
ternal load, the vector G aggregates forces applied
in the internal nodes (caused by gravity), F is vec-
tor of external load applied to the end-effector and
K
θ
= diag(K
θ1
,...,K
θn
) diagonal matrix with stiff-
ness of all virtual springs. Desired static equilibrium
configuration can be found using iterative algorithm
(Klimchik et al., 2014) .
F
i+1
= (J
(F)
θ
· K
−1
θ
· J
(F)T
θ
)
−1
· (t
i+1
− g(q,θ
i
)+
J
(F)
θ
i
· θ
i
− J
(F)
θ
· K
−1
θ
· J
(G)T
θ
· G
i
)
θ
i+1
= K
−1
θ
(J
(G)T
θ
· G
i
+ J
(F)T
θ
· F
i+1
)
(14)
and the Cartesian stiffness matrix K
C
can be computed
as follows
K
C
∗
∗ ∗
=
J
θ
· K
−1
θ
· J
T
θ
J
q
J
q
0
−1
(15)
this allows us to obtain force-deflection relation
∆t = K
−1
C
· F (16)
where ∆t end-effector deflections, and estimate com-
pliance errors caused by gravity forces.
For the considered humanoid robot the main
source of elasticity is related to the motor and gear-
box flexibility. So, for simplicity, all links are consid-
ered to be rigid while actuated joints are considered to
be deformable. Friction forces are not taken into ac-
count. According to the VJM notation 1 DoF virtual
springs will be added after each actuator.
(a) Left leg model. (b) Right leg model.
Figure 5: Robot VJM model.
For stiffness analysis of humanoid (similarly to
kinematic and dynamic analyses) two walking phases
should be addressed: single support phase (SSP) and
dual support phase (DSP). In dual support stage both
legs are on the ground. Assuming that there is no slip
between surface and robot feet, it can be represented
as parallel manipulator with two 6R serial chains. De-
flections from external forces will only affect position
of robot trunk and, assuming that deflections too small
to move robot center of mass (CoM) out of support
polygon, do not contribute to robot stability.
Most critical stage for bipedal robot where deflec-
tions can have a strong effect on stability is single sup-
port stage. In this stage one of the robot legs is swing
and deflections caused by gravity force or/and exter-
nal load can displace swaying leg closer to the ground
or collide them. This undesired contact may lead the
robot to fall. Robot VJM model in that stage can be
introduced as two serial chains (Figure 5a and 5b).
the first chain (Figure 5b) consist of 6 active joints
and 6 virtual joints, base fixed to the surface. In addi-
tion to gravity forces G
n
, there are external loadings
caused by weight of upper body and swing leg. Sec-
ond chain (Figure 5a) consists of 6 active joints and
6 virtual joints, base position can be found as end-
effector position of first chain plus deflections in the
end-effector of first chain. Second chain affected only
by gravity forces G
n
.
Total deflection can be calculated in 3 steps:
1. Calculate deflection for standing leg pelvis chain
with gravity load and external load in end-effector
that correspond to pelvis (upper body) mass +
swing leg mass.
2. Calculate deflections for pelvis swing leg chain
with swing leg gravity load.
3. Combine deflections from 2 chains.
Deflection magnitudes for different swing leg
heights (presented in Figure 3) within the reachable
workspace shown in Figure 6a, 6b, 6c, 6d. Right
leg configuration (fixed on the floor) used for these
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
71

(a) Distance between foot and the torso Z=325 mm.
(b) Distance between foot and the torso Z=350 mm.
(c) Distance between foot and the torso Z=375 mm.
(d) Distance between foot and the torso Z=430 mm.
Figure 6: Deflections magnitude of the left foot for different
swing leg hight.
figures is static and all joint coordinates are equal to
zero. It is shown that deflections are increasing near
the border of the workspace. The minimal deflections
can be achieved close to (0;0) point, but this configu-
ration is not reachable by the swing leg for the heights
less than 375 mm.
Deflection vector components for the swing leg
high 375mm are shown in Figure 7a, 7b, 7c. Ad-
ditional figures for other leg highs are presented in
Appendix (Figures 13-16). Deflections in X and Y di-
rections can be positive or negative, depending on the
leg configuration. This behavior is explained by shift-
ing robot center of mass. Deflections in Z direction
have maximum magnitude and are the most critical
ones, since they shift robot foot closer to the ground.
(a) Deflections in X directions.
(b) Deflections in Y directions.
(c) Deflections in Z directions.
Figure 7: Deflection vector components for distance be-
tween foot and the torso Z=375 mm.
5 TRAJECTORY PLANNING
The biped walking pattern was obtained using Zero
Moment Point (ZMP) preview control, proposed by
(Kajita et al., 2003). ZMP preview control allows to
obtain CoM trajectory based on ZMP-reference tra-
jectory as it is shown in Figure 8a, 8b. With CoM
trajectory and robot leg’s end-effector trajectories it
is possible to find joint angles with inverse kinemat-
ics described previously. Trajectory generated with
this method assumes that robot links and joints are
perfectly stiff. In order to include information about
possible deflections to trajectory generation, external
compensation technique is required.
The following algorithm for simple off-line com-
pensation for SSP is used:
1. Generate trajectory for CoM using ZMP preview
control.
2. Calculate deflections in each SSP for both legs for
all points on trajectory.
3. Find new legs end effector coordinates as p
new
=
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
72

(a) Robot motion in sagittal plane.
(b) Robot motion in lateral plane.
Figure 8: Walking pattern generated by preview control.
p − ∆t.
4. Recalculate inverse kinematics for new trajecto-
ries.
For simulation following walking pattern genera-
tion parameters were used:
• Step size - 6 cm
• CoM height - 43 cm
• Number of step phases = 15 (for demonstration)
• Control frequency - 50 Hz
• Leg lift - 5 cm
• Dual support phase - 20%.
Ankle trajectories in X, Y, Z plane are shown in
Figure 9a, 9b, 9c respectively. Deflections in X and
Y planes are small compared to Z. Table 6 shows nor-
malized position error value with and without com-
pensation. High improvement factor can be explained
by the linearity of the model. Joint trajectories with
and without compensation are presented in Figure 9d.
Knee, hip and ankle joints rotating around Y axis have
the most essential changes due to compensation, since
they correspond to movements of end-effector in Z di-
rection, where deflections have maximal magnitude.
Difference between reference and compensated con-
trol signal for left leg ankle shown in Figure 10. Since
only the SSP is considered for compensation, error for
intervals where the left leg placed on the ground are
equal to zero. Lower amplitude of error in the first
step can be explained by the fact that first step is ac-
tually a half-step.
(a) Ankle position X.
(b) Ankle position Y.
(c) Ankle position Z.
(d) Joint angles.
Figure 9: reference and non-compensated spatio-temporal
joint trajectories for robot gait.
Total stability improvement for the biped robot
can be observed by looking at ZMP position and
its position error compared to reference ZMP trajec-
tory. Trajectories obtained from preview control (Fig-
ure 8a, 8b) were examined with the robot model in
V-REP, after that ZMP trajectory were obtained from
virtual sensors. Figure 11a, 11b present ZMP po-
sition in Y and X plane over time. ZMP position
without compensation has a noticeable peak at the
point where foot of the robot contacted with ground
surface and because of deflections it’s happen before
DSP defined by the algorithm. This cause robot to
stumble and move its ZMP closer to the edges of sup-
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
73

Figure 10: Error between reference and compensated tra-
jectory for ankle position.
(a) Robot motion in sagittal plane.
(b) Robot motion in lateral plane.
Figure 11: Simulated robot walking trajectories with and
without compensation in V-REP.
port polygon. Maximum amplitude of difference be-
tween compensated/non-compensated and reference
ZMP position presented in Table 7. Figure 12 intro-
duce ZMP position with and without compensation
in XY plane (top view). Using compensation of de-
flections allowed to reduce error by 61% in X plane
(forward movements) and by 73% in Y plane (side
movements).
Figure 12: Simulated biped robot ZMP with and without
compensation in XY plane.
Table 6: Maximum end-effector position errors.
Error before
compensation
(∆t/(k · F))
Error after
compensation
(∆t/(k · F))
%
X 3.06 0.19 93.8
Y 2.22 0.09 95.9
Z 10.41 0.65 93.7
Table 7: Maximum ZMP errors compared to reference.
Error before
compensation
(mm)
Error after
compensation
(mm)
%
X 51.62 20.04 61.2
Y 68.41 18.27 73.3
The simulated ZMP trajectory was also validated
on the real 3D-printed robot prototype. During tests
robot demonstrated stable walking capability with
off-line generated joint trajectories.
6 DISCUSSION
Stiffness modeling for bipedal robots allow to reduce
position error for the robot legs, especially in Z di-
rection, that is critical for stable walking ability. In
this work only the joint compliance was used, but
it’s possible to further improve stiffness model by
implementing a link stiffness model in addition to
joint model. This improved model will allow to in-
crease error reduction depending on the robot struc-
ture (Klimchik et al., 2015). Link compliance is more
valuable for full-size humanoid robots, where mass
of the robot parts is relativity high. The robot used in
this work has small size and low mass and link com-
pliance could be ignored. But in the same time ma-
terial (ABS - plastic) has quite low Young’s modulus
value and process (Fused deposition modeling) used
for robot link creation will reduce total stiffness of the
robot links. Further experiments required in order to
understated how implementing of more complicated
model will increase performance of walking motion.
Another way of increasing error reduction is imple-
mentation of non-linear model that could further de-
crease error.
The current algorithm calculates deflection off-
line. For humanoid robot that could constantly re-
calculates moving trajectory based on its environment
on-line method should be implemented by computing
possible deflection each control cycle or by using pre-
viosly calculated patterns.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
74

7 CONCLUSIONS
The main goal of this work was to design low-
cost bipedal anthropomorphic robot, provide stiff-
ness analysis and implement error compensation tech-
nique. The biped robot was designed based on open
source Poppy Humanoid project with 10 DoF lower
limbs, but with enhancing their mechanical structure
and functionality with additional DoF at the ankle.
The robot’s lower body was modeled in V-REP sim-
ulator and prototyped using 3D printing technology.
Despite increasing DoF relative to Poppy humanoid,
we succeeded to reduce overall cost using hobby ser-
vomotors, inexpensive fabrication methods and cost-
efficient electronics components. As far as the cur-
rent robot design has a non-spherical hip joint, which
does not allow to use an analytical solution for the
inverse kinematics, we computed inverse kinematics
using hybrid and numerical methods. Stiffness model
of the robot was obtained using VJM for single sup-
port phase and main source of compliance in the robot
joints. Integration of stiffness model into gait pattern
generation algorithm allowed us to compensate de-
flections caused by link weights. These trajectories
were examined both with the robot model in V-REP
simulator and on the real 3D-printed lower body pro-
totype. The results of experiments demonstrated sta-
ble walking capability of the designed Poppy-inspired
humanoid with 12 DoF lower limbs.
Future work includes deep consideration of mo-
tion processes, creation and implementation of on-
line trajectory generation and compensation, using
stiffness model along with the variable stiffness ac-
tuators. For hardware part the main future tasks are
to enhance and to produce lower limbs with a higher
motion range, passive/active joints with spring sup-
port, and to design robots upper body.
ACKNOWLEDGEMENTS
This research has been suppotred by the grant of Rus-
sian Ministry of Education and Science 2017-14-576-
0053-7882 and Innopolis University
REFERENCES
Buss, S. R. (2004). Introduction to inverse kinematics with
jacobian transpose, pseudoinverse and damped least
squares methods. IEEE Journal of Robotics and Au-
tomation, 17(1-19):16.
Cisneros Lim
´
on, R., Ibarra Zannatha, J. M., and Ar-
mada Rodriguez, M. A. (2013). Inverse kinematics of
a humanoid robot with non-spherical hip: a hybrid al-
gorithm approach. International Journal of Advanced
Robotic Systems, 10:1–13.
Craig, J. J. (2005). Introduction to robotics: mechanics and
control, volume 3. Pearson Prentice Hall Upper Sad-
dle River.
Ferro, F. and Marchionni, L. (2014). Reem: A humanoid
service robot. In ROBOT2013: First Iberian Robotics
Conference, pages 521–525. Springer.
Gouaillier, D., Hugel, V., Blazevic, P., Kilner, C., Mon-
ceaux, J., Lafourcade, P., Marnier, B., Serre, J., and
Maisonnier, B. (2009). Mechatronic design of nao hu-
manoid. In Robotics and Automation, 2009. ICRA’09.
IEEE International Conference on, pages 769–774.
IEEE.
Ha, I., Tamura, Y., Asama, H., Han, J., and Hong, D. W.
(2011). Development of open humanoid platform
darwin-op. In SICE Annual Conference (SICE), 2011
Proceedings of, pages 2178–2181. IEEE.
Jazar, R. N. (2010). Theory of applied robotics: kinematics,
dynamics, and control. Springer Science & Business
Media.
Kajita, S., Kanehiro, F., Kaneko, K., Fujiwara, K., Harada,
K., Yokoi, K., and Hirukawa, H. (2003). Biped
walking pattern generation by using preview control
of zero-moment point. In Robotics and Automa-
tion, 2003. Proceedings. ICRA’03. IEEE International
Conference on, volume 2, pages 1620–1626. IEEE.
Khusainov, R., Shimchik, I., Afanasyev, I., and Magid, E.
(2015). Toward a human-like locomotion: Modelling
dynamically stable locomotion of an anthropomorphic
robot in simulink environment. In Informatics in Con-
trol, Automation and Robotics (ICINCO), 2015 12th
International Conference on, volume 02, pages 141–
148.
Klimchik, A., Chablat, D., and Pashkevich, A. (2014). Stiff-
ness modeling for perfect and non-perfect parallel ma-
nipulators under internal and external loadings. Mech-
anism and Machine Theory, 79:1–28.
Klimchik, A., Furet, B., Caro, S., and Pashkevich, A.
(2015). Identification of the manipulator stiffness
model parameters in industrial environment. Mech-
anism and Machine Theory, 90:1–22.
Lapeyre, M., N’Guyen, S., Le Falher, A., and Oudeyer,
P.-Y. (2014). Rapid morphological exploration with
the poppy humanoid platform. In 2014 IEEE-RAS In-
ternational Conference on Humanoid Robots, pages
959–966. IEEE.
Lapeyre, M., Rouanet, P., and Oudeyer, P.-Y. (2013a).
Poppy humanoid platform: Experimental evaluation
of the role of a bio-inspired thigh shape. In 2013 13th
IEEE-RAS International Conference on Humanoid
Robots (Humanoids), pages 376–383. IEEE.
Lapeyre, M., Rouanet, P., and Oudeyer, P.-Y. (2013b). The
poppy humanoid robot: Leg design for biped locomo-
tion. In 2013 IEEE/RSJ International Conference on
Intelligent Robots and Systems, pages 349–356. IEEE.
Pashkevich, A., Klimchik, A., and Chablat, D. (2011).
Enhanced stiffness modeling of manipulators with
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
75

passive joints. Mechanism and machine theory,
46(5):662–679.
Peiper, D. L. (1968). The kinematics of manipulators under
computer control. Technical report, DTIC Document.
Rohmer, E., Singh, S. P., and Freese, M. (2013). V-rep:
A versatile and scalable robot simulation framework.
In 2013 IEEE/RSJ International Conference on Intel-
ligent Robots and Systems, pages 1321–1326. IEEE.
Sakagami, Y., Watanabe, R., Aoyama, C., Matsunaga, S.,
Higaki, N., and Fujimura, K. (2002). The intelligent
asimo: System overview and integration. In Intelli-
gent Robots and Systems, 2002. IEEE/RSJ Interna-
tional Conference on, volume 3, pages 2478–2483.
IEEE.
Siciliano, B. and Khatib, O. (2008). Springer handbook of
robotics. Springer Science & Business Media.
Yamaguchi, J., Soga, E., Inoue, S., and Takanishi, A.
(1999). Development of a bipedal humanoid robot-
control method of whole body cooperative dynamic
biped walking. In Robotics and Automation, 1999.
Proceedings. 1999 IEEE International Conference on,
volume 1, pages 368–374. IEEE.
APPENDIX
Analytical Solution for Inverse Kinematic
In the sagittal plane (Figure 2b) we consider lengths
Z
3
, Z
4
and l
05
.
The position of the ankle T
x
, T
y
, T
z
can be obtained
from the inverse matrix of T 6 ∗ T 7 (1).
T 1 ∗ T 2 ∗ T 3 ∗ T 4 ∗ T 5 = T F ∗ (T 6 ∗ T 7)
−1
=
∗ ∗ ∗ T x + z6 · r13
∗ ∗ ∗ Ty + z6 · r23
∗ ∗ ∗ T z + z6 · r33
0 0 0 1
(17)
Then find distance l
05
as
(l
05
)
2
= (T
x
+ z
6
· r
13
)
2
+ (T
y
+ z
6
· r
23
)
2
+
(T
z
+ z
6
· r
33
)
2
(18)
The knee angle q4 can be calculated from the law
of cosines
q4 = cos
−1
l
05
2
− z3
2
− z4
2
2 · z3 · z4
(19)
Lengths l
06yz
and l
05yz
can be found in the frontal
plane (Figure 2a).
l
06yz
=
q
(T F
−1
(2,4))
2
+ (T F
−1
(3,4))
2
(20)
l
05yz
=
q
(T F
−1
(2,4))
2
+ (T F
−1
(3,4) − z6)
2
(21)
The ankle roll angle can be calculated by the law
of cosine
q6 = cos
−1
l
06yz
2
− l
05yz
2
− z6
2
2·l
05yz
· z6
!
(22)
T 1 ∗ T 2 ∗ T 3 ∗ T 4 = T F ∗ (T 5 ∗ T 6 ∗ T 7)
−1
(23)
Find q1 and q2 from (23), by comparing right
hand side (RHS) and left hand side (LHS) equations.
If we inverse T 1 ∗ T 2, T 6 ∗ T 7 and multiply them
with TF
T 3 ∗T 4∗T 5 = (T 1 ∗ T 2)
−1
∗T F ∗(T 6 ∗ T 7)
−1
(24)
Then RHS and LHS equations will be:
RHS =
∗ ∗ ∗ A
∗ ∗ ∗ B
∗ ∗ ∗ ∗
0 0 0 1
(25)
where
A = −T x · sin (q2)sin (q1)+
Ty · cos (q2) sin(q1) − T z · cos(q1)−
z6(r13 · sin(q1)sin (q2)−
r23 · cos(q2)sin (q1) +r33 · cos (q1))
(26)
B = −T x · cos (q2) − Ty · sin (q2)−
z6(r13 · cos(q2) + r23 · sin (q2))
(27)
LHS =
∗ ∗ ∗ C
∗ ∗ ∗ D
∗ ∗ ∗ ∗
0 0 0 1
(28)
where
C = (z3 + z4 · cos(q4))cos (q3)−
z4 · sin(q4)sin(q3)
(29)
D = z4 · sin(q4) cos (q3)+
(z3 + z4 · cos(q4)) sin(q3)
(30)
Solve it for q3 and then find q5 from known q3
and q4. Final equations for 6 DoF leg presented in
section 3.2.1
Deflections Maps for Biped Robot
Figures 13-16 shows X, Y, Z deflection vector com-
ponents for the left leg hight is presented in Figure 3.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
76

(a) Deflections in X directions.
(b) Deflections in Y directions.
(c) Deflections in Z directions.
Figure 13: Deflection vector components for distance be-
tween foot and the torso Z=325 mm.
(a) Deflections in X directions.
(b) Deflections in Y directions.
(c) Deflections in Z directions.
Figure 14: Deflection vector components for distance be-
tween foot and the torso Z=350 mm.
(a) Deflections in X directions.
(b) Deflections in Y directions.
(c) Deflections in Z directions.
Figure 15: Deflection vector components for distance be-
tween foot and the torso Z=430 mm.
Design and Stiffness Analysis of 12 DoF Poppy-inspired Humanoid
77

(a) Deflections in X directions.
(b) Deflections in Y directions.
(c) Deflections in Z directions.
Figure 16: Deflection vector components for distance be-
tween foot and the torso Z=400 mm.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
78
