An Adaptive Underfloor Heating Control with External Temperature

Compensation

Luca Ferrarini, Soroush Rastegarpour and Anacleto Petretti

Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, P.za L. da Vinci 32, 20133 Milano, Italy

Keywords: Temperature Control, Self-tuning Regulators, Building Energy Efficiency, Model-based Control.

Abstract: The paper describes an interesting combination of auto-tuning and adaptive scheduling approaches to design

and update a feedback/feedforward control of the temperature in buildings. The focus here is on residential

houses endowed with radiant floors, which are intrinsically complex to control due to large inertia and

operational constraints, and on the disturbance rejection of the external temperature. Pure auto-tuning

techniques may fail to converge if the initialization step is not done properly, due to the wide variety of

possible buildings and compensation hard to adapt in closed loop. The proposed approach combines a

classification of the typology of rooms based on physical parameters with auto-tuning, so that in a two-step

closed-loop procedure, the room cluster can be quickly identified, and consequently the feedback controller

and feedforward compensator be tuned. Numerical examples are provided to test the robustness of the

proposed approach.

1 INTRODUCTION

The problem of controlling temperature in buildings

has seen a growing importance due to the pressure

on energy efficiency on the one hand, and on the

need to increase the comfort level on the other hand.

Although temperature is well understood in many

process control applications, in residential buildings

with radiant floors temperature control is still an

issue in almost all applications, due the large inertia

of the pavement itself, to the limitations of the

operating range for inlet temperature, and to the

many disturbances affecting the system.

On the application side, building automation

systems are based on controllers (typically cascaded

PID schemes with saturation and linear/nonlinear

compensators), which are tuned by hand during the

installation phase by some technicians. The results are

that days, weeks or months later these systems must

be retuned, manually, with users’s discomfort in

between. The variety of buildings types, materials,

orientation and so on, makes the classic auto-tuning

techniques ineffective, if proper actions are not taken.

The goal of this paper is to design and test an

algorithm that allows to auto-tune a feedback

controller and a feedforward compensator, in closed

loop, starting from no notion at all of the residential

building with radiant panel under control.

Although the technical literature is dense of

theory and application of adaptive approaches

(Astrom & Wittenmark, 1995), there is a scarce

consideration on adaptive compensator in order to

achieve a high performance in disturbance rejection.

An adaptive control strategy based on RLS method

has been developed for a multizone airhandling unit

in (Nesler, 1986), but since the most contribution of

the collected data from building temperature is due

to heating system, the collected data is not rich in

information to identify the disturbance dynamics in

order to design the proper compensator.

In (Bakker, Brouwer, & Babuska, 2007) an

integration of adaptive control and model predictive

control has been developed, but the focus is on the

occupant behaviour and discomfort aspects and in

(Moon, 2012) an ANN-based (Artificial neural

network) predictive and adaptive thermal control for

disturbance rejection has been proposed. Although

the results of these methods are good, they strongly

depend on the quality of prediction and estimation,

which cannot be guaranteed at all in general, due to

the wide uncertainties and disturbances acting on the

building. Also, the stability, the quality of estimation

and the convergence rate of these methods are

affected by initial states and initial control

configuration.

Ferrarini, L., Rastegarpour, S. and Petretti, A.

An Adaptive Underﬂoor Heating Control with External Temperature Compensation.

DOI: 10.5220/0006432906290636

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 629-636

ISBN: 978-989-758-263-9

629

In addition, the adaptive control strategy is used

in (Adolph, Kopmann, Lupulescu, & Muller, 2014),

(Lauenburg & Wollerstrand, 2014) for radiator

heating systems and single room heating system. In

these systems, an operator decision is required to

adapt the control scheme. These methods are usually

named as push-button approach which are not so

user-friendly. In (Tanaskovic, Fagiano, Smith, &

Morari, 2014), (Landau, Lozano, M'saad, & Karimi,

2011), (Kim, Yoon, & Shim, 2008) an adaptive

procedure has been applied on the constrained

MIMO (multi input multi output) system to deal

with the constrains on the input (for example valve

saturation) and output. However, these adaptive

control approaches cannot deal with hard output and

input constraints and wrong initial states and initial

control configuration. And also, the state space

structure of the plant needs to be known. In all these

approaches, the system and initial control scheme

are required to be stable.

Among all, gain

scheduling is one of the most parsimonious method

of choice to rapidly adapt controller tuning to the

prevailing operating conditions in a mildly time

invariant system. (Yang, et al., 2015) (Leith &

Leithead, 2010) (Wilson & Jeff, 2000) (Azwar, et

al., 2014)

The approach proposed in the present paper, on

the contrary is able to update the compensator based

on a recursive cluster selection procedure which can

guarantee the stability and robustness of the system

even with poorly performing initial configuration for

feedback controller and feedforward compensator.

The convergence of this approach has been tested in

all situations defined by technical literature and it

can be shown that by using an appropriate starting

point the convergence rate will increase rapidly.

According to the adaptive approach the PID

controller will be updated to deal with constraints of

input and improve the transient behaviour of the

system. The main novelty of the presented paper is

in the application of a well-known algorithm

(adaptive startegy) for choosing the best cluster

among a wide range of buildings. Moreover, the new

clusterization has been conducted to cover majority

types of buildings ranging from old to new ones.

The rest of the paper is organized as follows. In

Sect. 2 the reference model and its control scheme

are given. Classification of residential buildings is

provided in Sect. 3, while in Sect. 4 closed-loop

auto-tuning techniques are described and tested

inside and outside a cluster. The overall adaptive

scheduling approach is analysed. Finally, some

concluding remarks are given in Sect. 6.

2 MODEL OF THE ROOM AND

ITS CONTROL

A generic building can be seen as a set of zones

(rooms) interconnected through heat exchange.

Rooms can be described with the same model. In a

radiant floor system all the rooms receive a heating

fluid (generally water) at the same temperature. The

fluid runs through pipelines under the pavement.

The returning water from all the rooms is collected

and mixed with hot water from a generator to have

the right water inlet temperature to keep heating the

rooms. The thermal behaviour of a room heated

through radiant panels has been here modelled as a

four-states dynamic linear system. The state

variables of the system are the following:

• T

: Average temperature of the air in the

room [°C];

• T

: Average temperat. of room walls [°C];

• T

: Average temperat. of pavement [°C];

• T

: Average temperature of the pipeline

water [°C].

The inputs of the system are:

• T

: Outside air temperature [°C];

• T

: Inlet temperature of pipeline water [°C].

The dynamic equations of the system come from

the energy balance of the room air, walls, pavement

and pipeline. The energy balance equation for the

room air is:

(1)

The energy balance equation for the room walls

is:

(2)

The energy balance equation for the room

pavement is:

(3)

where:

()

pePTERM

LAUP −

−

)1(

(4)

θρ

ArC

LAU

(5)

The energy balance equation for the pipeline is:

eppwtpwt

LAU

ewCwC

























−













−

−−

−

αα

(6)

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

630

The parameters used in equation (1) to (6) are the

following:

• C

: Heat capacity of the room air [J/K];

• U

wci

: Internal heat transfer coeff. of walls

[W/K];

• U

win

: Heat transfer coefficient of windows

[W/K];

• U

pav

: Heat transfer coefficient of pavement

[W/K];

• C

: Heat capacity of walls [J/K];

• U

wceo

: External heat transfer coeff. of walls

[W/K];

• C

: Heat capacity of pavement [J/K];

• A

: Pipeline external perimeter [m];

• U

: Pipeline thermal conductivity [W/mK];

• A

: Pipeline section [m

];

• L: Pipeline length [m];

•

: Velocity of water in the pipeline [m/s];

•

: Water density [Kg/ m

];

• C

: Heat capacity of pipeline water [J/K];

• C

pwt

: Water specific heat [J/kgK];

• w: Water mass-flow in the pipeline [kg/s].

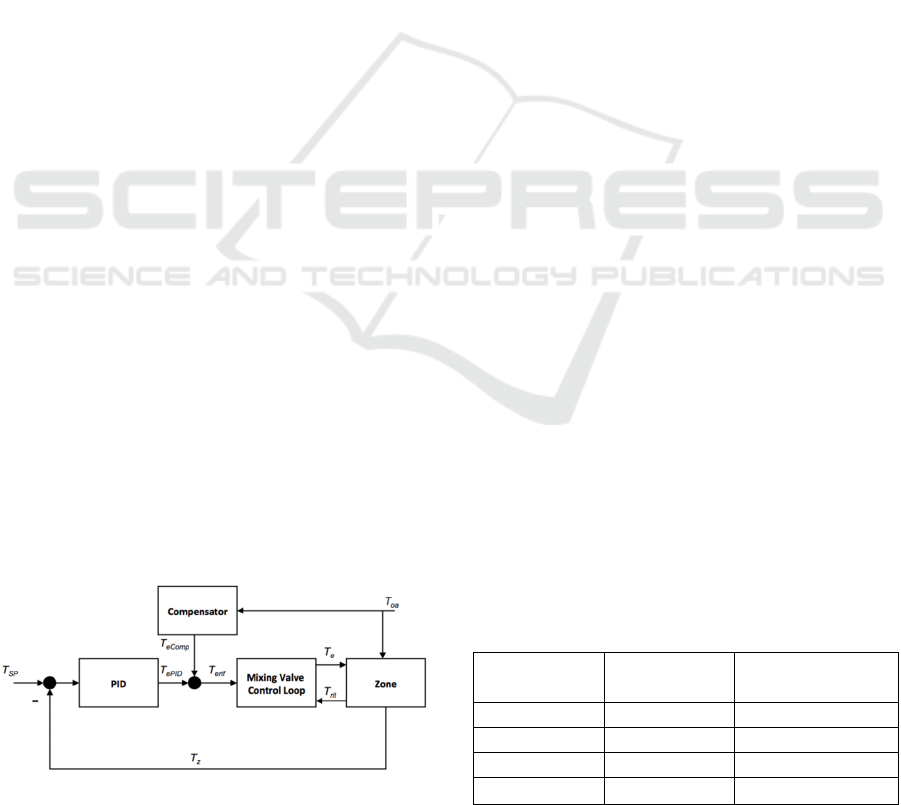
The control scheme here used is shown in

Figure

with a PID as feedback controller (FBC) and a

compensator (FFC) of the outside temperature

disturbance (T

). The aim of the control is to keep

the zone temperature equal to a set point chosen by

the user. The control variable is the reference (T

erif

)

of the inlet temperature of the water inside the

pipeline T

while the controlled variable is T

. The

PID computes T

ePID

based on the error between the

zone set point (T

) and the actual zone temperature

. The sum of T

ePID

and of the contribution of the

compensator T

eComp

is T

erif

. A second (inner) control

loop, consisting of a PID, controls the opening of the

valve mixing return water from the radiant panels

rit

) and hot water from the generator in order for T

to follow T

erif

. Clearly, there are saturations in both

cascaded controllers (each endowed with clamping

anti-windup), as well as ON/OFF valves combined

with a thermostat. All of these have been here

considered.

Figure 1: Temperature control scheme.

3 CLASSIFICATION OF

BUILDINGS

3.1 Clusterization Procedure

The control scheme previously described is the one

widely adopted in practice, with many possible

customization (e.g. in the compensation procedure).

One of the main problems is that the system under

control has a large inertia so that uncertainties and

disturbances can create overshoots and oscillations

which dramatically compromise the comfort.

However, buildings can be of very different types,

due to the wide range of their physical and

geometrical parameters. A purely adaptive approach

to control a generic old or a brand new building is

not effective and shows convergence problems. So,

the proposed approach is based on a suitable

combination of classification and adaptation.

Clusterization of buildings, i.e. the classification

of buildings based on the values of the most relevant

physical parameters, is the way here selected to

reduce the range of all the parameters. This way, a

reference model with contained uncertainty can be

computed for each identified cluster. The

clusterization procedure is based on historical and

statistical data about buildings and on data sheets of

construction materials. At the end of this procedure,

one gets to N

clusters, and, after the design stage, to

feedback controllers and N

feedforward

controllers. The main parameters analyzed in the

clusterization procedure are:

• u

pavi

: heat transfer coeff. of the pavement

[W/m

K];

• C

pav

: heat capacity of the pavement

[kJ/m

K];

• u

wall

: heat transfer coeff. of the walls

[W/m

K];

• C

wall

: heat capacity of the walls [kJ/m

K];

The initial range of the parameters (referred to

their average value between all the types of

buildings) can be seen in

Table 1

Table 1: Parameters average values, and range of

variations before clusterization.

Parameter Average Value Range

pavi

20 +340% -65%

pav

100 +60% -60%

wal

0.75 +75% -60%

wall

30 +100% -60%

An Adaptive Underﬂoor Heating Control with External Temperature Compensation

631

After the clusterization procedure an average

value of the parameters is determined for each

cluster and their variation range is reduced to

approximately 1/3 of the initial one.

3.2 Control Scheme Tuning

The reference model of the generic cluster can be

used to tune the PID and the compensator of the

control scheme proposed in Sect. 2.2. Starting from

the 4-state model described in Sect. 2.1 it is possible

to compute two transfer functions:

• G(s): Transfer function from the inlet

temperature T

to the temperature of the

room T

;

• H(s): Transfer function from the outside

temperature T

to the temperature of the

room T

In order to tune the PID controller, a simplified

transfer function can be identified from G(s):

(7)

According to the transfer function in (7), the PID

can be tuned as follows:

()

)1(

)(

sPID

τμ













(8)

Where K and N can be chosen to act on the

velocity of the control loop and τp is a high-

frequency pole for the controller feasibility.

As for the compensator M(s) it can be ideally

computed as:

)(

sM −=

(9)

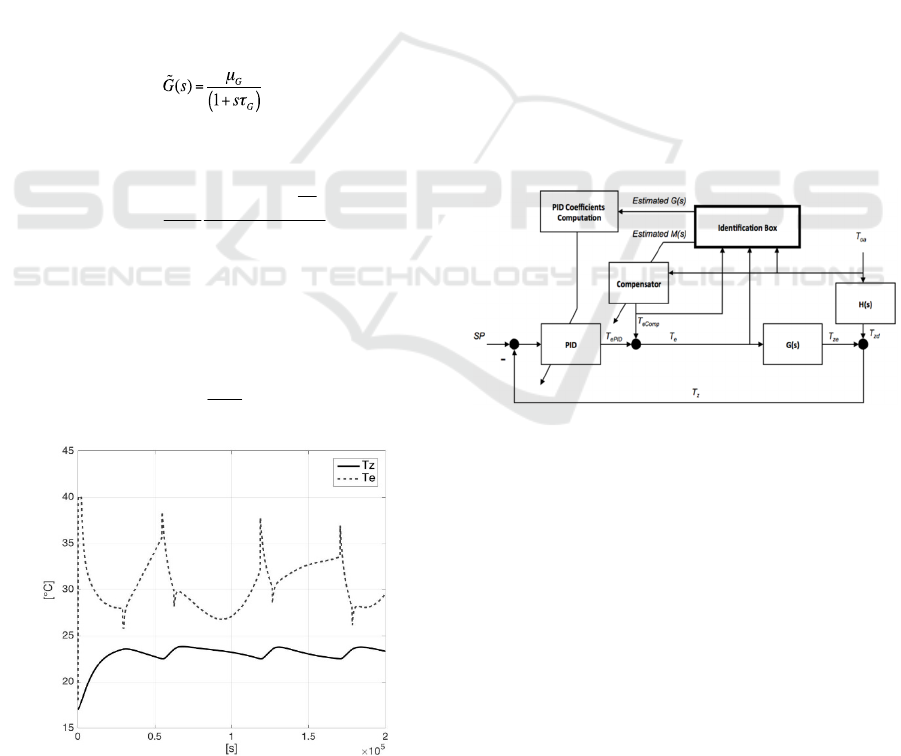
Figure 2: Example of performances when a control

scheme of a cluster is applied to a building belonging to

another cluster.

For each cluster a low frequency approximation

of M(s) can be found and used in the control scheme

as compensator of the disturbance Toa.

Notice that applying the control scheme of a

cluster to a building of another cluster may result in

unacceptable performance, as shown in Figure 2,

where Te and Tz are the inlet water temperature and

room temperature respectively.

4 CLOSED-LOOP AUTO-TUNING

OF ZONE TEMPERATURE

CONTROL

Adaptive control techniques are able to self-regulate

and update the parameters of a controller in presence

of various uncertainties and disturbances. Model

estimation is a vital part of the adaptation procedure.

The quality of adaptive scheme strongly depends on

the quality of the identified models, which in turn

depends on initial states and initial control

configuration. Apart from that, external disturbances

can cause big troubles in the model identification

procedure. The proposed adaptive strategy is

sketched in Figure 3.

Figure 3: Adaptive strategy block diagram.

The control scheme of Sect. 2.2 is tuned based

on an initial guess of the room cluster and applied to

the real plant.

Input and output data are collected and used in

the identification procedure to estimate the plant and

disturbance dynamics, i.etransfer functions G(s) and

H(s). In order to estimate G(s), which describes just

the effects of Te on Tz, a pure output signal without

any oscillatory behaviour, due to disturbances (Toa),

is required.

In an ideal case, the compensator would

guarantee a good disturbance rejection and therefore

it could be assumed that the measured Tz is not

influenced by Toa but only by TePID. Thanks to the

initial compensator, the output signal (T

) will be

pure enough to estimate G(s). However, in the worst

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

632

case in which Tz is not sufficiently rich, since the

most contribution of room temperature is due to the

heating loop so the identified model can be

acceptable for the first iteration. In an iterative

procedure, while the effects of disterbance is

alleviating, the estimated G can converge to the

optimal one, or very close to it. Once the estimation

of G(s) is obtained, the output of H(s) (T

) can be

calculated (T

) based on the output of the G(s)

estimation. The input and output data of the system

for the identification procedure can be organized as

follows:











−=

eCompe

sG :)(











−=

zez

sH :)(

A method based on state variable filter (SVF)

(Young & Jakeman, 1980), (Ljung, 2009) is used to

identify G(s) and H(s). Based on these identified

models, the compensator and the PID controller are

updated.

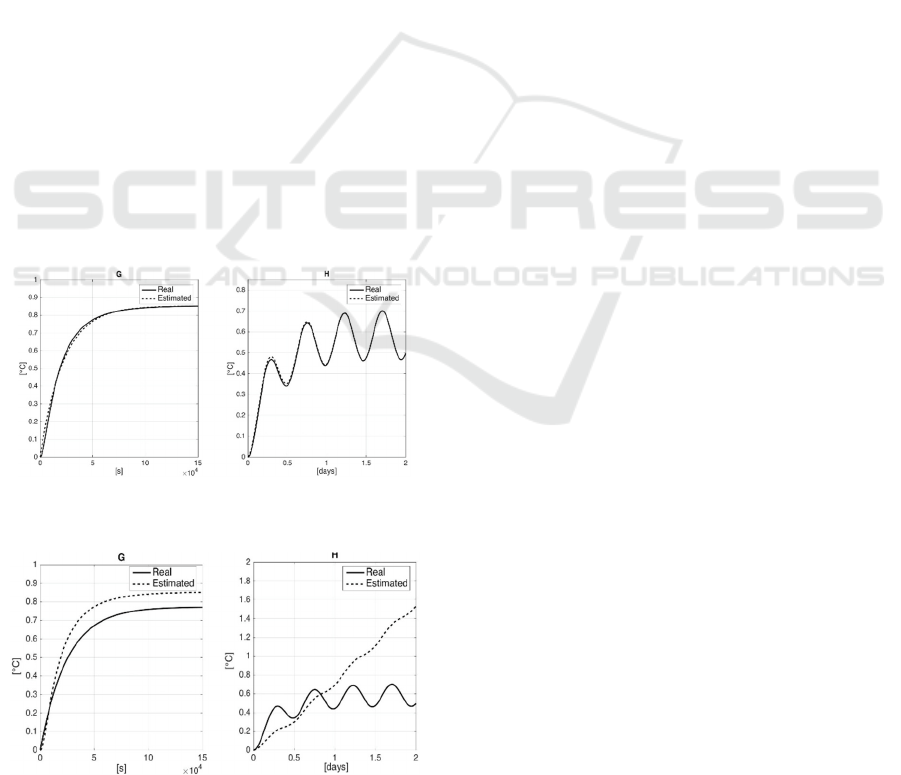
In order to evaluate how the estimation of G(s)

and in consequence H(s) are influenced by this

initial guess, the adaptive control strategy is applied

to the mentioned plant with different initial guess of

the cluster (i.e. parameters of the PID and of the

compensator) If the initial control scheme is chosen

from a cluster whose physical characteristics are far

away from those of the building under control, the

estimation of the real plant is inaccurate and,

Figure 4: Estimation of G(s) and H(s) with a good

initialization.

Figure 5: Estimation of G(s) and H(s) with a bad

initialization.

consequently, the identified model for disturbance

dynamics is completely wrong in the sense of time

and frequency properties Figure 5. Both the

estimation of G(s) and H(s) are accurate when

starting from good initialization

Figure

. Therefore, to choose the right cluster for

the building (i.e. the control scheme) is fundamental.

5 OVERALL ADAPTIVE

SCHEDULING APPROACH

5.1 Main Motivation and Possible Solution

A robustness problem in the classical auto-tuning

method arises when the estimated plant (G(s)) is

inaccurate. Because of the strong sensibility of

disturbance dynamic estimation (H(s)) to the

accuracy of estimated plant, classical self-tuning

approaches for updating the compensator are

unreliable. On the contrary, an adaptive scheduling

method (based on clustering approach) is a well-

known robust approach to adapt the compensator in

a proper way to guarantee the robustness, stability

and convergence behaviour of the system even in

presence of lack of accuracy in plant estimation.

According to the analysis conducted in Sect. 3

and 4, a hybrid adaptive approach has been

conceived. Basically, first we identify the cluster,

then we apply the control parameters of the

identified cluster and re-tune only the FBC using the

auto-tuning scheme presented in Section 4,

maintaining the FFC of the selected cluster. The

advantages of this hybrid procedure are: 1) as a first

step, it is easier to identify the most accurate cluster

to identify G(s) or H(s); 2) when estimating G(s),

some parts of disturbance dynamics are eliminated

before the reaction of compensator; 3) the estimation

of H(s) is avoided, thanks to the cluster

compensator; 4) the identified cluster is used “only”

for a correct initialization of the auto-tuning

procedure. Thus, this approach improves the

robustness and quality of estimated model of the real

plant which in turn leads to better re-tune the

compensator. The procedure to identify the cluster

should be iterative, since the variety of the buildings

is very high, so potentially the estimation should be

refined in a step-wise manner: first we get data from

the closed-loop system with a tentative controller,

then, after the plant estimation, better FBC/FFC

controllers are obtained and applied, so we can

restart, obtaining cleaner data. The closest cluster

can be found throughout the iterative cluster

An Adaptive Underﬂoor Heating Control with External Temperature Compensation

633

selection procedure. The convergence of the

mentioned iterative opertaion can be proved due to

the cluster selection criterion which is the time

constant and DC gain of the estimated linear

function. On one hand, the thermal characteristics

(thermal capacity and transmitance of the walls and

pavement) of the working building are represented

by the time constant and the DC gain of estimated

transfer function. On the other hand, the

clusterization has been done due to difference of

thermal capacity and transmitance of the walls and

pavement. It can consequantly be claimed that the

cluster selection procedure converges to the closest

cluster thanks to the accurate clusterization of the

possible biuildings. The convergence of the

aforesaid operation is also proved by different

analysis even with a randomely chosen cluster

Figure 7. In the case that the iterative procedure can

not converge to the specific cluster, i.e. switching

among 2 or 3 clusters, the average compensatore

will apply to the system and the proper PID

controller will retuned based on the estimated linear

model.

As for the initialization of the adaptive

scheduling approach, the control scheme is chosen

initially as the “average” PID/compensator. This is a

standard PID designed for the “average” building,

ranging from very old buildings to most recent ones

belonging to the Nc clusters. As it will be shown

later, the identification procedure of the cluster is

affected by the initial control scheme (i.e. a FBC and

a FFC), but only for the convergence rate.

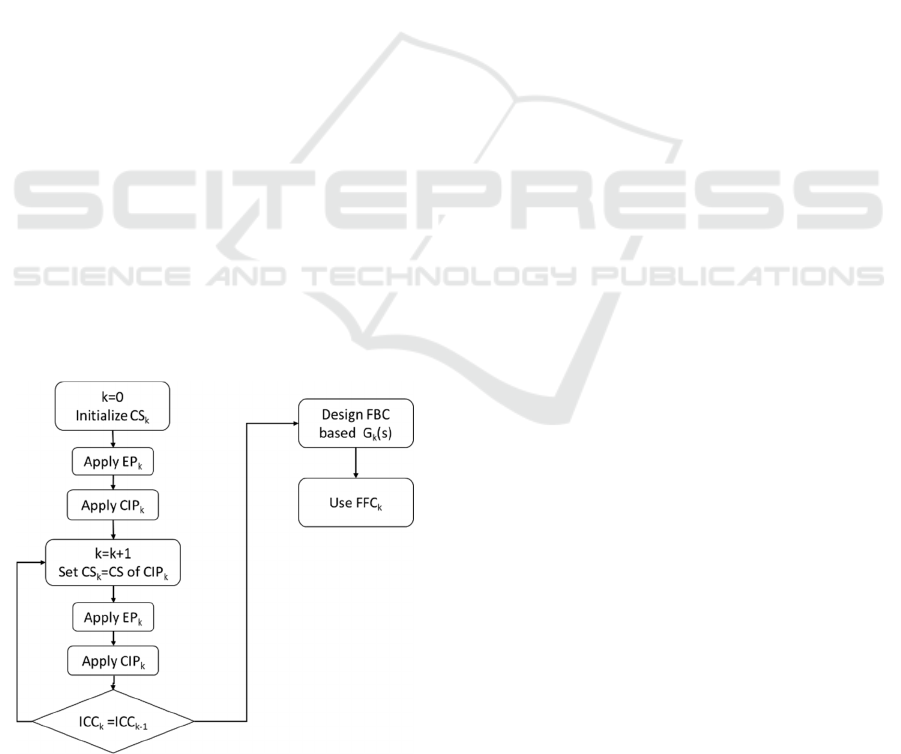
Data collection procedure and consequently a

preliminary estimation of the real plant are done

Figure 6: Adaptive scheduling algorithm flowchart.

based on the initial control scheme during a time

period Test (Test =2 days in the following analysis

and figures). In this step, the closest cluster (ICC,

Identified Closest Cluster) is identified iteratively

(through the CIP procedure). Once the cluster has

been selected, the final FBC is tuned based on the

estimation of the plant performed in the last

iteration, while the compensator is selected directly

from the identified cluster.

The mentioned adaptive scheduling algorithm is

summarized in the flowchart of Figure 6. The term

CS stands for control scheme, based on a FBC and a

FFC. The two acronyms EP and CIP stand for the

following two procedures.

Estimation procedure (EPk):

1- Apply the control scheme CS

2- Run the closed loop system and collect data

for time interval T

est

3- Estimate G(s).

Cluster Identification procedure (CIPk):

1- Select two clusters with closest dominant

time constant based on estimation

procedure (EP).

2- Select among those two the one with

closest gain.

3- Name this cluster as ICC

5.2 Simulation Results and

Comparison

A wide cross-validation between adaptive

scheduling and clustering approach and initial

control scheme (CS

) has been performed to

illustrate the beneficial effects of proposed

adaptation procedure on disturbance rejection,

stability and robustness of the system and also the

convergence to the most appropriate FFC and FBC

in an iterative procedure.

In the first test a modern building endowed with

an initial control scheme, randomly chosen among

the N

clusters, has been considered in order to

evaluate the robustness of the proposed approach.

As shown in

Figure 7

, this scheme CS

generates

unacceptable oscillatory behaviour and slow

transient response. Nevertheless, after the proposed

adaptation procedure, the behaviour of the building

temperature is completely smooth and the

disturbance rejection is achieved perfectly. The FFC

converges to the most appropriate one after 4

iterations (each iteration takes the same time interval

est

) and FBC regulates correctly.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

634

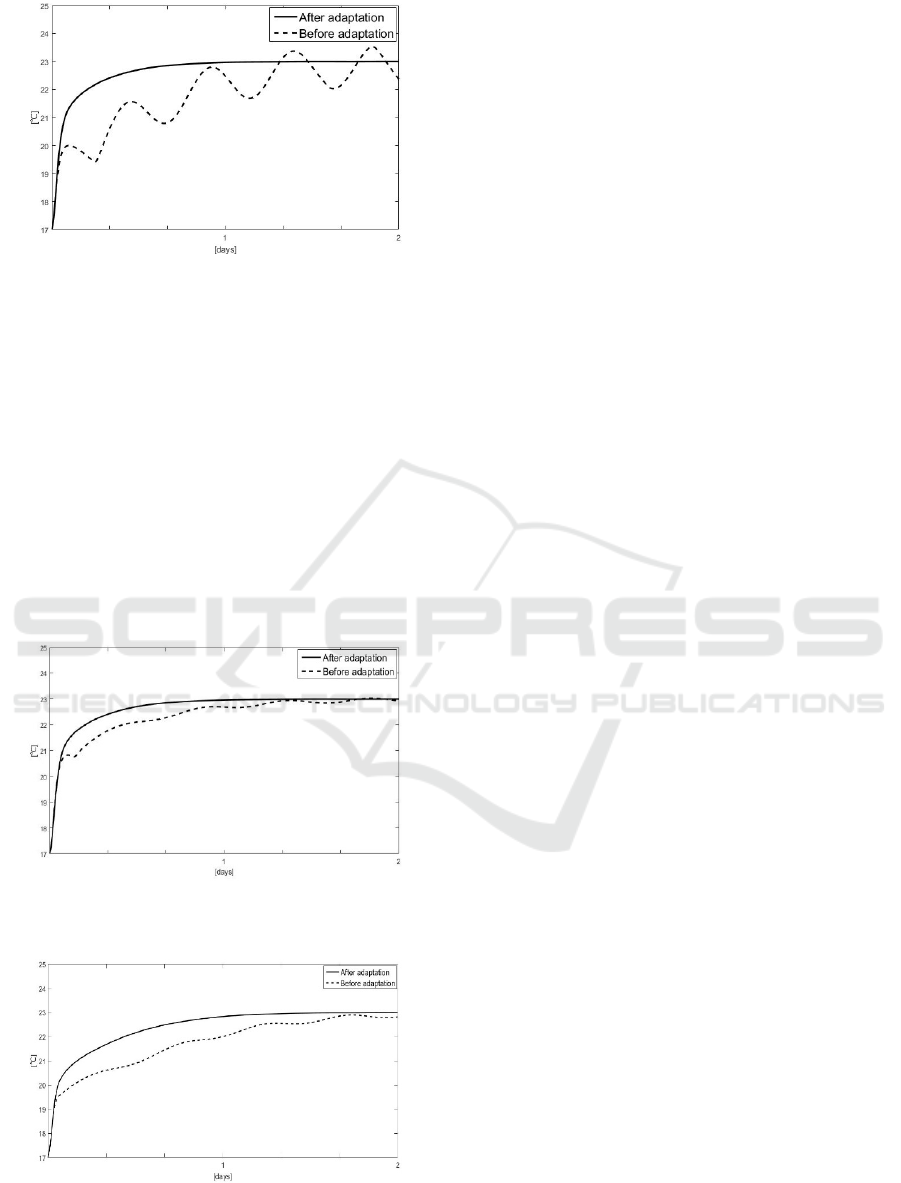
Figure 7: Temperature behaviour of a modern building

with a randomly chosen CS0.

In the second test, the same modern building is

considered, but this time the CS

has been initialized

based on the “average” building of the N

clusters.

This initial control scheme is more reliable than the

previous one. In this case, the same result of the

previous test is achieved

Figure 8, but the

convergence rate is two times faster: in this second

test, the adaptation procedure just took 2 iterations.

In the third test, a very old building is chosen.

Once again the CS

is initialized based on the

average building of the clusters. The adaptive

scheduling approach converges to the best working

cluster in 2 iterations as shown in

Figure 9.

Figure 8: Temperature behaviour of a modern building

with CS0 based on “average” building.

Figure 9: Temperature behaviour of a very old building

with CS0 based on “average” building.

Many other similar testing have been performed.

So, it can be claimed that, by using an interpolation

of all the clusters (ranging from very old buildings to

most recent ones) as the initial control scheme for

the adaptive scheduling approach, the minimum

iterations number for converging to the best working

cluster is guaranteed.

6 CONCLUSIONS

The paper addresses the general problem of

automatic tuning of temperature regulators for

buildings with radiant floors. In particular, the

problem is here considered for residential buildings

of any type (from a flat in a multi-residential

building to an isolated villa), of any construction

period (from ‘60s up to 2015), and of any energy

labels (classes A to D), which gives rise to a wide

variety of physical parameters. Also, the external

temperature rejection problem is considered. The

basic result here proposed is an adaptive procedure

based on a suitable combination of auto-tuning and

adaptive scheduling based on a clusterization of

buildings. Blind tests show that it proves to be

robust to parametric uncertainties always converging

to the expected control schemes, for any kind of the

above-mentioned rooms. Different sampling time

and estimation horizons have also been tested, with

similar performance. Models have also been tested

in a laboratory facility, where room with heated

pavement is build within another bigger room

playing the role of external ambient, and the first

results are encouraging. Formal proof of

convergence will be considered as a further result.

Although the external temperature is one of the

most effective disturbances on the building

temperature, there are many other disturbances

affecting the system, such as internal gains, due to

occupant behaviour and thermo-electrical

equipment, and solar radiation. The rejection of such

disturbances will be considered in the future

extension of the adaptive algorithm here illustrated.

In addition, future directions include tackling the

problem of measurement noise in the zone

temperature, inlet temperature and the disturbance

signals.

REFERENCES

Adolph, M., Kopmann, N., Lupulescu, B. & Muller, D.,

2014. Adaptive Control Strategies for Single Room

An Adaptive Underﬂoor Heating Control with External Temperature Compensation

635

Heating. Energy and Buildings, volume 68, P. 771–

778.

Astrom, K. & Wittenmark, B., 1995. Adaptive control

(2nd ed.). s.l.:Addison-Wesley..

Azwar, M. Y., Mohd, A. H. & Ahmad, K. A. W., 2014.

Modeling, optimization, and control of microbial

electrolysis cells in a fed-batch reactor for production

of renewable biohydrogen gas. International Journal

Energy Research.

Bakker, L. G., Brouwer, A. & Babuska, R., 2007.

Integrated Predictive Adaptive Control Of Heating,

Cooling, Ventilation, Daylighting And Electrical

Lighting In Buildings. International Journal of Solar

Energy, 21(2-3), pp. 203-217.

Kim, J., Yoon, T. & Shim, H., 2008. Switching adaptive

output feedback model predictive control for a class of

input-constrained linear plants. IET Control Theory &

Applications, pp. 573 - 582.

Landau, I., Lozano, R., M'saad, M. & Karimi, A., 2011.

Adaptive Control, Algorithms, Analysis and

Applications. New York: Springer.

Lauenburg, P. & Wollerstrand, J., 2014. Adaptive control

of radiator systems for a lowest possible distric

theating return temperature. Energy and Buildings,

Volume 72, p. 132–140.

Leith, D. & Leithead, W., 2010. Survey of gain-scheduling

analysis and design. International Journal of Control,

pp. 1001-1025.

Ljung, L., 2009. Experiments with Identification of

Continuous Time Models, Linköping, Sweden:

Linköpings universitet & 15th IFAC Symposium on

System Identification,Saint-Malo, France.

Moon, J. w., 2012. Performance of ANN-based predictive

and adaptive thermal-control methods for disturbances

in and around residential buildings. The International

Journal of Building Science and its Applications,

Volume 48, pp. 15-26.

Nesler, C. G., 1986. Adaptive control of thermal processes

in buildings. IEEE Control Systems Magazine, 6(4),

pp. 9-13.

Tanaskovic, M., Fagiano, L., Smith, R. & Morari, M.,

2014. Adaptive receding horizon control for

constrained MIMO systems. Automatica, Volume 50,

p. 3019–3029.

Wilson, R. & Jeff, S., 2000. Research on gain scheduling.

Automatica, 36(10), p. 1401–142.

Yang, L., Xiaojun, B., Fen, W. & H, L., 2015. A Gain-

Scheduling Control Approach for Takagi–Sugeno

Fuzzy Systems Based on Linear Parameter-Varying

Control Theory. Journal of Dynamic Systems,

Measurement, and Control, p. 9.

Young, P. & Jakeman, A., 1980. Refined instrumental

variable methods of time-series analysis: Part III,

extensions. International Journal of Control, Volume

31, p. 741–764.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

636