
Open Loop based Time Optimal PID Control Synthesis
Salim Bichiou, Mohamed Karim Bouafoura and Naceur Benhadj Braiek
LSA, Ecole Polytechnique de Tunisie, BP. 743, 2078 La Marsa, Tunisia
Keywords:
Minimum Time Control, Block Pulse Functions, PID Control, Optimization.
Abstract:
This paper deals with PID control tuning. The main objective being to minimize stabilizing/settling time of
linear control feedback. The presented method is based on an open loop time optimal control framework
reformulation into a closed loop system. Numerical tools such as orthogonal functions and optimization
algorithms are used to determine PID parameters that match a certain equivalent bang-bang control. Numerical
simulation of the obtained results shows the effectiveness of the proposed approach.
1 INTRODUCTION
Minimum time control has received a great attention
from researchers, this is particularly relevant since the
introduction of the maximum principe by (Pontryagin
et al., 1962). The methods used to solve such prob-
lems are numerous. Some of the approaches are ana-
lytical (shen et al., 2013) and are based on some affine
mapping and graphical resolution. Others are numer-
ical (Lasserre et al., 2005) and uses computational
algorithms (Piccagli and Visioli, 2007) etc. Linear
systems minimum time control, due to the saturation
on both the input and output, feature a generalized
bang-bang solution. Specifically, the solution input
is a combination of bang-bang functions and linear
combination of modes associated to the zero dynam-
ics (Consolini and Piazzi, 2006).
On the other hand, researchers have used the or-
thogonal polynomials in many fields like tracking
control (Warrad et al., 2015) and model order reduc-
tion (Qi et al., 2014). Some have used them to solve
the minimum time control problem like the work pre-
sented in (Piccagli and Visioli, 2007). Where Cheby-
shev polynomials had been used to find out the solu-
tion.
Furthermore, the orthogonal functions are a
widely used tool in the control field. They have been
used for state estimation (Chou and Horng, 1986) and
used for systems that feature delays (Mohan and Kar,
2010). To find a general solution for LTI system
with complex poles, orthogonal function were used
to solve the open loop problem (Bichiou et al., 2016).
In fact orthogonal function or polynomials like block
pulse functions (BPFs) are a powerful tool to solve
these problems numerically. It offers the advantage
of reducing the differential equations to a linear sys-
tem of algebraic equations through the use of the op-
erational matrix of integration and vector forms. It is
also noted that using piecewise orthogonal functions
such as block pulse instead of polynomial orthogonal
functions results in more relevant control. It captures
better discontinuities in the inputs (the control saught
is of type Bang-Bang).
In practice, one of the most popular control struc-
tures is the PID controller. This is due to its simplicity
and ability to achieve the desired performance with
various possible technologies (
˚
Astr¨om and H¨agglund,
1995). In this paper a PID controller of a particular
structure (Pradhan and Ghosh, 2015) is adopted in or-
der to find out the feedback signals that allows the
studied system to reach either its equilibrium state or
a desired steady state both in a minimum time.
Some issues in literature dealing with PID time
optimal control exists (Piccagli and Visioli, 2009). In
(Piccagli and Visioli, 2009), authors are interested to
derive a feedforward control for a closed loop system
with PID controller already designed. Then the objec-
tive is to improve the set-point following performance
of the controller. The system being constrained in
both input and output, so the open loop control is not
bang-bang.
In the proposed approach, we are basically search-
ing for PID parameters k
p
, k
i
and k
d
that permit to the
closed loop system to behave as it was controlled with
a minimum time bang-bang control.
The formulation of this problem, is mathemat-
ically simplified when using orthogonal function.
Then all system variables are expanded over that ba-
Bichiou, S., Bouafoura, M. and Braiek, N.
Open Loop based Time Optimal PID Control Synthesis.
DOI: 10.5220/0006433002790285
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 279-285
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
279

sis. Since then, in all the development, we will replace
states, output and control input with their coefficients
when the development is truncated to a finite number
of functions.
Moreover, introducing, operational matrix of inte-
gration and some tensor properties could help us to
pose properly the basis of the framework.
The paper is organised as follows The second sec-
tion is reserved for the description of the used orthog-
onal functions and their algebraic properties. In the
third section, a formulation of the time optimal open
loop problem is given. The formulation of the opti-
mization problem and simulation results are presented
in the fourth section. In the fifth section, a PID con-
troller structure is introduced. Discussion of the sim-
ulation results and discussion are shown in the sixth
section. Finally, concluding remarks and future works
are presented.
2 ORTHOGONAL FUNCTIONS
AND ALGEBRAIC
PROPERTIES
Using orthogonal functions (OF) to construct opera-
tional matrices was approached in the study of dy-
namic systems for modeling (Bouafoura et al., 2009),
identification (Rao and Sivakumar, 1981); (Pacheco
and Steffen, 2002) and control purposes (Mohan and
Kar, 2010).
2.1 Function Development over OF
Principle
Any analytical function absolutely integrable on the
time interval [0, T] can be approximated as follows:
f(t) =
∞
∑
i=0
f
i
φ
i
(t) (1)
where φ
i
(t) are the elementary orthogonal functions
and the coefficients f
i
are evaluated by the following
scalar product:
f
i
=
Z
T
0
f(t)φ
i
(t)dt (2)
For numerical purposes, a truncation of equation (1)
until a convenient number of elementary functions
must be done:
f(t)
∼
=
N−1
∑
i=0
f
i
φ
i
(t) = F
T
N
Φ
N
(t) (3)
where Φ
T
N
= [φ
0
(t),φ
1
(t),··· ,φ
N
(t)] constitutes the
orthogonal basis and F
T
N
= [ f
0
, f
1
,· ·· , f
N
] is the co-
efficient vector.
Integrating (3) transforms it as follows:
Z
t
0
f(t)
∼
=
F
T
N
P
N
φ
N
(t) (4)
where P
N
∈ R
n×n
is the operational matrix of integra-
tion depending on the considered orthogonal basis.
This approximation can fit both orthogonal piece-
wise functions and orthogonal polynomials, in fact
their operational matrices in the integer case were
largely found out and applied in systems science.
As a result, the differential equations describing
dynamic processes can be reduced into algebraic re-
lations allowing important simplifications in the syn-
thesis problems.
2.2 Properties of the Block Pulse
Functions
Block pulse functions (BPFs) constitute a complete
set of orthogonal functions and are defined over the
time interval [0,T] as follows (Wu et al., 2000):
ϕ
i
(t) =
1 if t ∈ [iT , (i+ 1)T]
i = 0, ...,N − 1
0 otherwise
(5)
A function f (t) can be approximately represented by:
f(t) ≃
N−1
∑
i=0
f
i
ϕ
i
(t) = F
T
φ(t) (6)
with
F = [ f
0
, f
1
,..., f
N−1
]
T
is the coefficient vector.
φ = [ϕ
0
(t),ϕ
1
(t),...,ϕ
N−1
(t)]
T
is the block pulse ba-
sis vector.
f
i
is given by:
f
i
=
T
N
Z
(i+1)T
iT
f(t)φ
i
(t)dt (7)
where N is the dimension of the operational matrix.
The operational matrix for the block pulse functions
is given as follows:
P
N
=
T
N
1
2
1 1 ... 1
0
1
2
1 ... 1
.
.
.
.
.
.
1
2
.. . 1
.
.
.
.
.
.
.
.
.
.
.
.
0 .. . ... 0
1
2
(8)
3 TIME OPTIMAL OPEN LOOP
PROBLEM
In this part, a general minimum time problem is for-
mulated for SISO linear time invariant systems.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
280

We are particularly interested with the class of
systems described by:
˙x(t) = Ax(t)+ Bu(t)
y(t) = Cx(t)
(9)
where x ∈ R
n
is the vector of states, u ∈ R
m
is the
control input and y ∈ R
p
is the output.
The objective here is to determine the controller
sequence that allows the system to move from a
known point A to another point B in the least possible
time. For this, time optimization is required. That
leads to minimizing this cost function (Kirk, 1970):
J =
Z
t
f
t
0
dt (10)
Applying The Pontryagin Maximum Principle (PMP)
(Pontryagin et al., 1962) and using the Hamiltonian
(Kirk, 1970), the the following control is derived.
This can be written as follows:
u(t) =
u
min
, if λ
T
B < 0
u
max
, if λ
T
B > 0
(11)
Thus, the obtained control is bang-bang.
To determine the control we need to determine the
sign of λ which is the co-state vector.
We remind here that this solution of the minimum
time control problem is solved in open loop.
4 BPFs BASED OPTIMAL
CONTROL SOLUTION
4.1 Formatting of the Control Problem
Finding the minimum time solution for system (9)
means solving multiple differential equations which
is a very difficult task. In order to make this problem
easier to solve, BPFs based approach is used.
Considering the system (9) written in state space
form, in order to derive the final time, a variable
change is considered as follows:
t = τt
f
(12)
This transformation allows us to go from the time
domain t ∈ [0,t
f
] to τ ∈ [0,1], the system states
become:
x(t) = ˜x(τ) (13)
Notice that, the latter variable change lead to a con-
stant time interval [0,1], for the used series. Since,
the final time t
f
is unknown, we deduce,
˙x(t) =
d ˜x(τ)
dτ
.
dτ
dt
=
1
t
f
˙
˜x(τ) (14)
The original system (9) is now equivalent to:
1
t
f
˙
˜x(τ) = A˜x(τ) + B ˜u(τ) (15)
The use of orthogonal functions consists on develop-
ing both, system states and input over that base:
˜x(τ) =
˜
X
T
N
· φ
N
(τ)
˜u(τ) = ˜u
T
N
· φ
N
(τ)
(16)
Furthermore, integrating equation (15) leads to
1
t
f
(
˜
X(τ) −
˜
X(0)) = A
Z
τ
0
(
˜
X(σ))dσ + B
Z
τ
0
˜u(σ)dσ
(17)
Introducing, coefficients of ˜x(τ), ˜u(τ) and operational
matrix of integration we obtain:
Z
τ
0
˜
X(σ)dσ =
˜
X
T
N
Z
τ
0
φ
N
(σ)dσ =
˜
X
T
N
P
N
φ
N
(τ) (18)
then we can write:
(
˜
X
T
N
−
˜
X
T
N
0
)φ
N
= t
f
(A
˜
X
T
N
P
N
+ B˜u
T
N
P
N
)φ
N
(19)
After the integration of equation (15) and the in-
troduction of coefficients ˜x(τ),˜u(τ) (Bichiou et al.,
2016), we can write:
˜
X
T
N
−
˜
X
T
N0
= t
f
(A
˜
X
T
N
P
N
+ B˜u
T
N
P
N
) (20)
where
˜
X
N0
depends on the chosen set of functions.
For the block pulse functions, the vector
˜
X
N0
is of the
following form:
˜
X
N0
=
˜
X(0)
˜
X(0) ···
˜
X(0)
4.2 Optimization Algorithm
Consider the system model defined in (9).
To find the transition time from the initial position to
the target one need to solve the following nonlinear
problem (NLP):
min(t
f
)
t
f
,u
N
,X
N
(21)
subject to
˙x(t) = Ax(t) + Bu(t) 0 ≤ t ≤ t
f
u ∈ [u
min
,u
max
]
x(0) = x
0
,x(t
f
) = x
f
(22)
then this problem is reported to the domain [0,1]. The
optimization algorithm in the orthogonalbase is of the
following form (OFNLP):
min (t f) (23)
subject to linear constraints:
˜u
Nmin
≤ ˜u
N
φ
N,bp
≤ ˜u
Nmax
˜
X
N f,bp
=
0 0 ·· · x
f
Open Loop based Time Optimal PID Control Synthesis
281
and nonlinear constraints:
˜
X
T
N
−
˜
X
T
N0
= t
f
(A
˜
X
T
N
P
N
+ B˜u
T
N
P
N
) (24)
The resolution of such optimization problem can be
done through interior point routines like the function
”fmincon” implemented in Matlab. As a result the fi-
nal time t
f
and the control sequence may be obtained.
5 SYSTEM WITH PID CONTROL
5.1 Closed Loop with PID
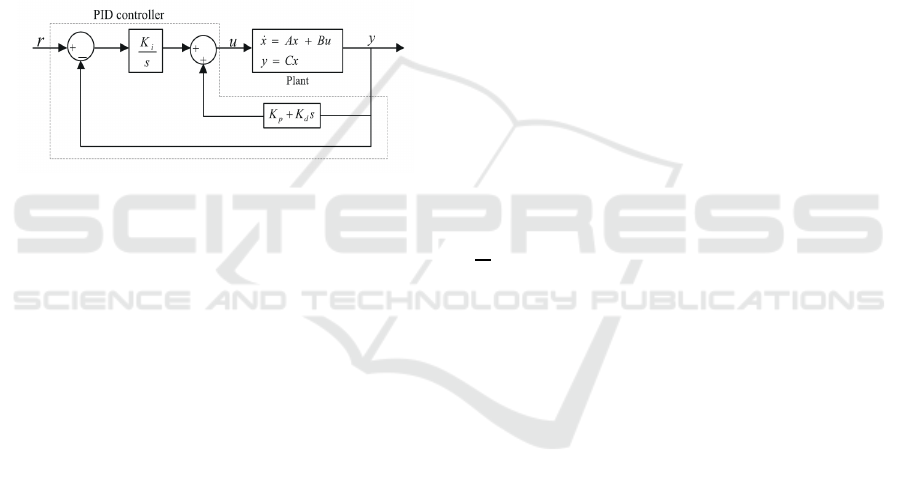
In this section, a PID controller is introduced to im-
prove the system performances. the considred feed-
back control is described by figure(1).
Figure 1: Feedback control structure.
the control effort is then given by:
u = k
p
Cx+ k
i
ξ+ k
d
C˙x (25)
where
ξ(t) =
Z
t
0
(r− y)dτ (26)
In this work, we aim to find the triplet {k
p
,k
d
,k
i
} that
steer the system from an arbitrary initial state to a
final one. Hence, both stabilization and tracking may
be investigated.
Equation (25) could be written:
u = k
p
Cx+ k
i
ξ+ k
d
C(Ax + Bu) (27)
Then the control u becomes:
u = (1 − k
d
CB)
−1
[k
p
Cx+ k
i
ξ+ k
d
C(Ax + Bu)] (28)
Let us note
¯
K = [
¯
k
p
¯
k
i
¯
k
d
] = (1− k
d
CB)
−1
[k
p
k
i
k
d
].
Hence, in the following section, we are interested
to investigate
¯
k, then pid controller gains could be
recovered as follows:
k
d
=
¯
k
d
(1+CB
¯
k
d
)
−1
(29)
k
p
=
¯
k
p
(1−CB
¯
k
d
) (30)
k
i
=
¯
k
i
(1−CB
¯
k
d
(31)
From the above, it is clear that finding PID controller
is possible iff both I − k
d
CB and I +CB
¯
k
d
are invert-
ible. Moreover, in (Zheng et al., 2002), it is proven
that the existence of invertibility I − k
d
CB is neces-
sary and sufficient for well-posedness of the MIMO
PID control problem.
5.2 PID Synthesis Formulation
In order to compute time optimal PID controller
gains, we propose firstly to consider the open loop
system and find the optimal coefficients of control ˜u
T
N
and system trajectory
˜
X
T
N
. Let us denote ˜u
T∗
N
and
˜
X
T∗
N
solutions of the optimization problem (OFNLP) pre-
sented in the last section.
The obtained control should obviously verify
equation (28):
˜u
T∗
N
=
¯
k
p
C
˜
X
T∗
N
+
¯
k
i
(r
T
N
−C
˜
X
T∗
N
)P
N
+
¯
k
d
CA
˜
X
T∗
N
(32)
For numerical convenience, the latter expression of
the control should be introduced into the state equa-
tion with respect to the time domain of resolution.
Then it comes:
˜
X
T∗
N
−
˜
X
T
N0
= t
f
(A
˜
X
T∗
N
P
N
+ B[
¯
k
p
C
˜
X
T∗
N
+
¯
k
i
(r
T
N
−C
˜
X
T∗
N
)P
N
+
¯
k
d
CA
˜
X
T∗
N
]P
N
) (33)
Rearranging equation (33), one may obtain:
1
t
f
(
˜
X
T∗
N
−
˜
X
T
N0
)− A
˜
X
T∗
N
P
N
= B
¯
K
C
˜
X
T∗
N
P
N
(r
T
N
−C
˜
X
T∗
N
)P
2
N
C
˜
X
T∗
N
P
N
(34)
Then
¯
K could be found with the following formula:
vec(
¯
K) = (F
T
⊗ B)
+
vec(G) (35)
with respect to the result (Brewer, 1978):
vec(XYZ) = (Z
T
⊗ X)vec(Y)
and where F is the last term of equation(34), while
G stands for the left hand side of the same equation,
⊗ denotes the Kronecker product (Brewer, 1978), vec
is the vectorization operator and (.)
+
is the Moore-
Penrose pseudoinverse of a matrix.
6 SIMULATION RESULTS AND
DISCUSSION
6.1 Example 1: Application to a Bridge
Crane
In this part, we intend to use the validated results on
a geometric model of a bridge crane (Ermidoro et al.,
2014).
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
282

The system is composed of the bridge, moving
along the Y axis and the trolley, moving along the X
axis. The load is connected to the trolley by a rope
and can oscillate along any direction as described in
figure (2).
Figure 2: The typical structure of a bi-dimensional bridge
crane.
The model of the bridge crane is described by a
classical state space model:
˙x(t) = Ax(t) + Bu(t)
y(t) = Cx(t)
(36)
where
A =
0 1
−
g
r
−
b
mr
2
B =
−
1
r
−
b
mr
3
C =
1 0
(37)
Note that the control input is saturated and u ∈
[u
min
,u
max
].
The state vector x = [x
1
,x
2
]
T
= [θ,
˙
θ]
T
. We need
to move the system from x
0
= [θ
0
,0]
T
to x
r
= [0,0]
T
.
Hence, in this example, we assume that r = 0, The
system is shifted to its equilibrium point.
The physical parameters of the bridge crane are as
follows:
m = 1000kg,r = 5m, g = 9.81m/s
2
,b = 12000
The bounds of the controller is [−10,10]. As found in
(Ermidoro et al., 2014) for time optimal control t
f
=
4.2717s.
The control sequence of the system in open loop
when minimizing (OFNLP) is illustrated in figure (3).
The state trajectories of the system are given in
figure(4).
In this example, we deal with a stabilization prob-
lem, then we propose to use a previous result (Bichiou
et al., 2016) to obtain a state feedback gain. Then a
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
Time (s)
-10
-8
-6
-4
-2
0
2
4
6
8
10
Control sequence
Figure 3: Bridge crane control sequence in open loop.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
Time (s)
-15
-10
-5
0
5
10
first state
second state
Figure 4: Bridge crane state trajectories in open loop.
method transforming that result to PID with the same
structure (figure 1) is applied (Pradhan and Ghosh,
2015).
The PID parameters are: k
p
= 488.7322, k
i
=
37.5069 and k
d
= 112.1876.
The system state trajectories are given in figure (5).
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time (s)
-8
-6
-4
-2
0
2
4
6
8
10
Closed loop first state
Closed loop second state
Figure 5: Bridge crane state trajectories using PID con-
troller.
Open Loop based Time Optimal PID Control Synthesis
283

6.2 Example 2: Fighter Aircraft
In this part, we intend to use a linearized longitu-
dinal dynamics of the McDonnell Douglas Tailless
Advanced Fighter Aircraft (TAFA) (Kefferp¨utz and
Adamy, 2011) for tracking purposes.
The general representation of the system is of the
following form:
˙x(t) = Ax(t) + Bu(t)
y(t) = Cx(t)
(38)
where
A =
−1 1
6 −2
; B =
0
8
C =
0 1
(39)
with x
1
is the deviation of the angle of attack (rad) and
x
2
is the body axis pitch rate (rad/s).
The control variable is limited to |u| ≤ 20/180π
rad/s.
The system control is given in figure (6).
0 0.05 0.1 0.15
Time (s)
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
Control sequence
Figure 6: Fighter aircraft control in open loop.
The PID parameters are: k
p
= −0.6447, k
i
=
6.8510 and k
d
= 0.0064.
The state trajectories of the system are given in
figure (7).
The system control is given in figure (8).
The system output is given in figure (9).
7 CONCLUSIONS
In this paper, a based minimum time control prob-
lem for linear systems is proposed. In fact, the open
loop control determined with orthogonal function op-
timization is transformed to a PID controller. Hence,
dynamics of the closed loop system may be enhanced
and final time could be reached in tracking as in a
classical bang-bang control. The whole development
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Time (s)
0
0.2
0.4
0.6
0.8
1
1.2
x1
x2
Figure 7: Fighter aircraft state trajectories in open loop.
0 1 2 3 4 5 6 7 8 9 10
Time (s)
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
Control
Figure 8: Fighter aircraft PID control.
0 1 2 3 4 5 6 7 8 9 10
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
System output
Step Response
Time (seconds)
Amplitude
Figure 9: Fighter aircraft output with PID controller.
is carried with block pulse functions and related oper-
ational matrices. Simulations illustrate the validity of
the approach.
In future work, we intend to generalize the PID time
optimal control problem to some classes of nonlinear
systems.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
284

REFERENCES
˚
Astr¨om, K. J. and H¨agglund, T. (1995). PID controllers:
Theory, Design, and Tuning. NC, second edition edi-
tion.
Bichiou, S., Bouafoura, M. K., and Braiek, N. B. (2016).
state feedback suboptimal time control method using
block pulse functions. In 24th Mediterranean Confer-
ence on Control and Automation (MED), pages 1224–
1229, Athens, Greece.
Bouafoura, M. K., Lanusse, P., and Braiek, N. B. (2009).
State space modeling of fractional systems using
block pulse fonction. In 15th IFAC Symposium on sys-
tem Identification SYSID’2009, St Malo, France.
Brewer, J. (1978). Kronecker products and matrix calculus
in system theory. IEEE Transactions on Circuits and
Systems, 25(9):772–781.
Chou, J. and Horng, I. (1986). State estimation using con-
tinuous orthogonal functions. International Journal of
Systems Science, 19(9):1261–1267.
Consolini, L. and Piazzi, A. (2006). Generalized bang-
bang control for feedforward constrained regulation.
In 45th IEEE Conference on Decision and Control,
pages 893–898, San Diego, CA.
Ermidoro, M., Formentin, S., Cologni, A., Previdi, F., and
Savaresi, S. M. (2014). On time-optimal anti-sway
controller design for bridge cranes. In American Con-
trol Conference, pages 2809–2814, Portland, OR.
Kefferp¨utz, K. and Adamy, J. (2011). A tracking controller
for linear systems subject to input amplitude and rate
constraints. In American Control Conference, pages
3790–3795, San Francisco, CA.
Kirk, D. (1970). Optimal Control Theory: An Introduction.
Dover Books on Electrical Engineering.
Lasserre, J. B., Prieur, C., and Henrion, D. (2005). Non-
linear optimal control: Numerical approximations via
moments and lmi relaxations. In 44th IEEE Confer-
ence on Decision and Control, pages 1648–1653.
Mohan, B. M. and Kar, S. K. (2010). Orthogonal functions
approach to optimal control of delay systems with re-
verse time terms. Journal of the Franklin Institute,
347(9):1723–1739.
Pacheco, R. P. and Steffen, V. (2002). Using orthogonal
functions for identification and sensitivity analysis of
mechanical systems. Journal of Vibration and Con-
trol, 8(7):993–1021.
Piccagli, S. and Visioli, A. (2007). Using a chebyshev tech-
nique for solving the generalized bang-bang control
problem. In 46th IEEE Conference on Decision and
Control, pages 4743 –4748, New orleans, LA.
Piccagli, S. and Visioli, A. (2009). Minimum-time feedfor-
ward technique for pid control. IET Control Theory
and Applications, 3(10):1341–1350.
Pontryagin, L. S., Boltyanskii, V., Gamkrelidze, R., and
Mischenko, E. (1962). The mathematical theory of
optimal processes. Interscience Publishers Inc, New
York.
Pradhan, J. K. and Ghosh, A. (2015). Multi-input and multi-
output proportional-integral-derivative controller de-
sign via linear quadratic regulator-linear matrix in-
equality approach. IET Control Theory and Applica-
tions, 9(14):2140–2145.
Qi, Z. Z., Jiang, Y. L., and Xiao, Z. H. (2014). Model order
reduction based on general orthogonal polynomials in
the time domain for coupled systems. Journal of the
Franklin Institute, 351(6):3200–3214.
Rao, G. P. and Sivakumar, L. (1981). Transfer function
matrix identification in mimo systems via walsh func-
tions. In IEEE proc., volume 69, pages 465–466.
shen, Z., Huang, P., and Andersson, S. B. (2013). Calcu-
lating switching times for the time-optimal control of
singleinput, single-output second-order systems. Au-
tomatica, 49(3):1340–1347.
Warrad, B. I., Bouafoura, M. K., and Braiek, N. B. (2015).
Tracking control synthesis of nonlinear polynomial
systems. In 12th International Conference on Infor-
matics in Control, Automation and Robotics, pages
517–523, colmar, Alsace, France.
Wu, J. L., Chen, C. H., and Chen, C. F. (2000). A uni-
fied derivation of operational matrices for integra-
tion in systems analysis. In International Conference
on Information Technology: Coding and Computing
(ITCC’00), pages 436–442, Washington, DC, USA.
Zheng, F., Wang, Q.-G., and Lee, T. (2002). On the de-
sign of multivariable pid controllers via lmi approach.
Automatica, 38(3):517–526.
Open Loop based Time Optimal PID Control Synthesis
285
