
Reputation Management in Online Social Networks
A New Clustering-based Approach
Sana Hamdi
1,2
, Alda Lopes Gancarski
1
, Amel Bouzeghoub
2
and Sadok Ben Yahia
1,2
1
University of Tunis El-Manar, Faculty of Sciences of Tunis, LIPAH-LR 11ES14, 2092 Tunis, Tunisia
2
SAMOVAR, Telecom SudParis, CNRS, Universit
´
e Paris-Saclay, 9 rue Charles Fourier, 91001 Evry Cedex, France
Keywords:
Social Networks, Reputation, Trust, Clustering.
Abstract:
Trust and reputation management stands as a corner stone within the Online Social Networks (OSNs) since
they ensure a healthy collaboration relationship among participants. Currently, most trust and reputation sys-
tems focus on evaluating the credibility of the users. The reputation systems in OSNs have as objective to help
users to make difference between trustworthy and untrustworthy, and encourage honest users by rewarding
them with high trust values. Computing reputation of one user within a network requires knowledge of trust
degrees between the users. In this paper, we propose a new Clustering Reputation algorithm, called RepC,
based on trusted network. This algorithm classifies the users of OSNs by their trust similarity such that most
trustworthy users belong to the same cluster. We conduct extensive experiments on a real online social net-
work dataset from Twitter. Experimental results show that our algorithm generates better results than do the
pioneering approaches of the literature.
1 INTRODUCTION
Reputation-based trust management has been used as
an effective solution to evaluate how much one user
can trust others, to help users to make the difference
between trustworthy and untrustworthy users and en-
courage honest users by rewarding them with high
trust values.
Despite reputation is closely related to the concept
of trust, it has not to be confused nor treated as trust.
In fact, trust is often considered as a personal and
subjective measure because it is computed primarily
based on a set of personalized factors and can be de-
rived from a combination of personal experience and
relationships (Hamdi et al., 2012). However, reputa-
tion is often considered as a collective and objective
measure of trustworthiness based on the transactional
experiences and direct interactions of different users.
In this paper, we propose an algorithm called
RepC for reputation management in Online Social
Networks (OSNs). The proposed algorithm is based
on direct and indirect trust values computed respec-
tively in previous works (Hamdi et al., 2012) and
(Hamdi et al., 2016).
RepC is truly unique since it is based on a clus-
tering approach. In fact, it divides OSNs users into
clusters (groups) such that trustworthy users belong
to the same cluster.
The remainder of this paper is organized as fol-
lows. Section 2 recalls the key notions used through-
out this paper. Section 3 reviews the related work ded-
icated to the reputation management in OSNs. Sec-
tions 4 and 5 introduce our approach that classifies the
OSNs’ users according to their reputation helping re-
questers to differentiate between benevolent and mali-
cious ones. Section 6 describes the evaluation proce-
dure as well as the results obtained from the real OSN
Twitter. The final section sketches our contributions
and points out avenues of future work.
2 BACKGROUND AND KEY
NOTIONS
In OSNs, a trust network is critical and it is the basis
for the reputation evaluation of users. In fact, it con-
tains some important information as direct trust re-
lations between users and social relations. Extracting
the trust network between users becomes a fundamen-
tal and essential step before performing the reputation
values of users and has important influences on their
evaluation.
For example, an OSN’s user A is looking for a
468
Hamdi, S., Gançarski, A., Bouzeghoub, A. and Yahia, S.
Reputation Management in Online Social Networks - A New Clustering-based Approach.
DOI: 10.5220/0006433104680473
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 468-473
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Tennis coach and B is a Tennis coach and member
on the same OSN. In such a situation, as indicated
in the theory of Social Psychology (Christianson and
Harbison, 1996) and Computer Science (Hamdi et al.,
2016), A can evaluate the trustworthiness of B based
on the trust social network.
We have defined on the basis of a previous work
(Hamdi et al., 2012) how to compute direct trust val-
ues in social networks. Yet, social actors are often
connected by more than one kind of relationship. Ac-
cordingly, our model titled IRIS, built direct trust
relations (local reputation) by aggregating different
ties in a multiplex network (the direct interactions
between users, their existing relationship types and
their interest similarity). In fact, multiplex networks
exist when actors are connected through more than
one type of socially relevant tie. The different ties
reflect the diverse roles played by users in the net-
work (Heaney, 2014). In an additional previous work
(Hamdi et al., 2016), we have proposed an accurate
model TISoN to infer trust in OSNs based on direct
relationships between users.
In the following, we briefly sketch the key notions
that will be of use in the remainder of this paper.
Definition 1.(TRUST) Trust is the subjective proba-
bility by which an individual, A, expects that another
individual, B, performs a given action on which its
welfare depends (Chen et al., 2011).
Definition 2.(DIRECT TRUST) In OSNs, a user A’s
trust in another user B is the subjective confidence,
faith or expectation of the user A receiving positive
outcomes through the transactions with the user B.
Definition 3.(INDIRECT TRUST) In OSNs, a user A’s
trust in another user B is the confidence, faith or ex-
pectation of the user A in the user B according to other
users.
Definition 4.(REPUTATION) In OSNs, a user A’s rep-
utation is the global perception of its trustworthiness
in the network. Furthermore, the trustworthiness can
be evaluated from its past and current behaviours.
In this paper, we propose a new algorithm for rep-
utation management in OSNs. The proposed algo-
rithm is based on direct and indirect trust values. The
different OSN users participate to help the requester
to have an idea about the reputation of an OSN user
(target). Some users, whom are indirectly connected
to the target, are observers and propagators, they ob-
serve direct interactions and, based on their experi-
ences, they propagate information about trust with the
different users. Other users (assessors), directly con-
nected to the target, are observers and evaluators since
they evaluate directly the trust in the target. The re-
quester can so scan the reputation of the target based
on direct and indirect trust.
3 RELATED WORK
In the literature, several approaches are designed to
describe how to identify the reputation of users. In
the remainder of this section, we present and describe
a set of some of the most representative reputation ap-
proaches for distributed networks.
3.1 SemanticWeb
SemanticWeb is a trust and reputation model specific
for social networks presented in (Zhang et al., 2006).
The trustworthiness between two users is computed
by searching all the paths connecting them; then, for
each path the ratings associated with each edge are
multiplied; finally, all the scores are added (normaliz-
ing that aggregation).
Let n be the number of paths from agent A to agent
B. D
i
denotes the number of users between A and B
on the i
th
path. The set of B’s friends or neighbours is
called M, m
i
denotes B’s direct friend or neighbour on
the i
th
path. w
i
denotes the weight of the i
th
path. The
weight of each path is computed as follows (giving a
higher weight to shorter paths):
w
i
=
1
D
i
∑
N
i=1
1
D
i
; (1)
The reputation of B from A’s point of view is com-
puted as follows:
R
A→B
=
N
∑
i=1
T
m
i
→B
×
∏
i→ j
R
i→ j
× w
i
; (2)
Where the reliable factor R
i→ j
denotes to which
degree i believes directly in j’s opinions or be-
haviours.
In this work, the authors did not compute a global
value reflecting the reputation of one user in the whole
network, their model only computes the reputation of
each user based on the opinion of other user. We can
consider these computed scores, simply, as indirect
trust between two users. In addition, these computed
values are essentially based on a direct trust (R
i→ j
).
However, authors did not show or mention how to cal-
culate them nowhere.
3.2 REMSA
Authors in (Lee and Oh, 2015) introduced a new
model named REMSA for reputation computation in
OSNs. The proposed model considers the informa-
tion associated to users to model how reputation is
spread within the social network. In REMSA, each
Reputation Management in Online Social Networks - A New Clustering-based Approach
469
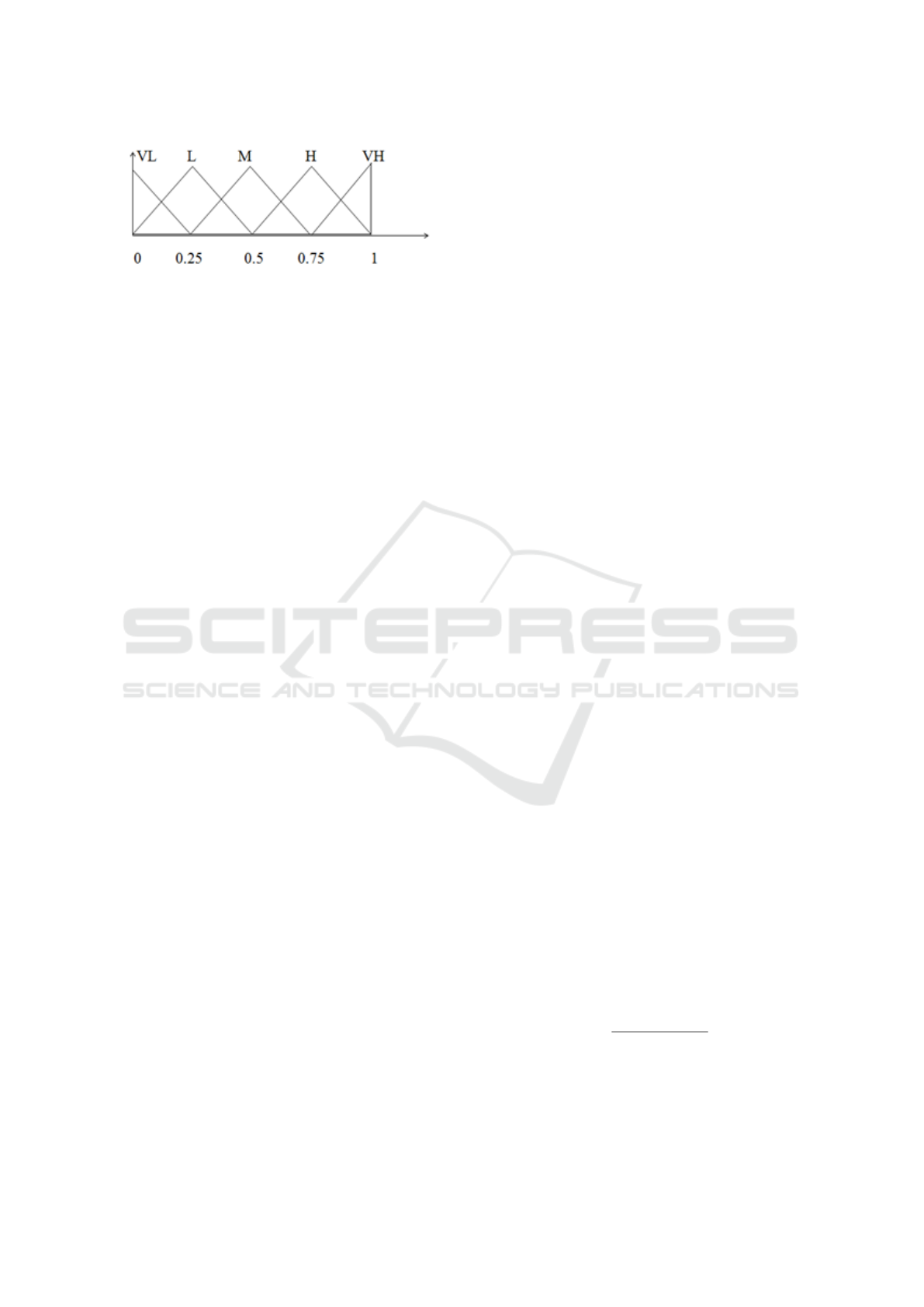
Figure 1: Stratification of reputation values.
user updates reputations values affected to his neigh-
bours based on the history of interactions and by con-
sidering the frequency of interactions in recent his-
tory. In addition, ReMSA, uses a voting mechanism
to aggregate neighbours’ opinions when updating rep-
utation values. The voting process is recursive and
aims to reach to every user in the network.
With REMSA, the reputation is only based on the
opinions of the neighbours. If one user has only one
friend, does the trustworthiness of its opinion guaran-
teed?
In this work, we propose a new algorithm called
RepC for reputation management in OSNs. RepC is
truly unique since it is based on clustering algorithms.
In fact, it aims to divide OSNs’ users into clusters
(groups) such that the most trustworthy users belong
to the same cluster.
4 CHOOSING THE INITIAL
CENTROIDS OF THE
CLUSTERS
We associate a Triangular Fuzzy Number (TFN), as
given in Figure 1, that enables us to specify a range
for a given reputation level instead of giving it a par-
ticular discrete value. The meaning of the different
linguistic values (fuzzy set) are defined as: Very Low
(VL), Low (L), Medium (M), High (H), and Very
High (VH), to range users from very untrustworthy to
very trustworthy. The advantage of this stratification
is that a reputation value denoted as ”high” of one user
is acknowledged by others as a high reputation value,
which is also true for the other values. Thus, we avoid
the problem of ”what does a reputation value of 0.2,
or 20%, mean? Is it high or low?”, for example.
Next section describes our algorithm RepC based
on a partitioning clustering algorithm. Indeed, the
time and space complexities of the partitioning algo-
rithms are typically lower than those of the hierarchi-
cal algorithms (Day, 1992). In fact, partitioning meth-
ods have advantages in applications requiring large
datasets as OSNs, which is not always the case for
hierarchical clustering for which the construction of a
tree is computationally expensive. In addition, the
problem of the choice of the number of desired output
clusters accompanying the use of a partitioning algo-
rithm is solved. In fact, each reputation strata shown
above, presents a cluster, thus, the number of clusters
(VL, L, M, H and VH) is 5.
5 REPC : A CLUSTERING
ALGORITHM FOR
REPUTATION MANAGEMENT
IN OSNS
In this Section, we introduce the RepC algorithm for
the clustering of OSNs’ users based on their reputa-
tion. In RepC, the global reputation of each user u is
weighted by aggregating the direct and indirect trust
values assigned to user u by other ones. In Subsection
5.1, we discuss how to aggregate these normalized
trust values in a sensible manner in order to obtain the
corresponding reputation values. Then, in Subsection
5.2, we tackle the problem of classifying users into
different clusters based on their reputation similarity
such that most trustworthy users belong to the same
cluster.
5.1 Aggregating Direct and Inferred
Trust Values
We have defined, on the basis of our previous work
(Hamdi et al., 2012), how to compute direct trust val-
ues in OSNs. Accordingly to our model titled IRIS,
we build direct trust relations by aggregating differ-
ent ties in a multiplex network (the direct interactions
between users, their existing relationship types and
their interest similarity). In addition, we use the ac-
curate model TISoN we proposed in (Hamdi et al.,
2016) to infer indirect trust in OSNs based on direct
relationships between users. The direct and indirect
computed values are normalized (all values are set be-
tween the unit interval) in the aim to lead to an elegant
probabilistic interpretation.
A natural way to evaluate the reputation of an
OSN user j is to aggregate the opinion of all users
about that user, i.e., to consider all direct and indirect
trust values assigned to him (c.f., Eq. 3).
r
j
=
∑
n
i=1
α.t
i j
/i 6= j
n + n
0
(3)
Here r
j
denotes the reputation of the OSN user
j based on all users’ opinions; t
i j
is the trust value
assigned to j by the user i; n is the number of OSN
users and n
0
is the number of direct relations in the
SECRYPT 2017 - 14th International Conference on Security and Cryptography
470

Algorithm 1: The RepC Algorithm.
Data: R: reputation vector with r
j
values,
j = 1 ...n.
C: the set of initialized centroids c
p
,
p = 1 . . . 5.
ε: error threshold, ε ≈ 0.
Result: G: the set of final clusters or groups
g
p
.
1 begin
2 k ← 0
3 V L ←
/
0; L ←
/
0; M ←
/
0; H ←
/
0 ; V H ←
/
0;
4 G ←
{(V L,c
1
);(L,c
2
);(M,c
3
);(H,c
4
);(V H, c
5
)};
5 repeat
6 k ← k + 1;
7 Update clusters ∈ G by assigning each
user j to one cluster g
p
such that
Min(
r
j
− c
p
/p ∈ [1 . . . 5]);
8 Recompute the vectors of centroids
C
k
= [c
p
]
k
by using Eq. 4;
9 until
C
k
−C
k−1
< ε;
OSN. The parameter α is defined as follows:
α =
(
1 if t
i j
is an inferred trust value
2 if t
i j
is a direct trust value
We can write this in matrix notation: if we define
T to be the square matrix [t
i j
], then R is the column
vector with r
j
values such as j ∈ [1..n]. This is a use-
ful way to have each user gain a view of the OSN that
is wider than his own experience.
5.2 Description of the RepC Algorithm
In RepC, we adopt the typical k-Means algorithm
(Hartigan and Wong, 1979), which is the simplest and
most used partitioning algorithm since it is easy to im-
plement and its time complexity is about O(n), where
n is the number of objects. K-means starts with a ran-
dom initial partition and keeps reassigning the object
to clusters based on the similarity between the object
and the cluster centroid until a convergence criterion
is met. In our work, as mentioned in Section 4, the
initial clusters are properly chosen and their number
is equal to 5. Thus, we do not face the major drawback
of k-means which is sensitive to the random selection
of the initial partition.
The process, used by RepC, is sketched by Algo-
rithm 1. First, in lines 3 to 4, RepC creates the set G
of 5 empty clusters (VL, L, M, H,VH) with the initial-
ized centroids such that c
1
= 0; c
2
= 0.25; c
3
= 0.5;
c
4
= 0.75; and c
5
= 1. Second, in line 7, the algorithm
assigns each user j to one cluster g
p
such that his rep-
utation r
j
is closer to this cluster centroid c
p
. Then,
in line 8, RepC recomputes the centroid of each clus-
ter as the mean of reputations of users belonging to
the cluster. The process of updating and recomputing
centroids of clusters as well as assigning users to the
adequate clusters is repeated until the stability condi-
tion is reached (line 9).
c
p
=
∑
g
p
r
j
l
, p ∈ [1 ...5],l ∈ [1 . . . n] (4)
In Eq. 4, n is the number of the OSN users, l is
the number of users j belonging to cluster g
p
with the
centroid c
p
.
6 EXPERIMENTS
In this section, we describe the experiments we lead
on the proposed algorithm RepC. In one hand, we
use different types of criteria for clustering evaluation
to validate the effectiveness of RepC. In the other
hand, we aim to test our results’ quality by compar-
ing RepC with the existing algorithm for reputation
management in OSNs REMSA.
Since trust is not randomly distributed, we con-
duct our experiments in the real OSN dataset Twit-
ter
1
.
6.1 Twitter Data Set
We use a data set
2
collected from the real social net-
work Twitter. This data set containing more than
250000 users and 320000 relations, uses a social la-
belled graph. Each node of the graph presents a Twit-
ter member and each edge denotes the number of
retweets one user gives to another user.
6.2 Accuracy Metrics
6.2.1 Validation of the Clusters
The clusters’ evaluation or the assessment of the qual-
ity of the obtained clusters presents an important topic
related to clustering. Most of cluster validity mea-
sures evaluate the trade-off between cluster compact-
ness and separability (Portmann, 2012). Other mea-
sures are used to evaluate how well a clustering ap-
proach performs on a dataset (Vendramin et al., 2010).
1
https://twitter.com/
2
https://snap.stanford.edu/data/higgs-twitter.html
Reputation Management in Online Social Networks - A New Clustering-based Approach
471

In our experiments, we adapt the internal crite-
ria indexes of Dunn (Dunn, 1974) as well as that
of Davies and Bouldin (Davies and Bouldin, 1979).
Both of these criteria consider a clustering algorithm
as good and successful whenever it generates clus-
ters with high intra-cluster homogeneity, good inter-
cluster separation and high connectedness between
neighbouring data objects.
The Dunn Index. The Dunn Index, I
D
, identifies
clusters which are well separated and compact. The
goal is therefore to maximize the inter-cluster dis-
tance while minimizing the intra-cluster distance. As
shown in Eq. 5, I
D
is the ratio between the maxi-
mum distance separating two users classified together
and the minimum distance between two users classi-
fied separately. For a good clustering, I
D
should be as
high as possible.
I
D
= min
1≤i≤n
[min
1≤ j≤n,i6= j
(
d(i, j)
max
1≤k≤n
d
0
(k)
)] (5)
With:
• d(i, j): the distance between clusters i and j
• d
0
(k): the diameter of cluster k
The Davies and Bouldin Index. Davies and Bouldin
Index, I
DB
, identifies clusters which are far from each
other. It is defined by the average of cluster evaluation
measures for all the clusters as described in Eq. 6.
For a good clustering, the I
DB
should be as low as
possible.
I
DB
=
1
n
n
∑
i=1
max
i6= j
(
σ
i
+ σ
j
d(c
i
,c
j
)
) (6)
With:
• n: the number of clusters.
• c
i
: the centroid of i
th
cluster
• σ
i
: the average distance between objects of cluster
i and the centroid c
i
• d(c
i
,c
j
): the distance between centroids c
i
and c
j
6.2.2 The F-score Metric
We adopt the commonly used metric in information
retrieval, F-score metric, defined in Eq. 7, to test the
accuracy of the proposed method. It is based on pre-
cision and recall metrics defined successively in Eq. 8
and Eq. 9. Parameters used to compute the accuracy
are as follows:
X = the set of users whom are actually trustworthy
(Reputation value greater than 0.5);
Y = the set of users that the algorithm suggests to
be trustworthy.
Table 1: The I
D
and I
DB
Cluster validity values for the RepC
algorithm.
#Users I
D
I
DB
100 0.25 0.52
500 0.25 0.53
1000 0.32 0.48
5000 0.38 0.45
10000 0.31 0.45
50000 0.31 0.56
100000 0.24 0.92
200000 0.23 1.23
F − score =
2 × (Pecision × Recall)
(Pecision + Recall)
(7)
Precision =
X
T
Y
Y
(8)
Recall =
X
T
Y
X
(9)
The higher the recall and precision are, the more
desirable the measures are for a good algorithm per-
formance. Thus, we make use of F-score to indi-
cate our algorithms performances. Obviously, high
F-score values are desirable.
6.3 Performance Study
In order to assess the performance of our algorithm,
we conduct different experiments. Firstly, we simu-
late the Twitter dataset with RepC and we run the pro-
grams computing the I
D
and I
DB
indexes by varying
the number of users. Then, we compute the F-score
measure for our algorithm RepC to find to which de-
gree RepC provides more relevant results, and we
compare it versus those obtained using the F-score for
the existing algorithm REMSA.
As shown in Table 1, after 5000 users, as far as
the number of users increases, the I
D
decreases and
the I
DB
increases. This finding is due to a decrease in
the minimum distance inter-cluster and an increase in
the maximum diameter intra-cluster. This is caused
by the rise in the number of clusters leading to the
cluster’s expansion (resp. an increase in a cluster di-
ameter), and thus a higher degree of clusters overlap
(resp. a decrease in the distance between clusters).
To compute the F-score values, we define, in
Eq.10, the importance degree notion I
D
i
, presenting
the actual reputation of a user i in Twitter. In fact,
the more a user is reputable and important in the net-
work, the higher the number of his shared (retweeted)
tweets is.
I
D
i
=
Tw
i
Tw
m
(10)
SECRYPT 2017 - 14th International Conference on Security and Cryptography
472
0
0.2
0.4
0.6
0.8
1
0 50000 100000 150000 200000
F-score
Users’ Number
REMSA
RepC
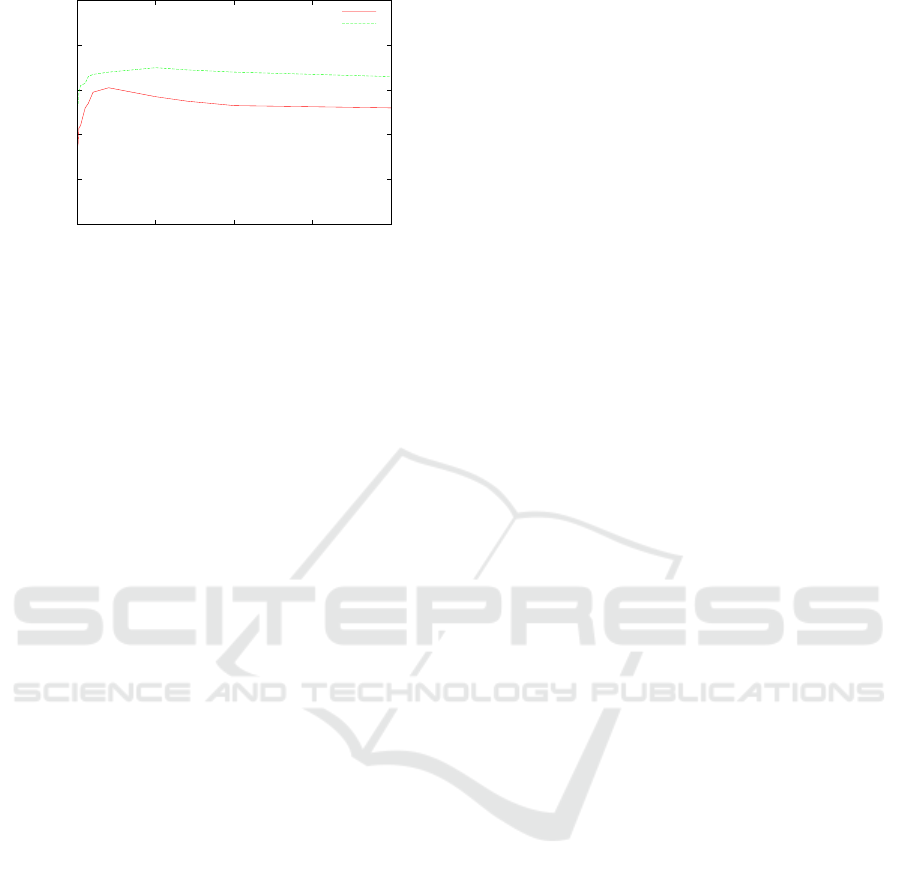
Figure 2: F-score results for RepC and REMSA with vary-
ing the number of users.
In Eq.10, Tw
i
is the number of shared tweets of
the user i and m is the user having the maximum num-
ber of shared tweets.
The simulation results, are shown in Figure 2.
The latter shows that RepC outperforms REMSA
whatever the number of users.
The F-score values for RepC increase as far as the
number of users increases. In fact, by increasing the
number of users, direct and indirect trust values, con-
sidered to compute reputation values, increase leading
to a rise in the authentication success trust rate. Then
reputation values are more accurate.
However, the accuracy of REMSA reaches its best
values for a number of users standing within the range
[5000, 20000], decreasing again when the number of
users exceeds 50000. In fact, considering only neigh-
bours of a user to compute its reputation instead of
the whole network, generates a decrease of precision
and recall values and consequently a decline of the F-
score. This is not the case of RepC which respects the
objectivity property of reputation and keeps produc-
ing correct results with an increasing of the number
of users.
7 CONCLUSION
In this paper, we have proposed a new reputation man-
agement algorithm RepC based on a trust network
generated in previous works. Our algorithm classi-
fies an OSN users into clusters by their trust simi-
larity such that most trustworthy users belong to the
same cluster. The evaluation results, based on the real
social network Twitter, show that our algorithm can
generate high quality results.
As forthcoming works, we plan to simulate a
fuzzy version of RepC and compare between the hard
and fuzzy methods.
REFERENCES
Chen, D., Chang, G., Sun, D., Li, J., Jia, J., and Wang, X.
(2011). Trm-iot: A trust management model based
on fuzzy reputation for internet of things. Computer
Science and Information Systems, (20):1207–1228.
Christianson, B. and Harbison, W. S. (1996). Why isn’t trust
transitive? In Proceedings of the Security Protocols
Workshop, Cambridge, United Kingdom, pages 171–
176.
Davies, D. L. and Bouldin, D. W. (1979). A cluster separa-
tion measure. IEEE Trans. Pattern Anal. Mach. Intell.,
1(2):224–227.
Day, W. H. E. (1992). Complexity theory: An introduction
for practitioners of classification, chapter 6, pages
199–235. World Scientific Publishing.
Dunn, J. C. (1974). Well separated clusters and optimal
fuzzy-partitions. Journal of Cybernetics, 4:95–104.
Hamdi, S., Ganc¸arski, A. L., Bouzeghoub, A., and Yahia,
S. B. (2016). Tison: Trust inference in trust-oriented
social networks. ACM Trans. Inf. Syst., 34(3):17.
Hamdi, S., Ganc¸arski, A. L., Bouzeghoub, A., and
BenYahia, S. (June 25-27, 2012). Iris: A novel method
of direct trust computation for generating trusted so-
cial networks. In Proceedings of the 11th IEEE Inter-
national Conference on Trust, Security and Privacy
in Computing and Communications, TrustCom 2012,
Liverpool, United Kingdom, pages 616–623.
Hartigan, J. A. and Wong, M. A. (1979). A K-means clus-
tering algorithm. Applied Statistics, 28:100–108.
Heaney, M. T. (2014). Multiplex networks and interest
group influence reputation: An exponential random
graph model. Social Networks, 36:66–81.
Lee, J. and Oh, J. C. (2015). A node-centric reputation com-
putation algorithm on online social networks. Appli-
cations of Social Media & Social Network Analysis,
pages 1–22.
Portmann, E. K. (2012). The fora framework: A fuzzy
grassroots ontology for online reputation manage-
ment. PhD thesis, Faculty of Sciences, University of
Fribourg, Switzerland.
Vendramin, L., Campello, R. J. G. B., and Hruschka, E. R.
(2010). Relative clustering validity criteria: A com-
parative overview. Stat. Anal. Data Min., 3(4):209–
235.
Zhang, Y., Chen, H., and Wu, Z. (2006). A social network-
based trust model for the semantic web. In Proceed-
ings of the Third International Conference on Auto-
nomic and Trusted Computing, ATC’06, pages 183–
192, Berlin, Heidelberg. Springer-Verlag.
Reputation Management in Online Social Networks - A New Clustering-based Approach
473
