A Min-Max Tchebycheff based Local Search Approach for MOMKP

Imen Ben Mansour, Ines Alaya and Moncef Tagina

National School of Computer Sciences, COSMOS Laboratory, University of Manouba, Manouba, Tunis, 2010, Tunisia

Keywords:

Multi-objective Multidimensional Knapsack Problem, Iterated Local Search, Scalarization Functions,

Tchebycheff Functions.

Abstract:

The multi-objective multidimensional knapsack problem (MOMKP) which is one of the hardest multi-

objective combinatorial optimization problems, presents a formal model for many real world problems. Its

main goal consists in selecting a subset of items in order to maximize m objective functions with respect to

q resource constraints. For that purpose, we present in this paper a resolution approach based on a Min-Max

Tchebycheff iterated Local Search algorithm called Min-Max TLS. In this approach, we propose designing a

neighborhood structure employing a permutation process to exploit the most promising regions of the search

space while considering the diversity of the population. Therefore, Min-Max TLS uses Min-Max N (s) as

a neighborhood structure, combining a Min-Extraction-Item algorithm and a Max-Insertion-Item algorithm.

Moreover, in Min-Max TLS two Tchebycheff functions, used as a selection process, are studied: the weighted

Tchebycheff (WT) and the augmented weighted Tchebycheff (AugWT). Experimental results are carried out

with nine well-known benchmark instances of MOMKP. Results have shown the efﬁciency of the proposed

approach in comparison to other approaches.

1 INTRODUCTION

Many real-life optimization problems can hardly be

formulated as a mono-objective problem, which ex-

plains the permanent growing interest in the ﬁeld of

multi-objective optimization. For instance, in trans-

portation problem there is more than one objective to

optimize. The cost of the transport, the duration and

the capacity of the transport, all of this could be objec-

tives to be optimized. In such problems, usually opti-

mizing one objective, leads to degrading other objec-

tives. Thus, ﬁnding a good trade-off between several

conﬂicting objectives is one of the main goals of the

multi-objective optimization problems (MOPs). So,

it consists in optimizing simultaneously several con-

ﬂicting objectives in order to ﬁnd a set of solutions

called Pareto front or set or non-dominated set.

The MOMKP modelizes many real world prob-

lems such as resource allocation (Shih, 2005), port-

folio optimization (Penn et al., 1994) and budget al-

location (Smeraldi and Malacaria, 2014). Moreover,

MOMKP can be modelized as a subproblem such as

the ﬂight crew choice (Ehrgott and Ryan, 2002) and

many other general integer programs. To solve the

MOMKP, several approaches based on metaheuris-

tics were proposed in the literature: In (Zitzler et al.,

2002), Zitzler et al. introduced the well-known

SPEA2 which is an elitist algorithm, based on a

ranking dominance procedure. Deb et al. proposed

the NSGAII (Deb et al., 2002), another well-known

multi-objective evolutionary algorithm that is also an

elitist approach and uses a different ranking domi-

nance procedure. In (Lust and Teghem, 2008), a

memetic algorithm integrates a tabu search method,

called MEMOTS, was devised. A generic ACO algo-

rithm (m-ACO) was presented and instantiated with

four variants In (Alaya et al., 2007). m-ACO is pa-

rameterized by the number of ant colonies and the

number of the pheromone structures. Recently, an

indicator based ant colony approach which is abbre-

viated as IBACO is proposed in (BenMansour and

Alaya, 2015). The algorithm uses the indicator op-

timization principle to guide ants during their search

in the most promising areas by reinforcing the best

solutions by rewarding pheromone.

Related Works. Local search approaches have been

widely employed on the NP-hard multi-objective op-

timization problems, including problems formulated

as a multi-objective multidimensional knapsack prob-

lem (Alsheddy and Tsang, 2009), (Vianna and Dianin,

2013) and(Liefooghe et al., 2013). Indeed, its sim-

ple and practical appearance has enabled it to be ef-

ﬁcient in many real-world problem such as railway

transportation, airline operations, portfolio optimiza-

140

Mansour, I., Alaya, I. and Tagina, M.

A Min-Max Tchebycheff based Local Search Approach for MOMKP.

DOI: 10.5220/0006433801400150

In Proceedings of the 12th International Conference on Software Technologies (ICSOFT 2017), pages 140-150

ISBN: 978-989-758-262-2

tion and computer networks (Ehrgott and Gandibleux,

2004). Motivated by the success of these meth-

ods, several papers propose scalarization-based local

search methods for MOMKP. These methods have re-

ceived a great interest from the scientiﬁc community

because of their success for solving multi-objective

problems. They represent a simple way to trans-

form a multi-objective problem into one single or a

family of single objective optimization problems. In

(Lust and Teghem, 2012), Lust and Teghem present

the two-phase Pareto local search (2PPLS). The al-

gorithm uses a Pareto-based local search combined

with a very-large scale neighborhood method based

on vectors weight. The 2PPLS combines Pareto lo-

cal search and aggregation to solve MOMKP, it con-

sists of two main phases. Phase 1 generates an ap-

proximation of all the supported solutions by solving

a number of linear aggregation problems. Phase 2

applies a Pareto local search to every solution gen-

erated in Phase 1 to ﬁnd non-supported Pareto opti-

mal solutions. In (Alves and Almeida, 2007), a ge-

netic algorithm based on Tchebycheff scalarization

function called MOTGA has been proposed. The al-

gorithm was applied to the MOMKP problem. The

Pareto front is divided into a few small parts. Each

part is approximated by a stage and each stage is

guided by a different Tchebycheff aggregation func-

tion. More recently, a memetic algorithm based on

decomposition (MOMAD) was proposed in (Ke et al.,

2014). MOMAD combines the ideas of the two ap-

proaches: the 2PPLS and the evolutionary algorithm

MOEA/D introduced in (Zhang and Li, 2007). In

MOMAD, a Pareto local search method is ﬁrst ap-

plied for the neighborhood search then a single objec-

tive local search is applied to each perturbed solution.

Motivations and Contributions. From the pre-

viously mentioned state-of-the-art algorithms, one

can say that scalarization and weighted based meth-

ods present promising approaches to solve MOMKP.

In the literature, various efforts have been directed

toward the use of the metaheuristics to solve the

MOMKP. Generally, these approaches present a good

way to solve NP-hard problems. However, if a heuris-

tic searching method is used these approaches may

be very time consuming, especially for the large size

instances. So, the challenge is optimizing both the

quality results and the time-consuming. In this work,

we propose an iterated multi-objective local search

based on Tchebycheff function: Min-Max TLS for

MOMKP. In order to investigate the impact of the

choice of the Tchebycheff function on the selection

process, the two well-known Tchebycheff functions

are studied in this work: the weighted Tchebycheff:

WT (Bowman, 1976) and the augmented weighted

Tchebycheff: AugWT(Steuer and Choo, 1983).

Moreover, one of the key aspects that has to be con-

sidered is the neighborhood structure since it plays

a central role in a local search algorithm. Min-Max

TLS integrates an efﬁcient weighted neighborhood

structure called Min-Max N (s) to explore the neigh-

borhood. Min-Max N (s) allows to establish an or-

der between items according to their proﬁtability. It

has the goal of ﬁnding the item that minimizes an ex-

traction ratio to permute it with items that maximize

an insertion ratio in order to improve the quality of

the obtained solutions in a small computational time.

Furthermore, in weighted based methods, the genera-

tion of the weight vectors presents a signiﬁcant point

and inﬂuences the quality of the generated solutions.

Thus, Min-Max TLS deﬁnes a weight vector genera-

tion method called Gw: Gradual weight vector gen-

eration method. Gw creates a set of weight vectors,

corresponding to search directions, guiding the search

gradually on almost all regions of the Pareto front.

The paper is organized as follows. In the next sec-

tion, we deﬁne the multi-objective optimization prob-

lems. In section 3, we present the multi-objective

multidimensional knapsack problem. In section 4,

the Tchebycheff functions used in this paper are de-

scribed. Section 5 presents our main contributions,

the proposed algorithm and its different main func-

tions. Then, in section 6, we discuss the experimental

results obtained from Min-Max TLS. Finally, in sec-

tion 7, we end the paper with the conclusion and our

perspectives.

2 MULTI-OBJECTIVE

OPTIMIZATION PROBLEMS

Before introducing the MOMKP, let us introduce

some useful notations and deﬁnitions related to a gen-

eral multi-objective optimization problem.

Let X denote the decision space of a general op-

timization problem, Z the corresponding objective

space and m objective functions f

,..., f

that assign

to each decision vector x ∈ X one objective vector

z=( f

(x),..., f

(x)) ∈ Z. In the following, we assume

that all objective functions are to be maximized:

• Deﬁnition 2.1. A solution z dominates a solution

z’, noted z  z’, iff ∀ i ∈ {1, ...,m}, f

(z) ≥ f

(z’)

and ∃ i ∈ {1,..., m}, f

(z) > f

(z’);

• Deﬁnition 2.2. A solution z is called weakly non-

dominated, if there exists no z’ ∈ Z such that for

all i ∈ {1, ...,m}, f

(z’) > f

(z);

• Deﬁnition 2.3. A solution z is Pareto-optimal or

non-dominated, if a solution z’ dominates z does

A Min-Max Tchebycheff based Local Search Approach for MOMKP

141

not exist.

The goal of a MOP is to ﬁnd the set of all non-

dominated solutions called Pareto set. When using a

metheuristic approach, the goal is to ﬁnd a Pareto set

approximation.

3 MOMKP FORMULATION

The multi-objective multidimensional knapsack prob-

lem could be formulated as follows:

Maximize

∑

j=1

k = 1, ...,m (1)

Sub ject to

∑

j=1

≤ b

i = 1, ...,q (2)

∈ {0,...,1} j = 1, ..., n

where n is the number of items, for each item I

assigned a decision variable x

equal to 1 if the item

is selected, 0 otherwise. Each item I

has a proﬁt p

relatively to the objective k and a weight w

relatively

to the resource i. The aim of the problem is to select

a subset of items in order to maximize m objective

functions while not exceeding q resource constraints.

is the total quantity available for the resource i.

In this paper, the considered instances assume that

the number of objective functions is equal to the num-

ber of resources (m=q).

4 TCHEBYCHEFF FUNCTIONS

For decomposing a multi-objective optimization

problem into one single-objective many scalariza-

tion functions exist. In following, we introduce two

among the most commonly-used methods based on

the Tchebycheff metric:

4.1 The Weighted Tchebycheff Function

W T (x|λ) = max

k=1...m

| f

(x) − r

∗

| (3)

where x is the solution to evaluate, λ=(λ

...λ

) is

the weight vector, such that λ

≥ 0 for all k = 1...m

and

∑

k=1

=1. The ideal point r

∗

= (r

∗

,...,r

∗

) is

used as a reference point, calculated as follows:

∗

= max

k=1...m

(x) (4)

The weighted Tchebycheff in (3) is minimized to

maximize each objective.

4.2 The Augmented Weighted

Tchebycheff Function

One of the main advantage of the weighted Tcheby-

cheff method is that by varying appropriately the

weight vectors and/or the reference point, every non-

dominated solution of the Pareto front of the stud-

ied MOP, explicitly includes non-convex and discrete

problems, can be found (Steuer, 1986). On the other

hand, the weighted Tchebycheff method generates

also the weakly non-dominated solutions which is of-

ten undesirable in MOP. In (Steuer and Choo, 1983),

Steuer and Choo suggested to add an l

-term, pa-

rameterized by ε, to W T (x|λ) that helps to avoid the

weakly non-dominated solutions. The resulting func-

tion is deﬁned as follows:

AugWT (x|λ) = max

k=1...m

| f

(x) − r

∗

+ ε

∑

k=1

| f

(x) − r

∗

| (5)

where ε ≥ 0 is usually chosen as a small positive

number and r

∗

is calculated as deﬁned in Eq. (4).

5 OUR PROPOSED APPROACH

MIN-MAX TLS: MIN-MAX

TCHEBYCHEFF BASED

LOCAL SEARCH

Let P be the current population of Min-Max TLS of

size N. Initially, a weight vector is selected from the

set V of H weight vectors, generated according to

the proposed Gw method. Then, for each solution

s of P the neighborhood is explored following the

proposed weighted neighborhood structure Min-Max

N (s), until a good solution is found i.e. one which

is better than at least the worst solution w in P in

terms of the used Tchebycheff function. This process

is iterated until all solutions in P are explored. All

the non-dominated solutions found during the local

search step are stored in the archive A. The algorithm

stops when a maximum number of iterations T max is

met and return the archive A. The algorithm 1 shows

a detailed description of the Min-Max TLS algorithm.

5.1 Weight Vectors Generation

In order to generate the set V , we propose the Gw

method: Let λ=(λ

...λ

) be the weight vector, such

that λ

≥ 0 for all k = 1...m and

∑

k=1

=1. For the

bi-objective case, the weight vectors are calculated as

ICSOFT 2017 - 12th International Conference on Software Technologies

142

Algorithm 1: Min-Max TLS algorithm.

1: Begin

2: V ← Generate Weight Vectors (H)

3: repeat

4: P ← Perturbation(P , N)

5: A ← Non-dominated solutions(P )

6: λ ← SelectWeightVector (V , H)

7: for all s ∈ P do

8: repeat

9: U pdateRe f erencePoint

10: s

∗

← Neighborhood(s)

11: if Acceptance(s

∗

, w, P ) then

12: P

← Replace(s

∗

, w, P )

13: end if

14: until s

∗

6= w

15: end for

16: A ← Non-dominated solutions(A ∪ P

)

17: until T max is reached

18: End

follow:

(t) = ln



4 ∗t ∗e



+ cos



2 ∗ π ∗t



(6)

(t) = 1.0 − λ

(t) (7)

where t is the iteration index and e is exp (1). The

weight vectors are controlled by FQ, which is the

weight change frequency. If the FQ is well set, the

population can move smoothly from one point to an-

other thus the whole regions can be explored and al-

most all points covering the Pareto front can be found

through this appropriate variation of research orien-

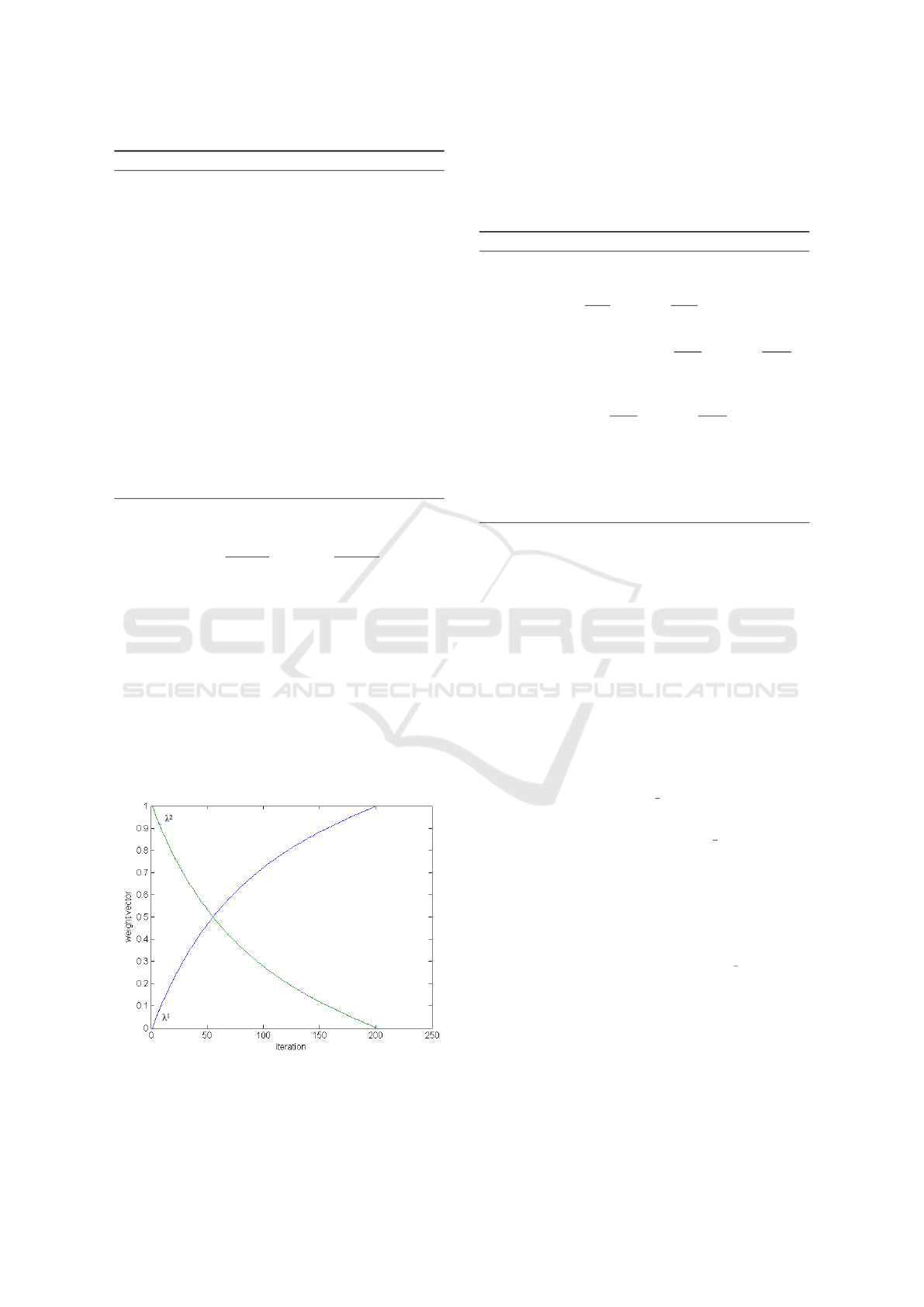
tations. Fig. 1 shows an example of how the weight

vector values λ

and λ

change within 200 iterations

during the local search process.

Figure 1: The weight vector value change within 200 itera-

tions.

The extension of the Gw method with more than

two objectives is theoretically straightforward. The

algorithm 2 shows the Gw, in case of m=4 objectives.

Algorithm 2: Gw algorithm.

1: Begin

2: for i f rom 0 to FQ/4 do

3: λ

=ln

h

4∗i∗e



+ cos



2∗π∗i

i

4: for j f rom 0 to FQ/4 do

5: λ

=(1.0−λ

)∗ln

h

4∗ j∗e



+ cos



2∗π∗ j

i

6: for k f rom 0 to FQ/4 do

7: λ

=(1.0 − λ

− λ

8: ln

h

4∗k∗e



+ cos



2∗π∗k

i

9: λ

=1.0 − λ

− λ

10: end for

11: end for

12: end for

13: End

The algorithm 2 is executed only once before the

beginning of the main loop of Min-Max TLS. Once

the initial population is generated, a weight vector is

selected from the set V , according to its order of gen-

eration by the Gw method and assigned to the solu-

tion to be evaluated in such way that all the member

of the population have the same weight vector during

the same iteration.

5.2 Initial Population Initialization

Like in most evolutionary approaches, the ﬁrst initial

population in Min-Max TLS is randomly created. In

Min-Max TLS, a solution s is composed of two sub-

sets I

={I

,...,I

} and I

−

={I

−

,...,I

−

} where

is the subset of the items selected in the solution

s, T is the number of taken items, I

−

is the subset

of the remaining items (unselected items) and NT is

the number of untaken items. To create a ﬁrst ran-

dom population, Min-Max TLS creates N random so-

lutions. Every solution s is created by selecting a ran-

dom item j among the n items and added it to the

solution s. If any resource capacity is violated by an

item j, the item is placed in the subset I

−

otherwise

the item is added to the subset I

. This process is

iterated until all items are placed.

5.3 Perturbation

After the update of the archive A, a new population is

generated. In order to reach different and new region

of the search space, where the exploration starts in the

A Min-Max Tchebycheff based Local Search Approach for MOMKP

143

next local search step, we propose to use a perturba-

tion function to generate the new population: At each

iteration, N new solutions are randomly selected from

the archive A if the size of A exceeds N, else if the

archive size is less than the size of the population, the

missing solutions are created randomly as done in the

ﬁrst initial population. Let µ be the rate of noise, for

every solution s we remove randomly (µ ∗ T ) items

from the subset I

and we add them to the subset I

−

of the solution s. Then, as long as we do not violate

any resource constraints. Items are randomly added

from I

−

to I

. In fact, this random move allows us to

reach new local optima. They can be weak or strong

noise which means moving to a near local optima or

jump totally to a new region where it is considerably

difﬁcult to ﬁnd a new local optima.

5.4 Update Reference Point

When a new solution is introduced in the population,

the reference point r

∗

is updated. After the initializa-

tion process of the population and after each neigh-

borhood exploration, the new maximal value of all

objective functions is calculated according to Eq. (4).

5.5 Neighborhood Structure

The generation of the neighborhood is one of the

most important part of a local search algorithm. In

this paper, we use a proposed weighted neighbor-

hood structure Min-Max N (s). By means of the

two proposed algorithms: Min-Extraction-Item algo-

rithm and Max-Insertion-Item algorithm, Min-Max

N (s) tries to gives a better neighbor of a solution s.

5.5.1 Min-Extraction-Item

For each taken item I

the ratio U(l

) is calculated

as follows:

U(l

) =

∑

k=1

(t)p

∑

i=1

(8)

where λ

(t) is the weight vector selected from the

set V ,

∑

k=1

(t)p

is the weighted proﬁt of the item

and

∑

i=1

its overall weight. The ratio U(l

)

measures the utility value of each item, the lower this

ratio is, the worst the item is.

Once the ratio U(l

) is calculated for all items

={I

,...,I

}, a list L

containing all the items I

is created and sorted in ascending order according to

the ratio U(l

) of each item. So that the worst items

that minimize the ratio U (l

) are placed on the top of

the list. The algorithm 3 outlined the Min-Extraction-

Item algorithm. This algorithm is executed only when

a new solution s is selected for neighborhood explo-

ration.

Algorithm 3: Min-Extraction-Item algorithm.

1: Begin

2: for l

f rom 1 to T do

3: Compute U(l

)

4: Add Item I

to L

5: end for

6: Sort L

in ascending order

7: End

5.5.2 Max-Insertion-Item

For each untaken item I

−

the ratio U(l), inspired from

(Alaya et al., 2004), is calculated. We deﬁne R

(s)=b

∑

l=1

as the remaining quantity of the resource i

after the construction of the solution s. The ratio

U(l)

of an item I

−

can be calculated as follows:

U(l) =

∑

k=1

(t)p

∑

i=1



(s)



(9)

where p

and w

are respectively the proﬁt and the

weight of the candidate item. The ratio U (l) measures

the quality of the candidate item according to the so-

lution s where the higher this ratio is, the better the

item is.

As done with the taken items in the Min-

Extraction-Item algorithm, a list L

containing all

the candidate items I

−

is created and sorted in de-

creasing order according to the ratio U(l) of each

item. So that the most proﬁtable items that maximize

the ratio U(l) are placed on the top of the list. The al-

gorithm 4 outlines the Max-Insertion-Item algorithm.

Algorithm 4: Max-Insertion-Item algorithm.

1: Begin

2: for l f rom 1 to NT do

3: Compute U(l)

4: Add Item I

−

to L

5: end for

6: Sort L

in decreasing order

7: End

5.5.3 Min-Max N (s)

A neighbor s

∗

is created by removing an item from

the list L

and adding items from the list L

as long

as no resource constraint is violated. The algorithm 5

describes the generation of a neighbor of a solution s.

ICSOFT 2017 - 12th International Conference on Software Technologies

144

Algorithm 5: Min-Max N (s).

1: Begin

2: Min-Extraction-Item(T )

3: while s

∗

is the worst do

4: Max-Insertion-Item(NT )

5: s

∗

← Remove L

) f rom s

6: while no constraint is violated do

7: s

∗

← Add L

(l) to solution s

8: end while

9: end while

10: End

5.6 Acceptance Criterion and

Replacement Function

In the local search algorithms, the neighborhood ex-

ploration stops at the ﬁrst better solution or when the

entire neighborhood is explored. In this work, we

choose to stop the exploration once the ﬁrst better

neighbor is found relatively to the used Tchebycheff

function. This choice is guided by one main reason

is that this mechanism allows to speed up the conver-

gence of the population.

The neighbor s

∗

is accepted in the population if

its ﬁtness value, calculated according to the Weighted

Tchebycheff function (Eq. 3) or the Augmented

Weighted Tchebycheff function (Eq. 5), is better than

the worst solution w in the current population. If so,

∗

replaces the worst solution w. Otherwise the neigh-

bor is rejected, the next item on the list L

is selected,

i.e. the item to be removed from the solution s, and

the algorithm 5 is executed again. This process is it-

erated until a neighbor s

∗

better than at least the worst

solution w is found.

6 EXPERIMENTAL RESULTS

The experiments carried out consider two versions

of Min-Max TLS: Min-Max TLS

W T

and Min-Max

TLS

AugW T

where the solutions are evaluated using

respectively the Weighted Tchebycheff function and

the Augmented Weighted Tchebycheff function. In

order to evaluate the quality of the proposed algo-

rithm and to have a fair comparison, we choose to

compare the two proposed versions of Min-Max TLS

with scalarizition-local search-based methods : the

MOMAD (Ke et al., 2014), the 2PPLS algorithm

(Lust and Teghem, 2012) and the MOTGA (Alves and

Almeida, 2007). For both of the two versions as well

as the compared algorithms, we considered the bench-

mark instances deﬁned in (Zitzler and Thiele, 1999),

that are widely used in testing several multi-objective

heuristics, containing nine instances with 250, 500

and 750 items, in combination with 2, 3 and 4 ob-

jectives.

6.1 Experimental Setup

The used parameter settings for Min-Max TLS are ad-

justed experimentally and presented as follow: The

population size N is set to 10, we choose a small

rate noise µ=0.05 to apply on selected solutions in or-

der to focus the search around the most useful solu-

tions. The parameter ε used in the AugWT function

is set to 10

−3

as suggested in (Steuer, 1986), to ensure

that weakly non-dominated solutions are avoided and

that all non-dominated solutions of the studied (poten-

tially non-convex) problem can be found. The change

frequency FQ is set according to the Table 1. In order

to let the weight vectors change smoothly from one

iteration to another and so the whole Pareto front will

be explored, the number of generated weight vectors

H and the stopping criterion T max is set to FQ/4

m−1

The MOMAD, 2PPLS and MOTGA were conﬁgured

as recommended by their authors, for each algorithm

and each instance 30 runs are considered.

Table 1: The change frequency FQ Setting.

Number of Objectives FQ

2 800

3 40

4 20

6.2 Performance Metrics

In order to evaluate the results generated by the dif-

ferent algorithms, we used three measures:

• The hypervolume Difference: which computes

the difference between a reference set, which cor-

responds to the set of the non-dominated solutions

obtained from the union of all solutions of the dif-

ferent runs, and the set of solutions to be evaluated

in terms of hypervolume as deﬁned in (Zitzler and

Thiele, 1999). The obtained values have to be as

close as possible to zero to prove the efﬁciency of

an algorithm against the other approaches;

• The Mann-Whitney Statistical Test: (Knowles

et al., 2005) is applied to the results obtained by

the hypervolume difference in order to prove that

the difference between two algorithms are statis-

tically signiﬁcant. We reject the null-hypothesis

”no signiﬁcant difference between the two algo-

rithms A and B” if the P-value is lower than the

signiﬁcance level 5%;

A Min-Max Tchebycheff based Local Search Approach for MOMKP

145

• The summary Attainment Surface: (Grunert Da

Fonseca et al., 2001) is used to compare the ap-

proach behaviors in a graphical way. The attain-

ment surface is deﬁned by the objective vectors

that have been attained by at least one approxima-

tion set of the tested algorithm. In the following

we compare the median (50%) attainment surface

of the fronts non-dominated solutions found for

30 runs of all the compared algorithms.

All the computational results were obtained by the

performance assessment software package PISA pro-

vided in http://www.tik.ee.ethz.ch/sop/pisa/.

6.3 Comparison Results

We performed 30 independent runs of each compared

algorithm on all the tested instances. In order to

have a good idea of the overall performance of each

approach, the average hypervolume is computed for

each algorithm and each instance. The hypervolume

difference results of the proposed algorithms Min-

Max TLS

W T

and Min-Max TLS

AugW T

, and the com-

pared algorithms MOMAD, 2PPLS and MOTGA ap-

pear in Table 2. Moreover, the Table 2 represents

the results obtained by the Mann-Whitney statistical

test. The M-W.T column contains the number of the

algorithm which is statistically outperformed by the

corresponding algorithm. For example, on the 2x250

instance, Min-Max TLS

W T

statistically outperformed

the algorithm number 3 and the algorithm number 5

which correspond to the MOMAD algorithm and the

MOTGA algorithm respectively. ” ” means that the

corresponding algorithm does not statistically outper-

form any other algorithm, as is the case with 2PPLS

on the 2x750 instance. mxn denotes the tested in-

stance, m is the number of objectives, n is the num-

ber of items and (N/A) denotes that the results are not

available.

By analyzing the Table 2, it is clear that our pro-

posed approach performs better than the other com-

pared algorithms. In fact, Min-Min TLS gives bet-

ter hypervolume difference results than MOMAD on

all the tested instances and better than MOTGA in

eight out of nine instances. Moreover, it seems that

the average results of MOMAD and MOTGA de-

crease according to the size of the problem. For

the largest and hardest instances, the quality of the

obtained results of MOMAD and MOTGA decease

clearly which is not the case of Min-Max TLS. Thus,

the difference between the compared approaches be-

came much more important with the largest instances.

By comparing Min-Max TLS with 2PPLS on the three

bi-objective instances, the two approaches obtained

about the same hypervolume values except on the

2x500 instance where 2PPLS preforms better than

Min-Max TLS. By analyzing the results of the Mann-

Whitney statistical test shown in the Table 2, the ﬁrst

important information that we can extract from the

table is that Min-Max TLS outperforms signiﬁcantly

MOMAD and MOTGA on all the largest and hard-

est instances with 3 and 4 objectives. However, MO-

MAD and MOTGA never signiﬁcantly outperform

the results returned by the proposed approach on these

instances. From the three bi-objective instances, we

can observe that Min-Max TLS outperforms signiﬁ-

cantly MOMAD and MOTGA on 2x750 and 2x250

instances. On the 2x500 instance, Min-Max TLS out-

performs only MOMAD.

Fig. 2 compares the average hypervolume differ-

ence of Min-Max TLS

W T

and Min-Max TLS

AugW T

according to the number of objectives. This ﬁgure

shows clearly the behaviors of the two versions. As

it was previously remarked, the hypervolume values

of Min-Max TLS

W T

are slightly better than Min-Max

TLS

AugW T

on the smallest instances (2 and 3 objec-

tives with 250 and 2 objectives with 500 items) while

with the largest instances with 4 objectives and with

500 and 750 items, Min-Max TLS

AugW T

ﬁnd slightly

better values than Min-Max TLS

W T

. As a conclusion,

one can say that, according to the Table 2 and ﬁgure 2,

Min-Max TLS

AugW T

slightly outperforms Min-Max

TLS

W T

for 5 out of the 9 instances in terms of the

average hypervolume difference but statistically there

is no signiﬁcant difference between the two versions:

Min-Max TLS

W T

and Min-Max TLS

AugW T

Table 3 gives the average computational time con-

sumed by each algorithm in seconds. From the ta-

ble, it is clear that our proposed approach Min-Max

TLS consumes signiﬁcant shorter CPU time than the

other approaches. In fact, the time consumed by

Min-Max TLS is shorter than the other approaches

for some instances about 8 times. When comparing

the CPU time of Min-Max TLS

W T

against Min-Max

TLS

AugW T

, one can observe that the two algorithms

consume almost the same running time. Nevertheless,

Min-Max TLS

AugW T

consumes slightly more running

time than Min-Max TLS

W T

on the same instances.

Fig. 3 shows the median attainment surfaces of

the approximation sets returned by the two versions

Min-Max TLS

W T

and Min-Max TLS

AugW T

, MO-

MAD, 2PPLS and MOTGA for the bi-objectives in-

stances 2x250, 2x500 and 2x750. The ﬁrst impor-

tant remarque that can be observed from this ﬁg-

ure is that all the tested approaches provide a well-

distributed Pareto front where the obtained points

cover almost all the Pareto front. For the instance con-

taining 250 items, the surfaces are almost confused,

it is difﬁcult to distinguish the algorithms. For the

ICSOFT 2017 - 12th International Conference on Software Technologies

146

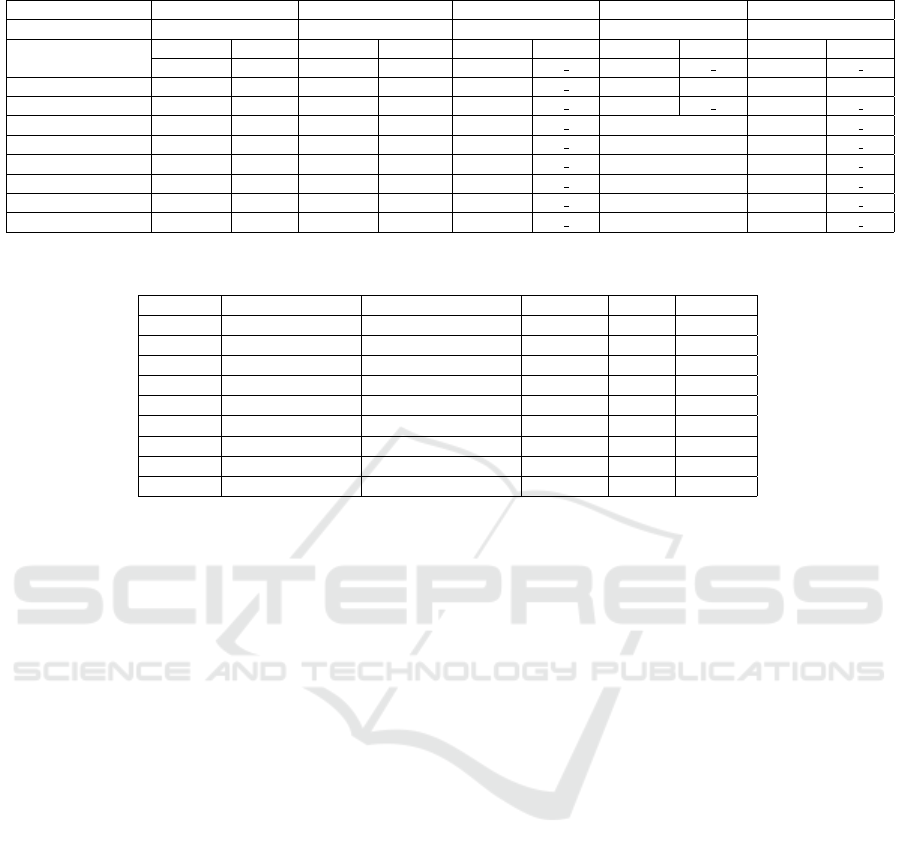
Table 2: Hypervolume Difference Average Values and Mann-Whitney Statistical Test Results.

Instances Min-Max TLS

W T

Min-Max TLS

AugW T

MOMAD 2PPLS MOTGA

Algorithm Number 1 2 3 4 5

Avg M-W.T Avg M-W.T Avg M-W.T Avg M-W.T Avg M-W.T

2x250 2.35E-01 3,5 2.52E-01 3 3.16E-01 2.32E-01 2.72E-01

2x500 1.93E-01 3 2.16E-01 3 3.56E-01 1.20E-01 1,2 1.41E-01 1,2

2x750 2.14E-01 3,5 2.13E-01 3,5 3.00E-01 2.10E-01 2.90E-01

3x250 2.12E-01 3,5 2.21E-01 3,5 3.93E-01 N/A 3.29E-01

3x500 2.27E-01 3,5 2.16E-01 3,5 4.56E-01 N/A 3.96E-01

3x750 1.91E-01 3,5 1.96E-01 3,5 4.31E-01 N/A 2.90E-01

4x250 2.20E-01 3,5 2.18E-01 3,5 3.76E-01 N/A 3.79E01

4x500 1.93E-01 3,5 1.84E-01 3,5 3.97E-01 N/A 3.97E-01

4x750 1.88E-01 3,5 1.76E-01 3,5 4.59E-01 N/A 4.27E-01

Table 3: Average CPU Time of Min-Max TLS

W T

, Min-Max TLS

AugW T

, MOMAD, 2PPLS and MOTGA in seconds.

Instances Min-Max TLS

W T

Min-Max TLS

AugW T

MOMAD 2PPLS MOTGA

2x250 0.6 0.8 5.2 3.1 0.9

2x500 1.9 2.3 15.5 14.8 3.3

2x750 4.0 4.3 23.5 25.1 9.6

3x250 1.0 1.0 7.5 N/A 8.8

3x500 3.4 3.7 19.1 N/A 15.2

3x750 5.8 6.4 35.7 N/A 40.7

4x250 4.8 5.0 10.7 N/A 8.6

4x500 13.6 16.1 25.5 N/A 27.4

4x750 24.3 28.8 45.7 N/A 43.2

other instances, the surfaces of MOMAD, 2PPLS and

MOTGA are slightly above the surfaces returned by

Min-Max TLS

W T

and Min-Max TLS

AugW T

on a small

middle region of the Pareto front. While through-

out the extremity, both of the surfaces of Min-Max

TLS

W T

and Min-Max TLS

AugW T

are close to those of

MOMAD, 2PPLS and MOTGA. We note that there

is no clear difference between the surfaces obtained

by Min-Max TLS

W T

and Min-Max TLS

AugW T

. Thus,

this graphic conﬁrms the numerical results obtained

previously, where we have found that, generally, for

the bi-objective instances the compared algorithms

are not signiﬁcantly different.

6.4 Discussion

As a conclusion of this experimentation section, the

results have shown that the proposed approach per-

forms better than the compared approaches. When

evaluating the Min-Max TLS algorithm for solving

the MOMKP, some useful conclusions can be ex-

tracted. First, the Min-Max TLS performs statistically

better especiallly for the largest and hardest instances

where the best values for the instances with 3 and 4

objectives are found by the two versions of Min-Max

TLS. Second, the difference between the two versions

Min-Max TLS

W T

and Min-Max TLS

AugW T

is very

small. Min-Max TLS performs slightly better using

AugWT function. Third, Min-Max TLS

AugW T

needs

more computational time than Min-Max TLS

W T

. In

fact, the augmented weighted Tchebycheff version

consumes slightly more CPU time than the weighted

Tchebycheff version, especially with the largest in-

stances but produces better results.

Finally, let us mention that the efﬁciency of the

proposed approach is due to many factors: the pro-

posed Gw method, the perturbation function, the

neighborhood structure, the acceptance criterion and

the replacement strategy. The Gw method has a sig-

niﬁcant role in Min-Max TLS. Like any weighted ap-

proach, the selection of the weights can lead to a bet-

ter performance. In fact, the Gw method tries to ap-

propriately varying the search directions, all the mem-

ber of population attempt to target almost all parts

on the Pareto front. Hence, different Pareto-optimal

points can be obtained. Furthermore, the initializa-

tion of the local search population is a very impor-

tant function. The used perturbation function allows

to generate a new population using information about

the good solutions obtained during the previous it-

erations. Also, the neighborhood structure is a cru-

cial part of the local search algorithm. Here, the pro-

posed Min-Max N (s) tries to remove the least valu-

able item and replace it with the most proﬁtable items

according to the current solution. Therefore, it pro-

vides an efﬁcient way to speed up the search while

leading the algorithm to converge. Lastly, the accep-

tance criterion and the replacement strategy. The used

replacement strategy in this work is a convergence-

promoting mechanism, it favors exploitation. While

the acceptance criterion, which can be considered as a

diversity-promoting mechanism, favors more the ex-

A Min-Max Tchebycheff based Local Search Approach for MOMKP

147

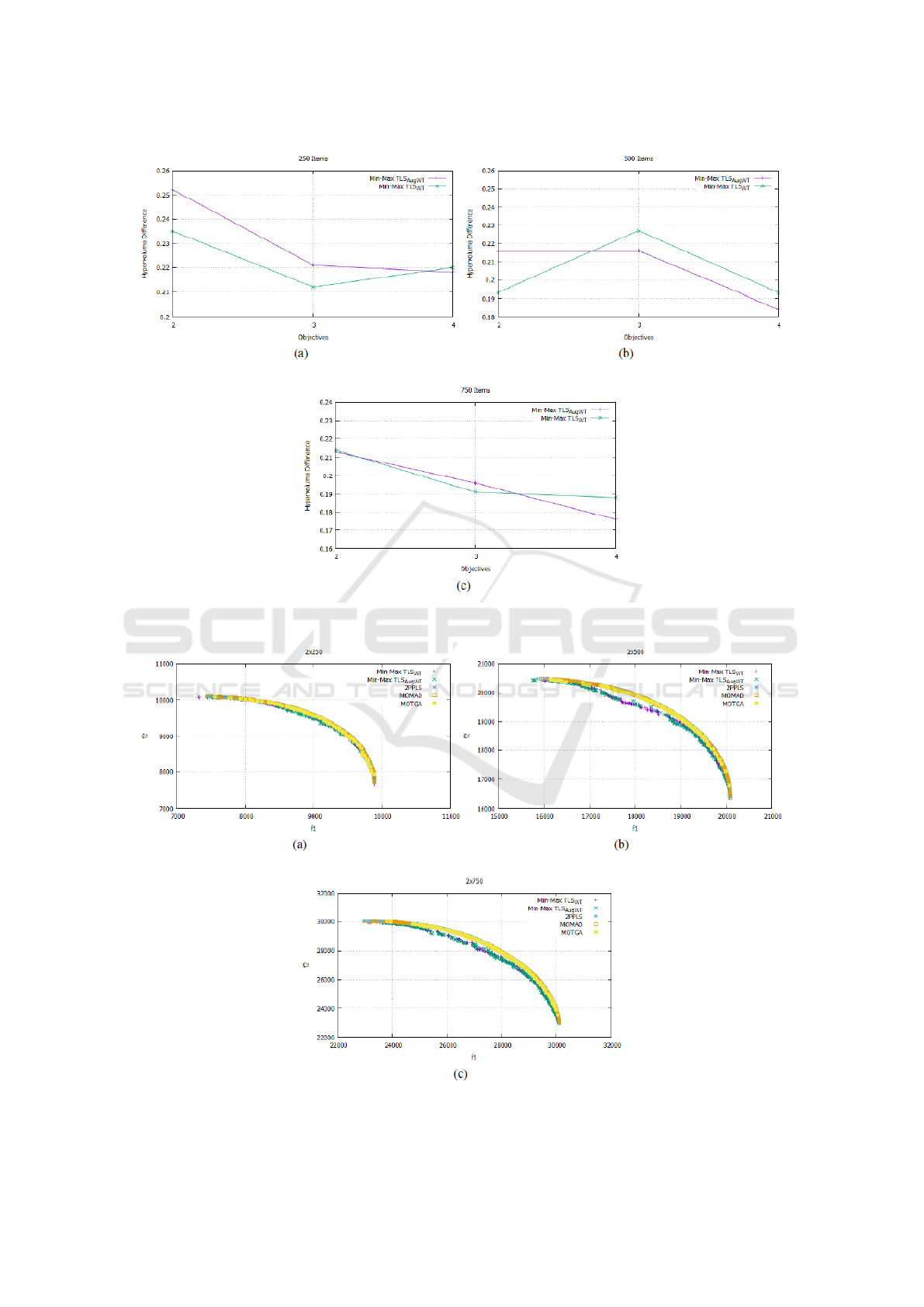
Figure 2: Average Hypervolume Difference of Min-Max TLS

W T

and Min-Max TLS

AugW T

with (a) 250, (b) 500 and (c) 750

Items.

Figure 3: Illustration of the Median Attainement Surfaces Obtained by Min-Max TLS

W T

, Min-Max TLS

AugW T

, MOMAD,

2PPLS, MOTGA with (a) 2x250, (b) 2x500 and (c) 2x750 Instances.

ICSOFT 2017 - 12th International Conference on Software Technologies

148

ploration. Thus, both of them help to provide a good

balance between exploration and exploitation during

the search process.

7 CONCLUSION AND

PERSPECTIVES

In this paper, we have presented a new multi-objective

local search using the scalarization concept. The

proposed approach Min-Max TLS has proved its ef-

ﬁciency for solving the multi-objective multidimen-

sional knapsack problem in comparison with three of

the well-known state-of-the-art algorithms. In fact,

Min-Max TLS is signiﬁcantly better than the com-

pared algorithms on almost all the tested instances.

In addition, experimental results have shown the per-

formance of the two proposed versions of Min-Max

TLS on a short processing time. As improvement of

this work, one potential direction of future research

would be to combine Min-Max TLS with another

metaheuristic method as the ant colony approach.

This metaheuristic could replace the initial population

function, since the use of an ant colony approach com-

bined with a local search method is known to perform

well on many problems. Another perspective of this

work is to apply this approach for solving other multi-

objective optimization problems. In fact, it would be

interesting to adapt Min-Max TLS to other optimiza-

tion problem to investigate its scalability and to have

an overview of its efﬁciency.

ACKNOWLEGMENT

We are grateful to the anonymous reviewers for their

insightful comments to improve our paper.

REFERENCES

Alaya, I., Solnon, C., and Gh

edira, K. (2004). Ant al-

gorithm for the multi-dimensional knapsack problem.

Proceedings of International Conference on Bioin-

spired Optimization Methods and their Applications

(BIOMA), 1:63–72.

Alaya, I., Solnon, C., and Gh

edira, K. (2007). Ant colony

optimization for multi-objective optimization prob-

lems. 19th IEEE International Conference on Tools

with Artiﬁcial Intelligence (ICTAI’07), 1:450–457.

Alsheddy, A. and Tsang, E. (2009). Guided pareto local

search and its application to the 0/1 multi-objective

knapsack problems. Proceedings of the eighth meta-

heuristic international conference (MIC09).

Alves, M. J. and Almeida, M. (2007). MOTGA: A multi-

objective tchebycheff based genetic algorithm for the

multidimensional knapsack problem. Computers &

OR, 34(11):3458–3470.

BenMansour, I. and Alaya, I. (2015). Indicator based

ant colony optimization for multi-objective knapsack

problem. Knowledge-Based and Intelligent Informa-

tion & Engineering Systems 19th Annual Conference,

60:448–457.

Bowman, V. J. (1976). On the relationship of the tcheby-

cheff norm and the efﬁcient frontier of multiple-

criteria objectives. In H. Thieriez and S. Zionts, ed-

itors, Multiple Criteria Decision Making, 1:76–85.

Deb, K., Pratap, A., S.Agarwal, and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

NSGA-II. IEEE Transaction on Evolutionary Com-

putation, 6(2):181–197.

Ehrgott, M. and Gandibleux, X. (2004). Approximative so-

lution methods for multiobjective combinatorial opti-

mization. Top, 12:1–63.

Ehrgott, M. and Ryan, D. M. (2002). Constructing robust

crew schedules with bicriteria optimization. Journal

of Multi-Criteria Decision Analysis, 11(3):139–150.

Grunert Da Fonseca, V., Fonseca, C. M., and Hall,

A. O. (2001). Inferential performance assessment

of stochastic optimisers and the attainment function.

1st International Conference on Evolutionary Multi-

criterion Optimization (EMO 2001)Lecture Note in

Computer Science, Springer, pages 213–225.

Ke, L., Zhang, Q., and Battiti, R. (2014). A simple

yet efﬁcient multiobjective combinatorial optimiza-

tion method using decompostion and pareto local

search. IEEE Trans on Cybernetics.

Knowles, J. D., Thiele, L., and Zitzler, E. (2005). A tutorial

on the performance assessment of stochastive multi-

objective optimizers. Technical report TIK-Report.

Liefooghe, A., Paquete, L., and Figueira, J. (2013). On

local search for bi-objective knapsack problems. Evol.

Comput., 21(1):179–196.

Lust, T. and Teghem, J. (2008). Memots: a memetic algo-

rithm integrating tabu search for combinatorial mul-

tiobjective optimization. RAIRO - Operations Re-

search, 42:3–33.

Lust, T. and Teghem, J. (2012). The multiobjective multi-

dimensional knapsack problem: a survey and a new

approach. International Transactions in Operational

Research, 19:495–520.

Penn, M., Hasson, D., and Avriel, M. (1994). Solving the

0/1 proportional knapsack problem by sampling. J.

Optim Theory Appl., 80:261–272.

Shih, H. (2005). Fuzzy approach to multilevel knapsack

problems. Computers and Mathematics with Applica-

tions, 49:1157–1176.

Smeraldi, F. and Malacaria, P. (2014). How to spend it:

Optimal investment for cyber security. Proceedings of

the 1st International Workshop on Agents and Cyber-

Security.

Steuer, R. E. (1986). Multiple Criteria Optimization: The-

ory, Computation and Application. John Wiley, New

York.

A Min-Max Tchebycheff based Local Search Approach for MOMKP

149

Steuer, R. E. and Choo, E. U. (1983). An interactive

weighted tchebycheff procedure for multiple objective

programming. Mathematical Programming, pages

326–344.

Vianna, D. S. and Dianin, M. F. (2013). Local search

based heuristics for the multiobjective multidimen-

sional knapsack problem. Production journal, 1:478–

487.

Zhang, Q. and Li, H. (2007). MOEA/D: a multiobjective

evolutionary algorithm based on decomposition. IEEE

Transactions Evolutionary Computation, 11:712–731.

Zitzler, E., Laumanns, M., and Thiele, L. (2002). SPEA2:

improving the strength pareto evolutionary algorithm

for multiobjective optimization. In Giannakoglou, K.

et al., editors, Evolutionary Methods for Design, Op-

timisation and Control with Application to Industrial

Problems (EUROGEN 2001), volume 1, pages 95–

100. International Center for Numerical Methods in

Engineering (CIMNE).

Zitzler, E. and Thiele, L. (1999). Multiobjective evolu-

tionary algorithms: A comparative case study and the

strength pareto approach. IEEE Transactions on Evo-

lutionary Computation, 1:257–271.

ICSOFT 2017 - 12th International Conference on Software Technologies

150