Parallel Robot Structure Optimizations for a Friction Stir Welding
Application
F. Dardouri
1,2
, G. Abba
1
and W. Seemann
2
1
Design, Manufacturing and Control Laboratory (LCFC), Arts et M
´
etiers ParisTech, 57078, Metz, France
2
Institut of Technical Mechanics (ITM), Karlsruhe Institut of Technology-KIT, 76131, Karlsruhe, Germany
Keywords:
Industrial Robot, Friction, Force, Deviation errors, Hybrid Systems, Actuators, Optimization.
Abstract:
Today industrial robots are used in many manufacturing applications because of their versatility and easy ap-
plicability. Notwithstanding their performance these robots are not suitable for some manufacturing processes
where uniform and high forces together with suitable precision of position are required. The present research
is focused on one of the high thrust operations, the friction stir welding (FSW). This method for connecting
two parts works while the connected materials are in the solid phase. For this reason a very high thrust force
is needed to soften the material during the welding process. Due to these high forces the position of the tool
of a serial robot deviates from the desired trajectory. In this paper the possibility of using a parallel structure
device is investigated to improve the load capacity and stiffness of a heavy manipulator robot. Such a system
may exert forces directly on the process tool. In this way the movement of the tool is mainly generated by the
industrial serial robot, while the parallel structure ensures the generation of very high thrust forces.
1 INTRODUCTION
Friction Stir Welding process is a comparatively new
method of welding. This process invented in 1991
by Wayne Thomas in The Welding Institute (TWI)
(Thomas et al., 1991). It enables joining material
in solid phase without reaching the melting temper-
ature. Comparing with other joining processes, FSW
has many benefits for welding metals. For this rea-
son, after its invention several industries have shown
great interest in this process, especially the aerospace
industry, mainly due to the exceptional mechanical
properties of welds, the absence of defects and typ-
ical porosities.
To use this process for welding linear joints, most
industrial applications use specified FSW machines.
One of the biggest specified machine was developed
by ESAB in cooperation with Boeing for the project;
space launch system (SLS), of NASA. The first ap-
plication of FSW in the aeronautics was the Delta II
in 1999, (ESAB, 2013). These machines are charac-
terized by high stiffness and thrust capacity, but they
require significant investments and have a low ma-
nipulapility. It is possible also to use parallel robot
(Tricept), see (Smith, 2007). Major research on FSW
using parallel structures were developed by HZG in
Germany (former GKSS), with a first test in 1998,
see (Strombeck et al., 2000). Despite the fact that this
type of structure is characterized by a high stiffness
but it has a great ability to push only in one direction.
To improve the thrust capacity in the other direction of
a parallel robot, Palpacelli proposed to join it to a sim-
ple cable-driven device whose moving platform was
rigidly attached to the robot end-effector. He applied
this concept to a tricept after a static and kinematic
modeling of the system (Palpacelli, 2016). The appli-
cation of FSW process using this solution may limit
the manipulapility of the structure due to the cables
use in the work plane. However, in industry, many ap-
plications require a large manipulapility to weld com-
plex joints, demanding machines with several degrees
of freedom. Because of that using an industrial robot
broadens this flexibility of application.
Of course, Comparing serial robot with many other
kinds of machines, they are characterized by low stiff-
ness. For this reason, their use is usually limited to
applications like packaging, assembling, or pick and
pack, where the positioning accuracy of the tool is
not a major factor and a large workspace is required.
High force operations like welding or machining are
preferably made by machines which have high stiff-
ness, thrust capacity and accuracy, resulting in a bet-
ter product quality. Nevertheless, their poor flexibility
limits many operations, e.g. in cases where a complex
372
Dardouri, F., Abba, G. and Seemann, W.
Parallel Robot Structure Optimizations for a Friction Stir Welding Application.
DOI: 10.5220/0006434203720381
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 372-381
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

path has to be realized and many places have to be
reached by the tool. This flexibility of application is
best done by a serial robot. Although In recent years,
current researchers tried to replace the dedicated ma-
chines by serial robots due to their low cost. The idea
in this paper is to use an industrial serial robot to per-
form the friction stir welding process (FSW).
Due to the high thrust force required for FSW, gener-
ally a heavy industrial robot uses to perform the pro-
cess. Usually, the heavy industrial robots are consid-
ered among rigid structures, this condition remains
valid unless the forces needed to be created by the
robot do not exceed its carrying capacity, which is
not the case such as this process requires a very high
thrust force that must be provided by the serial robot
to hold the contact between the tool and the workpiece
surface. For example, to assemble two pieces of alu-
minum with 6 mm depth, we need 10 kN. For that rea-
son, its positioning accuracy becomes very low, when
the effect of transmission elasticity is non-negligible.
The deformation of the whole industrial robot needs
to be considered especially, for applications that re-
quire a precise position of the tool as described by
(Soron, 2008) and (Voellner et al., 2007), as in our
case, it is necessary that the tool follow a defined tra-
jectory. Therefore, this deformation makes deflection
in each joint of the robot, which causes an error in
following a given trajectory, see (Strombeck et al.,
2000) and affects evidently the quality of the weld.
The magnitude of this error depends on the robot po-
sition in the work space and the direction of welding
(Voellner et al., 2007), (Zaeh and Voellner, 2010) and
(Qin et al., 2014). The deviation error can be reduced
by solving this difficulty. Several work on manipula-
tor control has been developed to correct the deviation
of the robot tool (Yoshikawa, 2000), (Chiaverini et al.,
1994), (Raibert and Craig, 1981), et (De Luca et al.,
1989). However, there is always a lack of precision,
for this reason, in this work, an assistance device has
been associated to an industrial robot.
The static performance and the stiffniss of an indus-
trial robot can be greatly improved by adding a device
in form of a parallel structure.This assisting device
has the architecture of a parallel structure but it is not
an existing parallel robot. It is just tree thrust branches
able to create together very high thrust forces on the
tool which can be controlled easily. In this paper we
develop an optimization algorithm to minimize the
deviation error. For the first time this algorithm allows
the optimization of the parameters defined the paral-
lel structure. In the second time, the optimization of
the three forces created by this structure. Thereafter,
we simulated the workspace of the whole structure to
have an idea about its flexibility of the applications.
2 FSW PROCESS
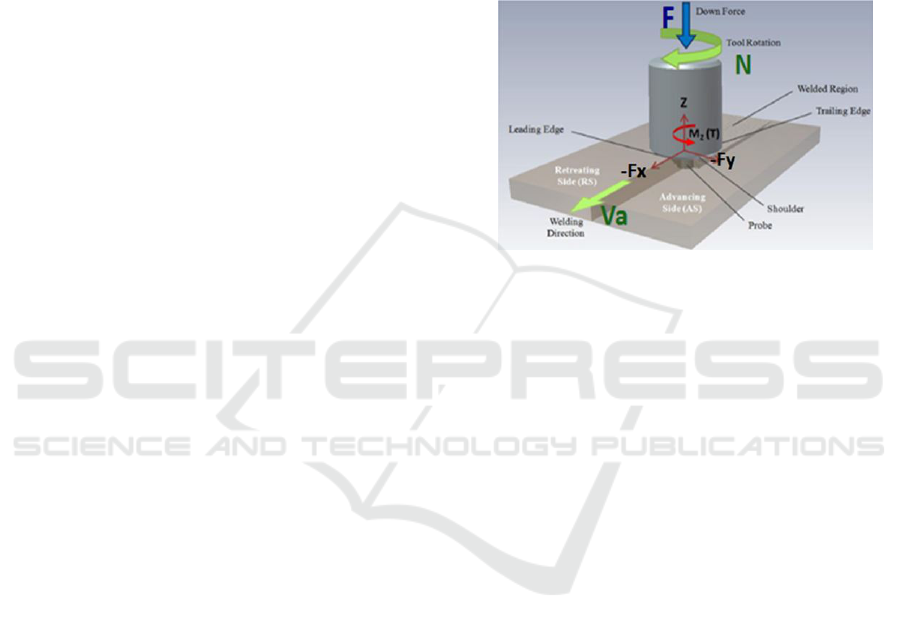
As shown in Fig. 1 the rotating tool used for the FSW
process consists of a probe and a shoulder. Moreover,
the external forces exerted on it are the thrust force F
exerted by the FSW machine, F
x
the axial force dur-
ing welding when the tool advances along the joint
line the material’s resistance generates a force along
x
0
and Fy, then during tool rotation the flow of mate-
rial pushes the tool which generates a force along y
0
.
Figure 1: Princible of the FSW Process (Gibson et al.,
2014).
FSW is typically described in three steps. The
first step is plunging. Here, the probe penetrates into
the weld joint between the two parts to be assembled.
This step stops when the shoulder touches the surface.
The second step is welding. It involves the rotation of
the tool and needs a high force which locally softens
and mixes the material. This process assists the ad-
vance of the tool along the welding line (Fuller 2007,
2007). The third step is retraction; in this step the
probe is pulled out vertically from the material.
The FSW process is defined by four parameters,
the thrust force F, the welding speed Va, the rotation
speed N and the tilt angle B. The force is necessary for
maintaining contact between the tool and the pieces
to be welded. Further, it softens the material in or-
der to assist the penetration of the probe into the joint.
N and Va describe how fast the tool traverses along
the interface and rotates, respectively. These two tool
speeds have considerable importance, and therefore
they need to be correctly set to get a successful weld-
ing cycle. There is a relationship between the heat
input, the rotation speed and the welding speed dur-
ing welding. It is arguable that decreasing the lat-
eral speed or increasing the rotation speed will cause
a hotter weld. FSW is characterized by a slower Va
comparing to other welding processes. The last pa-
rameter is B, it tilts the tool mostly between 1.5
◦
and
3.5
◦
degrees such that the front of the tool is higher
than the rear. This inclination assists to forge the ma-
terial. See (Balasubramanian, 2009). To use this pro-
Parallel Robot Structure Optimizations for a Friction Stir Welding Application
373

cess, these four parameters must to be set dependly on
the material of the parts to be assembled the depth of
the joint and the geometry of the tool and its material.
3 THE WRENCH CREATED ON
THE PLATFORM
3.1 Description
In the optimization of the deviation error, an industrial
robot KUKA KR 500-2MT was used. This is an artic-
ulated manipulator with 6 degrees of freedom (DOF)
consisting only of revolute joints. This a heavy robot
is able to carry in its end a load of 500 kg. Moreover,
the first three axes of this robot were modified, such
that the transmission are twice as rigid as the trans-
mission of the standard KR 500 Robot. This modifi-
cation doubles the torque of three motors. However,
owing to the high normal force needed for FSW the
compliance of the robot remains important and the er-
ror due to the deformation in the joints cannot be ne-
glected.
Fig. 2 shows a schematic of the parallel structure that
we propose to investigate and which is optimized.
The fixed base is connected to the moving platform
by three identical limbs. Each limb consists of a pris-
matic joint P , an universal joint U at point M
i
and a
spherical joint S at point P
i
, for i = 1, 2 and 3. The
prismatic joint is driven by actuator which creates a
force. Together the three limbs provide an additional
force required to minimize the positioning error of the
tool. Finally, to summarize This UPS parallel manip-
ulators produces only three forces F
1
,F
2
and F
3
on the
moving platform but not its actuation and it is con-
trolled in force by retracting or extending the actua-
tors. As shown in the figure r
b
is the distance O
M
M
i
and r
p
is the distance O
6
P
i
.
3.2 Modelling of the System
The reference frame (O
0
, x
0
, y
0
, z
0
) is fixed to the
ground, the reference frame (O
M
, x
M
, y
M
, z
M
) is fixed
to the base of the parallel structure while the refer-
ence frame (O
6
, x
6
, y
6
, z
6
) is moving with the plat-
form. In order to be able to locate the end-effector of
an industrial robot, it is necessary to specify its posi-
tions and its orientation in the workspace. There are
several methods to definie the rotation angles of the
transformation between two frames. So in this work
to calculate the orientation of the serial robot tool in
R
0
, the Euler method was used. Three successive ro-
Figure 2: Definition of the parallel structure.
tations are defined as follows:
R(z
0
, A), R(y
0
, B), R(x
0
, C)
(1)
The designated angles A, B and C shown in Fig. 3
describe the angles of roll, pitch and yaw. Each new
rotation is carried out with respect to one of the fixed
frame axes.
C is the rotation around the axis x
0
, B is the rota-
tion around the axis y
0
and A is the rotation around
the axis z
0
. In this work, the orientation of the end-
effector is represented to obtain the rotation matrix
depending these angles:
0
R
6
=


CACB CASBSC −CCSA SASC +CACCSB
CBSA CACC + SASBSC CCSASB −CASC
−SB CBSC CBCCi


Where CA, SA, CB, SB, CC and SC represent
cos(A), sin(A), cos(B), sin(B), cos(C) and sin(C) re-
spectively.
The direct geometric model defines the set of re-
lations which express the situation of the object j in
the space in terms of the articular variables vector of
the robot q.
q =

q
1
q
2
q
3
q
4
q
5
q
6

>
(2)
q
i
is the rotation angle of joint i. The situation of the
end-effector j in the frame R
0
is defined by:
T =

0
P
j
R
j

>
(3)
T =

x
j
y
j
z
j
A
j
B
j
C
j

>
(4)
There are several conventions to calculate these rela-
tions. Modified Denavit-Hartenberg (MDH) is usu-
ally used to model robots consisting of revolute or
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
374

Figure 3: Cordinite to define the tool orientation.
prismatic joints including the manipulator used in this
research work. The MDH parameters defined for this
robot and are used thereafter with the support of the
software SYMORO+ (Khalil and Creusot, 1997) to
determine the relationship:
T = f (q) i ∈ [1...6]
(5)
Where x
6
, y
6
and z
6
of the equation (4) represent the
coordinates of the point O
6
in the fixed frame R
0
. This
point was noted by:
0
P
6
=


x
6
y
6
z
6


Then the transformation matrix of the end-effector in
R
0
is given as :
0
T
6
=

0
R
6
0
P
6
0 1

The FSW tool is in direction of the 6th axis of the
manipulator with the same orientation of the frame
R
6
, The position of O
t
is
6
P
t
=


0
0
L
t


Where L
t
is the length of the tool, see Fig. 3.
0
P
t
=
0
P
6
+
0
R
6


0
0
L
t


And the transformation matrix of the tool in R
0
is :
0
T
t
=

0
R
6
0
P
t
0 1

To calculate the vector P
i
M
i
it is necessary to calcu-
late first the contact position between the platform and
limbs P
i
and the contact position between limbs and
the fixed base of the parallel structure M
i
in the fixed
frame R
0
of the industrial robot. As shown in Fig. 4,
the orientation of the frame of the parallel structure is
the same as of the fixed frame R
0
of the robot. The
coordinates of point O
M
in the robot frame are x
M
in
x
0
, y
M
in y
0
and H in z
0
direction. Then its position is
defined by:
0
P
M
=


x
M
y
M
z
M


Figure 4: Frames of the robot, the parallel structure and the
tool.
Therefore, the transformation matrix of the base
of the parallel structure is given by:
0
T
M
=

I
3
0
P
M
0 1

According to the geometry of the chosen base shown
in Fig. 2, the coordinates of point M
i
in frame R
M
is
expressed by:
M
P
M
1
=
h
−
r
M
2
−
√
3
2
r
M
0
i
>
M
P
M2
=

r
M
0 0

>
M
P
M
3
=
h
−
r
M
2
√
3
2
r
M
0
i
>
Parallel Robot Structure Optimizations for a Friction Stir Welding Application
375

The three contact positions between limbs and the
base of the parallel structure in the fixed frame R
0
were defined by:
M
i
=
0
P
M
i
+ I
3
M
P
M
i
(6)
The coordinates of the point P
i
in frame R
6
are
given by:
6
P
p
i
=


x
p
i
y
p
i
z
p
i


Such as the platform geometry was chosen like the
base geometry, for this reason the coordinates of the
points expressed in the end-effector frame R
6
are:
6
P
p
1
=
h
−
r
p
2
−
√
3
2
r
p
0
i
>
6
P
p
2
=

r
p
0 0

>
6
P
p
3
=
h
−
r
p
2
√
3
2
r
p
0
i
>
To calculate the contact positions between limbs and
the platform p
i
in the fixed frame R
0
the homogeneous
transformation is defined by:
P
i
=
0
P
6
+
0
R
6
6
P
p
i
(7)
As mentioned, in this work the industrial robot al-
lows to move and to position the tool while the paral-
lel structure allows to improve its stiffness. Then, to
correct the deviation of the end effector, we need to
calculate torques created by the parallel structure on
the platform. Each thrust limb of this parallel struc-
ture produces a wrench τ
i
on the moving platform in
point P
i
defined by:
τ
i
=

F
>
i
C
>
i

>
(8)
As shown in Fig. 2 the forces exerted by the limbs
are:
F
i
= f
i
Z
i
(9)
f
i
is the force created by the actuator i of the paral-
lel structure according to the direction Z
i
. Accord-
ing to the transformation matrices expressed in equa-
tions (6) and (7), it is possible to calculate the po-
sitions of the points P
1
, P
2
, P
3
, M
1
, M
2
, M
3
during
the movement of the industrial robot and for all these
configurations in the space. Using the coordinates of
these points expressed in the frame R
0
the vector Z
i
is
obtained as
Z
i
=
P
i
M
i
kP
i
M
i
k
(10)
The vector of moment Ci created by the actuator i
in point O
6
is:
C
i
= O
6
P
i
×F
i
(11)
O
6
P
i
is the vector from the origin of the coordinate
of the platform center defined to the point where the
force is exerted
O
6
P
i
= r
p
U
Pi
(12)
where r
p
is the distance between O
6
and P
i
along
the direction U
Pi
.
U
Pi
=
O
6
P
i
kO
6
P
i
k
(13)
The spindle of the FSW tool is located at the 6th axis
of the manipulator, which is supposed to remain in-
clined with the small tilt angle M during the process,
fig. 3. The FSW force is exerted on the robot tool
along its axis z
t
as shown in fig. 3. This force can be
defined in frame R
0
by:
F
FSW
=


−F
FSW
sin(B)
0
F
FSW
cos(B)


The wrench at point O
6
created by the FSW force
expressed in the fixed frame is:
τ
FSW
=

−F
FSW
sin(B) 0 F
FSW
cos(B) 0 0 0

>
(14)
Here, we neglet the torque created by the FSW
force on the robot tool C
FSW
.
The total wrench applied on the platform at its
center O
6
in the fixed frame R
0
is:
F
ext
= τ
FSW
+
∑
3
i=1
τ
i
(15)
4 DEVIATION ERROR
This paper presents an approach to improve the qual-
ity of friction stir welding using serial robot. The idea
is to minimize the deviation error of the tool due to
the application of the external forces. The position-
ing accuracy is depending on the tool orientation and
location (Deblaise et al., 2006).
4.1 The Error in the Joint Space
In the industrial robot flexibility is originated from
links and joints. However, many researchers claim
that, because of the larger stiffness in links, its flexi-
bility could be ignored. (Dumas, 2011) had analysed
in her research work that link flexibilities contribute
to 25% of the global deflection. For this reason, it
is generally admitted that in this kind of machine the
flexibility of the structure originates mainly from the
joints. The error in the joint space is typically asso-
ciated to the gearbox flexibility, including motors and
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
376

transmissions. This source of rotation is the most im-
portant contributor to positional inaccuracies (Duelen
and Schr
¨
oer, 1991), (Schr
¨
oer, 1993). Therefore, the
links of serial robots used in this work are condidered
as rigide and only the joint errors are considered, and
they are modelled by linear torsional springs (Bres
et al., 2010):
τ = K∆q
(16)
Then, τ is the vector of joint torques, and K is a
diagonal matrix for the joint stiffness. The difference
∆q = (q
d
− q) is the source of errors in the joint
space, where q
d
is the desired angle and q is the
actual angle. During the application of a load, this
model is used to calculate the deformation created in
the joints of the robot.
Dynamic model
Dynamic modeling of the robot is required for me-
chanical design, controls and simulations. A corre-
sponding model shows the relationship between po-
sitions of the manipulator joint, torques, speeds, ac-
celerations, friction and external forces. This leads
to a set of nonlinear differential equations of order
two. It gives the state of the robot at each moment
as it can analyse the stability of the control and per-
formance trajectory. The Euler-Lagrange formulation
for the joint space dynamic model is written as fol-
lows (Khalil and Kleinfinger, 1986) , (Wernholt and
¨
Ostring, 2003):
D(q) ¨q +C(q, ˙q) ˙q + F
v
˙q + F
s
sgn( ˙q) + G(q) = τ −τ
ext
(17)
D(q) is the robot inertia matrix, C(q, ˙q) ˙q repre-
sents Coriolis and centrifugal terms, F
v
is the viscous
friction matrix, F
s
is the static friction matrix, G(q)
is the gravitational torque vector, J
>
τ
ext
is wrench
vector due to force and torque on the end effector.
During FSW the welding speed Va is always con-
stant and very low, for this reason the acceleration
can be assumed to be zero. In this contribution, we
use a KuKa robot, which is characterized by a small
static friction, and therefore F
s
was neglected. Equa-
tion (17) can be reduced to equation (18)
τ = G(q)+ τ
ext
(18)
4.2 The Error in the Operational Space
Using the direct kinematic model the relationship be-
tween the error in the joint and in the operational
spaces can be written as follows:
∆X = J(q)∆q
(19)
Where J(q) is a 6 ×6 matrix which is known as a
manipulator Jacobian that relates Cartesian velocities
to joint velocities.
this jacobian matrix is composed of two parts:
J(q) =

J
v
J
w

J
v
calculates the cartesin velocity vector which is
obtained from the derivation of the platform position
vector
J
v
=
d
0
P
t
dq
i
(20)
J
v
=



dx
6
dq
1
dx
6
dq
2
...
dx
6
dq
6
dy
6
dq
1
dy
6
dq
2
...
dy
6
dq
6
dz
6
dq
1
dz
6
dq
2
...
dz
6
dq
6



J
w
calculates the vector of rotation speed of the tool
that is obtained by this expression:
J
w
= T
r
dR
t
dq
i
(21)
T
r
is a 3 ×3 matrix defined in (Siciliano and Khatib,
2016)
T
r
=


−SB 0 1
CBSC CC 0
CBCC −SB 0


Now combining (16) and (19) provides:
∆X = JK
−1
τ
(22)
Equations (18) and (22) provide the deviation error in
the operational space:
∆X = JK
−1
(G(q) + τ
ext
)
(23)
Among the applications of the Jacobian matrix is
to define a linear relationship between the external
forces exerted at the tool and torques required at the
joints of the industrial robot to support these forces.
But we cannot use the same Jacobian matrix calcu-
lated in the point because the forces exerted on the
patform in the point. For this reason, it is necessary
to calculate the jacobien in O
6
τ
ext
= J
>
6
F
ext
(24)
This expression allows to project all end-effector
forces at the joints. This important relationship not
just for the development of static forces but also can
be used for robot control. But we cannot use the
same Jacobian matrix calculated in point O
t
because
the forces were applied to the platform and not to the
welded parts. For this reason, it is necessary to calcu-
late the new Jacobian in O
6
J
6
(q) =

J
v
6
J
w
6

Parallel Robot Structure Optimizations for a Friction Stir Welding Application
377

R
6
and R
t
have the same orientation what gives us this
equality
J
w
6
= J
w
(25)
But,
J
v
6
=
d
0
P
6
dq
i
(26)
Integrating equation (15) in (24) and equa-
tion (24) in equation (23) provides:
∆X = JK
−1
(G(q) + J
>
6
(τ
FSW
+
∑
3
i=1
τ
i
))
(27)
∆X =







∆x
∆y
∆z
∆C
∆B
∆A







(28)
∆X =

∆P
(3×1)
∆R
(3×1)

(29)
with the deviation errors ∆P along the axes x
0
, y
0
and z
0
. Similarly ∆R contrains the orientation errors
about the axes x
0
, y
0
and z
0
.
5 THE OPTIMIZATION OF THE
ERROR
5.1 The Position Error (EP)
The EP occurs when the tool deviates laterally of the
desired weld line and contributes to positional inac-
curacies. The error created along the normal of the
workpiece during FSW does not affect the positional
accuracy of the tool in the welding plane. But can
be affect the welding quality then, the deviation er-
rors creted along the three axes in the space have been
minimized using the following expression:
EP =
p
∆x
2
+ ∆y
2
+ ∆z
2
(30)
With ∆x, ∆y and ∆z are the deviation along the axis
x
0
, y
0
and z
0
respectively.
5.2 The Orientation Error (ER)
Among the FSW parameters we defined the tilt an-
gle. In some applications, it is different from zero.
And a higher value of this angle generates a blocking
in advance, and a smaller value causes weld defects.
Therefore, this angle has to be chosen with care, be-
fore starting the welding. In addition, it is very im-
portant that it remains constant during welding. But
the action of the external loads changes the tool ori-
entation which leads to an undesired tilt angle value
and results an orientation error. Consequently, we get
an incorrect welding. The orientation error reads:
ER =
√
∆A
2
+ ∆B
2
+ ∆C
2
(31)
5.3 Optimization Results
For a good quality of welding an optimization algo-
rithm in MATLAB is developed that minimizes ER
and EP. This has been done by optimization the fol-
lowing function:
E = (λEP + ER)
2
(32)
Where, λ is the Lagrange multiplier.
The position and the orientation errors are in terms
of the parameters of the parallel structure which are
defined with the matrix:
V =





r
p
r
M
x
M
y
M
z
M





Then, as previously mentioned r
p
is the dimention of
the platform, r
M
is the dimention of the base, x
M
, y
M
and z
M
are the coordinates of the base center O
M
(see
Fig. 2). In addition, these errors depend on the forces
created by the three actuators of the parallel structure:
F
p
=


F
1
F
2
F
3


To minimize E, we developed an optimization algo-
rithm in MATLAB. This algorithm calculated the op-
timal parameters which correspond to the minimum
deviation. Thereafter this algorithm gives us the opti-
mal three forces which have to be realized by the par-
allel structure as a fonction of the position of the tool
during welding. These parameters and forces then
correspond to a minimum error.
Figure 5: External force created by the limb 1 of the parallel
structure.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
378

Figure 6: External force created by the limb 2 of the parallel
structure.
Figure 7: External force created by the limb 3 of the parallel
structure.
It is revealed that F
2
is totally different from F
1
and
F
3
. However, F
1
has approximately the same value as
F3 (see Fig. 5 and Fig. 7). As expected this is because
F
2
is applied directly on the welding line while F
1
and F
3
are applied symmetrically on both sides of the
welding line. Moreover, it has been observed that to
correct the error, forces created by the parallel struc-
ture are between 2500 N and 3500 N.
Therefore the parallel structure is technically feasible.
The dimensioning parameters of the parallel struc-
ture and the three forces estimated to minimize the
function E were used to calculate the position and ro-
tation error. As shown in Fig. 8, the maximum rota-
tional error is equal to 2.5 ×10
−3
rad. Similarly, as
shown in Fig. 9 the maximum position error is equal
to 8 ×10
−8
mm. The deviation of the tool is very well
corrected by adding the parallel structure.
Figure 8: The orientation error (ER).
Figure 9: The position error (EP).
5.4 The Workspace of the Structure
The idea to add a parallel structure allows improv-
ing the rigidity of the robot. However, it limits
the workspace and the index of the manipulability
(De Backer, 2014). The workspace of the hybrid
structure was not calculated in this work. However,
it has been simulated using the software Catia. This
simulation shows what happens by using a real system
and how this system works in the face of real distur-
bances. Furthermore, From this simulation it has been
observed that the tool can go up to y
0
= ±1.2m (be-
cause of the structure symmetry on the plane (x
0
, z
0
)).
Further, different configurations have been tested in
the plane y
0
= 1.2m using Catia as shown in Fig. 10.
It has been revealed that there is no collision between
the serial and the parallel structure in each configu-
ration. At an initial stage, the workplace can be es-
timated by a parallelepiped of the following dimen-
sions. the large length of the base equal 2.5m, the
small length of the base equal 2.5m and the height
equal 1m. To know the exact limits of the tool before
collision it is necessary to calculate the workspace
correctly.
6 CONCLUSIONS
The elasticity of industrial robots and limited force
capability are barriers for achieve a successful robotic
FSW which limits its use for high quality welding.
Usually, this elacticity causes errors to follow the de-
sired trajectory. There are two types of error; position
error (EP) and orientation error (ER). These two er-
rors are calculated in Cartesian space using the joint
stiffness model, the kinematic and dynamic models
of the manipulator. In this work a parallel structure
was added to polyarticulated robot to minimize them.
Optimization has been carried out using an algorithm
developed in Matlab. The algorithm calculates the
parameters of the parallel structural V and the three
forces generated by this structure F
p
to minimize the
Parallel Robot Structure Optimizations for a Friction Stir Welding Application
379

Figure 10: the workspace of the hybrid structure.
position and the orientation error during welding. For
ours example we obtained a small orientation error of
0.1
◦
and a very small position error of approximately
zero.
Using the software Catia we estimated approximately
the workspace of the serial and parallel robots by
a parallelepiped. The volume of the parallelepiped
equals 5.76m
3
.
With the proposed solution, the accuracy of position-
ing the tool and the FSW welding performance can
be greatly improved. This assist device allows to im-
prove the stiffness of an industrial robot. This ap-
proach allows us to gain in terms of stiffness, how-
ever, it limits the workspace. Moreover the main ad-
vantage of a serial robot is its workspace. But, de-
spite this limitation of the application flexibility, this
solution can ensure a process with good accuracy for
simple paths and also for complex paths as the angle
between the axis of the tool and the axis z
0
stays in
the workspace of the hybrid structure. So finally, the
structure can be useful for many industrial applica-
tions with the advantage of high welding quality.
ACKNOWLEDGEMENTS
The authors would like to thank the Doctoral School
SMI of Arts et metiers ParisTech and the Institut of
Technical Mechanics of KIT for their support.
REFERENCES
Balasubramanian, B. Gattu, R. S. M. (2009). Process
forces during friction stir welding of aluminium al-
loys. 14:141–145.
Bres, A., Monsarrat, B., Dubourg, L., Birglen, L., Perron,
C., Jahazi, M., and Baron, L. (2010). Simulation of
friction stir welding using industrial robots. Industrial
Robot, 37(1):36–50.
Chiaverini, S., Siciliano, B., and Villani, L. (1994).
Force/position regulation of compliant robot manip-
ulators. IEEE Transactions on Automatic Control,
39(3):647–652.
De Backer, J. (2014). Feedback control of robotic friction
stir welding. PhD thesis, University west.
De Luca, A., Manes, C., and Ulivi, G. (1989). Robust hy-
brid dynamic control of robot arms. In Decision and
Control, 1989., Proceedings of the 28th IEEE Confer-
ence on, pages 2641–2646. IEEE.
Deblaise, D., Hernot, X., and Maurine, P. (2006). A system-
atic analytical method for pkm stiffness matrix cal-
culation. In Robotics and Automation, 2006, pages
4213–4219. Proceedings of the 2006 IEEE Interna-
tional Conference on Robotics and Automation.
Duelen, G. and Schr
¨
oer, K. (1991). Robot calibra-
tion: method and results. Robotics and Computer-
Integrated Manufacturing, 8. 4.
Dumas, C. (2011). D
´
eveloppement de m
´
ethodes robotis
´
ees
pour le parach
`
evement de pi
`
eces m
´
etalliques et com-
posites. PhD thesis, Universit
´
e de Nantes.
ESAB (2013). Boeing selects esab for space launch system
project. (2013, 2013/09/06).
Fuller 2007 (2007). Friction Stir Welding and Processing,
chapter Chapter 2 Friction Stir Tooling: Tool Materi-
als and Designs, Friction Stir Welding and Processing.
ASM International. ISBN-13 978-0-87170-840-3.
Gibson, B., Lammlein, D., Prater, T., Longhurst, W., Cox,
C., Ballun, M., Dharmaraj, K., Cook, G., and Strauss,
A. (2014). Friction stir welding: process, automation,
and control. Journal of Manufacturing Processes,
16(1):56–73.
Khalil, W. and Creusot, D. (1997). Symoro+: A system for
the symbolic modelling of robots. Robotica, 15:153–
161.
Khalil, W. and Kleinfinger, J. (1986). New geometric no-
tation for open and closed-loop robots. pages 1174–
1179.
Palpacelli, M. (2016). Static performance improvement
of an industrial robot by means of a cable-driven re-
dundantly actuated system. Robotics and Computer-
Integrated Manufacturing, 38:1–8.
Qin, J., Leonard, F., and Abba, G. (2014). Nonlinear dis-
crete observer for flexibility compensation of indus-
trial robots. IFAC Proceedings Volumes, 47(3):5598–
5604.
Raibert, M. and Craig, J. (1981). Hybrid position/force con-
trol of manipulators. Journal of Dynamic Systems,
Measurement and Control, Transactions of the ASME,
103(2):126–133.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
380

Schr
¨
oer, K. (1993). Theory of kinematic modelling and nu-
merical procedures for robot calibration. Robot Cali-
bration, Chapman & Hall, London, pages 157–196.
Siciliano, B. and Khatib, O. (2016). Springer handbook of
robotics. Springer.
Smith, B. C. (2007). Friction Stir Welding and Processing,
chapter 11 Robots and machines for friction stir weld-
ing / processing, Friction Stir Welding and Processing.
ASM International.
Soron, M. (2008). Towards multidimensionality and flexi-
bility in fsw using an industrial robot system. Welding
in the World, 52(9-10):54–59.
Strombeck, A., Schilling, C., and Santos, J. (2000). 2D and
3D friction stir welding with articulated robot arm. In
Proc. of 2nd International Friction Stir Welding Sym-
posium, Gothenburg, Sweden.
Thomas, W. M., Nicholas, E. D., Needham, J. C., Murch,
M. G., Temple-Smith, P., and Dawes, C. J. (1991). In-
ternational patent application pct/gb92/02203. Tech-
nical report, The Welding Institute, London, UK.
Voellner, G., Zaeh, M., Silvanus, J., and Kellenberger, O.
(2007). Robotic friction stir welding. Technical re-
port, SAE Technical Paper.
Wernholt, E. and
¨
Ostring, M. (2003). Modeling and con-
trol of a bending backwards industrial robot. De-
partment of Electrical Engineering,Link
¨
oping, Swe-
den, page 38.
Yoshikawa, T. (2000). Force control of robot manipula-
tors. In Robotics and Automation, 2000. Proceed-
ings. ICRA’00. IEEE International Conference on,
volume 1, pages 220–226. IEEE.
Zaeh, M. F. and Voellner, G. (2010). Three-dimensional
friction stir welding using a high payload industrial
robot. Production Engineering, 4(2-3):127–133.
Parallel Robot Structure Optimizations for a Friction Stir Welding Application
381