Smooth Autonomous Take-off and Landing Maneuvers over a

Double-hulled Watercraft

Omar Velasco, Pablo J. Alhama Blanco and Jo

ao Valente

Departamento de Ingenier

ıa de Sistemas y Automatica, Universidad Carlos III de Madrid, Legan

es, Madrid, Spain

Keywords:

Aerial-marine Robotic System, Vertical Take-off and Landing, Classic Control, Dynamic Movement Primi-

tives.

Abstract:

This paper addresses the problem of vertical take-off and landing (VTOL) over a moving target in an inland

water environment. The maneuvers are carried out by a multi-rotor unmanned aerial system (UAS) over a

double-hulled watercraft unmanned surface vehicle (USV). The approach proposed employs a cascade PID

control architecture and is then improved with Dynamic Movement Primitives (DMP). The results presented

show that DMP can be used in combination with PID classical control for achieving a more safe and accurate

VTOL maneuver.

1 INTRODUCTION

Quality assessment of inland waters is one of the

most important action ﬁelds launched by the Euro-

pean Union until 2022 for biodiversity and habitat

conservation.

The branch of science that addresses the studies of

inland aquatic ecosystems is called limnology. Wa-

ter quality evaluation is achieved through the analy-

sis and classiﬁcation of different biophysical and bio-

chemical parameters. This parameters are usually ac-

quired locally with manual instrumentation close by

the water, and also through satellites or airborne im-

agery.

Manual sampling techniques have been used tra-

ditionally, but they involve tedious operations and

increase the probability of erroneous ﬁeld practices.

Moreover, satellite imagery is not always available

and the spatial resolution is limited for certain appli-

cations. Finally, airborne surveys are subject to strict

legislation for ﬂying over natural environments and

ungovernable logistics. It should also be highlighted

that all those approaches have increased associated

operation costs.

Unmanned aerial systems (UAS) have improved

remote sensing (RS) missions from different domains

by providing a personal channel of data delivery for

researcher and end-users. In this way, their usability

in limnology will also play an important role because

data may be delivered in short time windows and with

affordable operation costs.

The UAS can be successful used in aquatic en-

vironments (Ore et al., 2015), however they have a

very limited autonomy, and they might be vulnerable

to unexpected weather changes. In order to avoid ac-

cidents and damages to the platform it is important to

constantly have available an emergency landing plat-

form fot the UAS during the mission.

In this paper we present a set of control strategies

for autonomous vertical takeoff and landing (VTOL)

with a quadrotor and a double-hulled watercraft.

A multiple robot UAS-USV conﬁguration was

presented in (Djapic et al., 2015) focusing on the im-

plementation of the control approach and the com-

munication interfaces. In (Pinto et al., 2014) a more

complex collaboration system was designed for envi-

ronmental data gathering with autonomous operation,

including VTOL. Another aerial and marine collabo-

ration using a visual servoing algorithm is presented

in (Weaver et al., ).

The work presented herein can be distinguished

by the smaller scale of the aerial platforms in the

multi-robot team. This characteristic enables rapid

deployment in areas with difﬁcult access and hard to

survey. Moreover, a reliable path tracking controller

for smooth landing and take off sequences was de-

signed to minimize the risk of the quadcopter falling

into the water during the VTOL manoeuvres.

This paper is organized as follows: The back-

ground of the problem is ﬁrstly given. Then, the plat-

forms used, as well as the scenario, and the assump-

tions are introduced in Section 2. Section 3 explains

Velasco, O., Blanco, P. and Valente, J.

Smooth Autonomous Take-off and Landing Maneuvers over a Double-hulled Watercraft.

DOI: 10.5220/0006435303890396

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 389-396

ISBN: Not Available

389

how the platforms dynamic models were obtained,

followed by the control strategy applied in Section 4.

After that, DMPs are presented and used to improve

the previous control approach in Section 5. Simula-

tions results are presented in Section 6, and conclu-

sion remarks in Section 7.

2 ROBOTIC SYSTEM, SCENARIO

AND ASSUMPTIONS

This section presents the multi-robot team modelled

in this work, and covers the characteristics of the

modeling scenario.

2.1 Robotic System

The modelled aerial platform is based in the

AR.Drone quadcopter, while the USV is a built from

the scratch platform named Strider V1.0. The objec-

tive of this multi-robot solution is to provide a collab-

oration system to perform data collection tasks in rel-

atively still waters. The USV aims to provide longer

autonomy to the UAV behaving as a mobile landing

platform and charging station. The drone provides the

agility and ﬂexibility to access zones where the USV

cannot reach.

2.2 Scenario and Assumptions

The solution presented in this work is particularly des-

tined to inland water environments where wave in-

cidence is negligible. The assumptions made during

the dynamic modeling of both vehicles will be based

upon this conditions. Therefore, angle variation in the

USV’s roll, pitch and heave are not considered.

3 DYNAMIC MODELING

This section deals with the dynamic modeling of the

two autonomous vehicles presented in this work. We

consider the UAV and the USV as single rigid body

systems to obtain the models of their dynamics. The

Newton-Euler formalism will be used to describe the

motion of both autonomous platforms.

3.1 Quad-rotor Helicopter

Concerning quadcopter modeling, an inertial and a

ﬁxed-body frame will be deﬁned, following the no-

tation in Figure 1, where E is the inertial earth frame,

Figure 1: Coordinate system schematic and notation for the

quadcopter motion description.

following a right handed NED coordinate system con-

vention, and B is the body-ﬁxed frame, attached to

the quadcopter airframe and along the arms of the

quadrotor.

Let us then deﬁne the following workspace within

this two frames. Two vectors can be deﬁned to give

a generalized overview of the position and velocity of

the quadrotor in the space:

ξ =









(1)









(2)

Where ξ [+] represents the generalized position of

the body with in terms of the earth frame and ν

[+]

the generalized velocity of the quad-copter in terms of

the body frame. The vector V

[m s

−1

] represents the

linear velocity vector of the body frame with respect

to the inertial frame, being u

and ω

the veloc-

ities in the positive x

, y

and z

directions respec-

tively. Similarly, the vector ω

[rad s

−1

] represents

the angular velocity of the quadrotor with respect to

the inertial frame, being p

and r

the angular ve-

locities around the x

, y

and z

axis. Γ

[m] and Θ

[rad] represent the linear and angular position, being

and z

the position of the body frame with re-

spect to the earth frame and φ

stands for roll, θ

for

pitch and ψ

for yaw of the body frame with respect

to the inertial frame.

Before we delve into the expressions for the mo-

tion of the quadrotor we will set a series of assump-

tions in order to simplify this task:

1. The body-ﬁxed frame axes coincide with the prin-

cipal axes of inertia of the body

2. The moments of inertia are constant.

3. The body-ﬁxed frame origin o

is coincident with

the centre of mass.

4. Body symmetry with respect to the centre of mass

is assumed.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

390

5. Minor aerodynamic effects such as blade ﬂapping

or induced drag are not considered.

Using the previously deﬁned workspace we can

obtain an expression for the motion of the quadcopter.

Equation 3 expresses the generalized expression for

the motion of any rigid body based on the assump-

tions made before:



3×3







× (m

)

× (Iω

)







(3)

Where m

[Kg] is the mass and I [N m s

] is the in-

ertia matrix of the quadrotor, with respect to the body

frame, and τ

[N m] and F

[N] are the force and torque

with respect to the body frame. We can characterize

this expression to the quadcopter model by deﬁning

the force and torque vector at the right side of the

equation. In the case of the quadcopter model, this

force and torque vector, shown in equation 4, can be

divided into four components:







3×1



+ U



3×1



+ F

ext

(4)

Gravitational Contribution.This component comes

from the effect of gravity on the quadrotor. It can

be modelled as:

(Θ) = R

−1

= R



















−m

gs(θ)

gc(θ)s(φ)







(5)

Where F

is the force vector due to the gravita-

tional contribution expressed in the body frame

and c

= cos(α), s

= sin(α).

Input Contribution. From the actuation of the four

rotors of the quadcopter. Following the typical de-

scription of the four basic basic movements of a

quadrotor, namely Throttle (U

), Roll (U

), Pitch

) and Yaw (U

) this contribution can be deﬁned

as:



















−c

(Ω

+ Ω

)

l(Ω

− Ω

)

l(Ω

− Ω

)

(Ω

+ Ω

− Ω

)







(6)

Where T

and Ω

are the generated thrust and

speeds of each rotor respectively, starting by

the rotor located in the x

axis and counting

counter-clockwise, c

[N s

] and c

[N m s

] are

the thrust and drag coefﬁcients and l [m] is the

distance between the centre of the quadrotor and

the centre of the propeller.

Gyroscopic Effects Due to Propeller Rotation.

Due to the interaction between the rotating

elements of the quadcopter and the airframe.

The expression of this gyroscopic torque is given

by the following expression (Erginer and Altug,

2007):

∑

i=1

(ω

×e

)(−1)

i+1

Ω

∈ R

3×1

(7)

Where I

[N m s

] is the moment of inertia of the

propeller, e

is a unitary vector in the z

direction

and Ω

the speed of each rotor.

External and Other Forces. Comprising exogenous

forces to the quadcopter and other effects, such as

minor aerodynamic forces.

3.2 Double-hulled Watercraft

For the dynamic modeling of the Strider V1.0 a sim-

ilar rigid-body mechanical model to the one used in

the previous section is adopted. An inertial and a

body ﬁxed frame will be deﬁned to create a suit-

able workspace for the model. The SNAME (Society

of Naval Architects and Marine Engineers) provides

with a standard notation and sign convention for the

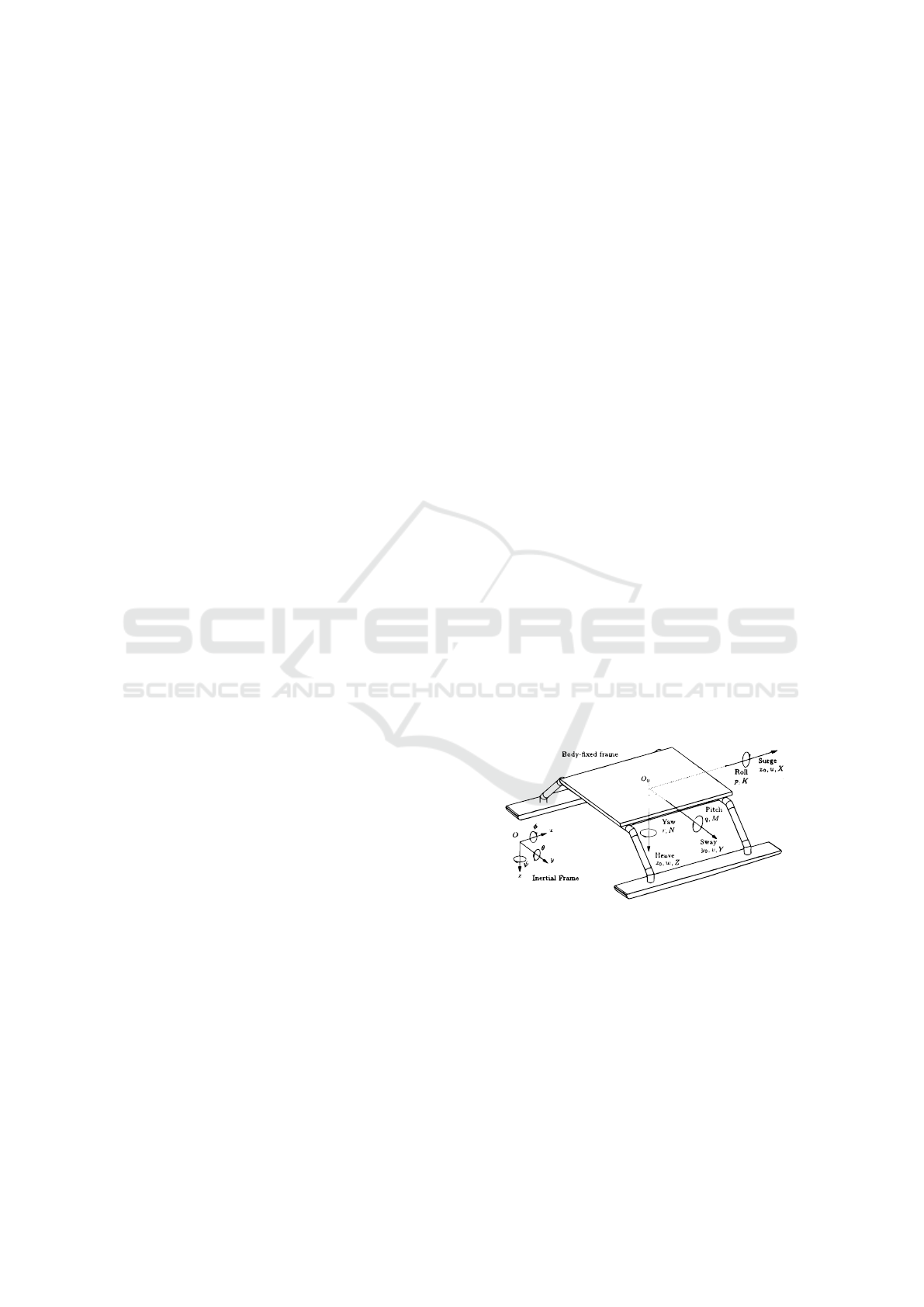
description of the motion of ships shown in Figure 2.

Figure 2: Standard notation and sign conventions for ship

motion description on the Strider V1.0.

Again, an inertial earth frame, following the NED

convention, and a body-ﬁxed frame, attached to the

vehicle’s platform, are deﬁned following the notation

shown in Figure 2. With this in mind the following

notation will be used:



x y z φ θ ψ



(8)



u v w p q r



(9)



X Y Z K M N



(10)

Smooth Autonomous Take-off and Landing Maneuvers over a Double-hulled Watercraft

391

Where η

[+] is the linear and angular position

with respect to the inertial frame, ν

[+] the linear and

angular velocity of the vessel with respect to the body

frame and Λ

[+] represents the forces and torques ap-

plied to the vessel in terms of the body ﬁxed frame.

In this work Manoeuvring Theory is adopted to

model our simulation. Manoeuvring Theory involves

the study of the vessel’s movement at a constant or

slowly varying positive speed. A three degrees of

freedom approach is commonly considered, where

only surge, sway and yaw are analysed since re-

stricted, calm water and still waves are assumed (Fos-

sen, 2011). The modelling approach selected in this

work, based on a three degrees of freedom (DOF) ma-

noeuvring theory, involves a set of assumptions, sum-

marized in the following list:

1. The body-ﬁxed frame axes coincide with the prin-

cipal axes of inertia of the body

2. The moments of inertia are constant.

3. Body symmetry with respect to the centre of mass

is assumed.

4. The body-ﬁxed frame origin O

is coincident with

the centre of mass.

5. Restricted, calm and still water bodies is assumed.

This implies that no currents or waves affect the

motion of the ship.

6. Heave, roll and pitch motions are neglected due to

a zero frequency wave excitation assumption.

7. Surge motion is decoupled from sway and yaw

motion due to the symmetry of the vessel hulls.

8. Added mass effects on the hulls are neglected

since only steady motion will be considered.

Now, taking from the generalized expression for the

motion of a rigid body in equation 3, still valid to the

model of the Strider V1.0 due to the made assump-

tions, we can deﬁne this 3DOF motion as:







0 0

0 m

0 0 I













˙u

˙v

˙r













0 −m

r 0

r 0 0

0 0 0































(11)

Where m

[Kg] is the mass of the vessel. We can

characterize this expression to the Strider V1.0 model

by deﬁning the forces and torques at play in the

motion of the vessel. In the case of the Strider V1.0

model, this force and torque vector can be divided

into three components:

Hydrodynamic Effects. This contribution comes

from the physical interaction of the hulls with the

water. The analytical expression for the hydrody-

namic forces is expressed in terms of the hydrody-

namic coefﬁcients. In this work the modelling ap-

proach made by Davidson and Schiff will be used

(Davidson and Schiff, 1946):

Y = Y

v +Y

r +Y

(12)

N = N

v + N

r + N

(13)

X = X(u)+ T (14)

Where, the constant coefﬁcients (Y

∂Y

∂v

∂Y

∂r

···) represent the hydro-

dynamic derivatives, X(u) is the hydrodynamic

resistance (which is a function of the forward

speed) and T is the thrust generated by the

propeller.

Control Surfaces and Propulsion. Generated by

the control surfaces (rudder, ﬁns, etc) and the

propulsion forces from the vessel thruster. The

propeller thrust is modelled directly as a force,

but rudder forces are analytically implemented

through the below expression (Perez and Blanke,

2002):

rudder

= −F

(u,V

,v, r,δ)sin(δ)

rudder

= F

(u,V

,v, r,δ)cos(δ)

rudder

= 0

(15)

Where F

is deﬁned as:







ρC

sin(

attack

stall

) i f |δ

attack

| < δ

stall

ρC

sign(δ

attack

) i f |δ

attack

| > δ

stall

(16)

Where ρ [Kg m

−

3] is the density of the water,

[−] is the lift coefﬁcient of the rudder, A

]

is the rudder area, V

[m s

−2

] is the average ﬂow

passing the rudder and δ

stall

[rad] is the stall angle

of the rudder. The function sign(k) gives back

the sign of k. The angle of attack δ

attack

[rad] is

the angle between the plane of the rudder and the

direction of the ﬂow passing by the rudder.

External Forces. Comprising exogenous forces to

the vessel such as wind or currents or any other

external disturbance.

4 PID CONTROL

PID control techniques are the most used linear regu-

lators. This is due to their simple structure and easy

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

392

implementation, good applicability to a wide arrange

of control problems and their tunability of ”blackbox”

systems, where the plant is not identiﬁed.

In the case of the quadrotor control system, a PID

cascade architecture has been used to obtain control

of the vehicle. Figure 3 illustrates the control archi-

tecture used in this work for the quadcopter. The

implemented architecture features three nested PID

feedback loops, each one controlling the position, ve-

locity and attitude of the quadcopter respectively.

Figure 3: Cascade loop architecture used for the control of

the quadcopter.

The control architecture of the Strider V1.0 is eas-

ier to implement than the quadrotor system since only

two degrees of freedom of the vessel will be con-

trolled. Two separate closed loop PID controllers will

command the surge speed u and the heading ψ of the

vessel through the actuation of the propeller’s thrust

and the rudder action respectively.

4.1 Trajectory Tracking

A trajectory tracking algorithm was also implemented

in the control architecture of the USV in order to per-

form planned sweeps and other autonomous path fol-

lowing tasks. Planned routes of any unmanned vehi-

cle can be represented in terms of way-points. Way-

points are deﬁned in Cartesian coordinates (x

)

for k = 1, 2, . . . , n. and represent an ordered database

of points in the working space (Fossen, 2011):

wpt.pos = (x

),(x

),... ,(x

) (17)

One of the simplest and common methods of im-

plementing path control based on way-point trajec-

tory planing is the use of Line Of Sight(LOS) guid-

ance. LOS guidance is based on the calculation of a

straight trajectory from the current position of the ve-

hicle and the following way-point using the following

expression:

(t) = tan

−1



(k) − y(t)

(k) − x(t)



(18)

Where ψ

(t) is the desired course angle, y

(k) and

(k) are the next way-point coordinates and y(t) and

x(t) the current vehicle position. Once the vehicle has

reached the way-point the next way-point is selected.

For this purpose, the concept of circle of acceptance is

adopted. When the vehicle resides within the borders

of a circle of radius ρ

[m] the next way-point in the

database is selected. This condition is translated into

the following inequality:

(k) − x(t)]

+ [y

(k) − y(t)]

≤ ρ

(19)

4.2 Vertical Take-off and Landing

Autonomous landing on a mobile platform proves to

be a difﬁcult task because of the involved complex-

ity of precise position estimation. The usual approach

to this problem is the use of Visual Servoing for po-

sition and tracking control as works such as (Heriss

et al., 2012) show. Although a Visual Servoing ser-

voing algorithm is out of the scope of this work, the

performance of VTOL tasks with the designed con-

troller can be evaluated.

The design of the autonomous landing controller

is based on the simple ﬂow chart shown in Figure 4.

During the approaching phase, the quadrotor is set to

track the vessel at an altitude z

∗

over the landing plat-

form. If the position error e is less than the selected

threshold e

∗

, the quadrotor is commanded to land.

Figure 4: VTOL controller ﬂowchart.

5 DYNAMIC MOVEMENT

PRIMITIVES (DMP)

The DMPs have been chosen for improving the VTOL

maneuvers because of their ability to operate with

all robot control parameters. They are based on

nonlinear differential equations. They also provide

smooth kinematic control parameters. This is essen-

tial to perform all the movements required in a ro-

bust and autonomous way. DMPs are well suited

to manage uncertainties, uncertain situations, unfore-

seen events, unexpected events, etc. This is possible

for several reasons, ﬁrst ensuring a smooth transition

from any unforeseen changes in the path target due to

sensory feedback; Second, because they provide the

framework for learning and adapting trajectories us-

ing learning and reinforcement algorithms; Thirdly, to

allow the learning of all types of trajectories based on

one or more of a given trajectory; and lastly because

they do not explicitly depend on time.

Smooth Autonomous Take-off and Landing Maneuvers over a Double-hulled Watercraft

393

5.1 Control Parameters as Dynamic

Systems

In this section is presented the theoretical founda-

tions of the motor representation developed accord-

ing to (Ijspeert et al., 2003) and (Schaal et al., 2005).

This documents deals with the discrete DMPs that en-

code discrete point-to-point motion control parame-

ters. For rhythmic DMPs, (Ijspeert et al., 2003) and

(Gams et al., 2009) can be consulted. A DMP path

with one degree of freedom is deﬁned by (Ijspeert

et al., 2013) with the following nonlinear differential

equations:

τ˙z

= α

(β

(g − y

) − z

) + f (x

), (20)

τ ˙y

= z

, (21)

τ ˙x

= −α

, (22)

Where: x

is the phase variable and z

is an auxil-

iary variable that represents the velocity, its derivative

is ˙z

. Moreover, β

, α

and α

are damping con-

stants, where α

= 4β

. The τ > 0 is constant, as a

temporal scaling factor. Their values are determined

in order to ensure the convergence of the system dy-

namics. This set of differential equations has a unique

attractor point y

= g (goal) with z

= 0. Finally,

f (x

) is deﬁned as a linear combination of nonlinear

radial basis functions, which allow the robot to follow

a smooth path from the initial position y

, to the ﬁnal

conﬁguration g.

f (x

) =

∑

i=1

)

∑

i=1

)

(g − y

), (23)

) = exp(−h

− c

)

), (24)

Where c

is the center of the Gaussian distribution

along the path phase and h

is its width. For a given

M and considering the time constant τ = τ

can be

deﬁned c

= exp(−α

i−1

M−1

), h

i+1

−c

)

= h

M−1

, i = 0,...,M. For each degree of freedom

in the cartesian space, the weight w

is estimated by

the measured data and using a regression according

to (Nemec et al., 2009), g being he last conﬁguration

saved during the trajectory. In this way the desired tra-

jectory is obtained. Since discrete DMPs have been

designed to represent discrete point-to-point move-

ments, the motion must pass smoothly and continu-

ously at the end of the path, that is, at time τ

0 2 4 6 8 10 12

t (s)

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0.2

X position (m)

P1 Lon Cmd

P2 Lon Cmd

P1 Measured Lon

P2 Measured Lon

Figure 5: Longitude commands and measured values during

the test.

0 2 4 6 8 10 12

t (s)

0.2

0.4

0.6

0.8

Lon position error (m)

P1 Lon position error

P2 Lon position error

Figure 6: Longitude position errors during the test.

6 EXPERIMENTS

This section will present the results obtained from the

simulation of several tests to evaluate the performance

of the designed controller.

6.1 Way-point Guidance Test

Way-point guidance was implemented for position

control of the Strider V1.0. Several tests were per-

formed with different path setups. Starting from the

coordinates origin, a constant speed of 1 m/s was

commanded to the vessel since this is the reference

speed used for the dynamic modeling of the forces.

Further analysis and results of the performance of this

controller can be found in (Omar, 2017).

6.2 DMP in Path Tracking Controllers

In this part, the performance of the proposed method

of improving a classic control with dynamic move-

ment primitives is evaluated. The base of experiments

is centered on three scenarios. A ﬁrst base scenario

P1 in which a control based on a cascade PID con-

trol architecture is performed. A second scenario P2

in which changes are introduced by the use of DMPs.

Finally a third scenario P3, where it is compared with

the case in which the operator handles the quadcopter

manually. One of the characteristics of the DMP

is the smoothness in the reproduction of movements.

For a smooth movement during the course of the tra-

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

394

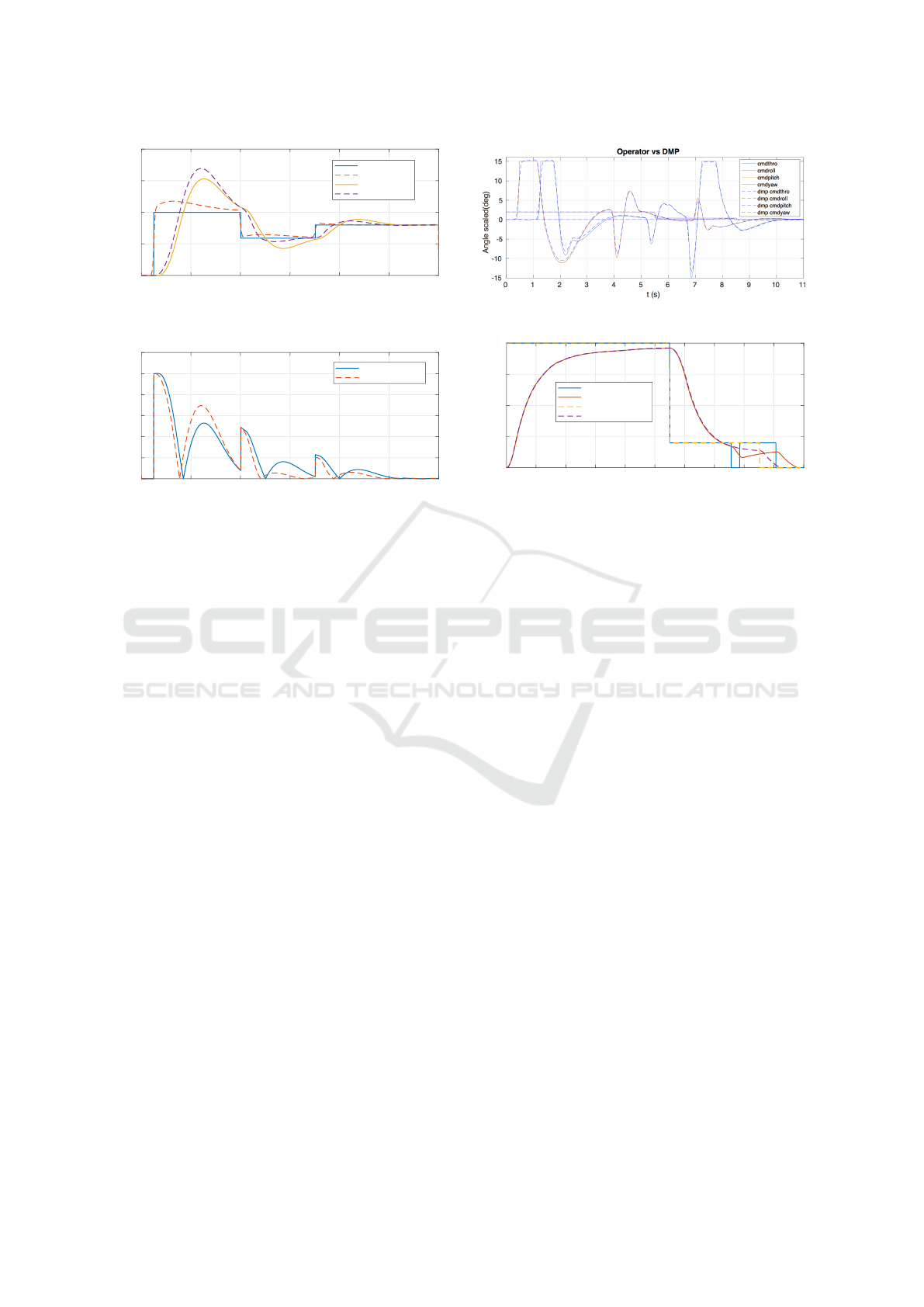
0 2 4 6 8 10 12

t (s)

0.5

1.5

Lat (m)

P1 Lat Cmd

P2 Lat Cmd

P1 Measured Lat

P2 Measured Lat

Figure 7: Latitude commands and measured values during

the test.

0 2 4 6 8 10 12

t (s)

0.2

0.4

0.6

0.8

1.2

Lat position error (m)

P1 Lat position error

P2 Lat position error

Figure 8: Latitude position errors during the test.

jectory, a treatment of the Cartesian control param-

eters is carried out using the UAV dynamic model.

Within the analyzed parameters we can highlight the

VTOL performance of the scenarios P1 and P2. Con-

cerning the path tracking performance, Figures 7 and

5 illustrate the system’s path tracking response during

tests P1 and P2. The position errors of the quadro-

tor during ﬂight are shown in 8 and 6. These errors

represent the distance between the original position

command (that of P1) and the measured latitude and

longitude during both tests. Another parameter ana-

lyzed is the settling time of the controller. As it can

be seen from the results in the ﬁgures, especially from

the analysis of the error plots, the results from P2

show a quicker settling time, which overall results in

a smaller average position error during the test. This

behavior, although more aggressive than P1 in some

cases (where the error from P2 is bigger than the error

from P1) provides a more tight path following perfor-

mance, which heavily beneﬁts autonomous take off

and landing duties. Regarding the behavior against

overshoots, it is where more signiﬁcant improvements

are obtained, In ﬁgure 9 it is possible to see in a dy-

namic way the abrupt changes made by the operator

of the scenario P3. In front of a soft control param-

eters thanks to the DMP. Despite of being a very in-

cipient experimentation it can be said that the prelimi-

nary results are satisfactory. It is intended to continue

to introduce characteristics of the DMP, such as the

treatment of rhythmic movements in surveying duties

(a typical task for drones) or dynamic evasion of ob-

stacles during VTOL.

Figure 9: Comparative between operator and DMPs.

1 2 3 4 5 6 7 8 9 10

t (s)

0.5

1.5

Altitude(m)

VTOL performance

P1 Altitude Command

P1 Altitude

P2 Altitude Command

P2 Altitude

Figure 10: Height values during P1 and P2 testing.

6.3 DMPs and VTOL Tests

We will evaluate the performance of the VTOL and

tracking algorithm comparing the two scenarios P1

and P2. The quadrotor is set to track the position of

the moving landing platform. It autonomously takes

off at the start of the test (t = 0s) and then the VTOL

controller is activated at 5,5 seconds and set to land-

ing mode. The controller parameters, from Figure 4,

used for the test were e

∗

= 0.12 m and h

∗

= 0.3 m.

Figure 10 shows the height measured values and

command of the quadrotor during tests P1 and P2.

The three phases of the algorithm can be easily iden-

tiﬁed by seeing the commanded height values during

the test, where the three height command levels rep-

resent each of the states of the controller respectively.

Figure 11 presents the absolute position error, repre-

senting the distance from the quadrotor to the cen-

tre of the landing pad. As it can be seen from both

ﬁgures, the performance of the DMP path tracking

(P2) yields a much smoother landing sequence. This

is thanks to the beneﬁts of the DMP, since the abso-

lute error gets reduced into the minimum landing er-

ror threshold.

It can be seen that the VTOL algorithm functions

properly and that the quadcopter is able to safely

land in the platform within the error constrains that

were set in both tests, however when treating the path

tracking controller with DMP the results provide with

lower landing times, reducing the inherent possibility

of hazard during this complicated manoeuvre, and a

more ﬂuid landing behaviour.

Smooth Autonomous Take-off and Landing Maneuvers over a Double-hulled Watercraft

395

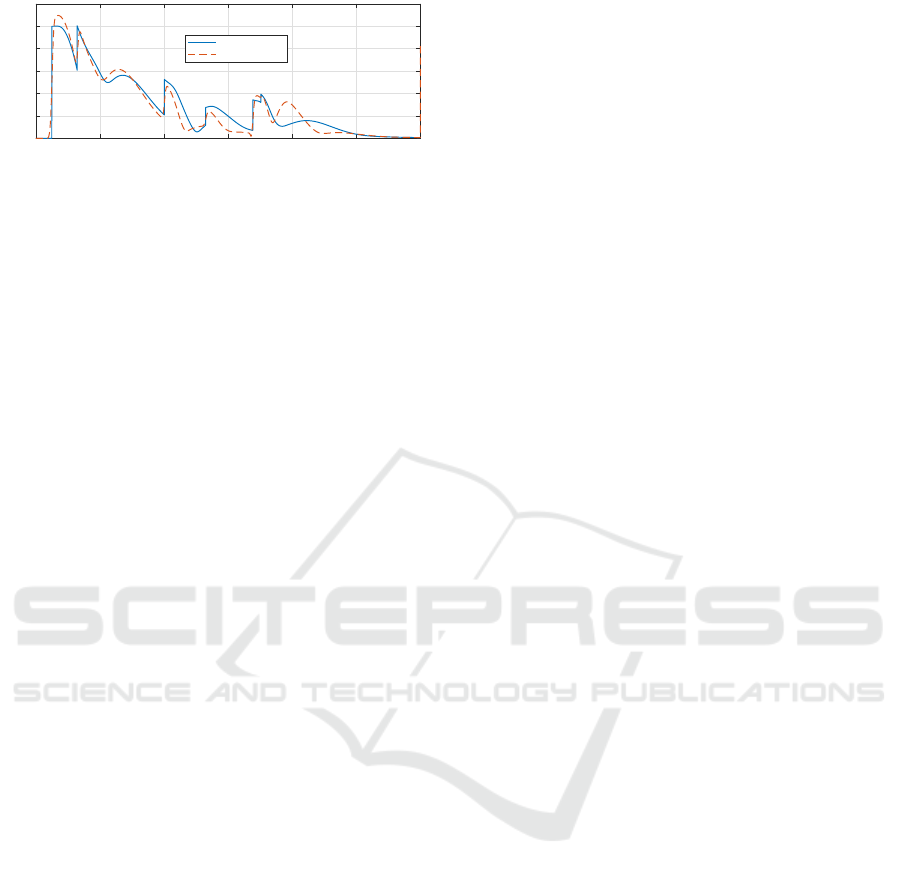
0 2 4 6 8 10 12

t (s)

0.2

0.4

0.6

0.8

1.2

Absolute position error (m)

P1 absolute error

P2 absolute error

Figure 11: Absolute position error of the quadcopter during

the VTOL test.

7 CONCLUSIONS

The approach proposed in this work shows how to im-

prove a classic control system dedicated to VTOL op-

erations over a moving target. In particular its shown

that the trajectory tracking error might be improved

and the UAS is able to perform a smooth VTOL ma-

noeuvre over the USV.

The stability and softness provided by the dy-

namic movement primitives might be able to improve

navigation manoeuvres subject to waves or even with

wind gusts, and including dynamic obstacle avoid-

ance capabilities. In spite of the early characteristic

of this experimentation, the preliminary results hint

of a sizeable improvement once more characteristics

of the DMP are introduced into the control architec-

ture.

Better performance could be expected, especially

when performing repetitive cyclic and rhythmical

tasks, typical in UAS based sensing techniques.

ACKNOWLEDGMENTS

The research leading to these results has received

funding from the RoboCity2030-III-CM project

(Rob

otica aplicada a la mejora de la calidad de vida

de los ciudadanos. fase III; S2013/MIT-2748), funded

by Programas de Actividades I+D en la Comunidad

de Madrid and cofunded by Structural Funds of the

EU.

REFERENCES

Davidson, K. and Schiff, L. (1946). Turning and course

keeping qualities of ships. Transactions of SNAME,

4:49.

Djapic, V., Prijic, C., and Bogartz, F. (2015). Autonomous

takeoff landing of small uas from the usv. In OCEANS

2015 - MTS/IEEE Washington, pages 1–8.

Erginer, B. and Altug, E. (2007). Modeling and pd control

of a quadrotor vtol vehicle. In 2007 IEEE Intelligent

Vehicles Symposium, pages 894–899.

Fossen, T. I. (2011). Handbook of marine craft hydrody-

namics and motion control. John Wiley & Sons.

Gams, A., Ijspeert, A. J., Schaal, S., and Lenar

c, J.

(2009). On-line learning and modulation of periodic

movements with nonlinear dynamical systems. Au-

tonomous robots, 27(1):3–23.

Heriss

e, B., Hamel, T., Mahony, R., and Russotto, F.-X.

(2012). Landing a vtol unmanned aerial vehicle on a

moving platform using optical ﬂow. IEEE Transac-

tions on Robotics, 28(1):77–89.

Ijspeert, A. J., Nakanishi, J., Hoffmann, H., Pastor, P., and

Schaal, S. (2013). Dynamical movement primitives:

learning attractor models for motor behaviors. Neural

computation, 25(2):328–373.

Ijspeert, A. J., Nakanishi, J., and Schaal, S. (2003). Learn-

ing attractor landscapes for learning motor primitives.

Advances in neural information processing systems,

pages 1547–1554.

Nemec, B., Tamo

unait

e, M., W

org

otter, F., and Ude, A.

(2009). Task adaptation through exploration and ac-

tion sequencing. In Humanoid Robots, 2009. Hu-

manoids 2009. 9th IEEE-RAS International Confer-

ence on, pages 610–616. IEEE.

Omar, V. A. (2017). Modelling and control of a uav-usv

collaboration scheme for ﬂuvial operations. Bache-

lor’s thesis, Univ. Carlos III de Madrid.

Ore, J.-P., Elbaum, S., Burgin, A., Zhao, B., and Detweiler,

C. (2015). Autonomous Aerial Water Sampling, pages

137–151. Springer International Publishing, Cham.

Perez, T. and Blanke, M. (2002). Mathematical ship mod-

elling for control applications. Ørsted-DTU, Automa-

tion.

Pinto, E., Santana, P., Marques, F., Mendonc¸a, R.,

Lourenc¸o, A., and Barata, J. (2014). On the design

of a robotic system composed of an unmanned surface

vehicle and a piggybacked vtol. In Doctoral Confer-

ence on Computing, Electrical and Industrial Systems,

pages 193–200. Springer.

Schaal, S., Peters, J., Nakanishi, J., and Ijspeert, A. (2005).

Learning movement primitives. In Robotics Research.

The Eleventh International Symposium, pages 561–

572. Springer.

Weaver, J. N., Frank, D. Z., Schwartz, E. M., and Arroyo,

A. A. Uav performing autonomous landing on usv

utilizing the robot operating system.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

396