
Trajectory Tracking based on Containment Algorithm Applied to a
Formation of Mobile Manipulators
Renato Vizuete, Jackeline Abad Torres and Paulo Leica
Departamento de Automatización y Control Industrial, Escuela Politécnica Nacional, Quito, Ecuador
Keywords: Multi-robot Formation, Distributed Control, Containment Algorithm, Consensus, Mobile Manipulator.
Abstract: This paper presents a distributed control for the formation control of mobile manipulators. We use a mobile
manipulator model that can be separated in a kinematic and a dynamic component. For the kinematic
component (formation control), we propose a distributed containment algorithm with a smooth function to
avoid the chattering phenomenon, which provides control actions applicable in real robots. For the dynamic
component, a controller based on the compensation of the dynamic forces and torques is applied. The structure
of the formation is given by: a group of virtual leaders, which are used as references and to delimit the physic
boundaries, and a group of follower robots. The distribution of the followers is determined by a Laplacian
matrix, which is built based on the desired positions of the robots inside the convex hull formed by the virtual
leaders. To validate the designed controllers, a simulation of formation and tracking trajectory of 8 mobile
manipulators is performed, considering as reference, a sinusoid in each coordinate axis.
1 INTRODUCTION
The formation control of robots has acquired
significant importance in the last decades because of
its civil and military applications including moving
objects of big dimensions (Eoh et al., 2011), rescue
activities (Liu et al., 2013), military convoys
(Maxwell et al., 2013), where it is necessary to use
multiple robots in a cooperative manner. In many
situations, it is crucial to use formations with an
irregular geometry according to the circumstances.
For instance, the transportation of objects with
irregular shapes and heterogeneous distribution of
mass requires the use of multiple mobile manipulators
in irregular distributions.
One of the challenges in the control of multiple
robots formations is the design of decentralized
control schemes that consider the complexity and
number of robots (or agents in networks), structure
and topology of the formation, information flow
among the agents, and robustness of the control
scheme. Classically, the coordination of multi robots
teams (or networks) in a formation uses a centralized
architecture, which requires all the network’s
information to compute the desired actions by the
central control. Meanwhile, in a decentralized
coordination scheme, every robot computes the
control actions based only on local information
(Johnson et al., 2016). In (De La Cruz and Carelli,
2006; Brandao et al., 2014), diverse centralized
control systems were developed for the formation
control of mobile robots. Despite the satisfactory
results of the centralized control schemes, they are
vulnerable to failures in the communication network
and the operation areas are limited. Further, the
scalability and geometric shapes of the formation are
other restrictions, which are usually solved by
rebuilding the control system.
Distributed control is one of the most relevant
techniques for the formation control due to its
robustness and scalability, whose most important
feature is the distribution of the control capabilities
through the system. In this type of architectures,
every robot computes the necessary control actions
using only the local information provided by its
neighbors, without knowing the state of all the
formation. Because the controller uses only local
information, it is robust to failures in the
communication network, which could be catastrophic
in a centralized formation control (Tron et al., 2016).
Additionally, a distributed formation control allows
adding agents and generating different formations
characterized by irregular geometric shapes without
redesigning the control structure.
Various distributed control methods for multiple
mobile robots have been investigated considering
limited communication capacity (Bock et al., 2016),
122
Vizuete, R., Torres, J. and Leica, P.
Trajectory Tracking based on Containment Algorithm Applied to a Formation of Mobile Manipulators.
DOI: 10.5220/0006435501220131
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 122-131
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

communication delays (Dai and Liu, 2015; Liu et al.,
2016), and noise (Dang et al., 2016). For instance, in
(Dai and Liu, 2017) a distributed cooperation control
considering time delays and obstacles is considered.
During the last decade, formation control has been
formulated as containment control problem, where
robots, considered followers, move into a geometric
space formed by other robots, considered leaders.
In (Ren and Cao, 2011) and (Cao et al., 2010),
several algorithms for the containment control
problem have been investigated. Specifically, (Cao et
al., 2010) proposes a distributed containment
algorithm for double-integrator dynamics, to drive a
group of followers into the convex hull spanned by
the leaders without considering a specific location of
each follower inside the geometric space. The
algorithm uses a PD-like controller and a sign
function to generate the control actions. The use of
this type of function guarantees that the errors of the
system converge to zero, but generates control actions
with chattering. This phenomenon behaves like a
high frequency noise due to the switching action of
the control law; consequently, the actuator signal is
not appropriate for real robots. To avoid this problem,
(Cheng et al., 2016) proposes a containment control
of multi-agent systems based on a
type approach
considering polynomial trajectories. In (Shtessel et
al., 2014) and (Ouyang et al., 2014), a smooth
function that approximates the behavior of the sign
function is proposed to solve the problem of
chattering. The use of smooth functions eliminates
the chattering in the control actions, but generates a
ball. These controllers cannot guarantee zero error,
but the error is confined inside the ball. Depending on
the system conditions and the type of these functions,
the boundary of the ball could become negligible,
getting acceptable results with control actions
applicable in a real system.
This work proposes to combine the use of both,
the convex hull and smooth functions, which provide
a distributed controller with a smooth control action
applicable to real manipulators. Here, a distributed
controller is designed for the kinematic component of
a mobile manipulator while for the dynamic
component of each agent another control law is
designed based on the dynamics’
compensation. Further, the formation is defined using
a graph that represents the interactions among the
mobile manipulators. The associated graph’s matrices
(Adjacency, Laplacian matrix among others) and its
properties play an important role in the development
of the control laws (Godsil and Royle, 2001), which
is typical in these types of network dynamics (Xue
and Roy, 2012; Jadbabaie et al., 2013; Olfati-Saber,
2006; Cao et al., 2013). Specifically, (Chen and Li,
2008; Chen and Li, 2006) propose an adaptive neural
network to control a formation whose geometric
pattern is determined by a relative matrix and the
interactions among the agents are modelled trough a
directed graph. In (Zavlanos and Pappas, 2007), the
connectivity of a graph represented by the smallest
eigenvalue of the Laplacian matrix associated is used
to control the movements of the agents in order to
track a leader.
In this paper, we aim to present a distributed
control system using a smooth function for a
formation of mobile manipulators with three degrees
of freedom (3 DOF), considering a dynamic model.
The paper is organized as follows. In Section II, we
formulate the problem of formation control of mobile
manipulators as distributed control problem on a
network dynamics. Section III presents the kinematic
and dynamic model of a mobile manipulator with 3
DOF used in the simulations. In Section IV, the
stability of the system including the distributed
control law is proved. Section V shows the simulation
results in the formation of eight mobile manipulators.
2 PROBLEM FORMULATION
The present work focuses on the problem of trajectory
tracking of a mobile manipulators formation. The
formation is given by a convex hull and a graph that
represents the information interchange among the
robots.
A convex hull is the minimum convex set formed
by a set of points in the Euclidian plane or space. The
use of this geometric space allows to delimit the
boundaries of the formation and guarantee the
location of the robots inside it. The convex hull is
formed generally by the leaders of the formation,
whose movements define the trajectory. In many
cases, the robot teams do not have real leaders, and it
is necessary to use virtual leaders as a reference for
the followers. For example, in (Droge, 2015; Yan et
al., 2016), a single virtual leader is used for a
formation control, while in (Li et al., 2016), multiple
leaders are used as references for the flocking of
multi-agent systems.
Formally, we consider a formation of agents
(mobile manipulators) composed by mobile
manipulators and virtual leaders. The
communication network among the agents, i.e.
mobile manipulators and virtual leaders, is modeled
through a directed graph (digraph) , with undirected
communication patterns among the followers and
directed paths from the virtual leaders to the
followers. The graph , is formed by a set of
Trajectory Tracking based on Containment Algorithm Applied to a Formation of Mobile Manipulators
123
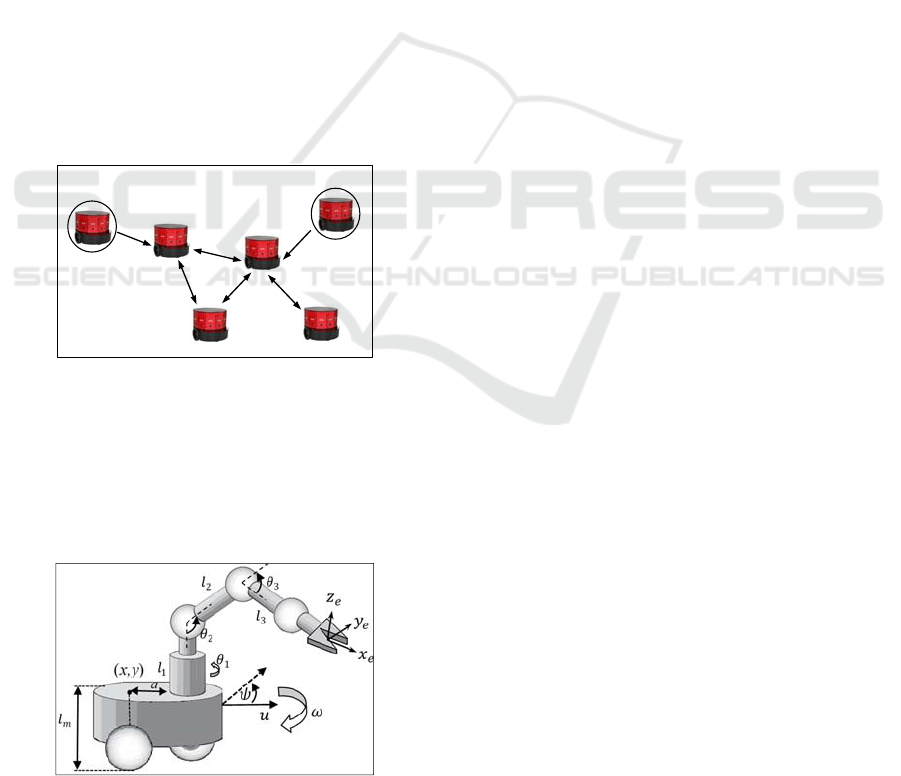
vertices
1,…,
that represents the
robots/mobile manipulators of the formation and a set
of edges ⊆
,
∈:
representing the
interactions among the robots. For example, if there
is a directed interaction between robot 1 and
robot 3 there is a directed edge
,
1,3
in
the digraph , as shown in Figure 1. The adjacent
matrix
is defined by
0 if
,
∈
and
0 otherwise. We define the Laplacian
matrix as ℓ
, where ℓ
∑
if ,
and ℓ
if . The adjacent matrix and the
Laplacian matrix are related by the expression
, where diag
,…,
and
∑
(see (Bapat, 2014) for details on graphs
definitions).
Notice that the first rows of the Laplacian
matrix corresponding to the virtual leaders are zeros
since there are not interactions from the followers to
the leaders or among the leaders, as observed in
Figure 1. Due to the fact that the virtual leaders are
the reference of the formation, there must be a path
from a virtual leader to every follower of the
formation. This means the existence of a connected
directed spanning tree in the graph of the formation.
Figure 1: Graph of a communication network among the
agents of a formation.
3 MOBILE MANIPULATOR
3.1 Kinematic Model
Figure 2: Diagram of a mobile manipulator with 3 DOF
(Molina and Suárez, 2016).
A kinematic model of a mobile manipulator with 3
DOF is shown in Figure 2. The effector position of
the robot is
,
,
and
are the values of the articulations 1, 2 and 3
respectively,
,
and
are the angles of
the articulations 1, 2 and 3 respectively,
is the centroid of the wheels of the
manipulator base, is the distance from the centroid
of the wheels of the mobile platform to the
manipulator base,
is the height of the manipulator
base; and are the linear and rotational velocities
of the platform and is the orientation of the
platform.
The kinematic model of the mobile manipulator is
given by:
, (1)
where
is the Jacobian matrix of the system defined
by:
(2)
;
;
;
;
;
;
;
;
;
;
0;
;
where
;
;
sin
;
;
cos
;
cos
;
;
sin
.
3.2 Dynamic Model
For the dynamic model, we have considered only the
dynamic component of the mobile platform because
in most of the mobile manipulators, the weight of the
manipulator arm is negligible compared to the
3
4
5
6
1
2
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
124

platform and hence the dynamic forces of the arm are
also negligible. Also, the rotational velocities of the
arm are not considerable compared to other dynamics
effects. The dynamic model of the mobile platform is
given by:
,
(3)
where
,
1
0
0
1
,
,
,
,
,
,
,
,
are the model parameters, and
is the input vector to the model. The values of
these parameters have been chosen for a unicycle
robot, according to (De la Cruz, 2006).
Combining the kinematic and dynamic model, the
complete model of the mobile manipulator can be
expressed as:
00
00
00
00000
1
0000
0
1
000
(4)
4 CONTROL SYSTEM
4.1 Distributed Containment Control
We have chosen a distributed containment control for
a double-integrator dynamics:
,
,
1,…,,
(5)
where
,
, and
represent position, velocity, and
acceleration respectively.
We have used the algorithm for multiple leaders
with nonidentical velocities specified in (Cao et al.,
2010). In this case, we have selected the sigmoid
function for the slide surface
. Thus, we
propose the following algorithm:
sigm
,(6)
where sigm
|
|
⋯
|
|
,
,…,
,
,…,
is the vector of
accelerations with the last entries equal to zero and
, , and are positive constants.
Considering
≜, the state error for the
consensus condition, the closed-loop system is given
by:
sigm
If we consider only the last entries of the system,
we get:
sigm
,
(7)
where
and
are the vectors containing only the
last entries and
∈
with
ℓ
, ,1,…,.
Remark: According to the problem formulation, is
a symmetric matrix with real coefficients. Further,
this matrix is diagonally dominant with positive
eigenvalues (Gershgorin’s circle theorem) (Godsil
and Royle, 2001).
In order to prove the system’s stability, let us
introduce the following matrices:
(8)
2
2
(9)
According to (Cao et al., 2010), these matrices are
symmetric positive definite if:
min
,
,
where
represents the minimum eigenvalue
of the matrix .
We use the Lyapunov function candidate:
1
2
1
2
1
2
(10)
Trajectory Tracking based on Containment Algorithm Applied to a Formation of Mobile Manipulators
125

Deriving 10, we obtain:
(11)
Then, by applying (7) in (11), the derivative of the
Lyapunov candidate is:
sigm
(12)
The product
sigm
is
equivalent to:
sigm
If 01, the following inequality is satisfied
when
/ :
sigm
1
Thus, (12) can be expressed as:
1
(13)
Using Hölder’s inequality and the property of the
vector norms
‖
‖
‖
‖
we get:
‖
‖
‖
‖
(14)
Finally, applying (14) in (13), the following
inequality is obtained:
1
‖
‖
To guarantee
0, the following condition must be
satisfied:
‖
‖
1
Consequently, the system is stable and the errors
are limited to a ball with a boundary
/. The size of the ball depends on the number of
followers , the size of the window of the sigmoid
function and a constant ∈
0,1
.
4.2 Dynamic Controller
The following dynamic controller is proposed:
sigm
0
0
, (15)
where
and
are positive constants. To prove
stability, the following Lyapunov function candidate
is used:
1
2
,
where
, and
is the reference generated
by the kinematic (distributed) controller. Taking
derivative of , we obtain:
sigm
sigm
0
0
sigm
sigm
sigm
sigm
Therefore,
0, and hence the system dynamics is
stable.
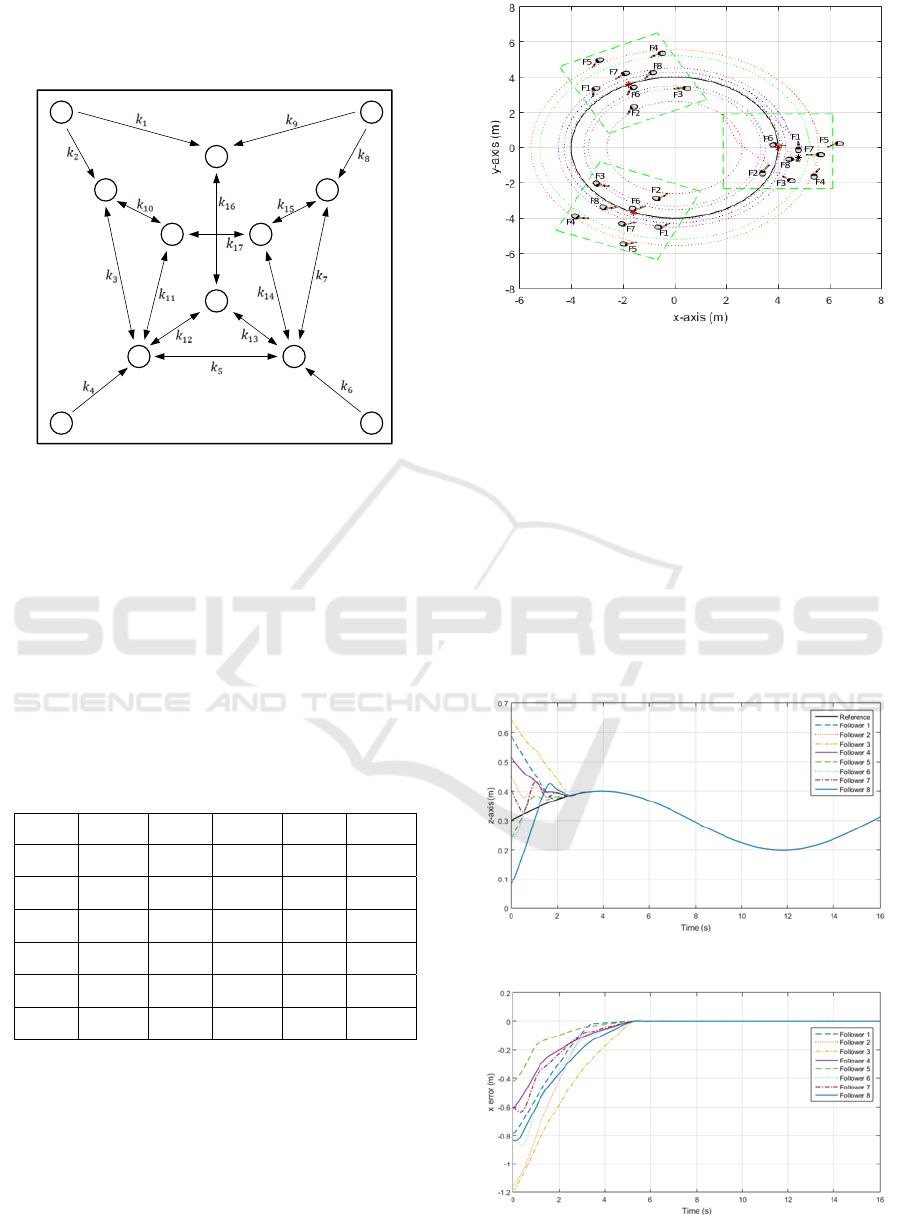
Applying the distributed containment algorithm
and the dynamic controller, the complete control
system of the formation tracking for each follower is
shown in Figure 3. In this figure,
,for 1,…,,
represent the neighbors of this follower, i.e. the ones
that interact with the follower according to the
Laplacian matrix, and
,
,
, for
1,…,, are the states of the virtual leaders.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
126
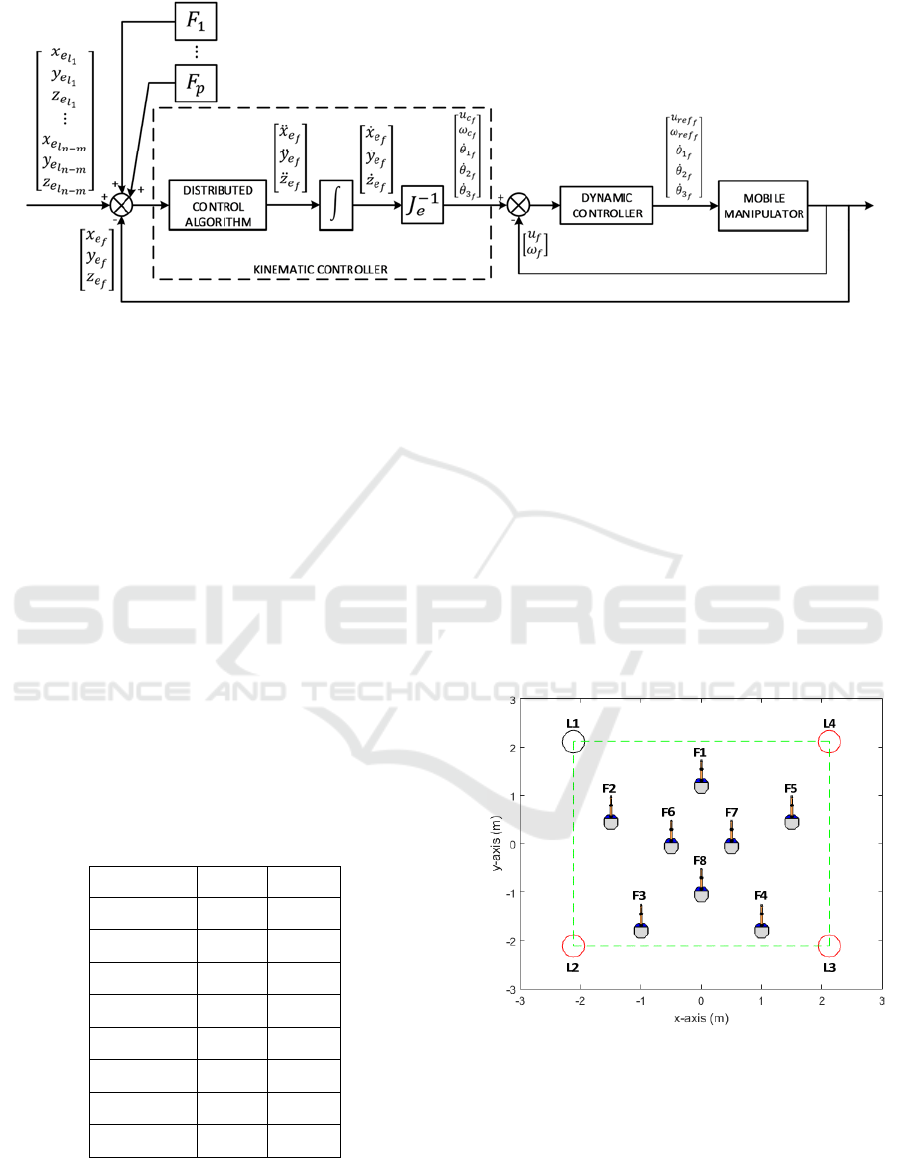
Figure 3: Control system of a follower of the formation.
5 SIMULATION
To validate the designed controllers, a simulation has
been performed, considering a mobile manipulator
with the following dimensions: 0.2,
0.383,
0.233 and
0.203.
The linear and rotational velocities of the mobile
platform are bounded according to the limits of the
robot Pioneer 3-DX specified in the datasheet and
used in (Yan et al., 2015) (1.21.2/
and 5.245.24/).
The formation uses 12 robots: 8 real followers and
4 virtual leaders. The positions of the virtual leaders
are given by a square inscribed in a circle with radius
3. Additionally, the states of the virtual leaders
are determined by the trajectory used as reference.
The desired positions of the followers are specified in
Table 1.
Table 1: Desired positions of the followers.
Follower x(m) y(m)
0.0 1.75
-1.5 1.0
-1.0 -1.25
1.0 -1.25
1.5 1.0
-0.5 0.5
0.5 0.5
0.0 -0.5
Figure 4 shows the formation of the mobile
manipulators, the convex hull spanned by the virtual
leaders and the distribution of the followers in it.
Figure 5 shows the graph associated with the
formation, which determines the references of each
follower.
To find the Laplacian matrix associated with the
formation, specifically the weights of the directed
edges in the graph, the following system of linear
equations is solved:
0
0
,
where and are the vectors containing the desired
positions of the virtual leaders as well as followers in
the formation.
Figure 4: Geometric distribution of the robot formation.
The coefficients of the Laplacian matrix are the
unknowns of the system. This is a homogeneous
system due to the zeros of the constant terms. For this
reason, it is necessary to choose an arbitrary value of
one of the coefficients to obtain a nontrivial solution
of the system since the robot formation can be formed
with an infinite combination of values of the
Trajectory Tracking based on Containment Algorithm Applied to a Formation of Mobile Manipulators
127
coefficients of the graph. In this case, the value
is
set to 1, which provides the solutions specified in
Table 2.
Figure 5: Graph of the formation.
Consequently, the Laplacian matrix of the system
is given by:
000000000000
000000000000
000000000000
000000000000
0.57 0 0 0.57 1.33 0 0 0 0 0 0 0.19
0.59 0 0 0 0 1.07 0.24 0 0 0.25 0 0
0 1 0 0 0 0.24 2.05 0.46 0 0.07 0 0.28
0 0 1 0 0 0 0.46 2.05 0.24 0 0.070.28
0 0 0 0.59 0 0 0 0.24 1.07 0 0.25 0
0 0 0 0 0 0.250.07 0 0 0.6 0.28 0
0 0 0 0 0 0 0 0.070.250.28 0.6 0
0 0 0 0 0.19 0 0.280.28 0 0 0 0.75
Table 2: Values of the coefficients of the Laplacian matrix.
Edge Value Edge Value Edge Value
0.57
0.24
0.28
0.59
0.59
0.07
0.24
0.57
0.25
1
0.25
0.19
0.46
0.07
0.28
1
0.28
For the experiment a circular trajectory has been
chosen for the plane, while a sinusoid is applied as
reference for the vertical movement of the effector in
the -axis. The equations of the trajectories are:
4cos0.08
4sin0.08
0.30.1sin0.15
Figure 6: Trajectory of the formation.
The robots start from random positions and
achieve the desired positions of the formation
quickly. Figure 6 shows the results of the tracking
trajectory of the formation in the plane. The
movement of the effectors in the -axis can be found
in Figure 7.
The position errors of the followers’ effectors are
presented in the Figure 8, Figure 9 and Figure 10.
Figure 11 shows the centroid error of the formation.
Finally the control actions of the mobile platform are
exposed in the Figure 12 and Figure 13. The control
actions are smooth and do not present the chattering
effect.
Figure 7: Movement of the effectors in the z-axis.
Figure 8: error of the followers.
F1
F2
F4F3
F7
F8
F5
F6
L1 L4
L2 L3
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
128
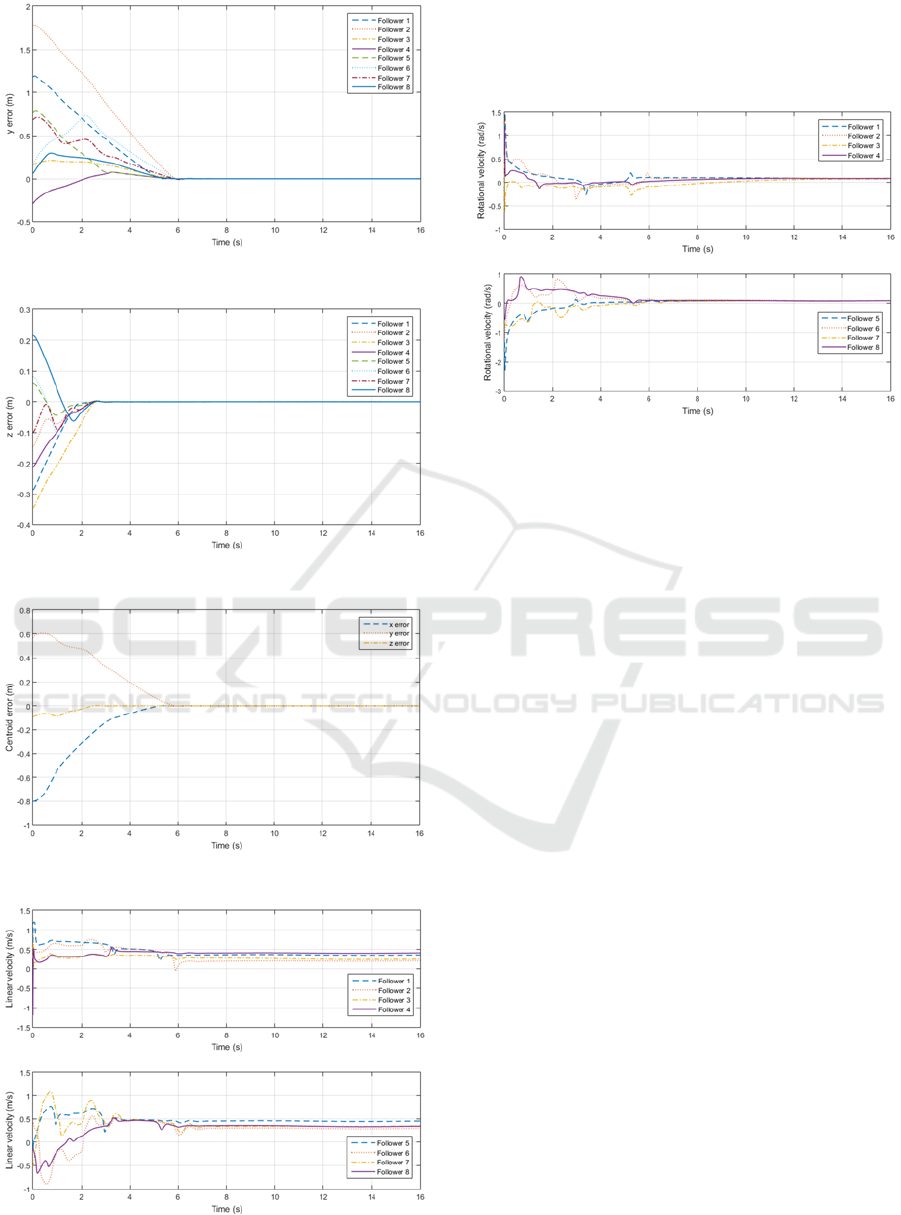
Figure 9: error of the followers.
Figure 10: error of the followers.
Figure 11: Centroid error of the formation.
Figure 12: Linear velocity of the followers.
A video of the simulation showing the movements
of the robots in the coordinate axes can be found at
https://www.youtube.com/watch?v=bc_S9HWAM0
g
Figure 13: Rotational velocity of the followers.
6 CONCLUSIONS
In this paper, we proposed a distributed control for the
formation control of mobile manipulators. A
distributed containment control was proposed for the
kinematic component. A controller based in the
compensation of the dynamic forces and torques was
proposed for the dynamic component. The two
controllers designed were applied using a cascade
control architecture. The structure of the formation
was given only by the Laplacian matrix, whose
coefficients were found solving a system of linear
equations obtained by considering the desired
positions of the followers inside the convex hull
spanned by the virtual leaders.
The virtual leaders were used as references and
determined only by the desired trajectory. The control
actions obtained did not show the chattering
phenomenon and were limited to the values of
velocities of a real robot.
ACKNOWLEDGEMENTS
The authors thanks Escuela Politécnica Nacional for
the grant support PII-DACI-01-2017 and PIJ-15-17.
REFERENCES
Bapat, R. (2014). Graphs and Matrices. London: Springer-
Verlag.
Trajectory Tracking based on Containment Algorithm Applied to a Formation of Mobile Manipulators
129

Bock, G., Hendrickson, R., Lamkin, J., Dhall, B., Wang, J.,
and Ahn, I. (2016). Experiments of distributed control
for multiple mobile robots with limited
sensing/communication capacity. In: IEEE
International Conference on Electro Information
Technology (EIT). Grand Forks, ND, USA.
Brandao, A., Barbosa, J., Mendoza, V., Sarcinelli-Filho,
M., and Carelli, R. (2014). A Multi-Layer Control
Scheme for a centralized UAV formation.
In: International Conference on Unmanned Aircraft
Systems (ICUAS). Orlando, FL, USA.
Cao, Y., Stuart, D., Ren, W., and Meng, Z. (2010).
Distributed Containment Control for Double-integrator
Dynamics: Algorithms and Experiments. In: American
Control Conference (ACC). Baltimore, MD, USA.
Cao, Y., Yu, W., Ren, W., and Chen, G. (2013). An
Overview of Recent Progress in the Study of
Distributed Multi-Agent Coordination. IEEE
Transactions on Industrial Informatics , 9(1), 427-438.
Chen, X., and Li, Y. (2006). Smooth Formation Navigation
of Multiple Mobile Robots for Avoiding Moving
Obstacles. International Journal of Control,
Automation, and Systems, 4(4), 466-479.
Chen, X., and Li, Y. (2008). Stability on Adaptive NN
Formation Control with Variant Formation Patterns and
Interaction Topologies. International Journal of
Advanced Robotic Systems, 5(1), 69-82.
Cheng, L., Wang, Y., Ren, W., Hou, Z.-G., and Tan, M.
(2016). Containment Control of Multiagent Systems
With Dynamic Leaders Based on a PIn-Type Approach.
IEEE Transactions on Cybernetics, 46(12), 3004-3017.
Dai, G.-B., and Liu, Y.-C. (2015). Leaderless and leader-
following consensus for networked mobile
manipulators with communication delays. In: IEEE
Conference on Control Applications (CCA). Sydney,
Australia.
Dai, G.-B., and Liu, Y.-C. (2017). Distributed Coordination
and Cooperation Control for Networked Mobile
Manipulators. IEEE Transactions on Industrial
Electronics, 64(6).
Dang, A., La, H., and Horn, J. (2016). Distributed formation
control for autonomous robots following desired shapes
in noisy environment. In: IEEE International
Conference on Multisensor Fusion and Integration for
Intelligent Systems (MFI). Baden, Germany.
De la Cruz, C. (2006). Control de Formación de Robots
Móviles. Tesis Doctoral, INAUT-UNSJ.
De La Cruz, C., and Carelli, R. (2006). Dynamic Modeling
and Centralized Formation Control of Mobile Robots.
In: IECON 2006 - 32nd Annual Conference on IEEE
Industrial Electronics. Paris, France.
Droge, G. (2015). Distributed virtual leader moving
formation control using behavior-based MPC. In:
American Control Conference (ACC). Chicago, IL,
USA.
Eoh, G., Jeon, J., Choi, J., and Lee, B. (2011). Multi-robot
cooperative formation for overweight object
transportation. In: IEEE/SICE International
Symposium on System Integration (SII). Kyoto, Japan.
Godsil, C., and Royle, G. (2001). Algebraic Graph Theory.
New York: Springer-Verlag.
Jadbabaie, A., Lin, J., and Morse, A. (2003). Coordination
of groups of mobile autonomous agents using nearest
neighbor rules.
IEEE Transactions on Automatic
Control, 48(6), 988-1001.
Johnson, L. B., Choi, H. L., and How, J. P. (2016). The Role
of Information Assumptions in Decentralized Task
Allocation: A Tutorial. IEEE Control Systems, 36(4),
45-46.
Li, Z., Na, C., and Xie, G. (2016). Flocking of Multi-Agent
Systems with Multiple Virtual Leaders Based on
Connectivity Preservation Approach. In: Proceedings
of the 2015 Chinese Intelligent Systems Conference,
Volume 1 (págs. 465-473). Berlin: Springer-Verlag.
Liu, Y., Nejat, G., and Vilela, J. (2013). Learning to
cooperate together: A semi-autonomous control
architecture for multi-robot teams in urban search and
rescue. 2013 IEEE International Symposium on Safety,
Security, and Rescue Robotics (SSRR). Linkoping,
Sweden.
Liu, Z., Chen, W., Lu, J., Wang, H., and Wang, J. (2016).
Formation Control of Mobile Robots Using Distributed
Controller With Sampled-Data and Communication
Delays. IEEE Transactions on Control Systems
Technology, 24(6), 2125-2132.
Maxwell, P., Rykowski, J., and Hurlock, G. (2013).
Proposal for the initiation of general and military
specific benchmarking of robotic convoys. In: IEEE
Conference on Technologies for Practical Robot
Applications (TePRA). Woburn, MA, USA.
Molina, L., and Suárez, J. (2016). Seguimiento de
trayectoria mediante tres estrategias de control basado
en espacio nulo, control en modo deslizante (SMC) y
tipo PID aplicadas a una formación de manipuladores
móviles. Thesis, Escuela Politécnica Nacional. Quito,
Ecuador.
Olfati-Saber, R. (2006). Flocking for multi-agent dynamic
systems: algorithms and theory. IEEE Transactions on
Automatic Control, 51(3), 401-420.
Ouyang, P. R., Acob, J., and Pano, V. (2014). PD with
sliding mode control for trajectory tracking of robotic
system. Robotics and Computer-Integrated
Manufacturing, 30(2), 189-200.
Pionner 3-DX Datasheet, Adept Technology, Inc. Rev. A.
http://www.mobilerobots.com/Libraries/Downloads/Pi
oneer3DX-P3DX-RevA.sflb.ashx.
Ren, W., and Cao, Y. (2011). Distributed Coordination of
Multi-agent Networks. London: Springer-Verlag.
Shtessel, Y., Edwards, C., Fridman, L., and Levant, A.
(2014). Sliding Mode Control and Observation. Basel:
Birkhäuser.
Tron, R., Thomas, J., Loianno, G., Daniilidis, K., and
Kumar, V. (2016). A Distributed Optimization
Framework for Localization and Formation Control:
Applications to Vision-Based Measurements. IEEE
Control Systems, 36(4), 22-24.
Xue, M., and Roy, S. (2012). Characterization of security
levels for the dynamics of autonomous vehicle
networks. In: IEEE 51st Annual Conference on
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
130

Decision and Control (CDC), (pp. 3916-3921). Maui,
HI, USA.
Yan, Z., Fabresse, L., Laval, J., and Bouraqadi, N. (2015).
Metrics for Performance Benchmarking of Multi-robot
Exploration. In: IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS). Hamburg,
Germany.
Yan, Z., Liu, X., Jiang, A., and Wang, L. (2016). Formation
control of multiple UUVs based on virtual leader. In:
35th Chinese Control Conference (CCC). Chengdu,
China.
Zavlanos, M., and Pappas, G. (2007). Potential Fields for
Maintaining Connectivity of Mobile Networks. IEEE
Transactions on Robotics, 23(4), 812-816.
Trajectory Tracking based on Containment Algorithm Applied to a Formation of Mobile Manipulators
131
