Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in

Urban Conditions

Nadir Ouddah, Lounis Adouane, Rustem Abdrakhmanov and Elkhatib Kamal

Institut Pascal/IMobS3, UCA/SIGMA - UMR CNRS 6602, Clermont-Ferrand, France

Keywords:

Heavy Hybrid Vehicle, Energy Management Strategy, Optimal Control, Pontryagin’s Minimum Principle.

Abstract:

In this paper, an energy management strategy (EMS) for a speciﬁc multi hybrid plug-in electric bus is designed.

This bus is equipped with an internal combustion engine, a hydraulic motor, an electric motor and battery.

Considering the physical characteristics of the studied hybrid electric bus (i.e., the system dynamics and the

power sources limits), an optimal control technique based on Pontryagin’s minimum principle (PMP) is used in

order to ensure that the bus achieve a signiﬁcant improvement in energy efﬁciency. Furthermore, information

of trafﬁc conditions obtained from intelligent transportation systems is used to further optimize the energy

management strategy and to accurately control the battery depleting rate. The work proposed in this paper is

conducted on a dedicated high-ﬁdelity model of the hybrid bus, that was developed on MATLAB/TruckMaker

software. The obtained results verify the effectiveness and validity of the developed energy management

strategy.

1 INTRODUCTION

A hybrid vehicle uses, by deﬁnition, at least two en-

ergy sources associated with the mechanical transmis-

sion to ensure its propulsion. The advantage of the

hybridization of vehicles is to overcome the two main

drawbacks of internal combustion engines that are the

low energy efﬁciency and the power irreversibility

which makes the engine unable to retrieve the energy

incurred during braking. Hybridization will therefore

draw on the strengths of different types of engines

by combining the excellent efﬁciency and reversibil-

ity of electric motors with the high energy density

of fossil fuels which increases the energetic auton-

omy, limits the vehicle weight and reduces refueling

time. The presence of additional power sources in the

HEV introduces additional degrees of freedom in con-

trolling the drivetrain, since at each time the driver’s

power request can be delivered by either one of the

on-board energy sources or their combination. The

additional degrees of freedom can be leveraged to re-

duce fuel consumption and pollutant emissions and

also to optimize other possible cost such as battery

life (Tang et al., 2015). This task is performed by

the energy management strategy which is the high-

est control layer of the drivetrain’s control strategy.

In commercially available HEV, the energy manage-

ment has been traditionally performed using heuristic

controllers in which rules are designed to manage the

on-board energy of the vehicle (Mashadi and Emadi,

2010) (Kamal et al., 2017). Such control strategies

are effective in real-time implementation but they re-

quire a careful calibration of the parameters (Mi et al.,

2011). A signiﬁcant improvement with respect to

such strategies is achieved with model based opti-

mal control methods. These methods can be divided

into numerical and analytical approaches. In numeri-

cal optimization methods like dynamic programming

(Ximing et al., 2015), the global optimum is found

numerically under the assumption of full knowledge

of the future driving conditions. Unfortunately,the re-

sults obtained through dynamic programming cannot

be implemented directly due to its high computational

demands. To remedy this problem, approximated dy-

namic programming (Johannesson et al., 2007) and

stochastic dynamic programming (Moura et al., 2011)

(Johannesson et al., 2007) had been suggested as pos-

sible solutions. Analytical optimization methods, on

the other hand, use a mathematical problem formula-

tion to ﬁnd an analytical solution that makes the ob-

tained solution faster than the purely numerical meth-

ods. Within this category, Pontryagin’s minimum

principle based energy management strategy is in-

troduced as an optimal control solution (Teng et al.,

2014). This approach can only generate an optimal

solution if implemented ofﬂine since in this case the

304

Ouddah, N., Adouane, L., Abdrakhmanov, R. and Kamal, E.

Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions.

DOI: 10.5220/0006436803040311

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 304-311

ISBN: 978-989-758-263-9

driving cycle is supposed to be known in advance. For

online implementation Equivalent Fuel Consumption

Minimization (ECMS) methods that lead to subopti-

mal solutions have been proposed for HEVs (Volkan

et al., 2011). ECMS is based on instantaneous op-

timization, and is simple enough to be implemented

in real-time applications. Model predictive control

based methods have been also applied to solve on-

line the energy management problem (Fengjun et al.,

2012). One of the main drawbacks of this approach

is the high computational power required to calcu-

late the optimal power split at each sampling interval.

This paper details the development of energy manage-

ment strategies to optimize the power distribution in

a plug-in hybrid bus actuated by three distinct types

of power (internal combustion engine, electric motor

and hydraulic motor). Among the energy manage-

ment strategies discussed above, Pontryagin’s mini-

mum principle based optimization turns out to be the

most appropriate approach to design an energy man-

agement strategy for the considered hybrid bus since

it can guarantee, under given conditions, near opti-

mality while keeping the methodology simple. Thus,

an adaptation of this optimization approach to a plug-

in multi hybrid bus is proposed in this work and the

obtained optimization algorithm is implemented in an

overall optimization scheme in order to achieve the

most efﬁcient way of bus operation. The key contribu-

tions are ﬁrstly in formulating the optimization prob-

lem so as all the sources of power of the studied hy-

brid bus are considered by the optimization algorithm.

Secondly, the general concepts initially presented in

literature are improvedby taking into account the mo-

tors dynamic limits. And ﬁnally, an overall optimiza-

tion scheme based on the use of predicted optimal ve-

locity trajectory of the bus is proposed. In fact, since

the route of the bus, roads levels variations and even

trafﬁc lights are well known, prediction of optimal

velocity trajectory for the trip can be carried out by

means of information obtained from intelligent trans-

portation systems (Wu et al., 2014). This available

knowledge of the future driving cycle is exploited, in

this latter contribution, to make the bus more efﬁcient

(even in the presence of exogenous and unpredictable

events such as the trafﬁc jam) and to ensure the de-

sired battery depleting level. The paper is structured

as follows: section 2 describes the studied hybrid bus

architecture and model. Section 3 introduces the pro-

posed energy management strategy. In section 4, sev-

eral simulations results are presented showing the ef-

ﬁciency of the proposed energy management strategy.

Finally, conclusions and some prospects are given in

the last section.

2 MODELING OF THE HYBRID

BUS

The aim of this section is to illustrate the architecture

and the mathematical model of the studied system,

i.e., BUSINOVA hybrid bus, developed by SAFRA

(cf. Figure 1)

. This bus is composed of an electric

motor, a hydraulic motor, an internal combustion en-

gine and battery as the propulsion drivetrain system

of the vehicle. The electric motor is a 103 kW perma-

nent magnet electrical machine from Visedo

devel-

oped especially for heavy duty applications. It has six

polepairs and its nominal voltage is 500 V (VISEDO,

2014). The internal combustion engine is produced

by VM Motori

. It delivers a maximum torque of

340 N.m at 1400 rpm and its maximum produced

power is 70 kW (VMMotori, 2015). The hydraulic

motor is a Parker

V14 series with a displacement

that varies between 22 and 110 cm

(Parker, 2014).

Figure 1: BUSINOVA hybrid bus.

2.1 Hybrid Bus Drivetrain Architecture

The model of the studied hybrid bus is based on a

series-parallel power-split hybrid architecture. A sim-

ple block diagram of the power ﬂows on the bus is

shown in Figure 2.

Figure 2: Block diagram of the drivetrain power ﬂows.

(ICE: internal combustion engine, HP: hydraulic pomp,

HM: Hydraulic motor, EM: electric motor).

The electric and hydraulic motors are both directly

connected to the transmission and can ensure simul-

taneously or independently the traction of the bus. On

http://www.businova.com

Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions

305

the other hand, the internal combustion engine is cou-

pled to a hydraulic pump for drivingthe hydraulic mo-

tor and therefore allowing the engine load shifting.

The rotational speeds of the hydraulic motor and the

electric motor are imposed by the wheels speed in

proportion to the reduction ratios of hydraulic and

electric motors respectively.

Moreover, the rotational speed ω

and the torque

of the hydraulic motor are expressed as a func-

tion of the rotational speed and the torque of the in-

ternal combustion engine as follows.











ICE

) =

.η

.ω

ICE

.η

(1a)

ICE

) =

.η

ICE

.η

(1b)

where ω

ICE

, T

ICE

are respectively rotational speed

and torque of the engine, and D

, D

, η

are respectively the displacements, me-

chanical efﬁciency and volumetric efﬁciency of the

hydraulic motor (HM) and the hydraulic pump (HP).

2.2 Control Oriented Model

The amount of residual energy of the battery, com-

monly represented by the estimation of the battery

state of charge SOC (Tang et al., 2015) or the bat-

tery state of energy SOE (Mura et al., 2015) is the

main dynamic state in optimal control of HEVs. In

particular, the state equation connects the variation

of the battery’s remaining energy to the control vari-

able of the system. In the formulation of the energy

management problem of the hybrid bus studied in this

paper, the SOE instead of the SOC, is considered as

the dynamic state x(t). There are several advantages

of using the estimated SOE to represent the battery

residual energy. Indeed, the energy loss on the inter-

nal resistance, the electrochemical reactions and the

decrease of the battery voltage are considered in the

SOE estimation (Xingtao et al., 2014). Based on the

previous assumption of using estimated SOE to rep-

resent the battery residual energy, the control oriented

model can be represented by:

˙x(t) = f (x(t), u(t), w(t)) (2)

where

x(t) = SOE(t), u(t) =





, w(t) =



wheel



(3)

u(t) is the control input and w(t) is an exogenous in-

put.

The above model can be rewritten as follows.

˙x(t) =

d SOE (t)

= −

BAT

max

= −

ηE

max

(4)

Depending on whether the battery is in discharg-

ing phase (

SOE ≤ 0) or in charging phase (

SOE ≥ 0),

η is deﬁned as follows (Tremblay et al., 2007):

η =



BAT

in discharging phase

1/η

BAT

in charging phase

(5)

Equation (4) is obtained from the battery internal re-

sistance model (Tremblay et al., 2007). In this equa-

tion, E

max

is the maximum energy that can be stored

in the battery, η

BAT

is the efﬁciency of the battery,

BAT

is the power delivred by the battery and P

the power consumed by the electric motor to produce

torque T

at speed ω

3 ENERGY MANAGEMENT

STRATEGY

The following section details the design procedure

of the proposed energy management strategy, which

aims to decide how to split the driver’s demanded

power between the different power sources of the hy-

brid drivetrain. This should allow to optimize the se-

lected criterion without sacriﬁcing the bus drivabil-

ity. The optimal control problem formulation is ﬁrstly

presented and then the analytical expression of the

proposed solution is described. These power man-

agement strategy is based on Pontryagin’s minimum

principle.

3.1 Optimal Control Problem

Formulation

Since our primary goal is to minimize the energy con-

sumption of the bus, the energy management prob-

lem is formulated as an optimal control problem.

The objective is to ﬁnd, at each sample time, the

optimal value of the control input that minimizes a

cost function representing the power consumption of

the drivetrain. This minimization of the cost func-

tion must be done under a certain number of con-

straints. In fact, the drivetrain components dimen-

sioning imposes minimum and maximum limits on

the exchanged powers. These limits form the follow-

ing constraints:

• The internal combustion engine and electric mo-

tor have limited operating ranges. Therefore, pro-

vided or absorbed torques must be comprised be-

tween minimum and maximum limits.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

306

min

≤ T

(t) ≤ T

max

(6)

min



min

ICE



≤ T

max

ICE

)

(7)

The maximum and minimum torque limits of

the internal combustion engine and electric motor

vary according to the variation of the system’s op-

erating point (torque-speed). Look-up tables are

therefore used to determine their values at each

time.

• The instantaneous power demand of the drivetrain

should always be satisﬁed, which results in,

ICE

) + ρ

(t) − T

wheel

(t) = 0

(8)

where ρ

and ρ

are the gearbox’ reduction ratios

of hydraulic and electric motors respectively. The

total torque at the wheels is equal to the sum of

the torques delivered by each of the motors pro-

portionally to the reduction ratios.

Compared with energy management problem for-

mulation for charge sustaining HEV (Mura et al.,

2015), there is no sustainability constraint on the ﬁ-

nal SOE for plug-in HEV allowing the charge de-

pleting operation. Thus, the energy consumed on the

entire cycle does not come exclusively from the fuel

since most of the available electrical energy is sup-

plied from the grid. This implies that the cost func-

tion must take into account all the energy sources used

to ensure the traction of the bus. This is why the

cost function J to be minimized over the time inter-

val [t

, t

] is deﬁned based on the total electric and

fuel energy consumed by the vehicle as follows.

t f

(u(t)) + P

BAT

(u(t))dt (9)

where P

is the instantaneous power of the fuel (en-

gine power input). As in several other papers dealing

with this topic (Mura et al., 2015), it is expressed in

terms of the fuel ﬂow rate ˙m

and the lower heating

value of the fuel (Q

LHV

= 43MJ/kg) using the formu-

lation given in equation (10).

( u(t)) = ˙m

(u(t)) Q

LHV

(10)

The control variables (T

and ω

) are linked

together trough the hydraulic motor dynamics, there-

fore, there can only be one target control value at a

time. In this paper, we have chosen to leave the rota-

tion speed free so that it will be imposed by the wheels

speed. The hydraulic motor torque is thus the only re-

maining control variable that can be used to decide

how to split the driver’s demanded power.

The optimization problem is then to ﬁnd the hy-

draulic torque that should be provided at every sample

time in order to minimize the total energy consumed

while checking the constraints thus mentioned above

(cf. equations (6) to (8)). To these constraints it is

added a new constraint (11) which aims to limit the

admissible control region in order to take into account

the limits of the hydraulic motor dynamics and conse-

quently taking into account the limits of the internal

combustion engine dynamics.

− ξ ≥ 0 (11)

with ξ is the maximum hydraulic torque variation

measured over a short period of time.

To introduce constraints in the optimization prob-

lem, these are transformed into equality constraints.

The constraint (11) can be rewritten as follows (Wang

and Wah, 1998).

− ξ−

= 0 (12)

where ε is a slack variable.

By using equation (8), it is possible to rewrite the

constraints (6) and (7) as a single constraint on the

control variable as follows.

min



min

max



≤ T

≤

max



max

min



(13)

with

min

= max(ρ

min

wheel

− ρ

max

) (14)

max

= max(ρ

max

wheel

− ρ

min

) (15)

It means that when the torque applied to the wheel

is too signiﬁcant to be only produced by the electric

motor, the

min

limit imposes a minimum torque on

the hydraulic motor. Additionally,

max

limit prevents

the electric motor torque set-point to become less than

min

Finally, using a 2

order approximation, the con-

straint (13) is written as the equivalent form given by

(16),

−T

+ αT

+ β = 0 (16)

with

α=

max

−

min

(17)

β=

max

min

(18)

Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions

307

3.2 Energy Management Algorithm

With the optimization problem fully deﬁned, Pontrya-

gin’s minimum principle can be used to give numer-

ical solution. According to Pontryagin’s minimum

principle, minimizing the cost function given in (9)

is equivalent to minimizing the Hamiltonian function

H of the system at each instant of time.

H (x(t), u(t), λ(t)) = P



(t),

(t)



−



λ(t)

ηE

max

− 1





(t),

(t)



(19)

where λ(t) is the costate (or the Langrange multi-

plier).

For the considered energy management problem,

an extended Hamiltonian function is deﬁned to ac-

count for the constraint (12) and (16). The additional

terms are introduced using a new Lagrange multiply-

ers (i.e., γ(t) et σ(t) respectively).

H (x(t), u(t), λ(t), γ(t) , σ(t)) =



(t),

(t)



−



λ(t)

ηE

max

− 1





(t),

(t)



+γ(t)



−T

+ αT



+β) + σ(t)



− ξ



(20)

The optimal control law which minimize the

Hamiltonian H must satisfy the following necessary

conditions for optimality:

∂H(t)

∂u(t)

∂H(t)

∂T

(t)

= 0 (21)

−

∂H(t)

∂x(t)

= −

∂H(t)

∂SOE(t)

∗

(t) (22)

∂H (t)

∂λ(t)

= ˙x

∗

(t) (23)

∂H(t)

∂γ(t)

= −T

+ αT

+ β = 0 (24)

∂H(t)

∂σ(t)



− ξ



ε (25)

The costate λ is determined by the condition (23).

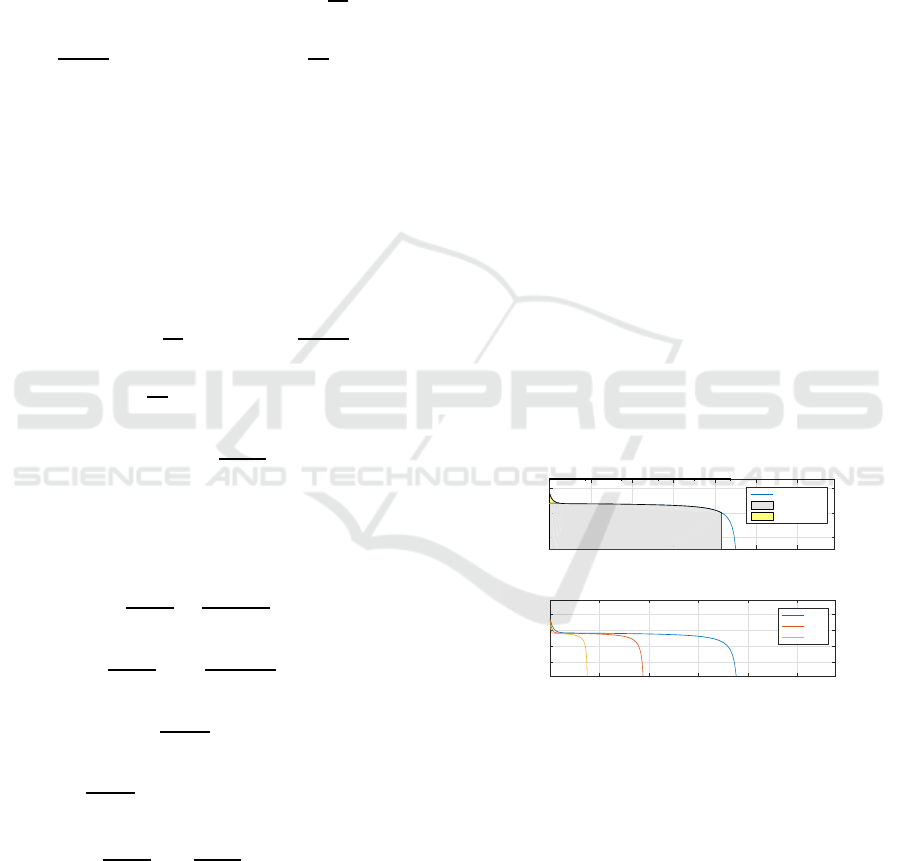
While taking into account the battery discharge

characteristics shown in Figure 4, it is clear that bat-

tery voltage is relatively independent on the battery

state of energy SOE and thus the power consumed by

the electric motor P

(t) is also independent on the

battery SOE (Kirk, 2012) (Lino and Sciarretta, 2007).

Under this assumption, it is straightforward to con-

sider that the costate λ is a constant value during the

entire driving cycle since the derivative of the Hamil-

tonian function H in (23) is null in this case.

The condition (21) determines the optimal control

trajectory T

∗

(t). If this necessary condition is sat-

isﬁed, then the optimal hydraulic torque T

∗

(t) must

be given by equation (26).

∗

(t) = arg min

∈U

H(SOE (t),T

(t),λ(t))

(26)

where U is deﬁned as the admissible control set.

After the hydraulic motor torque is obtained, the in-

ternal combustion engine torque and speed are calcu-

lated according to the desired speed and torque of the

hydraulic motor. Thanks to the displacement tuning

capability of the hydraulic motor, the internal com-

bustion engine load can be shifted freely to operate

this latter close to its maximum efﬁciency curve. Es-

pecially in this case, the speed of the internal combus-

tion engine is not imposed by the wheels speed and it

can be set to a nearly constant value where the engine

is the most efﬁcient. To reach this goal, the displace-

ment of the hydraulic motor is controlled online by

using equation (1a). Thereafter, the engine torque is

calculated as a function of the displacement and the

optimal torque of the hydraulic motor by using equa-

tion (1b).

Time (hours)

0 0.5 1 1.5 2 2.5 3

Voltage (Volts)

400

500

600

Nominal Current Discharge Characteristic at 108.6957 Amperes

Discharge curve

Nominal area

Exponential area

Time (hours)

0 10 20 30 40 50

Voltage (Volts)

450

500

550

600

Fully Charged Voltage: E0 = 581.6883 Volts, Internal Resistance: R = 0.02 Ohms

6.5 A

13 A

32.5 A

SOE

020406080100

Figure 3: Discharge characteristics of the used battery.

The energy management strategy could have

greater potential for power savings if an optimal speed

proﬁle is predicted for each trip of the bus based on

the actual driving conditions. Indeed, buses run on the

same route every day, stop invariably at similar loca-

tions and they could even have some dedicated lanes

of the road in some cities which facilitates driving

conditions prediction compared to other type of vehi-

cles. Therefore, several studies have been conducted

to optimize bus speed proﬁles (Dib et al., 2014). With

this approach in mind and to further improve the en-

ergy management strategy proposed in this paper, a

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

308

control scheme that uses the information on the op-

timal speed proﬁle is proposed in order to conﬁgure

the energy management algorithm developed previ-

ously. Therefore, the optimal speed proﬁle is ﬁrst de-

termined by using a dedicated speed proﬁle optimiza-

tion algorithm based on a predictive intelligent con-

trol (Gunter et al., 2016). Thereafter, at the beginning

of each new trip of the bus, the obtained optimal speed

proﬁle is utilized to search iteratively, using a shoot-

ing search method (Serrao et al., 2011), the value of

the costate λ that generates the correct ﬁnal SOE

the end of the daily duty time of the bus. In fact, for

a given driving cycle there exists only one value of

the costate for which the solution that minimizes the

Hamiltonian H at each sample time is also the one that

satisﬁes the terminal condition on the ﬁnal value of

SOE. This corresponds to the global optimal solution

of the problem. The obtained overall energy manage-

ment scheme is illustrated in Figure 4. As stated be-

fore, the choice of the costate value must be made to

ensure, in each trip of the bus, a charge-depleting rate

which allows to reach desired ﬁnal SOE

at the end

of a full day driving period. In this paper, it is con-

sidered that the initial value of SOE is 90% and the

desired ﬁnal value of SOE after eight hours of driving

is 17%. The working hypothesis behind this assump-

tion is to use the maximum amount of energy that can

be consumed from the battery in one day driving.

Figure 4: Block diagram of the proposed power manage-

ment strategy.

4 SIMULATION RESULTS

The implementation of the proposed energy manage-

ment strategy is carried out using a dedicated high-

ﬁdelity model of the hybrid bus, that was developed

on Matlab/TruckMaker software (cf. Figure 5), in or-

der to investigate their performance in a test platform

which reproducesaccurately the real operating behav-

ior of the bus.

Figure 5: TruckMaker test platform.

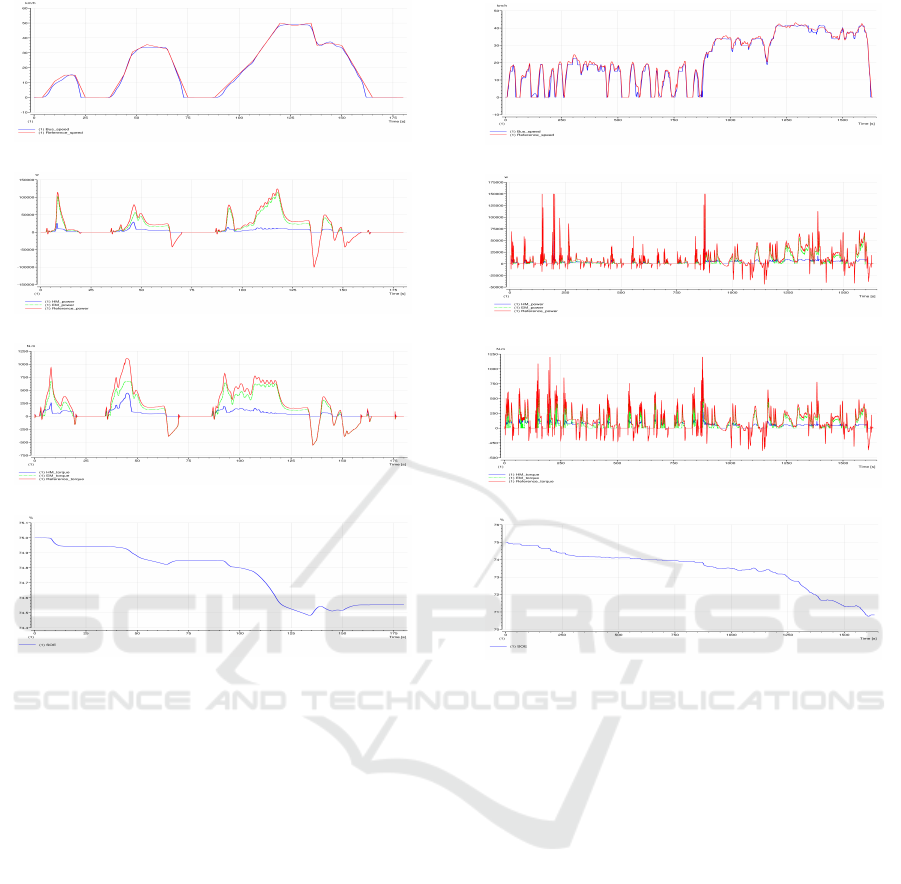
Figure 6 shows the overall simulation results

of the proposed energy management strategy over

an optimized driving cycle which represents differ-

ent usage conditions of the studied hybrid electric

bus including urban and extraurban driving environ-

ments. The video showing this overall demonstra-

tion using TruckMaker is available from this link:

https://goo.gl/8mJT3s.

Figure 6(a) gives an outline of the desired speed

and the actual bus speed when the designed opti-

mization algorithm is applied to calculate the optimal

power split. As one can observe in this ﬁgure, the bus

speed follows the reference speed curve with only a

small tracking error. This observed speed tracking er-

ror is due to the important response time of the mo-

tors. The contribution of the fuel energy and the elec-

tric energy to the total power and torque at the wheels

is illustrated in Figure 6(b) and 6(c) respectively. The

SOE proﬁle is also illustrated in Figure 6(d). Accord-

ing to Figure 6 (b), it is shown that the distribution of

the power demand between the electric motor and the

hydraulic motor is correctly assured and the required

power at the wheels is totally satisﬁed over the entire

driving cycle. The dynamic limits of the motors de-

ﬁned during the synthesis of the energy management

strategy are also respected as can be seen in these ﬁg-

ures. Since the driving cycle is known in prior, the

proposed energy management strategy ﬁnds the op-

timal power split which operates the engine around

its maximum efﬁciency curve to minimize the power

consumption of the drivetrain. The ﬂuctuation range

of the power delivered by the engine is directly related

to the amount of electric energy available for electric

assist and it allows to always satisfy the constraints of

the ﬁnal SOE of the battery. A battery discharge of

0.45% is observed at the end of the driving cycle sim-

Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions

309

(a)

(b)

(c)

(d)

Figure 6: Simulation results of the proposed energy man-

agement strategy: (a) driving cycle, (b) power distribution

proﬁle, (c) torque distribution proﬁle, (d) SOE proﬁle.

ulated in this test, which corresponds, by extrapola-

tion, to a discharge from 90% to 17% after 8 hours

driving period. Otherwise, the energy management

strategy doesn’t use the engine to charge the battery,

because its efﬁciency is too low and thus recharg-

ing the battery using fuel energy is not cost-effective.

deepen the analysis under more realistic and ex-

haustivetest conditions, the proposed energy manage-

ment algorithm is evaluated over the FTP-75 (Federal

Test Procedure) normalized driving cycle. This cy-

cle includes acceleration and deceleration phases in

urban and suburban environments. It thus constitutes

an interesting study support for evaluating the perfor-

mance of the energy management strategy in the dif-

ferent phases of operation of the real hybrid bus. The

results obtained from this test are presented in Figure

(a)

(b)

(c)

(d)

Figure 7: Simulation results of the energy management al-

gorithm on the FTP-75 driving cycle: (a) driving cycle, (b)

power distribution proﬁle, (c) torque distribution proﬁle, (d)

SOE proﬁle.

5 CONCLUSION

An optimal energy management strategy, based on

Pontryagin’s minimum principle, is designed in this

paper for a a plug-in multi hybrid bus. The proposed

approach combines the system’s dynamical equations

with the control objectives formulated in the form

of a cost function and constraints to determine at

each instant the optimal value of the control variable

which minimizes the power consumption of the hy-

brid bus. Furthermore, based on the characteristics

of the studied urban bus, which runs generally on the

same routes, the energy management strategy is fur-

ther improved by searching the optimal driving cycle

for each bus trip while using the available trafﬁc infor-

mation. The ﬁnal battery SOE level is also controlled

by selecting an appropriate value of the costate at each

time the bus starts a new lap. The validation tests re-

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

310

sults show that the proposed optimization approach

can ensure optimal operation for the hybrid bus while

having the advantage of being very simple to imple-

ment in practice thanks to its high computational ef-

ﬁciency. Nonetheless, to achieve this performance

level, good accuracy for estimating road trafﬁc con-

ditions is required. In future works, additional opti-

mization criterion such as: reduction of battery aging

and pollutant emissions will be added to the already

existing optimal control algorithm. The tradeoff be-

tween the different optimization criteria will be inves-

tigated in order to achieve the most efﬁcient drivetrain

operation.

ACKNOWLEDGEMENTS

This project is supported by the ADEME (Agence

De l’Environnement et de la Matrise de l’Energie) for

the national french program: Investissement d’Avenir,

through BUSINOVA Evolution project.

REFERENCES

Dib, W., Chasse, A., and Moulin, P. (2014). Optimal energy

management for an electric vehicle in eco-driving ap-

plications. In Control Engineering Practice, vol. 29.

IEEE.

Fengjun, Y., Junmin, W., and Kaisheng, H. (2012). Hybrid

electric vehicle model predictive control torque-split

strategy incorporating engine transient characteristics.

In Transactions on Vehicular Technology. IEEE.

Gunter, H., Marcus, S., Uli, W., and Oliver, S. (2016).

Predictive planning of optimal velocity and state of

charge trajectories for hybrid electric vehicles. In

Journal of Control Engineering Practice. Elsevier.

Johannesson, L., Asbogard, M., and Egardt, B. (2007). As-

sessing the potential of predictive control for hybrid

vehicle powertrains using stochastic dynamic pro-

gramming. In Transactions ITSC, vol. 8, no. 1. IEEE.

Kamal, E., Adouane, L., Abdrakhamanov, R., and Ouddah,

N. (2017). Hierarchical and adaptive neuro-fuzzy con-

trol for intelligent energy management in hybrid elec-

tric vehicles. In IFAC World Congress. Elsevier.

Kirk, D. (2012). Optimal Control Theory: An Introduction.

Dover, NY, USA, 2nd edition.

Lino, G. and Sciarretta, A. (2007). Vehicle propulsion sys-

tems. Springer-Verlag Berlin Heidelberg, Berlin, vol.

1 edition.

Mashadi, B. and Emadi, S. (2010). Dual-mode power-split

transmission for hybrid electric vehicles. In Transac-

tions on Vehicular Technology. IEEE.

Mi, C., Masrur, A., and Gao, D. W. (2011). Plug-in hybrid

electric vehicles, in Hybrid Electric Vehicles: Prin-

ciples and Applications With Practical Perspectives.

Wiley, NY, USA, 2nd edition.

Moura, S. J., H. Fathy, D. C., and Stein., J. (2011). A

stochastic optimal control approach for power man-

agement in plug-in hybrid electric vehicles. In Trans-

actions on Control Systems Technology, vol. 19, no. 3.

IEEE.

Mura, R., Utkin, V., and Onori, S. (2015). Energy man-

agement design in hybrid electric vehicles: A novel

optimality and stability framework. In Transactions

On Control Systems Technology, Volume: 23, Issue:

4. IEEE.

Parker (2014). Parker hy30-8223/uk catalogue. In :

https://goo.gl/bExyDj.

Serrao, L., Onori, S., and Rizzoni, G. (2011). A compara-

tive analysis of energy management strategies for hy-

brid electric vehicles. In Journal of Dynamic Systems,

Measurement, and Control, vol. 133, no 3. IEEE.

Tang, L., Rizzoni, G., and Onori, S. (2015). Energy man-

agement strategy for hevs including battery life opti-

mization. In Transactions on Transportation Electri-

ﬁcation.

Teng, L., Yuan, Z., De-xing, L., and Feng-chun, S. (2014).

Real-time control for a parallel hybrid electric vehicle

based on pontryagin’s minimum principle. In Confer-

ence and Expo in Transportation Electriﬁcation Asia-

Paciﬁc.

Tremblay, O., Dessaint., L., and Dekkiche, A. (2007). A

generic battery model for the dynamic simulation of

hybrid electric vehicles. In Vehicle Power and Propul-

sion Conference. IEEE.

VISEDO (2014). Visedo powerdrum pdr-xxs-3200-t310

technical features. In : https://goo.gl/Bg1q4q.

VMMotori (2015). Vm motori vm-r754eu5-05d/4 technical

features. In : https://goo.gl/7oLVD3.

Volkan, S., Metin, G., and Seta, B. (2011). A novel ecms

and combined cost map approach for high-efﬁciency

series hybrid electric vehicles. In Transactions on Ve-

hicular Technology, vol. 60, no 8. IEEE.

Wang, T. and Wah, B. (1998). Handling inequality con-

straints in continuous nonlinear global optimization.

In Journal of Integrated Design and Process Science,

vol. 2, no 3. iospress.

Wu, G., Boriboonsomsin, K., and Barth, M. (2014). De-

velopment and evaluation of an intelligent energy-

management strategy for plug-in hybrid electric ve-

hicles. In Transactions on Intelligent Transportation

Systems, vol. 15, no 3. IEEE.

Ximing, W., Hongwen, H., Fengchun, S., and Zhang, J.

(2015). Application study on the dynamic program-

ming algorithm for energy management of plug-in hy-

brid electric vehicles. In vol. 8, no 4. Energies.

Xingtao, L., W. Ji, Z. C., and Zonghai, C. (2014). A method

for state of energy estimation of lithium-ion batteries

at dynamic currents and temperatures. In Journal of

Power Sources, vol. 270. Elsevier.

Optimal Energy Management Strategy of Plug-in Hybrid Electric Bus in Urban Conditions

311