Using Inverse Compensation Vectors for Autonomous Maze

Exploration

Andrzej A. J. Bieszczad

Computer Science Program, California State University Channel Islands, One University Drive, Camarillo, U.S.A.

Keywords: Mobile Robotics, Obstacle Avoidance, Maze Running, Movement Correction.

Abstract: Autonomous exploration of mazes requires finding a “center of gravity” keeping the robot safe from colliding

with the walls. That is similar to the obstacle avoidance problem as the maze walls are obstacles that the robot

must avoid. In this report, we describe an approach to controlling robot movements in a maze using an Inverse

Compensation Vector (ICV) that is not much more computationally demanding than calculating a centroid

point. The ICV is used to correct the robot velocity vector that determines the direction and the speed, so the

robot moves in the maze staying securely within the passages between the walls. We have tested the approach

using a simulator of a physical robot equipped with a planar LIDAR scanner. Our experiments showed that

using the ICV to compensate robot velocity is an effective motion-correction method. Furthermore, we

augmented the algorithm with preprocessing steps that alleviate problems caused by noisy raw data coming

from actual LIDAR scans of a physical maze.

1 INTRODUCTION

The ciNeuroBot (Figure 1) has been designed to

simulate and explore goal-oriented behaviors

exhibited by rats running in mazes (Bieszczad, 2006).

The robot’s name is derived from the Neurosolver, a

neuromorphic high-level planner based on the

organization of columns in the brain cortex

(Bieszczad, 1998).

The ciNeuroBot is based on the DiddyBorg

platform integrated with a 360-degree LIDAR planar

scanner placed at the top. The robot has six wheels

groups: left and right. The hardware controller

utilizes RaspberryPI single-board-computer running

Raspbian version of Linux. There is also a high-

resolution video camera in front of the robot, but it is

not used for navigation. The code is written in Python

3 taking advantage of generous supply of modules

and a relatively high computational power of the

platform.

Figure 1: ciNeuroBot and ciNeuroBot in a reconfigurable maze.

Bieszczad, A.

Using Inverse Compensation Vectors for Autonomous Maze Exploration.

DOI: 10.5220/0006437203970404

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 397-404

ISBN: Not Available

397

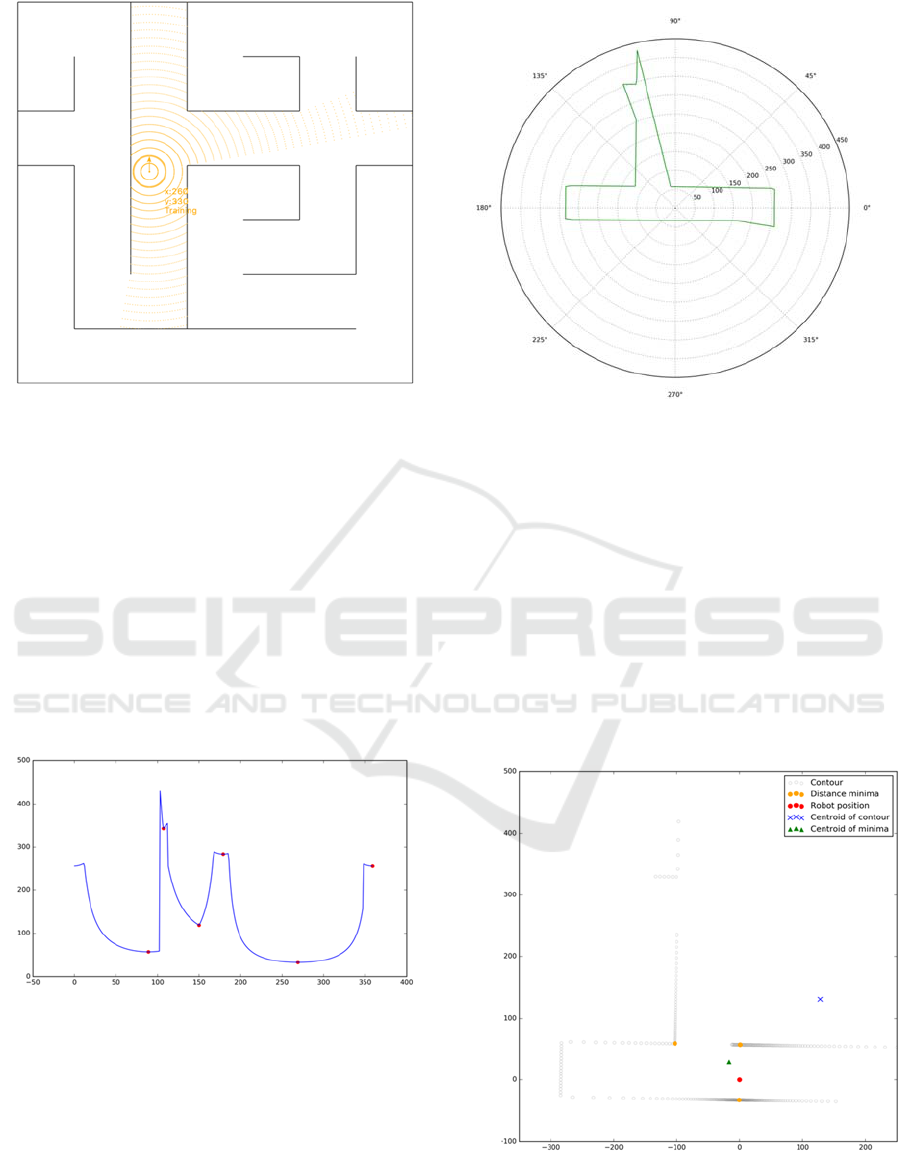
Figure 2: ciNeuroBot simulator with a LIDAR simulated

scan of the right t-section cue.

The ultimate high-level task of the robot is to

explore mazes like the one shown in Figure 1

searching for goals; for example, certain colors or

shapes on the walls (the video camera is used for that

purpose). Furthermore, the robot is to construct a map

of the maze and record the location of the goals, so in

the future it can construct a plan recalling – and

potentially optimizing – the paths to a specific goal.

The construction of the map is founded on the ability

to identify environmental cues; in the case of a maze,

the cues are perceived shapes such as cross-section, t-

section, right turn, left turn, etc.

Figure 3: LIDAR scan of the right t-section cue. The scan

readings (on the vertical axis) are shown as a function of an

angle from which the measurement was made. There are

360 measurements for a full rotation of the scanner. Also,

the minima on the curve are shown as red dots (the

rightmost minimum is there due to a cyclic wrap of the

curve). The scan starts from the back of the robot and

proceeds counter clockwise.

To realize the high-level objectives, the robot

needs low-level capabilities to autonomously explore

the maze staying clear of walls.

Figure 4: LIDAR scan readings of right t-section cue shown

in polar coordinates. The orientation is different than in

Figure 2 due to the 90-degree rotation. The robot is always

in the center of any coordinate system; in this case, polar.

We developed a simulator of the robot running

mazes (Figure 2) to ease – and in some cases, make

feasible – the experimentation and development. The

simulator is tightly correlated with the physical robot,

so the ideas implemented and tested in the simulator

can be used to create prototypes to be transferred to

the physical robot. As we found out however, the

physical world poses challenges that need attention

during the porting such as imperfections in the

accuracy of scanner readings.

Figure 5: Maze contour constructed from the LIDAR

readings of right t-section cue. The red dot demarcates the

position of the robot. The dot is also in the center of the

Cartesian coordinate system.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

398

The onboard LIDAR scanner is used for both the

high- and the low-level functionality. At the high-

level, the mapping and localization components need

cues that can be identified using the LIDAR readings

(Figure 3) (Bieszczad, 2015 and the ongoing research

on improving that capability).

The LIDAR readings (that are simply the

distances from the objects in the robot surroundings;

i.e., walls in a maze in this case) can also be used to

keep the robot away from the walls. The robot moves

are controlled by a velocity vector generated in

response to some mobility drive that may be coming

from a manual robot controller (e.g., our Android or

iOS apps), or from a higher-level planner like the

Neurosolver. To keep the robot away from the walls,

the velocity vector must be modified by analyzing the

LIDAR readings. The periodic compensation allows

the robot to stay within the walls while moving along

the modified velocity vector.

2 OBSTACLE AVOIDANCE

PROBLEM

The problem of avoiding obstacles is one of the most

critical in Robotics. A very good survey of the

approaches, especially techniques based on

commonly used potential fields is presented in

(Rajvanshi et al., 2015). The methods based on

potential fields (originally proposed in (Khatib,

1986)) assume presence of a target destination that

acts as an attractor force for the robot, while any

surrounding obstacles act as repellent forces. The

problem of exploring a maze is somewhat different,

as the obstacles are the enclosing walls, and there is

no global target. Rather than being repelled to some

open space by the obstacles, robot’s objective is to

stay within the maze walls in a position equidistant

from any wall while still maintaining the movement.

The overall problem can be summarized as a task

of moving as far as possible from each of the

obstacles at every step in the movement. While

conceptually the task is simple, it is an optimization

problem, and as such, it is computationally

demanding. The problem is especially challenging for

robots that have limited processing power and limited

information about the environment; for example, if

the robot – like ciNeuroBot – is equipped with just a

simple one-dimensional scanner (also referred to as

planar or 2D scanner). Simple methods – like

computing a centroid of certain “important” set of

points on the obstacles – fail in complex scenarios.

For example, if the robot is close to several obstacles

that are also close to each other, it will tend to move

towards the obstacles if the centroid is used as a

guidance. In a maze, quite often the centroid is

completely inaccessible; as exemplified by the point

marked with blue cross in Figure 5. A centroid of the

closest points – shown as a green triangle in the same

figure – might be better, but still fails in numerous

scenarios. Our experiments with computing a

centroid of the convex hull spanned by the closest

points from the robot to the walls also led to only

marginal improvements.

It appears that there is no known closed form

solution to the problem. While iterative solutions do

exist, they are computationally expensive (Eppstein,

Erickson, 1999). Most of the solutions that have been

proposed approximate the “center of view” (the point

as distant from each of the obstacles as possible;

sometimes also called the “center of gravity”) by

iteratively decomposing the map using triangles

(Shewchuk, 2008), or quad-trees (Agafonkin, 2016;

based on Finkel, 1974). The medial axis transform

(MTA) has also been used (Joan-Arinyo et al., 1997

based on Lee, 1982). Like the potential fields

methods, the MTA is used usually in context of path

planning; some researchers advocate separation of

path planning from the obstacle avoidance problem

and treating them as two distinct issues. Point

sampling was also attempted to approximate the

location that is optimally furthest from all obstacles

(Garcia-Castellanos, Lombardo, 2007).

An obstacle avoidance strategy based on direction

correction based on the distances from obstacles (that

could be viewed as a density of obstacles) was

reported in (Peng et al., 2015) as part of path planning

research.

3 INVERSE COMPENSATION

VECTOR (ICV)

We propose a simple and efficient way to compensate

the robot movement by computing a correction vector

that we call the Inverse Compensation Vector, or

ICV. As stated earlier, the direction and the speed of

a moving robot can be expressed as a velocity vector

(or force). It is the velocity vector that is affected by

applying the Inverse Compensation Vector to correct

the movement with the intention of staying away

from the walls. Ultimately, that motion compensation

operation implements a simple collision avoidance

algorithm.

In the following sections, we focus on the

construction of the ICV; the velocity vector is not

Using Inverse Compensation Vectors for Autonomous Maze Exploration

399

included in the figures as it may be arbitrarily

imposed at any time.

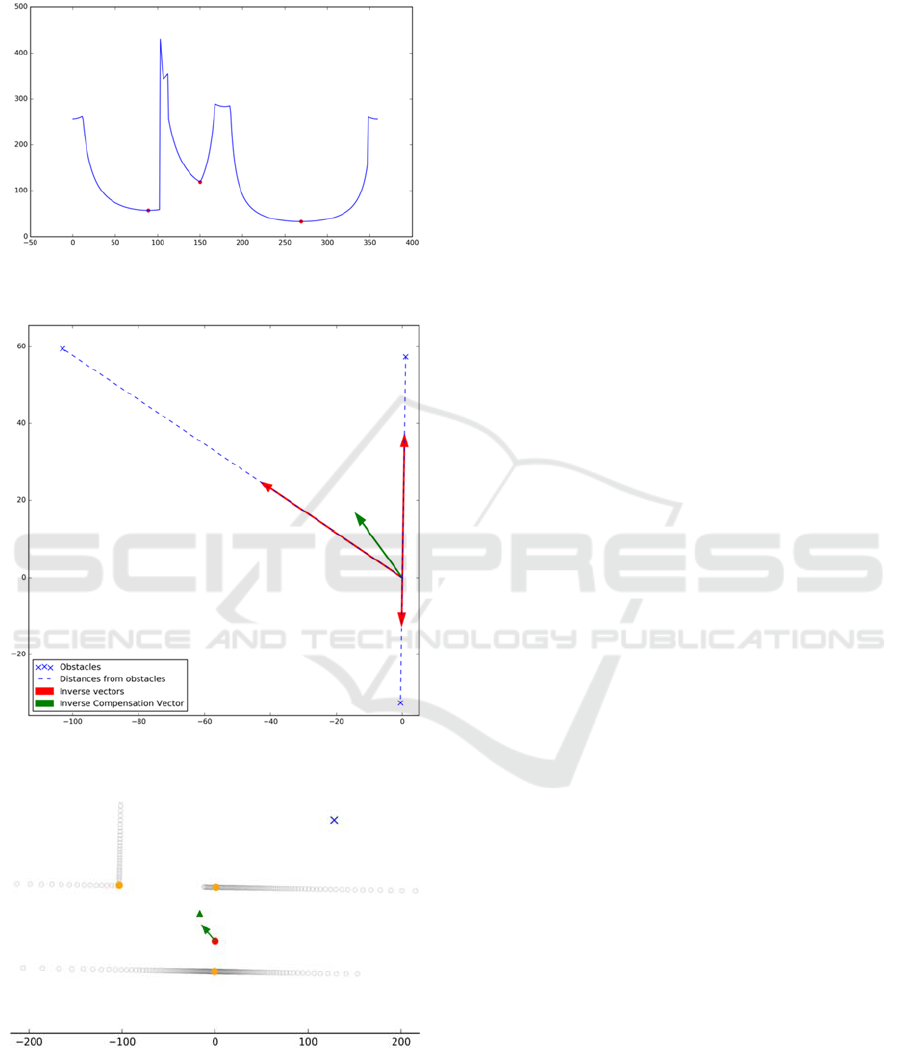
Figure 6: LIDAR scan readings for right t-section cue with

the three smallest minima shown as red dots.

Figure 7: Graphical illustration of constructing the Inverse

Compensation Vector (ICV) for the right t-section cue.

Figure 8: The ICV for the right t-section cue versus the

centroid of the contour and the centroid of the supporting

contour (see the text for explanation).

The ICV is constructed on the basis that the robot

should be kept away from each of the points in a

contour of the maze as far as possible. In contrast to

the potential fields approach, obstacles are seen as

attractors rather than repellents. Rather than pushing

the robot away, they pull it to a position in which all

forces are balanced. As stated earlier, finding such a

center of gravity is an optimization problem that is

computationally hard. However, the following

approach yields reasonable computational results in

simulations.

The algorithm assumes that the robot position is

always in the center of the coordinate system. We

compute a set of minima in the LIDAR scan reading

shown as red dots in Figure 3. Next, we select three

closest points in the contour (i.e., the smallest

minima). Figure 6 shows the same scan as in Figure

3, but with only three smallest minima. We already

discussed constructing a contour of the maze from the

LIDAR readings; an example is shown Figure 5.

Using the minima, we can select the closest contour

points for any set of minima; we call the set a

supporting contour. The points in two-dimensional

space correspond to vectors (with the center of the

coordinate system as the other end), so we call the

closest three contour points support vectors. Support

vectors are the basis for computing the ICV. To do

that, a mean distance to all points in the supporting

contour is computed. Then we calculate inverse ratios

of the mean to the support vectors; the smaller the

vector, the larger the ratio. The adjective inverse

refers to the fact that instead of normalizing the

vectors using their mean, inverses of these

normalizations are computed. The ratios are then used

to compute inverse vectors that attract the robot

towards the gaps between the robot and each of the

points in the supporting contour. The idea follows the

logic that the robot should move into empty spaces

between itself and the obstacles with the speed

inversely related to its distance to a given obstacle.

The further the obstacle (i.e., the larger the gap) the

more attractive it is to move towards the that obstacle

(relatively to the other obstacles). Hence, using the

metaphor from the potential field methods, the

obstacles attract the robot with a force relative to the

inversely normalized distance from the robot. We

refer to the operation as inverse compensation.

A Python 3 snippet to compute the ICV is shown

in Code Snippet 1. In the code, the support vectors are

passed as a parameter vs. In addition to the ICV, the

function also returns the compensation vectors as well

as their mean. The additional return values could be

used for scaling the ICV in some circumstances; for

example, in relation to the width of the maze

passages.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

400

Code Snippet 1: Python 3 code to compute the Inverse Compensation Vector icv of three vectors given as a Numpy array vs.

Figure 7 illustrates the process using a scan of the

right t-section cue as an example. The robot position

is in the center of the coordinate system (the base of

all shown vectors). The crosses demarcate the closest

obstacles with broken lines reflecting the distances.

The red vectors are the individual inverse

compensation vectors, and the green arrow is the total

inverse compensation vector (i.e., the mean of the

individual inverse vectors). That is the vector that

would be used to compensate the motion drive vector

of the robot.

The result of the computation in the context of the

contour, the centroid of all contour points, as well as

the centroid of the supporting contour is shown in

Figure 8. The difference with the centroid of all points

is dramatic, but not so much with the centroid of the

supporting contour. As shown in the following

experiments the difference may be much more

significant in other cases.

4 RESULTS

Currently, we have defined six cues in the maze: right

turn, left turn, t-section, cross-section, right t-section,

and left t-section. Figure 9 shows calculations of the

ICVs for arbitrary robot positions in approaching

each of the cues.

It is evident from the illustrations that ICVs

(shown as green arrows) provide much improved

correction to robot movement over using a centroid

of the supporting contour (shown as a green triangle).

While the centroid point often lays even closer to the

obstacles than the current robot position, the ICVs

direct the robot to much safer locations. It is worth

noting that using potential fields methods would

direct the robot away from all points on the

supporting contour and as such would not be suitable

for this application.

To gain some insight into the movement

compensation calculations for different robot

positions near a single cue, we conducted a series of

experiments in which we calculated ICVs for

different robot locations when near a selected cue.

Figure 10 illustrates how the ICV evolves with the

change of the robot position when approaching the t-

section cue (that we used earlier in this document to

demonstrate the process of constructing the ICV). We

can see that every correction to the position is very

reasonable and balances the overall distance from all

the obstacles. Experiments with other cues and other

locations also support that thesis.

import numpy as np

def compute_icv(vs):

# compute vector lengths

vs_len = np.sqrt((vs*vs).sum(axis=1))

# get a mean length

vs_mean_norm = np.mean(vs_len)

# compute inverse proportions

inv_factor = vs_mean_norm/vs_len

# calculate correction vectors by applying inverse

# proportions to the vectors

vs_inv_norm = vs - np.array([k * v for k,v in zip(inv_factor, vs)])

# compute the final correction vector as the mean

# of correction vectors

icv = vs_inv_norm.mean(axis=0)

return icv, vs_inv_norm, vs_mean_norm

# Example

vs = np.array([[ 23, -18],

[ -7, -24],

[ 19, 23],

[-14, 2],

[-24, -3]])

compute_icv(vs)

Using Inverse Compensation Vectors for Autonomous Maze Exploration

401

Figure 9: The ICVs (green arrows) for (from top to bottom):

right turn, left turn, left t-section, t-section, and cross-

section. The ICV for right t-section is shown in Figure 5.

5 HEURISTICS

5.1 Noisy Data

The LIDAR data collected in the simulator are perfect

as they are computed using Mathematically sound

formulas. However, the data that are collected from a

LIDAR residing on a physical robot placed in an

actual maze contain noise that constitutes a challenge

for a reliable identification of minima. Very often the

measured distances that are angularly close to each

other differ by small amounts due to the imperfect

accuracy of the LIDAR. That yields distance curves

that are rugged, and as such prone to containing

numerous local minima as shown in the upper plot of

Figure 11 as tightly located red dots (they look almost

as thick red lines).

To deal with that problem, we applied a

smoothing function that removes the excess of local

minima as shown in the lower plot in Figure 11.

5.2 Tight Support Contours

If the distance minima are close to each other both by

angle and by magnitude, the ICV may not have the

magnitude sufficient to repel the robot from the walls.

There are two ways of dealing with the problem. First

is to ensure that the minima are well distributed in the

span of the scan. Therefore, the LIDAR full 360

degrees range is divided in several equal zones, and

then minima are calculated for each of the zones. The

three smallest are then used in computing the ICV.

The minima shown in the lower plot of Figure 11

were obtained in the described way.

Another method that we tried was to use an

inverse of the variance in the distances to the

obstacles to modulate the magnitude of inverse

vectors. That method helped only in some cases; for

example, when the robot was close to three obstacles

located closely one to another. Applying zoning to

finding minima make such scenarios impossible, so

this approach was abandoned.

6 CONCLUSIONS

Our simulations show that correcting the robot

velocity vector by the Inverse Compensation Vector

(ICV) is a very simple yet effective approach to

keeping the robot away from the maze walls. The ICV

that corrects both the direction and the speed is

computed and applied periodically after each of the

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

402

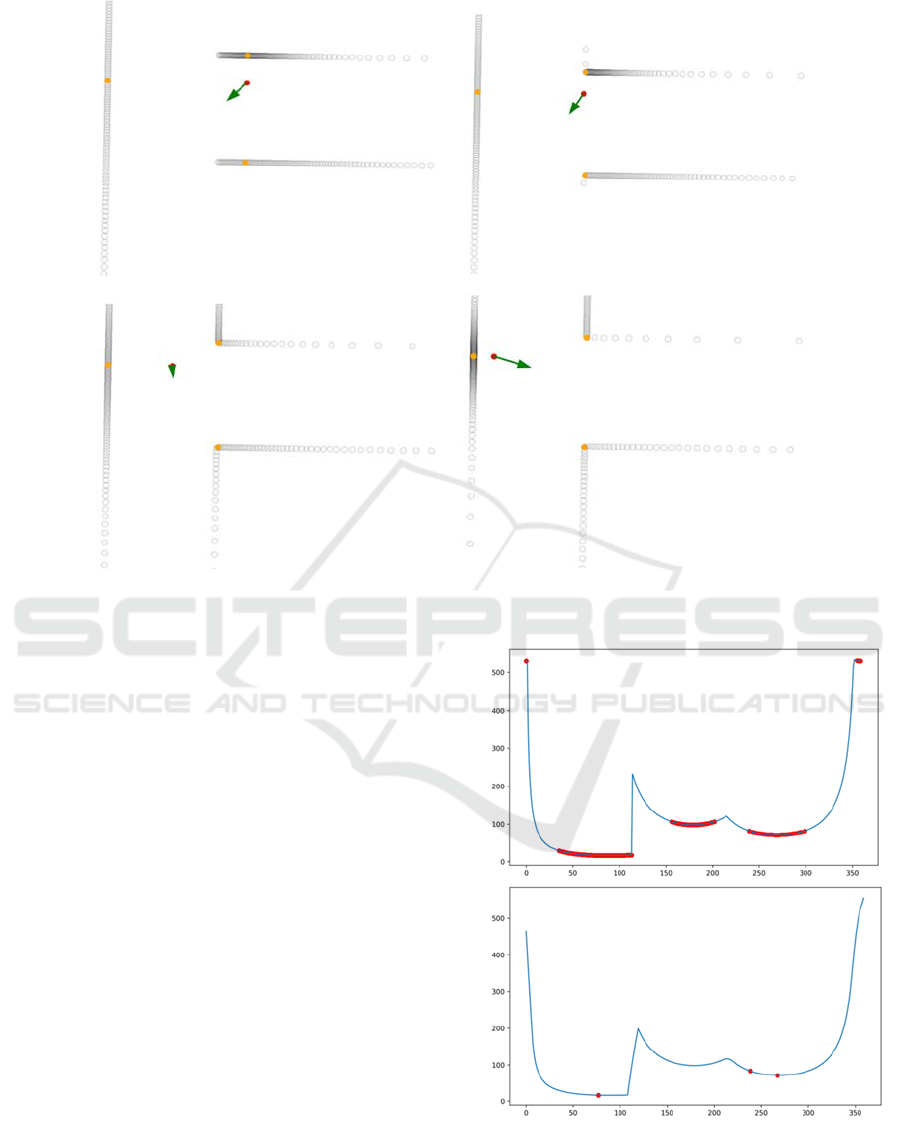
Figure 10: The ICVs computed for four different location of the robot near a t-section cue.

LIDAR scans (or as often as the processing power of

the robot controller allows).

The method does not yield an optimal solution to

the obstacle avoidance problem, but is much more

efficient than the iterative approaches to finding the

center of gravity discussed in the introduction.

Therefore, it can be applied in robots that employ

relatively slow processor boards.

7 FUTURE WORK

We are transferring the algorithms to the physical

robot. The simulator does not take into account the

volume of the robot, so some adjustments are

necessary to the use of the ICV.

We are also looking at the scaling of the speed

correction, since certain scenarios may yield ICVs

that, for example, just cancel out the motion drive

vector leading to halting the robot altogether. This is

not a problem with a remote controller as just more

forward movement might be applied. However, an

autonomous robot must have a logic to deal with such

issues. We theorize that a detection of a stop can be

used to modify the velocity vector. A stop detector is

easy to implement by comparing subsequent LIDAR

scans.

Figure 11: Cleaning up the noise data using smoothing and

ensuring distribution using zones. The upper plot shows

raw data, and the bottom shows the distance curve after it

was smoothened and divided in three sectors.

Using Inverse Compensation Vectors for Autonomous Maze Exploration

403

The further-reaching agenda includes the goal-

oriented behavior that we described in the

introduction. We are making progress using the

simulator, but to transfer the ideas to the physical

robot we must tackle other low-level tasks similar to

the ones described in this report.

ACKNOWLEDGEMENTS

The author would like to acknowledge assistance

from two research assistants and excellent senior

Computer Science students Jesus Bamford and Corey

Smith, who are implementing many of the ideas and

conduct a lot of tests, especially with the physical

robot. This work would not be possible without them.

Great thanks to both!

REFERENCES

Agafonkin, V., 2016 (snapshot). A new algorithm for

finding a visual center of a polygon.

https://www.mapbox.com/blog/polygon-center/.

Aichholzer, O., Aurenhammer, F., Alberts, D., and Gartner,

B., 1995. A novel type of skeleton for polygons. In

Journal of Universal Computer Science 1(12):752-761,

1995.

Bieszczad, A. and Pagurek, B., 1998. Neurosolver:

Neuromorphic General Problem Solver. In Information

Sciences: An International Journal 105 (1998), pp.

239-277, Elsevier North-Holland, New York, NY.

Bieszczad, A. and Bieszczad, K., 2006. Running Rats with

Neurosolver-based Brains in Mazes. In Proceedings of

International Conference on Artificial Intelligence and

Soft Computing, Zakopane, Poland.

Bieszczad, A., 2015. Exploring Machine Learning

Techniques for Identification of Cues for Robot

Navigation with a LIDAR Scanner. In Proceedings of

12th International Conference on Informatics in

Control, Automation and Robotics (ICINCO 2015),

Special Session on Artificial Neural Networks and

Intelligent Information Processing (ANNIIP 2015),

Cormal, France, CITEPRESS Digital Library.

DiddyBorg, 2017 (snapshot).

https://www.piborg.org/diddyborg

Eppstein, D., Erickson, J., 1999. Raising roofs, crashing

cycles, and playing pool: Applications of a data

structure for finding pairwise interactions. In Discrete

& Computational Geometry 22(4):569-592.

Finkel, R., Bentley, J.L., 1974. Quad Trees: A Data

Structure for Retrieval on Composite Keys. In Acta

Informatica 4 (1): 1–9.

Garcia-Castellanos, D., Lombardo, U., 2007. Poles of

Inaccessibility: A Calculation Algorithm for the

Remotest Places on Earth. In Scottish Geographical

Journal Vol. 123, No. 3, 227 – 233.

Joan-Arinyo, R., Pérez-Vidat, L., Gargallo-Monllau, E.,

1997. An Adaptive Algorithm to Compute the Medial

Axis Transform of 2-D Polygonal Domains. In

Proceeding CAD Systems Development: Tools and

Methods Pages 283-298, Springer-Verlag London, UK.

Khatib, O., 1986. Real-time obstacle avoidance for

manipulators and mobile robots. In International

Journal of Robotics Research, Volume 5 Issue 1, pp.

90-98, SAGE Publications.

Lee, D. T., 1982. Medial Axis Transformation of a Planar

Shape. In IEEE Transactions on Pattern Analysis and

Machine Intelligence Volume: PAMI-4, Issue: 4.

Peng, Y., Qu, D., Zhong, ,Y., Xie, S., Luo, J., Gu, J., 2015.

The Obstacle Detection and Obstacle Avoidance

Algorithm Based on 2-D Lidar. In Proceeding of the

2015 IEEE International Conference on Information

and Automation Lijiang, China.

Rajvanshi, A., Islam, S., Majid, H., Atawi, I., Biglerbegian,

M., and Mahmud, S., 2015. An Efficient Potential-

Function Based Path-Planning Algorithm for Mobile

Robots in Dynamic Environments with Moving Targets.

In British Journal of Applied Science & Technology

9(6): 534-550.

RPLIDAR, 2017 (snapshot).

https://www.seeedstudio.com/RPLIDAR-360-degree-

Laser-Scanner-Development-Kit-p-1823.html

Shewchuk, J. R., 2008. "General-Dimensional Constrained

Delaunay and Constrained Regular Triangulations, I:

Combinatorial Properties". 39 (1-3): 580–637.

Yan Peng, Y., Dong Qu, D., Yuxuan Zhong, ,Y., Shaorong

Xie, S., Jun Luo, J., Jason Gu, J., 2015. The Obstacle

Detection and Obstacle Avoidance Algorithm Based on

2-D Lidar. In Proceeding of the 2015 IEEE

International Conference on Information and

Automation Lijiang, China.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

404