
Index Clustering: A Map-reduce Clustering Approach using Numba
Xinyu Chen and Trilce Estrada
University of New Mexico, Albuquerque, U.S.A.
Keywords:
Scalable Clustering, Privacy Preserving, Big Data.
Abstract:
Clustering high-dimensional data is often a crucial step of many applications. However, the so called ”Curse
of dimensionality” is a challenge for most clustering algorithms. In such high-dimensional spaces, distances
between points tend to be less meaningful and the spaces become sparse. Such sparsity needs more data
points to characterize the similarities so more distance comparisons are computed. Many approaches have
been proposed for reduction of dimensionality, such as sub-space clustering, random projection clustering,
and feature selection technique. However, approaches like these become unfeasible in scenarios where data is
geographically distributed or cannot be openly used across sites. To deal with the location and privacy issues
as well as mitigate the expensive distance computation, we propose an index-based clustering algorithm that
generates a spatial index for each data point across all dimensions without needing an explicit knowledge of
the other data points. Then it performs a conceptual Map-Reduce procedure in the index space to form a final
clustering assignment. Our results show that this algorithm is linear and can be parallelized and executed
independently across points and dimensions. We present a Numba implementation and preliminary study of
this algorithm’s capabilities and limitations.
1 INTRODUCTION
Clustering technology has been challenged by the
rapid growing of data. In domains where data vol-
ume is continuously growing (e.g., climate simula-
tions - 32 PB, astronomy - 200 GB/day to 30 TB/day,
and high-energy physics - 500 EB/day), data move-
ment and centralized processing represent perfor-
mance bottlenecks that increase resource pressure on
storage, bandwidth, memory, and CPU (Tiwari et al.,
2012). The problem becomes even more challenging
as the number of distributed locations increases, or as
privacy and management impose restrictions to data
access. Two scenarios are of relevance for this work:
(1) In-situ data analysis of HPC simulations. Anal-
ysis has to be done on site, using local data, in real
time, along with as little communication as possible.
(2) Medical data analysis. Data volume may not be
too large to be efficiently moved across locations, but
privacy issues may restrict data sharing. In both sce-
narios, a global model has to be computed at run time
using only an incomplete view of the data. Our ques-
tion is if data cannot be moved, or shared, how can
we still learn from it?.
From the standpoint of scalability in parallel and
distributed environments and privacy bound applica-
tions, state of the art clustering techniques lack in one
or more of the following crucial aspects: (1) Tradi-
tional machine learning and data mining approaches
rely on expensive training phases and often require
gathering data in a centralized (
ˇ
S
´
ıma and Orponen,
2003), (Salakhutdinov and Hinton, 2009) or semi-
centralized (Kargupta et al., 2001), (Boyd et al., 2011)
way. (2) Existing distributed approaches either re-
quire synchronized communication (Bandyopadhyay
et al., 2006), are tied to a particular domain and do not
generalize (Estrada and Taufer, 2012), (Kawashima
et al., 2008), sacrifice accuracy for the sake of scala-
bility (Liu et al., 2013), (Gionis et al., 1999), (Aggar-
wal et al., 1999), or are affected by the curse of dimen-
sionality (Quiroz et al., 2012) (i.e., scaling the num-
ber of data features negatively affects an algorithm’s
predictive capabilities (Indyk and Motwani, 1998)).
None of these methods are all, scalable, accurate, and
general enough to be useful in privacy bound or dis-
tributed scenarios of Big Data.
Our goal is to build a clustering algorithm that is
able to organize large dimensional datasets without
relying on a global knowledge of the data or expen-
sive distance computations. This is a key step that
may eventually lead to a solution for location and pri-
vacy restricted situations: the clustering can be done
locally on each distributed site by exchanging only
summarized information, like bins and frequencies,
Chen, X. and Estrada, T.
Index Clustering: A Map-reduce Clustering Approach using Numba.
DOI: 10.5220/0006437402330240
In Proceedings of the 6th International Conference on Data Science, Technology and Applications (DATA 2017), pages 233-240
ISBN: 978-989-758-255-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
233

with other sites. Compared to moving the whole raw
dataset around, the summarized information is ex-
tremely small. Individual data points cannot be repro-
duced from such limited information on other sites so
that the privacy is well protected. With this in mind,
we propose Index Clustering, a new data clustering
approach based on indexing individual data points
across their whole high dimensional space, and then
using only the indexes to build final clusters. Without
distance computation, our algorithm has a linear time
complexity with regards to both the number of points
and dimensions. More specifically, the processing of
each point can be done in a constant time. Finally, un-
like most density-based clustering methods, our algo-
rithm can benefit from a large number of dimensions.
This paper’s contributions are as follow:
• A linear time complexity clustering approach that
is able to group data across multiple dimensions
even with a very limited view of the data.
• A parallel implementation of our algorithm in
GPU using Numba.
• A preliminary evaluation of our algorithm’s scal-
ability and generality using synthetic and real
datasets.
The remainder of this paper is organized as fol-
lows: in section 2, we briefly summarize some algo-
rithms that have influence on our algorithm as well
as other related approaches. Section 3 presents our
index-based clustering algorithm, which combines a
map-reduce like approach with Numba to accomplish
the parallel clustering tasks. In section 4 we explain
the experimental results. Section 5 presents our dis-
cussion regarding our algorithm’s limitations, reason-
ing behind parameter selection, and overview of fu-
ture works that can improve the robustness of our
method. Finally, section 6 concludes the paper.
2 RELATED WORK
Scalable methods, closely related to our techniques,
are density-based clustering. One of the first ap-
proaches is DBSCAN (Ester et al., 1996). Another
successful example is the Decentralized Online Clus-
tering (Quiroz et al., 2012) that was used in the con-
text of distributed systems monitoring and resource
provisioning. Our approach is similar to these tech-
niques in the sense that it groups points in a density-
based way; but it is different in that we use indexed
bins to define dense regions that contain enough
points instead of defining some core points that have
enough neighbors.
Other methods have been proposed to capture
low-dimensional semantics of data features with the
final purpose of accelerating searches for similar
items. Successful methods in this category include
Latent Semantic Analysis (LSA), Semantic Hashing,
and Lazy Learning (Indyk and Motwani, 1998; Bar-
rena et al., 2010; Omercevic et al., 2007). Latent Se-
mantic Analysis (Deerwester et al., 1990) uses the
SVD decomposition to extract low dimensional se-
mantic structure of the word-document co-occurrence
matrix. LSA enables document retrieval engines to
base their searches on semantic structure, rather than
using individual word counts. This property greatly
reduces the time complexity of the algorithms. How-
ever, computing the SVD decomposition becomes un-
feasible as data size grows large.
Sub-space Clustering algorithms gave inspi-
ration to our algorithm. Grid-based hierarchi-
cal clustering algorithms that use bottom-up search
strategies are most related and influential to us.
CLIQUE (Agrawal et al., 1998) and MAFIA (Goil
et al., 1999) first find dense regions in lower-
dimensional spaces. Then they merge these lower-
dimensional regions into bigger higher-dimensional
hyper-cubes if they can find a common-face between
two regions. The limitation of these two algorithms
is the expensive combinations of all possible lower
dimensional regions so they didn’t show scalability
when the dimensionality goes to several hundred.
3 ALGORITHM
Most traditional clustering techniques rely on com-
puting pairwise distances between points or regions
to form clusters. These computations are exponen-
tially expensive as the number of points and the num-
ber of dimensions grow. Other more efficient tech-
niques such as dimensionality reduction, need prior
knowledge of the data (e.g. its principal components,
covariance matrix, or some other statistical proper-
ties). However, when data needs to be analyzed as a
stream, in situ, or on different geographical locations,
and the i.i.d.(independent and identically distributed)
property cannot be guaranteed, then these methods
fail.
For an algorithm to work in such circumstances,
the main question is: if we cannot compute pairwise
distances, how can we decide whether two points are
similar? To efficiently answer this question, we took
inspiration from Locality Sensitive Hashing (Gionis
et al., 1999). Similar to the family of hashed val-
ues, we map data points to indexes along every di-
mensions. By organizing these indexes into bins and
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
234

merging bins to primary clusters, we get a list of pri-
mary cluster identifiers like the fingerprints for each
point which we call it a index. Then, forming clus-
ters can be done in this projected space, and is al-
most as easy as performing a reduction on finger-
prints. The A-priori algorithm for mining frequent
patterns (Agrawal et al., 1994) is behind our final
grouping approach: Points belong to one higher di-
mensional cluster also stay together in each lower di-
mensional regions; Points with different fingerprints
belongs to different clusters. Two crucial aspects of
this process are: (1) the space of indexes represents
summarized knowledge of the raw data, which allows
us to preserve privacy, and (2) the reduction on finger-
prints instead of distance comparisons, which allows
us to improve scalability.
3.1 Methods
We want to cluster a dataset m of size M × N, where
M is the number of data points and N is the number of
features. We denote m = {cor
i, j
|i < M, j < N}, with i
being the unique identity of a data point and j its jth
feature. Without lack of generality we could assume
M = 1 for a data stream scenario or multiple m’s for a
distributed case. For descriptive purposes we will call
m as our raw data for the rest of the paper. The steps
of our method are as follows:
1. Assign a list of indexes to a point. Every index
is associated with a bin in the specific dimension.
As points get their indexes, bins update their den-
sity. This step only involves the point itself and
the value range of each dimension. In the dis-
tributed scenario this can be done with only local
data.
2. Building primary clusters. A primary cluster is
a partial clustering assignment viewed from one
particular dimension. This step merge adjacent
bins into what we call primary clusters if they ex-
ceed the density threshold.
3. Assigning points to final clusters. Once primary
clusters are built, every point can be mapped to a
specific set of primary clusters in all of its dimen-
sions. They use their indexes to get a index. This
leads to a final global clustering assignment.
3.1.1 Assigning a List of Indexes to a Point
A point
i
’s coordinate are converted to idx, a list of
indexes indicating a relative location along each di-
mension. The number of bits per index is defined by
the user as the depth of our algorithm. This depth
also determines the number of bins per dimension as
B = 2
depth
. Then, idx
i, j
, which is the index for x
i, j
is
in range of [0,2
depth
− 1].
The function getindex as shown in Algorithm 1,
receives as parameters the depth of indexes, an es-
timated lower and upper boundaries of the specific
dimension, and the point’s coordinate. Then, it recur-
sively divides the range on one dimension into equal
halves for depth number of steps. This procedure is
conceptually building a depth deep binary tree to ac-
commodate the range. Each leaf contains a sub re-
gion of the bounded dimension. The point’s coordi-
nates are then converted into indexes of leaves. The
getindex function is applied to x
i, j
∀i, j independently.
Thus, it can be efficiently implemented in parallel, not
only per data point but also per feature.
Algorithm 1: getindex.
1: procedure GETIDX(max depth,lower,upper,x
i, j
)
2: for depth < max depth do
3: µ
j,depth
← 1/2(lower + upper)
4: if x
i, j
≥ µ
j,depth
then
5: append 1 to idx
i, j
6: lower ← µ
j,depth
7: else
8: append 0 to idx
i, j
9: upper ← µ
j,depth
10: return idx
i, j
return leaf index
3.1.2 Building Primary Clusters
Primary clusters are sets of bins organized in a par-
tial clustering assignment for a single dimension.
Our algorithm follows a bottom-up strategy. Un-
like CLIQUE(Agrawal et al., 1998) and MAFIA(Goil
et al., 1999), we build primary clusters on each di-
mension then directly reduce to the entire dimensional
clusters and skip all intermediate lower-dimensional
dense regions. A bin is instantiated only when there
is a data point whose index on this dimension is as-
sociated to that bin. bins = {dbin
b, j
|b < B, j < N}.
dbin
b, j
is the density of bin b on the jth dimension.
To build primary clusters we merge adjacent bins
if their density is larger than a predefined threshold
minDensity. For very sparse clustering, this thresh-
old can be set to zero. A primary cluster represents
an agglomeration of points viewed from one particu-
lar dimension. We refer them as pc where {pc
b, j
|b <
B, j < N} contains a unique identifier (e.g. PCid) for
the primary cluster in that dimension, with B and N
being the number of bins and the number of dimen-
sions respectively. Algorithm 2 shows the procedure
for building primary clusters. A while loop for gener-
ating point’s indexes and updating bins’ density, and
a for loop for merging adjacent bins forming primary
Index Clustering: A Map-reduce Clustering Approach using Numba
235

clusters. The only communication needed would be
the final bin densities, which is considerably smaller
than raw data and has no sensitive information that
could compromise privacy.
Algorithm 2: Build Primary Clusters.
1: M = numberOfPoints
2: N = numberOfDimension
3: minD = minimumDensityInBin
4: depth = depthOfindex
5: B = 2
depth
numberOfBins
6: while not EOF do generate indexes, fill bins
7: cor ← one data point from raw data
8: idx ← getindex(depth, cor)
9: for j = 1 to N do
10: dbin
j,idx
j
+ = 1 increase bin density
11: PCid ← 0 initialize for noise
12: for i = 1 to N do merge bins
13: k ← 1, f lag ← f alse
14: while k ≤ B do
15: if dbin
i,k
> minD AND not f lag then
16: PCid ← k
17: f lag ← true
18: else if dbin
i,k
<= minD AND f lag then
19: PCid ← 0
20: f lag ← f alse
21: pc
i,k
← PCid
22: k ← k + 1
3.1.3 Assigning Points to Final Clusters
The final step makes a final assignment of points to
their respective clusters. The aggregated clusters are
represented as FC = { f c
m
|m < M}. The index for a
final cluster is just the concatenation of PCids of each
one-dimensional primary cluster. The intuition being
that if points belong together in a high dimensional
cluster, they will be together with high frequency in
lower dimensional clusters. Although the possible
combination of primary cluster indexes is vast, the
real worst case is each point forms a unique ”group”.
So we can bound the maximum number of final clus-
ters to be M. Algorithm 3 shows the procedure of
building final clusters. This procedure consists on
concatenating the set of primary clusters assigned to
a point to build a global index which determines the
point membership to a specific final cluster.
In figure 1(a) we illustrate the algorithm with an
intuitive example. Two primary clusters are formed
on dimension
a
,dimension
b
, and one primary cluster
forms on dimension
c
. Final clusters are built upon
points sharing the same concatenation of their PCids.
p
1
, p
2
are from the red and black group respectively.
Figure 1(b) shows their specific primary clusters
Algorithm 3: Final clustering.
1: M = numberOfPoints
2: N = numberOfDimensions
3: pc = primaryClusters
4: for i = 1 to M do concatenate PCids
5: for k = 1 to N do
6: fcindex ← concatenate pc
i,k
7: f c
f cindex
+ = 1 increase cluster density
(a) 2 final clusters and bin densities.
pointID PCid
a
PCid
b
PCid
c
fcindex
p
1
1 1 1 111
p
2
2 2 1 221
(b) Example of primary clusters and final clusters in-
dexes
Figure 1: Didactic example of how our algorithm will
merge adjacent bins into primary clusters and reduce on
PCids to form a global arrangement.
across the three dimensions. The column fcindex
shows their final clustering assignments. Note that
with this arrangement, it is very easy to collapse a par-
ticular dimension and form completely different clus-
tering assignments without having to reiterate through
the data.
3.2 Parallel Implementation with
Numba
We used Numba to accelerate the above algorithm.
Numba is an Open Source NumPy-aware optimizing
compiler for Python that generates machine code for
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
236

both CPUs and NVIDIA GPUs. To Assign indexes
is the most time consuming section. We parallelized
the function getindexGPU and fillBinsGPU with one
GPU thread per coordinate. To build primary clusters,
the buildPClustersGPU function is implemented in a
limited parallel manner. The algorithm only launches
one thread per dimension. The location to merge bins
starts from the lowest bin. Since this step is not the
most computationally expensive in our method, we
leave it in a simple parallel approach. The Numba
sequence of steps is described in Algorithm 4.
Algorithm 4: Parallel map-reduce clustering algorithm.
1: M = numberOfPoints
2: N = numberOfDimension
3: B = numberOfBins
4: wt ← rand(w
1
,w
2
,...,w
N
)
T
kw
i
∈ (0,1)
5: m ← readFile get cor
i, j
6: k ← getindexGPU get idx
i, j
7: dbin ← fillBinsGPU get dbin
i,k
8: pc ← buildPClustersGPU get pc
i,k
9: cg ← getPrimaryClusterindex additional step
10: cm ← cg · wt additional step
11: ck ← getindexGPU additional step
12: hc ← fillBinsGPU additional step
13: for i = 1 to M do output final clusters
14: if hc
f cindex
≥minThreshold then
15: output final cluster
f cindex
The current version of Numba has no direct string
operations. Our implementation uses four additional
steps (lines 9 to 12 in Algorithm 4) to accomplish
the final clustering assignment. To emulate the se-
rial implementation of concatenating each of the pri-
mary cluster indexes in a point’s dimensions, we
first fetch the primary cluster indexes into a ma-
trix cg = {cid
i, j
|i < M, j < N}. Then we multiply
c with a random N dimensional real vector wt =
(w
1
,w
2
,...,w
N
)
T
,w
i
∈ (0,1). The result is a column
vector cm = {hk
i
|i < M}. So we get an unique real
number hk
i
to replace the concatenation of primary
cluster indexes. We will discuss the correctness of
this later in section 5.
The above two steps generate a 1 dimensional
array of real number final cluster indexs for every
points. We use an additional generate index step to
scatter these indexes onto a deeper binary tree. This
converts the vector cm = {hk
i
∈ R} of real numbers
into the integer vector ck = {ck
i
∈ I} with unique in-
tegers per bin. Our worst case is still when each point
has an unique final cluster index. To assure each of
the resulting leaf indexes are unique, the additional
getindex step uses a new depth > log(M). The last
additional step consists on keeping track of the den-
sity of bins in ck.
3.3 Time Complexity
In Algorithm 1, getindex uses a constant depth steps
to convert coordinates to indexes. The while loop
in Algorithm 2 goes one pass through all M points
to convert coordinates to indexes and accumulate the
bin densities on all N dimensions. This pass will be
O(M × N). The for loop goes one pass through bins
on N dimensions to merge them into Primary Clus-
ters. The number of bins is 2
depth
. This adds up
to O(2
depth
× N). The Algorithm 3 goes through all
M points on all N dimensions adds up to O(M × N).
The overall time complexity will be O(M × N) +
O(2
depth
× N). Normally, we set depth to 10 to 15 so
M > 2
depth
. The time complexity is still O(M × N).
The Numba implementation can parallelize the above
computations to the number of GPU threads P. So
The overall time complexity reduces to O(M ×
N
P
).
As P and N are fixed for a given dataset, our algorithm
can be seen as linear to the number of data points with
time complexity = O(M).
4 EXPERIMENTS AND RESULTS
We empirically evaluate the scalability and generality
of our Index Clustering algorithm through three tests.
First we compare performance between the serial and
the GPU implementations to quantify gains obtained
from the algorithm’s parallelization. Then, we per-
form controlled scalability tests to quantify perfor-
mance when we varied the number of points or the
number of dimensions. Finally, we use the algorithm
on real datasets to understand its predictive capabil-
ities. All the experiments ran on an 8 core Intel
Haswell 2.4GHz machine with a 640 Maxwell core
0.9GHz SMM graphic card. The host RAM is 8G and
the device RAM is 2G.
4.1 Performance Gain from GPU
Our first experiment is to quantify the improvement of
performance of GPU parallelization. We used simple
synthetic data to allow us control over the dimension-
ality and size of the datasets. We used the data gen-
erator from gpumafia(Canonizer, ) to generate 1 mil-
lion 20-dimensional points grouped into 5 hypercubic
clusters with 10% uniformly distributed noises. We
sum up the additional steps on the GPU implementa-
tion to get an equivalent timing for the final clustering
step on CPU. Figure 2 shows the time for clustering
1 million 20 dimensional points into 5 groups. The
algorithm successfully found five groups with recall
and precision equal to 1.0. The GPU implementation
Index Clustering: A Map-reduce Clustering Approach using Numba
237
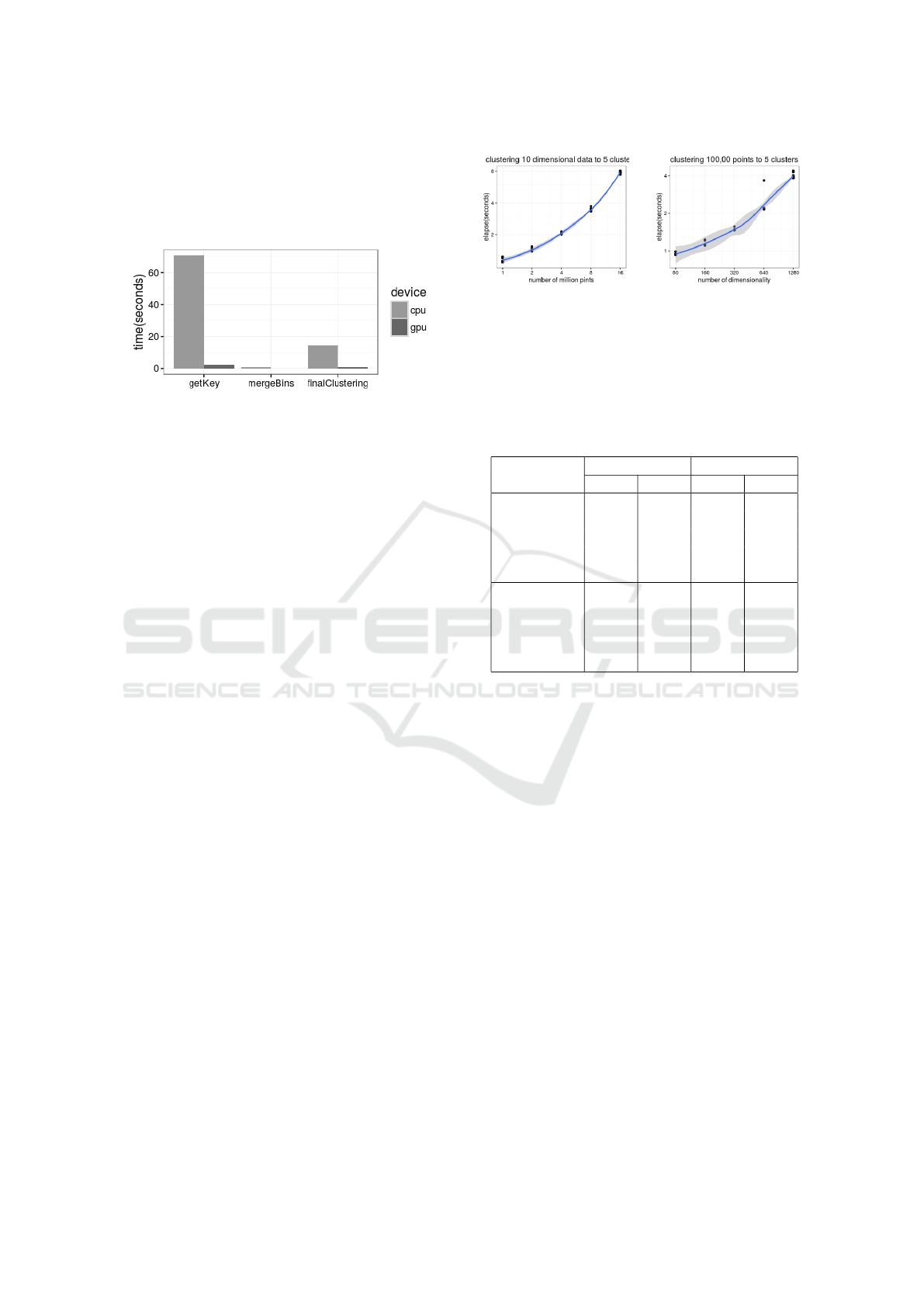
is about 30 time faster than CPU. Performance is ex-
pected to plateau as the number of data dimensions
approach the maximum number of threads. However,
this is a limitation of the hardware rather than of the
algorithm.
Figure 2: Elapsed time consumed by each step on CPU and
GPU in clustering 1 million low dimensional points.
4.2 Scalability
Our second set of experiments are designed to test the
algorithm’s weak scalability as the number of points
or the number of dimensions grow.
We first fixed the dimensions to 10 and number of
clusters to 6. Then we varied the number of points
from 1 million to 16 million with intermediate mea-
sures at 2, 4, and 8 million. Figure 3(a) shows the
relationship between time and size of the datasets is
close to linear. Through experimentation we observed
that the depth = 15 and minpt = 10 produced accu-
rate clusters for the 1 million dataset, and minpt = 100
for the 16 million dataset. Even though it is apparent
that the depth parameter is weakly correlated to the
data size, its relative growth is so small that it does
not have a considerable effect on the time complexity
of the algorithm.
Next we fixed the number of points to 100,000 and
varied the number of dimensions from 80 to 1280(i.e,
80, 160, 320, 640, 1280). Again, the algorithm suc-
cessfully divided the points into 5 groups. Figure 3(b)
shows that the relationship between time and dimen-
sionality is close to linear.
4.3 Comparison with K-means
It’s better to compare with density-based algorithms.
However, DBSCAN failed to finish 1 million data
points due to its quadratic complexity. So we com-
pare our algorithm with the K-Means due to its high
performance and widely acceptance in many disci-
plines. We picked the implementation of K-means in
scikit-learn package 0.17.1. To avoid hardware dif-
ference, only accuracy is compared. We simply give
K-means the ground truth value of k. Table 1 con-
tains averaged recall and precision of 10 runs for each
row. This comparison shows the generated separa-
(a) Scalability as data
points increases
(b) Scalability as dimen-
sionality increases
Figure 3: Scalability as dataset size and dimensionality in-
crease. Above: time for clustering 10 dimensional data with
size of 1, 2, 4, 8,and 16 million points. Below: time for
clustering 100,000 points with 80, 160, 320, 640 and 1280
dimensions.
Table 1: Index Clustering (idxc) VS. K-Means (kms).
Recall Precision
idxc kms idxc kms
1m-10d 0.999 0.798 1.0 0.788
2m-10d 0.999 0.799 1.0 0.841
4m-10d 0.999 0.800 0.999 0.791
8m-10d 0.999 0.799 1.0 0.806
16m-10d 0.999 0.800 1.0 0.601
100k-80d 0.999 0.800 1.0 0.984
100k-160d 0.999 0.804 1.0 0.746
100k-320d 0.998 0.799 1.0 0.738
100k-640d 0.998 0.797 1.0 0.736
100k-1280d 0.996 0.801 1.0 0.741
ble boundaries of synthetic hypercubes help our al-
gorithm achieve high accuracy. But the pairwise dis-
tances trick K-Means to lower accuracy.
4.4 Clustering Real Data
We tested our algorithm on the Daily and Sports Ac-
tivities Data Set(Altun et al., 2010) from the UCI
Machine Repository. The data set contains 45-
dimensional signals measured from different physical
activities performed by eight persons.
The first experiment is to identify different activi-
ties of the same person. We considered sitting, walk-
ing on a treadmill and jumping. Each activity contains
7,500 records. The total observations per person are
22,500. Without further preprocessing, our algorithm
separates the signals into three well defined groups.
The algorithm discards a few observations (in the or-
der of 20 per person) as noise. However, it correctly
assigns 99.9% of the data to the correct activities.
The second experiment aims to identify differ-
ent people doing a particular activity. In this case
total 60,000 points per activity for 8 persons. Our
algorithm consistently identified nine distinct clus-
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
238

ters. The nine-th cluster can be explained as noisy
inputs and inconsistencies of participants performing
the physical activity during the data collection.
5 DISCUSSION
In this section, we discuss the limitations of our algo-
rithm. This will help us to decide whether and when
the algorithm can accomplish its tasks.
Our algorithm works well with the assumption
that all dimensions are orthogonal to each other.
Adding one orthogonal dimension only stretches
points farther. However, adding one non orthogonal
dimension may compress points closer. To avoid this
problem, our algorithm makes it easy to collapse di-
mensions. If the collapse produces radically different
clustering assignments, it is possible to determine that
some dimensions are not orthogonal and need to be
revised.
Another limitation is the situation where the dense
bins of two clusters overlap. Figure 4 shows a com-
mon situation in a 2 dimensional space, where the
projected dense bins of cluster
1
and cluster
2
over-
lap on both dimensions. Our algorithm would fail
if they overlap in all dimensions. If p
i
is the prob-
ability of overlapping on the ith dimension, then the
probability that our algorithm fails is
∏
N
i=1
p
i
, which
becomes small quickly as dimensionality increases.
Thus, our algorithm is likely to perform better with
high dimensional data. To ameliorate the overlapping
problem, we can check dimension
b
in Figure 4 to ob-
serve a bimodal distribution of densities. An analy-
sis of the modes per range would give us indications
that the data is actually forming two clusters instead
of one. Again, as the number of dimensions increase,
the probability of successfully identifying this phe-
nomena just increases.
Unique Final Cluster indexes. In Section 3.2, we
convert the row vector of primary cluster into a real
value as the final index. We accomplish this goal
by multiplying this row vector with a random col-
umn weight vector wt = (w
1
,w
2
,..,w
N
)
T
,w
i
∈ (0,1).
In Table 2, the column PCid
1
and PCid
2
are primary
cluster indexes. We can generalize the number of pri-
mary clusters in dimension
1
and dimension
2
to be X
and Y . The maximum number final cluster indexes. is
X ×Y .
Let the weight vector be wt = (
1
a
,
1
a+1
) where a
is an integer and a · (a + 1) ≥ X ·Y . The dot product
of the matrix of PCids with wt is an 1-dimensional
column vector of real values. The results are within
the range of [
2a+1
a(a+1)
,
X(a+1)+aY
a(a+1)
]. The minimum step
between two values will be
1
a(a+1)
. This value range
Figure 4: Algorithm cannot separate two clusters when his-
tograms overlap on both dimensions. This happens more
often in lower dimensional spaces.
Table 2: Generate unique cluster indexes.
PCid
1
PCid
2
Weight Result
1 1 (1/2,1/3)
T
5/6
1 2 (1/2,1/3)
T
7/6
1 3 (1/2,1/3)
T
9/6
2 1 (1/2,1/3)
T
8/6
2 2 (1/2,1/3)
T
10/6
2 3 (1/2,1/3)
T
12/6
contains a(X + Y − 2) + X points. Solve the above
inequality we have a ≥
q
XY +
1
4
−
1
2
. Given X,Y,a
are all integers, we can simplify the inequality to be
a > min(X,Y ). This will give us the lower bounds of
the number of unique points XY + (X
2
− X),(X ≥ Y )
or XY + (Y
2
−Y ),(Y ≥ X ). For both cases, the lower
bound will be larger than the maximum number of
all possible final cluster indexes. In the above ex-
ample, X = 2,Y = 3. We choose a = 2 such that
a(a + 1) ≥ XY . Then wt = (1/2,1/3)
T
. The result
final cluster indexes are all unique. We can choose
wt = (
1
a
,
1
b
)
T
instead of (
1
a
,
1
a+1
)
T
as long as |a − b|
is still small, and a · b ≥ X · Y . Our algorithm uses
random real numbers within (0,1) to simulate such
a weight vector. For the purpose of querying a new
point’s cluster index, we can generate a fixed weight
vector as the index generator.
6 CONCLUSIONS
In this paper we presented the Index Clustering algo-
rithm, a parallel clustering algorithm tailored for sce-
narios with very limited view of the data. Our algo-
rithm, is able to organize large dimensional datasets
without pair-wise point comparisons. This enables
us to form clusters under location and privacy re-
stricted situations. The communication is extremely
small compared to the whole raw dataset and indi-
Index Clustering: A Map-reduce Clustering Approach using Numba
239

vidual data points cannot be reproduced from it. Our
algorithm shows weak scalability with the number of
points/dimensions. The limitation of dimension or-
thogonality and overlapping is discussed. Such sit-
uation shall be rare as dimensionality grows higher.
Domain knowledge can benefit our algorithm by pro-
viding guidelines for collapsing particularly noisy or
non-orthogonal dimensions. Finally, this work shows
the potential power of Numba in high-dimensional
data analysis.
ACKNOWLEDGEMENTS
This research was supported by the National Science
Foundation for the grant entitled CAREER: Enabling
Distributed and In-Situ Analysis for Multidimensional
Structured Data (NSF ACI-1453430).
REFERENCES
Aggarwal, C. C., Wolf, J. L., Yu, P. S., Procopiuc, C., and
Park, J. S. (1999). Fast algorithms for projected clus-
tering. SIGMOD Rec., 28(2):61–72.
Agrawal, R., Gehrke, J., Gunopulos, D., and Raghavan, P.
(1998). Automatic subspace clustering of high dimen-
sional data for data mining applications. ACM SIG-
MOD Record, 27(2):94–105.
Agrawal, R., Srikant, R., and Others (1994). Fast algo-
rithms for mining association rules. In Proc. 20th
int. conf. very large data bases, VLDB, volume 1215,
pages 487–499.
Altun, K., Barshan, B., and Tunc¸el, O. (2010). Comparative
study on classifying human activities with miniature
inertial and magnetic sensors. Pattern Recognition,
43(10):3605–3620.
Bandyopadhyay, S., Giannella, C., Maulik, U., Kargupta,
H., Liu, K., and Datta, S. (2006). Clustering dis-
tributed data streams in peer-to-peer environments. In-
formation Sciences, 176(14).
Barrena, M., Jurado, E., M
´
arquez-Neila, P., and Pach
´
on, C.
(2010). A flexible framework to ease nearest neighbor
search in multidimensional data spaces. Data Knowl.
Eng., 69(1):116–136.
Boyd, S., Parikh, N., Chu, E., Peleato, B., and Eckstein, J.
(2011). Distributed optimization and statistical learn-
ing via the alternating direction method of multipliers.
Found. Trends Mach. Learn., 3(1):1–22.
Canonizer. Implementation of mafia subspace clustering on
nvidia gpus. https://github.com/canonizer/gpumafia.
open source code 2012.
Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer,
T. K., and Harshman, R. (1990). Indexing by latent
semantic analysis. Journal of the American Society
for Information Science, 41(6).
Ester, M., Kriegel, H.-P., Sander, J., Xu, X., and Others
(1996). A density-based algorithm for discovering
clusters in large spatial databases with noise. In Kdd,
volume 96, pages 226–231.
Estrada, T. and Taufer, M. (2012). On the effectiveness of
application-aware self-management for scientific dis-
covery in volunteer computing systems. In Proceed-
ings of the International Conference on High Perfor-
mance Computing, Networking, Storage and Analysis,
pages 80:1–80:11. IEEE Computer Society Press.
Gionis, A., Indyk, P., and Motwani, R. (1999). Similarity
search in high dimensions via hashing. In Proceedings
of the 25th International Conference on Very Large
Data Bases, pages 518–529. Morgan Kaufmann Pub-
lishers Inc.
Goil, S., Nagesh, H., and Choudhary, A. (1999). MAFIA:
Efficient and scalable subspace clustering for very
large data sets. . . . Discovery and Data Mining,
5:443–452.
Indyk, P. and Motwani, R. (1998). Approximate nearest
neighbors: Towards removing the curse of dimension-
ality. In Proceedings of the Thirtieth Annual ACM
Symposium on Theory of Computing, pages 604–613.
Kargupta, H., Huang, W., Sivakumar, K., and Johnson, E.
(2001). Distributed clustering using collective princi-
pal component analysis. Knowledge and Information
Systems, 3(4):422–448.
Kawashima, H., R. Sato, R., and Kitagawa, H. (2008).
Models and issues on probabilistic data streams with
Bayesian Networks. In Proc. of the International Sym-
posium on Applications and the Internet (SAINT).
Liu, Y., Jiao, L. C., Shang, F., Yin, F., and Liu, F. (2013). An
efficient matrix bi-factorization alternative optimiza-
tion method for low-rank matrix recovery and com-
pletion. Neural Netw., 48.
Omercevic, D., Drbohlav, O., and Leonardis, A. (2007).
High-dimensional feature matching: Employing the
concept of meaningful nearest neighbors. In IEEE
11th International Conference on Computer Vision,
pages 1–8.
Quiroz, A., Parashar, M., Gnanasambandam, N., and
Sharma, N. (2012). Design and evaluation of decen-
tralized online clustering. ACM Trans. Auton. Adapt.
Syst., 7(3):34:1–34:31.
Salakhutdinov, R. and Hinton, G. (2009). Semantic hashing.
Int. J. Approx. Reasoning, 50(7):969–978.
Tiwari, D., Vazhkudai, S. S., Kim, Y., Ma, X., Boboila,
S., and Desnoyers, P. J. (2012). Reducing data move-
ment costs using energy-efficient, active computation
on ssd. In 2012 Workshop on Power-Aware Comput-
ing and Systems. USENIX.
ˇ
S
´
ıma, J. and Orponen, P. (2003). General-purpose com-
putation with neural networks: A survey of complex-
ity theoretic results. Neural Computing, 15(12):2727–
2778.
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
240
