Optimization for Solving Workcell Layouts using Gaussian Penalties for

Escaping Local Minima

Thomas Fridolin Iversen and Lars-Peter Ellekilde

The Maersk McKinney Moller Institute, University of Southern Denmark, Campusvej 55, 5230, Odense M, Denmark

Keywords:

Robot Workcell Optimization, Optimization Algorithms, Industrial Robotics.

Abstract:

The main contribution of this paper is a method for optimizing the layout of workcells taking into consid-

eration both the reachability of the robot as well as the expected cycle time. To analyse the reachability for

systems using sensors to pose estimate objects, the method uses a combination of discrete samples over the

space in which objects are located and a manipulability measure based on the determinant of the manipulator

Jacobian. To compute the expected cycle time for the robot, the method includes a simulated controller, which

is optimized to estimate the performance of the physical robot. For the optimization of the workcell layout the

proposed method based on applying Gaussian penalties in local minima is compared to three existing methods

for global optimization. For the optimization of the simulated controller three different local methods are

compared along with one global.

1 INTRODUCTION

Utilizing robots in industrial tasks, such as bin-

picking and product assembly, means having the

robots work in environments, which includes a mul-

titude of entities such as machines, ﬁxtures, feeders,

bins with randomly placed objects etc. Optimizing

the layout of a workcell to ensure that all entities are

reachable can be challenging and even more so when

the location of objects are not know before hand, but

identiﬁed online using a sensor system. Trying man-

ually to adjust the workcell layout to reduce the cycle

time can be even more challenging, as a longer but

simpler trajectory might well be faster than one being

shorter but more complex.

In this paper, a formulation of the workcell lay-

out problem is suggested where the objective includes

both reachability, but also an estimate of the actual

execution times for the robot. To support scenarios

where objects poses are estimated in a bin or on a

feeder, the method will use a combination of discrete

samples over the space of expected object poses and

a manipulability measure based on the determinant

of the manipulator Jacobian. To estimate the exe-

cution times for the robot, a simulation of the robot

controller is needed. To that end, a model based

on parabolic blends (Petersen and Ellekilde, 2011) is

used, and parameters scaling the acceleration and ve-

locity limits as well as blend values are optimized for

tuning the model to match the properties of the phys-

ical robot. The input to this optimization is a collec-

tion of representative trajectories executed on the real

robot. Collecting these data can be time consuming,

hence four different optimization algorithms has been

compared to see how well they perform on a limited

set of data.

The use of the manipulability metric helps smooth

the objective compared to just using discrete samples,

but it is impossible to guarantee that the objective will

have no local minima. Also when combined with the

estimates of execution times, we risk introducing lo-

cal minima in the overall objective function. To cope

with these, this paper proposes an optimization algo-

rithm based on the complete Fill Algorithm (Morris,

1993), which seeks to escape local minima by adding

a virtual force, pushing it away. Even though the pro-

posed algorithm is not proven complete in the sense

that it will always ﬁnd the optimal solution, then we

will argue that in the limit it will be equivalent to the

Fill Algorithm. Furthermore when tested in practice

it performs very well on the layout optimization prob-

lem.

To further improve the optimization, a starting

point sampling method is suggested, using spherical

sampling around the robot. Additionally is a com-

parison done, where three other global algorithms are

tested against the suggested one, with and without

starting point sampling. The tested algorithms are

110

Iversen, T. and Ellekilde, L-P.

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima.

DOI: 10.5220/0006438201100121

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 110-121

ISBN: Not Available

chosen to represent the three main categories of global

derivative free optimization methods being determin-

istic, model-based and stochastic.

The rest of this paper is organized with related

work in Section 2, the overall objective function is

introduced in Section 3, the description of the opti-

mized simulation of the robot controller in Section 4,

a description and discussion of the proposed method

along with a presentation of the tests in Section 5, ex-

perimental results in Section 6 and a conclusion in

Section 7.

2 RELATED WORK

This section is divided in two parts, the ﬁrst being

work related to the optimization of robotic workcells

and the second part being general optimization tech-

niques.

2.1 The Robotic Workcell Layout

Problem

A problem closely related to the optimization of

robotics workcells is the facility layout problem

(FLP) (for a general introduction see (Arabani and

Farahani, 2012)). FLP is generally concerned with

placing a number of machines to minimize a cost

function, typically transportation time of objects, and

comes in many forms: Static and dynamic FLP vari-

ations are concerned with whether the cost function

is changing over time; for lower dimensionality the

Single-row facility layout problem is utilized and both

discrete and continuous versions are described in lit-

erature.

An important difference between FLP and the pre-

sented workcell optimization is that for FLPs the ver-

tical dimension of the environment is not considered,

constraining the problem to 2D position and a sin-

gle rotation around the vertical axis. Furthermore the

robot kinematics and dynamics are ignored, hence the

cost function only depends on distances and ﬂows

between machines, see e.g. (Zhang and Li, 2009),

(Gonc¸alves and Resende, 2015) or (Guan and Lin,

2016) for applications of FLP.

A 3D case of workcell optimization is found in

(Cagan et al., 1998), where components are decom-

posed into containers and the objective is to maxi-

mize the packing density. (Gueta et al., 2009) also

optimizes workcell layouts in 3D, but the objective

function only consists of a simple time measure and

spatial requirements, thus the reachability and robot

execution times are not considered.

In (Lim et al., 2016) the authors utilize 5 different

nature inspired algorithms to optimize a workcell lay-

out for assembly tasks. Although only considering the

discrete 2D case, robot kinematics are considered via

the manipulability of the robot along with execution

time and layout area. These include the same objec-

tives as used in this paper, but calculated and weighted

differently. The layout area is weighted the most, fol-

lowed by the execution time and lastly the manipu-

lability. As our manipulability measure also covers

how many objects the robot can reach, it is weighted

the highest and the execution time is then prioritized

second. Furthermore our approach depends on a more

elaborated simulation of the execution times, includ-

ing path planning and a simulation of execution times

optimized to approximate the physical robot. Min-

imizing the layout area, even though considered an

important property for transporting objects in a facil-

ity (Koopmans and Beckmann, 1957), is for now not

a part of our objective function and we rely on bound-

ary constraints to prevent components from moving

outside the space of the workcell.

2.2 Optimization Algorithms

A common property of the optimization objectives

considered in this paper is, that they are not analyt-

ically differentiable, hence we will have to rely on

methods for derivative-free optimization, for which a

general review can be found in (Rios and Sahinidis,

2013), together with an evaluation of different soft-

ware packages. Details of the chosen algorithms are

given in Sections 4.1 and 5.4 in connection with the

objective functions and the results.

A speciﬁc problem in optimization is overcoming

local minima, for which research have been carried

out within different domains. In motion planning,

(Barraquand and Latombe, 1991) uses Brownian mo-

tions to escape local minima, while (Barraquand et al.,

1992) maps local minima in the workspace with a

potential ﬁeld planner and connects those in a graph

structure which can be searched for a path. The work

in (Park and Lee, 2003) places virtual obstacles in an

environment to avoid getting stuck in local minima,

when applying a potential ﬁeld planner. In (Morris,

1993) two methods are presented, the ﬁrst being the

Breakout algorithm applying forces to the different

parameters trying to force it out of a local minima

and secondly the more abstract Fill Algorithm, which

is proven to be complete for discrete problems. The

proposed method in the paper is very similar to the

Breakout and Fill Algorithms, but is concretized with

a Gaussian penalty for ﬁlling.

Simulated annealing, ﬁrst proposed for combina-

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima

111

torial problems by (Kirkpatrick et al., 1983) and later

generalized for continuous problems by (B

elisle et al.,

1993), is a probabilistic algorithm that tries to over-

come local minima by taking steps, that does not nec-

essarily optimize the objective function, based on a

decreasing probability reminiscent of that of a an-

nealing mechanical system. The method shares prop-

erties with the also probabilistic Evolutionary Algo-

rithm (Holland, 1975) which is used for testing in sec-

tion 6.

3 OPTIMIZATION OBJECTIVE

The main goal of the optimization is to ﬁnd a layout of

the workcell that maximizes the reachability, referred

to as r(x) of the robot while minimizing the execution

times, referred to as t(x). Details of how the reacha-

bility and execution times are deﬁned can be found

below in Sections 3.1 and 3.2. Alternative criteria

such as e.g. safety (average clearance between robot

and obstacles) or energy consumption could also be

considered as objectives, but would require the deﬁni-

tion of appropriate objective functions that can either

replace or supplement the reachability and execution

time.

Having a dual purpose a scaling is required to

weigh the objectives, hence the overall objective func-

tion becomes

minimize

x∈X

f (x) = w

·t(x) − w

· r(x) (1)

where w

and w

are the scaling of reachability and

execution times, respectively. X is the space of all

feasible parameter values, meaning those where the

entities are not colliding and all ﬁxed and required

targets are reachable. x is a concrete set of parameters

corresponding to a speciﬁc pose of all entities in the

workcell. Here it is important to choose the parameter

set to be minimal, as the optimization problem may

otherwise not have a well deﬁned minimum.

While the theoretical deﬁnition of X is rather

straight forward, it is hard to deﬁne practically. To ef-

fectively restrict the solutions to X the objective func-

tion will return large values for infeasible states. To

still guide the optimization towards feasible areas this

value will depend on how many of the required targets

that are indeed reachable.

3.1 Reachability

When considering applications that include picking

randomly placed objects from feeders and bins, it is

important that the reachability measure reﬂects the

ability to pick as many objects as possible. In these

cases targets are distributed across a bounded sub-

space of SE(3), meaning that we can approximate the

distribution with a ﬁnite set of samples, S. Just count-

ing the number of samples that are reachable would

result in the objective becoming a step function and

would require a very large number of samples to rep-

resent the reachability well. To get a more smooth

function the manipulability proposed in (Yoshikawa,

1985) is used to indirectly score reachable samples

depending on how likely it is, that nearby objects

would also be reachable. This measure is computed

det(J(q)J(q)

), where J(q) is the manipulator

Jacobian and q is the joint conﬁguration for reaching

the target. For unreachable points without an inverse

kinematics solution a manipulability measure of 0 is

used. The manipulability score for a parameter set x

and sample s can thus be described as:

m(x, s) =

(

det(J(q)J(q)

), if IK(x,s) 6= 0.

0, otherwise.

(2)

where q = IK(x, s) is the inverse kinematics solu-

tion for sample s and the parameter set x. If no inverse

kinematics solution exists IK(x, s) will return 0.

To penalize conﬁgurations with close-to zero ma-

nipulability, the measure can be raised to a constant

0 < p < 1, where we empirically found that p =

gives good results for our scenarios. The complete

reachability score is then computed over all samples

r(x) =

N−1

∑

m(x, s)

(3)

where N is the number of samples in S.

3.2 Execution Times

When working in industrial environments, time spent

moving a robotic arm is generally a limiting factor

when considering cycle times and productivity. It is

therefore considered in the objective function by

t(x) =

N−1

∑

i=0

(x) (4)

where M is the number of cycles, equal to the

number of reachable samples, and t

(x) is the time

taken for the cycle associated with the i

th sample and

estimated using the simulation optimized to mimic the

physical robot, as described in Section 4.

To actually deﬁne the robot motions in a cycle a

motion planner is used to determine the trajectories.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

112

A challenge with classic planning techniques, such as

the Rapidly-Exploring Random Tree (LaValle, 1998),

is that they are probabilistic, meaning that the objec-

tive score may change between two evaluations. To

overcome this problem the deterministic TrajOpt al-

gorithm is chosen, see (Schulman et al., 2014), as

it has shown promising results to similar cases in

(Iversen and Ellekilde, 2017). To remove further

noise in the objective function, the upper and lower

10% of execution times are removed when calculat-

ing the mean execution time of all cycles to get rid of

outliers.

4 OPTIMIZATION OF

EXECUTION TIMES

SIMULATION

To minimize execution times in the workcell opti-

mization it is necessary to efﬁciently estimate the

duration of robot motions. Some manufacturers of-

fer ofﬂine simulations of their robot controllers, e.g.

(Universal Robots, 2017), (ABB Robotics, 2017) and

(FANUC, 2017), but these work in real time and are

not easily integrated into an optimization problem. To

have a more computationally efﬁcient estimate of ex-

ecution times and avoid a full dynamic simulation of

the robot, the model of (Petersen and Ellekilde, 2011)

based on parabolic blends and velocity and accelera-

tion limits is used.

Real world execution times might be inﬂuenced

by other things beside acceleration and velocity lim-

its, hence the model is not completely accurate. How-

ever, to enhance predictions an optimization of the

method is implemented, where the parameters to be

optimized are velocity and acceleration scalings along

with a scaling of the blends distances. The accel-

eration and velocity scalings are multiplied with the

given accelerations and velocities limits when run-

ning the model, while the blend scaling is used to

alter the maximum allowed deviation when blending

through conﬁgurations. While some robots, such as

the Universal Robots, blends in Cartesian coordinates

while (Petersen and Ellekilde, 2011) utilizes blends

in conﬁguration space, the blend scaling parameter

helps adapt between the two. Blending in different

spaces means that paths joint conﬁguration will dif-

fer from each other, however only the time taken to

move the robot is needed and the path differences can

be ignored.

The objective function to optimize for tuning the

simulation thus becomes

minimize

α,β,γ

N−1

∑

i=0

(α, β, γ) −t

k (5)

where N is the number of executed paths, t

and

are respectively the time estimated by the parabolic

blend method and the actual execution time on the

robot for the i

th path. α, β and γ are the velocity, ac-

celeration and blend scalings, respectively.

Collecting the paths for optimizing the simulation

parameters can be time consuming, hence it is de-

sirable to compare how different optimization meth-

ods performs on the same set of data. Section 4.1

presents these results for four different optimization

algorithms.

4.1 Test of Execution Times Simulation

250 paths are executed on a real-life Universal Robots

UR5 robot to obtain data, of which 80% are used for

training and 20% for veriﬁcation. The paths should

be representative for the problem, hence they are ex-

tracted from running the application with an unopti-

mized workcell.

Assuming that the optimization problem is rather

well-behaved, four optimization algorithms are used

to optimize the parameters. The ﬁrst two are the con-

jugate gradient descent (CGD) and Broyden-Fletcher-

Goldfarb-Shanno (BFGS) algorithms both from the

dlib library (King, 2009). These are purely local and

tested to determine the impact of using a numerical

estimate of the gradient.

Also from (King, 2009) BOBYQA (Powell, 2009)

is tested as it have shown good performance in (Rios

and Sahinidis, 2013). BOBYQA relies on an inter-

polation forming quadratic models of a trust region

and is derivative free. Still being rather local, it uses

a more complex analysis of the neighborhood com-

pared to that of CGD and BFGS.

To test a global algorithm, RBFopt (Costa and

Nannicini, 2014) is chosen to see whether a global

approach will converge to the same result as the local

ones. RBFopt uses Radial Basis functions to approxi-

mate the objective function and uses multiple approx-

imations with cross validation to select the best ﬁt.

Updating the approximation is done with balancing

exploration and exploitation on a global scale, mak-

ing it a global solver in contrast to the other three.

The algorithms are tested with 500 different seed

points and their end results are veriﬁed. Using dif-

ferent random seed points for CGD and BFGS is

straight forward, but it is somewhat more complex

for BOBYQA and RBFopt. Since BOBYQA requires

a trust region around seeds it is necessary to limit

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima

113

the sampling space. Thus, when using a thrust re-

gion of 1/10 of the range of the parameters, the seed

points for BOBYQA can only be placed in mid 8/10

of the range. To gain a fair comparison, seed points

for CGD and BFGS are therefore also only placed in

this space. RBFopt relies on multiple seed points to

form the initial function approximation. To generate

these seed points RBFopt uses Latin Hypercube sam-

pling. Given the different seed sampling methods, it

is hard to do a completely fair comparison, but the

differences should be close to negligible.

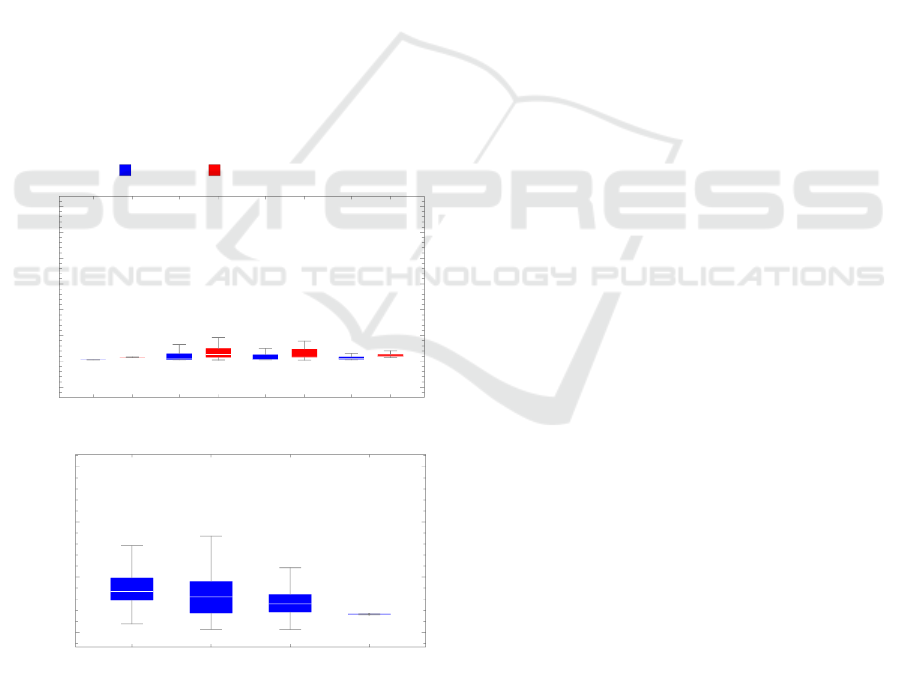
Results from the test can be seen in Figure 1 and

Table 1, where scores obtained on training data and

on veriﬁcation data are presented along with number

of objective function evaluations. BOBYQA manages

to ﬁnd the best set of parameters, both for the evalu-

ated objective function and for the veriﬁcation. It does

so at a cost though, as it requires more than twice as

many function evaluations as RBFopt, for ﬁnding a

slightly better solution. In general all solutions varies

under 0.2 seconds in mean time from the executed

path times on the real robot, which given the length

of the executed paths of 6-8 seconds are a maximum

error of 3% and down to 1.25% for BOBYQA.

Training Verification

••••••••••••••••

•

••

•

••

•

••

•

••

•

••

•

••

•

••

•

•••

•

••

•

••

•

BOBYQA CG BFGS RBFopt

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

f(x)

(a) Scores.

•

BOBYQA CG BFGS RBFopt

500

1000

1500

Function Evaluations

(b) Number of evaluations.

Figure 1: Boxplots showing ﬁnal scores on the training and

veriﬁcation data sets and number of function evaluations of

each algorithm on the robot controller simulation optimiza-

tion problem.

5 GLOBAL WORKCELL LAYOUT

OPTIMIZATION

This section describes the actual workcell optimiza-

tion. To illustrate the method two scenarios are ﬁrst

described and the challenge in optimizing the objec-

tive is analysed. Secondly the section presents the

proposed method of using Gaussian penalties for es-

caping local minima, followed by a strategy for sam-

pling of starting points utilizing knowledge of the

workcell. At the end the section introduces alterna-

tive optimization algorithms used for comparison in

the experiment section.

5.1 Scenarios

Two scenarios are used for the workcell optimization.

Both scenarios include picking randomly placed ob-

jects based on camera information and placing them

for further operations.

5.1.1 Scenario 1: Bin Picking

The bin picking scenario (BP), Figure 2(a), contains

a 6 degree of freedom (DOF) Universal Robots UR5,

a bin with randomly placed objects, a re-picking sta-

tion and a place table. The robot picks objects from

the bin and places them on the re-picking station for

a more precise grip, before placing on the table. The

reachability for this scenario is calculated from ob-

jects randomly placed in the bin and the execution

times consists of moving the robot from the grasp po-

sition via the re-picking station and to the place table.

To reduce redundancy in the optimization the robot is

ﬁxed in the workcell, but the three other components

can be translated in XYZ and rotated around Z, giv-

ing a total of 12 parameters to optimize. The lower

and upper bounds is set to assure that no part of the

components are placed outside the frame comprising

the workcell. Reachability in this scene is weighted

ten times higher than execution times in the objective

function.

5.1.2 Scenario 2: Industrial Assembly

The industrial assembly scenario (IA), Figure 2(b),

consists of a Kuka LBR IIWA 7 robot with 7 DOF

and an attached Weiss WGS25 gripper, an Adept

AnyFeeder with randomly placed objects on its feed

surface, two feeders with ﬁxed object positions and

a ﬁxture for assembling all the parts. Three different

objects are picked from the AnyFeeder and one object

from each of the two feeders with ﬁxed objects. The

objects are assembled in the ﬁxture by simply placing

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

114

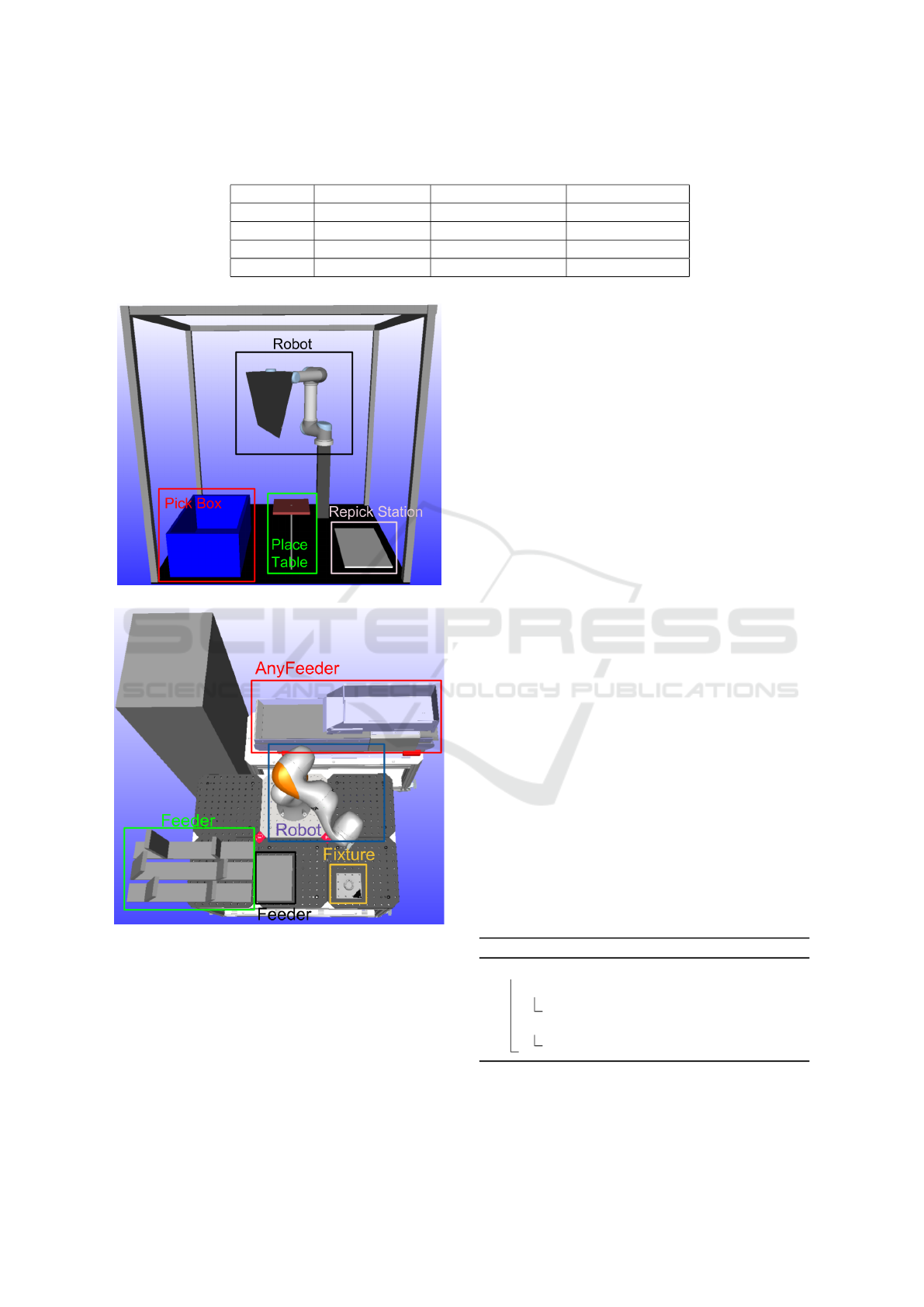
Table 1: Results of the robot controller simulator optimization after 250 runs, shown as mean scores on the training- and

veriﬁcation set and function evaluations along with their 99% conﬁdence intervals.

Training Scores Veriﬁcation Scores Fnc. Evaluations

BOBYQA 0.106±0.00055 0.116±0.00110 407.1±19.4

CGD 0.127±0.00944 0.140±0.00943 340.7±22

BFGS 0.174±0.04630 0.186±0.04658 255.6±12.5

RBFopt 0.113±0.00120 0.123±0.00120 164.4±0.2

(a) Bin picking scenario

(b) Industrial assembly scenario.

Figure 2: The two scenes used for workcell layout optimiza-

tion. Figure 2(a) shows the Bin Picking scenario and Figure

2(b) shows the industrial assembly scenario.

them on top of each other. The AnyFeeder is ﬁxed

in this scenario, meaning that the robot, the ﬁxture

and the two feeders can be translated in XYZ and ro-

tated around the Z axis, giving a total of 16 parame-

ters to optimize. The bounds make sure that none of

the components can leave the platform on which they

are located, but they can be raised above it to a cer-

tain height. The reachability is weighted 100 times

more than the execution time in this scene, as execu-

tion times are longer than in the BP scenario due the

higher number of motions. As the robot is a 7 DOF

robot, there might potentially exist inﬁnitely many in-

verse kinematics solutions to each of the transforma-

tions the TCP has to reach. One solution is to use

a Jacobian based inverse kinematics solver (see e.g.

(Buss, 2004)), ﬁnding only a single solution which

may risk being in collision or violate joint limits. In-

stead an inverse kinematics solver is used, where the

fourth joint is given an arbitrary conﬁguration after

which a closed form solver gives up to 8 possible in-

verse kinematics solutions. For the ﬁrst pick position

these are sorted favoring solutions where all joints are

close to the middle of their limits, while for the next

positions, solutions are sorted based on their distance

in joint space to the previous chosen solution.

5.2 Gaussian Penalty Optimization

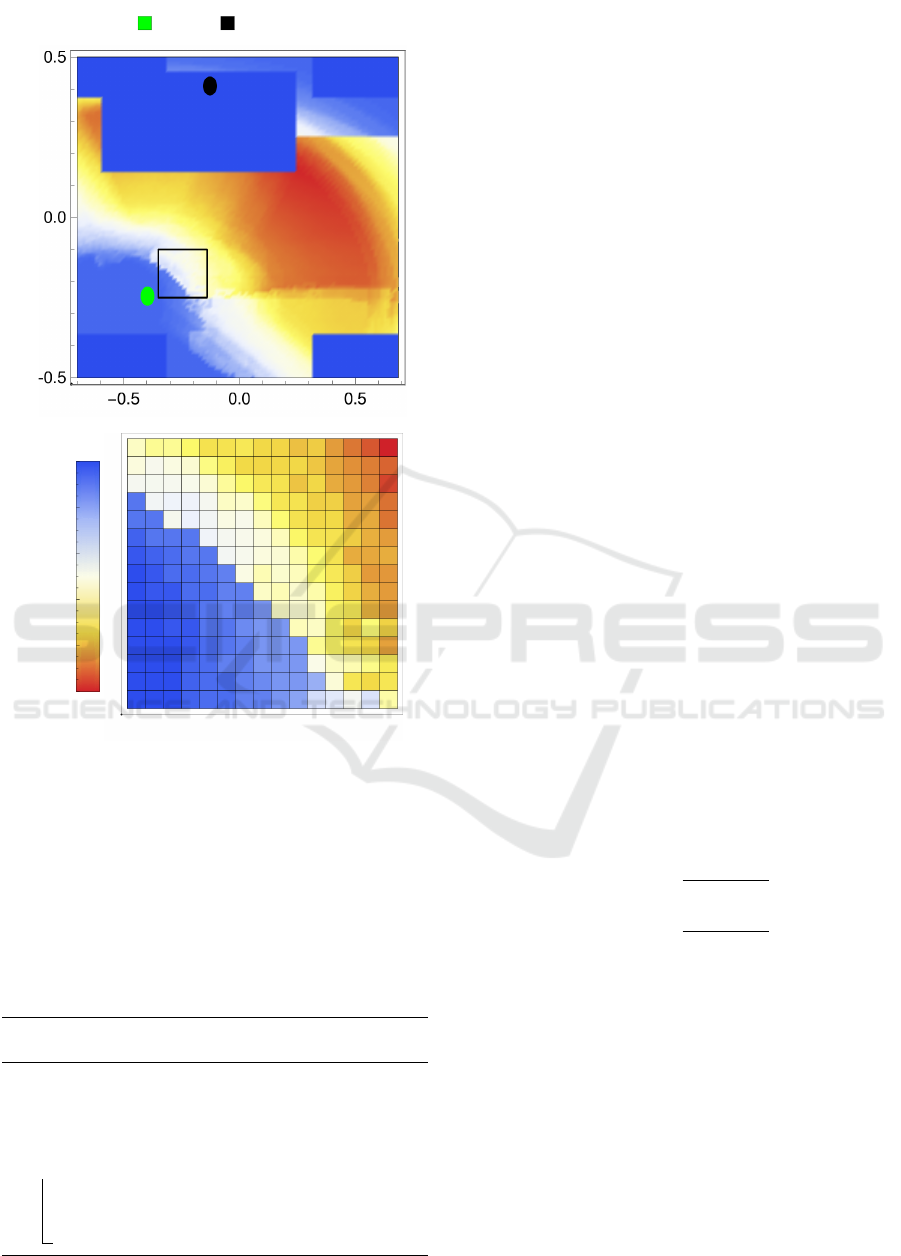
Slices of the objective function can be visualized as

in Figure 3, where a discrete heat map is used to il-

lustrate the objective function as the XY position of

the pick area in the BP scenario is changed. From

these views it becomes evident that the objective suf-

fers from local minima, especially in the region con-

necting the blue to the red areas. These local min-

ima will create problems for local optimization meth-

ods. Since the local minima appears to be shallow,

the proposed method attempts to locally modify the

objective and is based on the Fill Algorithm (Morris,

1993), presented in Algorithm 1.

Algorithm 1: Fill Algorithm.

while current state IS NOT solution do

if current state IS NOT local minimum then

make local change reducing cost

else

increase cost of current state

The Fill Algorithm is only proven complete in dis-

crete cases, but we will argue that as the resolution

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima

115

Robot Place

Y[m]

X[m]

0.0

0.2

0.4

0.6

0.8

1.0

Figure 3: A slice of the discreteized objective function when

ﬁxing all parameters of the BP scenario except XY transla-

tion of the pick box, along with an example close up of the

marked square.

goes towards inﬁnity, the found solution will go to-

wards the solution in the continuous case. In the con-

tinuous case we cannot just increase the cost of a sin-

gle state, but will rather locally modify the objective

using a Gaussian kernel. This idea is illustrated in

Algorithm 2.

Algorithm 2: GPopt - Gaussian Penalty Optimiza-

tion.

Input:

Starting guess x, Objective function f (x)

f (x) ← f (x)

ˆx ← x

while NOT DONE do

˜x ← OptimizeLocal( ˆx,

f (x))

f (x) ←

f (x) + N ( ˜x, | ˜x − ˆx| · τ).

ˆx ← ˜x

Informally the algorithm, which is referred to as

Gaussian Penalty Optimization (GPopt), searches for

a local minimum from the current starting point us-

ing a local optimization algorithm and penalizes that

minimum in the objective function with a Gaussian

normal distribution. The standard deviation is chosen

based on the distance between the local minimum and

the starting point, multiplied by a constant, τ, depend-

ing on the range of the objective function.

The stopping criterion of the algorithm can be

chosen as either a maximum of time, iterations or im-

provement ratio. In this paper the local optimization

is done with BOBYQA while the stopping criterion is

based on the improvement ratio.

5.3 Improved Sampling Utilizing Robot

Workspace Knowledge

Unlike general global optimization methods, GPopt

relies on ﬁnding a feasible starting point from which

it will search for a solution. The quality of the chosen

starting point is therefore important for how quickly

the algorithm ﬁnds the solution. The simplest strategy

is to randomly sample until a feasible starting point

is found, but by integrating some knowledge of the

workcell into the sampling, better starting points can

be found.

To that end, a sampling strategy exploiting the

robots reach is implemented. Components are sam-

pled in a band on a sphere around the robots base.

One way of doing so, is to randomly sample spher-

ical coordinates θ and φ, but this approach is biased

towards the poles. Instead the method proposed by

(Marsaglia et al., 1972) is used, where random points

and x

are sampled from uniform distributions (-

1, 1) and rejected if x

+ x

≥ 1, for the not-rejected

points

x = 2x

1 − x

− x

(6)

y = 2x

1 − x

− x

(7)

z = 1 − 2



+ x



(8)

have a uniform distribution on the unit sphere and can

be scaled to a desired radius. As only a band around

the robot is wanted and not a full sphere, coordinates

are translated to spherical coordinates and rejected de-

pending on limits of θ.

This method do neglect parts of the sampling

space, but it seems a fair assumption that feasible

starting points lie within a sphere surrounding the

robot, and since an arbitrary number of starting points

can be sampled, the method is asymptotically com-

plete in the space covered by this sphere.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

116

In the IA scenario, where the AnyFeeder is ﬁxed,

the robots base coordinates are ﬁrst sampled in a

sphere around the AnyFeeder, and afterwards com-

ponents in the scene are sampled around the robot.

5.4 Algorithms

The algorithms tested against GPopt, is described un-

derneath. Only global derivative-free algorithms are

chosen, assuming there exists a lot of local minima in

the objective function and the derivative only can be

found numerically. To cover the spectrum of different

types of optimization algorithms, one deterministic,

one model-based and one stochastic algorithm is cho-

sen.

5.4.1 DIRECT

The DIRECT (DIviding hyperRECTangle) algorithm

(Jones et al., 1993) is chosen to represent the deter-

ministic category. DIRECT is a development of the

classic Lipschitzian based methods, where a known

Lipschitz constant is used to partition the search space

until a solution is found. The two drawbacks of these

methods are that the Lipschitz constant is unknown

and that function evaluations increases exponentially

with the parameter space. DIRECT ﬁxes these prob-

lems by terminating once a predeﬁned limit of itera-

tions is reached and evaluating function values in the

center of partitions instead of the extreme points. The

implementation of the DIRECT algorithm is from the

DAKOTA library, see (Adams et al., 2016).

5.4.2 RBFopt

RBFopt (Radial Basis Function optimization), (Gut-

mann, 2001), is the chosen model-based approach. It

relies on Radial Basis Functions as surrogate mod-

els for approximating the objective function and guid-

ing the search in the right direction. The model

is reﬁned to balance exploitation and exploration on

global scale, and the used implementation is from

(Costa and Nannicini, 2014).

5.4.3 EA

The EA (Evolutionary Algorithm) is chosen as the

stochastic optimization algorithm. It was ﬁrst intro-

duced in (Holland, 1975) and relies on an approach

resembling that of natural selection and reproduction

guided by rules dictating survival of the ﬁttest. Indi-

viduals are associated with a ﬁtness score (objective

function value) that probabilistically determines their

chance of survival and reproduction. The used imple-

mentation is also from the DAKOTA library.

6 EXPERIMENTAL RESULTS

This section presents the experimental results of the

paper. In Section 6.1 a small experiment determining

the number of sample points to use is described. This

is then followed by the actual workcell optimization

in Section 6.2, which includes both some quantita-

tive results comparing the different optimization algo-

rithm and qualitative results of the workcell layouts.

6.1 Test of Number of Objects to

Simulate

To determine how the number of samples used in the

objective function inﬂuences the quality a set of ex-

periments has been performed where a random work-

cell layout is generated and the objective function is

calculated for 1 and up to 150 samples. In Figure 4 re-

sults are presented, where the objective function eval-

uations can be seen.

0 20 40 60 80 100 120 140

0.10

0.15

0.20

0.25

0.30

0.35

0.40

# Objects

f(x)

(a) BP

0 50 100 150

-8

-6

-4

-2

# Objects

f(x)

(b) IA

Figure 4: Evaluations the objective function on different

number of simulated objects.

The differences in evaluations never reach 0 in any

of the two scenarios, but manages to settle down on a

more stable level when 30 objects are used in the BP

scenario and 40 in the IA. These numbers of objects

are therefore used in the optimization.

6.2 Test of Algorithms on Workcell

Layout

Figure 5 shows how the different optimization algo-

rithms improves the objective as a function of the

number of evaluations.

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima

117

Evaluating the objective score per simulated ob-

ject takes approximately 0.85 and 1.25 seconds for the

two scenarios respectively. Given that 30 and 40 ob-

jects are simulated in each of the scenarios per func-

tion evaluation, is the computational burden of the op-

timization algorithms themselves considered negligi-

ble. Hence, only the number of evaluated scenarios

are examined in the results.

Since the RBFopt, EA and GPopt algorithms all

depends on a sampling they have been run 50 times

to reliably compute the means and standard devia-

tions illustrated in the ﬁgure. For the GPopt algorithm

a standard version using random samples as well as

a variation, GPopt W. Samling, using the improved

sampling technique of Section 5.3 are included. The

DIRECT method is deterministic, hence has no vari-

ance associated. In Table 2 the algorithms are com-

pared based on their ﬁnal best score for each run and

the number of valid evaluations, meaning number of

objective function evaluations where the workcell lay-

out did not result in collisions or lacking inverse kine-

matics solutions for required target positions.

All in all the EA and RBFopt performs the worst

in the two scenarios looking at both the function

scores and the number of valid evaluations, where

EA in average only evaluates 0.56% valid work-

cell layouts on the BP scenario, and RBFopt only

6.47%. These numbers are presumably also the rea-

son for their low objective function scores, as the in-

valid workcell layouts gives little or no information of

where to look for good workcell layouts in the param-

eter space. The DIRECT algorithm has more valid

evaluations than the two aforementioned algorithms,

but not as many as the two proposed methods. Even

so, it manages to ﬁnd an equally good solution in the

IA scenario while a bit worse on the BP scenario.

GPopt with and without spherical sampling ﬁnds

the best solutions. For the BP scenario, utilizing

workspace knowledge for sampling is a bigger ad-

vantage than in the IA scenario, where results with

and without are similar. Noteworthy for both scenar-

ios, is that GPopt W. Sampling evaluates more invalid

workcell layouts than without, but still reaches equal

or better scores, indicating that the sampler manages

RBFopt

Direct

GPopt

GPopt W. Sampling

0 500 1000 1500 2000

-2

Evaluations

f(x)

(a) BP

RBFopt

Direct

GPopt

GPopt W. Sampling

0 500 1000 1500 2000

-200

-100

100

200

300

400

Evaluations

f(x)

(b) IA

Figure 5: Workcell optimization results for the two scenar-

ios, results are shown as the mean along with 2 standard

deviations of the mean. The results are generated based on

50 optimizations for each of the algorithms.

to ﬁnd more optimal layouts that lies in between in-

valid layouts in the parameter space.

In Figure 7 a single run on the BP scenario for

each of the algorithms are shown. Each orange dot

corresponds to the score of a single evaluation and the

blue line shows the minimum. Corresponding well

with results in Table 2, EA and RBFopt evaluates a lot

of invalid parameter sets. EAs evaluations seems to

be coming rather sporadically whereas RBFopt man-

ages to evaluate chunks of valid parameters sets. DI-

RECT ﬁnds more and more valid parameter sets as it

moves along, due to its exploitation strategy. For the

GPopt with and without spherical sampling, 5 and 6

start points are investigated respectively, where each

starting leads to a lot of local minima. For the GPopt

one optimization from starting point to the found min-

ima is marked inside two dashed lines. Notable is

that the spherical sampling has better starting points,

therefore also reaches a better result in the end.

The workcell layouts that get the highest scores

Table 2: Results of workcell optimization on the two scenes. Results are shown as mean along with ± two standard deviations

for the evaluation scores.

BP IA

Valid Evaluations Scores Valid Evaluations Score

EA 0.56% 0.64463±0.871404 2.07% -218.457±7.94465

RBFopt 6.47% -0.0495001±0.747906 18.43% -229.132±4.35685

DIRECT 72.3% -0.45452±0 50.91% -234.435±0

GPopt 85.15% -0.894707±0.386961 88.45% -234.939±1.68963

GPopt W. Sampling 80.77% -1.49056±0.0978638 87.22% -234.944±4.90666

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

118

(a) Bin Picking

(b) Industrial Assembly

Figure 6: The best workcell layouts accomplished with the

optimization algorithms, both come from GPopt with spher-

ical sampling.

can be seen in Figure 6. Both layouts have compo-

nents placed in a circle around the robot, in the band

where reachability of the robot is highest and placed

close together to lower the execution times as much

as possible. In both scenarios are components rear-

ranged compared to Figure 2 to accommodate for the

order in which objects are moved. Furthermore is the

robot placed higher than the other components in both

scenarios, presumably to gain even more reachability.

7 CONCLUSION

This paper has presented the problem of optimizing

workcell layouts for two different industrial work-

cell setups, and suggested an optimization method

for solving such problems, where a lot of local min-

ima exist. The objective function is dependent on the

Samples Minimum

0 500 1000 1500 2000

-2

INV

Evaluations

f(x)

(a) EA

0 500 1000 1500 2000

-2

INV

Evaluations

f(x)

(b) RBFopt

0 500 1000 1500 2000

-2

INV

Evaluations

f(x)

0 500 1000 1500 2000

-2

INV

Evaluations

f(x)

(d) GPopt

0 500 1000 1500 2000

-2

INV

Evaluations

f(x)

(e) GPopt with spherical sampling

Figure 7: Evaluations of the 5 algorithms on the BP sce-

nario. Invalid parameter evaluations are deﬁned as INV in

the plots.

robots reachability and time spent on moving objects

in the workcell estimated by an optimized simulation

of the robot controller. Based on the Fill Algorithm,

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima

119

which is proven to ﬁnd an optimum if one exists,

this paper suggests an optimization algorithm that it-

eratively optimizes towards local minima and tries

to escape by penalizing the state by adding a Gaus-

sian kernel to the objective function. As the algo-

rithm depends on a starting point, a sampling method

is suggested that samples workcell components in a

sphere around the robot to maximize reachability of

the robot. The algorithm is tested against other global

optimization methods and a performance increase is

demonstrated on the two scenarios.

REFERENCES

ABB Robotics (2017). Robotstudio. http://new.abb.com/pr

oducts/robotics/robotstudio. [Online; accessed 10-

May-2017].

Adams, B. M., Coleman, K., Hooper, R. W., Khuwaileh,

B. A., Lewis, A., Smith, R. C., Swiler, L. P., Turin-

sky, P. J., and Williams, B. J. (2016). User Guidelines

and Best Practices for CASL VUQ Analysis Using

Dakota. Technical report, Sandia National Laborato-

ries (SNL-NM), Albuquerque, NM (United States).

Arabani, A. B. and Farahani, R. Z. (2012). Facility lo-

cation dynamics: An overview of classiﬁcations and

applications. Computers & Industrial Engineering,

62(1):408–420.

Barraquand, J., Langlois, B., and Latombe, J.-C. (1992).

Numerical potential ﬁeld techniques for robot path

planning. IEEE Transactions on Systems, Man, and

Cybernetics, 22(2):224–241.

Barraquand, J. and Latombe, J.-C. (1991). Robot mo-

tion planning: A distributed representation approach.

The International Journal of Robotics Research,

10(6):628–649.

elisle, C. J., Romeijn, H. E., and Smith, R. L. (1993). Hit-

and-run algorithms for generating multivariate dis-

tributions. Mathematics of Operations Research,

18(2):255–266.

Buss, S. R. (2004). Introduction to inverse kinematics with

jacobian transpose, pseudoinverse and damped least

squares methods. IEEE Journal of Robotics and Au-

tomation, 17(1-19):16.

Cagan, J., Degentesh, D., and Yin, S. (1998). A sim-

ulated annealing-based algorithm using hierarchical

models for general three-dimensional component lay-

out. Computer-aided design, 30(10):781–790.

Costa, A. and Nannicini, G. (2014). RBFOpt: an open-

source library for black-box optimization with costly

function evaluations. Optimization Online, (4538).

FANUC (2017). ROBOGUIDE - FANUC Simulation Soft-

ware. http://robot.fanucamerica.com/products/vision-

software/roboguide-simulation-software.aspx. [On-

line; accessed 10-May-2017].

Gonc¸alves, J. F. and Resende, M. G. (2015). A biased

random-key genetic algorithm for the unequal area fa-

cility layout problem. European Journal of Opera-

tional Research, 246(1):86–107.

Guan, J. and Lin, G. (2016). Hybridizing variable neigh-

borhood search with ant colony optimization for solv-

ing the single row facility layout problem. European

Journal of Operational Research, 248(3):899–909.

Gueta, L. B., Chiba, R., Arai, T., Ueyama, T., and Ota, J.

(2009). Compact design of work cell with robot arm

and positioning table under a task completion time

constraint. In Intelligent Robots and Systems, 2009.

IROS 2009. IEEE/RSJ International Conference on,

pages 807–813. IEEE.

Gutmann, H.-M. (2001). A radial basis function method for

global optimization. Journal of global optimization,

19(3):201–227.

Holland, J. H. (1975). Adaptation in natural and artiﬁcial

systems. an introductory analysis with application to

biology, control, and artiﬁcial intelligence. Ann Arbor,

MI: University of Michigan Press.

Iversen, T. F. and Ellekilde, L.-P. (2017). Benchmarking

motion planning algorithms for bin-picking applica-

tions. Industrial Robot: An International Journal,

44(2):189–197.

Jones, D. R., Perttunen, C. D., and Stuckman, B. E. (1993).

Lipschitzian optimization without the lipschitz con-

stant. Journal of Optimization Theory and Applica-

tions, 79(1):157–181.

King, D. E. (2009). Dlib-ml: A machine learning

toolkit. Journal of Machine Learning Research,

10(Jul):1755–1758.

Kirkpatrick, S., Gelatt, C. D., Vecchi, M. P., et al.

(1983). Optimization by simulated annealing. Sci-

ence, 220(4598):671–680.

Koopmans, T. C. and Beckmann, M. (1957). Assign-

ment problems and the location of economic activi-

ties. Econometrica: journal of the Econometric Soci-

ety, 25(1):53–76.

LaValle, S. M. (1998). Rapidly-exploring random trees a

new tool for path planning. Tech. rep., Iowa State

Univ., Comp Sci. Dept.

Lim, Z. Y., Ponnambalam, S., and Izui, K. (2016). Na-

ture inspired algorithms to optimize robot workcell

layouts. Applied Soft Computing, 49:570–589.

Marsaglia, G. et al. (1972). Choosing a point from the sur-

face of a sphere. The Annals of Mathematical Statis-

tics, 43(2):645–646.

Morris, P. (1993). The breakout method for escaping from

local minima. In Proceedings of the Eleventh National

Conference on Articial Intelligence, volume 93, pages

40–45.

Park, M. G. and Lee, M. C. (2003). A new technique

to escape local minimum in artiﬁcial potential ﬁeld

based path planning. KSME international journal,

17(12):1876–1885.

Petersen, H. G. and Ellekilde, L.-P. (2011). Modeling

motions of a KUKA KR30 robot. Technical report,

The Maersk Mc-Kinney Moller Institute, University

of Southern Denmark.

Powell, M. J. (2009). The BOBYQA algorithm for bound

constrained optimization without derivatives. Techni-

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

120

cal report, Department of Applied Mathematics and

Theoretical Physics, University of Cambridge.

Rios, L. M. and Sahinidis, N. V. (2013). Derivative-free

optimization: a review of algorithms and comparison

of software implementations. Journal of Global Opti-

mization, 56(3):1247–1293.

Schulman, J., Duan, Y., Ho, J., Lee, A., Awwal, I., Brad-

low, H., Pan, J., Patil, S., Goldberg, K., and Abbeel, P.

(2014). Motion planning with sequential convex op-

timization and convex collision checking. The Inter-

national Journal of Robotics Research, 33(9):1251–

1270.

Universal Robots (2017). Universal robots simulator soft-

ware. https://www.universal-robots.com/download.

[Online; accessed 10-May-2017].

Yoshikawa, T. (1985). Manipulability of robotic mech-

anisms. The international journal of Robotics Re-

search, 4(2):3–9.

Zhang, J. and Li, A.-P. (2009). Genetic algorithm for robot

workcell layout problem. In Software Engineering,

2009. WCSE’09. WRI World Congress on, volume 4,

pages 460–464. IEEE.

Optimization for Solving Workcell Layouts using Gaussian Penalties for Escaping Local Minima

121