
Considerations on 2D-Bin Packing Problem: Is the Order of
Placement a Relevant Factor?
Gia Thuan Lam
1
, Viet Anh Ho
2
and Doina Logofătu
2
1
Vietnamese-German University, Le Lai Street, Hoa Phu Ward, Thu Dau Mot City, Binh Duong Province, Vietnam
2
Frankfurt University of Applied Sciences, Nibelungenplatz 1, Frankfurt am Main, Germany
Keywords: 2D Bin Packing, Order of Placement, Placement Algorithm, Optimization Techniques, First-Fit, Area
Decreasing Order.
Abstract: The problem of packing a given sequence of items of 2-dimensional (2D) geometric shapes into a minimum
number of rectangle bins of given dimensions is called the 2D bin packing problem. This problem has
various applications across many industries such as steel-, paper- and wood- industries where objects of
certain shapes are needed to be cut from large rectangle panels with the most efficient use of materials. This
problem, however, belongs to the class of NP-Hard problems, implying that no perfect solution exists. Many
proposed solutions involve the use of advanced metaheuristic search techniques such as Local Search,
Simulated Annealing or Genetic Algorithm, but most of them are still greedy-based, which means some
greedy technique such as First-Fit is still used as their core placement algorithm and optimization techniques
are employed only to search for a good ordering or orientation (rotation angles) of the objects so that the
placement procedure can yield the best possible results. Practice has shown that greedy placement algorithm
on the simple area decreasing order can produce excellent results comparable to those on orderings
generated from advanced optimization techniques. This paper discusses the relevance of the order of
placement in the 2D bin packing problem.
1 INTRODUCTION
The 2-dimensional (2D) bin packing is the problem
of packing a list of objects of different geometric
shapes into rectangle bins of fixed dimensions while
minimizing the number of used bins (Lodi et al.,
2010). It is related to many important problems
across a variety of practical areas. In steel industry,
for example, to cut out metal components of
different shapes from a metal sheet, the engineers
always try to minimize the wasted material that will
be thrown away. This problem is a generalization
from the well-known 1D packing problem and can
be generalized to even higher dimensions such as 3D
packing problem which has important applications
in transportation or delivery service where all items
should be transferred using as few vehicles as
possible. Let’s consider the following example.
A hand-made shop needs to produce some
objects of metal in different shapes. These objects
will be used to decorate their new store. This shop
always buys metal panels in forms of rectangle of
fixed dimensions and the objects must be cut from
them in a way that the amount of wasted material
can be minimized.
Figure 1 shows an example where the shop wants
to produce 20 objects of different shapes. A simple
but inefficient placement of objects as shown in
figure 1 costs 3 panels of metal and the wasted area
(blank area) is large. As a result, it makes the price
of material much more expensive.
Figure 1: Example for simple placement.
Figure 2 shows a better placement in which the
280
Lam, G., Ho, V. and Logofatu, D.
Considerations on 2D-Bin Packing Problem: Is the Order of Placement a Relevant Factor?.
DOI: 10.5220/0006440302800287
In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 280-287
ISBN: 978-989-758-265-3
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

number of panels can be reduced to 2, which is
visually an optimal solution. The wasted area is
much smaller compared to that in figure 1. That
means the material has been utilized efficiently. In
mass production, the amount of saved material may
be significant and generate a huge economic value.
Figure 2: A better placement for items from figure 1.
Due to its large application domain, 2D bin
packing has been one of the core research topics for
many years. However, in computational complexity
theory, it is a combinatorial NP-hard problem.
Hence no optimal deterministic algorithms exist.
Although many sophisticated algorithms have been
developed for it, naïve and simple greedy
approaches such as Best-Fit and First-Fit (Dósa and
Sgall, 1998) strategies seem to yield very good
results in practice compared to those using advanced
search techniques such as Local Search, Simulated
Annealing or Evolutionary Approaches, leading us
to the question whether those advanced techniques
are useful in this problem.
Analyzing many previous algorithms, we
recognize that numerous algorithms in this topic
followed a common pattern. They only concentrated
on improving the order of placement of objects. That
is the sequence deciding which objects should be
placed before others. This paper will demonstrate
that the order of placement it not a useful factor in
solving this problem by testing the First-Fit
algorithm on some random permutations of objects
and comparing the results with that of the area
decreasing order. The reason why First-Fit, a naïve
and simple algorithm, is used and why the area
decreasing order is used as a standard for
comparison will be shown in section 3. In section 4,
an implementation of the First-Fit algorithm will be
presented and most importantly, experimental results
to prove our claim will be presented in section 5.
2 PROBLEM DESCRIPTION
The 2D bin packing is divided into 2 main branches:
one only concerned with rectangle objects, namely
regular bin packing, and the other concerned with
both rectangle and non-rectangle objects called
irregular bin packing which is the focus of our study.
A solution to this problem will process a set of n
objects, each is represented as a sequence of points
P
i
= {p
1
, p
2
, p
3
… p
k
} for some k forming a polygon
of k vertexes and 1 ≤ i ≤ n, and output a placement
of objects inside rectangle bins of given dimensions.
The placement must satisfy the condition that no two
objects intersect with each other and the number of
bin used must be as minimal as possible.
Figure 3 and figure 4 shows an example of the
input and output of a 2D bin packing algorithm,
respectively. The first line of the input gives
dimensions, the width and height of all rectangle
bins, the second line represents the number of items
to place n, followed by n lines, each of which
describes an item as a polygon by listing a sequence
of points.
Figure 3: Sample input for 5 items.
The output in figure 4 is simply a graphical
visualization of an optimal placement. In this case,
we only need 1 bin, which is also an optimal
solution.
Figure 4: Sample output for the placement of 5 items.
Unlike the above example where an optimal
solution can be found easily, the complexity of this
problem in theory is NP-Hard, implying that it is
only possible to find a good approximation in
general case.
Considerations on 2D-Bin Packing Problem: Is the Order of Placement a Relevant Factor?
281

3 BACKGROUND
Both the regular and irregular 2D bin packing
problems have been intensively studied (Lodi et al.,
2002; Bennell et al., 2008). Albeit it is impossible to
solve this problem optimally, numerous efficient
solutions have been proposed and proved extremely
sufficient in practice, especially for the regular
version. The most fundamental but also an excellent
approach in practice is the First-Fit algorithm.
Although a variety of more advanced algorithms
using complicated optimization techniques such as
Local Search (Alvim et al., 1999), Simulated
Annealing (Rao and Iyengar, 1994) or Evolutionary
Algorithm (Junkermeier, 2015) have been
developed, the majority are still based on some
greedy algorithm like First-Fit as the placement
procedure. Different search techniques are
commonly used only to find a good ordering or
orientation (rotation angles) of objects so that the
core placement procedure can produce the best
possible result.
Ferreira (2015) tested the First-Fit algorithm with
1 heuristic and 3 different metaheuristics: First Fit
on area decreasing order (FFD), local search (LS),
simulated annealing (SA) and genetic algorithm
(GA). His experimental results imply a hidden but
disappointing fact that there is almost no distinction
in efficiency among the 4 algorithms regardless of
their varying levels of complexity. Table 1
summarizes his experimental results. N is the
number of objects for input. From his original data,
for each value of N, there are 6 classes of test cases.
Nonetheless, due to the limitation of space, table 1
only stores the average value of all tests of 6 classes
for each input of size N of each algorithm.
Table 1: Summary of Ferreira’s experimental results.
N FFD LS SA GA
20 3.78 3.69 3.62 3.65
40 6.96 6.93 6.84 6.94
60 10.34 10.18 10.20 10.38
80 13.87 13.68 13.72 14.13
100 16.35 16.11 16.20 16.70
From the table, the maximum difference between
any two algorithms given the same input size is less
than 0.59. The bigger the input size, the worse SA
and GA get compared to others, whilst for LS and
FFD, they get better with larger input size.
Nonetheless, considering the complexity of LS, SA
and GA, their performance was so poor compared to
that of FFD, which is not explained in the paper and
becomes the inspiration for our paper to discover
why they are so inefficient. After careful analysis, a
common pattern among these 4 algorithms is that
their optimization objective was only the order of
placement, leading to the question if that is the
problem making advanced optimization techniques
so inefficient. To investigate that question, we repeat
his experiment but only use the FFD as the standard
and compare it against First-Fit on random orderings
of input instead of those generated from advanced
search methods. The reason why First-Fit is chosen
is because of its simplicity and usefulness in
practice, and why area decreasing order is
considered as the standard is already explained by
data from table 1. If random orderings are also good
comparatively to the area decreasing ordering, it is
obvious that there should be no further investigation
into the order of placement in further researches on
this topic.
4 IMPLEMENTATION OF THE
PLACEMENT ALGORITHM
After careful consideration, the core placement
strategy of our study has been decided to be First-Fit
algorithm. For the sake of convenience, we employ
the open source Java implementation of Baly (2016)
which is a variant of First-Fit algorithm. His
implementation is, however, not very optimized and
likely to produce non-optimal results that are too far
from optimality, which may badly affect the
experiment. Therefore, the implementation needs
improving to meet our needs. Firstly, an overview of
his original algorithm will be presented in subsection
4.1. Some improvements will be made and shown in
subsection 4.2 and 4.3. Finally, in subsection 4.4, a
comparison between our improved version and the
original version will be presented to verify if it can
produce acceptable results for the main experiment.
4.1 Overview of the Original Algorithm
The idea of the algorithm is to apply regular bin
packing algorithm for irregular bin packing by
considering that each non-rectangle object is
bounded by a rectangle box which will be treated as
the object itself. By so doing, we can utilize the
advances in regular packing, the field in which
researches have already reached a high level of
maturity (Jylänki, 2010), for the newer field of
irregular bin packing. In regular packing, there are
better alternative techniques, but for the sake of
simplicity, the strategy used in this study is still
First-Fit.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
282

The first feature is named “try and replace”.
Each bounding box is a rectangle but it is not solid.
The object inside it may leave some free space large
enough to store some smaller objects. By
rearranging objects that have already been placed
(putting smaller ones into bigger bounding boxes),
more empty space can be created. This feature gives
more opportunities of being placed in the current bin
to those objects that fail to be placed by First-Fit.
Last, but not least, the most important feature is
the “gravity system” which simulates real gravity
and directs all objects towards the top-left corner.
The use of this feature is of paramount importance in
that it can compress all currently placed objects
inside a bin to create more free space so that more
objects can be considered. Another use of this
feature is to randomly “drop” objects into the bin
like throwing balls into a container and they will
automatically roll around to find their place. Figure
5 shows the pseudocode for the whole algorithm.
While SomeObjectsAreLeft do
Create new bin
While TheCurrentBinNotFull do
For each object p left do
If FirstFit(p) = success then
continue
endIf
endFor
call TryAndReplace()
call GravitySystem()
drop objects randomly
endWhile
endWhile
Figure 5: Pseudocode for The Algorithm.
Many optimizations can be done for this
algorithm, two of which will be shown in the next
two subsections 4.2 and 4.3.
4.2 Minimum Bounding Box
The first place that needs improving is the idea of
treating the bounding box of each object as the
object itself. There is no problem with that idea, but
the technique for finding the bounding box
employed in the original algorithm by only finding
the highest and lowest vertical coordinates and the
leftmost and rightmost horizontal coordinates in the
set of vertexes is too trivial and unlikely to generate
acceptable results. Instead of finding any bounding
box, the minimum bounding box in which the
wasted area is minimal should be preferred. It can be
found by rotating the objects through all angles of
integer value from 1 to 180 degree, and selecting the
best one after each rotation using the old method.
This is known as the minimal enclosing box problem
(O'Rourke, 1985).
4.3 Nested Testing to Emphasize
Current Order of Placement
The original implementation is inefficient in the way
that the order of placement is underestimated. An
object failing the First-Fit strategy the first time does
not mean it has no chance of being placed and
should be put behind those coming after it in the
initial order. The positions of “try and replace” and
“gravity system” cannot utilize their full potential of
creating opportunities for each object. Each object
should be given more opportunity of being placed by
those features right after failing the First-Fit
strategy. By so doing, the likelihood of the current
object being added will increase, which may reduce
additional use of new bins. As a result, the order of
placement can be enhanced. Figure 6 shows the
pseudocode for the new version from figure 5. The
difference lies in the positions of “try and replace”
and “gravity system”. They are nested inside the
same loop with the First-Fit strategy and right after
the First Fit strategy fails.
While SomeObjectsAreLeft do
Create new bin
While TheCurrentBinNotFull do
For each object p left do
If FirstFit(p) = success then
continue
endIf
call TryAndReplace()
call GravitySystem()
If FirstFit(p) = success then
continue
endIf
endFor
call GravitySystem()
drop objects randomly
endWhile
endWhile
Figure 6: Pseudocode for the New Algorithm.
These modifications should be enough to
produce acceptable results for our main experiment.
A comparison by experimental results between the
original and the improved version is shown in
subsection 4.4.
4.4 Comparison between the Old and
New Implementation
In this study, 120 test cases representing 4 classes of
Considerations on 2D-Bin Packing Problem: Is the Order of Placement a Relevant Factor?
283
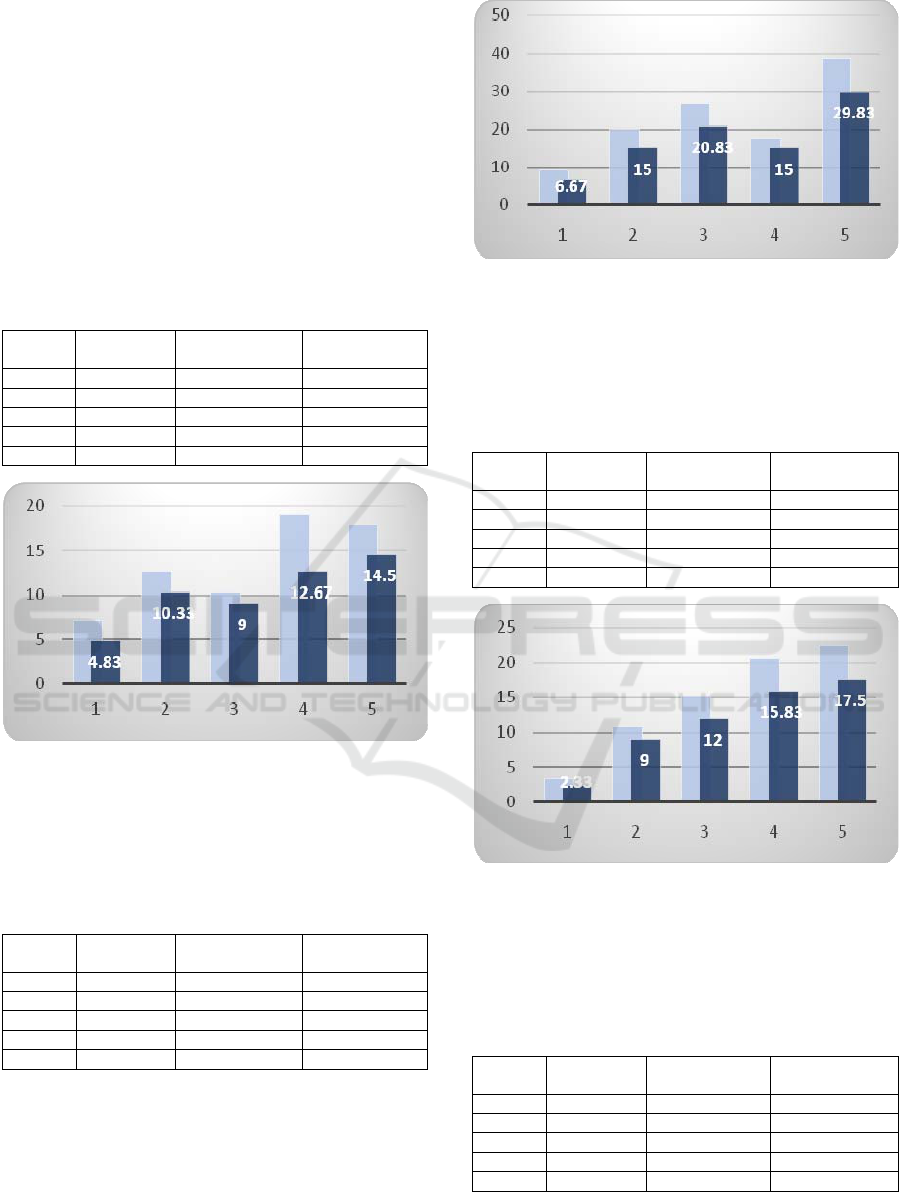
objects, Stars, Polygons, Circles and Mixed (all of 3
types), are randomly and independently constructed
for experiment. Each class is consisted of 30 tests
and is further divided into 5 subclasses in relation
with their input sizes of 20, 40, 60, 80 or 100 items.
This set of test cases will also be used for section 5.
Table 2, 3, 4, 5 will show the average number of bin
used for input of type Star, Polygon, Circle and Mix,
respectively. Following right after each table is its
corresponding bar chart illustrating its data. In this
case, only the area decreasing order is considered.
Table 2: Average number of used bins for input of type
Star.
Index
Number of
items
Original
Version
Improved
Version
1 20 7.17 4.83
2 40 12.67 10.33
3 60 10.33 9.00
4 80 19.00 12.67
5 100 17.83 14.50
Figure 7: Visualisation of the results for input of type Star
(average of used bins) from Table 2. The original
algorithm – light grey and our modified algorithm – dark
grey. X-axis: simulation number (20 to 100 items, step
20), Y-axis: average number of used bins.
Table 3: Average number of used bins for input of type
Polygon.
Index
Number of
items
Original
Version
Improved
Version
1 20 9.33 6.67
2 40 19.99 15.00
3 60 26.67 20.83
4 80 17.67 15.00
5 100 38.83 29.83
Figure 8: Visualisation of the results for input of type
Polygon (average of used bins) from Table 3. The original
algorithm – light grey and our modified algorithm – dark
grey. X-axis: simulation number (20 to 100 items, step
20), Y-axis: average number of used bins.
Table 4: Average number of used bins for input of type
Circle.
Index
Number of
items
Original
Version
Improved
Version
1 20 3.33 2.33
2 40 10.67 9.00
3 60 15.17 12.00
4 80 20.50 15.83
5 100 22.50 17.50
Figure 9: Visualisation of the results for input of type
Circle (average of used bins) from Table 4. The original
algorithm – light grey and our modified algorithm – dark
grey. X-axis: simulation number (20 to 100 items, step
20), Y-axis: average number of used bins.
Table 5: Average number of used bins for input of mixed
types.
Index
Number of
items
Original
Version
Improved
Version
1 20 5.00 3.67
2 40 7.00 5.17
3 60 12.50 9.67
4 80 17.00 12.83
5 100 18.00 14.17
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
284

Figure 10: Visualisation of the results for input of type
mixed types (average of used bins) from Table 5. The
original algorithm – light grey and our modified algorithm
– dark grey. X-axis: simulation number (20 to 100 items,
step 20), Y-axis: average number of used bins.
The 4 tables 2, 3, 4, 5 have shown that our
program always outperforms the original program in
all cases. In addition, the 4 figures 7, 8, 9, 10 have
demonstrated that the difference between our
program and the original program increases when
the input size increases. In other words, our program
works better with bigger data set. These results
shown that our program seems to be able to yield
acceptable results for the main experiment in section
5.
5 EXPERIMENTAL RESULTS
This section is the central component of our paper
where experimental results are produced to support
our claim that the order of placement is not relevant
in solving the problem of 2D bin packing. In this
section, the same algorithm described in section 4 is
employed. The algorithm will be run on the same set
of test cases from subsection 4.4, and for each test
case, 3 different orderings will be considered: the
first two orderings will be randomly generated
whilst for the final, it is the area decreasing order,
the results of which have already been available in
subsection 4.4. Our experimental results are
summarized in the following tables and figures.
Table 6, 7, 8 and 9 will summarize our results for
input objects of different types Star, Polygon, Cycle
and Mixed (combination of Star, Polygon and
Cycle), respectively, followed by their
corresponding figures giving an overview of their
data.
Table 6: Average number of bin used for input of type Star
– random orders versus area decreasing order.
Number of
items
Random 1 Random 2
Area
Decreasing
20 5.00 5.00 4.83
40 10.67 10.67 10.33
60 9.83 9.83 9.00
80 13.00 13.33 12.67
100 15.50 15.67 14.50
Figure 11: Visualisation of the results for Star-type items
(average of used bins) form Table 6. The random 1 order –
light grey, random 2 – grey and the area decreasing order
– dark grey. X-axis: Number of items, Y-axis: average
number of used bins.
According to table 6, the program yields the best
results on area decreasing order of input. The
differences range from 0.17 to 1.17 bin. However,
figure 11 shows that their differences are visually
insignificant compared to the number of bins
needed.
Table 7: Average number of bin used for input of type
Polygon – random orders versus area decreasing order.
Number
of items
Random 1 Random 2 Area
Decreasin
g
20
7.67 8.00 6.67
40
16.00 15.33 15.00
60
22.00 21.83 20.83
80
15.67 15.83 15.00
100
32.33 32.00 29.83
Table 7 shows that the area decreasing order of
input is still the best ordering. However, as can be
seen from figure 12, there is visually not much
difference when input size is less than 100.
Considerations on 2D-Bin Packing Problem: Is the Order of Placement a Relevant Factor?
285
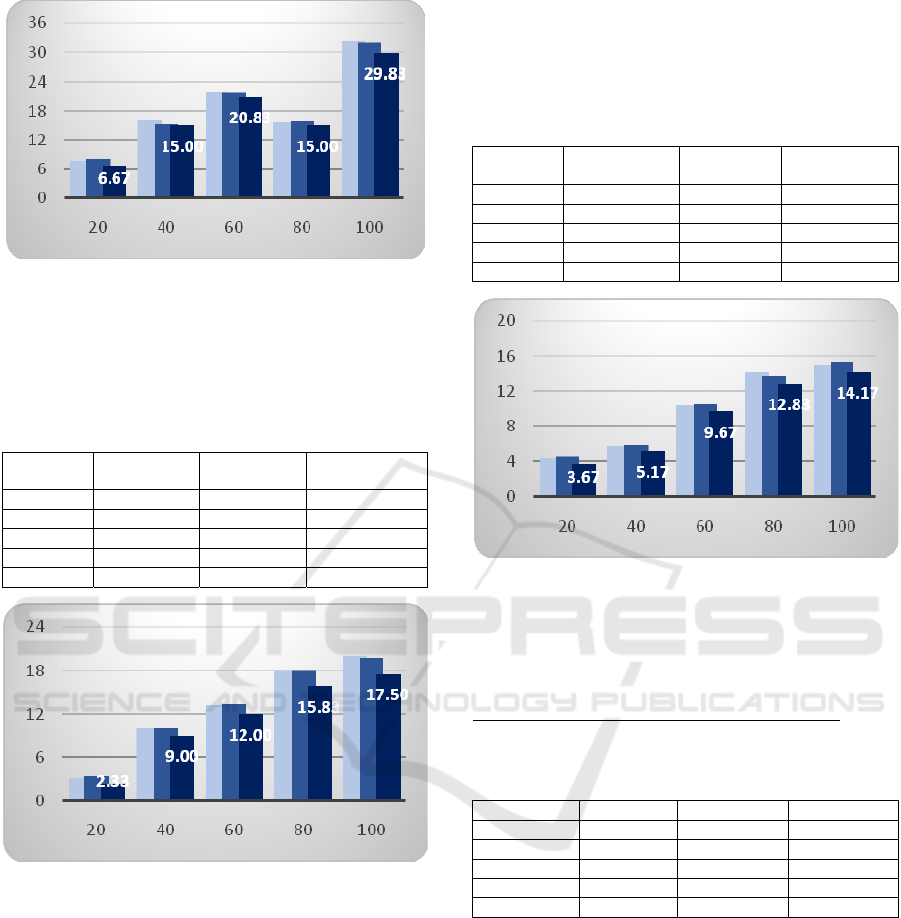
Figure 12: Visualisation of the results for Polygon-type
items (average of used bins) form Table 5. The random 1
order – light grey, random 2 – grey and the area
decreasing order – dark grey. X-axis: Number of items, Y-
axis: average number of used bins.
Table 8: Average number of bin used for input of type
Circle – random orders versus area decreasing order.
Number
of items
Random 1 Random 2
Area
Decreasing
20 3.17 3.33 2.33
40 10.00 10.00 9.00
60 13.17 13.33 12.00
80 18.00 18.00 15.83
100 20.00 19.67 17.50
Figure 13: Visualisation of the results for Circle-type
items (average of used bins) form Table 5. The random 1
order – light grey, random 2 – grey and the area
decreasing order – dark grey. X-axis: Number of items, Y-
axis: average number of used bins.
In table 8, the area decreasing order remains as
the best ordering. Albeit the differences are wider
between the three compared to previous results, they
are at most 2.5 for input size of 100 which is still an
acceptable result considering the height of its
corresponding bar. Figure 13 shows that the three
bars for each input size seem very close in height.
Table 9 shows results for inputs of mixed types
which are the most general case in the experiment.
The area decreasing order is still the best, but closer
analysis on the relationship between the maximum
difference between the three orderings and the best
number of bin used can reveal an interesting pattern.
For each input size, consider the following ratio.
Table 9: Average number of bin used for input of mixed
types – random orders versus area decreasing order.
Number
of items
Random 1 Random 2
Area
Decreasing
20 4.33 4.50 3.67
40 5.67 5.83 5.17
60 10.33 10.50 9.67
80 14.17 13.67 12.83
100 15.00 15.33 14.17
Figure 14: Visualisation of the results for items of mixed
types (average of used bins) form Table 5. The random 1
order – light grey, random 2 – grey and the area
decreasing order – dark grey. X-axis: Number of items, Y-
axis: average number of used bins.
M
axValueO
f
Bin –
M
inValueO
f
Bin
(1)
M
inValueO
f
Bin
Table 10: Results for comparison following formula (1).
Input Size Max Min Ratio (1)
20 4.50 3.67 22.6%
40 5.83 5.17 12.8%
60 10.50 9.67 8.6%
80 14.17 12.83 10.4%
100 15.33 14.17 8.2%
The ratio values tend to decrease as the input size
increases. In other words, the program performs
more similar on different orderings for larger input
size. Even for the small input size like 20, though
the fraction seems high but the real difference is just
0.83 bin. For each input size, all results are still
relatively close as illustrated in figure 14. This
comparison is only made for this input since this is
the most general case where objects are more
diverse in shapes. The other types of input are too
specific and may require more tests of a more
variety of sizes for the pattern to be clearly present.
All results confirm that random orderings are
good since they are not too far away from the area
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
286

decreasing order which has already been known as
an excellent order. In all test cases, the average
difference between the area decreasing order and
random orders never exceeds 2.5 bins for input size
of 100. The 4 figures also show that there is visually
not much difference between them. An important
consideration is that results on the two randomly
generated orderings are almost identical. The
maximum difference between them is 0.67 bin as
shown in table 7 for input size of 40. If the order of
placement is an important factor, there is no possible
way that they do not differ by even 1 bin in all 120
test cases. That implies that all possible orders of
placement should generally yield very close results.
Considering our results and results from
Ferreira
shown in table 1
, we strongly believe that the order of
placement is not relevant for researches in this topic.
Our experimental results do not demonstrate that the
order of placement has no effect at all in this
problem, but they confirm that the influence is so
little that even a random permutation of input should
be good comparatively to the best one. Hence there
is no practical benefit in using complicated
optimization techniques, which should be about
hundreds of times slower than a normal greedy
approach especially for large input size, to find the
best order of placement. Further researches into this
topic should investigate into other dimensions such
as the placement method.
6 CONCLUSION AND FUTURE
WORK
Our study investigates the relevance of the order of
placement, which has been one of the main
objectives of optimization, in the 2D bin packing
problem, and conclude that its influence is so little
that it does not deserve the attention of researchers
in this topic by using experimental results to show
that even random orderings may yield very good
results comparable to a good ordering.
Improvements should be made on the placement
method instead of the order of placement. We
believe an advanced placement method with a
simple order of placement would outperform a
simple method with complicated order of placement.
Even though our experiment yields generally
acceptable results, it is not up to our expectation. We
believe that the differences between the three
orderings in section 5 may be even closer if a better
placement algorithm is used. Our placement
algorithm is acceptable, but it is based on a regular
packing algorithm which is not fully intended for the
irregular problem.
In future experiments, we will continue
investigating into other placement methods that are
designed for the irregular packing problem to
produce better experimental results. In addition, we
would like to make one-to-one comparisons between
random orderings with orderings generated from
advanced search techniques such as Simulated
Annealing or Evolutionary Algorithm to point out
how little the algorithm may improve at the huge
cost of resource consumption.
REFERENCES
Duarte Nuno Gonçalves Ferreira, 2015. Rectangular Bin-
Packing Problem: a computational evaluation of 4
heuristics algorithms. U. Porto Journal of Engineering,
1:1 (2015) 35-49.
Moises Baly, 2016. Java Implementation for 2D Bin
Packing. [Online]. [Accessed on 20 April 2017].
Available from https://github.com/mses-bly/2D-Bin-
Packing.
Alvim, A.C.F., F. Glover, C.C. Ribeiro, and D.J. Aloise.
1999. “Local Search for the Bin Packing Problem.” In
Extended Abstracts of the 3rd Metaheuristics
International Conference, Angra dos Reis, pp. 7-12.
R.L. Rao, S.S. Iyengar, 1994. Bin-Packing by Simulated
Annealing. Computers Math. Applic. Vol. 27, No. 5,
pp. 71-82.
Jordan Junkermeier, 2015. A Genetic Algorithm for the
Bin Packing Problem. Evolutionary Computation, St.
Cloud State University, Spring 2015.
György Dósa, Jiří Sgall, 1998. First-Fit bin packing: A
tight analysis. 1998 ACM Subject Classification F.2.2
Nonnumerical Algorithms and Problems.
A. Lodi, S. Martello, M. Monaci, D. Vigo, 2010. Two-
Dimensional Bin Packing Problems. In Paschis V. Th.
Paradigms of Combinatorial Optimization,
Wiley/ISTE, p. 107-129.
Andrea Lodi, Silvano Martello, Daniele Vigo, 2002.
Recent advances on two-dimensional bin packing
problems. Discrete Applied Mathematics 123 (2002)
379–396.
Bennell, J.A, and Oliveria, J.F, 2008. 50 years of irregular
shape packing problems: a tutorial/ Southampton, UK
(Discussion Papers in Centre for Operational
Research, Management Science and Information
Systems, CORMSIS-08-14).
Jukka Jylänki, 2010. A Thousand Ways to Pack the Bin - A
Practical Approach to Two-Dimensional Rectangle
Bin Packing. [Online]. [Accessed on 20 April 2017].
Available from http://clb.demon.fi/files/RectangleBin
Pack.pdf.
Joseph O'Rourke, 1985. Finding minimal enclosing boxes.
International Journal of Computer & Information
Sciences June 1985, Volume 14, Issue 3, pp 183–199.
Considerations on 2D-Bin Packing Problem: Is the Order of Placement a Relevant Factor?
287
