
Analysing Dynamical Systems
Towards Computing Complete Lyapunov Functions
Carlos Arg
´
aez
1
, Peter Giesl
2
and Sigurdur Hafstein
1
1
Faculty of Physical Sciences, University of Iceland, 107 Reykjav
´
ık, Iceland
2
Department of Mathematics, University of Sussex, Falmer BN1 9QH, U.K.
Keywords:
Dynamical System, Complete Lyapunov Function, Meshless Collocation, Radial Basis Functions.
Abstract:
Ordinary differential equations arise in a variety of applications, including e.g. climate systems, and can ex-
hibit complicated dynamical behaviour. Complete Lyapunov functions can capture this behaviour by dividing
the phase space into the chain-recurrent set, determining the long-time behaviour, and the transient part, where
solutions pass through. In this paper, we present an algorithm to construct complete Lyapunov functions. It is
based on mesh-free numerical approximation and uses the failure of convergence in certain areas to determine
the chain-recurrent set. The algorithm is applied to three examples and is able to determine attractors and
repellers, including periodic orbits and homoclinic orbits.
1 INTRODUCTION
In this paper, we describe a new algorithm to analyse
the behaviour of a dynamical system. Let us consider
a general autonomous ordinary differential equation
(ODE)
˙
x = f(x), where x ∈ R
n
.
A classical (strict) Lyapunov function (Lyapunov,
1992) is a scalar-valued function that can be used to
analyse the basin of attraction of one attractor such as
an equilibrium or a periodic orbit. It attains its mini-
mum at the attractor, and is otherwise strictly decreas-
ing along solutions of the ODE.
A generalization of this idea is the notion of a
complete Lyapunov function (Conley, 1978a; Con-
ley, 1988; Hurley, 1995; Hurley, 1998), which charac-
terizes the complete behaviour of the dynamical sys-
tem. It is a scalar-valued function V : R
n
→ R, de-
fined on the whole phase space, not just in a neighbor-
hood of one particular attractor. It is non-increasing
along solutions of the ODE. The phase space can be
divided into the area where the complete Lyapunov
function strictly decreases along solution trajectories
and the one where it is constant along solution trajec-
tories. The area where the complete Lyapunov func-
tion is strictly decreasing along solution trajectories
characterizes the gradient-like flow. There solutions
pass through and the larger this area is, the more in-
formation is obtained from the complete Lyapunov
function. Note that, by definition, the complete Lya-
punov function needs to be constant along solution
trajectories on each transitive component of the chain-
recurrent set.
Note that there are other methods to analyse the
general behaviour of dynamical systems: The di-
rect simulation of solutions with many different ini-
tial conditions, however, is costly and can only give
limited information about the general behaviour of
the system, unless estimates are available, e.g. when
shadowing solutions. More sophisticated methods in-
clude the computation of invariant manifolds, form-
ing the boundaries of basins of attraction of attractors
(Krauskopf et al., 2005); here, additional analysis of
the parts with gradient-like flow is necessary. The cell
mapping approach (Hsu, 1987) or set oriented meth-
ods (Dellnitz and Junge, 2002) divide the phase space
into cells and compute the dynamics between these
cells, see also for example (Osipenko, 2007); these
ideas have also been used to compute complete Lya-
punov functions, see Section 2.1.
In this paper we focus on a new algorithm of tack-
ling a mathematical problem numerically. Inspired
by a method to compute classical Lyapunov functions
for an equilibrium, we approximate the solution of
V
0
(x) = −1, where V
0
(x) = ∇V (x) · f(x) denotes the
orbital derivative, the derivative along solutions of the
ODE. We use mesh-free collocation with Radial Basis
Function to approximately solve this partial differen-
tial equation (PDE): we choose a finite set of collo-
cation points X and compute an approximation v to V
which solves the PDE in all collocation points.
134
Argáez, C., Hafstein, S. and Giesl, P.
Analysing Dynamical Systems - Towards Computing Complete Lyapunov Functions.
DOI: 10.5220/0006440601340144
In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 134-144
ISBN: 978-989-758-265-3
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Note, however, that the PDE cannot be fulfilled
at all points of the chain-recurrent set, such as an
equilibrium or periodic orbit. We use the failure of
the method to approximate in certain areas to identify
these areas. We split the collocation points X into a
set X
0
, where the approximation fails, and X
−
, where
it works well. A complete Lyapunov function should
be constant in X
0
, so in the next step we solve the
PDE V
0
(x) = 0 for all x ∈ X
0
and V
0
(x) = −1 for
all x ∈ X
−
, which is an approximation of a complete
Lyapunov function.
The computed function v gives us the follow-
ing information about the ODE under consideration:
the set X
0
, where v
0
(x) ≈ 0 approximates the chain-
recurrent set, including equilibria, periodic orbits and
homoclinic orbits, while the set X
−
, where v
0
(x) ≈ −1
approximates the area with gradient-like flow, where
solutions pass through. The function v, through its
level sets, gives information about the stability and
attraction properties: minima of v correspond to at-
tractors, while maxima represent repellers.
Let us give an overview over the paper: in Section
2 we discuss complete Lyapunov functions as well as
mesh-free collocation to approximate solutions of a
general linear PDE. In Section 3 we present our algo-
rithm to compute a complete Lyapunov function. In
Sections 4 and 5 we apply the method to three exam-
ples and discuss the results in detail.
2 PRELIMINARIES
2.1 Complete Lyapunov Functions
We will consider a general autonomous ODE
˙
x = f(x), where x ∈ R
n
. (1)
A complete Lyapunov function (Conley, 1978b; Con-
ley, 1978a) is a continuous function V : R
n
→ R
which is constant on the chain-recurrent set, includ-
ing local attractors and repellers, and decreasing else-
where. In contrast to classical Lyapunov functions
(Lyapunov, 1992), which are defined on the basin of
attraction of just one attractor, a complete Lyapunov
function characterizes the flow on the whole phase
space and distinguishes between the chain-recurrent
set and the gradient-like flow. Thus, it captures the
long-term behaviour of the system.
Conley (Conley, 1978b; Conley, 1978a) proved
the existence of complete Lyapunov functions for dy-
namical systems on a compact metric space. The idea
is to consider corresponding attractor-repeller pairs
and to construct a function which is 1 on the repeller,
0 on the attractor and decreasing in between. Then
these functions are summed up over all attractor-
repeller pairs. This was generalized to more general
spaces by Hurley (Hurley, 1992; Hurley, 1995; Hur-
ley, 1998).
The smaller the part of the phase space where the
complete Lyapunov function is constant, the more in-
formation is provided by a complete Lyapunov func-
tion. There exists a complete Lyapunov function
which is only constant on the generalized chain-
recurrent set (Auslander, 1964), thus providing fur-
ther information about the system as the generalized
chain-recurrent set is a subset of the chain-recurrent
set.
In (Kalies et al., 2005; Ban and Kalies, 2006;
Goullet et al., 2015) a computational approach to
construct complete Lyapunov functions was consid-
ered. A discrete-time system was given by the time-
T map and the phase space was subdivided into cells
and the dynamics between them computed through an
induced multivalued map using the computer pack-
age GAIO (Dellnitz et al., 2001). An approximate
complete Lyapunov function is then computed using
graph algorithms (Ban and Kalies, 2006). This ap-
proach requires a high number of cells even for low
dimensions. We will use a different methodology, in-
spired by the construction of classical Lyapunov func-
tions, which is faster and works well in higher di-
mensions. In (Bj
¨
ornsson et al., 2014a), the approach
of (Ban and Kalies, 2006) is compared to the RBF
method for equilibria (see below) for one particular
example; here, the method of (Ban and Kalies, 2006)
works well only on the chain-recurrent set, while the
RBF method is very efficient on the gradient-like part.
In (Bj
¨
ornsson et al., 2015), a complete Lyapunov
is constructed as a continuous piecewise affine (CPA)
function, affine on a fixed simplicial complex. How-
ever, it is assumed that information about local attrac-
tors is a available, while the proposed method in this
paper does not require any information about the sys-
tem under consideration.
2.2 Mesh-free Collocation
For classical Lyapunov functions, several numerical
construction methods have recently been proposed,
e.g. (Johansson, 1999; Johansen, 2000; Marin
´
osson,
2002; Giesl, 2007; Hafstein, 2007; Bj
¨
ornsson et al.,
2014b; Kamyar and Peet, 2015; Anderson and Pa-
pachristodoulou, 2015; Doban, 2016; Doban and
Lazar, 2016) see also the recent review (Giesl and
Hafstein, 2015). Our algorithm will be based on the
RBF (Radial Basis Function) method, a special case
of mesh-free collocation, which approximates the so-
lution of a linear PDE, specifying the orbital deriva-
Analysing Dynamical Systems - Towards Computing Complete Lyapunov Functions
135

tive.
Mesh-free methods, particularly based upon Ra-
dial Basis Functions, provide a powerful tool for solv-
ing generalized interpolation problems efficiently. We
assume that the target function belongs to a Hilbert
space H of continuous functions (often a Sobolev
space) with reproducing kernel ϕ : R
n
× R
n
→ R,
given by a suitable Radial Basis Function Φ through
ϕ(x,y) := Φ(x − y), where Φ(x) = ψ(kxk) is a ra-
dial function. Examples for Radial Basis Functions
include the Gaussians, multiquadrics and inverse mul-
tiquadrics; we, however, will use the compactly sup-
ported Wendland functions in this paper, which will
be defined below.
We assume that the information r
1
,... ,r
N
∈ R of
a target function V ∈ H generated by N linearly inde-
pendent functionals λ
j
∈ H
∗
is known. The optimal
reconstruction of the function V is the solution of the
minimization problem min{kvk
H
: λ
j
(v) = r
j
,1 ≤ j ≤
N}. It is well-known (Wendland, 2005) that the solu-
tion can be written as v(x) =
∑
N
j=1
β
j
λ
y
j
ϕ(x,y), where
the coefficients β
j
are determined by the interpolation
conditions λ
j
(v) = r
j
, 1 ≤ j ≤ N.
In our case, we consider the PDE V
0
(x) = g(x),
where g(x) is a given function. We choose N points
x
1
,. .. ,x
N
∈ R
n
of the phase space and define func-
tionals λ
j
(v) := (δ
x
j
◦ L)
x
v = v
0
(x
j
) = ∇v(x
j
) · f(x
j
),
where L denotes the linear operator of the orbital
derivative LV (x) = V
0
(x) and δ is Dirac’s delta dis-
tribution. The right-hand sides are V
0
j
= g(x
j
) for all
1 ≤ j ≤ N. The approximation is then
v(x) =
N
∑
j=1
β
j
(δ
x
j
◦ L)
y
Φ(x − y),
where Φ is a positive definite Radial Basis Function,
and the coefficients β
j
∈ R can be calculated by solv-
ing a system of N linear equations. A crucial ingre-
dient is the knowledge on the behaviour of the er-
ror function |V
0
(x) − v
0
(x)| in terms of the so-called
fill distance which measures how dense the points
{x
1
,. .. ,x
N
} are, since it gives information when the
approximate solution indeed becomes a Lyapunov
function, i.e. has a negative orbital derivative. Such
error estimates were derived, for example in (Giesl,
2007; Giesl and Wendland, 2007), see also (Nar-
cowich et al., 2005; Wendland, 2005).
The advantage of mesh-free collocation over other
methods for solving PDEs is that scattered points can
be added to improve the approximation, no triangula-
tion of the phase space is necessary, the approximat-
ing function is smooth and the method works in any
dimension.
In this paper, we use Wendland functions (Wend-
land, 1998) as Radial Basis Functions through
ψ(x) := ψ
l,k
(ckxk), where c > 0, k ∈ N is a smooth-
ness parameter and l = b
n
2
c + k + 1. Wendland
functions are positive definite functions with com-
pact support, which are polynomials on their sup-
port; the corresponding Reproducing Kernel Hilbert
Space is norm-equivalent to the Sobolev space
W
k+(n+1)/2
2
(R
n
). They are defined by recursion: for
l ∈ N, k ∈ N
0
we define
ψ
l,0
(r) = (1 − r)
l
+
ψ
l,k+1
(r) =
R
1
r
tψ
l,k
(t)dt
(2)
for r ∈ R
+
0
, where x
+
= x for x ≥ 0 and x
+
= 0 for
x < 0.
As collocation points X ⊂ R
n
we use a hexagonal
grid with α ∈ R
+
constructed according to
(
α
n
∑
k=1
i
k
w
k
: i
k
∈ Z
)
, where
w
1
= (2e
1
,0, 0,. .. ,0)
w
2
= (e
1
,3e
2
,0, .. ., 0)
.
.
.
.
.
.
w
n
= (e
1
,e
2
,e
3
,. .. ,(n + 1)e
n
) and
e
k
=
s
1
2k(k + 1)
, k ∈ N.
We set ψ
0
(r) := ψ
l,k
(cr) with positive constant c
and define recursively ψ
i
(r) =
1
r
dψ
i−1
dr
(r) for i = 1, 2
and r > 0. The explicit formulas for v and its orbital
derivative are
v(x) =
N
∑
j=1
β
j
hx
j
− x,f(x
j
)iψ
1
(kx − x
j
k),
v
0
(x) =
N
∑
j=1
β
j
h
− ψ
1
(kx − x
j
k)hf(x),f(x
j
)i
+ ψ
2
(kx − x
j
k)hx − x
j
,f(x)i · hx
j
− x,f(x
j
)i
i
where β is the solution of A · β = r, r
j
= V
0
(x
j
) and A
is the N × N matrix with entries
a
i j
= ψ
2
(kx
i
− x
j
k)hx
i
− x
j
,f(x
i
)ihx
j
− x
i
,f(x
j
)i
− ψ
1
(kx
i
− x
j
k)hf(x
i
),f(x
j
)i
for i 6= j and
a
ii
= −ψ
1
(0)kf(x
i
)k
2
.
More detailed explanations on this construction are
given in (Giesl, 2007, Chapter 3).
If no collocation point x
j
is an equilibrium for the
system, i.e. f(x
j
) 6= 0 for all j, then the matrix A is
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
136
positive definite and the system of equations Aβ = r
has a unique solution. Note that this holds true inde-
pendent of whether the underlying discretized PDE
has a solution or not, while the error estimates are
only available if the PDE has a solution.
3 ALGORITHM
Starting with scattered collocation points X, we solve
the equation V
0
(x) = −1, where V
0
(x) := ∇V (x)· f(x)
denotes the orbital derivative, the derivative along so-
lutions of (1). Note that the equation V
0
(x) = −1 does
not have a solution on chain-recurrent sets in general;
e.g. along a periodic orbit, the orbital derivative must
integrate to 0. However, as mentioned above, we can
still compute a (unique) approximation by the method
described in Section 2.2.
In the next step we check for each collocation
point x
j
in X whether the approximation was poor
(then x
j
∈ X
0
) or good (then x
j
∈ X
−
). Then we ap-
proximate the solution of the new problem V
0
(x) =
−1 for x ∈ X
−
and V
0
(x) = 0 for x ∈ X
0
; the set X
0
indicates the (generalized) chain-recurrent set.
To determine whether the approximation was poor
or good, we evaluate v
0
(x) for test points x around
each collocation point x
j
– for a good approximation
we expect v
0
(x) ≈ −1. In view of our goal to compute
a complete Lyapunov function, we classify colloca-
tion points as poor if the orbital derivative near them is
larger than 0 or a chosen critical value, i.e. v
0
(x) > γ,
for certain points x near the collocation point x
j
. As
points to check near a collocation point x
j
we choose
points on two circumferences around each collocation
point x
j
. They are distributed around each collocation
point and we place 64 checking points per each col-
location point. In particular, in R
2
, for a collocation
point x
j
∈ R
2
, we use the following checking points
Y
x
j
:
x
j
± rα(cos(θ),−sin(θ))
x
j
± rα(sin(θ),cos(θ))
x
j
±
r
2
α ∗ (cos(θ), sin(θ))
x
j
±
r
2
α ∗ (cos(θ), −sin(θ))
(3)
where r is a scaling parameter and θ =
0.0,11.25, 22.5,45, 56.25,67.5,75 and 105 degrees;
this is shown in Figure 1.
The algorithm can be summarized as follows.
1. Create the collocation points X and compute the
approximate solution v of V
0
(x) = −1
2. For each collocation point x
j
, compute v
0
(x): if
v
0
(x) > γ for a point x ∈ Y
x
j
, then x
j
∈ X
0
, oth-
erwise x
j
∈ X
−
, where γ ≤ 0 is a chosen critical
value
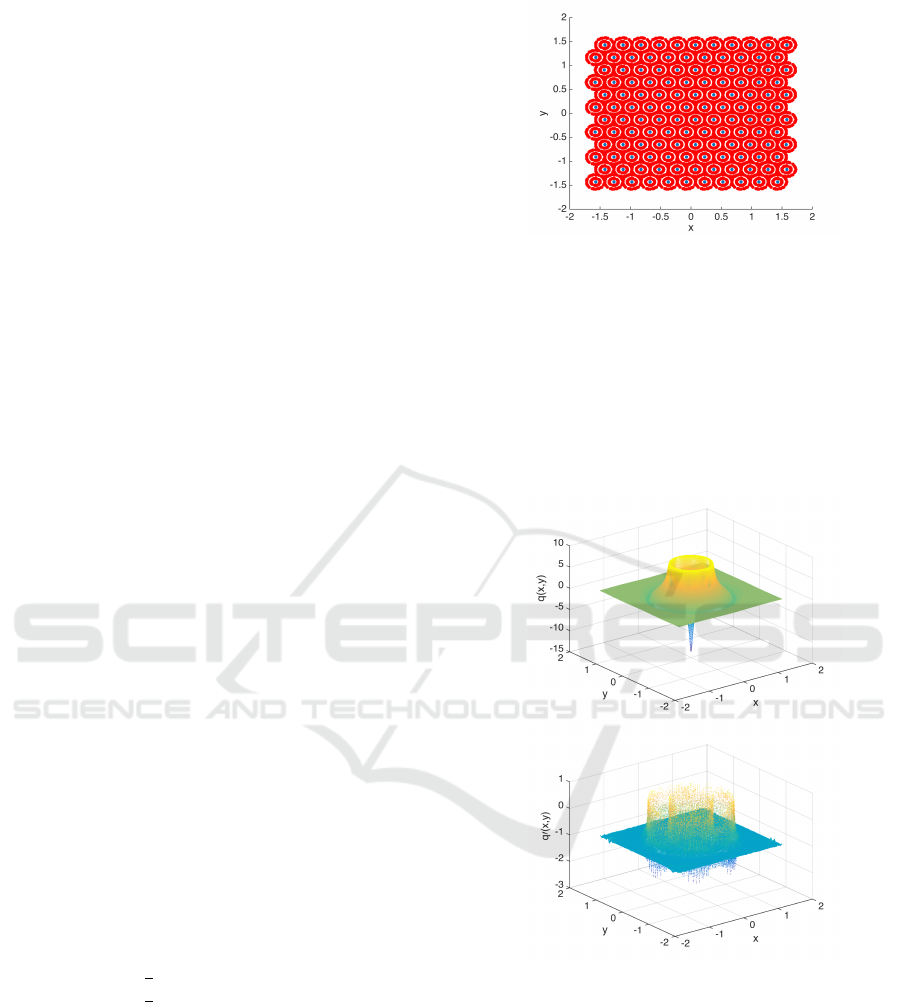
Figure 1: The figure shows the collocation points (blue)
and the checking points (red) around each collocation point.
The collocations points are used to construct the Lyapunov
function and the checking points are used to evaluate the
orbital derivative of the complete Lyapunov function.
3. Compute the approximate solution v of V
0
(x) =
−1 for x ∈ X
−
and V
0
(x) = 0 for x ∈ X
0
4. Repeat steps 2. and 3. until no more points are
added to X
0
Figure 2: Lyapunov function for (4). The upper figure
shows the approximated complete Lyapunov function. The
lower figure shows its orbital derivative. The minima in the
upper figure correspond to the asymptotically stable equi-
librium and periodic orbit with radius 1, while the maxi-
mum is attained at the repelling periodic orbit of radius 1/2.
The orbital derivative fails to be negative on the periodic or-
bits and the equilibrium.
Analysing Dynamical Systems - Towards Computing Complete Lyapunov Functions
137

Figure 3: The figures show the checking points x around
each collocation point, where v
0
(x) > γ for different values
of γ. Upper: γ = −0.5. Middle: γ = −0.25. Lower: γ = 0.
In all cases, α = 0.02, r = 0.5.
4 EXAMPLES
In the following we apply the method to three exam-
ples and then analyse the behaviour of the method
with respect to certain parameters. In this section we
only consider the first step of the method, and we will
discuss the iterations in Section 5. Note that in all
examples we use the notation x = (x,y).
4.1 Two Circular Periodic Orbits
We consider system (1) with right-hand side
f(x,y) =
−x(x
2
+ y
2
− 1/4)(x
2
+ y
2
− 1) − y
−y(x
2
+ y
2
− 1/4)(x
2
+ y
2
− 1) + x
,
(4)
which has an asymptotically stable equilibrium at the
origin, an asymptotically stable periodic orbit with ra-
dius 1, and a repelling periodic orbit with radius 1/2.
To compute the Lyapunov function with our
method we used ψ
5,3
as Wendland function with c =
1. The collocation points were set in (−1.5,1.5) ×
(−1.5,1.5) ⊂ R
2
and we used α = 0.02.
In Figure 2 we see how the derivative fails to
be negative in both periodic orbits and the equilib-
rium. In the next step of the algorithm, we use points
around each collocation points to check whether the
orbital derivative is above the critical value γ. Figure
3 shows the results for different values of γ, namely
γ = 0,−0.25,−0.5 and a fixed scaling parameter r =
0.5 for (3).
Clearly, γ = 0 is not enough to find all failing
points, since some chain-recurrent sets, such as the
equilibrium at the origin, are not detected.
4.2 Van Der Pol Oscillator System
We consider system (1) with right-hand side
f(x,y) =
y
(1 − x
2
)y − x
. (5)
System (5) is the two dimensional form of the Van der
Pol oscillator. This describes the behaviour of a non-
conservative oscillator reacting to a non-linear damp-
ing. The origin is an unstable focus, and the system
has an asymptotically stable periodic orbit.
We used our method with the Wendland function
ψ
4,2
and c = 1. The collocation points were set in
(−4,4) × (−4,4) ⊂ R
2
with α = 0.1.
In Figure 4 we see how the derivative fails to be neg-
ative at the points of the periodic orbit. In Figure
5 we show the points in X
0
for three critical val-
ues γ = 0,−0.25,−0.5 and a fixed scaling parameter
r = 0.5.
For γ = 0 and γ = −0.25 we do not detect all points
of the periodic orbit, but we can already see its shape
(see Figure 5), while for γ = −0.5 the whole periodic
orbit is covered. However, we obtain points in the
gradient-like flow where the orbital derivative fails to
be negative, and thus overestimate the chain-recurrent
set.
4.3 Homoclinic Orbit
We consider system (1) with right-hand side f(x, y) =
x(1 − x
2
− y
2
) − y((x − 1)
2
+ (x
2
+ y
2
− 1)
2
)
y(1 − x
2
− y
2
) + x((x − 1)
2
+ (x
2
+ y
2
− 1)
2
)
.
(6)
This system has an unstable focus at the origin and
an asymptotically stable homoclinic orbit at a circle
centered at the origin and with radius 1.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
138
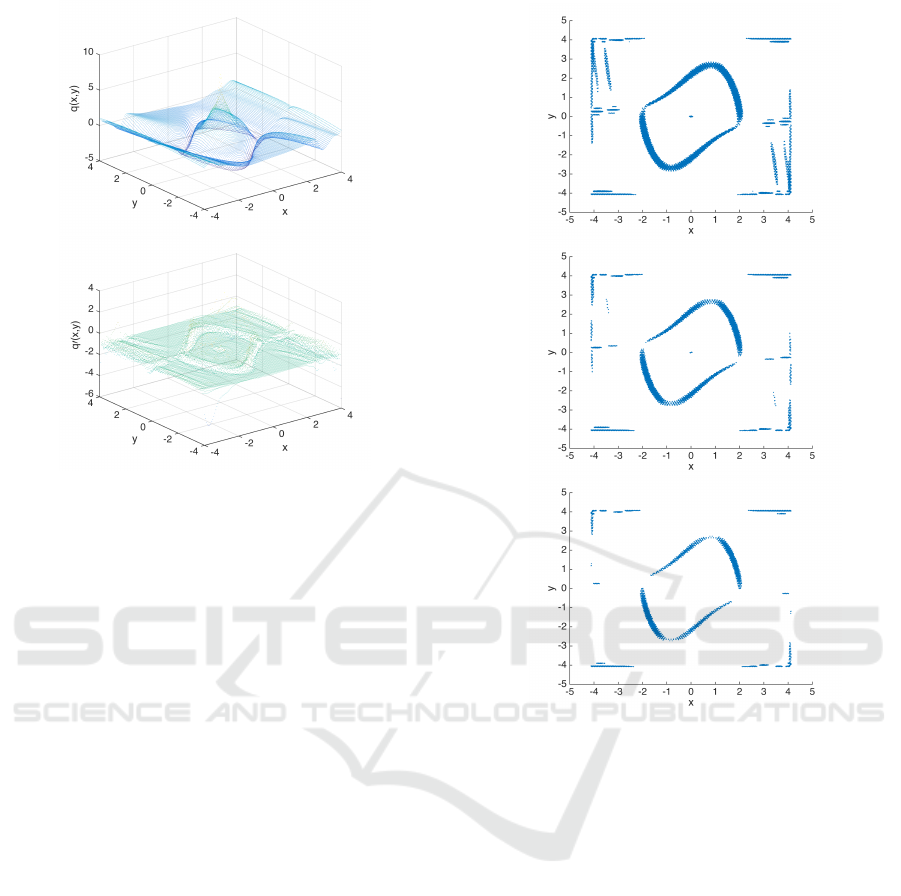
Figure 4: Approximated complete Lyapunov function for
(5). The upper figure shows the complete Lyapunov func-
tion; the minimum corresponds to the asymptotically stable
periodic orbit and the maximum to the unstable equilibrium
at the origin. The lower figure shows the orbital derivative
of the complete Lyapunov function. The collocation points
in both cases have α = 0.1. The lower figure is able to detect
the periodic orbit.
We use our method with the Wendland function
ψ
4,2
and c = 1. The collocation points were set in
(−1.5,1.5) × (−1.5,1.5) ⊂ R
2
with α = 0.02.
The method detects the points of the homoclinic orbit
well, but has problems at the unstable equilibrium at
(1,0), corresponding to the homoclinic orbit. Here,
the approximation also fails at points which belong to
the gradient-like flow.
In Figure 7 we see how the derivative fails to be
negative at the points of the homoclinic orbit, and also
beyond. We show the points in X
0
for three critical
values γ = 0, −0.25,−0.5 and a fixed scaling radio
r = 0.5.
4.4 Dependence on the Collocation Grid
and the Verification Points
A very interesting behaviour is observed by varying
the density of the collocation grid. A natural way to
vary it is by changing the value of the parameter α in
(3): the larger the α the fewer collocation points we
have for a defined area.
In Figure 8 we can observe how our algorithm
converges to the chain-recurrent set for example (4).
We observe that in order to be able to detect the dy-
Figure 5: The figures show the points x around each collo-
cation point, where v
0
(x) > γ for different values of γ. Up-
per: γ = −0.5. Middle: γ = −0.25. Lower: γ = 0. In all
cases, α = 0.1, r = 0.5.
namical behaviour, the collocation grid needs to be
sufficiently dense. This corresponds to error estimates
between the solution of a PDE and its approximation
using mesh-free collocation which proves that the er-
ror is bounded by a constant times the fill distance,
measuring the density of the collocation points. In
our case, however, the PDE does not have a solution
and thus these error estimates do not apply.
In Figure 9 we consider example (6) and vary the
radius r for the checking points, used to determine
poor and good collocation points. We are only able to
detect the whole homoclinic orbit with a sufficiently
large radius. This is to be expected, since at the col-
location points we have v
0
(x) = −1 and since v
0
is
continuous it will be negative close enough to the col-
location points.
Analysing Dynamical Systems - Towards Computing Complete Lyapunov Functions
139
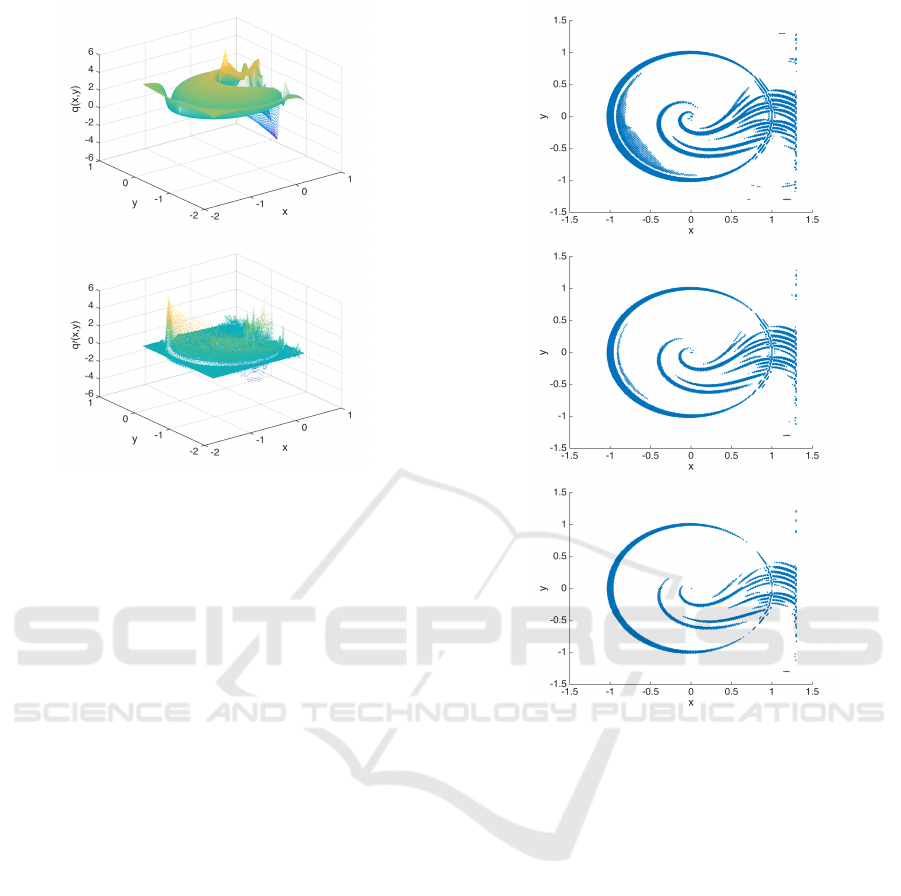
Figure 6: Approximated complete Lyapunov function for
(6). The upper figure shows the approximated complete
Lyapunov function; the homoclinic orbit corresponds to the
minimum, while the origin is a maximum. The lower figure
shows its orbital derivative. The collocation points in both
cases have α = 0.02.
5 ITERATION STEPS OF THE
ALGORITHM
After splitting the set of collocation points X into the
set X
0
, where the approximation is poor, and the re-
maining points X
−
, in the next step, our method will
solve the problem V
0
(x) = 0 for x ∈ X
0
and V
0
(x) =
−1 for x ∈ X
−
. This is done by solving Aβ = r with
an updated right-hand-side r and we look again for
collocation points where the approximation is poor.
This procedure should then be iterated until no more
collocation points are added to X
0
.
For the Van der Pol system (5) the results of this
procedure with γ = −0.25 and α = 0.1 can be seen
in Figures 10 to 12. Figure 10 shows the complete
Lyapunov v for each step, which does not change sig-
nificantly after the first step; observe, that the range
of v is slightly reduced. Figure 11 shows its orbital
derivative; again, there is no significant change after
the first step, only the range of v
0
is slightly reduced
and the values near the chain-recurrent set are now 0
rather than different values above the critical value.
Figure 12, finally, displays the set of checking
points where the orbital derivative is larger than the
critical value γ = −0.25; these points should approx-
imate the chain-recurrent set, in this case the unstable
equilibrium at the origin and the asymptotically sta-
Figure 7: The figures show the points x around each collo-
cation point, where v
0
(x) > γ for different values of γ. Up-
per: γ = −0.5. Middle: γ = −0.25. Lower: γ = 0. In all
cases, α = 0.02, r = 0.5.
ble periodic orbit. We observe that the set of points
increases and nearly covers the whole periodic or-
bit. However, collocation points away from the chain-
recurrent set also are included, mainly at the bound-
ary of the domain under consideration as the values of
v
0
(x) become more extreme.
After the first step there is no significant change
in the figures, although a close study reveals that the
algorithm still adds points, see Table 1. There are
boundary effects, such that points near the boundary
of the considered domain do not behave as expected.
We are currently studying these phenomena and ex-
pect that a more elaborate way of fixing the values of
v
0
at the collocation points will improve the perfor-
mance of the method.
For all examples (4) to (6) we show a table of how
many points we find by iterating this procedure. The
corresponding parameters are given in Table 2.
In Table 1 the number of total collocation points and
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
140

Figure 8: Example (4) with collocation grids of varying
density. Upper α = 0.5. Middle up α = 0.3. Middle down
α = 0.1. Lower α = 0.02. The radii for the test circles for
all of them were set to r = 0.5 and the critical value was
γ = −0.25.
the total number of points in X
0
with poor approxi-
mation in each step iteration are shown. For system
(4) we see that after the fourth step no more points
are added to X
0
, while for the other two examples the
method keeps adding points.
Figure 9: We consider example (6) with fixed α = 0.02,
fixed critical value γ = 0.0 and varying r. Upper r = 0.2.
Middle up r = 0.3. Middle down r = 0.4. Lower r = 0.5.
6 CONCLUSIONS AND
OUTLOOK
We have presented a method to compute a complete
Lyapunov function and thus to determine the quali-
tative behaviour of a given ODE, using both the val-
ues of the complete Lyapunov function and its orbital
derivative. A complete Lyapunov function V is con-
stant along solutions in the chain-recurrent set, i.e. the
Analysing Dynamical Systems - Towards Computing Complete Lyapunov Functions
141
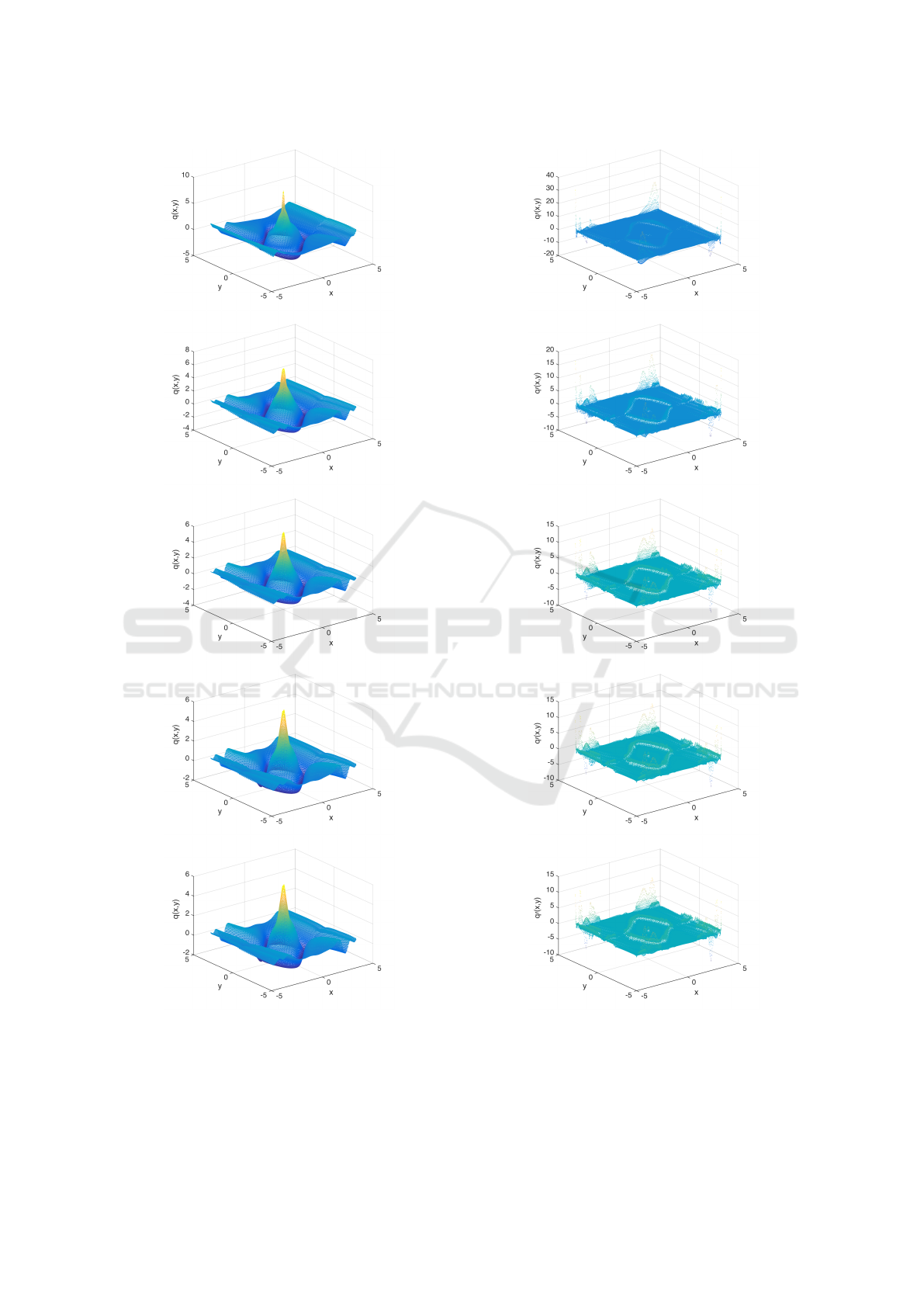
Figure 10: Evolution of the complete Lyapunov function
approximation v(x) for the Van der Pol problem with critical
value γ = −0.25, α = 0.1, r = 0.5. The top figure shows the
first iteration of the method, the second, third and fourth
show the corresponding iterations. The figures only change
very slightly after the first step; one can observe that the
range of values is reduced.
Figure 11: Evolution of the complete Lyapunov function
approximation v
0
(x) for the Van der Pol problem for the
steps of the method. After the first step, where points with
poor approximation have orbital derivatives with positive
values, they are close to zero in subsequent steps. There are
no significant changes in the later steps.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
142

Figure 12: Evolution of the checking points with orbital
derivative larger than the critical value γ = −0.25 for the
Van der Pol problem over several steps. It can be seen
that after the first step visibly more points are added, which
nearly cover the whole periodic orbit, while in later steps
there are no significant changes. Apart from the chain-
recurrent sets, also points at the boundary of the domain
are marked as poor approximations.
Table 1: In this table we list the overall number of colloca-
tion points as well as the collocation points in X
0
in each
step of the algorithm for each of the examples (4) to (6). In
example (4), no further points are added after step 4, while
for the other two examples we keep adding points to X
0
.
system (4) (5) (6)
collocation points 29440 7708 19500
step 1 1358 762 2517
step 2 1362 956 2751
step 3 1368 1034 2802
step 4 1370 1072 2820
step 5 1370 1092 2829
Table 2: Parameters to obtain results shown in table 1.
system (4) (5) (6)
α 0.02 0.1 0.02
γ -0.25 -0.25 0
r 0.5 0.5 0.5
orbital derivative is zero (V
0
(x) = 0), and it is strictly
decreasing along solutions in the gradient-like set, i.e.
V
0
(x) < 0. Minima of the complete Lyapunov func-
tion correspond to attractors and maxima to repellers.
The method approximately solves the PDE
V
0
(x) = −1 with mesh-free collocation. As this PDE
does not have a solution in the chain-recurrent set,
we examine where the approximation is poor (the set
X
0
) and thus can determine the chain-recurrent set.
In the subsequent steps of the algorithm we adjust
the PDE problem by solving V
0
(x) = 0 for x ∈ X
0
and V
0
(x) = −1 elsewhere to approximate a complete
Lyapunov function.
While the method works well in several exam-
ples to detect the dynamical behaviour, it does not
always converge to a fixed set of points in X
0
and
X
−
= X \ X
0
, but keeps on adding points. Further-
more, points at the boundary of the domain are in-
cluded in X
0
, although they belong to the gradient-
like part. The reason could be that we set the or-
bital derivative to 0 and −1, rather than a continuous
function. Further research will consider replacing this
with a more elaborate method, e.g. by replacing the
jump function by a smooth function of the distance to
the detected chain-recurrent set.
ACKNOWLEDGEMENTS
First author in this paper is supported by the Ice-
landic Research Fund (Rann
´
ıs) grant number 163074-
052, Complete Lyapunov functions: Efficient numer-
ical computation. Special thanks to Dr. Jean-Claude
Berthet for all his good comments and advices on
C++.
Analysing Dynamical Systems - Towards Computing Complete Lyapunov Functions
143

REFERENCES
Anderson, J. and Papachristodoulou, A. (2015). Advances
in computational Lyapunov analysis using sum-of-
squares programming. Discrete Contin. Dyn. Syst. Ser.
B, 20(8):2361–2381.
Auslander, J. (1964). Generalized recurrence in dynamical
systems. Contr. to Diff. Equ., 3:65–74.
Ban, H. and Kalies, W. (2006). A computational approach
to Conley’s decomposition theorem. J. Comput. Non-
linear Dynam, 1(4):312–319.
Bj
¨
ornsson, J., Giesl, P., and Hafstein, S. (2014a). Al-
gorithmic verification of approximations to complete
Lyapunov functions. In Proceedings of the 21st In-
ternational Symposium on Mathematical Theory of
Networks and Systems, pages 1181–1188 (no. 0180),
Groningen, The Netherlands.
Bj
¨
ornsson, J., Giesl, P., Hafstein, S., Kellett, C., and Li,
H. (2014b). Computation of continuous and piece-
wise affine Lyapunov functions by numerical approx-
imations of the Massera construction. In Proceedings
of the CDC, 53rd IEEE Conference on Decision and
Control, Los Angeles (CA), USA.
Bj
¨
ornsson, J., Giesl, P., Hafstein, S., Kellett, C., and Li, H.
(2015). Computation of Lyapunov functions for sys-
tems with multiple attractors. Discrete Contin. Dyn.
Syst. Ser. A, 35(9):4019–4039.
Conley, C. (1978a). Isolated Invariant Sets and the Morse
Index. CBMS Regional Conference Series no. 38.
American Mathematical Society.
Conley, C. (1978b). Isolated Invariant Sets and the Morse
Index. CBMS Regional Conference Series no. 38.
American Mathematical Society.
Conley, C. (1988). The gradient structure of a flow i. Er-
godic Theory Dynam. Systems, 8:11–26.
Dellnitz, M., Froyland, G., and Junge, O. (2001). The algo-
rithms behind GAIO – set oriented numerical methods
for dynamical systems. In Ergodic theory, analysis,
and efficient simulation of dynamical systems, pages
145–174, 805–807. Springer, Berlin.
Dellnitz, M. and Junge, O. (2002). Set oriented numer-
ical methods for dynamical systems. In Handbook
of dynamical systems, Vol. 2, pages 221–264. North-
Holland, Amsterdam.
Doban, A. (2016). Stability domains computation and sta-
bilization of nonlinear systems: implications for bio-
logical systems. PhD thesis: Eindhoven University of
Technology.
Doban, A. and Lazar, M. (2016). Computation of Lyapunov
functions for nonlinear differential equations via a
Yoshizawa-type construction. IFAC-PapersOnLine,
49(18):29 – 34. 10th IFAC Symposium on Nonlinear
Control Systems NOLCOS 2016, Monterey, Califor-
nia, USA, 23-25 August 2016.
Giesl, P. (2007). Construction of Global Lyapunov Func-
tions Using Radial Basis Functions. Lecture Notes in
Math. 1904, Springer.
Giesl, P. and Hafstein, S. (2015). Review of computational
methods for Lyapunov functions. Discrete Contin.
Dyn. Syst. Ser. B, 20(8):2291–2331.
Giesl, P. and Wendland, H. (2007). Meshless collocation:
error estimates with application to Dynamical Sys-
tems. SIAM J. Numer. Anal., 45(4):1723–1741.
Goullet, A., Harker, S., Mischaikow, K., Kalies, W., and
Kasti, D. (2015). Efficient computation of Lyapunov
functions for Morse decompositions. Discrete Contin.
Dyn. Syst. Ser. B, 20(8):2419–2451.
Hafstein, S. (2007). An algorithm for constructing Lya-
punov functions. Monograph. Electron. J. Diff. Eqns.
Hsu, C. S. (1987). Cell-to-cell mapping, volume 64 of Ap-
plied Mathematical Sciences. Springer-Verlag, New
York.
Hurley, M. (1992). Noncompact chain recurrence and at-
traction. Proc. Amer. Math. Soc., 115:1139–1148.
Hurley, M. (1995). Chain recurrence, semiflows, and gradi-
ents. J Dyn Diff Equat, 7(3):437–456.
Hurley, M. (1998). Lyapunov functions and attractors
in arbitrary metric spaces. Proc. Amer. Math. Soc.,
126:245–256.
Johansen, T. (2000). Computation of Lyapunov functions
for smooth, nonlinear systems using convex optimiza-
tion. Automatica, 36:1617–1626.
Johansson, M. (1999). Piecewise Linear Control Systems.
PhD thesis: Lund University, Sweden.
Kalies, W., Mischaikow, K., and VanderVorst, R. (2005).
An algorithmic approach to chain recurrence. Found.
Comput. Math, 5(4):409–449.
Kamyar, R. and Peet, M. (2015). Polynomial optimization
with applications to stability analysis and control – an
alternative to sum of squares. Discrete Contin. Dyn.
Syst. Ser. B, 20(8):2383–2417.
Krauskopf, B., Osinga, H., Doedel, E. J., Henderson, M.,
Guckenheimer, J., Vladimirsky, A., Dellnitz, M., and
Junge, O. (2005). A survey of methods for computing
(un)stable manifolds of vector fields. Internat. J. Bifur.
Chaos Appl. Sci. Engrg., 15(3):763–791.
Lyapunov, A. M. (1992). The general problem of the sta-
bility of motion. Internat. J. Control, 55(3):521–790.
Translated by A. T. Fuller from
´
Edouard Davaux’s
French translation (1907) of the 1892 Russian orig-
inal, With an editorial (historical introduction) by
Fuller, a biography of Lyapunov by V. I. Smirnov, and
the bibliography of Lyapunov’s works collected by J.
F. Barrett, Lyapunov centenary issue.
Marin
´
osson, S. (2002). Lyapunov function construction for
ordinary differential equations with linear program-
ming. Dynamical Systems: An International Journal,
17:137–150.
Narcowich, F. J., Ward, J. D., and Wendland, H. (2005).
Sobolev bounds on functions with scattered zeros,
with applications to radial basis function surface fit-
ting. Mathematics of Computation, 74:743–763.
Osipenko, G. (2007). Dynamical systems, graphs, and al-
gorithms. Springer, Berlin. Lecture Notes in Mathe-
matics 1889.
Wendland, H. (1998). Error estimates for interpolation by
compactly supported Radial Basis Functions of mini-
mal degree. J. Approx. Theory, 93:258–272.
Wendland, H. (2005). Scattered data approximation, vol-
ume 17 of Cambridge Monographs on Applied and
Computational Mathematics. Cambridge University
Press, Cambridge.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
144
