A Simulation–based Optimization Approach for Stochastic Yard

Crane Scheduling Problem with Crane Mobility Constraints

Frobin M. Mnale

, Mohamed S. Gheith

and Amr B. Eltawil

Department of Industrial Engineering and Systems Management, Egypt-Japan University of Science and Technology,

Alexandria, Egypt

Production Engineering Department, Alexandria University, Alexandria, Egypt

Keywords: Container Terminals, Stochastic Scheduling, Mobility Constraints, Simulation-based Optimization.

Abstract: With the fast-paced growth in containerized trade market the need for effective and efficient operations at

container terminals is a critical factor in freight transport. One major contributing factor of terminal efficiency

is the productivity of Yard Cranes (YC) resulting from YC scheduling. In this paper, the stochastic YC

Scheduling Problem (YCSP) is presented aspiring to provide a new yard cranes analysis through operational

attributes of the container handling process. A stochastic mixed integer programming model is proposed, and

a simulation-based optimization procedure introduced to build YC schedules that account for the dynamic

and uncertainty nature of container handling process in container terminals.

1 INTRODUCTION

Over the past 30 years, freight transportation has

rapidly developed, it is now an indicator of the

economic growth of countries in global freight

operations. Therefore, the effective and efficient

management of Container Terminal (CT) is important

in the contribution of economic growth. These

advancements in freight transportation and

information technology have brought new challenges

and complications that associate with CT operations.

As of 2014, it was estimated that the container flows

from largest ports in the world to be 68.4 Million TEU

(twenty-foot equivalent unit; a 20 ft. × 8ft× 8.5 ft.).

This increase raised a logistic concern all over the

most important ports and the world (UNCTAD 2015).

Nowadays, terminal competitiveness in global

freight network is directly affected by the storage

yard activities (Zhen 2013a). This is due to

containerization growth which leads to high vessel

turn around time. However, alleviation of vessel

turnaround time requires integration between various

operations to ensure better performance of terminal

operations (Vis and De Koster 2003). Consequently,

It is important to decide on the planning of

operational activities as well as selecting right

handling equipment on storage yard activities to

facilitate a seamless flow of containers in the port

(Wiese et al. 2010).

A container terminal is an essential node in an

open system and dynamic flow of containers

materials. Terminals operate under two external

interfaces of operations to serve container vessels

(Steenken et al. 2005). Moreover, container terminal

can be classified into five main areas namely; berth,

quay, transport areas, yard storage, and terminal gate.

Berth and quay areas considered as the seaside

operations, while the yard and gate areas are in the

landside operations (Vis and De Koster 2003). For

instance, (Lau and Zhao 2008) addressed vessel

operations comprise of loading and discharging tasks,

where containers are loaded and unloaded to/ from a

ship and stacked or retrieved in a storage yard.

Furthermore, they explained three types of material

handling equipment; Quay Cranes (QCs), Automated

guided vehicles (AGVs), and Automatic Stacking

Cranes (ASCs) that connect seaside and landside

operations.

Fig. 1.Show the schematic diagram of automated

container terminal whereas, the storage yard is

composed of multiple blocks perpendicular to vessel

Each yard block contains an adjacent stretch of slots

(40 -60 slots) and each slot denoted as a rectangle in

a diagram can store 6 – 9 containers.

296

Mnale, F., Gheith, M. and Eltawil, A.

A Simulation–based Optimization Approach for Stochastic Yard Crane Scheduling Problem with Crane Mobility Constraints.

DOI: 10.5220/0006440902960303

In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 296-303

ISBN: 978-989-758-265-3

Figure 1: Schematic diagram of an automated container

terminal.

In the automated terminal, container handling from/to

the transportation trucks is carried at the extremities

of the storage blocks. Consider, for example, Hong

Kong international terminal is one of the busiest

terminals in the world, this terminal received over

10,000 trucks and 15 containers ships a day (Phan and

Kim 2016). Fig. 2. Show the trends of the global

turnover of the largest seaports.

In this paper, yard crane scheduling problem

(YCSP) is presented, and framework approach of a

problem based on current research trends is

demonstrated. We have established literature review

classification following leading attributes that arise in

the scheduling of storage equipment in the block; (1)

yard layouts, (2) yard crane mobility characteristics,

(3) solution methods approach, and (4) Performance

measure and uncertainty. These attributes will be

more or less in chronological order in our work.

Figure 2: World turnover of largest seaport (IHS 2016).

The remainder of the paper is organized as follows, in

section 2 of the paper detailed description of the

storage yard crane problem followed by yard storage

analysis in section 3 and section 4, simulation

framework of the YCSP. In section. Five conclusions

and the future prospect are summarized.

2 PROBLEM DESCRIPTION

In this section, yard crane scheduling problem

(YCSP) is modeled as an integer program. We seek

to develop a mathematical model describing the

attributes of yard crane schedule to sequence the

stacking and retrieving of containers in a block. Based

on two main factor, mobility rules and uncertainty,

some important assumption for the formulation have

been constructed.

a) The planning horizon is apportioned into T

small time periods (weeks, beginning t = 1)

b) The volume of a particular task group should

not exceed the capacity of the YC given that

all tasks in a single bay should be a group of

one task.

c) The YC movements are within a block and

should be non-crossing with a safety

distance between cranes.

d) All job in a block are assumed as discrete

operations, and the task will be grouped in a

different segment of the block whereas

arriving vessels and external truck represent

the tasks to be handled.

e) At the beginning of rolling horizon, all yard

cranes are available, the estimated time of

operation and start time of processing of

tasks are known.

f) Each yard crane has same productivity.

Parameter

I set of all jobs I = {1, 2…n} to be handled

K set of identical yard cranes K= {1, 2}

ready time of job i

location of job i

time required for yard cranes to travel from L

to L

h time required by a yard crane to handle one

job.

Decision variables

) the handling time window for job I

the time at which the yard crane assigned to

handle job i

completion time of job i

arrival time of the yard crane assigned to job i

ϴ completion time of the yard crane k







1 if yard crane k handle job i before job j

20,1

20,6

24,2

30,9

36,5

0, 10, 20, 30, 40,

Hong Kong

Ningbo

Shenzhen

Singapore

Shanghai

Throughput (in Milion TEUs)

A Simulation–based Optimization Approach for Stochastic Yard Crane Scheduling Problem with Crane Mobility Constraints

297

0 otherwise.

YC assigned to handle job i

The model follows below

 





(1)











    

(2)











    

(3)

 













   

(4)





















   

(5)

= U

+ h, i = 1… n

(6)

= max {Rt

, t

}, i = 1… n

(7)

- V

≥ Tt

+ h – (1-





M, i, j = 1… n

|i ≠ j

(8)

– Y

) (L

– L

) > 0 if











 

i, j = 1…, n | i  j

(10)

+ Tt

– ϴ ≤ M (1–





), j=1… n, k=1..m

(11)







 {0, 1}, i, j = 1… n, k = 1… m

(12)

, U

, t

, ϴ ≥ 0, i = 1… n, k = 1… m

(13)

 {1, 2…} i = 1… n

(14)

The objective is to minimize the completion time

of the yard crane operation by constraint (1).

Carrying out all group task sequence: constraints (2)

-(4), to ensure the completion of all workgroup by

yard crane. Each task should be carried out by single

YC and should follow after the last task group

handled by YC. Constraint (5) ensure the balance

flow of cranes during travels. Handling time requests

constraints (6) – (7), to make sure that the start time

of the task group to be later than its estimated time,

also the start time of task group should be later than

YC completion time. Movement of yard crane

constraints (8) – (9) define the move time for each

yard crane from the current location to the next one.

Then, ensure mobility integration (non-crossing) of

yard crane in the block. Constraint (10) ensure that

the completion time for each yard crane is defined.







Binary variable by constraint (11). Non-negative

integer variables in constraints (12) and (14)

This study has considered, deviation of process

time and start time of handling a task simultaneously.

These deviance factors arise due to the lateness

arrival of the vessel or external truck that leads to

work delays.

3 YARD STORAGE OPERATION

This section discusses yard storage operations and

introduces cranes as primary equipment in yard

block. The cranes perform stacking and retrieving

operations of the containers while integrating with

quay cranes and transport vehicles (Zhen 2013a). In

the various practical and theoretical studies, yard

crane scheduling problem has been presented in two

categories; Rail Mounted Gantry Crane (RMGC) and

Rubber Tire Gantry Crane (RTGC). The two types

operate in different rules. RMGCs are automated and

work in intra-block operation. On contrary RTGCs

are manually operated, and work on various zones in

the yard storage (Gharehgozli et al. 2014).

3.1 Yard Storage Layout

A typical yard storage layout determines the

containers placement and a network of operations;

each block has material handling equipment (yard

crane) serving a block or multiple blocks. A standard

block is made of several rows each with bays so that

container can be stored in several tiers depending on

the capability of equipment used to stack them (Liu et

al. 2004). There are two types of yard layout

configurations; (1). Non-automated (2) Automated

yard layout. The main differences observed in their

design is the position of the input/output point (

container exchange position of yard vehicle and

cranes), the level of automation used and the block

position to quay; horizontal/vertical (Lee and Kim

2013).

Conventional yard layout configuration mostly

used in container terminals in the world. It has blocks

arranged parallel/horizontal to the quay. Fig.3. Show

the schematic diagram of the typical configuration of

conventional yard storage layout. Usually, one or

more rows in each block are reserved for internal and

external transfer vehicles as truck lanes. In this

configuration, cranes travel in vehicle lanes for

stacking and retrieving tasks. Each yard block

contains adjacent slots and each slot denoted as

rectangle in a diagram can store 6 – 9 containers. On

contrary automated yard layout mostly employed in

Europe and few Asia ports, blocks are perpendicular/

vertical to the quay. Input and output points are

located at both ends of the storage block where

automatic guided vehicle pick up containers at

seaside and external truck at land.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

298

Figure 3: Schematic diagram of conventional terminal

layout.

3.2 Crane Mobility Characteristics

Dispatching standards and setting of yard cranes

routes indicate the operational mobility attributes

employed in the storage area. Yard crane follow the

dispatching rule in the block finding the optimal

paths. (Narasimhan and Palekar 2002) studied yard

operation by considering a single YC which retrieves

and stack container in a single block. Some of the

articles have also addressed retrieval and stacking

requests operation simultaneously. (Zhang et al.

2002) formulated a mixed integer programming

model for YC problem under a given workload in

multiple blocks. Their objective was to minimize the

unfinished workload defined as either retrieval or

stacking.

(Ng et al. 2005) studied multiple crane scheduling

problem for non-crossing cranes in a single block.

They developed a branch and bound algorithm for a

large size problem to minimize the total delay time

for all requests. (Lee et al. 2006) presented loading

sequence requirements in the schedule considering

two non-crossing yard crane in separate blocks. The

authors developed a genetic algorithm to find the

solution. Likewise, (Li et al. 2009) introduced a

discrete time model for automatic stacking cranes to

minimize the earliness and lateness combination of all

request in their due course. They proposed a dynamic

rolling horizon algorithm, to ensure the real-time

update of the schedule for all tasks. (Vis and Carlo

2010) formulated the same setting. However, the

stacking cranes can pass through one another, but

they cannot work in the same bay. the request of all

activities has neither due times nor sequence. They

developed a mathematical model to minimize

makespan for both cranes and applied simulated

annealing-based heuristic to solve the large instance

of the problem; the authors concluded that numerical

solution based on heuristic solutions are within 2% of

the large instance and 6% for a small instance of the

problem.

3.3 Solution Method Approaches

Most of the research papers in yard cranes scheduling

problem in literature are described in mathematical

modeling. Such as; linear, nonlinear, and mixed

integer programming models. Due to the

computational complexity of solving these models to

optimality, advanced techniques such as heuristics,

meta-heuristic, and algorithms used to address the

problem to approximate solution. Therefore, we

categorize these into two branches; exact solution

methods and approximate solution methods.

3.3.1 Exact Solution Methods

Exact solutions are widely used in formulating

mathematical models for the purpose of developing

adjusted patterns in some parameter to get exact

solutions.(Cheung et al. 2002) formulate a mixed

integer program of the YC scheduling problem to

minimize the total workload of tasks. Numerical

experiment results, concluded the solution approach

was effective and efficient for large-sized problems.

Moreover, (Lee et al. 2007) developed a

mathematical model for scheduling of two transtainer

systems. The objective was to reduce total loading

time on two-yard crane moving in the separate blocks.

They used simulated annealing (SA) to solve the

proposed model. Numerical experiment results

concluded that the completion time of SA introduced

was 10% above lower bound and performance of the

algorithm is extraneous to some of the containers

loaded. In some cases YC problems use combination

exact and approximate solutions in finding a result,

for instance (Cao et al. 2008) formulated a mixed

integer program to provide an efficient operation

strategy for loading outbound container. Using a dual

rail mounted gantry crane they developed a greedy

heuristic algorithm and simulated annealing

algorithm to solve the problem. (Wiese et al. 2010)

formulated integer linear program for container

layouts in yard operations, they expressed restricted

model to a square storage yard and added a Variable

Neighbourhood Descent (VND) heuristic for solving

yard operations’ problems with an arbitrary shape.

Their study shows that the VND heuristic provides

the trade-off of time and solution quality by economic

results for 43% of the instances.

3.3.2 Approximate Solution Methods

Due to the compound nature of YC scheduling

problems, research studies use approximate solutions

to achieve a near optimal results in solving large

instances of the problems. In their paper (Kozan and

A Simulation–based Optimization Approach for Stochastic Yard Crane Scheduling Problem with Crane Mobility Constraints

299

Preston 1999) introduced genetic algorithms for the

optimization of container transfer in maritime

terminals. The goal was to find the optimal storage

strategy and schedule for handling container in a yard.

(Chen et al. 2004) addressed yard storage

optimization in Singapore port, to minimize space

allocation of cargo in a designated yard and satisfy

space requirement. They used the combinatory

heuristic method to solve the problem. Results

concluded that a traditional heuristic approach

achieves relatively better results in a short time by

10% above margin.

(Dell’Olmo and Lulli 2004) considered container

as a network of complex substructures or platform to

address resource allocation problem to minimize the

total delay time in the overall system and on the time

horizon. They introduced a dynamic programming

approach tackling large size problem and conclude

that the percent is 6.3% above the lower bound of the

solution. In recent years (Burke et al. 2012) proposed

an empirical analysis on comparing Monte Carlo

based hyper-heuristics for solving capacitated

timetabling problems in the automated terminals.

They applied a simulated annealing to accompany the

hyper-heuristic on finding the approximate solution.

Their proposed approach claims to prove the new

precisely technique to schedule automated cranes.

3.4 Performance Measure and

Uncertainty

Dynamic operations that subsist during loading and

unloading of the container may affect the

performance of cranes operations if overlooked. The

effects may occur due to the failure of equipment,

delay of vessel/truck arrival time, incorrect

information of vehicles or ship and human errors.

3.4.1 Uncertainties

The arrival time of ships/external trucks may affect

the performance of the terminal, for example, (Zhen

et al. 2011) proposed an optimization model for berth

allocation problem under uncertainty of vessel arrival

time and handling time to obtain a robust schedule.

However, the same settings were used in (Zhen and

Chang 2012) to formulate a mathematical model

under two objectives on stochastic consideration of

vessel arrival and operation time. (Zhen 2013b)

presented the decision support system (DSS) that

replaced the traditional system of operation. By

introducing real-life events of uncertainty in yard

allocation problem. This decision support system

enabled port operators to cope with the adjustable

volume of arriving containers.

(Golias et al. 2014) proposed a berth scheduling

problem. The schedule minimizes the total service

times for serving all vessels, they formulated a

discrete mathematical model and used a heuristic to

find a robust schedule.Furthermore, (Jun-Liang et al.

2016) addressed yard crane scheduling where,

handling time, vessel and truck arrival were assumed

to be dynamic with different service priorities. They

developed mixed integer programming, and

simulation based genetic algorithm search was

applied to develop a robust YC schedule.

3.4.2 Performance Measure

Performance metrics such as crane makespan, crane

utilization, and vessel turnaround time indicate the

level of efficiency achieved by the terminals during

processes. For instance, (Petering and Murty 2009)

considered a restriction on the system would prevent

the system from being disturbed by outside factors

such as trucks/vessel arrival, they developed

performance measures using the rule-based control

system that deploys cranes among blocks on the same

zone of operation. (Borgman et al. 2010) investigated

the effect of vessel departure time and stacking point

of container on the overall performance of container

terminal. The discrete-event simulation tool was

developed for analysis, and it was found that

minimizing departure time proved to be significant on

reshuffle and performance of container terminals.

Furthermore (Bortfeldt and Forster 2012) proposed a

heuristic tree search procedure for container

relocation problem taking into account effect of the

height of stacks in the overall performance of the

stacking operations. They compared their method

with.

3.4.3 Emerging Issues

The performance of the container terminal is

measured on the capacity to accustom a large number

of vessels and minimum vessel turnaround time.

However, handling capacity increase with an increase

in the size of the terminal. Recently large operating

terminals have considered a direct impact of handling

equipment on the cost of energy consumption. In (Xin

et al. 2014) addressed the energy-aware control in

scheduling automated terminal by considering the

behavior of the terminal under two operating level;

higher level and lower level represented by discrete

event dynamics and continuous dynamics

respectively. They further elaborated latter level

obtained of minimal value to achieve minimum

energy consumption while maintaining operational

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

300

time constraints. Also, (He et al. 2014) addressed the

pollutants generated from the yard activities

mentioning carbon dioxide as a threat to the

environment. They developed mixed integer

programming model and solved the problem in a

vehicle routing procedures. To account for the total

energy associated in yard crane.

4 SIMULATION FRAMEWORK

OF STOCHASTIC YARD

CRANE SCHEDULING

PROBLEM

A proposed framework seek to develop a yard crane

schedule considering the effects of mobility and

capture realistic environment. This framework put

together an optimization program and a simulation

model of a yard crane operations. The objective is to

minimize the total yard crane completion time and

penalty costs that are associated with operational

uncertainties. The optimization program will generate

an initial feasible solution to be used into the

simulation model as initial input data. Initially, the

simulation model will evaluate the current and total

costs based on the positional values of crane and

efficiency measures (such as speed, start time and

recovery time of operation, when there is equipment

failure or late arrival of ship/trucks). Then model

outputs will be returned to the optimization program

checking the optimality. Consequently, this

simulation-based optimization is an optimization on

the basis of the simulation results to capture the

dynamic nature of operations and the uncertainties. As

it can be seen in fig.4 simulation model of yard crane

is the core component, while the optimization is the

central program for evaluation.

Optimization Program: the program constitutes of

mathematical model built with mixed integer

programming, and it will follow the following steps;

 Initial data generation of the yard activities

this will include block characteristics, the

number of cranes, handling efficiency and

the distribution of crane service time also

berth and gate features which include

vessel/truck size and their probabilities of

arrival and the distribution of inter-arrival

time between successive vessel/truck.

 Simulation initiation: The optimization

program transfer the initial data into the

simulation, and activates evaluation process

in the simulation program to get vessel/truck

waiting times and the berth utilization ratio.

 Objective function assessment: After the

simulation is complete, the program returns

the results to the optimization program, and

the optimization program evaluates the total

time and costs.

 Decision: optimization program assesses the

initial solution from the simulation by

comparing the total costs. If the designed

total cost is minimal, the system stops and

outputs the optimal design and schedule and

the corresponding decision. Otherwise, it

returns to data generation stage and go on to

the next iterative operation

Simulation Model: This involves submodule for

vessel/truck arrival and handling operation module.

To help capture the realistic part of the yard operation

especially in a block, berth, and gate. To be able to

incorporate the effect of crane utilization on the

schedule that will reduce unnecessary penalty cost that

may occur during the process.

5 CONCLUSIONS

This paper conducted analysis and introduced a new

classification of the stochastic yard crane scheduling

problem. Although, few articles have addressed the

stochastic nature of the problem, yet the majority of

research paper have overlooked its effects in

scheduling cranes. A mathematical model was

developed, and simulation-based optimization

framework is proposed for solving these new

attributes of the problem. Hence, based on the analysis

of literature introduced, no study has addressed the

integration of uncertainty factors and mobility settings

in scheduling yard cranes. This confirms a gap for

future work which will focus on the generation of

optimal solutions results and improvements that

would allow considering larger instances of the

problem.

A Simulation–based Optimization Approach for Stochastic Yard Crane Scheduling Problem with Crane Mobility Constraints

301

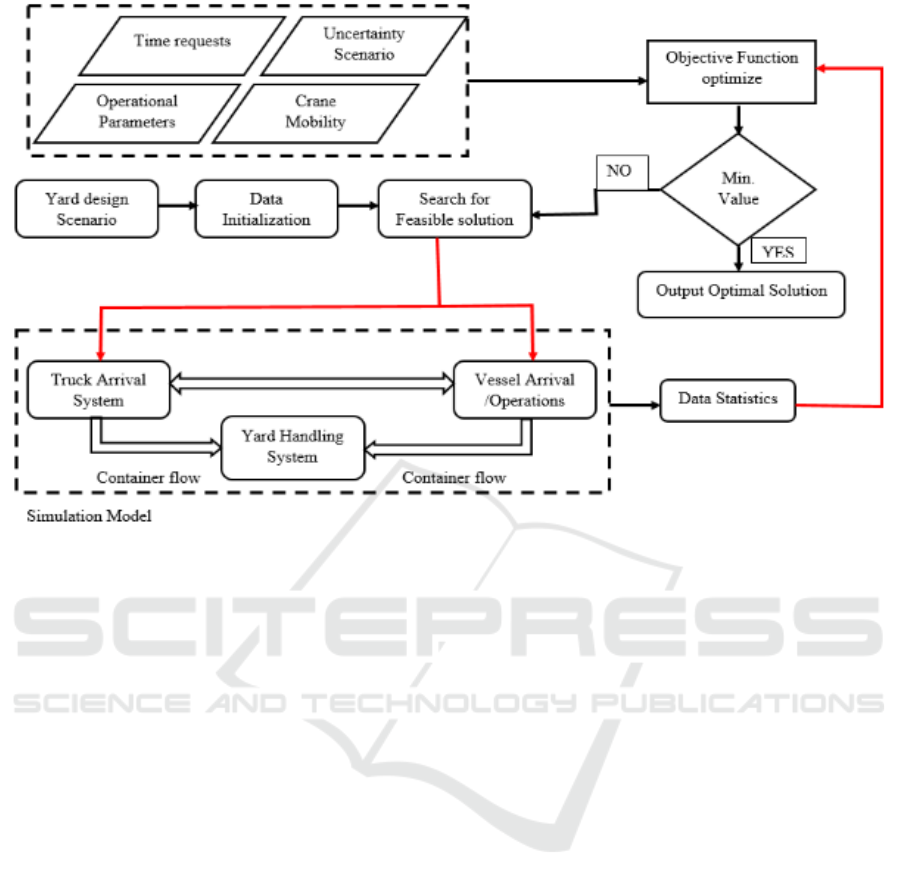
Figure 4: Simulation-based optimization flowchart for YCSP.

ACKNOWLEDGEMENTS

This research project is sponsored by the Pharco

Corporation Graduate Scholarship to the Egypt-Japan

University of Science and Technology (E-JUST) and

support of the Japanese International Cooperation

Agency (JICA).

REFERENCES

Borgman, B., van Asperen, E., and Dekker, R. 2010.

“Online rules for container stacking,” OR Spectrum

(32:3), pp. 687–716.

Bortfeldt, A., and Forster, F. 2012. “A tree search procedure

for the container pre-marshalling problem,” European

Journal of Operational Research (217:3), pp. 531–540.

Burke, E. K., Kendall, G., Misir, M., and Özcan, E. 2012.

“Monte Carlo hyper-heuristics for examination

timetabling,” Annals of Operations Research (196:1),

pp. 73–90.

Cao, Z., Lee, D. H., and Meng, Q. 2008. “Deployment

strategies of double-rail-mounted gantry crane systems

for loading outbound containers in container

terminals,” International Journal of Production

Economics (115:1), pp.

Chen, P., Fu, Z., Lim, A., and Rodrigues, B. 2004. “Port

yard storage optimization,” IEEE Transactions on

Automation Science and Engineering (1:1), pp. 26–37.

Cheung, R. K., Li, C.-L., and Lin, W. 2002. “Interblock

Crane Deployment in Container Terminals,”

Transportation Science (36:1), pp. 79–93.

Dell’Olmo, P., and Lulli, G. 2004. “Planning activities in a

network of logistic platforms with shared resources,”

Annals of Operations Research (129:1990), pp. 155–

169.

Gharehgozli, A. H., Laporte, G., Yu, Y., and de Koster, R.

2014. “Scheduling Twin Yard Cranes in a Container

Block,” Transportation Science (49:3), pp. 686–705.

Golias, M., Portal, I., Konur, D., Kaisar, E., and Kolomvos,

G. 2014. “Robust berth scheduling at marine container

terminals via hierarchical optimization,” Computers &

Operations Research (41), pp. 412–422.

He, J., Huang, Y., and Yan, W. 2014. “Yard crane

scheduling in a container terminal for the trade-off

between efficiency and energy consumption,”

Advanced Engineering Informatics (29:1), Elsevier Ltd,

pp. 59–75.

IHS. 2016. “The largest container ports worldwide - cargo

throughput 2015 | Ranking,” (available at

https://www.statista.com/statistics/264171/turnover-

volume-of-the-largest-container-ports-worldwide/;

retrieved September 11, 2016).

Jun-Liang, H., Wei, Y., Yu-Ting, Z., and You-Fang, H.

2016. “A Proactive Approach for Yard Crane

Scheduling Problem with Stochastic Arrival and

Handling Time,” International Journal of Hybrid

Information Technology (9:2), pp. 389–406.

Kozan, E., and Preston, P. 1999. “Genetic algorithms to

schedule container transfers at multimodal terminals,”

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

302

International Transactions in Operational Research

(6), pp. 311–329.

Lau, H. Y. K., and Zhao, Y. 2008. “Integrated scheduling

of handling equipment at automated container

terminals,” International Journal of Production

Economics (112:2), pp. 665–682.

Lee, B. K., and Kim, K. H. 2013. “Optimizing the yard

layout in container terminals,” OR Spectrum (35:2), pp.

363–398.

Lee, D.-H., Cao, Z., and Meng, Q. 2007. “Scheduling of

two-transtainer systems for loading outbound

containers in port container terminals with simulated

annealing algorithm,” International Journal of

Production Economics (107:1), pp. 115–124.

Lee, D.-H., Meng, Q., and Cao, Z. 2006. “Scheduling Two-

Transtainer Systems for Loading Operation of

Containers Using Revised Genetic Algorithm.,”

Li, W., Wu, Y., Petering, M. E. H., Goh, M., and Souza, R.

de. 2009. “Discrete time model and algorithms for

container yard crane scheduling,” European Journal of

Operational Research (198:1), pp. 165–172.

Liu, C. I., Jula, H., Vukadinovic, K., and Ioannou, P. 2004.

“Automated guided vehicle system for two container

yard layouts,” Transportation Research Part C:

Emerging Technologies (12:5), pp. 349–368.

Narasimhan, A., and Palekar, U. S. 2002. “Analysis and

Algorithms for the Transtainer Routing Problem in

Container Port Operations,” Transportation Science

(36:1), pp. 63–78.

Ng, W. C., Mak, K. L., and Taylor, P. 2005. “An effective

heuristic for scheduling a yard crane to handle jobs with

different ready times,” Engineering Optimization

(37:731604565), pp. 867–877.

Petering, M. E. H., and Murty, K. G. 2009. “Effect of block

length and yard crane deployment systems on overall

performance at a seaport container transshipment

terminal,” Computers and Operations Research (36:5),

pp. 1711–1725.

Phan, M. H., and Kim, K. H. 2016. “Collaborative truck

scheduling and appointments for trucking companies

and container terminals,” Transportation Research

Part B: Methodological (86), Elsevier Ltd, pp. 37–50.

Steenken, D., Vo??, S., and Stahlbock, R. 2005. “Container

terminal operation and operations research - A

classification and literature review,” Container

Terminals and Automated Transport Systems: Logistics

Control Issues and Quantitative Decision Support, pp.

3–49.

UNCTAD. 2015. Review of Maritime Transport 2015

Unctad.

Vis, I. F. A., and Carlo, H. J. 2010. “Sequencing Two

Cooperating Automated Stacking Cranes in a Container

Terminal,” Transportation Science (44:2), INFORMS

, pp. 169–182.

Vis, I. F. A., and De Koster, R. 2003. “Transshipment of

containers at a container terminal: An overview,”

European Journal of Operational Research (147:1), pp.

1–16.

Wiese, J., Suhl, L., and Kliewer, N. 2010. “Mathematical

models and solution methods for optimal container

terminal yard layouts,” OR Spectrum (32:3).

Xin, J., Negenborn, R. R., and Lodewijks, G. 2014.

“Energy-aware control for automated container

terminals using integrated flow shop scheduling and

optimal control,” Transportation Research Part C:

Emerging Technologies (44), pp. 214–230.

Zhang, C., Wan, Y., Liu, J., and Linn, R. J. 2002. “Dynamic

crane deployment in container storage yards,”

Transportation Research Part B: Methodological

(36:6), pp. 537–555.

Zhen, L. 2013a. “A Review on Yard Management in

Container Terminals,” Industrial Engineering &

Management Systems (12:4), pp. 289–304.

Zhen, L. 2013b. “Storage allocation in transshipment hubs

under uncertainties,” International Journal of

Production Research (52:1), Taylor & Francis, pp. 72–

88.

Zhen, L., and Chang, D.-F. 2012. “A bi-objective model for

robust berth allocation scheduling,” Computers &

Industrial Engineering (63:1), pp. 262–273.

Zhen, L., Lee, L. H., and Chew, E. P. 2011. “A decision

model for berth allocation under uncertainty,”

European Journal of Operational Research (212:1), pp.

54–68.

A Simulation–based Optimization Approach for Stochastic Yard Crane Scheduling Problem with Crane Mobility Constraints

303