Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle

Evgeni Magid

, Roman Lavrenov

and Airat Khasianov

Intelligent Robotics Department, Higher School of Information Technology and Information Systems,

Kazan Federal University, Kremlyovskaya str. 35, Kazan, Russian Federation

Higher School of Information Technology and Information Systems, Kazan Federal University, Kremlyovskaya str. 35,

Kazan, Russian Federation

Keywords:

Path Planning, Voronoi Diagram, Potential Field, Mobile Robot.

Abstract:

Potential function based methods play signiﬁcant role in global and local path planning. While these methods

are characterized with good reactive behavior and implementation simplicity, they suffer from a well-known

problem of getting stuck in local minima of a navigation function. In this article we propose a modiﬁcation of

our original spline-based path planning algorithm for a mobile robot navigation, which succeeds to solve local

minima problem and adds additional criteria of start and target points visibility to help optimizing the path

selection. We apply a Voronoi graph based path as an input for iterative multi criteria optimization algorithm.

The algorithm was implemented in Matlab environment and simulation results demonstrate that we succeeded

to overcome our original algorithm pitfalls.

1 INTRODUCTION

Today most robotic applications are targeting for in-

dustrial production speed and quality improvement

as well as for human replacement in various scenar-

ios, which range from social-oriented human-robot

interaction scenarios (Pipe et al., 2014) to danger-

ous for a human urban search and rescue scenar-

ios (Magid et al., 2011). The later scenarios may in-

clude indoor and outdoor environments and require

good performance in autonomous navigation within

unknown environments (Indelman et al., 2015), abil-

ity to deal with computational complexity of simul-

taneous localization and mapping (SLAM) (Buyval

et al., 2016), capabilities of negotiation and collab-

oration (Panov and Yakovlev, 2017) with other robots

within a team (Rosenfeld et al., 2015) or swarm con-

trol (Ronzhin et al., 2016) and other functionality.

Path planning is probably the most essential part

of autonomous navigation for a mobile robot, which

is responsible for providing a collision-free path be-

tween initial and goal positions of the robot. A good

path planning algorithm should guarantee its com-

pleteness, i.e. the robot should reach its goal position

or conclude explicitly that a path, which could con-

nect the start and the goal positions, does not exist.

The completeness property is by default incorporated

into all global path planning methods, but for local

path planning in order to satisfy this property vari-

ous strategies are applied. The classical global path

planning approach, which is referred as piano movers

problem, utilizes complete a priori knowledge about

environment: a robot is aware of its own shape, ini-

tial and goal position and orientation, and a set of 2D

or 3D environment obstacles, where each obstacle in-

formation includes precisely deﬁned shape, position,

orientation in space and other task-related data (e.g.,

texture or traversability index (Seraji, 1999)). Next,

the robot searches for a continuous path from the ini-

tial position to the goal position, while negotiating

with static obstacles of the environment along its way.

In order to simplify the procedures, often the concept

of multi-dimensional conﬁguration space (Latombe,

2012) is applied for the planning. In such settings,

the path planning operation becomes an off-line one-

time operation since a complete knowledge about the

environment is available in advance. This allows op-

timizing a solution with regard to various criteria in

order to obtain an optimal or at least sub-optimal path

relatively to these criteria. The path search algorithm

should consider such qualities as ability to generate a

collision free path, time and space complexity, ability

to discover a path if it does exist, efﬁcient computa-

tional scheme, and the later is actually the main difﬁ-

culty of the piano movers approach. Yet, in real world

scenario the robot does not possess a complete knowl-

edge about environment - except some very limited or

artiﬁcial application cases. For this reason the robot

132

Magid, E., Lavrenov, R. and Khasianov, A.

Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle.

DOI: 10.5220/0006442601320141

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 132-141

ISBN: Not Available

should continuously collects sensory data from its po-

tentially dynamic environment and plan the path ac-

cordingly, which requires a reasonable combination

of local and global methods of path planning.

When a robot uses incoming sensory data to create

a global world map as it traverses the environment, we

refer to such approach as global sensor-based plan-

ning. Next, the created map is used for path plan-

ning. Main weakness of global sensor-based plan-

ning approach is a signiﬁcant computational burden

on the robot while creating and maintaining a global

model as well as excessive memory requirements in

order to store the model and the large amount of sen-

sory information, which is associated with the model.

Purely local path-planners avoid these issues by uti-

lizing only local sensory information; this allows to

reactively negotiate environmental obstacles but does

not guarantee global convergence. This way, in order

to provide a superior performance, a well-balanced

integration of global and local path-planners is essen-

tial.

A classical and popular path planning ap-

proach applies potential ﬁeld method (Tang et al.,

2010), (Khatib and Siciliano, 2016), which is based

on an artiﬁcial potential ﬁeld concept that marks a

goal position as an attractive pole and obstacles are

represented with repulsive surfaces. Then a robot pur-

sues the potential gradient in the direction of its min-

imum. Potentials are generated either at a global or

a local level and this is a matter of available envi-

ronmental information (Andrews and Hogan, 1983).

Potential ﬁeld methods gained their popularity due

to algorithm simplicity and a capability of fast re-

active avoidance of mobile and stationary obstacles.

However, potential ﬁeld methods are typically fea-

tured with such drawbacks as path oscillations for

certain conﬁgurations of obstacles (e.g., narrow pas-

sages) and local minima problem, which captures a

robot in a potential function local valley and requires

special escape procedure in order to proceed (e.g., se-

quence of random steps in arbitrary direction).

In our previous research we had proposed a path

planning spline-based algorithm for a car-like mobile

robot within a well-known environment (Magid et al.,

2006). It uses potential ﬁeld method for obstacle

collision avoidance to provide a locally sub-optimal

path with regard to path length, path smoothness and

safety optimization criteria. While a typical path-

planning algorithm applies ﬁnal smoothing of a path

at the last stages only (Fleury et al., 1995), (Elban-

hawi et al., 2015), our algorithm special feature is the

smoothness criterion integration into path optimiza-

tion from the ﬁrst stage of the algorithm. Other crite-

ria (path length and safety) played secondary role in

optimization procedure and thus collision-free but not

sufﬁciently smooth path was treated as a low quality

one. In order to improve the original algorithm per-

formance, to add ﬂexibility for path optimization and

a possibility for a fast dynamic replanning in a case

the initially off-line selected path becomes unavail-

able, we integrate Voronoi Diagram approach into our

algorithm (Choset and Burdick, 1995).

The rest of the paper is organized as follows. Sec-

tion 2 brieﬂy describes our previous research within

spline-based path planning. In section 3 we present

new criteria that improve the algorithm performance

and add more ﬂexibility for the user while select-

ing path evaluation measures. Section 4 presents

our modiﬁcation of the spline-based algorithm, which

successfully overcomes the weaknesses of the initial

approach. Section 5 demonstrates the original and

the new algorithm trial examples, where the new al-

gorithm shows successful solution of the original al-

gorithm failures. Section 6 discusses our future work.

Finally, we conclude in Section 7.

2 SPLINE-BASED ROBOT

NAVIGATION WITH ORIGINAL

POTENTIAL FIELD APPROACH

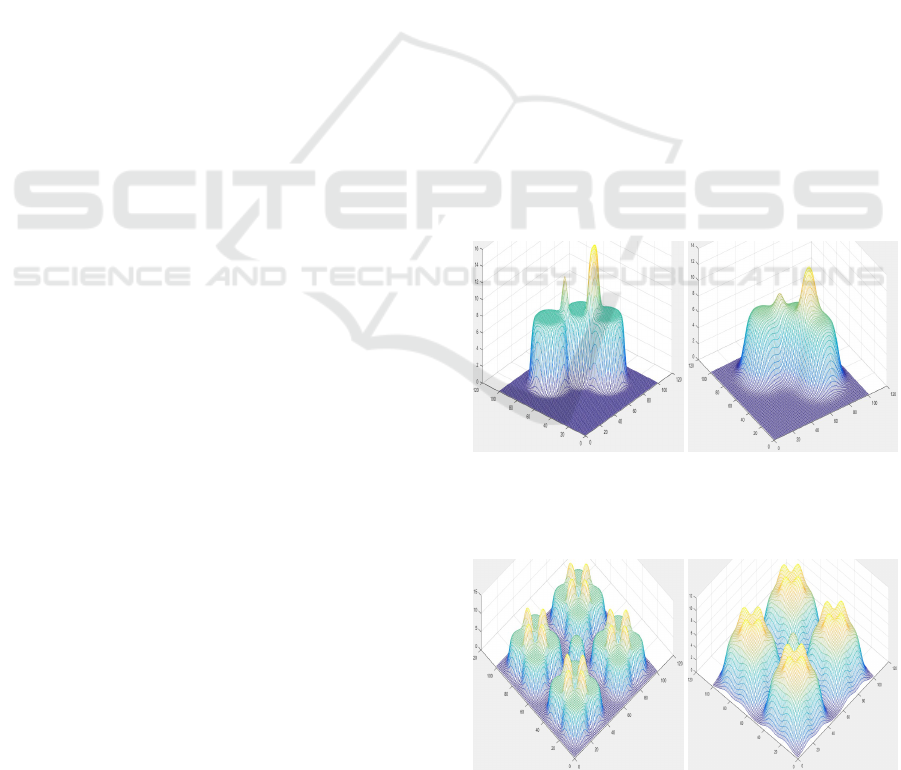
Figure 1: Repulsive potential function of eq. 1 for α = 0.5

(left) and α = 0.2 (right) that corresponds to the obstacles

in Figure 4.

Figure 2: Repulsive potential function of eq. 1 for α = 0.5

(left) and α = 0.2 (right) that corresponds to the obstacles

in Figure 5.

Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle

133

The spline-based method, proposed by Magid

et.al. about a decade ago (Magid et al., 2006) navi-

gates a car-like robot in a planar known environment

populated with static obstacles. The algorithm is con-

sidering an omnidirectional circle-shape robot which

reduces a search space by one dimension (an orienta-

tion) and all further actions are performed for a point

robot in a 2D conﬁguration space. An obstacle is pre-

sented with a set of intersecting circles of different

sizes and each set may contain just a single circle or a

ﬁnite number of circles. The idea behind such restric-

tion is based on the assertion that any arbitrary ob-

stacle could be well-approximated with a ﬁnite set of

circles. Next, given a complete information about the

environment, a start and a target positions of the robot,

the robot searches for a collision-free path which is

guided by a pre-determined cost function. The de-

tails of the algorithm could be found in (Magid et al.,

2006), while in this section we brieﬂy describe the se-

lected cost functions and overview the algorithm, and

demonstrate a successful example of its execution and

two failing examples. Finally, we explain the origins

of these failures in subsection 2.3 and further suggest

its modiﬁcation in Section 4.

2.1 Cost Function

To provide the collision free path, a repulsive poten-

tial function is featured with a high value inside an

obstacle and on its border and a small value within

free space. This way, high value of the potential

function in the obstacle’s centre pushes all points of

a path outside in order to minimize path cost during

local optimization procedure. The potential ﬁeld be-

gins to drastically change (decline) on obstacle’s bor-

der, keeps decreasing with distance as a point moves

away from the border and becomes zero rather fast in

a close vicinity of the obstacle. Assuming the robot’s

position at q(t) = (x(t), y(t)) for a time-stamp t, a con-

tribution of a single circle (where the circle is a part of

an obstacle) repulsive potential to the global potential

function is deﬁned with the following equation:

rep

(q) = 1+tanh(α(ρ−

(x(t) − x)

+ (y(t) − y)

))

(1)

where ρ is the radius of the obstacle with the centre at

(x, y) and α is an empirically deﬁned parameter that is

responsible for pushing a path outside of an obstacle.

Figure 1 demonstrates the examples of two different

selections of α parameter (α = 0.5 in the left sub-

ﬁgure and α = 0.2 in the right) for the environment

with a single obstacle that is formed by three inter-

secting circles, shown in Figure 4. Similarly, Figure 2

demonstrates the examples of α = 0.5 (in the left sub-

ﬁgure) and α = 0.2 (in the right sub-ﬁgure) for the en-

vironment with one circular obstacle in the centre and

four symmetrical complicated concave obstacles (that

are formed by four intersecting circles each), which

correspond to the map in Figure 5. In the later ex-

ample, potential function has clear peaks at the circle

intersections.

Topology T (q) is a function that takes into an ac-

count all N obstacles of the environment and their in-

ﬂuence on the robot along the whole path, which is

deﬁned as a parametric function within [0,1]:

T (q) =

N−1

∑

j=0

t=0

rep

(q) · δl(t) · dt (2)

where δl(t) is simply a length of a segment:

δl(t) =

(t))

+ (y

(t))

(3)

A function for smoothness property of the path

is referred as Roughness R(q) and is also integrated

along the path:

R(q) =

t=0

(t))

+ (y

(t))

dt (4)

A function that accounts for the path length L(q) sim-

ply sums up the lengths of all path segments:

L(q) =

t=0

δl(t)· dt (5)

Then, the ﬁnal path cost function accumulates all the

three above components:

F(q) = γ

T (q) + γ

R(q) + γ

L(q), (6)

where γ

i=1..3

are the weight factors that set an inﬂu-

ence of the corresponding component on a total cost

of the path. In particular obstacle penalty inﬂuence

component is empirically deﬁned as γ

, where β

ranges over a predeﬁned array, which correlates with

array of α parameters from eq.1 (Magid, 2006).

2.2 The Algorithm

The original algorithm of spline-based path planning

works iteratively, beginning with start point S and tar-

get point T , and utilizes the environment obstacles as

its input data. An initial path is suggested as a straight

line between points S and T , which serves as a ﬁrst

spline-based path and its spline is deﬁned with three

points: S, T and a equidistant point that lies on the

straight line between them. Equation 6 sets a current

path cost, which is further optimized with Nelder-

Mead Simplex Method (Lagarias et al., 1998) in or-

der to minimize the path cost. A resulting better path

serves as an initial guess for the next iteration.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

134

The optimization procedure operates only with

those points of the path, which deﬁne its spline, while

path evaluation accounts for all points of the path.

The path-deﬁning spline is rebuilt at each iteration us-

ing information from a previous stage, increasing the

number of spline’s points by one and adjusting pa-

rameters of the target cost function. Once the path

is free of obstacles, a few more iterations are con-

ducted in order to improve the resulting path locally.

The algorithm terminates if iteration count exceeds a

user-deﬁned limit or if a new iteration does not suc-

ceed to improve a previous one, while increasing the

spline complexity. Figure 3 demonstrates an example

of the algorithm successful execution within a simple

convex obstacles environment that resembles a plaza

with ideal geometrical placement of equal columns or

ﬂowerbeds (a view from the above): the initial path is

an optimized with regard to eq.6 spline with a single

via point between S and T (Figure 3a); after four iter-

ations the spline has four via points but still collides

with the obstacles (Figure 3b); after seven iterations

the 7-via-points-spline could be already applied for

navigation (Figure 3c), but two more iterations suc-

ceed to improve path’s length and smoothness prop-

erties (Figure 3d, 9th iteration); further increase of via

points number does not provide any improvement of

the path. It took 9 minutes to obtain the ﬁnal path

after 9 iterations of the algorithm.

(a) (b)

Figure 3: Simple convex obstacles: (a) the initial state, (b) 4

iterations, (c) 7 iterations, (d) the ﬁnal path after 9 iterations.

Figure 4: Simple concave obstacle: the ﬁrst iteration path

(left) and the ﬁnal path after 12 iterations (right).

Figure 5: Two complicated concave obstacles: the ﬁrst iter-

ation path (left) and the ﬁnal path after 17 iterations (right).

2.3 Drawbacks of the Approach

The original spline-based method succeeds to obtain

a collision free smooth path for any complexity of the

environment if each obstacle is approximated with a

single circle under the condition of non-intersecting

obstacles and some minimal distance between the ob-

stacles, which would provide a safety gap for the

moving along a path mobile robot. In this case, since

the potential function diminishes rapidly as we move

away from the obstacle boundary, we could neglect

the probability of getting stuck in a local minima.

However, when the obstacles are to be approximated

with a number of intersecting circles, the intersections

introduce potential ﬁeld local maxima. Moreover, if

in such settings an initial spline passes through in-

tersection of several obstacles, the cost function F(q)

concentrates on pushing the spline out of intersection

area that forms a local maximum; upon successful

pushing out, a further solution often gets stuck in a lo-

cal minima and a next iteration spline can not ”jump

over” some obstacle components due to a local nature

of the optimization process. Figure 4 presents a sim-

ple case of an obstacle that is formed by three inter-

secting circles and the corresponding potential ﬁeld is

presented in Figure 1; after 12 iterations the algorithm

stops as no further improvements are possible - while

a spline succeeds to optimize the path locally so that

it avoids a local maximum, it is still stuck at a local

minimum and the resulting path could not be used for

Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle

135

navigation due to obstacle collision. Figure 5 demon-

strates an example with ﬁve complicated concave ob-

stacles and a narrow pass in between. Due to multi-

ple intersecting circles, which generate their own lo-

cal repulsive potentials, the corresponding global ﬁeld

conceals the pass (Figure 2) and permits only a local

optimization of the path. The local optimization suc-

cessfully avoids local maxima, but even after 37 iter-

ations that continued for 44 minutes, the ﬁnal path is

still occluded with obstacles and thus useless for nav-

igation.

3 INTEGRATING ADDITIONAL

OPTIMIZATION CRITERIA

The original spline-based algorithm uses just three

criteria within cost function (eq. 6): topology, rough-

ness and length of path. In this section we introduce

two new additional criteria - start and target point vis-

ibility time - and explore their inﬂuence on the result-

ing path. Point visibility time refers to the path length

where the robot keeps the start point (or target point

respectively) within its direct line of sight without any

obstacle occlusions.

These two criteria are important if a robot needs to

maximize the time of a direct visual or radio contact

with a monitoring device or a router, which supports

path planning, localization or any other functionality

of the robot. The criterion should consider the ra-

tio of visible and invisible from the start (or target)

points segments of a path. Thus, we need to maxi-

mize the time when the robot is visible from the start

point while following the selected path before it dis-

appears behind some obstacle for the ﬁrst time. In

other words, we minimize the time (which is actually

measured as a length of the path assuming a constant

speed of the robot - in our future work we also extend

this to the cases of varying speed along the path) after

the robot becomes occluded for the ﬁrst time, which

we refer as invisibility of the start point S:

= 1 − lim

δt,δl(t)→0

∑

t=0

dist(A(t), A(t +δt))

t=0

δl(t)· dt

(7)

such that

∀t ∈ [0, u + δt] : [A(t), S] ∩ (∪

j=1

Obs

) =

0 (8)

where the numerator of the fraction in Eq. 7 reﬂects

the path length of a visible from the start position S

segment and the denominator of the fraction reﬂects

path length from Eq. 5. A(t) is a position of the robot

at timestamp t, and short segments of the path that

were travelled between timestamp t and t + δt, which

are denoted by dist(A(t), A(t + δt), are accumulated.

Eq. 8 describes the visibility property, which means

that a straight segment [A(t), S] does not intersect any

obstacle Obs

where j = 1..N and N is a number of

obstacles in the environment. Thus, the last visible

point from the start point while the robot follows the

selected path before disappearing behind an obstacle

for the ﬁrst time is described with A(u + δt). Simi-

larly, we describe the criterion that shows the ratio of

visible and invisible from the target point segments

of a path, which we refer as invisibility of the target

point T :

= 1 − lim

δt,δl(t)→0

∑

1−δt

t=w

dist(A(t), A(t +δt))

t=0

δl(t)· dt

(9)

such that

∀t ∈ [w, 1] : [A(t), T ] ∩ (∪

j=1

Obs

) =

0 (10)

Eq. 9 and 10 describe the ﬁrst point A(w) of a path

segment [A(w), A(1) = T ] that marks the beginning of

the last segment of the path which is featured by a

guaranteed constant visual contact between the robot

and the target position T while the robot follows the

selected path.

The cost function that combines all ﬁve criteria is

deﬁned as follows:

F(q) = γ

T (q)+γ

R(q)+γ

L(q)+γ

+γ

, (11)

where γ

and γ

are the weight factors that set the line-

of-sight criteria inﬂuence on a total cost of the path

for start S and target T points respectively. Figure 6

demonstrates the two criteria inﬂuence on the path

in the vicinity of start and target points: while with

=10 and γ

=10 these criteria do not contribute any

signiﬁcant inﬂuence (left sub-ﬁgure), with γ

=20 and

=20 the path changes are clearly visible, especially

as the robot approaches the target position (right sub-

ﬁgure); other parameters are deﬁned as γ

=1, γ

=1,

and γ

=0.5 for both cases (both sub-ﬁgures).

As the path optimization with regard to Eq. 11 is

performed only locally, the inﬂuence of the two addi-

tional parameters is also local. As a part of our future

work we plan to apply the optimization at a global

scale, which will allow the path to vary different ho-

motopy sets in order to satisfy and emphasize a par-

ticular user-deﬁned criterion inﬂuence.

4 VORONOI DIAGRAM BASED

SOLUTION

We recognize that the local nature of the optimiza-

tion procedure creates a strong dependence of algo-

rithm success or failure on initial spline. In order to

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

136

Figure 6: Start and target points visibility time inﬂuence

on the path quality: γ

=10, γ

=10 (left) and γ

=20, γ

=20

(right).

provide a good initial spline that could be further im-

proved locally with regard to user selection of the cost

weights, we apply Voronoi Diagram approach (Toth

et al., 2004). This helps to avoid the spline seizing at

local minima.

Assuming the above deﬁnition of environment ob-

stacles and potential ﬁeld, prior to Voronoi graph con-

struction, the two following steps are performed in or-

der to prepare the environment:

1. Register obstacles by grouping intersecting cir-

cles together in order to form a single obstacle. Ini-

tially, every circle is marked as idle and has its own

index i = 1..M, where M is a ﬁnite number of circles

within the environment. We start from an arbitrarily

circle, assign it to obstacle O

and mark as an acti-

vated one. Next, we iteratively grow O

by search-

ing for all idle circles that intersect with O

, assign

them to obstacle O

and mark as activated as well.

The iterative growth of O

continues until no more

idle circles that intersect O

are left in the environ-

ment. When the iterative growth of O

is completed

but there are still idle obstacles available, we select

another arbitrarily idle circle, assign it to obstacle O

and repeat the growth procedure. Obstacles registra-

tion is completed when all circles of the environment

become activated. For example, there are ﬁve obsta-

cles that are formed by groups of circles in Figure 7

and twelve obstacles in Figure 8. While performing

the registration, each pair of intersecting circles i and

j provides their intersection point ω

i j

in a case there

is a single joint point (i.e., boundary touch) and a pair

of points ω

i j

, ω

in a case of joint two points (i.e.,

boundary intersection).

2. Find outer and inner boundaries of each obsta-

cle of set Obst = {O

, O

, ..., O

}, where k is a num-

ber of compound obstacle within the environment.

Starting from an arbitrary circle within O

obstacle,

boundaries of all circles that belong to O

are split

into short segments of length σ, merged via intersec-

tion points ω

i j

(or ω

) and labelled. Parameter σ is

predeﬁned in advance and correlates with a radius of a

smallest circle of the environment in order to further

match a shortest polygonal edge of contours. Thus,

during the procedure, two segments receive the same

label if there exists a continuous path between them,

which is built of boundary segments. This procedure

is repeated for each obstacle and upon its completion

we receive a set of obstacles’ boundaries. If the size

of the latter set exceeds the size of Obst, it points out a

presence of inner boundaries that were formed by in-

ternal contours. To get rid of such contours, for each

particular obstacle O

we encapsulated every contour

of O

into a convex hull, verify which of the result-

ing contours forms outer boundary of O

and remove

the rest. For example, this procedure has successfully

removed four tiny diamond-shape internal contours

inside complicated obstacles of environment in Fig-

ure 7. Finally, we obtain several non-convex poly-

gons, one for each obstacle within Obst, and tightly

encapsulate them into a square map.

Figure 7: External contours of group of obstacles.

Next, Voronoi graph is constructed as follows, based

on a classical brushﬁre approach (Choset, 2005):

1. Parse free space with rays that originate from ob-

stacles’ edges and square map boundary. Figure 8

(the bottom image) demonstrates an example of

Voronoi graph construction for the environment in

the top image of the ﬁgure. Thick blue lines de-

pict borders of obstacles of Obst set and thin blue

lines are emerging outwards and inwards rays.

2. Calculate rays intersection points and connect

them with segments for neighbouring ray. These

Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle

137

segments are equidistant to nearest obstacles, and

all together form Voronoi graph, which is depicted

with a thin red line in Figure 8 (the bottom image)

Figure 8: Environment with obstacles (top) and Voronoi

graph building procedure (bottom).

Upon obtaining Voronoi graph V G, we select nearest

to start position S and target position T points (S

and

respectively) within V G so that segments [S, S

] and

[T, T

] lie in the free space of the environment. Next,

shortest paths between S

and T

are found within

V G applying Dijkstra algorithm (Dijkstra, 1959); they

are depicted with thick red lines in Figure 9). Any

path (S, T ) on Voronoi graph V G is guaranteed to be

collision free and maximally safe with regard to dis-

tance from obstacle boundaries, and thus could pro-

vide a good initial spline for the original spline-based

method (Magid et al., 2006).

If we use points S, T and Voronoi graph V G nodes

(thick red points on Figure 9), which are a part of

some selected path (S, T ), in a role of via points for

Figure 9: The obtained Voronoi graph and a path within the

graph.

initial spline, such sparse selection may fail to guar-

antee a good start of the spline-based method. On the

opposite, selecting every point of some selected path

(S, T ) provides us with a dense and excess amount of

via points. Our trade-off solution that uses a small

set of special points of V G (that belong to the path)

utilizes only via points that would properly charac-

terize path’s features yet avoid redundant complexity

of a spline. At a ﬁrst step, S is selected as a active

point and a farthest visible from S point of the path,

V P

, is calculated. S is added to {L}, while V P

re-

ceives a status of a next active point and again a far-

thest visible from V P

point of the path, V P

, is cal-

culated. V P

is added to {L}, V P

becomes a next ac-

tive point and the process continues until target point

T becomes visible. Here, point VP

i+1

is visible from

point V P

if they could be connected with a straight

segment that does not collide with any obstacle of the

environment. After the process ﬁnishes, the points of

{L} are utilized as via points for initial spline of the

spline-based method (Magid et al., 2006).

5 SIMULATIONS

In order to verify our approach the new smart spline-

based algorithm was implemented in Matlab environ-

ment and an exhaustive set of simulations was per-

formed. Particular attention was paid to the cases

where the original algorithm failed (Magid et al.,

2006). The cost function of Eq. 11 was applied with

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

138

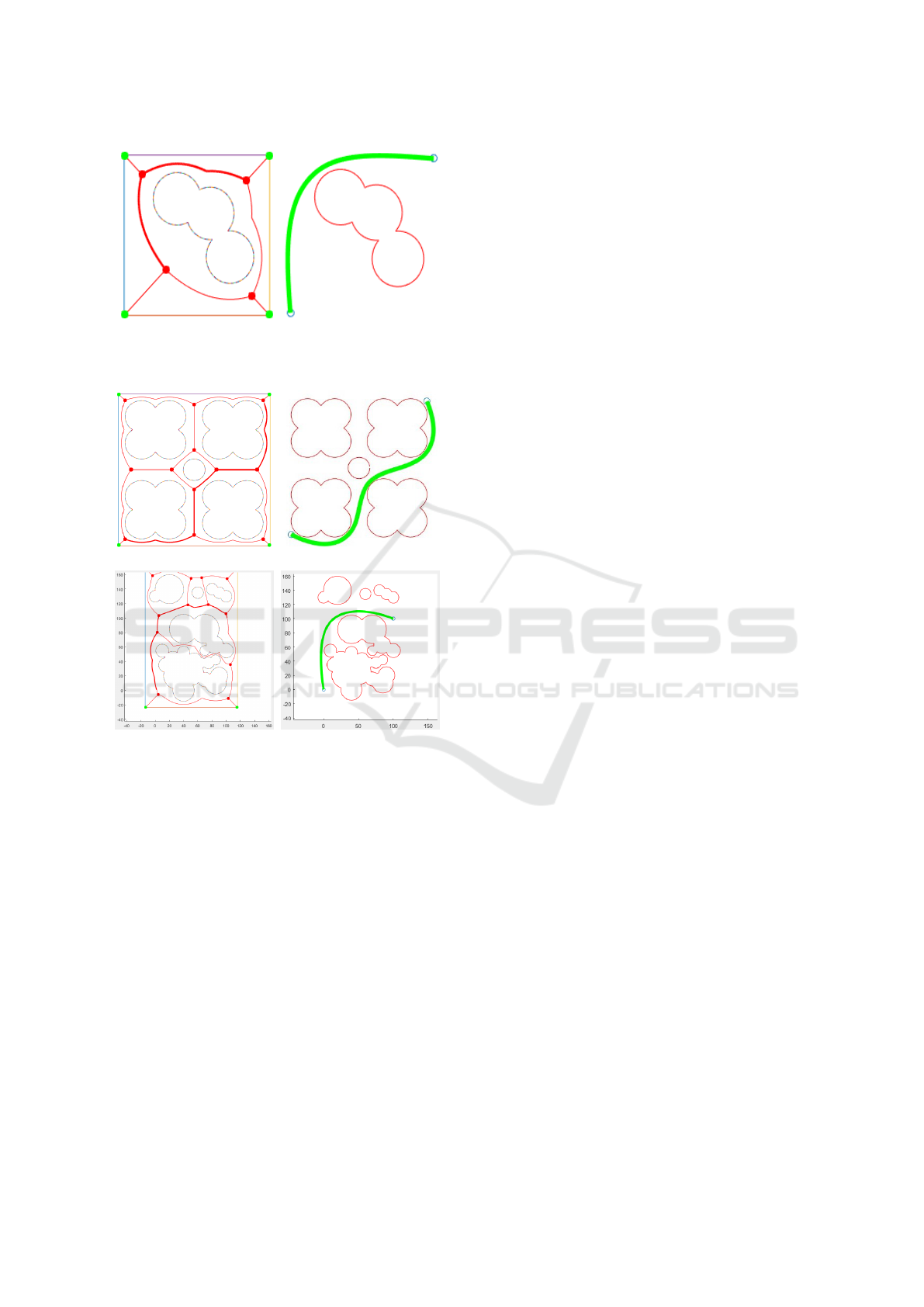
Figure 10: Path planning results: path on Voronoi graph

(left) and the corresponding spline-based optimal path

(right).

(a) (b)

Figure 11: Path planning results: paths within Voronoi

graph (a,c) and the corresponding spline-based optimal

paths (b,d).

the following empirical parameter selection: γ

=1,

=1, γ

=0.5, γ

=5, and γ

=5. The algorithm suc-

ceeded to provide collision-free paths in all cases,

which was a natural consequence of applying initial

Voronoi-based path as an input of our iterative algo-

rithm at the ﬁrst stage of the procedure.

Figure 11 demonstrates two environments, where

the original spline-based algorithm had failed (e.g.,

the example in sub-ﬁgure (b) corresponds to Fig-

ure 5). Voronoi graph provides us with a safe path

without obstacle collision or may barely touching the

obstacle boundaries in a case of very narrow passages

between distinct obstacles (of conﬁguration space).

Therefore, this good initial path ensures that the mod-

iﬁed spline-based algorithm would calculate a ﬁnal

path within a signiﬁcantly smaller number of itera-

tions. Our preliminary concern about the time com-

plexity of Voronoi graph construction turned out to be

obsolete as the simulations empirically demonstrated

that Voronoi graph calculations take acceptably small

amount of time (at least for our reasonably simple

cases, while more simulations in complicated large-

size environments are scheduled as a part of the future

work).

For example, for the environment of Figure 11(a)

the Voronoi-based initial path calculation took only 2

seconds, while for Figure 11(c) - 6 seconds. The total

running time of the new algorithm decreased in three

times in average with regard to the original algorithm.

This way, the ﬁnal path of Figure 11(b) was calcu-

lated in just 2 iterations within 2.5 minutes in Matlab,

while the original spline-based algorithm had spent 17

iterations and 44 minutes to conclude on its failure to

provide an acceptable path from start to target point.

Similarly, the original algorithm required 9 iterations

and 15 minutes to provide a good path within Figure 3

environment, while the new algorithm required 5 it-

erations and 4 minutes. In another case of Figure 4

the original algorithm failed to ﬁnd a path, while a

Voronoi-based algorithm successfully completed the

task within 3 iteration and 2 minutes (Figure 10).

6 DISCUSSION AND FUTURE

WORK

The computation time in minutes per iteration of our

currently implemented spline-based algorithm in its

Matlab prototype is an obstacle for dynamical on-line

planning with changing or dynamic environments in

practical applications. However, we emphasize that a

full-scale Voronoi graph construction and path plan-

ning are performed off-line before a search and res-

cue mission starts in order to select an initial path

of the vehicle. Then, as the vehicle discovers new

or dynamical obstacles on its way, the graph could

be rebuilt only locally (e.g., using techniques similar

to (Kalra et al., 2009) or creating a local virtual gener-

alized Voronoi graph (Choset et al., 2000)) and local

replanning is performed. Local replanning, as well as

implementation speed up and optimization, are parts

of our ongoing and future work. We strongly believe

that C++ implementation will signiﬁcantly increase

all computations.

The selection of gamma

(n=1, , 5) coefﬁcients in

equation (11) is very important for a successful path

planning in practical applications. Currently, the se-

lection is performed empirically, which in our opinion

is a rather weak point of the algorithm. As one of the

possible further extensions of this work, a separate

project for theoretical or comparative approach with

Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle

139

exhaustive simulations and further analysis of the ob-

tained data would be of a great value for proper selec-

tion of these parameters.

Figure 12: Unior robot, courtesy of Avrora robotics com-

pany, Russia.

Figure 13: Servosila Engineer mobile robot, courtesy of

Servosila company, Russia.

As a part of our future work we plan to introduce

some new parameters of cost function, including

varying speed of the robot along the path. The al-

gorithm will be tested in large-size environments in

order to verify the acceptability of the Voronoi-graph

construction time for more complicated cases. We

would like to apply optimization procedure at a global

scale, which will allow the path to vary different ho-

motopy sets in order to satisfy and emphasize a par-

ticular user-deﬁned criterion inﬂuence. Moreover,

we consider extending the algorithm for 3D envi-

ronment and adding new parameters of cost function

that are associated with 3D surfaces. The algorithm

will be bundled into a ROS package with C++ im-

plementation and further veriﬁed with real navigation

of a heterogeneous robotic team operating in an ur-

ban search and rescue scenario. Real experimenta-

tion in real world, both static and dynamic, are op-

timistically scheduled for 2018 and will be executed

utilizing Unior car-type mobile robots 12 and a group

of DJI Phantom quadcopters. Additional testing will

be performed with our crawler ”Servosila Engineer”

mobile robot 13, in ROS-Gazebo simulation (Sokolov

et al., 2016), as well as with a real hardware in order

evaluate the applicability of the algorithm for crawler-

type robots. In addition, it will be interesting to com-

pare our solution with the adaptive elliptic trajecto-

ries for smooth and safe mobile robot navigation ap-

proach (Adouane et al., 2011) and trying another rep-

resentation of complex shaped obstacles in harmonic

potential ﬁelds (Daily and Bevly, 2008).

7 CONCLUSIONS

A typical difﬁculty of path planning with potential

function methods is getting stuck in local minima of a

navigation function. In this paper we have presented

a combined method for calculating a smooth and safe

path for mobile robot in static planar environment.

The introduced modiﬁcations of our original spline-

based path planning algorithm for a mobile robot nav-

igation helped avoiding local minima problem and

added more ﬂexibility for path optimization. We so-

phisticated the cost function by introducing additional

criteria that maximized the time of keeping the robot

within direct line of sight from start and target points

while the robot follows the path. We also integrated a

Voronoi graph approach into the algorithm in order to

produce a good starting path for iterative spline-based

optimization. The new smart spline-based method al-

gorithm was implemented in Matlab environment and

its results were explicitly compared with our origi-

nal algorithm. The new approach requires less opti-

mization iterations that the original algorithm due to

a smart selection of an initial spline. While the origi-

nal algorithm fails to ﬁnd an existing path in compli-

cated environments with multiple concave obstacles,

its smart version was successful in all simulated tests

because of the Voronoi graph approach nature.

ACKNOWLEDGEMENTS

This work was partially supported by the Russian

Foundation for Basic Research (RFBR) and Ministry

of Science Technology & Space State of Israel (joint

project ID 15-57-06010). Part of the work was per-

formed according to the Russian Government Pro-

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

140

gram of Competitive Growth of Kazan Federal Uni-

versity.

REFERENCES

Adouane, L., Benzerrouk, A., and Martinet, P. (2011). Mo-

bile robot navigation in cluttered environment using

reactive elliptic trajectories. IFAC Proceedings Vol-

umes, 44(1):13801–13806.

Andrews, J. R. and Hogan, N. (1983). Impedance control

as a framework for implementing obstacle avoidance

in a manipulator. Master’s thesis, M. I. T., Dept. of

Mechanical Engineering.

Buyval, A., Afanasyev, I., and Magid, E. (2016). Compar-

ative analysis of ros-based monocular slam methods

for indoor navigation. 9th International Conference

on Machine Vision (ICMV), Nice, France.

Choset, H. and Burdick, J. (1995). Sensor based planning.

i. the generalized voronoi graph. In Robotics and

Automation, 1995. Proceedings., 1995 IEEE Interna-

tional Conference on, volume 2, pages 1649–1655.

IEEE.

Choset, H., Walker, S., Eiamsa-Ard, K., and Burdick,

J. (2000). Sensor-based exploration: Incremental

construction of the hierarchical generalized voronoi

graph. The International Journal of Robotics Re-

search, 19(2):126–148.

Choset, H. M. (2005). Principles of robot motion: theory,

algorithms, and implementation. MIT press.

Daily, R. and Bevly, D. M. (2008). Harmonic potential ﬁeld

path planning for high speed vehicles. In American

Control Conference, 2008, pages 4609–4614. IEEE.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische mathematik, 1(1):269–

271.

Elbanhawi, M., Simic, M., and Jazar, R. N. (2015). Con-

tinuous path smoothing for car-like robots using b-

spline curves. Journal of Intelligent & Robotic Sys-

tems, 80(1):23–56.

Fleury, S., Soueres, P., Laumond, J.-P., and Chatila, R.

(1995). Primitives for smoothing mobile robot trajec-

tories. IEEE transactions on robotics and automation,

11(3):441–448.

Indelman, V., Carlone, L., and Dellaert, F. (2015). Planning

in the continuous domain: A generalized belief space

approach for autonomous navigation in unknown en-

vironments. The International Journal of Robotics Re-

search, 34(7):849–882.

Kalra, N., Ferguson, D., and Stentz, A. (2009). Incremen-

tal reconstruction of generalized voronoi diagrams on

grids. Robotics and Autonomous Systems, 57(2):123–

128.

Khatib, O. and Siciliano, B. (2016). Springer handbook of

robotics. Springer.

Lagarias, J. C., Reeds, J. A., Wright, M. H., and Wright,

P. E. (1998). Convergence properties of the nelder–

mead simplex method in low dimensions. SIAM Jour-

nal on optimization, 9(1):112–147.

Latombe, J.-C. (2012). Robot motion planning, volume 124.

Springer Science & Business Media.

Magid, E. (2006). Sensor-based robot navigation. Master’s

thesis, Technion - Israel Institute of Technology.

Magid, E., Keren, D., Rivlin, E., and Yavneh, I. (2006).

Spline-based robot navigation. In Intelligent Robots

and Systems, 2006 IEEE/RSJ International Confer-

ence on, pages 2296–2301. IEEE.

Magid, E., Tsubouchi, T., Koyanagi, E., and Yoshida, T.

(2011). Building a search tree for a pilot system of a

rescue search robot in a discretized random step en-

vironment. Journal of Robotics and Mechatronics,

23(4):567.

Panov, A. I. and Yakovlev, K. (2017). Behavior and Path

Planning for the Coalition of Cognitive Robots in

Smart Relocation Tasks, pages 3–20. Springer Inter-

national Publishing, Cham.

Pipe, A., Dailami, F., and Melhuish, C. (2014). Cru-

cial challenges and groundbreaking opportunities for

advanced hri. In System Integration (SII), 2014

IEEE/SICE International Symposium on, pages 12–

15. IEEE.

Ronzhin, A., Vatamaniuk, I., and Pavluk, N. (2016). Auto-

matic control of robotic swarm during convex shape

generation. In Electrical and Power Engineering,

2016 International Conference and Exposition on,

pages 675–680. IEEE.

Rosenfeld, A., Agmon, N., Maksimov, O., Azaria, A., and

Kraus, S. (2015). Intelligent agent supporting human-

multi-robot team collaboration. In Proceedings of

the 24th International Conference on Artiﬁcial Intelli-

gence, pages 1902–1908. AAAI Press.

Seraji, H. (1999). Traversability index: A new concept for

planetary rovers. In Robotics and Automation, 1999.

Proceedings. 1999 IEEE International Conference on,

volume 3, pages 2006–2013. IEEE.

Sokolov, M., Lavrenov, R., Gabdullin, A., Afanasyev, I.,

and Magid, E. (2016). 3d modelling and simulation of

a crawler robot in ros/gazebo. In Proceedings of the

4th International Conference on Control, Mechatron-

ics and Automation, pages 61–65. ACM.

Tang, L., Dian, S., Gu, G., Zhou, K., Wang, S., and Feng,

X. (2010). A novel potential ﬁeld method for obsta-

cle avoidance and path planning of mobile robot. In

Computer Science and Information Technology (ICC-

SIT), 2010 3rd IEEE International Conference on,

volume 9, pages 633–637. IEEE.

Toth, C. D., O’Rourke, J., and Goodman, J. E. (2004).

Handbook of discrete and computational geometry.

CRC press.

Modiﬁed Spline-based Path Planning for Autonomous Ground Vehicle

141