Review of the Best MPPT Algorithms for Control of PV Sources

RUCA Tracking Algorithm

Nacer K. M’Sirdi

, Abdelhamid Rabhi

and Bechara Nehme

Aix Marseille Universit

e, CNRS, ENSAM, Universit

e de Toulon, LSIS UMR 7296, 13397, Marseille, France

MIS, Laboratory of Modeling Information and Systems, Picardie Jules Vernes University, Amiens, France

Keywords:

Maximum Power Point Tracking, Perturb and Observ Algorithm (PO), IncCond, Hill Climbing, Boost

Converter, Robust Uniﬁed Control Algorithm (RUCA).

Abstract:

Renewable energies, has generated more and more interest of research in control of the HyRES. Thousand of

papers deal with MPPT (Maximum Power Point Tracking) to optimize harnessing solar energy. The intent of

this paper is to review the most interesting Algorithm and to propose a Robust Uniﬁed Tracking Algorithm.

1 INTRODUCTION

The conversion systems of renewable energy sources,

as they include commutations and discontinuities, are

VSAS (Variable Structure Automatic Systems) and

highly dependent on variations in climate parameters,

such as temperature and irradiation (Schaefer, 1990).

A great variety of MPPT methods have been pro-

posed by the researchers and competition between

the algorithms to be implemented continues. A good

classiﬁcation will help future applications in PV sys-

tems and give a convenient reference on the required

system features.

In this paper, we present a review of the existing

methods, propose a classiﬁcation and try to ﬁnd the

best of them. Three categories of MPPT schemes

exist: open loop, closed loop and hybrid methods;

They can also be classiﬁed with regard to model based

methods or robust optimisation. Then we propose

a new technique which unify and robustify the al-

gorithms. The Robust Uniﬁed Control Algorithm is

proposed to track the maximum power point (VSAS-

MPPT) based on Variable Structure Automatic Sys-

tems approach.

The purpose of this study is also to analyze

and compare execution efﬁciency for the proposed

RUCA-MPPT algorithms to well known power con-

trol type MPPT methods, including Perturbation and

Observation (P&O), Incremental Conductance (In-

Cond) and Hill Climbing (HC) methods, simulated

in Matlab/Simulink environment in order to compare

their performance (Yu and Shen, 2009; Tavares et al.,

2009; Xiao and Dunford, 2004).

The paper is organized as follows. The second

section presents standard photovoltaic system equa-

Figure 1: Equivalent circuit model of PV panel.

tions and features. Section three reviews the differ-

ent control algorithms proposed for tracking the max-

imum power point (MPP) and then in section four the

analysis and discussion lead us to introduce our new

algorithm. After VSAS-MPPT deﬁnition, we com-

pare the results of the RUCA with the widely used

MPPT algorithms; the performance is evaluated on

the energy point of view, in simulation, considering

different actual solar irradiation measured variations.

Finally, a conclusion summarizes the work and pro-

poses perspectives.

2 RENEWABLE ENERGY

SOURCES

PV modules (panels) are composed by combination of

several solar cells, connected in series and in parallel

circuits, to generate higher power (Liu et al., 2008).

The equivalent circuit of the general model, as il-

lustrated in left of ﬁgure 1, consists of a photo-current,

diodes, a parallel resistor expressing a leakage cur-

rent, and a series resistor describing an internal resis-

tance to the current ﬂow.

The PV circuit is connected to the load (R

) trough

a DC-DC converter in order to adjust (adapt) the op-

318

M’Sirdi, N., Rabhi, A. and Nehme, B.

Review of the Best MPPT Algorithms for Control of PV Sources - RUCA Tracking Algorithm.

DOI: 10.5220/0006461503180325

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 318-325

ISBN: 978-989-758-263-9

erating voltage and current of the PV panel at optimal

values to maximize the harnessed power. The control

of the boost has to tracks the Maximum Power Point

(ﬁgure 2).

Mathematical description of I(V) Input/Output

characteristics for a PV cell has been studied for over

the past four decades. The PV system exhibits then

a nonlinear I(V) characteristic which depend on the

temperature and the solar radiation which vary during

a day. The PV characteristics (I = f (V) and Ppv =

f (V)) are represented by the ﬁgure 2 under constant

temperatures (Ta=10, 30, 50 and 70

◦

C) and irradia-

tion Gs=1000 w/m2.

Figure 2: a) I-V characteristic I = f (V

) and b) P-V char-

acteristic curve P

= f (V ) of PV module.

Te DC-DC converter is used as a power interface

circuit between the PV panel and the load or bat-

tery. This circuit consists, in its simple way, of only a

switch (typically a MOSFET), an inductor, and a ca-

pacitor connected as shown in ﬁgure 1. To achieve

the optimum matching and track the power Maximis-

ing point, a good control of the DC-DC is necessary.

3 THE MPPT CONTROL

3.1 The Open Loop Methods for MPPT

3.1.1 Fixed Operating Point

The problem is to ﬁnd the voltage V

MPP

or the cur-

rent I

MPP

at which the PV array delivers the maxi-

mum power under a given temperature T and irradi-

ance G. Then the method automatically puts the PV

in this condition. The ﬁrst remark was that the MPP

varies in a small region and that on the left part of the

P-V characteristic, the slope P/V is roughly constant.

Fractional Open-circuit Voltage. The ﬁrst method

uses the observation that, the ratio between array volt-

age at maximum power V

MPP

to its open circuit volt-

age V

is nearly constant.

MPP

≈k

. The factor k

is not constant but, has been remarked to be between

0.71 and 0.78. Once the constant k1 is known, V

MPP

can be computed.

This method consists in measuring V

periodi-

cally and then ﬁxing V

MPP

= k

The implementation is simple and cheap, but the

tracking efﬁciency is relatively low due to inaccurate

values of the constant k

in the computation of V

MPP

Fractional Short-circuit Current. This method is

based on the remark that the current at maximum

power point I

MPP

is approximately proportional to the

short circuit current I

of the PV array. I

MPP

≈k

The factor k

is not constant but, has been re-

marked to be between 0.78 and 0.92. Once the con-

stant k1 is known, V

MPP

can be computed.

The accuracy of this method and its tracking ef-

ﬁciency depend on the accuracy of knowledge of k

and the periodic measurement of short circuit current

3.1.2 Artiﬁcial Neural Networks, ANN for

MPPT

ANN are well known to provide universal approxi-

mators providing non-linear models which are com-

plementary to the conventional modeling techniques.

Back propagation ANN are used as pattern classi-

ﬁer or as non-linear layered feed-forward networks to

give a global approximations to a non-linear input-

output mapping (Reisi et al., 2013). The ﬁrst applica-

tion of ANNs to MPPT, has been proposed by Hiyama

et al (Hiyama and Kitabayashi, 1997).

In general a three layer structure, i.e. input layer,

hidden layer and output layer are used with the back

propagation. After a good learning, ANN are able

to make generalizations in regions of the phase space

where little is known or no data are available. The

Neural network is composed by neuron cells, placed

in 3 layers (or may be more) connected to all neurons

through weights see ﬁgure below. The input variables

are PV parameters like V

and I

, atmospheric data

(Irradiance and Temperature). The output of ANN

gives reference signals, like the reference voltage or

the duty cycle signal used to drive the power converter

to operate at or close to the MPP.

The three layers of neural network have a hyper

tangent sigmoid function (Noguchi et al., 2002). The

algorithm used for training is back-propagation. The

back-propagation training algorithm needs inputs and

the desired output to adapt the weight by MSE.

The characteristics of a PV array are nonlinear and

time-varying, this implies that the neural network has

to be trained to guarantee accurate tracking of MPP.

This is a time consuming process. Note also that it can

use as inputs the voltage and current measurement,

to become a closed loop method or a combination of

both.

Review of the Best MPPT Algorithms for Control of PV Sources - RUCA Tracking Algorithm

319

3.1.3 Fuzzy Logic Method (FL)

Fuzzy logic controllers offer the advantage of work-

ing capability with imprecise inputs, and do not need

an accurate mathematical model. They can han-

dle nonlinearities, and have fast convergence. Their

learning ability and accuracy depend on the number

on the fuzzy levels and the the membership functions.

The decision-making uses rules speciﬁed by a set of

IF–THEN statements to deﬁne the control which pro-

duce the desired behavior. The defuzziﬁcation stage,

operates the reverse function to get numerical vari-

ables for analog control using the membership func-

tion.

In order to track MPP, the error is computed based

on irradiance and temperature or instantaneous values

such as power and voltage (Algazar et al., 2012). The

output signal is either the duty cycle itself, or V

MPP

and I

MPP

reference to generate the duty cycle.

The membership function associated with fuzzi-

ﬁcation and defuzziﬁcation, as well as the antecedent

and the consequent fuzzy rules are determined by trial

and error. This can be time-consuming. This method

can be used in open loop or in closed loop when us-

ing as feedback (in real time) the output variables like

current, voltage and the power.

3.2 The Closed Loop MPPT

3.2.1 Perturb and Observe Methods

The most commonly used MPPT algorithm is the Per-

turbation and Observation (P&O) due to its easy im-

plementation. It uses the P-V characteristics P

f (V ) of the PV module shown in ﬁgure 3 (b). Note

that the point of maximum power P(n)=V(n)I(n) is ob-

tained when the condition

= 0 is accomplished, re-

gardless of the sun irradiance magnitude (Kim et al.,

2001). In actual experiments, the system oscillates ar-

roumd the MPP. To minimize the oscillations ampli-

tude, we can reduce the perturbation step size. How-

ever, small step size slows down the convergence of

the MPPT.

The Modiﬁed Enhanced Perturb and Observe

(MEPO) algorithm uses and adaptive step adjustment

gain and simplify the implementation using on com-

mutation functions. This algorithm have been revis-

ited, its rationale behind have been clariﬁed and then

implementation obviated using commutation func-

tions (Msirdi and Nehme, 2015).

3.2.2 Incremental Conductance Methods

The incremental conductance (IncCond) (Femia et al.,

2004), method is based on the fact that the slope (or

the PV conductance G =

) of the PV array, in the

power curve is zero at the MPP and it is positive (con-

stant) on the left of the MPP. The slope becomes neg-

ative on the right of th MPP.

3.2.3 Hill Climbing Method

The basic idea of the HC (Hill Climbing) method is

the same as P&O method. It tests if P(n) is greater

than P(n-1) or not, to reach MPP. The PO method uses

instead a test on dP/dV to determine whether the max-

imum power point has been found or not. However,

the HC method uses a test condition on P(n)-P(n-1).

3.2.4 Extremum Seeking Control Method (ESC)

Krstic et al. (Ariyur and Krstic, 2003), from au-

tomatic control community interested on robust and

adaptive control techniques, proposed an adaptive

ESC methodology which has been proved to be ro-

bust against parametric uncertainties for non linear

dynamic uncertain systems. It is based on theories

namely averaging theory, adaptive control and singu-

lar perturbation techniques. This real-time optimiza-

tion ESC method has been successfully applied in var-

ious systems and has been speciﬁcally adapted for PV

systems in order to track MPP (Leyva et al., 2006;

Brunton et al., 2010). Extension to ESC by Newton

Like optimisation has been also considered and com-

pared to other ESC based methods (Zazo et al., 2012).

The objective of ESC is to rapidly reach the MPP de-

spite uncertainties and disturbances on the PV panel

and the load.

The reference current is perturbed by a sinusoidal

modulation. The power got at the output of the PV

system is high pass ﬁltered, to get only effect of

the perturbation (4P(t)) on the obtained power P(t).

Then, after the ripple demodulation to get the pro-

duced power perturbation observed (ξ(t)), integration

with an adaptive gain C(p) of this effect gives the ref-

erence current. The adaptation gain C(p) is adjusted

by a theoretical study to get fast convergence to the

optimum power (MPP). The controller will, therefore,

adjust the reference current until MPP is reached.

The main advantages of ESC are that the power

optimization is got by a dynamic adaptation-based

feedback for a sinusoidal perturbation and conver-

gence to the MPP is guaranted. This approach does

not require any parametrization or structural formal-

ization of the modeling uncertainty. The disadvantage

of ESC is its complexity and the implementation dif-

ﬁculties regard to PO and MEPO.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

320

3.2.5 RSMCA: Robust Sliding Mode Control

Algorithm

A lot of algorithms have been proposed based on

Sliding Mode. The most of them are not very pre-

cise when deﬁning the objective of the algorithm and

chosing the sliding surface. They simply has been de-

velop as alternative to use of a standard regulator like

PID controller. This reduces the efﬁciency of the Slid-

ing Mode Approach and does not tackle the robustnes

problem. The most of them use a sliding surface to

reach the MPP. The best choice seems to be given by

the proposed criteria in equations (1 and 2).

In the following we propose an MPPT based on

the VSAS and the Lyapunov theory which general-

izes all the previous algorithms. The desired objective

to get is that the MPP reached when the maximum

power is obtained

= 0.

Note that the optimization is done versus time be-

cause P varies during time in function of the voltage

V and the current I. Only if current I (respectively

the voltage V) is maintained constant we can consider

P(V) (respectively P(I)) characteristic. Note also that

in real weather condition the Operating Point do not

moves on a unique (P-V) characteristic. If the irradia-

tion or the temperature changes the MPP varies from

one curve to another one.

Then as P(t) = V (t).I(t) = f (V, I,t), the power is

function of the voltage, the current and time, then the

required Maximum Power Point to Track is really de-

ﬁned by the following objective function which we

propose to take as the generic sliding surface:

dV I

= I

= 0 (1)

Let us consider the control in case of discrete

time, like do all the above presented algorithms,

with the previously deﬁned variables (see equation

5) the fetched MPPT may be deﬁned by ∆P(k) = 0,

then as

= 0 can be approximated by ∆P(k) =

(I(k)∆V (k) +V (k)∆I(k)).4t

The objective function that we propose in

(M’Sirdi et al., 2014) becomes then:

∆P(k) = I(k)∆V (k) +V (k)∆I(k) = 0 (2)

The control variable is either, in the ﬁrst case,

(k) = 4V (k), which means that the voltage per-

turbed and the current is ﬁxed u

(k) = 4I(k) = 0,

or in the second case, the control variable is u

(k) =

4I(k), the current is pertubed and the voltage is ﬁxed

(k) = 4V (k) = 0. In control context, the previously

presented MPPT controllers use only one control

variable u

or u

and impose the second to zero. Let

us consider the MPP reaching condition

dP(t)

= 0 and

note that the maximum power is always P

max

≥ P(t)

every where and at any time. We can choose as Slid-

ing Surface s(t) = P

max

− P(t) which goes to zero (or

at least to its minimum) when P(t) = P

max

(Msirdi

and Nehme, 2015). We can also take zero instead of a

positive constant P

max

= 0.

Let us then consider the Lyapunov like function

W (t) = s

= [P

max

− P(t)]

> 0 which is strictly pos-

itive every where except at the MPP where it goes to

zero. Lyapunov based control design is well known

to give robust algorithms.

The derivative of this Lyapunov function W (t) =

> 0, is

W = s ˙s = −[P

max

− P(t)] .

dP(t)

This term is negative when −

dP(t)

= −I

−

<0. This equation is similar to the proposed Slid-

ing Surface equations (1 2 12). Please note also the

similarity with the InCond equation (13). This means

obviously that we only need, from control, to make

dP(t)

> 0, to reach the MPP.

as we impose

= 0, we get

W = −I

It can be made negative by choosing the appro-

priate control laws u

(k) = 4V (k) and u

(k) = 0.

Note that this can be reached by choosing the sign

of u

(k) = V (k), such as to get

W < 0.

Choosing u

(k) = 4V (k) =

4P(k).α.sign(4V (k)) and knowing that we

impose u

(k) = 4I(k) = 0 like in the con-

trol algorithm, we have previously proposed

MEPO (Msirdi and Nehme, 2015). This gives us

4W = −α.4P(k).sign(4V (k))I(k). If the gain

parameter α is positive constants, we then get a

negative derivative

4W = −α.∆V (k).sign(4V (k))I

(k) < 0 (3)

This method, called MEPO (Modiﬁed Enhanced

Perturb and Observ) gives an enhanced and variable

step size algorithm. The step size is adjusted in pro-

portionally to the power variation produced in the pre-

vious step. The step adjustment gain K = α.4P(k) is

used for weighting this adjustment step. It may be

useful for oscillation avoidance and noise sensitivity.

This proves, theoretically the convergence of the

RSMC algorithm and shows that Robust Sliding

Mode Control is equivalent to the MEPO algorithm

got by enhancement of the P&O.

We propose, as a modiﬁed PO Algorithm which

will be more robust, the reference voltage is given by

V re f = V k + α.4P.sign(4V ) (4)

The algorithms have been tested under various oper-

ating conditions. The obtained results have proven

that the MPPT is tracked even under sudden change

of irradiation level.

Review of the Best MPPT Algorithms for Control of PV Sources - RUCA Tracking Algorithm

321

3.2.6 RUCA: Robust Uniﬁed Control Algorithm

VSAS (Variable Structure Automatic Systems) con-

trol methodology was applied to clarify the rationale

behind Maximum Power Point Tracking and get the

best optimization algorithm. We have seen previously

that the control is either on voltage or on current in-

put or both. For the proposed RUCA algorithm, both

controls can be used if we look for adjusting both vari-

ables (V and I), either at each control step or alterna-

tively.

Two new algorithms can be developed, using this

approach, the Modiﬁed and Enhanced Perturb and

Observe Algorithm (MEPO) if the control input is

on the voltage or the Modiﬁed Enhanced InCond

(MEInCond) if the control input is on the current.

For the MEPO and the RSMC, we take for esti-

mation of the power variation ∆P(k) = I(k)∆V (k), the

current is assumed constant.

For the Modiﬁed Enhaced InCond (MEInCond),

we consider the current as the only input control and

we take ∆P(k) = V (k)∆I(k), the voltage is assumed

constant.

The Robust Uniﬁed Control Algorithm (RUCA)

will do both of them alternatively. Note that the hard-

ware have to be considered in consequence. Com-

pared to the other algorithms like Perturb and Observe

(PO), Hill Climbing, Incremental Conductance (In-

Cond) The RSMC approach it is proven more efﬁcient

and faster despite using low frequency commutation.

It can be noticed that all the previous algo-

rithms can be considered as particular cases of this

one (RUCA), when simplifying the proposed control

method.

The implementation of the proposed RUCA con-

troller can be summarised as follows:

1. The reference voltage is set be equal to the PV

open circuit voltage.

2. Measurement of the of input signals (PV voltage,

PV current and Load voltage).

3. Estimate the PV power at the sample time k :

(k) = I

(k)V

(k)

4. Calculate the PV current and the power incre-

ments.











∆I = I

(k) − I

(k − 1)

∆V = V

(k) −V

(k − 1)

∆P = P

(k) − P

(k − 1)

(k) = V

(k).I

(k)

(5)

The reference voltage V

re f

(k) is calculated as below,

where α is the perturbation variation step (control

gain). Note that ∆V

re f

= α.sign(∆P∆V ) produces ex-

atly the same result as the classical PO algorithm with

a much more simple implementation (one formula in-

stead of an algorithm chart).

Recall that the system equations have been used

also to deﬁne the classical Sliding Mode based algo-

rithms by means of choosing a commutation (sliding)

surface s. The proposed MPPT has several advan-

tages: simplicity, high convergence speed and is in-

dependent on PV array characteristics. In conclusion

let us say that RUCA enhances and generalizes all

the best algorithms presented in litterature and sug-

gest new algorithmes like MEPO and MEInCond.

3.3 Hybrid Tracking Methods HTM

It is well known that combination of OLM (Open

Loop Method) for anticipation with robust feedback

(CLM: Closed Loop Method) gives the best way

to control and track trajectories of uncertain and

time varying systems. In HTM, the control sig-

nal associates OLM, determined according to atmo-

spheric conditions temperature and irradiance, and

CLM based on feedcback control to track MPP. In a

hybrid method consisting of two loops is proposed.

In the ﬁrst loop MPP is estimated based on the open

circuit voltage at a constant temperature. Several au-

thors use Neural Networks or Fuzzy Logic or combine

Neuro Fuzzy Logic to anticipate on temperature and

radiation effects. Tina et al proposed to use a simpli-

ﬁed model used to evaluate the MPP power in (Tina

and Scrofani, 2008). It seems to be the most efﬁcient

way to predict the MPP.

4 COMPARATIVE STUDY

In this section we present simulations based compar-

ison between different MPPT algorithms. Several al-

gorithms are compared the classical P&O (Perturb

and Observe), the MEPO (Modiﬁed Enhanced Per-

turb and Observe), IncCond (Incremental Conduc-

tance), RUCA (Robust Uniﬁed Control Algorithm),

and NL-ESC (Newton-Like Extremum Seeking Con-

trol).

The ﬁrst step, for validation of the implementa-

tion, uses the same simulated model as in the paper

of Zazo et al (Zazo et al., 2012) to compare the dif-

ferent algorithms. The second step is simulation with

the PSIM software of the model of the experimental

setup.

4.1 Simulations with PSIM Software

The physical model of a PV panel is used with a Boost

DC-DC converter using a MOSFET as a switch. The

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

322

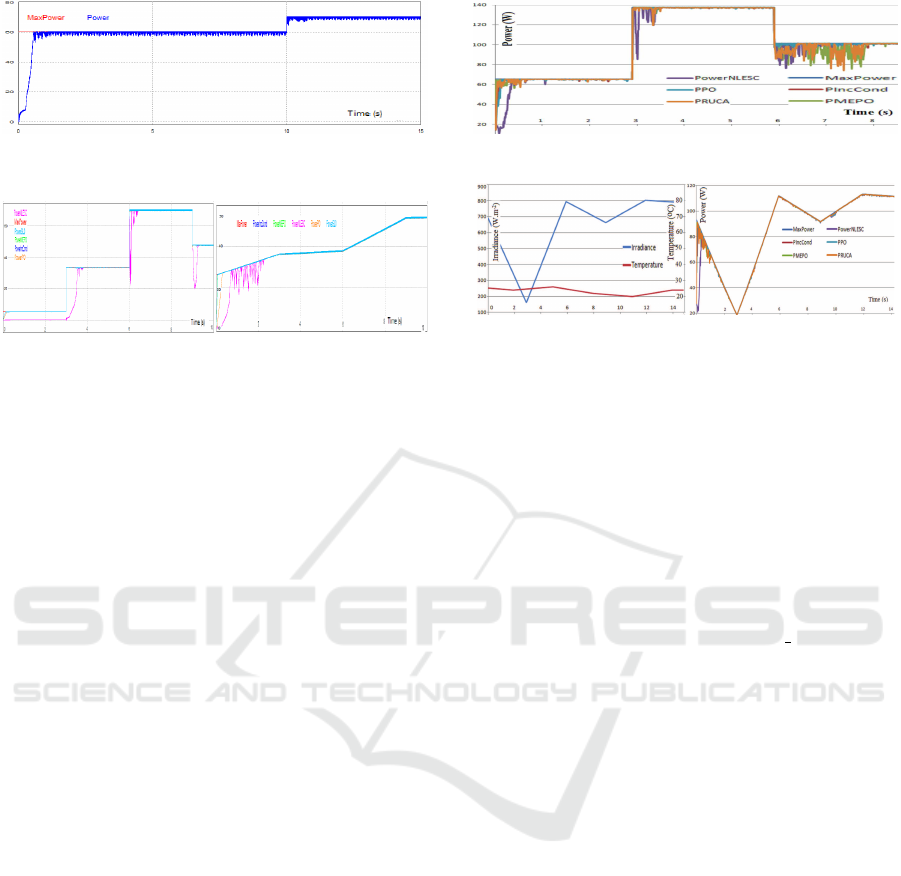
Figure 3: Power output of a PV panel with sudden variation

in irradince controlled with the NL-ESC algorithm.

Figure 4: First order interpolation comparison of the 5 al-

gorithms with real data. Zero order sample and hold com-

parison of the 5 algorithms.

panel is considered to have 36 cells. A boost con-

verter is built;The load is a 100Ω resistor. The al-

gorithms are implemented in a C block and the duty

cycle is calculated from Vref using another C block.

The actual, measured irradiation and panel tempera-

ture, when used, are read from a txt ﬁle as input to the

simulation.

We start ﬁrst by retrieving all the simulation of

the paper of Zazo et al (Zazo et al., 2012) and then

compare to the other algorithms.

In order to compare the 5 algorithms we build un-

der Psim software 5 identical PV systems. Each sys-

tem is controlled by a different MPPT algorihm. The

second simulation is done with the same input irradi-

ance and temperature for the 5 systems. Zero order

sample and hold is applied. The result is shown in

ﬁgure 4.

The third simulation is done with ﬁrst order inter-

polation and shown in ﬁgure 5. In this simulation real

weather data and real PV temperature are used.

4.2 Simulation Results

The simulation was performed under Psim software.

The simulated process is composed of two PV pan-

els, a DC/DC converter, and 4 batteries. Each PV

panel is composed of 10 cells mounted in serie. The

panel short circuit current is 5.1 A and it can gen-

erate 62W in STC. The two panels are mounted in

series. The DC/DC converter is a boost (step up con-

verter) mainly made of a capacitor, a self, a diode and

a switching device. The batteries are connected in se-

ries delivering 4 × 12 = 48V .

In order to compare the 5 algorithms we built 5

identical simulation systems. All systems have the

Figure 5: Brutal change in irradiance and temperature.

Figure 6: Simulation for change in irradiance and tempera-

ture. Interpolated change in irradiance and temperature.

same irradiance and temperature inputs.

The step of the P&O algorithm is ﬁxed to 0.1V.

The step of the IncCnd algorithm is also ﬁxed to 0.1V.

The gain of the MEPO algorithm is chosen 25. The

gain of the RUCA algorithm is chosen 25. The gain

of the NL-ESC is 0.15 and the gain of the hessian is

3000.

For the ﬁrst simulation, we consider an irradiance

of 1000W.m

-2

and a temperature of 25

C. We can

see that all the algorithms reach the maximum power

point in less than 0.5 seconds. The NL ESC presents

the less oscillations. The RUCA is the fastest with

decreasing oscillations. Also the MEPO present the

same features. The IncCnd and PO present high os-

cillation and takes time to reach the MPP.

For the second simulation, we consider a zero or-

der sample and hold for the irradiance and tempera-

ture that change. The irradiance and temperature rise

and fall brutally during as shown in ﬁgure 3. The sim-

ulation of ﬁgure 4 shows how all algorithms manage

to reach the MPP after the brutal variation of environ-

mental conditions. The NL-ESC presents the high-

est oscillation amplitude after the brutal change. The

RUCA and MEPO presents oscillation before stabi-

lizing in the MPP after the brutal change. This is

explained because these last algorithms uses the gra-

dient of power to calculate the step, and after brutal

change of environmental conditions, the power gradi-

ent is high.

For the third simulation, we consider a variation

in irradiance and temperature with ﬁrst order interpo-

lation. Real data are taken from measurement done

on the 16/5/2012. We can see that all algorithms

reaches the MPP. Oscillations do not occurs because

the power gradient is low.

In summary, the simulation comparison between

the 5 algorithms showed a convergence of all the al-

Review of the Best MPPT Algorithms for Control of PV Sources - RUCA Tracking Algorithm

323

gorithms. Algorithms based on ﬁxed step as P&O and

IncCond must run at high frequency in order to reach

the MPP. Algorithms based on the power gradient as

MEPO and RUCA can operate at lower frequencies.

MEPO, RUCA, and NL-ESC present oscillations in

front brutal variation of irradiance and temperature.

5 CONCLUSION

The best MPPT algorithms of the litterature have been

reviewed and analyzed in this work. This comparison

allowed us to select ﬁve of them to be compared in

simulations and experimental application. The sim-

ulations was performed under PSIM software to use

realistic physical models.

The analysis has shown the rationale behind

MPPT and the generalization leading to a uniﬁed

framework RUCA, as a Robust Uniﬁed Control Algo-

rithm. The well known algorithms can be viewed as

particular cases of the RUCA. The proposed approach

RUCA generalizes the PO, the InC, the ESC and the

Sliding Mode Control schemes to non linear systems

with commutations. The proposed MPPT has several

advantages: simplicity, high convergence speed, and

is independent on PV array characteristics. The ob-

tained results have proven that the MPPT is tracked

even under sudden change of irradiation level or tem-

perature.

The algorithms are tested under various operating

conditions. Realistic simulations are used to show

ease of implementation of our new algorithm, and to

compare its execution efﬁciency and accuracy to the

the studied MPPT methods.

In summary the best algorithms are those designed

using the SASV-MPPT approach and Lyapunov de-

sign method considering that the PV system can move

from one characteristic to another. The proposed al-

gorithms are the most efﬁcient despite using low fre-

quency commutation. They are the faster converging.

REFERENCES

Algazar, M. M., El-Halim, H. A., Salem, M. E. E. K.,

et al. (2012). Maximum power point tracking using

fuzzy logic control. International Journal of Electri-

cal Power & Energy Systems, 39(1):21–28.

Ariyur, K. B. and Krstic, M. (2003). Real-time optimization

by extremum-seeking control. John Wiley & Sons.

Brunton SL, Rowley CW, Kulkarni SR, Clarkson C. Max-

imum power point tracking for photovoltaic opti-

mization using ripple-based extremum seeking con-

trol. IEEE Transactions on Power Electronics 2010;

25(10): 2531-40.

Femia, N., Petrone, G., Spagnuolo, G., and Vitelli, M.

(2004). Optimizing duty-cycle perturbation of p&o

mppt technique. In Power Electronics Specialists

Conference, 2004. PESC 04. 2004 IEEE 35th Annual,

volume 3, pages 1939–1944. IEEE.

Hiyama, T. and Kitabayashi, K. (1997). Neural network

based estimation of maximum power generation from

pv module using environmental information. IEEE

Transactions on Energy Conversion, 12(3):241–247.

Kim, T.-Y., Ahn, H.-G., Park, S. K., and Lee, Y.-K. (2001).

A novel maximum power point tracking control for

photovoltaic power system under rapidly changing so-

lar radiation. In Industrial Electronics, 2001. Proceed-

ings. ISIE 2001. IEEE International Symposium on,

volume 2, pages 1011–1014. IEEE.

Leyva R, Alonso C, et al. MPPT of Photovoltaic Sys-

tems using Extremum- Seeking control. IEEE Trans-

actions on Aerospace and Electronic Systems 2006;

42(1) :249-58.

Liu, F., Kang, Y., Zhang, Y., and Duan, S. (2008). Com-

parison of p&o and hill climbing mppt methods for

grid-connected pv converter. In Industrial Electronics

and Applications, 2008. ICIEA 2008. 3rd IEEE Con-

ference on, pages 804–807. IEEE.

Msirdi, N. and Nehme, B. (2015). The vsas approach gives

the best mppt for solar energy sources. Renewable

Energy and Sustainable Development, 1(1):60–71.

M’Sirdi, N., Nehme, B., Abarkan, M., and Rabbi, A.

(2014). The best mppt algorithms by vsas approach

for renewable energy sources (res). In Environmental

Friendly Energies and Applications (EFEA), 2014 3rd

International Symposium on, pages 1–7. IEEE.

Noguchi, T., Togashi, S., and Nakamoto, R. (2002). Short-

current pulse-based maximum-power-point tracking

method for multiple photovoltaic-and-converter mod-

ule system. IEEE Transactions on Industrial Electron-

ics, 49(1):217–223.

Reisi, A. R., Moradi, M. H., and Jamasb, S. (2013). Clas-

siﬁcation and comparison of maximum power point

tracking techniques for photovoltaic system: A re-

view. Renewable and Sustainable Energy Reviews,

19:433–443.

Schaefer, J. (1990). Review of photovoltaic power plant

performance and economics. IEEE Transactions on

Energy Conversion, 5(2):232–238.

Tavares, C. A., Leite, K. T., Suemitsu, W. I., and Bellar,

M. D. (2009). Performance evaluation of photovoltaic

solar system with different mppt methods. In Indus-

trial Electronics, 2009. IECON’09. 35th Annual Con-

ference of IEEE, pages 719–724. IEEE.

Tina, G. and Scrofani, S. (2008). Electrical and thermal

model for pv module temperature evaluation. In Elec-

trotechnical Conference, 2008. MELECON 2008. The

14th IEEE Mediterranean, pages 585–590. IEEE.

Xiao, W. and Dunford, W. G. (2004). A modiﬁed adap-

tive hill climbing mppt method for photovoltaic power

systems. In Power Electronics Specialists Conference,

2004. PESC 04. 2004 IEEE 35th Annual, volume 3,

pages 1957–1963. Ieee.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

324

Yu, T.-C. and Shen, Y.-T. (2009). Analysis and simulation

of maximum power point tracking for photovoltaic

systems. In Proceedings of the 30th ROC Symposium

on Electrical Power Engineering, Taoyuan, Taiwan,

pages 92–96.

Zazo, H., Del Castillo, E., Reynaud, J. F., and Leyva, R.

(2012). Mppt for photovoltaic modules via newton-

like extremum seeking control. Energies, 5(8):2652–

2666.

Review of the Best MPPT Algorithms for Control of PV Sources - RUCA Tracking Algorithm

325