Hierarchical Petri Net Simulator: Simulation, Design Validation, and

Model Checking Tool for Hierarchical Place/Transition Petri Nets

Yojiro Harie and Katsumi Wasaki

Interdisciplinary Graduate School of Science and Technology, Shinshu University,

4-17-1, Wakasato, Nagano, Nagano, Japan

Keywords:

Petri Nets, HiPS, Hierarchical Modeling, Property Analysis, Event based Veriﬁcation.

Abstract:

This paper introduces the Hierarchical Petri net Simulator (HiPS), a Petri net design tool implemented using

C# and C++, the .NET Framework, and an interprocess communication channel. HiPS supports hierarchical

modeling and can analyze the dynamic and structural properties of a Petri net by generating state spaces. The

state space generation engine in HiPS provides a memory-saving technique and high-speed execution. We

have devised an Extended Coverability Graph (ECG) mechanism for liveness and persistence properties to

accurately maintain transition information. In this paper, we extend HiPS to include a liveness analyzer that

utilizes the ECG mechanism and an on-the-ﬂy model checker for event-based systems. We also describe an

algorithm that generates state spaces by multi-threading. Furthermore, we propose priority ﬁring estimation

with on-the-ﬂy model checking for Linear Temporal Logic (LTL).

1 INTRODUCTION

The increasing implementation of embedded systems

in IT has led to communication complexity and com-

plex architectures. A Petri net is a graphical and math-

ematical modeling tool that can describe many sys-

tems, such as logic circuits, data communication, and

distributed cloud applications (Iakushkin et al., 2016).

The set of all possible system states is called the state

space. State space structures in Petri nets are pre-

sented in the form of reachability graphs. For com-

plex hierarchical models, large simulations have high

processor and memory requirements, and generating

state spaces to analyze system behavior can overtax

these resources. Thus, high efﬁciency throughput and

reasonable run times are important.

Model checking (Clarke et al., 2001), which can

be applied to eliminate bugs, is an automatic ver-

iﬁcation method that employs mathematical analy-

sis. However, with large complex system models, the

number of states can increase signiﬁcantly. On-the-ﬂy

execution has been proposed to increase the efﬁciency

of model veriﬁcation by checking the model and gen-

erating the state space simultaneously.

This paper describes the Hierarchical Petri net

Simulator (HiPS) and extensions to HiPS. HiPS is a

Petri net design tool implemented in C# and C++,

the .NET Framework, and an interprocess commu-

nication (IPC) channel. HiPS can support hierarchi-

cal modeling and can analyze dynamic and structural

properties by generating state spaces.

Hierarchical Queuing Petri Net (HQPN) model-

ing tools are similar to HiPS (Falko Bause and Kem-

per, 1996). HiPS differs from HQPN tools depending

on whether the subpage module deals with the aspect

of the place. We focus on the temporal aspects and

consider two classes of Petri nets, that is, timed Petri

nets (TPNs) and stochastic Petri nets (SPNs) (Reisig,

1985). Colored Petri nets (CPNs) are a backward-

compatible extension of the concept of Petri nets be-

cause its tokens can hold data. CPN Tools (Wester-

gaard and Verbeek, 2016) is a modeling and analy-

sis tool for CPNs, and PIPE 2 (Dingle and Knotten-

belt, 2016), a platform independent Petri net editor,

is a modeling and simulation analysis tool for TPNs

and SPNs. In this paper, we do not consider CPNs;

however, HiPS2 has been developed and released for

modeling based on CPNs.

The state space generation engine embedded in

HiPS provides a memory-saving technique and high-

speed execution. The state space generation engine

employs parallel execution based on Intels Threading

Building Blocks (TBB), a widely used library for par-

allel task execution (Reinders, 2007). The engine was

conﬁgured according to the operating parameters of

each data structure, that is, hash table size and tree

356

Harie, Y. and Wasaki, K.

Hierarchical Petri Net Simulator: Simulation, Design Validation, and Model Checking Tool for Hierarchical Place/Transition Petri Nets.

DOI: 10.5220/0006463803560361

In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 356-361

ISBN: 978-989-758-265-3

Figure 1: HiPS tool user interface (ellipses, small rectangles, plain arrows, and red circles represent places, transitions, arcs,

and tokens, respectively).

depth; thus, it provides a suitable container for the

structure of the model and the marking appearance.

To minimize memory space, we use special limited 4-

bit memory (i.e., 4BIT

INT). The size and structure

can be varied such that we can emphasize minimiz-

ing the use of another resource; for example, by using

the 4BIT

INT mode, we can emphasize memory efﬁ-

ciency rather than execution speed.

Petri nets havetwo sets of properties, that is, struc-

tural and dynamic. Structural properties are related to

the structure of the net and dynamic properties de-

pend on the initial marking. Note that HiPS can an-

alyze both sets. We introduced Extended Coverabil-

ity Graphs (ECGs) for liveness and persistence prop-

erties to maintain accurate information about transi-

tions. The existing coverability graph generator can-

not incorporate ﬁring sequences without maintaining

transition information. By introducing ECGs, we can

perform the required fairness analysis uncondition-

ally.

We have extended the HiPS tool to include a live-

ness analyzer to utilize the ECG mechanism and an

on-the-ﬂy model checker for event-based systems. In

this paper, we describe an algorithm that generates

state spaces by multi-threading. Furthermore, we pro-

pose the concept of priority ﬁring estimation with on-

the-ﬂy model checking for Linear Temporal Logic

(LTL).

The remainder of this paper is organized as fol-

lows. Section 2 describes the HiPS tool environment

and concept. Section 3 deﬁnes state space and de-

scribes the achieved improvements. Petri net proper-

ties are discussed in Section 4, and model checking

for HiPS is described in Section 5. Conclusions and

suggestions for future work are given in Section 6.

2 HIPS DEVELOPMENT

HiPS has been designed to improve operability and

execution speed by introducing multi-threading into

a system that generates a state space. Figures 1 and

2 show an overview of the HiPS user interface and

a function diagram of the HiPS tools, respectively.

The architecture of the HiPS graphical user interface

(GUI) framework is organized around a Petri net de-

signer and the simulator. When implementing a ver-

iﬁcation environment, it is vital to simulate and ana-

lyze the properties and behaviors of the given system.

In addition to the shown functions in Figure 2, HiPS

can also analyze other properties (liveness, deadlock,

etc.) of a system model. It is important that the sys-

tem design such as the reactive system needs to run

continuously anytime without unexpected stopping,

that is, the system does not include deadlock. Prop-

erty analyzer is useful for detecting potential bugs.

Useful functions of the HiPS tool improve visually

the display results of structural analysis such as T-

invariant and the speciﬁcation support function for

model checking (Harie and Wasaki, 2015).

A Petri net is a particular type of bipartite directed

graph consisting of two types of nodes (i.e., places

and transitions) (Murata, 1989). Arcs are either from

a place to a transition or from a transition to a place.

Hierarchical Petri Net Simulator: Simulation, Design Validation, and Model Checking Tool for Hierarchical Place/Transition Petri Nets

357

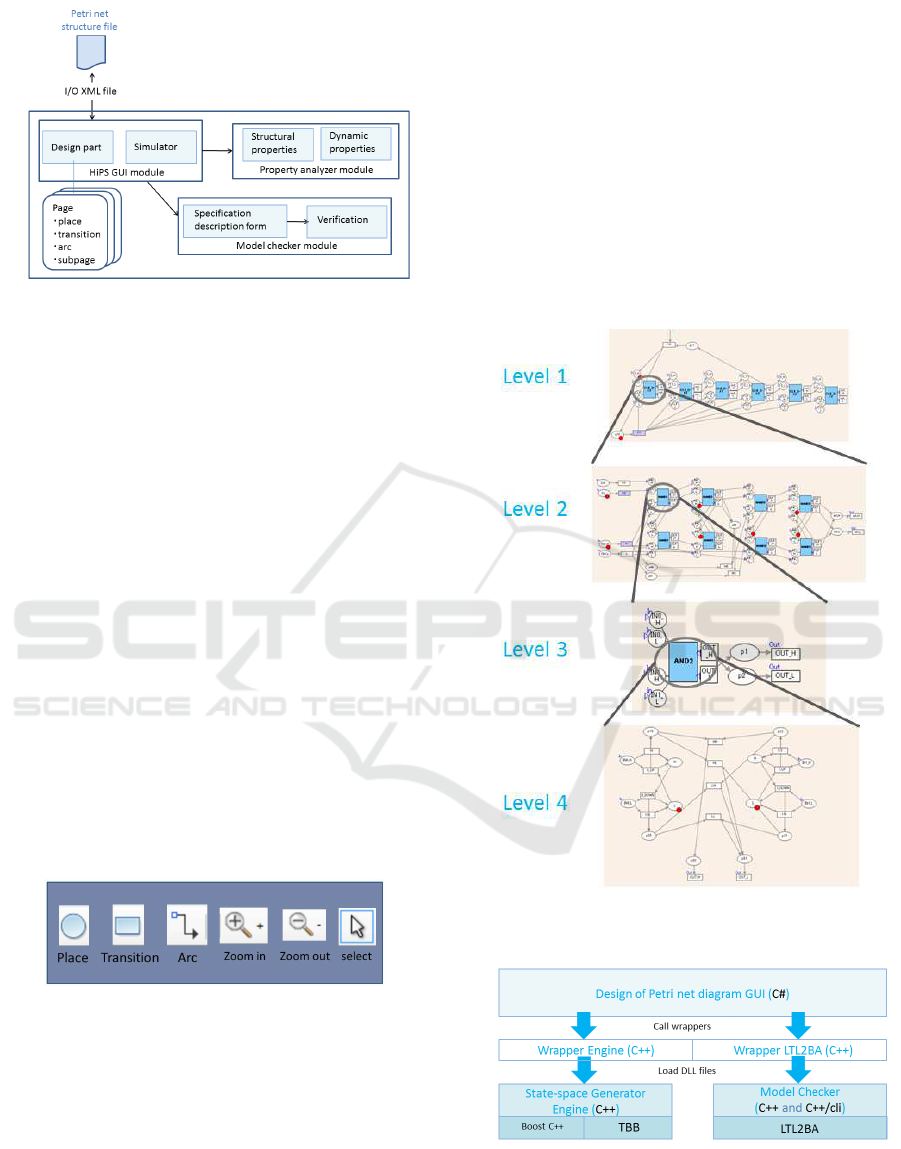
Figure 2: HiPS tool function diagram.

Petri net design can be performed intuitively to con-

nect components on the main screen, such as transi-

tions, places, and arcs. HiPS can observe the behav-

iors of the design model by simulating random walks

from the initial marking. The Petri net data struc-

ture in HiPS comprises several pages. The page in-

stance has many elements, for example, place, transi-

tion, arc, and subpage. The HiPS GUI uses the .NET

Framework, which has a container implemented in

C#.

The main HiPS window includes standard menu

panels to load/save ﬁles, edit models, call the Petri net

analyzer, and help users (Figure 1). The GUI buttons

to create models are shown in Figure 3. By clicking

on the buttons (e.g., arc, transition, and place), the

applications operation mode can be switched to edit

mode. After selecting these buttons, the user can add

a new responding element by clicking on the canvas.

After clicking the “Select” button, the user can select

elements on the canvas. A place is represented by an

empty ellipse. When positioning tokens, we edit the

place attribute information. Note that ﬁreable transi-

tions are represented by small blue rectangles.

Figure 3: HiPS model design buttons.

We exploit a hierarchy to adjust logic synthesis

in order to describe the logic circuits in an embed-

ded system. The tool can generate a hierarchical and

timed Petri net design by considering a subpage that

describes the Petri net model relative to a given ob-

ject. HiPS can apply hierarchical modeling to connect

lower subpage instances, as shown in Figure 4 where

subpage instances are represented by large blue rect-

angles. A subpage instance possesses transition ports

or place ports.

Figure 5 shows the system construction of the

composition framework in HiPS. The Petri net design

and simulator can be constructed on top of the inter-

face. When performingveriﬁcations, such as dynamic

analyses, the HiPS GUI loads the state space gener-

ation engine in the background using the “wrapper-

engine” wrapper application. The core portion of the

tool is implemented in C#. HiPS is also implemented

in the C++ language for state space generation be-

cause C++ has a rich parallel collection and good ex-

ecution speed. Note that we use the Intel C++ com-

piler, which is an optimizing compiler, and Intel TBB,

which is a C++ parallelization library.

Figure 4: Example hierarchical structure with subpage in-

stances.

Figure 5: HiPS composition framework.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

358

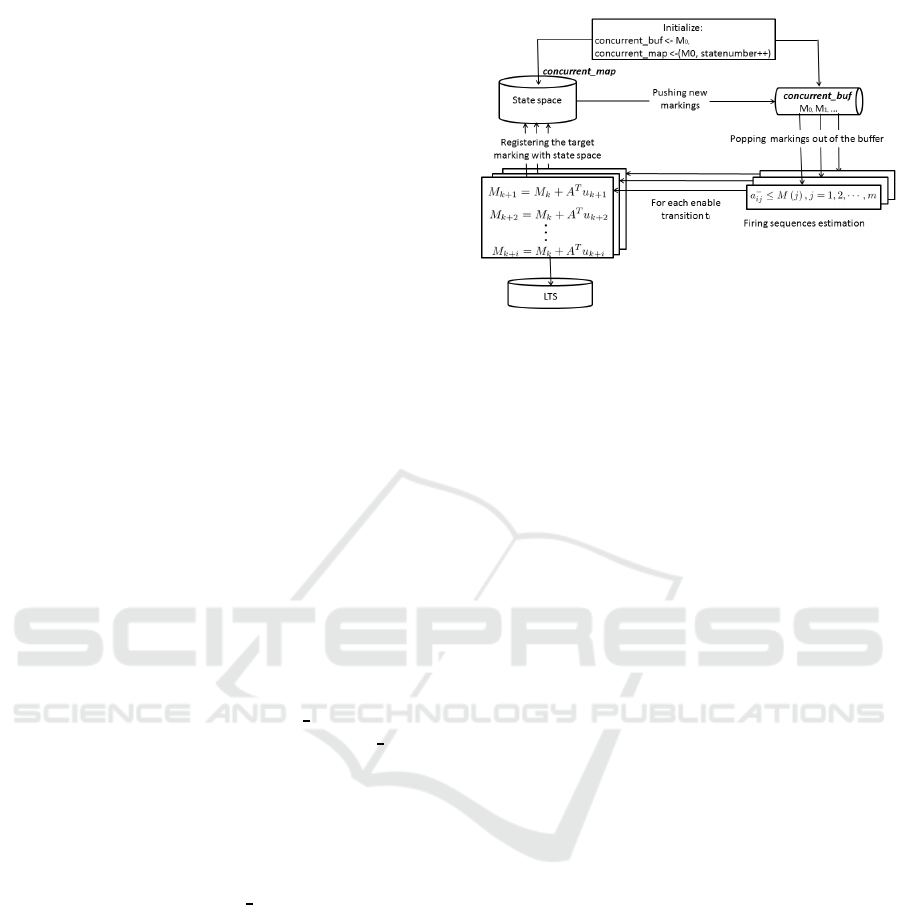
3 EXHAUSTIVE STATE SPACE

GENERATION BY PARALLEL

THREADS

The state space generator presents all possible behav-

iors of the entire system as a labeled transition system

(LTS), which comprises the set of all states reachable

from the initial state (Ohta and Wasaki, 2013). State

spaces are expressed by the LTS and are output in

Aldebaran automaton format, which is a ﬁle format

of the LTS. The LTS labels the transitions between

states and describes the system behavior based on an

event.

To speed up generation of the state space, we im-

plement multi-threading in the generator engine. Fig-

ure 6 shows the ﬂow of the algorithm for the ex-

haustive state space generation using parallel threads.

The generation algorithm of the reachable graph is

shown (Murata, 1989). Since the ﬁring evaluation

of the marking can be determined, generation of

the next marking is ﬁnished in a ﬁnite step. The

choice of marking from the next marking list is non-

deterministic and state space does not depend in the

order of marking selection. Therefore, it is possible

to parallelize the loops for selecting markings from

the next marking in the generation algorithm.

By adopting TBB container, we have imple-

mented state space generator by multi-threading in

HiPS tool. Newly generated marking(s) in state space

would be contained in “concurrent buf”, and the

generated state space is stored in “concurrent map”

Each container is used to be implemented thread-safe

container by TBB. The parallel executions operate a

series of processes, that is, the ﬁring sequence esti-

mation, inserting and searching a new marking, and

obtaining transition relations. The generating process

adds a marking to the state space if it ﬁnds a new

marking from the “concurrent

map”.

4 DYNAMIC BEHAVIOR AND

STRUCTURAL ANALYSIS

4.1 Dynamic Behavior Properties

Examples of dynamic property analysis include

reachability graph analysis, (extended) coverability

graph analysis, deadlock analysis, k-bounded analy-

sis, reversibilityanalysis, and synchronic distance and

fairness analysis. The dynamic properties depend on

the initial marking and are in fact analyzed by gener-

ating the set of reachable state spaces.

Figure 6: Algorithm ﬂow for exhaustive state space genera-

tion by parallel threads.

4.1.1 Reachable Analysis

A marking M

is said to be reachable from marking

if there exists the ﬁring sequence σ s.t. M

−→ M

For a net (N, M

), the set of all markings reachable

from M

is denoted R(N, M

). Reachability analysis

in HiPS enumerates all reachable markings from the

initial marking and the transition relations between

markings.

4.1.2 Coverability Graph Analysis

A marking is coverable if there exists M

in R(N, M

)

s.t. M

(p) ≤ M(p) for all places p in the given net.

The coverability analyzer constructs a ﬁnite graph

structure to represent a reachable marking as a tree

node and the ﬁring transition as a tree connection by

introducing ω to cut off an unbounded net. If a mark-

ing reachable from the initial marking is detected, the

transition between the markings is listed.

Note that the current coverability graph generator

cannot introduce ﬁring sequences without maintain-

ing information about transitions because the ω no-

tation would lose information about speciﬁc behav-

iors only to manage information about more than one

token. Therefore, we introduce ECGs and perform

unconditional fair analysis. Note that an ECG is ex-

pressed by three special symbols, that is, N

, N

, and

, rather than ω.

4.2 Structural Properties

Structural properties depend on the topological struc-

ture of the Petri nets. These properties are charac-

terized by incidence matrices and homogeneous ex-

pressions related to these matrices. Structural prop-

erties are independent of the initial marking in that

they maintain their properties for any initial marking

Hierarchical Petri Net Simulator: Simulation, Design Validation, and Model Checking Tool for Hierarchical Place/Transition Petri Nets

359

or are concerned with the existence of certain ﬁring

sequences from some initial marking. Note that we

assume all Petri nets are pure when analyzing struc-

tural properties.

HiPS can check for seven characteristics, that is,

structurally bounded, (partially) conservative, (par-

tially) repetitive, (partially) consistent, structurally

unbounded, unconservative, and inconsistent charac-

teristics.

When A is the incidence matrices of the Petri net

and x is the ﬁring count vector, the integer solution

x of equation A

x = 0 is considered T-invariant, and

when A is the incidence matrices of the Petri net and

y is the ﬁring count vector, the integer solution y of

Ay = 0 is considered S-invariant. The partially con-

servative and partially repetitiveproperties are present

if and only if there exists such an invariant solution.

Thus, the properties analyzer can also calculate the

invariant.

5 ON-THE-FLY MODEL

CHECKING

5.1 Fluent LTL On-the-ﬂy Model

Checking in HiPS

Automatic model checking methods are based on

state space exploration. However, exploring an en-

tire state space incurs signiﬁcant memory and time

costs. On-the-ﬂy checking reduces the effort required

to generate and search the state space (Schwoon and

Esparza, 2005). In on-the-ﬂy checking, the search

process operates concurrently with the state space

generation process. In addition, on-the-ﬂy checking

can terminate searching to generate a state space ear-

lier rather than constructing the overall state space

when an acceptable sequence is detected.

In association with CADP tools (VASY/INRIA,

2015), HiPS can perform model checking. However,

currently, it is essential toconstruct the full state space

for model checking. We have addressed this require-

ment by implementing on-the-ﬂy model checking to

HiPS(Harie and Wasaki, 2015). Of the many for-

mal languages available, we introduce LTL, which

is a well-known language used in SPIN (Bell Labs,

2016). To apply LTL model checking to event-based

systems, ﬂuent, which is a truth-value predicate de-

ﬁned by events, and ﬂuent LTL (FLTL) have been

proposed (Giannakopoulou and Magee, 2003). Note

that the FLTL speciﬁcation does not differ from LTL.

We attemptedto implement an FLTL on-the-ﬂy model

checker.

To achieve on-the-ﬂy model checking, we im-

plemented a veriﬁcation process for parallel execu-

tion of the state space generator. The IPC channel

(Stevens et al., 2003) is deﬁned as a communication

service within the same machine for remoting in .NET

Framework. By using the IPC channel, the state space

generator can be expanded to include an LTS transfer

function. The state space generation process and the

veriﬁcation process can transmit and receivesuch data

using a remote object to transfer LTS data.

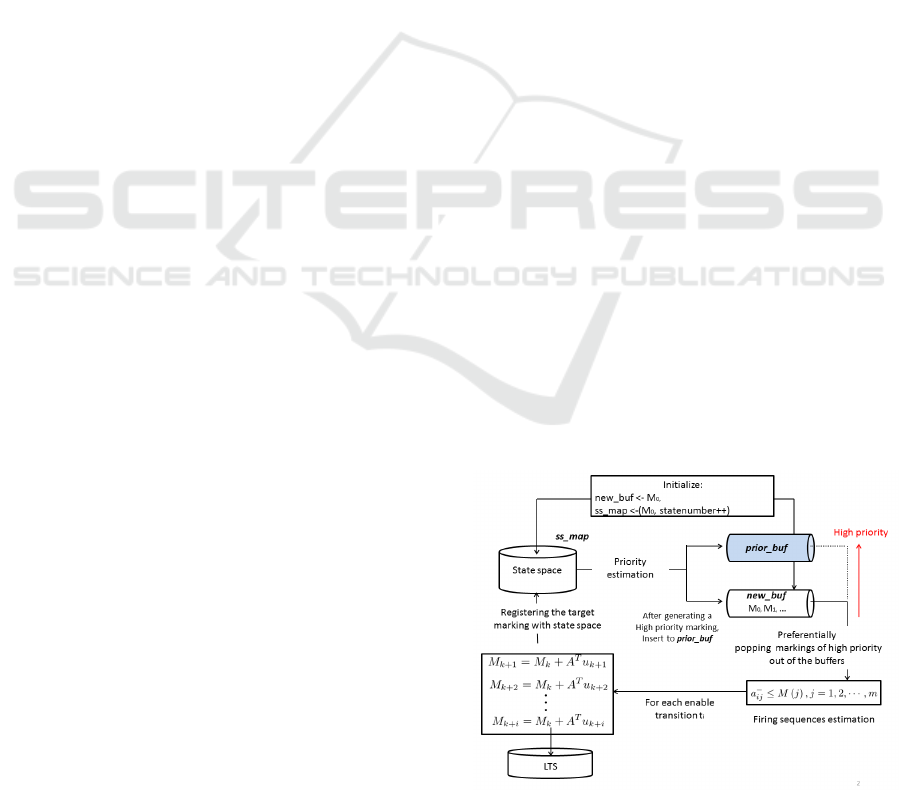
5.2 Priority Estimation for State Space

Generation

We aim to improve the efﬁciency of the implementa-

tion of on-the-ﬂy model checking. We implemented

on-the-ﬂy model checker by using the Nested-DFS al-

gorithm (Harie and Wasaki, 2016). By operating the

implemented model checker, we state the following

results. IPC information transfer creates overhead;

thus, one approach is to improve the transfer method.

Considering the data transfer overhead, it is desirable

to transfer data collectively rather than sequentially.

Recently, we use an LTS, in which transferred data

are represented by a data structure that uses vector

classes. We seek to redeﬁne this format to its data

format in order to generate more compact data (e.g.,

unsigned integers).

Here, we describe our state space generation ap-

proach. The Nested-DFS algorithm searches accept-

able sequences in synchronization automaton. So a

Path to acceptable sequences depends on speciﬁca-

tion, it is desirable to generate state space on speciﬁ-

cations. We consider a strategy in which the transition

in the given speciﬁcation is considered high priority.

Note that a high priority transition is ﬁred preferen-

tially. Figure 7 shows the state space generation ﬂow

with the priority estimation strategy.

Figure 7: Algorithm ﬂow of state space generation with the

priority estimation strategy.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

360

Note that information about transitions with

higher priority can be obtained before the state space

is generated. Currently, in state space generation, a

single buffer is used to store new markings. There-

fore, when a new marking is generated, the ﬁring pos-

sibility is evaluated from the marking, and the highest

priority marking is selected if a given condition ap-

plies. If a priority marking is selected, it is inserted

into the priority generation buffer; otherwise, it is in-

serted into the normal buffer. After generating a high

priority marking, the algorithm inserts it into the be-

ginning of the normal buffer.

Here, we consider methods to prioritize transi-

tions. One approach is to set priorities by analyzing a

speciﬁcation automaton in advance. The rating anal-

ysis for a speciﬁcation automaton is expected to be

calculated relatively quickly because the number of

states in the speciﬁcation automaton is much smaller

than that of the state space. Another approach is to

update priority relative to transition appearance fre-

quency in the set of priority transitions when generat-

ing the state space.

6 CONCLUSION

In this paper, we have shown how the HiPS tool can

be used to simulate hierarchical modeling of Petri

nets and analyze the structural and dynamic proper-

ties of Petri nets. The current release supports ECGs

with synchronic distance. In addition, the HiPS tool

incorporates on-the-ﬂy model checking to describe

LTL (FLTL) and accomplish speciﬁcation descrip-

tion support. The technology described in this paper

has potential as an integrative execution system. Fu-

ture work includes support for model correction and

model checking by simulating obtained counter ex-

amples. SPEC PATTERNS have been proposed to

describe property speciﬁcations for ﬁnite-state veri-

ﬁcation (SAnToS laboratory, 2015).

REFERENCES

Bell Labs (2016). Verifying Multi-threaded Software with

Spin. http://spinroot.com/spin/whatispin.html.

Clarke, E. M., Grumberg, O., and Peled, D. (2001). Model

checking. MIT Press.

Dingle, N. and Knottenbelt, W. (2016). QPN-Tool

for the Speciﬁcation and Analysis of Hier-

archically Combined Queueing Petri Nets.

http://pipe2.sourceforge.net/.

Falko Bause, P. B. and Kemper, P. (1996). Platform

Independent Petri net Editor 2. http://ls4-

www.cs.tu-dortmund.de/QPN/QPN-TOOL

arti-

cle/article/article.html.

Giannakopoulou, D. and Magee, J. (2003). Fluent model

checking for event-based systems. In Proceedings of

the 11th ACM SIGSOFT Symposium on Foundations

of Software Engineering 2003 , 2003, pages 257–266.

ACM.

Harie, Y. and Wasaki, K. (2015). On-the-ﬂy LTL Model

Checker on the Petri Net Design Tool : HiPS. In 14th

Forum on Information Technology, FIT2015, pages

139–142.

Harie, Y. and Wasaki, K. (2016). Formal Veriﬁcation of the

Safety Testing for Remote Controlled Consumer Elec-

tronics Using the Petri Net Design and Tool: HiPS. In

5th IEEE Global Conference on Consumer Electron-

ics, GCCE2016, pages 290–294.

Iakushkin, O., Shichkina, Y., and Sedova, O. (2016). Petri

Nets for Modelling of Message Passing Middleware

in Cloud Computing Environments, pages 390–402.

Springer International Publishing, Cham.

Murata, T. (1989). Petri nets: Properties, analysis and ap-

plications. In Proceedings of the IEEE, volume 77,

pages 541–580.

Ohta, I. and Wasaki, K. (2013). Model Designing using A

Petri Net Tool and State Space Generation Algorithm

for Post-Veriﬁcation Tool. In 12th Forum on Informa-

tion Technology, FIT2013, pages 171–174.

Reinders, J. (2007). Intel Threading Building Blocks.

O’Reilly & Associates, Inc., Sebastopol, CA, USA,

ﬁrst edition.

Reisig, W. (1985). Petri Nets: An Introduction, volume 4

of EATCS Monographs on Theoretical Computer Sci-

ence. Springer.

SAnToS laboratory (2015). Spec Patterns.

http://patterns.projects.cis.ksu.edu/.

Schwoon, S. and Esparza, J. (2005). A note on on-the-ﬂy

veriﬁcation algorithms. In Proc. Tools and Algorithms

for the Construction and Analysis of Systems, 11th In-

ternational Conference, TACAS 2005, pages 174–190.

Stevens, W. R., Fenner, B., and Rudoff, A. M. (2003). UNIX

Network Programming, Vol. 1. Pearson Education, 3

edition.

VASY/INRIA (2015). CADP toolbox. http://cadp.inria.fr/.

Westergaard, M. and Verbeek, H. E. (2016). CPN tools.

http://cpntools.org/.

Hierarchical Petri Net Simulator: Simulation, Design Validation, and Model Checking Tool for Hierarchical Place/Transition Petri Nets

361