An End-to-end Formal Verifier for Parallel Programs
Soumyadip Bandyopadhyay
1
, Santonu Sarkar
1
and Kunal Banerjee
2
1
BITS Pilani, K K Birla Goa Campus, Goa, India
2
Indian Institute of Technology, Kharagpur, India
Keywords:
Equivalence Checking, Petri Net based Representation for Embedded Systems (PRES+) Model, Finite State
Machine with Datapath (FSMD) Model, High-level Language.
Abstract:
Among the various models of computation (MoCs) which have been used to model parallel programs, Petri net
has been one of the mostly adopted MoC. The traditional Petri net model is extended into the PRES+ model
which is specially equipped to precisely represent parallel programs running on heterogeneous and embedded
systems. With the inclusion of multicore and multiprocessor systems in the domain of embedded systems, it
has become important to validate the optimizing and parallelizing transformations which system specifications
go through before deployment. Although PRES+ model based equivalence checkers for validating such trans-
formations already exist, construction of the PRES+ models from the original and the translated programs was
carried out manually in these equivalence checkers, thereby leaving scope for inaccurate representation of the
programs due to human intervention. Furthermore, PRES+ model tends to grow more rapidly with the pro-
gram size when compared to other MoCs, such as FSMD. To alleviate these drawbacks, we propose a method
for automated construction of PRES+ models from high-level language programs and use an existing transla-
tion scheme to convert PRES+ models to FSMD models to validate the transformations using a state-of-the-art
FSMD equivalence checker. Thus, we have composed an end-to-end fully automated equivalence checker for
validating optimizing and parallelizing transformations as demonstrated by our experimental results.
1 INTRODUCTION
Embedded systems are becoming increasingly com-
plex and pervasive with each passing day. Appli-
cations running in embedded devices demand large
compute resources and they have started exploiting
the parallelism as the underlying compute infrastruc-
ture is becoming more and more powerful (Gay et al.,
2003; Marwedel, 2006). Designer of such applica-
tions uses compiler’s optimizing transformation on
the code (Smith et al., 1992; Raghavan, 2010); which
if carried out by untrusted compilers, can result in
software bugs
1
. Thus, for embedded systems, there
is a growing concern to validate the applications be-
fore its deployment.
It is important to verify whether the implemented
code faithfully represents the intended functionality,
which is commonly known as the translation vali-
dation process. Here, each individual translation is
followed by a validation phase to establish the be-
havioural equivalence of the source code and the tar-
1
As a case in point, consider an unpredictable bug
in gcc v4.9.2 https://gcc.gnu.org/bugzilla/show bug.cgi?
id=64490
get code (Pnueli et al., 1998; Necula, 2000; Kundu
et al., 2008; Rinard and Diniz, 1999). Verifica-
tion techniques of applications for embedded systems
based on formal models have been well researched
over the last two decades (Edwards et al., 1997; Lee
and Parks, 1995). Out of several models proposed,
Petri net based models, specially the PRES+ model
has been found to be highly suitable for modeling
concurrent behavior, simple computation over basic
data types (integer, real), modeling general data struc-
ture and modeling timing behavior of a parallel ap-
plication. This model allows tokens to carry infor-
mation (Cort´es et al., 2000) and it has a well-defined
semantics for precise representation of systems.
A major limitation of these methods is that they
can verify only structure preserving transformations
and invariably fails for schedulers that alter the con-
trol structure of a program (Camposano, 1991). To
alleviate this shortcoming, a path based equivalence
checker for the FSMD models (which are essentially
sequential control and data flow graphs (CDFGs))
was proposed in (Karfa et al., 2012) which was later
modified to handle more sophisticated uniform, non-
uniform code motions and code motions across loops
388
Bandyopadhyay, S., Sarkar, S. and Banerjee, K.
An End-to-end Formal Verifier for Parallel Programs.
DOI: 10.5220/0006464503880393
In Proceedings of the 12th International Conference on Software Technologies (ICSOFT 2017), pages 388-393
ISBN: 978-989-758-262-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

in (Banerjee et al., 2014). They, however, cannot han-
dle thread-level parallelizing transformations mainly
because FSMD, being a sequential mode of computa-
tion, cannot capture a parallel behaviour straightway.
The work described in (Bandyopadhyay et al.,
2012) proposed a translation algorithm from a PRES+
model to an FSMD model and then used the exist-
ing FSMD equivalence checker of (Karfa et al., 2012)
to establish an equivalence between the initial and
the optimized versions of a program, modeled using
the PRES+ formalism. However, in this method, the
model construction from the original programs was
a manual process. The authors of (Voron and Kor-
don, 2008) reported a method for automated construc-
tion of Petri net models from a high-level language
program where the source program is converted into
an intermediate representation form such as, abstract
syntax tree, for various modules. However, in their
method, only control structure is captured, and the
data flow analysis is not performed. We present a
technique for automated construction of value based
PRES+ models (Cort´es et al., 2000) from parallel pro-
grams capturing both control and data flow. Subse-
quently the PRES+ model is used for formal verifica-
tion of two programs. The major contributions in this
paper are as follows:
1. The proposed approach captures maximal
block level and instruction level parallelism during
PRES+ model construction.
2. Our verifier is generic and portable as the
underlying model is generic. For instance, we have
demonstrated that it is possible to integrate an FSMD
based equivalence checker(Banerjee et al., 2014) to
accept our PRES+ model for program validation. For
this purpose, we haveused a PRES+ to FSMD transla-
tor (Bandyopadhyayet al., 2012). One can seamlessly
integrate a PRES+ based checker with our model in-
stead of an FSMD based one to build yet another val-
idator.
The experimental results demonstrate the effi-
ciency of the tool.
Rest of the paper has been organized as follows.
The automated construction of PRES+ model from
high-level language programs is mentioned in sec-
tion 2. The results obtained when the procedure was
tested on some examples can be found in section 3.
The paper is finally concluded in section 4.
2 AUTOMATED PRES+
CONSTRUCTION METHOD
We demonstrate our automated model construction
method in the following subsection. The functional
modules are depicted in Algorithm 2 – Algorithm 5
with Algorithm 1 being the top level module.
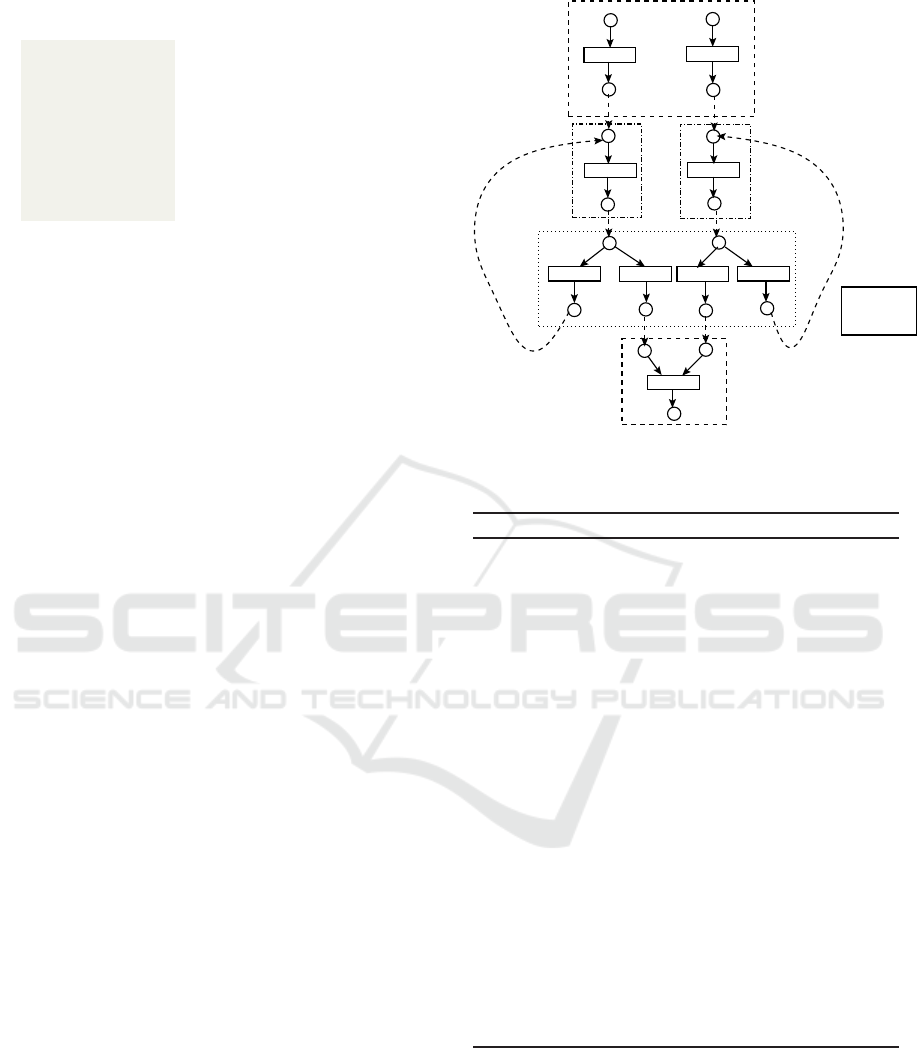
2.1 A Brief Example
Figure 1 (a) depicts a simple parallel program which
can be easily converted to a 3 address code along
with the basic block information as shown in Fig-
ure 1(b) using tools like flex and bison. The func-
tion
creatPRES (Algorithm 1) checks the proper-
ties of each basic block. For the basic block
bb2, the function
creatPRES calls the function
subNetForAssignMentBB (Algorithm 2). The func-
tion subNetForAssignMentBB constructs a data de-
pendency graph (DDG) for bb2. Then, the function
performs the reaching definition analysis on the DDG
that results in sets of instruction-level parallel state-
ments in bb2. For each member in the set of par-
allel statements, the method creates places for each
operands, i.e., {p
1
, p
2
} shown in Figure 2. Next,
the function constructs the transitions and out-places.
Now, the transitions and out-places of the sub-net of
the PRES+ model are {t
1
,t
2
} and {p
3
, p
4
}, respec-
tively. Then the function
subNetForAssignMentBB
(Algorithm 2) identifies that there are two basic block
information associated with goto statement, i.e., bb4
and bb6. The function
subNetForAssignMentBB
identifies the basic blocks bb4 and bb6 as parallel
blocks. Then the control goes to the caller func-
tion,
creatPRES (Algorithm 1). which checks that
set of parallel blocks is non empty. Hence, it calls the
function
subnetForParallelBB (Algorithm 5). In
this example, there are also two parallel basic blocks,
bb4 and bb6 respectively. For bb4, the function
subnetForParallelBB identifies that bb4 is a con-
dition containing block. Therefore, it calls the func-
tion
subnetForCondBB (Algorithm 3). The function
subnetForCondBB identifies the conditional state-
ment in three address code and the operator used in
the condition. For each operands of the condition,
two mutually exclusive transitions are created hav-
ing one pre-place. Then for each transition one post
is created. Then it identifies that the basic block in-
formation associated with
goto statement, e.g., bb3
whose id is less than the id of currently processed
basic block i.e., bb4. Hence bb3 is inferred as loop
containing basic block. For the block bb3, the func-
tion
subnetForCondBB (Algorithm 3) calls the func-
tion subnetForLoopBB which in turn calls the func-
tion subNetForAssignMentBB (Algorithm 2). Then
for each element in bb3, the function constructs a
loop variable sets. For each of these member in the
set, the function computes the used-defined variable
pairs. In this example, the variable associated with
An End-to-end Formal Verifier for Parallel Programs
389

1 i n t i =1 , j =1 ,k ;
2 #pragma scop
3 while ( i <=10)
4 i ++;
5 while ( j <=10)
6 j ++;
7 #pragma scop
8 k= i + j ;
9 r e t urn k ;
(a)
int k,j,i;
<bb2>: i = 1;j = 1;
goto <bb3>;
goto <bb5>;
<bb3>: i = i + 1;
<bb4>:
if (i <= 9) goto <bb3>;
else goto <bb7> ;
<bb5>: j = j + 1;
<bb6>:
if (j <= 9) goto <bb5>;
else goto <bb7>;
<bb7>: k = i + j;
(b)
Figure 1: A simple parallel program and the corresponding
basic blocks.
the place p
5
corresponds to the used-defined pair;
therefore, the place p
5
contains a back edge. Next
the function
subnetForParallelBB (Algorithm 5)
processes the basic block bb6 in identical manner.
Then the control goes to the caller function. For
the block bb7, the caller function calls the function
subNetForAssignMentBB (Algorithm 2) and then it
constructs the corresponding subnet. Finally, all the
PRES+ subnets are attached according to the updated
symbol table information. If the same variable is as-
sociated with two different places, those two places
are then merged into a single place. In Figure 2, the
place p
3
is merged with p
5
as the variable i is associ-
ated with both the place p
3
and p
5
. Symbolically, it
is represented as p
3
" p
5
. In Figure 2, the dotted ar-
row between the place to place indicates the merging
operation. The graphical representation is depicted in
Figure 2.
3 EXPERIMENTAL RESULTS
The tool has been tested on parallel examples on
a 2.0 GHz Intel(R) Core(TM)2 Duo CPU machine
(using only a single core). We have carried out
the experiments on a set of parallel examples in a
systemic manner. Here, we have transformed five
sequential programs into parallel programs using a
prominent thread-level parallelizing compiler PLuTo
(Bondhugula et al., 2008). The experimental set up is
as follows:
1. Preparation of the example suite: We have
taken five sequential source programs. The list of
the source programs and their functionality are as
follows:
a) BCM : A toy example on basic code motion
without writable shared variables which illustrates
computational vs. executional optimality.
bb 2
bb 4
&
bb 6
bb 3
bb 5
bb 7
1
1
+1
+1
id
id
id id
+
[c
1
]
[~c
1
]
[c
2
]
[~c
2
]
c
1
: i<=9
c
2
: j <=9
p
1
p
2
p
3
p
4
p
5
p
6
p
7
p
8
p
9
p
10
p
11
p
12
p
13
p
14
p
15
p
16
p
17
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
(c)
Figure 2: Constructed PRES+ model.
Algorithm 1: PRES+ creatPRES (BB, PB).
Inputs: Set of basic blocks along with informations and
parallel block.
Outputs: PRES+ model N.
1: N =
/
0; PB =
/
0;
2: for each basic block b in BB do
3: if (b is normal assignment block) then
4: subNetForAssignMentBB(b, N, PB);
5: else
6: if (b is loop containing ) then
7: subnetForLoopBB(b, N, PB);
8: else
9: if (PB 6=
/
0 ) then
10: subnetForParallelBB(b, N, PB);
11: else
12: if (b is conditional basic block) then
13: subnetForCondBB(b, N, PB);
14: end if
15: end if
16: end if
17: end if
18: end for
19: Merge all the subnet according to the symbol table in-
formation.
20: return N;
b) MINANDMAX-P: Computes sum of the maxi-
mum of four numbers n
1
, n
2
, n
3
, n
4
and the mini-
mum of the four numbers n
1
, n
5
, n
6
and n
7
(having
n
1
as the common element).
c) LUP: It computes “LU Decomposition with
Pivoting”. In this experimentation, we have only
taken the pivoting routine which does not contain
ICSOFT 2017 - 12th International Conference on Software Technologies
390

Algorithm 2: STRUCT2TUPLE subNetForAssign-
MentBB (b, N, PB).
Inputs: A basic block, a PRES+ model N, set of parallel
blocks
Outputs: Two tuple structures. The elements of this
structure are as follows: 1.sub-net of the PRES+ model and
2. parallel block list
1: G =
/
0;
2: G = G∪ creatDDG (b);
/*Construction is carried out by GauTe Tool*/
3: L = reachingDefinitionAnalysis (G);
/* The function returns a set of lists. Each list contains
set of statements. Every statement in a list is indepen-
dent to the other statements present in that list. This
analysis is carried out by NuSMV*/
4: for each list l in L do
5: P =
/
0;
6: for each element e in l do
7: P = P∪ {p};
/* The function takes an element and creates
places for every used variable of that element */
8: T = T ∪ {t};
9: for each t in T do
10: /* Construct normalize expression and guard
condition using SMT solver*/
11: end for
12: P
out
= P
out
∪ {p
out
};
/*The function creates an output place for the
transition T and update the symbol table for
places and transitions */
13: Attach p, t and p
out
14: end for
15: end for
16: if number of block associated with goto >1 then
17: The blocks along with goto statement are put in to
PB
new
;
18: PB = PB∪ PB
new
; //update the parallel block lists
19: end if
20: Update N
21: return hN, PBi;
any array. The detailed functionalityof this source
program is given in PLuTo example suite (Bond-
hugula et al., 2008).
d) DEKKER’s and PATTERSON’s algorithms:
Implementations of the classical solutions to the
mutual exclusion problem of two concurrent pro-
cesses. Since our mechanism does not handle
writable shared variables among parallel threads,
we have considered a single process in each of
these cases; also we have introduced a series of
dummy assignment statements within the critical
section.
2. Transforming the programs: The above five se-
quential programs are transformed by a prominent
thread level parallelizing compiler, PLuTo (Bond-
hugula et al., 2008); the transformed versions ac-
Algorithm 3: STRUCT2TUPLE subnetForCondBB
(b, N, PB).
Inputs: A basic block, a PRES+ model, a set of parallel
blocks
Outputs: Two tuple structures. The elements of this
structure are as follows: 1.sub-net of the PRES+ model and
2. parallel block list
1: cond = getCond (b);
/* The function gets condition of execution of the block
b. The condition is easily obtainable from 3 address
code using SMT solver */
2: expr = getExpr (b);
/* The function returns operator used in the condition
*/
3: P =
/
0;
4: P = P∪ {p};
/* The function determines input places for condition */
5: T
1
= T
1
∪ {t
1
};
6: P
out
1
= P
out
1
∪ {p
out
1
};
7: Attach p,t
1
, p
out
1
;
8: T
1
= T
2
∪ {t
2
}
9: P
out
2
= P
out
2
∪ {p
out
2
};
10: Attach p,t
2
, p
out
2
;
11: P
out
= P
out
1
∪ P
out
2
;
/* The function accumulates all the output places */
12: if current process block Id > block Id associated with
goto then
13: subnetForLoopBB(b, N, PB);
14: end if
15: if number of block associated with goto >1 then
16: The blocks along with goto statement are put in to
PB
new
;
17: PB = PB∪ PB
new
; //update the parallel block lists
18: end if
19: Update N
20: return hN, PBi;
cordingly have parallel structures. Table 1 depicts
the type of transformations applied for each of the
above examples. It is to be noted that for testing
our tool, (in the context of parallelizing transfor-
mations) we have five sequential programs and the
five parallel programs are obtained using PLuTo
compiler.
3. The automated model constructor constructs two
PRES+ models – one from the original code and
the other from the transformed program. The
two PRES+ models are then translated into corre-
sponding FSMD models using (Bandyopadhyay
et al., 2012) and finally equivalence checking is
carried out using the FSMD equivalence checker
of (Banerjee et al., 2014). It is to be noted that
all the above parallel examples do not contain any
writable shared variable.
An End-to-end Formal Verifier for Parallel Programs
391

Algorithm 4: STRUCT2TUPLE subnetForLoopBB (b, N,
PB).
Inputs: A basic block, a PRES+ model N, set of parallel
blocks
Outputs: Two tuple structures. The elements of this
structure are as follows: 1.sub-net of the PRES+ model and
2. parallel block list
1: subNetForAssignMentBB(b, N, PB);
2: L =
/
0
3: for each element e in b do
4: L = L ∪ getVariables(e);
5: end for
6: for each variable v in L do
7: P
1
= findLastPlace(v);
/* Find the last place of the variables updated in the
loop */
8: P
2
= findReturnPlace(v);
/* Values need to be sent back through back edges in
case of loop. It finds the place to which values are
sent back. */
9: P
1
= P
2
10: end for
11: if number of block associated with goto >1 then
12: The blocks along with goto statement are put in to
PB
new
;
13: PB = PB∪ PB
new
; //update the parallel block lists
14: end if
15: Update N
16: return hN, PBi;
Table 1: Transformations carried out using parallelizing
compilers.
Example Transformations
BCM Boosting up
MINANDMAX-P Thread level parallelization
LUP Thread level parallelization
DEKKER Thread level parallelization
PATTERSON Thread level parallelization
Analysis
Table 2 depicts the size of PRES+ models in terms
of number of places and transitions, PRES+ model
construction time from both original and transformed
programs and PRES+ to FSMD translation times for
both original and transformed PRES+ models. In this
experimentation, we have also carried out a compar-
ative study between FSMD and PRES+ equivalence
checking methods. The last two columns indicate
the FSMD equivalence checking and direct PRES+
equivalence checking times (Bandyopadhyay et al.,
2015a; Bandyopadhyay et al., 2015b; Bandyopad-
hyay et al., 2016a), respectively. It is to be noted
that FSMD equivalence checking includes PRES+ to
FSMD translation time, path construction time and
the equivalence checking time. On the other hand, di-
Algorithm 5: STRUCT2TUPLE subnetForParallelBB (b, N,
PB).
Inputs: A basic block, a PRES+ model N, set of parallel
blocks
Outputs: Two tuple structures. The elements of this
structure are as follows: 1.sub-net of the PRES+ model and
2. parallel block list
1: for each b in PB do
2: if (b is normal assignment block). then
3: subNetForAssignMentBB(b, N,PB);
4: else
5: if (b is loop containing ) then
6: subnetForLoopBB(b, N,PB);
7: else
8: if (b is conditional basic block) then
9: subnetForCondBB(b, N, PB);
10: end if
11: end if
12: end if
13: end for
14: return hN, PBi;
rect PRES+ equivalence checking includes path con-
struction time and equivalence checking time. By
comparing the numbers in the columns
FSMD Eqiv
and PRES+ Eqiv , we notice that FSMD equivalence
checking time is faster than the PRES+ equivalence
checking time because the path construction method
of the PRES+ model is complicated compared to the
FSMD model (Bandyopadhyay et al., 2016b). It
is also to be noted that earlier FSMD equivalence
checker reported in (Banerjee et al., 2014) is not ca-
pable of validating thread-level parallelizing transfor-
mation. However, FSMD equivalence checking mod-
ule which is integrated within our automated model
constructor is capable of handling those paralleliz-
ing transformations. As PRES+ to FSMD translation
module uses both symbolic execution as well as seri-
alization technique, FSMD captures parallelism using
serialized form.
4 CONCLUSION
In this work, an automated model construction
method is presented for obtaining PRES+ models
from high-level languages. Our tool when integrated
with the PRES+ to FSMD translator of (Bandyopad-
hyay et al., 2012) and the FSMD equivalence checker
of (Banerjee et al., 2014) provides an end-to-end fully
automated verifier for optimizing and parallelizing
transformations. An overview of this entire tool is
provided here. Through experiments over a set of
parallel examples, the efficacy of the verifier, and es-
ICSOFT 2017 - 12th International Conference on Software Technologies
392

Table 2: Experimentation using parallel examples.
Example Original Transformed Time (µs)
Lines Place Trans Time (µs) Lines Place Trans Time (µs) FSMD Eqiv PRES+ Eqiv
Model Const. Translation Model Const. Translation
BCM 11 34 21 650 234 11 32 20 628 232 3001 8345
MINANDMAX-P 20 42 20 983 312 20 41 20 982 312 3421 8451
LUP 32 80 73 1025 775 32 80 71 1028 771 5152 10678
DEKKERS 29 53 45 994 702 29 53 41 979 623 4352 10414
PETTERSON 29 53 45 992 710 29 53 41 989 673 4758 10612
pecially that of the automatic PRES+ constructor, is
demonstrated. Some of the possible future extensions
of our work are as follows. Optimization of the con-
structed PRES+ model is a short-term goal. More-
over, PRES+ models permit specifications of timing
behaviours too; enhancing the present tool for timing
analyses seems promising as well.
ACKNOWLEDGMENTS
Santonu Sarkar has been partially supported by Sci-
ence and Engineering Research Board, Govt. of India
project (SB/S3/EECE/0170/2014) for this research
work.
REFERENCES
Bandyopadhyay, S., Banerjee, K., Sarkar, D., and Man-
dal, C. A. (2012). Translation validation for pres+
models of parallel behaviours via an fsmd equivalence
checker. In VDAT, pages 69–78.
Bandyopadhyay, S., Sarkar, D., Banerjee, K., and Mandal,
C. A. (2015a). A path-based equivalence checking
method for petri net based models of programs. In
ICSOFT-EA, pages 319–329.
Bandyopadhyay, S., Sarkar, D., and Mandal, C. (2015b).
An efficient equivalence checking method for petri net
based models of programs. In 37th IEEE/ACM Inter-
national Conference on Software Engineering, ICSE
2015 (Poster), Florence, Italy, May 16-24, 2015, Vol-
ume 2, pages 827–828.
Bandyopadhyay, S., Sarkar, D., and Mandal, C. (2016a). An
efficient path based equivalence checking for petri net
based models of programs. In Proceedings of the 9th
India Software Engineering Conference, Goa, India,
February 18-20, 2016, pages 70–79.
Bandyopadhyay, S., Sarkar, D., Mandal, C. A., Banerjee,
K., and Duddu, K. R. (2016b). A path construction al-
gorithm for translation validation using PRES+ mod-
els. Parallel Processing Letters, 26(2):1–25.
Banerjee, K., Karfa, C., Sarkar, D., and Mandal, C. (2014).
Verification of code motion techniques using value
propagation. IEEE TCAD, 33(8).
Bondhugula, U., Hartono, A., Ramanujam, J., and Sadayap-
pan, P. (2008). PLuTo: A practical and fully automatic
polyhedral program optimization system. In PLDI 08.
Camposano, R. (1991). Path-based scheduling for synthe-
sis. IEEE transactions on computer-Aided Design of
Integrated Circuits and Systems, Vol 10 No 1:85–93.
Cort´es, L. A., Eles, P., and Peng, Z. (2000). Verification
of embedded systems using a petri net based repre-
sentation. In ISSS ’00: Proceedings of the 13th inter-
national symposium on System synthesis, pages 149–
155, Washington, DC, USA. IEEE Computer Society.
Edwards, S., Lavagno, L., Lee, E. A., and Sangiovanni-
Vincentelli, A. (1997). Design of embedded systems:
Formal models, validation, and synthesis. In Proceed-
ings of the IEEE, pages 366–390.
Gay, D., Levis, P., von Behren, R., Welsh, M., Brewer, E.,
and Culler, D. (2003). The nesC language: A holistic
approach to networked embedded systems. In PLDI,
pages 1–11.
Karfa, C., Mandal, C. A., and Sarkar, D. (2012). For-
mal verification of code motion techniques using data-
flow-driven equivalence checking. ACM Trans. De-
sign Autom. Electr. Syst., 17(3):30.
Kundu, S., Lerner, S., and Gupta, R. (2008). Validating
high-level synthesis. In Computer Aided Verification,
CAV ’08, pages 459–472.
Lee, E. A. and Parks, T. M. (1995). Dataflow process net-
works. Proceedings of the IEEE, 83(5):773–799.
Marwedel, P. (2006). Embedded System Design.
Springer(India) Private Limited, New Delhi, India.
Necula, G. C. (2000). Translation validation for an optimiz-
ing compiler. In PLDI, pages 83–94.
Pnueli, A., Siegel, M., and Singerman, E. (1998). Transla-
tion validation. In TACAS, pages 151–166.
Raghavan, V. (2010). Principles of Compiler Design. Tata
McGraw Hill Education Private Limited, New Delhi.
Rinard, M. and Diniz, P. (1999). Credible compilation.
Technical Report MIT-LCS-TR-776, MIT.
Smith, M. D., Horowitz, M., and Lam, M. S. (1992).
Efficient superscalar performance through boosting.
In ASPLOS-V: Proceedings of the fifth international
conference on Architectural support for programming
languages and operating systems, pages 248–259,
New York, NY, USA. ACM Press.
Voron, J.-B. and Kordon, F. (2008). Transforming sources
to Petri nets: A way to analyze execution of parallel
programs. In SimuTools, page 13.
An End-to-end Formal Verifier for Parallel Programs
393