PAnTHErS: A Prototyping and Analysis Tool for Homomorphic
Encryption Schemes
Cyrielle Feron
1
, Vianney Lapotre
2
and Lo
¨
ıc Lagadec
1
1
UMR 6285, Lab-STICC, ENSTA Bretagne, 29806, Brest Cedex 9, France
2
UMR 6285, Lab-STICC, Univ. Bretagne-Sud, F-56100, Lorient, France
Keywords:
Homomorphic Encryption, Security, Cloud Computing.
Abstract:
Homomorphic Encryption (HE) enables third parties to process data without requiring a plaintext access to
it. Its future is promising to solve Cloud Computing security issues. Still, HE is not yet usable in real cases
due to complexity issues. For every new HE scheme, evaluation is of primary importance, but performances
(execution time and memory cost) for various sets of parameters are currently difficult to estimate ahead of
practical implementations. This paper introduces PAnTHErS, a Prototyping and Analysis Tool for Homomor-
phic Encryption Schemes that alleviates the need for implementation to estimate the performances of any new
HE scheme. PAnTHErS supports parametric modeling of HE schemes and provides analysis features. In this
paper, PAnTHErS is illustrated over some HE schemes and shows promising results.
1 INTRODUCTION
Homomorphic Encryption (HE) aims at answering se-
curity issues of Cloud Computing by allowing a user
to delegate computations on confidential encrypted
data to a third party. In 2009, Gentry (Gentry, 2009)
constructed the first Fully Homomorphic Encryption
(FHE), which is based on ideal lattices. He created a
Somewhat Homomorphic Encryption (SHE) scheme
and introduced a bootstrapping phase that permits to
refresh the noise in ciphertexts. As bootstrapping
is a costly operation, decryption circuit is simplified
(squashing step) to have a lower multiplicative depth.
Then, it is possible to evaluate the decryption cir-
cuit. A FHE scheme needs to have circular secu-
rity. This means that it is safe to encrypt the private
key under its own public key (Brakerski et al., 2012).
Since then, a lot of HE schemes have been created.
They are based on different hardness assumptions as
approximate-GCD (Dijk et al., 2010), Learning With
Error (LWE) (Lindner and Peikert, 2011), Ring-LWE
(R-LWE) (Brakerski and Vaikuntanathan, 2011b) or
approximate-eigenvector (Gentry et al., 2013). Sev-
eral open-source implementations of HE are avail-
able. HElib (Halevi and Shoup, 2014) is the most
known.
Despite all existing schemes and implementations,
HE is still not usable in real world applications. One
of the big challenges is that HE consumes a lot of
memory resources. It implies large data transfers
from the user to the server, due to the fact that the en-
crypted data is much larger than the plaintext. More-
over, computations on ciphertext exhibit an important
complexity.
HE could solve security concerns in Cloud Com-
puting. Nevertheless, no HE scheme fits every appli-
cation efficiently. One possible alternative is to deter-
mine the best HE scheme given an application. Cri-
terion are bounded by limitations of the server and
application constraints like, among others, execution
time (complexity), number of homomorphic opera-
tions that are processed, memory usage and secu-
rity strength. As HE can be very memory and time
consuming, analyzing every existing HE scheme by
varying their input parameters would involve inten-
sive software simulations.
In this work, we present a tool named PAn-
THErS that aims to help analyzing and prototyping
HE schemes. PAnTHErS workflow is illustrated in
Figure 1: it proposes to build functional models of HE
schemes (step 1 ) which can be analyzed and con-
figured regarding the application requirements (step
2 ). Then, a set of schemes can be selected to be par-
tially implemented on FPGA to provide hardware ac-
celeration for HE computing (step 3 , 4 and 5 ).
This paper focuses on steps 1 and 2 of the pro-
posed flow.
Feron, C., Lapotre, V. and Lagadec, L.
PAnTHErS: A Prototyping and Analysis Tool for Homomorphic Encryption Schemes.
DOI: 10.5220/0006464703590366
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 359-366
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
359

Figure 1: High-level illustration of PAnTHErS workflow.
The remainder of this paper is organized as fol-
lows. Section 2 introduces the modeling approach
and Section 3 details analysis methods. Then, Section
4 describes the insight of PAnTHErS implementation
and utilization. Section 5 presents PAnTHErS results
on four HE schemes. Finally, Section 6 concludes and
presents future works.
2 MODELING
In PAnTHErS, a HE scheme is modeled into a set
of functions which are stored in a library and shared
among HE models.
Actually, HE schemes modeling (step 1 ) pro-
duces both an executable model and an analysis
model of a HE scheme. The first one is forwarded to
model transformation (step 3 ), while the second is
used for HE schemes analysis (step 2 ). While, the
details regarding analysis functions is given in Section
4, this section details HE scheme modeling through
atomic, specific and HE basic functions.
2.1 Atomic Functions
In this paper, an atomic function represents a basic
operation that can be operated in a HE scheme. Func-
tions such as addition, multiplication, division, mod-
ulo, round and their variants for polynomials, matrix
of integers and matrix of polynomials are some exam-
ples of atomic functions. These are basic blocks used
to build more complex functions, i.e. specific func-
tions. As an example, matrices addition and scalar
matrix multiplication are stored as below in the li-
brary:
addMat(int[][] A, int[][] B, int[][] C) :
//adds two matrices.
C = A + B
multScalMat(int a, int[][] B, int[][] C) :
//Multiplies a scalar with a matrix.
C = a*B
Algorithm 1: distriLWE (mathematical algorithm).
Require: q,n,m,k integers, χ a Gaussian distribu-
tion, R a ring, s a vector of size n.
Ensure: distriLWE(q,n, m,k,χ, R,s)
A ← R
m×n
q
b ← χ
m
b ← (A.s + k.b) mod q
return A ∈ R
m×n
q
,b ∈ R
m
q
2.2 Specific Functions
A specific function is a set of atomic functions. Some
schemes based on the same problem (e.g. R-LWE)
use identical instructions. These instructions form
then a specific function that is flushed to the library.
For example, the following equation:
addTimes(A,b,C) = A + b ×C (1)
with A, C matrices and b an integer, can be modeled
as a specific function using a set of atomic functions.
Thus, it is stored in the library as:
addTimes(int[][] A, int b, int[][] C,
int[][] D) :
multScalMat(b,C,D) // D ← b × C
addMat(A,D,D) // D ← A + D
Obviously, specific functions can be defined with
both atomic and specific functions. Moreover, to be
used in several HE schemes, they may be general-
ized. As an example, a function named distriLWE,
presented in Algorithm 1, appears in (Fan and Ver-
cauteren, 2012) using k = 1 and in (Brakerski and
Vaikuntanathan, 2011a) using k 6= 1. Using functions
available in the library, Algorithm 1 is rewritten as a
set of atomic and specific functions resulting in func-
tion distriLWE written below. This new produced
specific function is then integrated in the library for
reusing purposes.
distriLWE(int q, int n, int m, int k, Set χ,
Set R, poly[] s, poly[][] A, poly[] b) :
rndMat(R, m, n, A) // A ← R
m∗n
rndMat(χ, m, 1, b) //b ← χ
m
multMat(A, s, c) //c ← A.s
addTimes(c, k, b, b) //b ← (c + k.b)
modMat(b, q, b) //b ← b mod q
SECRYPT 2017 - 14th International Conference on Security and Cryptography
360

Table 1: Representation of memory and complexity after executing analysis functions of distriLWE. Parameter d is the maxi-
mal degree of a polynomial.
(a) Memory table.
Name A c b
Object POLY POLY POLY
Dimensions (n,m) (m,1) (m,1)
(b) Complexity table: operations.
Mult Add Div Mod Rnd Round
INT m ×d 0 0 0 0 0
POLY n ×m n ×m 0 m (n + 1) ×m 0
2.3 HE basic Functions
A HE scheme is composed of five functions: key
generation (KeyGen), encryption (Enc), decryption
(Dec), addition (Add) and multiplication (Mult). In
this paper, these are referred as HE basic functions
which are built using atomic and specific functions
from the library. In option, a function which ”re-
freshes” a HE scheme can be added to the HE basic
functions and so, can be modeled too. Contrary to
atomic and specific functions, HE basic functions are
not stored in the library: they are only created for one
particular HE scheme.
Atomic, specific and HE basic functions enable
modeling any kind of HE schemes. More generally,
the modeling process can be used in another cryptog-
raphy context or even in a mathematical context. In
our work, 25 atomic and 31 specific functions were
produced and included in the library. These functions
made possible the modeling of 14 HE schemes of the
literature. To model future schemes, other atomic or
specific functions can be created and added to the li-
brary if necessary. In this section, HE scheme exe-
cutable modeling has been explained. This modeling
enables analysis modeling which is described in the
next section.
3 LIBRARY FUNCTIONS
ANALYSIS
Previous section shows how HE schemes can be mod-
eled into sets of atomic, specific and HE basic func-
tions. To analyze a modeled HE scheme, each atomic
and specific function of the library is linked to analy-
sis functions: one for memory and one for complex-
ity. This section explains how these two functions are
created. HE basic functions possess also their proper
memory and complexity analysis functions which are
created using the same construction model as specific
functions.
3.1 Memory Analysis Function
Memory cost analysis function evaluates the maximal
amount of integers and polynomials that need to be
stored at the same time during the execution of atomic
and specific functions. The memory is represented by
a table that keeps parameter names, dimensions and
objects they contain (integers or polynomials). For
instance, Table 1a shows how temporary variables and
outputs of distriLWE are saved.
All variables of HE schemes are stored in the
memory table. A variable can be either temporary
or an output. At the end of each atomic, specific or
HE basic function, variables created during the func-
tion are sorted. That way, it is possible to see memory
evolution through the execution. This memory evo-
lution permits to return the maximal memory needed
for a HE scheme.
Below, the function Memory.multScalMat is the
memory analysis function of multScalMat which is
an atomic function. Memory table is filled thanks to
Memory.new function call.
Memory.multScalMat(int a, int[][] B,
int[][] C ) : // adds outputs of multScalMat
// in Memory table.
n = Memory.rows(B) //# of rows of B
m = Memory.cols(B) //# of columns of B
Memory.new(C,INT,n,m) //adds C to memory
//table or changes its dimensions
As a specific function is a set of atomic func-
tions, its associated memory analysis functions con-
stitute then a set of related memory analysis func-
tions. Memory.addTimes shows an example of mem-
ory evaluation for the specific function addTimes pre-
sented in Section 2.2.
Memory.addTimes(int[][] A, int b, int[][] C,
int[][] D) :
Memory.multScalMat(b,C,D)
Memory.addMat(A,D,D)
3.2 Complexity Analysis Function
In this paper, complexity represents the number of op-
erations executed. It is determined on the basis of six
operations: multiplication, addition, division, mod-
ulo, random and round. Those operations exhibit dif-
ferent complexities if they are used with integers or
PAnTHErS: A Prototyping and Analysis Tool for Homomorphic Encryption Schemes
361

polynomials only. Complexity is calculated for inte-
gers on one hand and for polynomials on the other
hand.
A table operations is conceived to store complex-
ity in those terms. For an evaluated function, the table
is updated with the total of each type of operations
performed. The operations table is represented in Ta-
ble 1b after calling complexity function of distriLWE.
Characteristics of parameters created and/or mod-
ified are stored and updated if needed through com-
plexity analysis. Indeed, to calculate complexity of
each function, dimensions of objects used in that
function are needed. For that, dimensions required
for the complexity evaluation are extracted from pa-
rameter characteristics. Then, cells of the table oper-
ations, containing global complexity, are incremented
by the number of operations executed in the evaluated
algorithm. After that, characteristics of output param-
eters affected by current operation are updated. As
an example, the function Complexity.multScalMat,
written below, evaluates computational complexity of
multScalMat.
Complexity.multScalMat(int a, int[][] B,
int[][] C ) :
n = B.rows()
m = B.cols()
t = B.type() //returns type of B
operations[INT][MULT] += n * m
C.update(t, n, m) //updates info about C
To evaluate complexity of specific functions, an
associated complexity analysis function is created
by identifying atomic functions used and calling
their related complexity analysis function. Most
of the functions are as simple as distriLWE which
is a set of atomic functions. However, complexity
evaluation remains difficult for few specific func-
tions. The main issue comes with while loops with a
non-deterministic condition or with conditions based
on another function like finding a prime number. In
this work, the worst case is considered.
In the end of the modeling phase, the library con-
tains atomic and specific functions and their associ-
ated memory and complexity analysis functions. As
specific and HE basic functions templates are similar
to their associated analysis functions, these last ones
can be automatically generated at the creation of a
specific or HE basic function. It enables fast analy-
sis of modeled HE schemes which is one of the main
goals of PAnTHErS.
4 PAnTHErS IMPLEMENTATION
AND APPLICATION
At this stage, the library can be filled with atomic,
specific and their corresponding analysis functions.
PAnTHErS can be used to evaluate HE schemes. This
section gives information about PAnTHErS imple-
mentation and describes its easy utilization from a
user and a HE expert point of view.
4.1 Implementation
PAnTHErS is implemented in Python using Sage.
Each type of functions (e.g. atomic) is defined
by a class (e.g. AtomicFunction class) allow-
ing creating HE schemes executable. Moreover,
each type of functions has also two associated
classes corresponding to complexity and memory
cost analysis (e.g. AtomicFunctionComplexity and
AtomicFunctionMemory classes). A design pattern
Visitor can be used to generate analysis functions
automatically (e.g. Memory.addTimes and Complex-
ity.multScalMat functions presented in Section 3). A
Visitor is an operation performed on elements of an
object structure of a class without changing the class
itself (Lasater, 2007).
In addition, for each HE scheme that has to be
model a distinct class is created. HE basic functions
are implemented in each HE scheme class. Other
functions can be added in those classes for optional
calculations. For instance, a function called Depth
was added in HE scheme classes for our case stud-
ies in Section 5. This function calculates the multi-
plicative depth: the number of operations which can
be done homomorphically. A mathematical equation
is needed to compute the depth of a HE scheme. Fi-
nally, a Main class is created to represent the appli-
cation. This class models the application i.e. the suc-
cession of HE basic functions. As an example, the ap-
plication begins by KeyGen and made the following
operations: three Enc, one Add and two Mult. And,
the application finishes with one Dec.
It is important to point out that complexity/mem-
ory cost are first expressed in number of opera-
tions/polynomials in some ring R
q
. However, func-
tions implemented in PAnTHErS permits to convert
complexity as number of multiplications and memory
cost as number of 32-bit integers stored.
Converting all operation complexities as number
of multiplications allows having one global complex-
ity. Operations on polynomials in some ring R
q
are
converted first in operations on integers in R
q
. Then,
by comparing the execution time of the six operations,
ratios are found. After calculating several execution
SECRYPT 2017 - 14th International Conference on Security and Cryptography
362

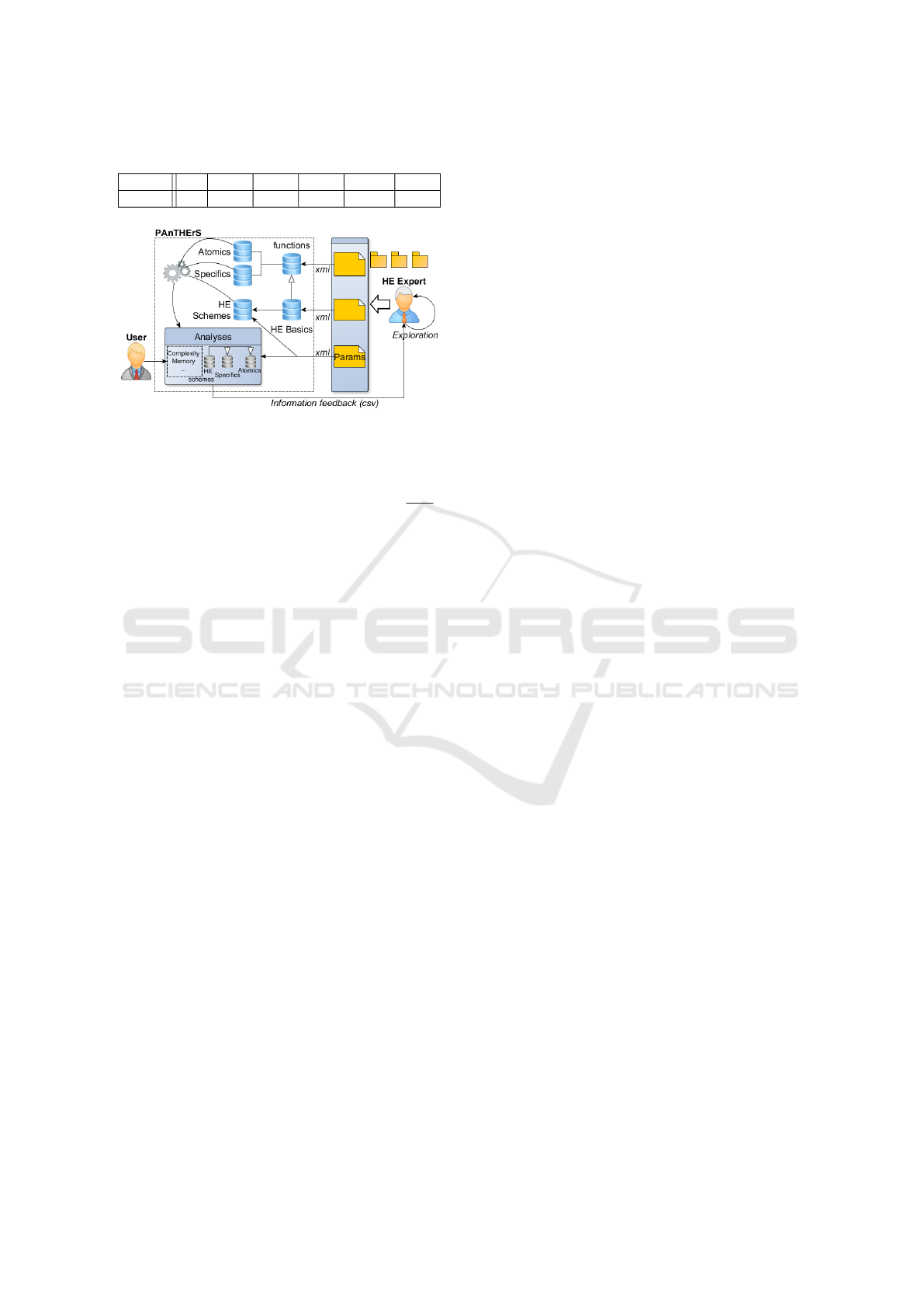
Table 2: Ratios calculated between different operations.
Ope. × + / % Rand ≈
Ratio 1 2.32 0.18 1.56 0.18 0.38
Figure 2: PAnTHErS utilization workflow.
times for each operation, the mean (m) and the median
(M) of those execution times are computed. Then, the
mean between m and M is calculated (mean =
m+M
2
).
A normalization process is performed on means to
take multiplication operation execution time as refer-
ence. So, each mean is divided by the mean of multi-
plication to get the ratio. For each operation, we pro-
duce a list of execution times on an Intel Core-i5 ma-
chine using Sage. From those lists, ratios, presented
in Table 2, were found taking multiplication as refer-
ence. For instance, time execution of 1 multiplication
equals to time execution of 2.32 additions. In PAn-
THErS, a user can change these ratios with custom
values adapted to his own architecture.
4.2 PAnTHErS Usage
Figure 2 shows PAnTHErS utilization workflow by
a HE expert and a user. A HE expert, who can be
also a user, can interact with PAnTHErS in order to
make an exploration of his HE schemes. PAnTHErS
usage depends on the number of specific functions
available in the library. PAnTHErS library contains
all atomic functions but the library does not necessar-
ily have any specific functions. Here, the expert starts
with a library empty of specific functions to illustrate
how PAnTHErS is populated.
First of all, the expert creates specific functions
to fill the library (e.g. addTimes function in Section
2). He starts creating a specific function by giving its
name, input and output parameters. The function is
composed of atomic functions where the expert has
specified their inputs and outputs. The description of
the specific function is given in a XMI file. Validating
a function can permits the automated creation of its
analysis functions. This generation, possible with a
Visitor, is represented by gearwheels on Figure 2. He
repeats this operation for every specific function he
needs for his HE scheme.
HE expert has to model the HE basic functions
of his HE scheme whose skeletons are written down
in XML file. As for creating a specific function, the
expert uses functions in the library to write HE basic
functions and specifies their inputs and outputs.
Once HE basic analysis functions are created, the
expert enters sets of input parameters (a range and a
step for each one) to analyze HE schemes; Moreover,
he fixes the number of HE basic functions executed
and their execution order i.e. his application mod-
eled. This sequence is analyzed regarding each set of
parameter and final results are returned in CSV for-
mat to the expert. Final results correspond to memory
cost, computational complexity and depth. Finally,
he can do an exploration of all of his HE schemes and
their possible input parameters.
PAnTHErS feedback contains useful information
for the HE expert as maximal computational com-
plexity and sum of all memory cost of HE basic func-
tions. The study of these analyses enables the expert
choosing the best parameters to fit its application.
Equally important, a user can interact on analysis
part by adding other analysis calculations for HE
schemes. Indeed, he has access to atomic and specific
functions which are visible to anyone. This way,
PAnTHErS is extended by various analyses that are
interesting for future HE experts’ exploration. More-
over, he takes part in making implementation choices
to improve HE schemes execution. Having analysis
results on a particular HE scheme, he knows, for
instance, where it is interesting to do parallelization
or hardware acceleration.
Knowing PAnTHErS utilization, a HE expert can
easily model and analyze any HE scheme. By varying
their input parameters, several analyses are produced
for each HE scheme. Thanks to these analyses, the
expert is able to select the most interesting one and a
set of parameter guaranteeing a computational com-
plexity, a memory cost and a depth adapted to his ap-
plication. Also, PAnTHErS can be extended by other
analyses implemented by a designer.
5 CASE STUDIES
This section shows PAnTHErS results considering
four HE schemes. PAnTHErS is applied on FV (Fan
and Vercauteren, 2012), YASHE (Bos et al., 2013), F-
NTRU (Dor
¨
oz and Sunar, 2016) and SHIELD (Khedr
et al., 2016) which are all based on R-LWE. To model
the first two schemes, we consider using PAnTHErS
PAnTHErS: A Prototyping and Analysis Tool for Homomorphic Encryption Schemes
363

Figure 3: Specific functions distribution between FV,
YASHE, F-NTRU and SHIELD schemes.
with a library filled of atomic functions only. Then,
each modeled scheme takes benefit of the previous
models leading to rapid modeling. Schemes are then
analyzed regarding several sets of input parameters.
Finally, PAnTHErS draws curves which show evolu-
tion of computational complexity, memory cost and
multiplicative depth.
5.1 Modeling
Figure 3 gives the distribution of specific func-
tions between FV, YASHE, F-NTRU and SHIELD
schemes. In this figure, each circle pictures a HE
scheme. When a number is in an intersection of cir-
cles, it represents the number of shared functions be-
tween the HE schemes. Figure 3 shows that, from
four modeled schemes, 60 % of their specific func-
tions are used in at least two schemes. Reusing spe-
cific functions from the library makes modeling eas-
ier. Starting from scratch to model FV and YASHE,
11 specific functions are created but already five are
shared between the two schemes. Then, three new
specific functions are needed to model F-NTRU and
finally, only one new is required to model SHIELD.
5.2 Experimental Setup
Each considered HE scheme has been modeled as de-
scribed in Section 2. In addition, a function to cal-
culate multiplicative depth was added to each class
except for SHIELD. Indeed, depth calculation is not
fully detailed in (Khedr et al., 2016). To compute the
depth of FV and YASHE, the bound of noise is given
in (Lepoint and Naehrig, 2014).
For the proposed experimentations, the analysis
step has been configured to cover one execution of
KeyGen, Enc, Dec, Add, Mult and Depth. In this
case, each ciphertext is considered ”refreshed” in
Mult function after the multiplication. In the end,
PAnTHErS returns computational complexity, mem-
ory cost of each HE basic function and depth depend-
ing of input parameters, by summing up partial con-
tributions, besides, with no need of time consuming
evaluation.
Table 3: Time execution of all PAnTHErS analysis ex-
pressed in minutes.
Schemes FV YASHE F-NTRU SHIELD
Time 6.279 9.864 3.731 0.598
Table 4: Time execution of one PAnTHErS analysis versus
time execution of real HE scheme execution expressed in
seconds.
Schemes FV YASHE F-NTRU SHIELD
Analysis 0.058 0.088 0.079 0.069
Execution 6.44 35.13 53.64 48.80
Before performing any analysis, input parame-
ters must be configured. For each set of parameters,
each scheme provides 80-bit of security considering
input parameters given by (Migliore et al., 2017).
In all HE schemes, computations are made in R =
Z[X]/(Φ
d
(X)) where Φ
d
(X) is the irreducible dth cy-
clotomic polynomial. In F-NTRU and SHIELD, d is a
power of 2. Polynomials of R have a maximal degree
of n = ϕ(d). All polynomial operations are located in
R
q
= R/qR with q the modulus. In FV and YASHE,
the plaintext to cipher is in R
t
= R/tR. An integer
base w is provided in FV, YASHE and F-NTRU; it is
used in some functions to decompose words in base
w. All schemes need two Gaussian distributions χ
key
and χ
err
bounded by respectively B
key
and B
err
.
In each scheme, parameters n and q are inter-
dependents on each other. To choose n with regards
to q, there is a maximum log
2
(q). We took n and
log
2
(q) presented in (Migliore et al., 2017). Our tests
cover all log
2
(q) ∈{40,48,...,500}. Making sure that
w < q, we took log
2
(w) ∈ {2, 32,64, 128} for FV and
YASHE analysis and log
2
(w) ∈ {1, 8,16,32} for F-
NTRU analysis. Finally, for FV and YASHE, we vary
t by taking t ∈{2,8,32,64}. And, we set B
key
= 1 and
B
err
= 9.2 ×2
√
n to calculate depth.
To evaluate PAnTHErS efficiency, a benchmark
of 100 executions has been performed. Table 3 re-
caps time execution of PAnTHErS for each scheme
depending on the number of evaluated sets of param-
eters. Varying parameters as explained before imply
6904 analyses for FV and YASHE, 1840 for F-NTRU
and 460 for SHIELD. Table 4 compares one analy-
sis execution time versus one real execution time. All
these executions were made using Sage, version 7.6.
5.3 Results
This section presents and analyzes the results ob-
tained for the considered HE schemes. One of the
main objectives of the proposed approach is to deter-
mine a set of adequate HE schemes and their associ-
ated input parameters which fit for requirements of an
SECRYPT 2017 - 14th International Conference on Security and Cryptography
364

0 100 200 300 400 500
log2(q)
0
0.5
1
1.5
2
Number of multiplications
10
9
FV t, = 32
YASHE t, = 32
FV t, = 64
YASHE t, = 64
(a) FV and YASHE complex-
ity.
0 100 200 300 400 500
log2(q)
0
0.5
1
1.5
2
2.5
3
3.5
Number of multiplications
10
13
F-NTRU = 8
F-NTRU = 16
F-NTRU = 32
SHIELD
(b) SHIELD and F-NTRU
complexity.
Figure 4: Evolution of computational complexity in func-
tion of log
2
(q) expressed in number of multiplications. We
fix ω = log
2
(w).
application. When taking each scheme individually,
there is no way to decide which one best fits to an
application since this choice is driven by the applica-
tion requirements. Analysis must target these features
to select an interesting candidate. If several schemes
match the application, thanks to tests and results, they
can be compared to detect the most interesting one.
Figures 4, 5 and 6 show analysis results i.e. evo-
lution of complexity, memory cost and multiplica-
tive depth of the four HE schemes in function of
log
2
(q). Breaks, visible in each figure, correspond
to the change of n. When complexities and mem-
ory costs of the four schemes are drawn together on
the same graph, we notice that the scale difference is
too important to be well displayed. To ensure good
graph readability, we choose to focus on two algo-
rithms comparisons only at a time, resulting on two
sets graphs, comparing respectively FV with YASHE
and F-NTRU with SHIELD.
From Figure 4a, it is clear that w impacts on FV
and YASHE complexity. For an application with
computational complexity constraints, a user will pre-
fer use a bigger w which implies a lower complexity.
FV is the most interesting because it is the less com-
plex. Additional analyses show that the impact of t
on computational complexity is non-existent. From
Figure 4b, SHIELD seems a better candidate than F-
NTRU (with a small w) for an application with com-
plexity constraints. Nonetheless, F-NTRU tends to
have a lower complexity while w increases.
Figure 5a shows that, for FV and YASHE, Mult
memory cost falls as w grows up. Moreover, this
Figure illustrates that for log
2
(w) = 64, YASHE is
less memory consuming than FV. If log
2
(w) = 32,
YASHE is more interesting until around log
2
(q) =
400. However, Figure 5b shows that Add function
of FV consumes more memory than Add function of
YASHE for all q. Additional analyses illustrate that
the same variations than Mult function exist for Key-
Gen function but that w and t have no influence on
Enc and Dec functions for both schemes. Among
F-NTRU HE basic functions, the Dec function con-
sumes the less of memory. Analyses show that Mult
and Add are identical and that they are the most mem-
ory consuming. Figure 5c illustrates that, despite a
high w, Enc function of SHIELD remains the less
consuming in term of memory than Enc function of
F-NTRU. Figure 5d shows it is the contrary for Key-
Gen function.
Theoretical multiplicative depth is represented by
an integer. For FV, YASHE and F-NTRU, growing
w implies a lower complexity and a lower memory
cost, however, it implies also a lower depth. Figure
6a illustrates that FV tends to have a greater depth
comparing to YASHE by taking the same input
parameters. Theoretically, depth curves of FV,
YASHE and F-NTRU are closed: F-NTRU depth
is lower. Nonetheless, depth of FV and YASHE is
slightly smaller if t increases. Analyses show that the
difference between depths in function of t seems to
become more important as q raises up. In practice,
it is possible to have a greater depth. For instance,
Figure 6b shows that F-NTRU depth is usually 1.5
times greater in average than theoretically. For a
fixed depth, a user will choose a HE scheme less
complex and less consuming in memory: FV and
YASHE seems more interesting.
These case studies show PAnTHErS utilization on
four HE schemes of the literature. Moreover, this
section demonstrates that as functions are shared be-
tween HE schemes, the modeling is faster. Thanks
to several analyses, we were able to detect two kinds
of schemes. Among results showed in this section,
SHIELD seems to have a lower memory cost than F-
NTRU and FV is clearly less complex than YASHE.
The proposed approach realizes a fast analysis of
various HE schemes and display comparative results,
enabling HE experts to select viable candidates for
their application. PAnTHErS helps them to focus
on analysis and development of the best HE schemes
matching their needs and their application constraints.
6 CONCLUSION AND FUTURE
WORKS
This paper presents PAnTHErS, a tool that provides
a way of evaluating HE schemes. Besides, this ap-
proach offers scalability and incremental design. It
dispenses with the need for software implementation
and simulations of HE schemes. The schemes are
modeled as sets of reusable functions that are stored
in the library. After the modeling phase, PAnTHErS
PAnTHErS: A Prototyping and Analysis Tool for Homomorphic Encryption Schemes
365

0 100 200 300 400 500
log2(q)
0
2
4
6
8
10
12
Number of 32-bit integers
10
7
FV t, = 32
YASHE t, = 32
FV t, = 64
YASHE t, = 64
(a) FV and YASHE Mult
memory cost.
0 100 200 300 400 500
log2(q)
0
0.5
1
1.5
2
2.5
3
3.5
Number of 32-bit integers
10
6
FV t
YASHE t
(b) FV and YASHE Add
memory cost.
0 100 200 300 400 500
log2(q)
0
1
2
3
4
5
6
Number of 32-bit integers
10
10
F-NTRU = 8
F-NTRU = 16
F-NTRU = 32
SHIELD
(c) SHIELD and F-NTRU
Enc memory cost.
0 100 200 300 400 500
log2(q)
0
2
4
6
8
10
12
Number of 32-bit integers
10
6
F-NTRU
SHIELD
(d) F-NTRU and SHIELD
KeyGen memory cost.
Figure 5: Evolution of memory cost in function of log
2
(q) expressed in number of 32-bit integers stored. We fix ω = log
2
(w).
0 100 200 300 400 500
log2(q)
0
2
4
6
8
10
12
14
16
Depth
FV t, = 32
YASHE t, = 32
FV t, = 64
YASHE t, = 64
(a) FV and YASHE depth.
0 100 200 300 400 500
log2(q)
0
5
10
15
20
25
30
Depth
= 8, in theory
= 8, in average
= 32, in theory
= 32, in average
(b) F-NTRU depth in theory
and in average.
Figure 6: Evolution of multiplicative depth in function of
log
2
(q). We fix ω = log
2
(w).
returns valuable information about HE schemes in
terms of computational complexity, memory cost and
multiplicative depth. This analysis is a lightweight
operation as the functions of the library have already
been analyzed. Evaluating PAnTHErS results enables
to determine if the scheme is an interesting candidate
for a particular application using HE. Future works
will focus on optimizing PAnTHErS. The analysis
step will be extended with new metrics. Then, an
extra feature of PAnTHErS will address automated
generation of hardware accelerators targeting a FPGA
implementation for HE schemes. This will rely on an
open-source high-level synthesis environment.
REFERENCES
Bos, J. W., Lauter, K. E., Loftus, J., and Naehrig, M. (2013).
Improved Security for a Ring-Based Fully Homomor-
phic Encryption Scheme. In Proc. Cryptography and
Coding IMA, pages 45–64, Oxford, UK.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2012).
(Leveled) Fully Homomorphic Encryption without
Bootstrapping. In Proc. Innovations in Theoretical
Computer Science Conference, pages 309–325.
Brakerski, Z. and Vaikuntanathan, V. (2011a). Effi-
cient Fully Homomorphic Encryption from (Standard)
LWE. FOCS 2011, pages 97–106.
Brakerski, Z. and Vaikuntanathan, V. (2011b). Fully Homo-
morphic Encryption from Ring-LWE and Security for
Key Dependent Messages. In Proc. CRYPTO, pages
505–524, Santa Barbara, CA, USA.
Dijk, M. V., Gentry, C., Halevi, S., and Vaikuntanathan, V.
(2010). Fully Homomorphic Encryption over the In-
tegers. In Proc. EUROCRYPT, pages 24–43, French
Riviera.
Dor
¨
oz, Y. and Sunar, B. (2016). Flattening NTRU for eval-
uation key free homomorphic encryption. IACR Cryp-
tology ePrint Archive, 2016:315.
Fan, J. and Vercauteren, F. (2012). Somewhat Practical
Fully Homomorphic Encryption. IACR Cryptology
ePrint Archive, 2012:144.
Gentry, C. (2009). Fully homomorphic encryption using
ideal lattices. In STOC, pages 169–178.
Gentry, C., Sahai, A., and Waters, B. (2013). Homomorphic
Encryption from Learning with Errors: Conceptually-
Simpler, Asymptotically-Faster, Attribute-Based. In
Proc. CRYPTO, pages 75–92, Santa Barbara, CA,
USA.
Halevi, S. and Shoup, V. (2014). HElib - An im-
plementation of homomorphic encryption.
https://github.com/shaih/HElib.
Khedr, A., Gulak, P. G., and Vaikuntanathan, V. (2016).
SHIELD: scalable homomorphic implementation of
encrypted data-classifiers. IEEE Trans. Computers,
65(9):2848–2858.
Lasater, C. G. (2007). Design Patterns. Wordware Appli-
cations Library. Wordware Pub, 1 edition.
Lepoint, T. and Naehrig, M. (2014). A Comparison of the
Homomorphic Encryption Schemes FV and YASHE.
In Proc. AFRICACRYPT, pages 318–335, Marrakesh,
Morocco.
Lindner, R. and Peikert, C. (2011). Better Key Sizes (and
Attacks) for LWE-Based Encryption. In Proc. - CT-
RSA 2011, pages 319–339, San Francisco, CA, USA.
Migliore, V., Bonnoron, G., and Fontaine, C. (2017). Deter-
mination and exploration of practical parameters for
the latest Somewhat Homomorphic Encryption (SHE)
schemes. Working paper or preprint.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
366