On Efficient Access Control Mechanisms in Hierarchy using
Unidirectional and Transitive Proxy Re-encryption Schemes
Gaurav Pareek and Purushothama B. R.
National Institute of Technology Goa, Ponda, India
Keywords:
Cryptographic Access Control, Proxy Re-encryption, Access Control in Hierarchy, Unidirectional-transitive,
Key Management.
Abstract:
Proxy re-encryption is a cryptographic primitive used to transform a ciphertext under one public key such
that it becomes a ciphertext under another public key using a re-encryption key. Depending on the properties
featured by a proxy re-encryption scheme, it can be applied to a variety of applications. In this paper, we target
one such application of proxy re-encryption – access control in hierarchy, to highlight an important research
gap in its design. We study how a proxy re-encryption scheme that is both unidirectional and transitive can
be useful for enforcing hierarchical access control with constant computation and storage overhead on its
users irrespective of the depth of the hierarchy. Also, we present improvements on the existing re-encryption
schemes to make it applicable to hierarchical key assignment and achieve performance closer to that in case
of a unidirectional transitive proxy re-encryption scheme.
1 INTRODUCTION
Cloud computing is gaining importance as more and
more enterprises are switching to cloud for provid-
ing storage and computing services to its users. To
maintain confidentiality of the data, it is encrypted. A
cloud customer willing to enforce cryptographic ac-
cess control (Vimercati et al., 2010) uses proxy re-
encryption (Blaze et al., 1998) to delegate decryption
rights of a data item to any other party. This dele-
gation of decryption rights (or simply delegation) re-
quires re-encryption to be done using a special key
called re-encryption key (or delegation key). Anyone
can use a re-encryption key rk
A→B
to transform mes-
sage encrypted for A such that can be decrypted by B.
The re-encryption procedure does not reveal anything
about the underlying plaintext or secret keys A and B.
First proposed by Blaze et al. (Blaze et al., 1998), re-
visited by Dodis et al.(Dodis and Fazio, 2003), the
desirable properties of proxy re-encryption were first
presented by Ateniese et al. (Ateniese et al., 2006).
The properties include unidirectionality, transitivity,
collusion safety, proxy invisibility, key optimality,
temporary delegation and non-transferability. Various
applications of proxy re-encryption require different
combinations of these properties to be satisfied.
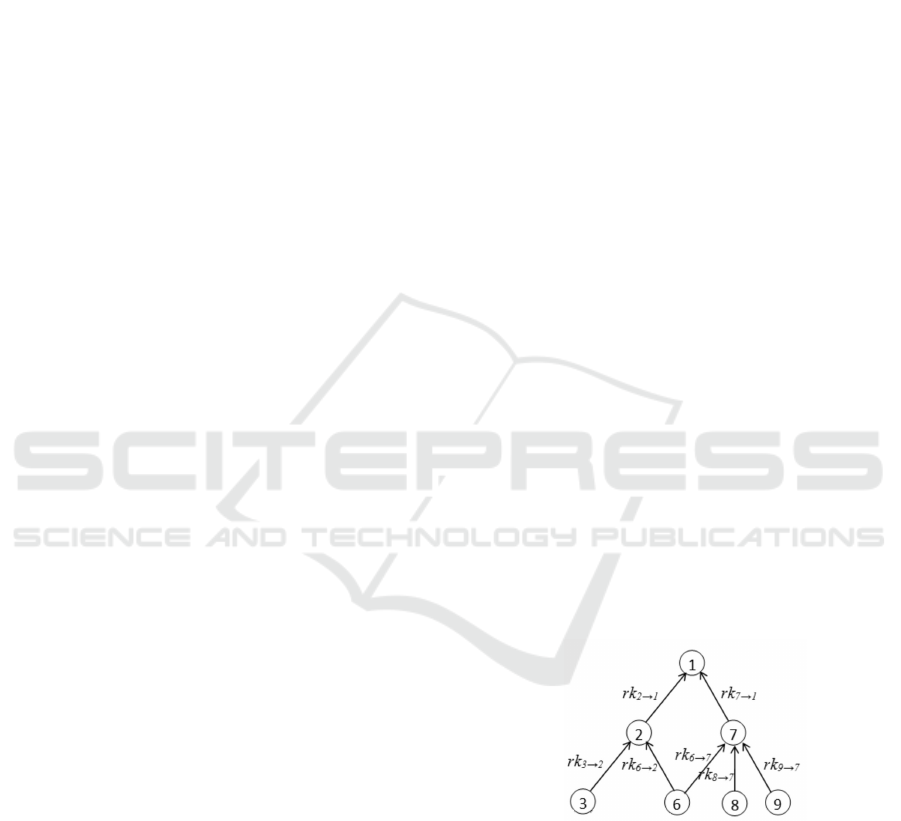
Consider an application scenario where cryptographic
access control in a hierarchy of security classes is pro-
vided using key management (Atallah et al., 2009).
The set of users is divided into a disjoint collection
of classes depending on the security clearance of the
users. The hierarchy of classes forms a POSET (par-
tially ordered set) under the partial order . Here,
C
j
 C
i
means that users in a class C
i
have access to
data items encrypted for all the classes C
j
in addition
to the data items directly encrypted for users in C
i
.
Figure 1: Hierarchical Key Assignment using Proxy Re-
encryption.
Proxy re-encryption can be applied for manag-
ing access in this scenario by assigning re-encryption
keys rk
i→ j
to each edge in the access hierarchy as
shown in Figure 1. Suppose users in C
1
wish to ac-
cess ciphertext CT
2
of class C
2
. Users in C
1
can get
CT
2
re-encrypted using rk
2→1
. But if users in C
1
want
to access ciphertext CT
6
, due to unavailability of re-
encryption key rk
6→1
, CT
6
must be first transformed
into CT
2
using rk
6→2
and then into CT
1
using rk
2→1
.
Pareek, G. and R., P.
On Efficient Access Control Mechanisms in Hierarchy using Unidirectional and Transitive Proxy Re-encryption Schemes.
DOI: 10.5220/0006466405190524
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 519-524
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
519

In general, the number of re-encryptions required is
at most equal to the depth of the hierarchy. Also,
schemes that support repeated re-encryption and only
in one direction i.e., unidirectional and multi-hop
re-encryption schemes (Shao et al., 2011; Chandran
et al., 2014) are computationally very costly to realize
and require extremely costly operations for each re-
encryption. But if the re-encryption scheme is transi-
tive and unidirectional, then given rk
6→2
and rk
2→1
, it
is possible to derive rk
6→1
. So, it avoids repeated re-
encryptions and requires only one re-encryption fol-
lowed by one decryption.
However, we note that there is no proxy re-encryption
scheme that satisfies both unidirectionality and tran-
sitivity. In this paper, we open an interesting prob-
lem of designing a unidirectional-transitive proxy re-
encryption scheme. Our claims are based on the ex-
isting security requirements and state-of-the art de-
sign of proxy re-encryption schemes. For this, we
capture high level design goals in the form of func-
tions. We also propose the ways by which existing re-
encryption schemes can be modified to obtain perfor-
mance close to the case with unidirectional-transitive
proxy re-encryption.
The remainder of the paper is organized as follows.
Section 2 presents system definitions for hierarchical
access control. Section 3 defines a unidirectional and
transitive proxy re-encryption scheme along with its
security requirements. Section 4 discusses our math-
ematical claims regarding the possibility of design of
a unidirectional-transitive proxy re-encryption.
2 ACCESS CONTROL IN
HIERARCHY
We present a formal model for access control in hi-
erarchy. This includes definitions of procedures in-
volved and security definition.
2.1 System Model
Let C
1
,C
2
,... ,C
n
be a disjoint partition (security
classes or simply classes) of the set of users U in the
system. Let S = {C
1
,C
2
,... ,C
n
} be partially ordered
by the binary relation . If C
j
 C
i
, then users in
classC
j
havethe right to access information meant for
users in class C
i
. However, the reverse is not allowed.
We use following notations in context of access con-
trol in hierarchy:
• parent(C
i
)/ances(C
i
) denotes the set of classes
C
j
∈ S such that C
i
 C
j
and C
j
is one/more than
one level higher in the hierarchy than C
i
.
• child(C
i
)/desc(C
i
) denotes the set of classes C
j
∈ S
such that C
j
 C
i
and C
j
is more than one/more
than one level lower in the hierarchy than C
i
.
All the users in a classC
i
share a class secret key,CSK
i
and the corresponding class encryption key CEK
i
is
published. All these users in a security class C
i
com-
municate with each other through messages encrypted
using a symmetric secret key K
i
. Users in a class C
j
may want to access data items encrypted for a class
C
i
where C
i
 C
j
. For this, symmetric secret key K
i
has to be obtained by users of C
j
. A class addition
or deletion from the hierarchy may take place. There
exists a central trusted Key Generation Center (KGC)
which generates the CSK and CEK for every class.
2.2 Definitions
Any hierarchical key assignment scheme can be de-
fined as a collection of the following algorithms:
1. Set: This algorithm takes security parameter as
input and computes the public system parameters.
2. Gen: In this algorithm, each class C
i
is assigned
CSK
i
to be kept secret by the class members and
a CEK
i
which is made public. This phase also
generates public parameters corresponding to the
edges in the hierarchy tree which may be used for
key derivation.
3. Derive: This procedure enables users of a class
C
j
∈ {ances(C
i
) ∪ parent(C
i
)} to derive decryp-
tion key of class C
i
.
2.3 Security
Security definition for key management for hierarchy
captures the inability of a probabilistic polynomial
time (PPT) adversary A to have a non-negligible ad-
vantage over the challenger C in the following game:
• Initiate: C executes Set and Gen and gives all the
public parameters and CEK
i
to the adversary.
• Query-1: A can request K
i
for the set of corrupted
security classes for number of times polynomial
in the security parameter k.
• Challenge: When A decides that the query pro-
cedure is over, she can specify a target security
class C
i
∗
such that C
i
∗
/∈ {desc(C
i
) ∪ child(C
i
)}
∀C
i
asked in the above query phase. C now picks
a bit h randomly such that h ∈
R
{0,1} and sends
a random output (other than the key)
K
i
∗
if h = 0
and the actual key K
i
∗
if h = 1.
• Query-2: A can issue more queries for classes C
j
such that C
j
/∈ {ances(C
i
∗
) ∪ parent(C
i
∗
)}.
• Guess: Now A outputs her best guess h
′
and A is
declared winner of the game if h = h
′
.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
520

A’s advantage in the game above= |Pr[h = h
′
]−1/2|.
In addition to the above security definition, hierarchi-
cal key management must also support forward and
backward secrecy. Backward Secrecy requires that if
a new security class C
l
joins in, the users in C
l
must
not be able to obtain data encrypted for all the classes
C
k
such that C
k
 C
l
prior to C
l
’s joining. To main-
tain Forward Secrecy, a class C
l
′
that leaves the sys-
tem must not be able to access data encrypted for all
classes C
k
such that C
k
 C
l
′
after C
l
′
leaves.
3 UNIDIRECTIONAL AND
TRANSITIVE PROXY
RE-ENCRYPTION
A proxy re-encryption scheme uses a re-encryption
key rk
A→B
for transformation of ciphertext under a
public key pk
A
such that it becomes a ciphertext under
pk
B
and is decrypted by sk
B
. While a unidirectional
proxy re-encryption prevents delegation in reverse di-
rection, transitivity makes it possible for anyone to
derive a direct re-encryption key using various single-
hop re-encryption keys.
3.1 Definition
We define a proxy re-encryption scheme which is
same as in (Ateniese et al., 2006) except that it has
an additional procedure for direct re-encryption key
derivation.
Definition 1. A proxy re-encryption scheme can be
defined as a collection Π =(Setup, KeyGen, Enc
1
,
Dec
1
, Enc
2
, Dec
2
, ReKeyGen, ReEnc, Derive) of al-
gorithms defined as follows:
• Setup(1
λ
)→ param: This algorithm inputs secu-
rity parameter 1
λ
to produce system parameters.
• KeyGen(i)→ (sk
i
, pk
i
): Public-secret key pair
(sk
i
, pk
i
) can be generated using this procedure.
• Enc
1
(pk
i
,m)→ CT
i
: This produces a first-level ci-
phertext CT
i
that can be decrypted using sk
i
.
• Enc
2
(pk
i
,m)→ CT
′
i
: This produces a second-
level ciphertextCT
′
i
which can be re-encrypted us-
ing a valid re-encryption key.
• Dec
1
(sk
i
,CT
i
)→ m: The first-level ciphertext CT
i
can be decrypted by this procedure using sk
i
.
• Dec
2
(sk
i
,CT
′
i
)→ m: This algorithm decrypts the
second-level ciphertext under pk
i
using sk
i
.
• ReKeyGen(sk
i
, pk
j
)→ rk
i→ j
: This algorithm gen-
erates a re-encryption key rk
i→ j
that transforms
CT
′
i
into CT
j
.
• ReEnc(rk
i→ j
,CT
′
i
) → CT
j
: Given a valid rk
i→ j
,
anyone can transform CT
′
i
into CT
j
.
• Derive
RK
({rk
1→2
,...,rk
(n−1)→n
}) → rk
1→n
:
Given a sequence of all the one-hop re-encryption
keys on the path from first delegator to the last
delegatee, a direct re-encryption key can be
derived using this procedure.
3.2 Correctness
1. A first-level ciphertext must decrypt correctly.
Dec
1
(sk
i
,Enc
1
(pk
i
,m)) = m
2. A second-level ciphertext must decrypt correctly.
Dec
2
(sk
i
,Enc
2
(pk
i
,m)) = m
3. A re-encrypted ciphertext must decrypt correctly.
Dec
1
(sk
j
,ReEnc(ReKeyGen(sk
i
, pk
j
),
Enc
2
(pk
i
,m))) = m
4. Derivation of direct re-encryption key given all
the intermediate keys, must be correct. That is,
Derive
RK
(ReKeyGen(sk
1
, pk
2
),... ,
ReKeyGen(sk
n−1
, pk
n
)}) → rk
1→n
3.3 Security
We define security requirements for the proposed
proxy re-encryption scheme against a PPT adversary
(A) that tries to distinguish two second-level cipher-
texts as under:
Pr[(pk
i
∗
,sk
i
∗
) ← KeyGen(i
∗
),{(pk
B
,sk
B
) ←
KeyGen(B)}, {(pk
X
,sk
X
) ← KeyGen(X)},
{rk
B→i
∗
← ReKeyGen(sk
B
, pk
i
∗
)},
{rk
X→i
∗
← ReKeyGen(sk
X
, pk
i
∗
)},
{rk
X→B
← ReKeyGen(sk
X
, pk
B
)}, (m
0
,m
1
,α) ←
A(pk
i
∗
,{pk
B
},{(pk
X
,sk
X
)},{rk
B→i
∗
}, {rk
X→i
∗
},
{rk
X→B
},CT
i
∗
, b ← {0,1},
b
′
← A
k
(α,Enc
2
(pk
i
,m
b
))) : b = b
′
] <
1
2
+
1
poly(k)
Set of key-pairs of the honest users as {(sk
B
, pk
B
)},
set of key-pairs of set of corrupted users as
{(sk
X
, pk
X
)} and key-pair of the target user as
(sk
i
∗
, pk
i
∗
). The definition means that a colluding ad-
versary is able to distinguish two direct ciphertexts
despite the availability of all the re-encryption keys,
with negligible advantage.
3.4 Hierarchical Key Assignment
We define hierarchical key assignment (Set, Gen and
Derive) as an application of a unidirectional transitive
proxy re-encryption scheme. (See Table 1):
1. Set: It uses SetUp defined in Section 3.1 to gen-
erate system parameters.
2. Gen: It calls KeyGen defined in Section 3.1
and generates key pairs (CEK
i
= pk
i
,CSK
i
= sk
i
)
∀C
i
∈ S. Re-encryption keys rk
i→ j
,∀C
i
,C
j
∈ S
On Efficient Access Control Mechanisms in Hierarchy using Unidirectional and Transitive Proxy Re-encryption Schemes
521

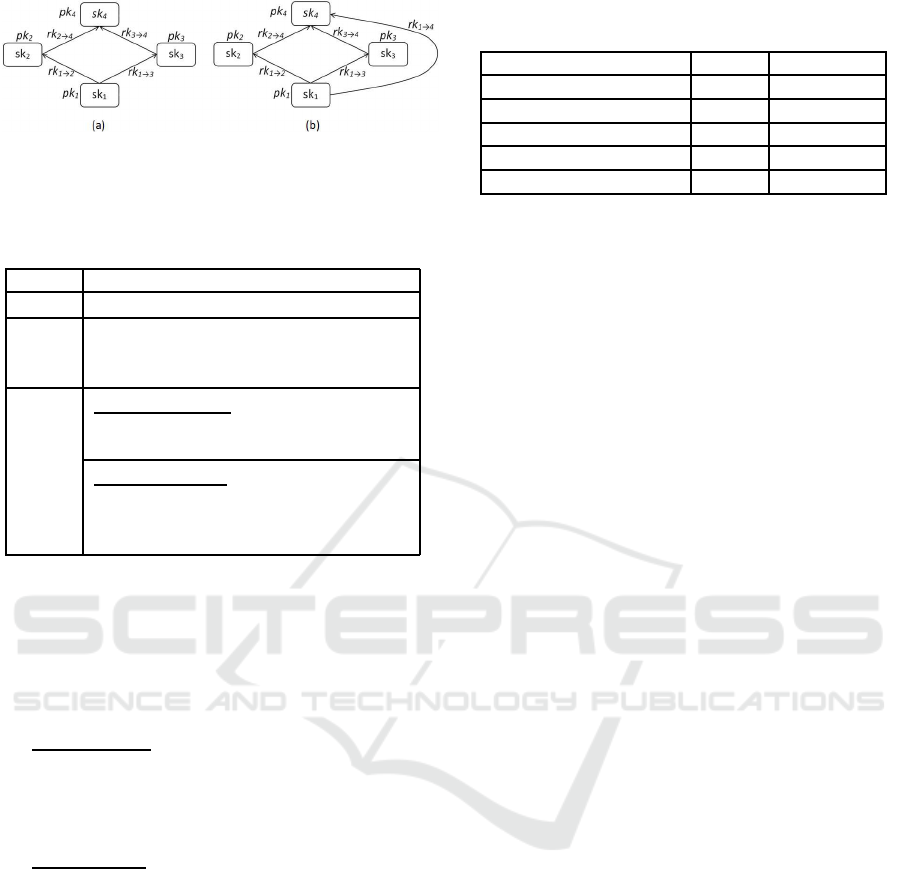
Figure 2: (a) Key assignment and (b) re-encryption
key derivation in a unidirectional-transitive proxy re-
encryption.
Table 1: Operation of access control in hierarchy using uni-
directional and transitive proxy re-encryption scheme.
HKA PRE procedures
Set SetUp(1
λ
)→ params
Gen
KeyGen(i)→ (CSK
i
= sk
i
,CEK
i
= pk
i
)
ReKeyGen(CSK
i
,CEK
j
)→ rk
i→ j
Enc
2
(CEK
i
,K
i
)→ CT
′
i
Derive
If C
i
∈ child(C
j
):
ReEnc(rk
i→ j
,CT
′
i
)→ CT
j
Dec
1
(CSK
j
,CT
j
)→ K
i
If C
i
∈ desc(C
j
):
Derive
RK
ReEnc(rk
i→ j
,CT
′
i
)→ CT
j
Dec
1
(CSK
j
,CT
j
)→ K
i
such that C
i
∈ child(C
j
) are generated and as-
signed to the corresponding edges by ReKey-
Gen(CSK
i
,CEK
j
). ∀C
i
∈ S. K
i
encrypted using
Enc
2
(CEK
i
,K
i
) to produce CT
′
i
is published.
3. Derive: When any user from C
j
wishes to access
K
i
of class C
i
, following two cases are possible:
C
i
∈ child(C
j
):
Re-encryption key rk
i→ j
should be
available as a result of the procedure Gen defined
above. For users in C
j
to access K
i
, anyone can
compute ReEnc(rk
i→ j
,CT
′
i
) to get CT
j
. This can
be decrypted using Dec
1
(CSK
j
,CT
j
).
C
i
∈ desc(C
j
):
In this case, rk
i→ j
would not be
available. The procedure Derive
RK
is used
with all the one-hop re-encryption keys on the
path from C
i
to C
j
to compute rk
i→ j
(see Fig-
ure 2). This rk
i→ j
can now be used for re-
encryption as in the previous case (where C
i
∈
child(C
j
)) to produce CT
j
. CT
j
can be decrypted
as Dec
1
(CSK
j
,CT
j
) to obtain K
i
.
3.4.1 Dynamic Access Hierarchy
To preserve backward secrecy, K
i
and the individ-
ual key pair (CSK
i
,CEK
i
) for all classes C
i
such that
C
i
∈ {desc(C
l
) ∪ child(C
l
)} are updated to K
′
i
and
(CSK
′
i
,CEK
′
i
) respectively. The new symmetric se-
cret key K
′
i
is now encrypted using Enc
2
(CEK
′
i
,K
′
i
).
As a result of changing the individual key pairs of ev-
ery class C
i
∈ {desc(C
l
) ∪ child(C
l
)}, corresponding
Table 2: Components stored by a security class C
i
in the hi-
erarchy with storage requirement (public/private) and size.
Key Component Type No.s
CEK
i
public 1
CSK
i
private 1
K
i
private 1
rk
i→ j
,∀C
j
∈ parent(C
i
) public |parent(C
i
)|
CT
′
i
= Enc
2
(pk
i
,K
i
) public 1
re-encryption keys rk
i
′
→ j
where C
j
∈ parent(C
i
) are
also updated using ReKeyGen(CSK
i
,CEK
j
). Similar
procedure is followed in case a class is removed from
the hierarchy to preserve forward secrecy.
3.4.2 Performance Analysis
Storage cost: As shown in Table 2, users in C
i
have to
store only one CSK
i
and one symmetric secret key K
i
irrespective of the depth d
i
of C
i
.
Computation cost: As can be seen in Table 1, to derive
symmetric secret key K
i
of any class C
i
∈ {desc(C
j
) ∪
child(C
j
)} it requires the users in class C
j
to perform
only one decryption. In case of a change in the access
hierarchy, total computation cost for a class C
j
equals
that of one encryption and generation of |parent(C
j
)|
re-encryption keys.
3.4.3 Security
Since K
i
is encrypted and re-encrypted using algo-
rithms defined in Section 3.1, security of the hierar-
chical access control depends on security of the uni-
directional transitive proxy re-encryption defined in
Section 3.3.
4 DESIGNING DESIRED PROXY
RE-ENCRYPTION SCHEME
So far, it has been discussed that using a unidirec-
tional and transitive proxy re-encryption scheme for
key management in hierarchy, we can achieve:
1. Constant key derivationcost for users of any class,
2. Constant storage overhead on the users,
3. Efficient forward an backward secrecy,
4. No repeated transformation of ciphertext.
We note, however, that there is no proxy re-encryption
scheme in the existing literature that is both unidirec-
tional and transitive. We present claims that have the
potential to establish that transitivity has to be com-
promised while achieving unidirectionality and vice
versa. We also present improvements by which unidi-
rectionality and transitivity can be “closely” imitated.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
522

4.1 Assumptions
Following are the assumptions subject to which we
state and prove our claims regarding transitivity and
unidirectionality of a proxy re-encryption scheme:
1. Secret keys required for re-encryption key gener-
ation are a member of a finite group of prime or-
der (say Z
p
) and resulting re-encryption keys are a
member of finite cyclic group of prime order (G
1
)
2. A re-encryption key rk
i→ j
is a function f : Z
2
p
→
G
1
i.e., rk
i→ j
= f(sk
i
,sk
j
). The order of ap-
pearance of the function input is important as
f(sk
j
,sk
i
) = rk
j→i
. Also, f(x, x) = e, where e is
the identity element of G
1
with respect to the op-
eration defined by the function f
′
defined next.
3. There exists a function f
′
: G
2
1
→ G
1
such
that f
′
( f(u,v),(w,x)) = f
′
( f(u,x), f(v,w)). High
level intuition of re-encryption key derivation for
transitive re-encryption keys is captured by f
′
.
4. A unidirectional re-encryption key f(sk
i
,sk
j
) is a
trapdoor function with no trapdoor information to
recover either sk
i
or sk
j
.
4.2 Desirable Conditions for Derive
RK
1. Unidirectionality of the re-encryption key, that is,
given rk
i→ j
, it is not possible to compute rk
j→i
.
2. No secret keys are revealed during the process.
3. Derive
RK
(rk
i→ j
,rk
i→ j
) must correctly produce
rk
i→k
. That is:
Derive
RK
(f(sk
i
,sk
j
), f(sk
j
,sk
k
)) = f(sk
i
,sk
k
)
We can think of the procedure Derive
RK
as the func-
tion f
′
defined in the assumptions above. So,
f
′
( f(sk
i
,sk
j
), f(sk
j
,sk
k
))=f
′
( f(sk
i
,sk
k
), f(sk
j
,sk
j
))
= f
′
( f(sk
i
,sk
k
),e) = f(sk
i
,sk
k
) = rk
i→k
.
4.3 Our Claims
In this section, we state and argue for our claims
which establish that given the current state-of-the-art
design for a proxy re-encryption scheme, it is hard to
satisfy both unidirectionality and transitivity.
Claim 1. To achieve transitivity in the re-encryption
key derivation, unidirectionality has to be sacrificed.
Argument: As mentioned earlier, the Derive
RK
func-
tion defined in Section 3.1 can be modelled using
function f
′
defined in Section 4.1.
Derive
RK
(rk
j→k
,rk
i→ j
)=f
′
( f(sk
j
,sk
k
), f(sk
i
,sk
j
))=
f
′
( f(sk
j
,sk
j
), f(sk
k
,sk
i
))=f
′
(e, f(sk
k
,sk
i
))=rk
k→i
.
So, using Derive
RK
defined using function f
′
, we
may obtain a reverse re-encryption key rk
k→i
.
Claim 2. To achieve unidirectionality in re-
encryption key generation, transitivity in key
derivation has to be sacrificed.
Argument: Given rk
i→ j
and rk
j→k
, definition of
Derive
RK
using function f
′
in Section 4.2 requires
that the secret key sk
j
be separated from the re-
encryption key defined using the function f. This
is in contradiction to the assumptions we made in
Section 4.1 which states inseparability of the secret
keys of the communicating parties from the proxy re-
encryption keys.
4.4 Alternate Methods
We present the idea of achieving direct re-encryption
key derivation using the existing properties of proxy
re-encryption. First we exploit the transferability and
then we present another potential method by deriving
a decryptionkey of the class lower down the hierarchy
which can be used to obtain direct re-encryption key.
4.4.1 Bottom-up: Exploiting a transferable PRE
Almost all the initial proxy re-encryption schemes
were transferable (Blaze et al., 1998; Ateniese et al.,
2006; Canetti and Hohenberger, 2007; Green and
Ateniese, 2007; Libert and Vergnaud, 2008). For a
transferable proxy re-encryption scheme, it is pos-
sible to generate rk
i→k
given rk
i→ j
, rk
j→k
and se-
cret keys sk
j
, sk
k
. For example, re-encryption key
in (Ateniese et al., 2006) takes the form rk
i→ j
=
g
sk
j
/sk
i
where g ∈ G
1
is one of the generators of
a cyclic group of prime order G
1
. One can ob-
tain the decryption key dk
i
= (rk
i→ j
)
sk
−1
j
= g
1/sk
i
.
This decryption key can be used to generate rk
i→k
using (g
1/sk
i
)
sk
k
. Therefore, the task of direct re-
encryption key derivation can be reduced to mak-
ing the decryption key g
1/sk
i
available to the user
with public key pk
k
securely. More formally, sup-
pose pk
1
, pk
2
,... , pk
n
is a collection of public keys
and rk
1→2
,rk
2→3
,... ,rk
(n−1)→n
are the re-encryption
keys. A direct re-encryption key rk
1→n
can be de-
rived using all these re-encryption keys as well as the
secret keys sk
2
,sk
3
,... ,sk
n
. As can be seen, this ap-
proach demands active participation of each interme-
diate user which is unrealistic.
4.4.2 Top-down: Transferring Decryption Keys
The unrealistic approach described in the previous
section works bottom-up. The top-down approach
discussed here is more practical and requires partic-
ipation of only one secret key thereby making it more
suitable for access control in hierarchy. We assume
On Efficient Access Control Mechanisms in Hierarchy using Unidirectional and Transitive Proxy Re-encryption Schemes
523

existence of a light-weight encryption scheme E that
involves (at most) one modular exponentiation or one
multiplication such that E (x,y) gives the encryption
of y using x as the key. Decryption of this encryption
can be done using another procedure D(x, E (x, y))
to obtain y. Consider the same collection of pub-
lic keys pk
1
, pk
2
,... , pk
n
with the sequence of re-
encryption keys being rk
1→2
,rk
2→3
,... ,rk
(n−1)→n
.
As has been discussed in the bottom-up approach,
decryption key dk
i
can be obtained using secret key
sk
i+1
and rk
i→(i+1)
. Now if decryption key dk
i−1
is encrypted using E (dk
i
,dk
i−1
) and stored as ad-
ditional component of re-encryption key (as shown
in Table 3) rk
(i−1)→i
, then using rk
(i−1)→i
,rk
i→(i+1)
and sk
i+1
, one can obtain not only dk
i
but also dk
i−1
using D(dk
i
,E (dk
i
,dk
i−1
)). Therefore a direct re-
encryption key rk
(i−1)→(i+1)
can be derived using
dk
(i−1)
and sk
(i+1)
. Note that in this process, only
one secret key (sk
i+1
) is involved. So, participation of
only one user is required. This would facilitate deriva-
tion of dk
1
using sk
i
alone in the general case where
rk
1→2
,... ,rk
(n−1)→n
and pk
1
,... , pk
n
are given as se-
quences of re-encryption keys and public keys respec-
tively. Since this procedure requires chain of depen-
dent computations for obtaining subsequent decryp-
tion keys, these computations cannot be outsourced.
However, the direct re-encryption key obtained as a
result of this process can be given to anyone to carry
out re-encryption.
Table 3: Public, secret and re-encryption key components
and their values for approach defined in Section 4.4.2.
Component name Content
Public keys pk
i
Secret keys sk
i
,dk
i
= f
′
(sk
i
)
Re-encryption key (rk
(i−1)→i
)
f(dk
i−1
,ek
i
)
E (dk
i−1
,dk
i
)
5 CONCLUSIONS
In this paper, we have proposed an idea of using
proxy re-encryption satisfying special properties for
hierarchical key management. We observed that key
derivation cost in hierarchy can be reduced to a con-
stant (independent of depth) with all the computa-
tions to be done on re-encryption key level if a proxy
re-encryption scheme is unidirectional and transitive.
We note that there is no re-encryption scheme in lit-
erature that is both unidirectional and transitive. This
leads us to prove the concrete requirements for such a
re-encryption scheme. We claim that given the state-
of-the-art design of proxy re-encryption scheme, both
unidirectionality and transitivity cannot be achieved
simultaneously. We also suggest improvementson the
existing re-encryption schemes to achieve efficiency
comparable to the case with transitive-unidirectional
proxy re-encryption.
REFERENCES
Atallah, M. J., Blanton, M., Fazio, N., and Frikken, K. B.
(2009). Dynamic and efficient key management for
access hierarchies. ACM Transactions on Information
and System Security, 12(3):18:1–18:43.
Ateniese, G., Fu, K., Green, M., and Hohenberger, S.
(2006). Improved proxy re-encryption schemes with
applications to secure distributed storage. ACM Trans-
actions on Information and System Security, (TIS-
SEC’06), 9(1):1–30.
Blaze, M., Bleumer, G., and Strauss, M. (1998). Divert-
ible protocols and atomic proxy cryptography. In Ad-
vances in Cryptology-EUROCRYPT’98, pages 127–
144. Springer.
Canetti, R. and Hohenberger, S. (2007). Chosen-ciphertext
secure proxy re-encryption. In ACM Conference on
Computer and Communications Security, (CCS’07),
pages 185–194. ACM.
Chandran, N., Chase, M., Liu, F.-H., Nishimaki, R., and
Xagawa, K. (2014). Re-encryption, Functional Re-
encryption, and Multi-hop Re-encryption: A Frame-
work for Achieving Obfuscation-Based Security and
Instantiations from Lattices, pages 95–112. Springer,
Berlin, Heidelberg.
Dodis, Y. and Fazio, N. (2003). Public key trace and re-
voke scheme secure against adaptive chosen cipher-
text attack. In Proceedings of the 6th International
Workshop on Theory and Practice in Public Key Cryp-
tography: Public Key Cryptography, PKC ’03, pages
100–115, London, UK. Springer-Verlag.
Green, M. and Ateniese, G. (2007). Identity-based
proxy re-encryption. In 5th International Confer-
ence on Applied Cryptography and Network Security,
(ACNS’07), volume 4521 of Lecture Notes in Com-
puter Science, pages 288–306. Springer.
Libert, B. and Vergnaud, D. (2008). Unidirectional chosen-
ciphertext secure proxy re-encryption. In 11th Inter-
national Workshop on Practice and Theory in Public-
Key Cryptography, pages 360–379. Springer Berlin
Heidelberg.
Shao, J., Liu, P., Cao, Z., and Wei, G. (2011). Multi-
use unidirectional proxy re-encryption. In 2011 IEEE
International Conference on Communications (ICC),
pages 1–5.
Vimercati, S. D. C. D., Foresti, S., Jajodia, S., Paraboschi,
S., and Samarati, P. (2010). Encryption policies for
regulating access to outsourced data. ACM Transac-
tions on Database Systems, 35(2):12:1–12:46.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
524