Privacy-preserving Disease Susceptibility Test with Shamir’s Secret
Sharing
Guyu Fan
1
and Manoranjan Mohanty
2
1
New York University Abu Dhabi, Abu Dhabi, U.A.E.
2
Center for Cyber Security, New York University Abu Dhabi, Abu Dhabi, U.A.E.
Keywords:
Shamir’s Secret Sharing, Genome Based Disease Susceptibility Test, Single Nucleotide Polymorphism (SNP).
Abstract:
Recent advances in genomics have facilitated the development of personalized medicine, in which a patient’s
susceptibility to certain diseases and her compatibility with certain medications can be determined from her
genetic makeup. Although this technology has many advantages, privacy of the patient is one of the major
concerns due to the sensitivity of genomic data. In this paper, we propose a privacy-preserving scheme for
computing a patient’s susceptibility to a particular disease. Our scheme stores genomic data in hidden form and
performs the disease susceptibility test in the hidden domain. To hide the data, we use Shamir’s (l, n) secret
sharing, which can be homomorphic to a fixed number of multiplications and unlimited additions. Using
Shamir’s secret sharing, we create n shares and store the shares at n datacenters. The datacenters perform the
susceptibility test on their shares and send the result (which is also hidden) to a hospital. Finally, the hospital
obtains the secret result of the test by accessing at least k datacenters, where k = 2l −1. In comparison to other
works, our approach is more practical as it minimizes the involvement of the patient and incurs less overhead.
1 INTRODUCTION
The success of the Human Genome Project and the
rapid increase of computational power have resulted
in a variety of applications of genomic data (Naveed
et al., 2015). For example, in health care, doctors can
now compute a patient’s susceptibility to a certain dis-
ease using the patient’s genome data. Although this
genome-based disease susceptibility test (DST) (Butts
et al., 2016) is cost-effective and mostly accurate, pri-
vacy of the patient is a major concern (Naveed et al.,
2015) (Ayday et al., 2013).
A patient’s genomic data can reveal various sen-
sitive information of the patient and her blood rela-
tives. For instance, disease information derived from
genomic data can be used for discrimination, and in-
ferred physical features such as skin color may be
used to identify the individual. Moreover, the privacy
implications of genomic data is not fully known yet as
the scientific community is far from completely un-
derstanding the human genome. Therefore, genomic
data must be protected from unauthorized access us-
ing tight security measures and legislations (Naveed
et al., 2015).
Hospitals often lack the expertise to protect their
patients’ genomic data (Ayday et al., 2013). Due to
the large size (several gigabytes per person) of the
data (Naveed et al., 2015), it is usually difficult for
hospitals to securely store, process, and maintain the
genomic data of patients when they have limited re-
sources. For instance, hospitals may not have the lat-
est technologies or adequate manpower to success-
fully prevent new hacking attempts (Ayday et al.,
2013). A possible solution to this problem is to out-
source the storage and processing of genomic data
to a third-party service provider (e.g., a cloud dat-
acenter) in a privacy-preserving way (Ayday et al.,
2013). The service provider can better handle the
data by providing more efficient and more secure stor-
age and processing technologies. It is, however, im-
perative that the service provider not know the data
in plaintext. Based on third-party outsourcing, Ay-
day et al. proposed the first privacy-preserving DST
scheme that stores encrypted genomic data in a third-
party server (Ayday et al., 2013). Their scheme uses
Paillier encryption to encrypt genomic data, which
allows them to perform encrypted domain DST us-
ing the weighted-averaging method (Kathiresan et al.,
2008). However, their scheme is not practically suit-
able as it incurs high overhead and requires patients to
be well educated in the field of genomics. Although
certain follow-up studies (Danezis and De Cristofaro,
Fan, G. and Mohanty, M.
Privacy-preserving Disease Susceptibility Test with Shamir’s Secret Sharing.
DOI: 10.5220/0006467105250533
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 525-533
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
525

2014) (Djatmiko et al., 2014) (Barman et al., 2015)
have built upon Ayday et al.’s scheme, they still re-
quire further improvement (details will be discussed
in Section 2).
In this paper, we propose a privacy-preserving
DST framework based on Shamir’s secret shar-
ing (Shamir, 1979). Our scheme incurs less overhead
and minimizes the participation of a patient in the pro-
cess. Using Shamir’s (l, n) secret sharing, we create n
shares of the genomic data, and distribute the shares
to n datacenters. Any group of less than l datacenters
will learn nothing about the secret data. Our approach
allows one multiplication and unlimited additions of
the shared (i.e., encrypted) values. Unlike Ayday et
al.’s scheme, we do not store additional multiplied
values, therefore the data overhead is reduced. To fur-
ther improve efficiency, we outsource the DST com-
putations from the hospital to the datacenters, which
usually have more computational resources. Finally,
to prevent the datacenters from inferring the disease
from the DST, we camouflage the DST computation
by introducing dummy genomic data (i.e., operands)
and dummy SNP weights. In our experimental setup,
our scheme runs 10, 000 times faster than Ayday et
al.’s scheme.
The rest of this paper is organized as follows. Sec-
tion 3 provides background information on genomics
and Shamir’s secret sharing. Section 2 presents re-
lated work. In Section 4, we discuss our framework
based on secret sharing, and in Section 5, we present
analysis and experimental results. Section 6 con-
cludes our work.
2 RELATED WORK
2.1 Ayday et al.’s Scheme
The main idea behind Ayday et al.’s scheme (Fig-
ure 1) (Ayday et al., 2013) is to store the SNPs in
a third-party Storage and Processing Unit (SPU, i.e.,
a datacenter) in encrypted form, and allow a medi-
cal center (MC, i.e., a hospital) to access part of the
SNPs. Given the biological sample of a patient, a
trusted entity called Certified Institution (CI) first se-
quences the sample to obtain the patient’s SNPs in
digital form, and then encrypts the states and posi-
tions of the SNPs. The state of a SNP is encrypted us-
ing Paillier double encryption scheme (Bresson et al.,
2003), whereas the position is encrypted using sym-
metric encryption. The encrypted SNPs are stored in
the SPU. When an MC wants to perform a DST, it
sends the location of the required SNPs to the patient.
The patient checks whether the MC has permission
to access the SNPs, and if so, sends the encrypted
SNP positions (encrypted using the same symmetric
encryption scheme) to the SPU. The SPU fetches the
SNPs, re-encrypts the SNPs using the modified Pail-
lier cryptosystem, and sends the encrypted SNPs to
the MC. The MC performs the weighted-averaging-
based DST (i.e., computes S
X
P
) on encrypted SNPs,
and sends the encrypted result to the SPU. The SPU
partially decrypts the result and sends it to the MC,
where the result is fully decrypted.
However, Ayday et al.’s scheme has several prac-
tical issues. Firstly, the use of the modified Paillier
cryptosystem results in high storage and computation
overhead as a 2-bit SNP state (i.e., 0, 1, or 2) will
be represented as an 8192-bit ciphertext-pair (because
2048-bit keys are recommended for the Paillier cryp-
tosystem). Secondly, since the Paillier cryptosystem
is not homomorphic to multiplications, the CI must
pre-compute the squared values of SNP states and
store the squared values at the SPU. Finally, patients
are actively involved in this scheme, which is gener-
ally undesirable. Not only do they have to perform
symmetrical encryptions with their smartcard, they
also need to be knowledgeable about genomics to de-
cide if the MC’s SNP requests are legitimate. The
participation of the patient is both user-unfriendly and
insecure as a wrong decision by the patient can leak
sensitive information (and the patient will be respon-
sible).
2.2 Other Schemes
After the seminal work of Ayday et al., several studies
have been carried out to improve and extend Ayday et
al.’s scheme.
In (Danezis and De Cristofaro, 2014), Danezis et
al. proposed a SNP-encoding scheme that eliminates
the need for ciphertext multiplications. They used the
faster El-Gamal cryptosystem instead of the Paillier
cryptosystem. Although the overhead is decreased,
the patient is still required to participate in the test.
The patient also needs to store the encryption keys
in a smart card, which when lost could cause a se-
curity breach. Furthermore, Danezis et al.’s scheme
discloses the number of SNPs to a third-party server.
Compared to their scheme, our keyless scheme is
more secure as it completely eliminates the need for
a smartcard, and hides the number of SNPs from the
server using data obfuscation.
Djatmiko et al. (Djatmiko et al., 2014) proposed
a Paillier-based scheme that can securely store and
compute linear combinations of genomic data on
a user’s mobile device. Similar to Ayday et al.’s
scheme, their scheme also incurs high overhead.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
526

Figure 1: Ayday et al.’s privacy-preserving DST protocol(Ayday et al., 2013).
Moreover, storing and computing genomic data at the
user-end can be less secure than in a datacenter.
In addition to private genome-based DST, signifi-
cant work has also been done in related areas. For ex-
ample, Huang et al. (Huang et al., 2015) presented a
honey encryption-based genomic data storage frame-
work that can protect data from brute-force attacks.
Jha et al., (Jha et al., 2008) presented a privacy-
preserving way to perform dynamic-programming-
based sequence alignment. Karvelas et al. (Karve-
las et al., 2014) proposed an Oblivious RAM-based
scheme that can securely store and compute genomic
data in a third-party server.
3 PRELIMINARIES
3.1 Genome-based DST
Genome-based DST uses the SNPs (Single
Nucleotide Polymorphism) of an individual’s
genome (Johnson and O’Donnell, 2009) (Ayday
et al., 2013). A SNP is a position in the genome that
holds a nucleotide that varies from one person to
another. There are approximately 4 million SNPs in
an individual’s genome, and there are approximately
50 million total SNPs across the human population.
An allele (i.e., nucleotide) in a SNP can either occur
frequently or infrequently in the human SNP pool.
The frequent allele is referred to as the major allele,
and the infrequent minor. Since a SNP contains one
allele from each parent, it has three possible states:
state 1 (exactly one minor allele), state 2 (two minor
alleles), and state 0 (no minor alleles). To carry out a
DST, it is sufficient to know the states and positions
of the relevant SNPs (Ayday et al., 2013).
One of the advanced methods of computing
disease susceptibilities is the weighted-averaging
method (Kathiresan et al., 2008) (Ayday et al., 2013).
This method is discussed in Ayday et al. and will be
considered in this paper, too. Below is a description
of this method.
Let SNP
P
i
represent the state of SNP
i
for patient
P at position i, where SNP
P
i
∈ {0, 1, 2}. Suppose
that the susceptibility of disease X is determined by
a set of SNPs whose positions are given in the set
L
X
. Each such SNP has a contribution to disease
X based on its state. More specifically, these con-
tributions are state-sensitive probabilities as follows:
p
i
0
(X) = Pr(X|SNP
P
i
= 0), p
i
1
(X) = Pr(X|SNP
P
i
= 1),
and p
i
2
(X) = Pr(X|SNP
P
i
= 2). In addition, each
SNP also has a general, state-agnostic contribution
to disease X, and the general contribution of SNP
i
is denoted C
X
i
. Together, the C
X
i
’s and p
i
j
(X)’s are
called the SNP weights for disease X. Given C
X
i
’s and
p
i
j
(X)’s for each SNP
i
, patient P’s susceptibility to
disease X can be computed as:
S
X
P
=
1
∑
i∈L
X
C
X
i
×
∑
i∈L
X
C
X
i

p
i
0
(X)
(0 − 1)(0 −2)
(SNP
i
− 1)
(SNP
i
− 2) +
p
i
1
(X)
(1 − 0)(1 −2)
(SNP
i
− 0)(SNP
i
− 2)
+
p
i
2
(X)
(2 − 0)(2 −1)
(SNP
i
− 0)(SNP
i
− 1)

. (1)
Note that in S
X
P
, one SNP state is multiplied by
another SNP state exactly once.
3.2 Shamir’s Secret Sharing
Shamir’s (l, n) secret sharing (Shamir, 1979) is a well
established cryptosystem that hides a secret S by cre-
Privacy-preserving Disease Susceptibility Test with Shamir’s Secret Sharing
527

ating n shares of the secret such that less than l shares
will not reveal any information about S. The shares
are distributed among n participants (e.g., datacen-
ters), and it is assumed that no group of l or more
participants will collude.
To create shares from S, we first pick a prime num-
ber p such that p > S. Then we define a (l −1)-degree
polynomial
F(x) = (S + α
x
) mod p, (2)
where α
x
=
∑
l−1
i=1
a
i
x
i
and a
i
< p is a random number
in GF(p). Finally, using this polynomial, the q
th
share
of S is generated by setting x = q and sent to the q
th
participant.
To restore the secret S from the shares, at
least l shares {z
0
, z
1
, . . . z
l−1
} such that z
i
= F(x
i
)
are required. Using these shares and their corre-
sponding share numbers {x
0
, x
1
, . . . x
l−1
}, the polyno-
mial F(x) is reconstructed using Lagrange interpo-
lation as L(x) =
∑
l−1
i=0
z
i
m
i
(x) mod p, where m
i
(x) =
∏
m−1
j=0, j6=i
x−x
j
x
i
−x
j
is the Lagrange basis function. S is
found by setting x = 0 in L(x) (which is equivalent
to F(x)).
Shamir’s secret sharing is homomorphic to addi-
tions and scalar multiplication. If the participants are
holding shares of a set of secrets S = {S
1
, S
2
, ..., S
j
},
then without communicating amongst themselves,
they can compute the shares of the secret
∑
j
i=1
I
i
S
i
,
where I
i
is an integer. Using this property, a number
of privacy-preserving medical imaging schemes have
been proposed (Mohanty et al., 2012) (Mohanty et al.,
2013b) (Mohanty et al., 2013a).
However, we would like to note that with slight
modifications, Shamir’s secret sharing can also be
homomorphic to a fixed number of multiplica-
tions (Gennaro et al., 1998). If the participants are
holding shares of a set of secrets S = {S
1
, S
2
, ..., S
j
},
then without communicating amongst themselves,
they can compute the shares of the secret
∏
j
i=1
S
i
,
where j is a pre-determined number. If the operand
shares (i.e., shares of S
i
’s) are obtained from a (l −
1)-degree polynomial, then the resultant share (i.e.,
shares of
∏
j
i=1
S
i
) will be a j(l − 1)-degree polyno-
mial. Therefore, to obtain the secret
∏
j
i=1
S
i
, at least
j(l − 1) + 1 distinct shares will be required. In our
case, one share (i.e., SNP state) will be multiplied by
another share only once. Thus, we need at least 2l − 1
shares to obtain the secret.
4 OUR APPROACH
In this section, we present our privacy-preserving
DST scheme. We employ Shamir’s secret sharing
to hide a patient’s SNPs and store the hidden SNPs
in a number of datacenters. Upon request from the
hospital, the datacenters perform an obfuscated ver-
sion of the weighted-averaging-based DST computa-
tion in the encrypted domain without any involvement
of the patient. With the encrypted DST results col-
lected from these datacenters, the hospital obtains the
final result in plaintext. We discuss the architecture
and workflow of our scheme below.
4.1 Architecture
As shown in Figure 2, our framework contains 4 par-
ties (a) a patient, (b) a trusted entity (TE), (c) n data-
centers, and (d) a hospital. Our threat model assumes
that (i) the patient is trusted, i.e., the patient honestly
performs all required operations and does not leak her
genomic information; (ii) the TE is trusted; (iii) the
datacenters are honest but curious, i.e., they perform
their operations honestly but can be curious to know
the secret information from the DST (e.g., by analyz-
ing the data they operate on); and (iv) the hospital
is usually honest but curious, although it can also be
a malicious entity that deliberately deviates from the
protocol in order to learn unauthorized information.
Finally, we assume that communications between dif-
ferent parties (e.g., between the patient and the TE)
are secured, and that the datacenters do not collude.
Our framework has the following security and per-
formance requirements. First, the datacenters must
not infer any information from the stored SNPs, so
both the states and positions of SNPs must be stored
in encrypted form. To meet this requirement, we use
Shamir’s (l, n) secret sharing scheme to hide the SNP
states and a symmetric encryption scheme to hide the
SNP positions. We also assume that an adversary can-
not access l ≤ n or more datacenters at any time. Our
second security requirement is that the hospital must
not know any information other than the result of the
DST. To meet this requirement, we perform the DST
operations at the datacenters and send the encrypted
result to the hospital. Our final security requirement
is that the datacenters must not infer any information
about the nature of the DST from the data they re-
ceive from the hospital. We use our own obfuscation
techniques to achieve this goal. As for performance
concerns, we need to ensure that both the storage and
computational overheads of our framework are low.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
528

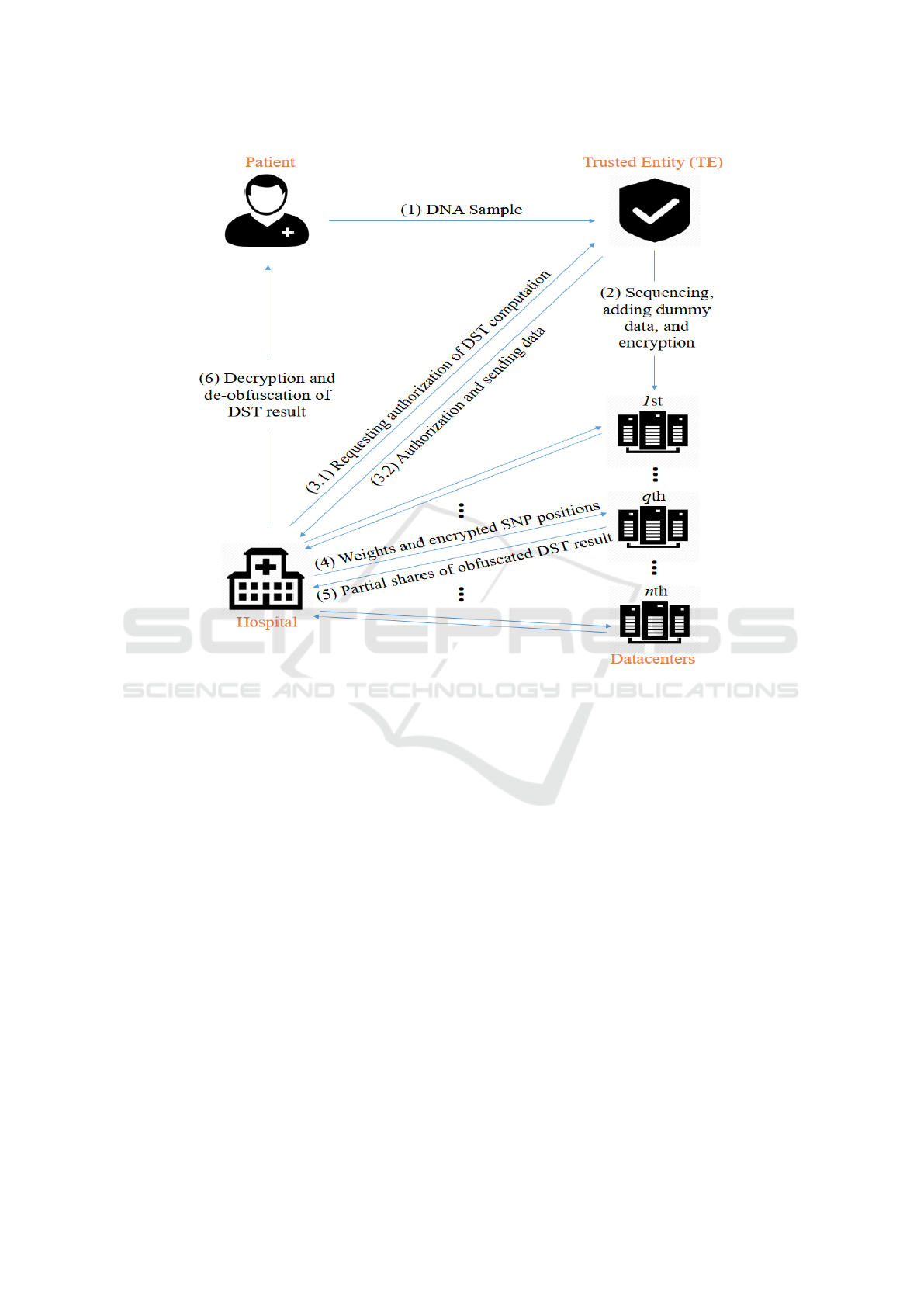
Figure 2: The architecture and workflow of our scheme.
4.2 Workflow
The working of our scheme is summarized in Figure
2 and explained below step-by-step.
Step 1 [Preliminary Step]. Our scheme begins with
the patient sending her biological DNA sample to the
TE for sequencing and future processing. The patient
is involved in this step only.
Step 2 [Preprocessing and Distribution]. In this
step, the TE first sequences the DNA sample, and then
obtains the SNP states and positions in digital format.
Next, the TE creates a number of dummy SNPs and
mix them with the actual SNPs (SNPs obtained from
sequencing). The introduced dummy SNPs will be
used by the hospital to obfuscate the DST operations.
These SNPs are finally encrypted by the TE and sent
to the datacenters. Note that this step and the previous
step (Step 1) are one-time operations. Also note that
in the rest of the paper, the term SNPs refers to the
mix of actual and dummy SNPs.
The TE encrypts a SNP by encrypting its state
and position. The position is encrypted with the same
symmetric encryption method as the one used by Ay-
day et al. (Ayday et al., 2013). We will therefore omit
a detailed discussion on the encryption of positions
in this paper, but note that in our scheme, the sym-
metric key used for position encryption is established
between the TE and the hospital.
We use Shamir’s secret sharing to encrypt SNP
states. From Section 3, we know that the state of
a SNP (which is the secret) is an integer from the
set {0, 1, 2}. To encrypt a state, the TE chooses a
prime number p, and using Equation 2, obtains the
q
th
(where 1 ≤ q ≤ n) share as
F(SNP, q) = (SNP + α
q
) mod p.
The TE then sends F(SNP, q) along with the en-
crypted SNP position to the q
th
datacenter.
Step 3 [DST Authorization]. In this step, the hos-
pital seeks DST authorization from the TE for a par-
ticular disease. To obtain authorization, the hospital
requests from the TE the list of actual SNPs that is
required to perform the DST. The TE then decides
whether the hospital’s request is legitimate, and if so,
Privacy-preserving Disease Susceptibility Test with Shamir’s Secret Sharing
529

the TE sends the encrypted positions of the actual
SNPs to the hospital. The TE also sends the states and
positions of a number of dummy SNPs to the hospital.
The exact number and type of dummy SNPs will be
addressed in detail in Section 5.
Step 4 [Obfuscation and Computation Request].
In this step, the hospital obfuscates the DST opera-
tions to prevent datacenters from learning any infor-
mation about the nature of the DST. Since a datacen-
ter might be able to infer the type of the disease be-
ing tested for if it knows the number of actual SNPs
used in the DST or the weights associated with these
SNPs, the hospital cannot simply send the positions
and plaintext weights of actual SNPs to the datacen-
ters. Instead, the hospital produces a mixture of actual
SNPs and dummy SNPs (obtained from TE in Step 3)
and generates dummy weights for dummy SNPs. This
mixture of actual and dummy SNPs, along with the
actual and dummy weights, are then sent to the dat-
acenters. For additional security, the hospital should
also split the DST computation into multiple parts by
simply dividing the SNP mixture into multiple parts.
Each part of the DST computation can then be carried
out independently with the hospital sending each cor-
responding part of the SNP mixture to the datacenters.
In the end, the hospital will be able to aggregate the
partial results and produce the desired disease suscep-
tibility.
Step 5 [Encrypted Domain DST]. In this step, the
datacenters first fetch the required SNP states (in the
form of encrypted shares) from their database using
the encrypted SNP positions they have received from
the hospital. Using these shares of SNP states, i.e.,
F(SNP
i
, q)’s, and the plaintext weights provided by
the hospital, i.e., C
X
i
’s and p
i
j
(X)’s, the datacenters
can perform the obfuscated DST computation. We
use L
X
0
to denote the set of dummy SNPs involved
in the obfuscated DST computation, and L
X
to denote
the union of dummy and actual SNPs. In the end, each
datacenter will obtain a share of the obfuscated DST
result. We denote the obfuscated result S
X
P
0
and the
qth share of the result F(S
X
P
0
, q).
One technical difficulty arises from the fact that
SNP weights are floating point numbers, which are
incompatible with the modular prime operations per-
formed by Shamir’s secret sharing. To overcome this
issue, the datacenters must convert the floating point
numbers to integers. Given a precision d, the data-
centers will first round a float to d decimal places and
then multiplying the roundoff value by 2 × 10
d
. The
multiplication by 2 is necessary here because the DST
formula contains divisions by 2. For simplicity, we
will also denote the integral SNP weights using C
X
i
and p
i
j
(X) in this paper.
After converting SNP weights to integers, the dat-
acenters will be ready to compute their respective
shares of the obfuscated disease susceptibility and
send the shares back to the hospital. The computa-
tion is done by using Equation 1 as:
F(S
X
P
0
, q) =
1
∑
i∈L
C
X
i
×
∑
i∈L
C
X
i

c
0
· F(SNP
i
, q)
2
+ c
1
· F(SNP
i
, q) + p
i
0
(X)

,
where
c
0
=
1
2
[p
i
0
(X) − 2p
i
1
(X) + p
i
2
(X)]
and
c
1
=
1
2
[−3p
i
0
(X) + 4p
i
1
(X) − p
i
2
(X)].
By substituting F(SNP
i
, q) = (SNP
i
+ α
q
) mod p
in the above equation, we get
F(S
X
P
0
, q) = (S
X
P
0
+ β
q
) mod p,
where
β
q
=
1
∑
i∈L
C
X
i
×
∑
i∈L
C
X
i
h
c
0
· α
2
q
+ (2c
0
× SNP
i
+ c
1
) ·α
q
i
is a constant.
Note that since α
q
is a value of an (l − 1)-degree
polynomial, β
q
is a value of a (2l − 2)-degree poly-
nomial. Thus, F(S
X
P
0
, q) is a share created from a
(2l − 1)-degree secret sharing polynomial:
F(x) = (S
X
P
0
+ β
x
) mod p.
Step 6 [Obtaining the DST Result]. In the final
step of our scheme, the hospital obtains the final DST
result (S
X
P
) from the shares it received from the data-
centers in Step 5. Since the hospital divided the DST
computation into a number of smaller parts in Step 4,
the hospital would have also received in Step 5 mul-
tiple partial shares from each datacenter correspond-
ing to the parts. Therefore, to obtain the final DST
result, the hospital first needs to reconstruct a com-
plete share from the partial shares received from each
datacenter. The hospital then recovers the obfuscated
DST result in plaintext from the complete shares. Fi-
nally, the hospital de-obfuscate the obfuscated result
by removing the noise introduced by dummy SNP and
their weights, obtaining the final DST result.
Suppose the hospital split the DST computation
into t parts. The SNPs included in the mth part
are denoted L
m
(L
m
⊂ L, and ∪
t
m=1
L
m
= L), and let
SECRYPT 2017 - 14th International Conference on Security and Cryptography
530

F
m
(S
X
P
0
, q) be the partial share that the qth datacenter
produced in the mth part of the DST computation. Us-
ing all t F
m
(S
X
P
0
, q)’s, the hospital can reconstruct the
complete share F(S
X
P
0
, q) as follows:
F(S
X
P
0
, q) =
∏
t
m=1
h
F
m
(S
X
P
0
, q) ·
∑
i∈L
m
C
X
i
i
∑
t
m=1
∑
i∈L
m
C
X
i
.
After reconstructing complete shares from at least
(2l − 1) datacenters, the hospital uses Lagrange inter-
polation to recover the obfuscated DST result, S
X
P
0
, in
plaintext. Finally, the hospital de-obfuscates S
X
P
0
and
obtains the final DST result S
X
P
using:
S
X
P
= S
X
P
0
·
∑
i∈L
X
C
X
i
∑
i∈L
C
X
i
−
∑
i∈L
0
X
, j=SNP
i
C
X
i
· P
i
j
(X)
∑
i∈L
X
C
X
i
.
5 ANALYSIS AND EXPERIMENT
In this section, we present the security assurance and
performance overhead of our system. We also com-
pare the our scheme with Ayday et al.’s scheme.
We implemented a prototype of our scheme us-
ing Java and simulated the scheme on a PC with Intel
i5 − 5300U and 12 GB of RAM running on Windows
10. Our prototype uses Shamir’s (3, 6) secret sharing
with 6 datacenters, and shares of at least 5 datacenters
are required to recover the secret DST result. To con-
vert floating point SNP states to integers, our proto-
type rounds them to 4 decimal places. Using the same
technology, we also implemented and simulated Ay-
day et al.’s scheme with a 2048-bit key Paillier cryp-
tosystem
1
.
In our experiment, we used real patient SNP data
obtained from (Personal-Genome-Project, 2016) and
disease markers from (Eupedia, 2016). We used (db-
SNP, 2016) to determine SNP states of the patient, and
generated SNP weights by choosing a random floating
point number in [0, 1). We validated the correctness of
our scheme by comparing the result of our encrypted-
domain DST with the result of the plaintext DST.
5.1 Security Analysis
We believe that the use of Shamir’s (l, n) secret shar-
ing makes our scheme more secure than Ayday et al.’s
scheme. Our scheme does not require an encryption
key and enables the hospital to verify the integrity of
test results when the number of shares required to ob-
tain the secret DST result (i.e., k = 2l − 1) is less than
1
The code of the proposed method can be found at
https://github.com/guyu96/encrypted-domain-DST
the number of deployed datacenters (i.e., n ). In such
cases, the secret result can be obtained by the hospi-
tal in

n
k

ways, and any inconsistency would indicate
that at least one datacenter has been compromised.
Moreover, as shown by Barman et al., malicious
hospitals are able to infer SNP states by carefully
crafting the SNP weights that are to be used in DST
computations (Barman et al., 2015). Unlike Ayday
et al.’s scheme, our scheme is secure against such at-
tacks because plaintext SNP weights are exposed to
the datacenters, and the datacenters can simply termi-
nate the DST computation when they see suspicious
weights (e.g., 0’s and consecutive powers). However,
it is also important to note that the number and val-
ues of plaintext SNP weights are sensitive informa-
tion that could be used to infer the type of the disease
being tested for. Our scheme addresses this vulner-
ability through the use of dummy SNP and dummy
weights, and this obfuscation technique merits a more
detailed discussion.
Dummy SNPs and dummy weights have two func-
tions. Their first function is to hide the number of ac-
tual SNPs involved in a particular DST. Given that no
disease listed on (Eupedia, 2016) is linked to more
than 100 SNPs, only a few dozen dummy SNPs are
required for this purpose in each DST. Even if we
take into account the need to choose a different set
of dummy SNPs for different DSTs, the total number
of dummy SNPs that need be stored at the datacenters
is trivial compared to 4 million, the average number
of SNPs in an individual’s genome.
The second function of dummy SNPs and weights
is to introduce noise to the values of actual SNP
weights. Note that in order to effectively accomplish
this goal, the hospital cannot simply randomly gener-
ate dummy SNP weights for every DST computation.
Consider the following scenario. The hospital tests
several patients for the same disease, and for each pa-
tient, the hospital sends, along with actual encrypted
SNP positions and their plaintext weights, a num-
ber of dummy encrypted SNP positions and randomly
generated dummy weights to the datacenters. Since
the dummy weights are randomly generated, they will
likely be different for different patients. However, the
actual SNP weights will be exactly the same because
the patients are all being tested for the same disease.
Exploiting this discrepancy in patterns, the datacen-
ters will likely be able to separate the actual SNPs
from the dummy SNPs by identifying a set of SNP
weights that are present in the DST for every patient.
To overcome this threat, our scheme requires the
hospital to associate a set of fixed dummy weights
with each disease in order to ensure that no only ac-
tual SNP weights, but also dummy SNP weights, are
Privacy-preserving Disease Susceptibility Test with Shamir’s Secret Sharing
531

consistent across different patients. For added secu-
rity, our scheme also requires that the hospital divide
a single DST computation into multiple parts, as ex-
plained in Step 4 of our workflow, making it impos-
sible for datacenters to determine the exact mixture
of actual and dummy SNPs involved in any particular
DST. Again, note that a few dozen dummy SNPs are
sufficient for camouflaging the values of actual SNP
weights as long as dummy weights are carefully and
consistently chosen.
5.2 Data Overhead
We analyze the amount of storage required by both
our scheme and Ayday et al.’s scheme in this section.
Since the number of dummy SNPs is smaller than
the number of actual SNPs by several orders of mag-
nitude, for our scheme, we only consider the data
overhead incurred by the use of Shamir’s secret shar-
ing. For each 2-bit SNP state, we create n shares, each
of which is a 64-bit integer. Each 2-bit SNP state
therefore requires 64n bits of storage. In our imple-
mentation, n = 6 and as a result 192 times as much
storage is required compared to the unencrypted-
domain DST. However, our scheme significantly im-
proves upon Ayday et al.’s scheme and requires ap-
proximately 40 times less space. To store the states
of 4 million SNPs (average number of SNPs in an
individual), our scheme requires 183 MB of storage
whereas Ayday et al.’s scheme requires 7.63 GB of
storage.
Communications between different parties during
the DST computation are also much more efficient
in our scheme. Suppose that z
1
actual SNPs and z
2
dummy SNPs are involved in the computation, and
the hospital splits the computation into t parts. As
shown in the security analysis, setting z
2
= z
1
is suf-
ficiently secure and we denote this value z. Since
our implementation rounds SNP weights to 4 deci-
mal places, the integral weights can be represented by
16-bit integers.
In our scheme, three transmissions are involved in
the DST computation: (1) the TE sends dummy SNP
states and encrypted SNP positions (both actual and
dummy) to the hospital (which requires 258z bits); (2)
the hospital sends SNP weights and encrypted SNP
positions to n datacenters in t parts (288nz bits); and
(3) each of the k datacenters sends t partial shares
to the hospital (64tk bits). Therefore, in our scheme
(258 + 288n)z +64tk bits are transmitted in total.
On the other hand, Ayday et al.’s scheme includes
four transmissions: (1) the patient sends encrypted
SNP positions to the datacenter (128z bits); (2) the
datacenter sends encrypted SNP states to the hospi-
tal (8192z bits); (3) the hospital sends the encrypted
DST result to the datacenter (8192 bits); and (4) the
datacenter sends the partially decrypted result to the
hospital (8192 bits). In total, 8320z + 16384 bits are
transmitted in Ayday et al.’s scheme.
In our implementation, we have n = 6, k = 5, and
t = 8. Thus the total amount of data transmitted in
our scheme is 1986z + 2560 bits, which is more than
4 times less than the amount of transmission required
by Ayday et al.’s scheme.
5.3 Computational Cost
We compare the computational costs of our scheme
with that of Ayday et al.’s scheme in this section.
Since the encryption and distribution of SNP data
can be preprocessed, we are only concerned with the
encrypted-domain DST computation.
Since we use Shamir’s secret sharing, we need
only additions, multiplications and divisions of 64-
bit integers. Ayday et al.’s scheme, however, requires
more expensive operations on larger numbers (i.e.,
multiplications and modular exponentiations of 4096-
bit integers). Therefore, our scheme incurs a signifi-
cantly smaller computational cost than Ayday et al.’s
scheme. We carried out DST computations on 21
SNPs related to Type-2 Diabetes, and on average, our
scheme runs 10, 000 times faster than Ayday et al.’s
scheme, taking less than 1 millisecond compared to
Ayday et al.’s 8 seconds.
6 CONCLUSION
Human genome-based disease susceptibility test
(DST) has serious privacy concerns, and previous at-
tempts at making DST secure all have notable draw-
backs, including high storage overhead, slow com-
putation speed, reliance on patient involvement and
even vulnerabilities to certain kinds of attacks. To ad-
dress these issues, we propose in this paper a more
practical privacy-preserving DST scheme that lever-
ages the additive and pseudo-multiplicative homo-
morphism of Shamir’s secret sharing. As demon-
strated by both theoretical analysis and empirical ev-
idence, our scheme is more secure and has signifi-
cantly improved space and time efficiencies in com-
parison to the seminal work by Ayday et al..
REFERENCES
Ayday, E., Raisaro, J. L., Hubaux, J.-P., and Rougemont, J.
(2013). Protecting and evaluating genomic privacy in
SECRYPT 2017 - 14th International Conference on Security and Cryptography
532

medical tests and personalized medicine. In WPES,
pages 95–106.
Barman, L., Elgraini, M. T., Raisaro, J. L., Hubaux, J. P.,
and Ayday, E. (2015). Privacy threats and practical
solutions for genetic risk tests. In IEEE SPW, pages
27–31.
Bresson, E., Catalano, D., and Pointcheval, D. (2003). A
simple public-key cryptosystem with a double trap-
door decryption mechanism and its applications. In
ASIACRYPT, volume 2894, pages 37–54.
Butts, C., KamelReid, S., Batist, G., and et al (2016). Ben-
efits, issues, and recommendations for personalized
medicine in oncology in canada. Current Oncology,
20(5):e475–e483.
Danezis, G. and De Cristofaro, E. (2014). Fast and private
genomic testing for disease susceptibility. In WPES,
pages 31–34.
dbSNP (2016). Home page. http://www.ncbi.nlm.nih.gov/
projects/SNP/.
Djatmiko, M., Friedman, A., Boreli, R., Lawrence, F.,
Thorne, B., and Hardy, S. (2014). Secure evaluation
protocol for personalized medicine. In WPES, pages
159–162.
Eupedia (2016). List of alleles (snp’s) linked to physical and
physcological traits, medical conditions and diseases.
http://www.eupedia.com/genetics/medical dna test.s
html.
Gennaro, R., Rabin, M. O., and Rabin, T. (1998). Simplified
VSS and fast-track multiparty computations with ap-
plications to threshold cryptography. In ACM PODC,
pages 101–111, Puerto Vallarta, Mexico.
Huang, Z., Ayday, E., Fellay, J., Hubaux, J. P., and Juels, A.
(2015). Genoguard: Protecting genomic data against
brute-force attacks. In IEEE S&P, pages 447–462.
Jha, S., Kruger, L., and Shmatikov, V. (2008). Towards
practical privacy for genomic computation. In IEEE
S&P, pages 216–230.
Johnson, A. D. and O’Donnell, C. J. (2009). An open access
database of genome-wide association results. BMC
Medical Genetics, 10(1):1–17.
Karvelas, N., Peter, A., Katzenbeisser, S., Tews, E., and
Hamacher, K. (2014). Privacy-preserving whole
genome sequence processing through proxy-aided
oram. In WPES, pages 1–10.
Kathiresan, S., Melander, O., Anevski, D., and et al. (2008).
Polymorphisms associated with cholesterol and risk of
cardiovascular events. NEJM, 358:1240–1249.
Mohanty, M., Atrey, P. K., and Ooi, W. T. (2012). Secure
cloud-based medical data visualization. In ACMMM,
pages 1105–1108, Nara, Japan.
Mohanty, M., Ooi, W. T., and Atrey, P. K. (2013a). Scale
me, crop me, know me not: supporting scaling and
cropping in secret image sharing. In IEEE ICME, San
Jose, USA.
Mohanty, M., Ooi, W. T., and Atrey, P. K. (2013b). Secure
cloud-based volume ray-casting. In IEEE CloudCom,
Bristol, UK.
Naveed, M., Ayday, E., Clayton, E. W., and et al. (2015).
Privacy in the genomic era. ACM Computing Surveys,
48(1):6:1–6:44.
Personal-Genome-Project (2016). Public genetic data.
https://my.pgp-hms.org/public genetic data.
Shamir, A. (1979). How to share a secret. Communications
of the ACM, 22(11):612–613.
Privacy-preserving Disease Susceptibility Test with Shamir’s Secret Sharing
533