Modular Modelling of an Embedded Mobile CPU-GPU Chip for Feature

Estimation

Oussama Djedidi, Mohand Arab Djeziri, Nacer K. M’Sirdi and Aziz Naamene

Laboratoire des Sciences de l’Information et des Syst`emes (LSIS), Aix-Marseille University, Marseille, France

Keywords:

Embedded Chips Central Processing Units, Graphics Processing Units, Modelling Simulation.

Abstract:

This paper deals with the modelling of a CPU-GPU chip embedded in an Android phone. The model is used for

the estimation of variables that characterise the operating state of System on Chip (SoC). The proposed model

is built to demonstrate the causal relationships between the variables, through its interconnected structure of

subsystems. This structure allows the extension of other components or the easy exchange of subsystems in

the case of a change in components or operating mode. The model developed here requires no additional

instrumentation—other than the one present on the phone—which facilitates its implementation. It is used for

the estimation of the state of the system and can also be used for monitoring and behaviour prediction. The

model is validated and the results are promising for further implementation.

1 INTRODUCTION

Modelling of Central Processing Units (CPU) and

Graphics Processing Units (GPU) chips is done for a

multitude of purposes. The ﬁrst and foremost is to en-

sure performance reliability which can be done either

by selecting the algorithms to be implemented and

predicting their performance (M’Sirdi et al., 2016;

Williams et al., 2009; Meng and Skadron, 2011), or

running background programs in parallel that are able

to predict the performance output of some compo-

nents (Ardalani et al., 2015), or even by thoroughly

studying the component itself (Kim et al., 2012a).

However, in this work, we are more interested in the

monitoring of the operating state of the chip. Hence,

we focus our modelling on the physical variables i.e.

frequency, voltage, power consumption, and temper-

atures in the SoC.

Reducing power consumption and improving bat-

tery life in mobile phones is a very active research

area. Thus, several models estimating the power con-

sumption of embedded CPU-GPU chips were devel-

oped. For instance, Zhang et al. propose a model

called ”PowerBooter” to the estimate power con-

sumption of a smartphone through its battery sen-

sors (Zhang et al., 2010). Another study used sys-

tem calls to estimate the power consumptions (Pathak

et al., 2011), while others used polynomial and re-

gression models in a series of works to estimate the

power consumption of smartphone components in-

cluding the CPU and the GPU (Minyong Kim et al.,

2012; Kim et al., 2012b; Kim and Chung, 2013; Kim

et al., 2015). These studies offer simple modelling

techniques and also show a clear dependence between

frequency and power consumption.

Furthermore, several other notable studies focused

on the power consumption of just the GPU. For in-

stance, Leng et al. estimate the power consumption,

in a discrete GPU, as a sum of three components,

the dynamic power (power consumed by the GPU

while running computations), the leakage power (es-

sentially linked to transistor leakage currents in the

architecture of the chip) and idle power (assumed con-

stant) (Leng et al., 2013). Additionally, in their work,

Adhinarayanan et al. present a GPU power estima-

tor based on multiple regression techniques, that uses

performance counters and temperature to deliver ac-

curate power estimation at runtime (Adhinarayanan

et al., 2016).

As Temperature is an important variable in the

functioning and life cycle of CPU and GPU, several

models were developed in the literature to study its

proﬁle and behaviour, such as the model developed by

Hong et al., which is a switched system with two ﬁrst

order models, one for the rise in temperature and the

second for cooling. The time constants of these mod-

els were identiﬁed experimentally, and static gains are

presented as a function of the maximum temperature

of the system, power consumption, and memory in-

tensity (Hong and Kim, 2010).

338

Djedidi, O., Djeziri, M., M’Sirdi, N. and Naamane, A.

Modular Modelling of an Embedded Mobile CPU-GPU Chip for Feature Estimation.

DOI: 10.5220/0006470803380345

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 338-345

ISBN: 978-989-758-263-9

Amongst the works mentioned above, there are

ﬁne grained models of the CPU-GPU chips, like the

model proposed by Kim et al. which models perfor-

mance as a function of of memory warps and models

temperature as a function of memory intensity (Kim

et al., 2012a). Nonetheless, such models use variables

which are neither measurable nor accessible to read,

such as the memory intensity for instance or are spe-

ciﬁc to certain GPU brands like the warps.

Moreover, because of the complexity of the sys-

tem and physical phenomena, inputs of the models

constructed by machine learning are not the subject

of a formal proof of the interaction between the inputs

and estimated outputs. The choice of model inputs is

often the result of observations and experimental tests

in various operating conditions. These models are of-

ten built to give developers feedback on on perfor-

mance, and power consumption, which will be used

for program optimisation. The temperature estima-

tion is, generally, used to set temperature thresholds

for thermal throttling to keep the component out of

harm’s way.

The model proposed in this paper is built in a

modular structure, and is composed of a set of inter-

connected subsystems, where the control components

(subsystems for frequency and voltage) are clearly

distinguished from the operating ones (power and

temperature), allowing thus the model to adapt to

changes in the system operating modes. The sub-

systems are inspired by those presented in the stud-

ies above and the algorithms given by manufacturers.

The developed model is then used to estimate a set

of variables characterising the operating state of the

CPU-GPU system. Our main goal behind the devel-

opment of this model is to use its generated estimation

to monitor the state of the chip.

This paper is organised as follows. The targeted

system is described is Section 2. In Section 3, we de-

scribe the data aquisition, then the modelling method

and the models of each subsystem are detailed in Sec-

tion 4. In Section 5, the model is validated by compar-

ing the real and estimated outputs, then, the results are

discussed. Finally, a conclusion is given in Section 6.

2 TARGETED SYSTEM

DESCRIPTION

The electronic devices market proposes differ-

ent CPU and GPU architectures. Each fam-

ily of architecture comes with its own advantages

and—naturally—complexities. One of the main goals

of this work is to construct a general dynamic model

for embedded CPU-GPU chips. Thus, for testing and

undertaking experimental validation, the choice of a

System on Chip (SoC) to be studied is ﬁrstly based

on the software it runs.

For this study, we settled on an Android

phone.

Android

phones are very popular, and with its pro-

gramming framework, aoolications are effortlessly

transferable to other devices. Moreover, Android is

built on top of the popular open source operating sys-

tem (OS) Linux. The availability of the code for this

OS makes some of the needed parameters accessible

for reading. Furthermore, the system’s terminal, via

Android Debugging Bridge (ADB), gives access to

all system ﬁles, some of which are used for variables

reading.

The smartphone we used in this study runs on

Android

Marshmallow 6.0, and is equipped with a

SoC harbouring a quad-core processor with variable

frequencies—through frequency and voltage scal-

ing—ranging between 300MHz–2.45 GHz. It also

sports an OpenGL

ES 3.0 capable GPU with fre-

quencies ranging between 200MHz–578 MHz. The

SoC also contains the systems 2GB RAM.

3 VARIABLES AND DATA

ACQUISITION

To analyse and model the dynamics of the CPU-GPU

chip, one must initially recover the relevant readings

characterising the operating state of the system. For

our modelling purposes, the needed readings are the

loads of both the CPU and the GPU, the working fre-

quencies, temperatures of the cores and other com-

ponents, the voltage of each core and the power de-

livered by the battery. All of these variables–except

for the temperature–have very fast variations. There-

fore, the quality of the results depends directly on the

chosen sampling period. Hence, we choose the min-

imum period necessary to follow the changes of the

fast changing variable: the frequency. Frequency is

evaluated by by frequency Governor (see paragraph

4.1). Hence, the minimum period for this program

to reevaluate the load and change of the frequency

accordingly was set as sampling period (in this case

study, T

= 20ms).

Since we do not wish to hinder the normal be-

haviour of the system while reading the variables, we

have written a lightweight application for data acqui-

sition. However,during periods of high loads, the sys-

tem will give priority to the user interface and system

operations over background services (like our app),

which sometimes leads to the scheduling of our ap-

plication excecution being pushed back, and thus the

chosen sampling period T

being not respected. Fig. 1

Modular Modelling of an Embedded Mobile CPU-GPU Chip for Feature Estimation

339

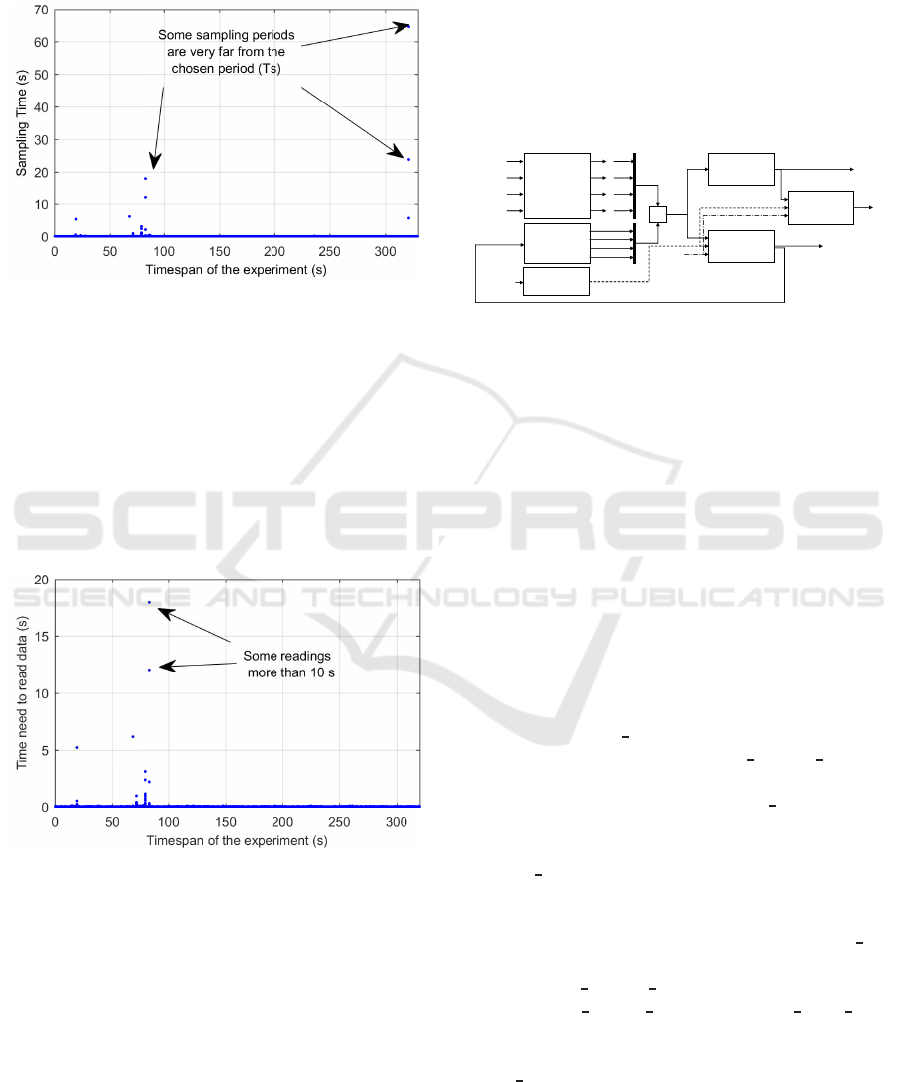
shows the evolution of the sampling periods during a

reading experience where some sampling values are

well beyond the chosen period T

and even reaching

tens of seconds.

Figure 1: Sampling time variation over time.

The second difﬁculty in reading the variables is

related to the management of instruction queues by

the OS. Again, during periods of high the CPU loads,

we came to notice that reading time—the time differ-

ence between the start of the reading process and its

end—is sometimes very long, even reaching seconds

(See Fig. 2), leading to the conclusion that the reading

was interrupted. This renders the values taken during

the said reading false (unsynchronized data, measure-

ments delays and missing data).

Figure 2: Reading time evolution and variation over time.

These two problems of data acquisition are taken

into account and the data acquired during long sam-

ple times or interrupted readings will be automatically

deleted from the database used in the next section for

learning and model assessment.

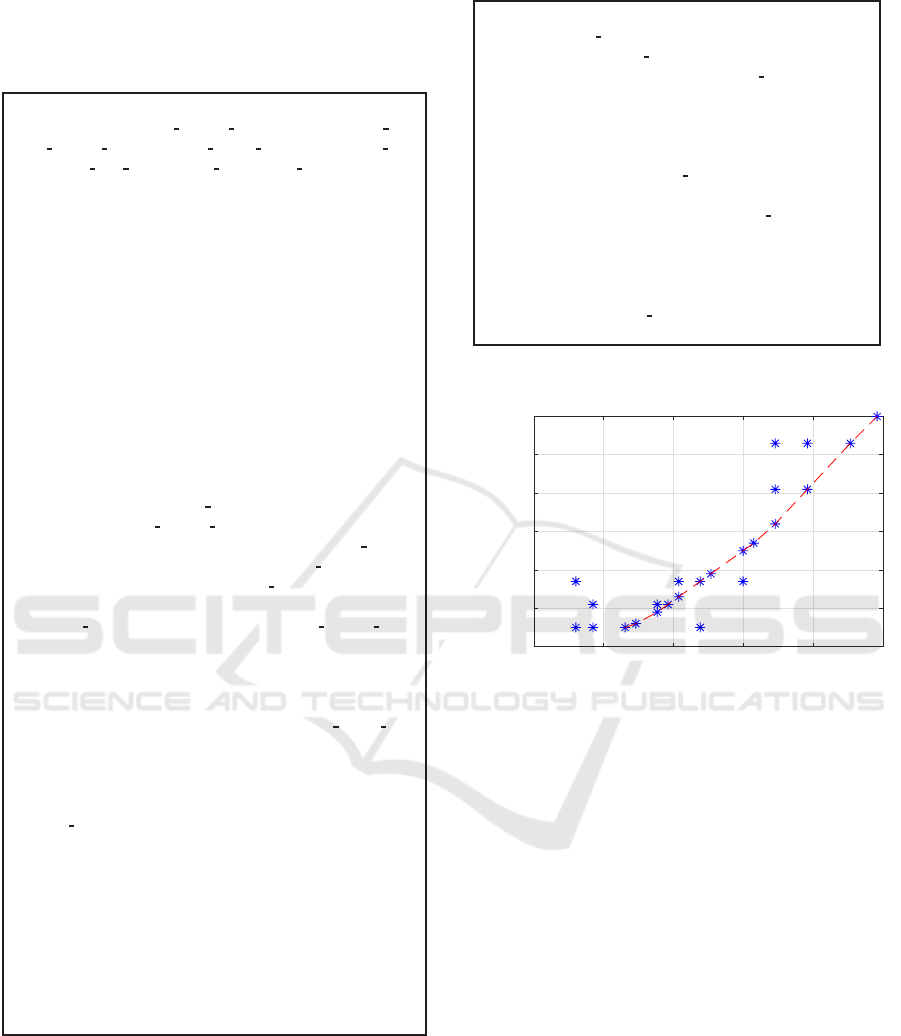
4 SYSTEM MODELLING

The CPU-GPU chip is a complex system with vari-

able structure, whose dynamics are nonlinear and not

continuous. Hence, a gradual approach and a modu-

lar structure are adopted for its modelling as shown in

Fig. 3. This modular approach provides for a gradual

analysis and modelling each of the subsystems and

account for the variable structure of the system. It

also allows easy integration of subsystems in case of

any changes. Fig. 3 shows a global vision of the in-

terconnected and gradual modelling approach. In the

following paragraphs, each of the subsystems will be

detailed.

⋮

Governor

Load

⋮

Thermal

Regulator

On/Off

Power

Model

Voltage

Model

Thermal

Model

GPU

Governor

Load

GPU

, V

…

, T

… T

consumed

MOR

Figure 3: Diagram of the proposed model of the CPU-GPU

system.

4.1 The Frequency Scaling Governor

Frequency scaling is carried out via Governors. On

the studied system, several frequency governors exist.

These governors calculate the frequency according to

usage needs as well as several other factors (speed,

power consumption). The governor we are modelling

in this work is the interactive governor. However,

thanks to the modular structure of the model, any

governor can replace the one considered in this case

study.

The interactive governor increases and decreases

the frequency of each core as a function of the load

and speciﬁc timers. When the CPU is back from the

idle state, the governor starts a countdown timer with

a predeﬁned timer

rate value at the end of which, if

the load exceeds a given value (go hispeed load), the

governor calculates a new frequency for which the

load will be equal or closest to target

load value.

The governor also takes into account sudden

heavy loads by directly scaling up the frequency to

hispeed

freq if the current frequency is below it for

better reactiveness and to avoid unexpected CPU bot-

tlenecks and sluggish performance. In addition, if the

frequencyof a core is greater or equal to hispeed

freq,

the core must stay on the same frequency at least a pe-

riod of above

hispeed delay, before scaling up, and a

period of min

sample time (or sampling down factor

if the current frequency is the maximum frequency)

before scaling down. The last time constant, noted

timer

slack, is an additional period of time that the

core has to wait before shutting down if the load is

equal to zero. The governor modelling algorithm is

given in Fig. 4 and Fig. 5. This model is engineered

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

340

from the original source code available in the code de-

posits of the manufacturer of the studied smartphone

(Samsung, 2016).

procedure INTERACTIVE(Load, Time,currentFrequency)

deﬁne

above hispeed delay

hispeed freq

go hispeed load

min sample time

target load

sampling down factor

timer slack

timer rate

if Initialisation = 0 then

currentHiSpeedTimer ← 0

currentTimers ← 0

currentDownTimers ← 0

currentTimersSlack ← 0

oldTime ← Time;

Initialisation ← 1

else

currentHiSpeedTimer ← currentHiSpeedTimer + (Time −

oldTime)

currentTimers ← currentTimers+ (Time− oldTime)

currentDownTimers ← currentDownTimers + (Time −

oldTime)

currentTimersSlack ← currentTimersSlack + (Time −

oldTime)

end if

if (currentTimers ≥

timer rate

) then

if (Load ≥

go hispeed load

) then

if (currentFrequency <

hispeed freq

∧

ChooseFreq(Load,currentFrequency) <

hispeed freq

) then

newFrequency ←

hispeed freq

else if (ChooseFreq(Load, currentFrequency) >

hispeed freq

) ∧ (currentHiSpeedTimer ≥

above hispeed delay

)

then

newFrequency ←

ChooseFreq(Load,currentFrequency)

else if (ChooseFreq(Load, currentFrequency) <

currentFrequency) ∧ (currentDownTimers ≥

min sample time

)

then

newFrequency ←

ChooseFreq(Load,currentFrequency)

else if (Load = 0) ∧ (currentTimersSlack ≥

timer slack

) then

newFrequency ← 0

end if

currentHiSpeedTimer ← 0

currentDownTimers ← 0

end if

else

newFrequency ← currentFrequency

end if

return newFrequency

end procedure

Figure 4: The Interactive Governor algorithm (I—The gen-

eral algorithm).

4.2 Voltage Model

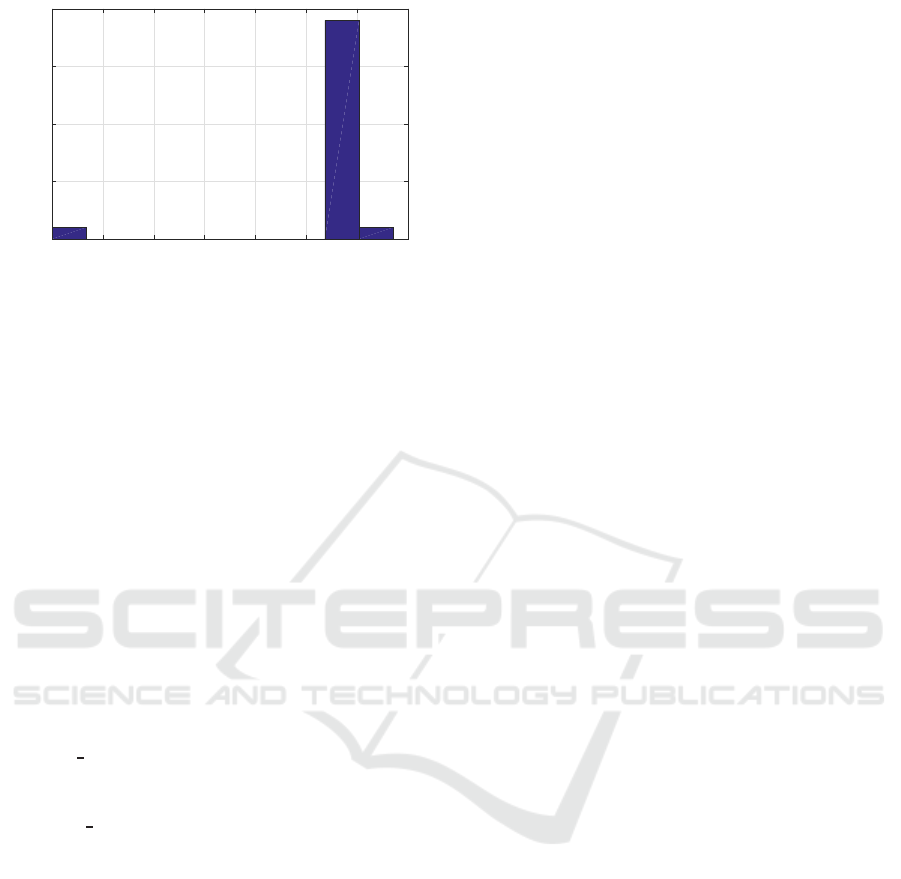
Recovered readings show that, like frequency, volt-

age is discrete and varies in a set of well-deﬁned val-

ues. Voltage readings are plotted against the frequen-

cies, in Fig. 6, in order to see the relationship between

procedure CHOOSEFREQ(Load, currentFrequency)

deﬁne target

load

deﬁne FREQUENCY

TABLE

freq = currentFrequency× (Load/target

load)

TableSize ← 16 ⊲ In our study case

Minimum ← freq;

BestIndex ← 0;

while (index < TableSize) do

if | freq− FREQUENCY

TABLE(index)| ≤ Minimum then

BestIndex ← index

Minimum ← | freq− FREQUENCY

TABLE(index)|

else

index ← index+ 1

end if

end while

return FREQUENCY

TABLE(BestIndex)

end procedure

Figure 5: The Interactive Governor algorithm (II—The

Choose frequency procedure).

0 0.5 1 1.5 2 2.5

Frequency per core (Ghz)

0.75

0.8

0.85

0.9

0.95

1.05

Voltage per core (V)

Figure 6: Voltage values drawn against frequency value

with the almost linear trend in red.

these two variables. It shows an almost linear trend in

the middle where 98% of the values are concentrated,

hinting that a ﬁxed voltage value is associated with

each frequency value. However, Fig. 6 also shows

that some frequencies are linked to multiple voltage

values, this is due to the fact that the core needs to in-

crease its voltage before scaling up the frequency,and

decrease the frequency before lowering the voltage.

Furthermore, by analyzing the measurements, we

ﬁnd 15 frequency values (plus a zero frequency for a

turned-off core) against 14 voltage values, leading to

the belief that some frequencies share the same volt-

age value. Thus, to better investigate the relationship

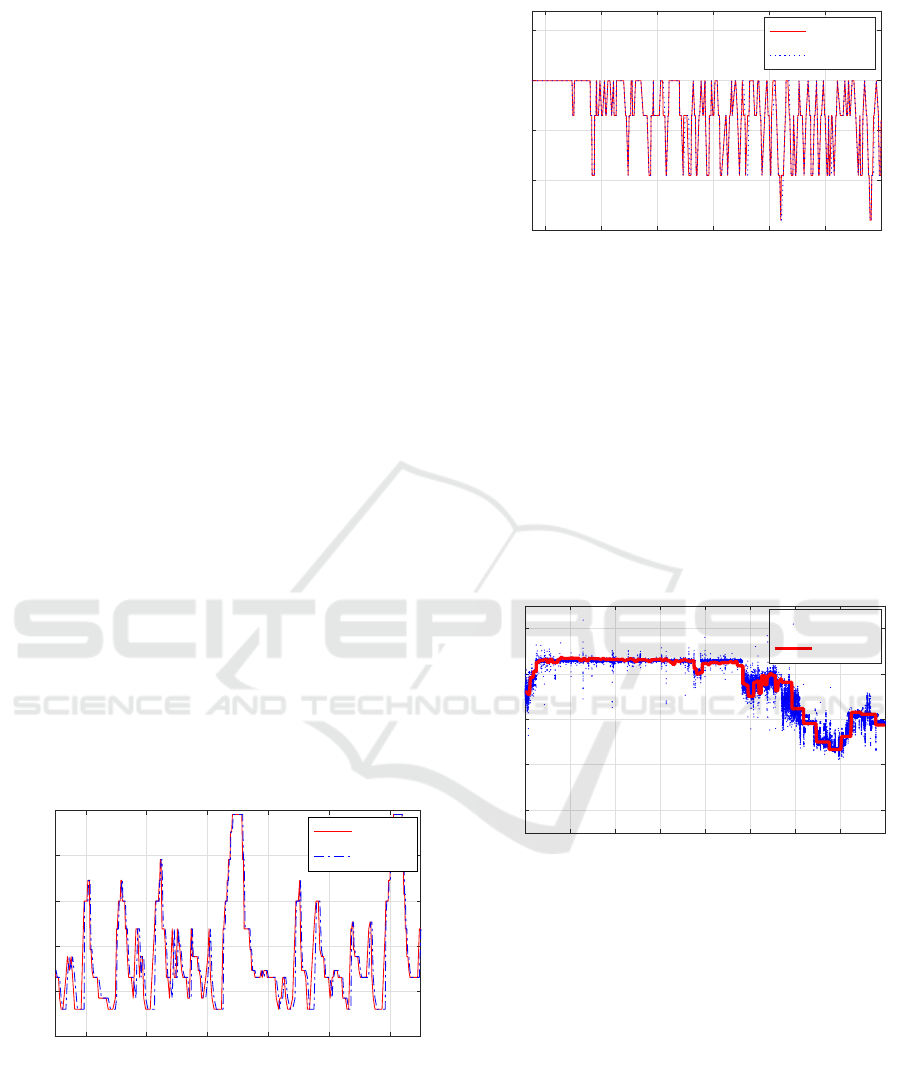
between the frequencies and voltages, a histogram

of voltage values for each frequency is constructed.

Fig. 7 shows the histogram of voltage values for f =

300MHz indicating that the voltage associated with

this frequency value is clearlyV

300MHz

= 0.775V. All

other voltage values are obtained following the same

fashion.

Modular Modelling of an Embedded Mobile CPU-GPU Chip for Feature Estimation

341

0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85

Voltage of the core (V)

Number of times read (n)

Figure 7: Histogram of voltage values for f = 300MHz.

4.3 The Thermal Regulator

Thermal management is a very important task, espe-

cially during boot and system startup periods where

the temperature can become excessively high. The al-

gorithms used during startup are generally ﬁxed and

not accessible to the programmer. However, in the

user space, SoC manufacturers generally implement

programmable algorithms for programmers to use.

In the smartphone we are studying, the SoC manu-

facturer implemented three types of regulators from

which the programmercan choose to manage the tem-

perature of the SoC. The implemented regulators are

Proportional Integral Derivative (PID), Single Step,

and ﬁnally, the one used by the manufacturer of the

studied smartphone a Monitor.

This algorithm samples the temperature every

sampling

ms. If the temperature of the core is higher

than a predeﬁned thresholds, the core is shutdown.

Once the temperature of the said core drops below

thresholds

clr, it can be turned on again.

4.4 Power Model

In the relevant literature, some works, such as the one

presented by Wang et al., use battery measurements to

estimate the power consumed by applications (Wang

et al., 2013). Others track kernel queries to determine

power consumption (Pathak et al., 2011). Other tech-

niques, like the one presented in (Kim et al., 2012b;

Kim and Chung, 2013; Kim et al., 2015) involve the

construction of polynomial models to estimate the

power consumption as a function of the frequency

and of the load. In this case study, we use battery

readings. However, the obtained value of the current

supplied by the battery is a constant, and the value of

voltage varies in a set of ﬁxed values which results

in staircase-like power output signal, and makes any

convergence of polynomial and auto-regressive mod-

els (ARX, ARMA, ...) impossible. Additionally, in

order to minimise the inﬂuence of the other compo-

nents of the smartphone, all communication and sec-

ondary peripherals (WiFi, screen, cameras ...) were

disabled and assumed to consume a static constant

amount of power in that state.

Before starting the modelling process, it is neces-

sary to determine the model inputs. In the case of the

CPU, the power consumption is often given by the re-

lation (Adam Kerin, 2013) :

CPU

= f ×V

×C (1)

where f denotes the frequency, V the voltage and C

the electric charge stored in the CPU, which is rel-

atively constant. Thus, the CPU power becomes a

function of the frequency and voltage. It was shown

in the previous subsection that the voltage is itself a

function of frequency. For the GPU, voltage mea-

surements are not available in this case study, thus its

frequency is used as input of the model (Kim et al.,

2015). The last input is the Memory Occupation Rate

(MOR)—the ratio of the occupied memory to the full

memory—which will help include the memory power

consumptionin the model, since it is a part of the SoC.

The model developed to estimate power consump-

tion is a neural network with two layers. A hidden

layer whose activation function is a sigmoid, and con-

taining 8 neurons, and an output layer containing a

single neuron with a linear transfer function.

4.5 Temperature Model

Heat transfer and temperature modelling have been

studied quite extensively in the relevant literature.

However, in this work, we will not focus on the me-

chanics of heat generation and transfer since its aim is

to estimate temperature for monitoring and diagnosis

purposes. Thus we focused our attention on ﬁnding

variables affecting it i.e. correlations.

Temperature dynamics are different from those of

the other studied variables; for one it does not range

in a speciﬁc set of values. Furthermore, it does not de-

pend only on the inputs, but also on its own previous

values. It is directly correlated with the frequency of

the CPU and the GPU. However, as shown in (Hong

and Kim, 2010), we note that the correlation in the

measurements between the recorded temperature and

power consumption is imperceptible, which was con-

ﬁrmed by our own results. Therefore, the considered

inputs of the model of the SoC temperature are the

frequencies and the MOR.

The temperature readings (Fig. 11) show two main

trends for which we should account. The ﬁrst is

the rise (warming) and fall (cooling) of temperature

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

342

occurring over relatively long periods of time, and

the second is the high-frequency small temperature

changes. To better represent these dynamics, we

chose to use an autoregressive–moving-average (AR-

MAX) model. ARMAX models use the regression of

inputs and previous outputs, along with the moving

average to simulate or predict the current output:

y(k) = P

y(k− 1) + ... + P

y(k− n)

+ Q

u(k− 1) + ... + Q

u(k− m)

+ e(k) + H

e(k− 1) + ... + H

e(k− r) (2)

Equation (2) is the linear difference equation of

an ARMAX (n, m,r) (orders of the model), with y(k)

being the output to compute, u the exogenous (X)

variable or system input, and e is the moving av-

erage (MA) variable ((Fung et al., 2003)). In the

case of this work, temperature T

SoC

is the output

y(k) to be estimated, and the system input is u(k) =

[ f

,..., f

, f

GPU

,MOR]. The parameters P, Q, and H

are constants evaluated by iterative search algorithms.

5 EXPERIMENTAL AND MODEL

VALIDATION

The experimental results presented in this section are

obtained through the application then compared with

estimations made by the model. The evolutions of the

measured frequenciesof one core, and the frequencies

estimated by the model are given in Fig. 8. The plots

are nearly identical, with a slight delay at the instants

of frequency changes. The maximum delay recorded

= 0.2s. This result validates the frequency model.

3474 3476 3478 3480 3482 3484

Time (s)

0.5

1.5

2.5

Frequency f (GHz)

Reading

Simulated

Figure 8: Frequency model estimations vs system readings.

Fig. 9 shows the evolution of the measured volt-

age of one core, compared to the estimated one. As

for frequencies, the plots are again nearly identical,

with a slight delay at the instants of voltage changes.

The maximum delay recorded τ

= 0.22s. Thus, the

voltage model is, also, validated.

282 284 286 288 290 292 294

Time (s)

0.9

0.95

1.05

1.1

Core Voltage (V)

Readings

Simulated

Figure 9: Voltage model estimations vs system readings.

The measured power delivered by the battery

compared to the estimated power by the neural net-

work model are given in Fig. 10. This result shows

the good accuracy of the model during the slow vari-

ations and static phase. However, there is also notice-

able noise during the phase of rapid changes, espe-

cially between t = 50s and t = 60s. The Mean Abso-

lute Error (MAE) recorded is 0.0083W over 2 × 10

samples, with a maximum error of 6.60%, while the

Mean Squared Error (MSE) is 2.3896 × 10

−4

. Thus,

the power model is validated.

0 10 20 30 40 50 60 70 80

Time (s)

1.5

1.6

1.7

1.8

1.9

Power (W)

Simulated

Readings

Figure 10: Power model estimations vs system readings.

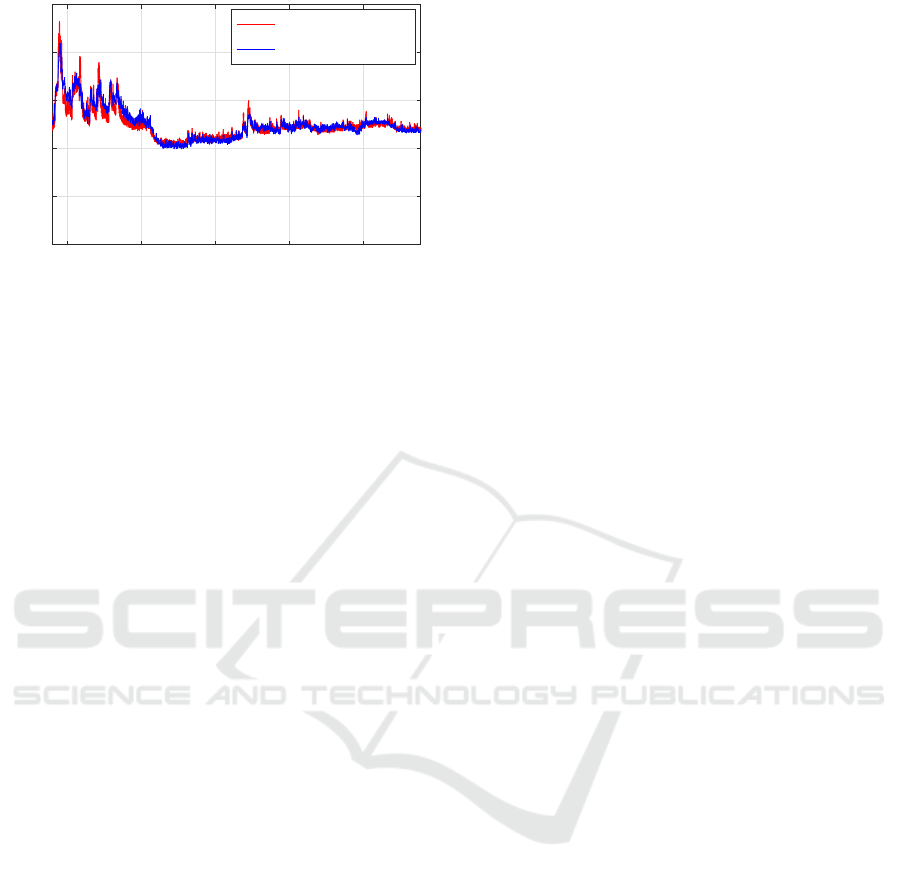
Fig. 11 shows the evolution of the estimated

temperature compared with the measured tempera-

ture. The model accurately follows the dynamics of

the measured temperature during temperature change

(heating and cooling), and also during phases with

weak temperature changes. Fig. 11 also shows that

the model takes into account the initial conditions of

temperature. It has an MAE of 0.9947

◦

C, with a

one time maximum of 8.14%, and an MSE of 1.8584.

Hence, the temperature model is also validated.

Modular Modelling of an Embedded Mobile CPU-GPU Chip for Feature Estimation

343

400 600 800 1000 1200

Time (ms)

Temperature(°C)

Temperature

Reading

Temperature

Simulated

Figure 11: Temperature model estimations vs system read-

ings.

6 CONCLUSION

A data acquisition and estimation systems have been

developed for a CPU-GPU embedded chip. Measure-

ments are acquired on the ﬂy for operational state es-

timation.

The estimation model developed is validated ex-

perimentally. The parameter and variable estimation

is structured as an interconnected system with vari-

able structure. The modularity of the estimation sys-

tem is easily adaptable to changes in the system struc-

ture and its operation modes.

In future works, the next step after developing the

model is to use it to monitor the operating state and

drifts in characteristics of the chip.

ACKNOWLEDGEMENT

This paper is a part of the MMCD project supported

and funded by the BPI, to whom we address our

thanks along with the FUI 19 project partners : IN-

RIA, IRTS, and Nolam ES.

REFERENCES

Adam Kerin (2013). Power vs. Performance Management

of the CPU.

Adhinarayanan, V., Subramaniam, B., and Feng, W.-c.

(2016). Online Power Estimation of Graphics Pro-

cessing Units. In IEEE/ACM International Sympo-

sium on Cluster, Cloud and Grid Computing (CC-

Grid), number May, Colombia.

Ardalani, N., Lestourgeon, C., Sankaralingam, K., and Zhu,

X. (2015). Cross-architecture performance prediction

(XAPP) using CPU code to predict GPU performance.

Proceedings of the 48th International Symposium on

Microarchitecture - MICRO-48, pages 725–737.

Fung, E. H., Wong, Y., Ho, H., and Mignolet, M. P. (2003).

Modelling and prediction of machining errors using

ARMAX and NARMAX structures. Applied Mathe-

matical Modelling, 27(8):611–627.

Hong, S. and Kim, H. (2010). An integrated GPU power

and performance model. In ACM SIGARCH Com-

puter Architecture News, volume 38 of {ISCA} ’10,

page 280, New York, NY, USA. ACM.

Kim, H., Vuduc, R., Baghsorkhi, S., Choi, J., and Hwu,

W.-m. (2012a). Performance Analysis and Tun-

ing for General Purpose Graphics Processing Units

(GPGPU), volume 7. Morgan & Claypool publishers.

Kim, M. and Chung, S. W. (2013). Accurate GPU power

estimation for mobile device power proﬁling. Digest

of Technical Papers - IEEE International Conference

on Consumer Electronics, pages 183–184.

Kim, M., Kong, J., and Chung, S. W. (2012b). En-

hancing online power estimation accuracy for smart-

phones. IEEE Transactions on Consumer Electronics,

58(2):333–339.

Kim, Y. G., Kim, M., Kim, J. M., Sung, M., and Chung,

S. W. (2015). A novel GPU power model for ac-

curate smartphone power breakdown. ETRI Journal,

37(1):157–164.

Leng, J., Hetherington, T., ElTantawy, A., Gilani, S., Kim,

N. S., Aamodt, T. M., and Reddi, V. J. (2013).

GPUWattch: Enabling Energy Optimizations in GPG-

PUs. Proceedings of the 40th Annual International

Symposium on Computer Architecture - ISCA ’13,

41:487.

Meng, J. and Skadron, K. (2011). A performance study for

iterative stencil loops on GPUs with ghost zone opti-

mizations. International Journal of Parallel Program-

ming, 39(1):115–142.

Minyong Kim, Joonho Kong, and Sung Woo Chung (2012).

An online power estimation technique for multi-core

smartphones with advanced display components. In

2012 IEEE International Conference on Consumer

Electronics (ICCE), pages 666–667. IEEE.

M’Sirdi, S., Godard, W., and Pantel, M. (2016). A Multi-

Core Interference-Aware Schedulability Test for IMA

Systems, as a Guide for SW/HW Integration. In 8th

European Congress on Embedded Real Time Software

and Systems (ERTS 2016), TOULOUSE, France.

Pathak, A., Hu, Y. C., Zhang, M., Bahl, P., and Wang, Y.-

M. (2011). Fine-Grained Power Modeling for Smart-

phones Using System Call Tracing. Proceedings of

the sixth conference on Computer systems EuroSys 11,

page 153.

Samsung (2016). Samsung Opensource Release Center.

Wang, C., Yan, F., Guo, Y., and Chen, X. (2013). Power

estimation for mobile applications with proﬁle-driven

battery traces. Int Symp on Low Power Electronics

and Design, pages 120–125.

Williams, S., Waterman, A., and Patterson, D. (2009).

Rooﬂine: An Insight Visual Performance Model for

Multicore Architectures. Communications of the

ACM, 52(4):65.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

344

Zhang, L., Tiwana, B., Qian, Z., Wang, Z., Dick, R. P.,

Mao, Z. M., and Yang, L. (2010). Accurate on-

line power estimation and automatic battery behav-

ior based power model generation for smartphones.

In IEEE/ACM/IFIP int conf Hardware/software code-

sign and system synthesis - CODES/ISSS ’10, page

105, New York, New York, USA. ACM Press.

Modular Modelling of an Embedded Mobile CPU-GPU Chip for Feature Estimation

345