A Hybrid Method Using Temporal and Spatial Information for 3D Lidar

Data Segmentation

Mehmet Ali C¸ a

grı Tuncer and Dirk Schulz

Cognitive Mobile Systems, Fraunhofer FKIE, Fraunhoferstr, 20, 53343 Wachtberg, Germany

Keywords:

Object Segmentation, Distance Dependent Chinese Restaurant Process, Mean Shift, 3D Lidar Data.

Abstract:

This paper proposes a novel hybrid segmentation method for 3D Light Detection and Ranging (Lidar) data.

The presented approach gains robustness against the under-segmentation issue, i.e., assigning several objects

to one segment, by jointly using spatial and temporal information to discriminate nearby objects in the data.

When an autonomous vehicle has a complex dynamic environment, such as pedestrians walking close to

their nearby objects, determining if a segment consists of one or multiple objects can be difﬁcult with spatial

features alone. The temporal cues allow us to resolve such ambiguities. In order to get temporal information,

a motion ﬁeld of the environment is estimated for subsequent 3D Lidar scans based on an occupancy grid

representation. Then we propose a hybrid approach using the mean-shift method and the distance dependent

Chinese Restaurant Process (ddCRP). After the segmentation blobs are spatially extracted from the scene, the

mean-shift seeks the number of possible objects in the state space of each blob. If the mean-shift algorithm

determines an under-segmented blob, the ddCRP performs the ﬁnal partition in this blob. Otherwise, the

queried blob remains the same and it is assigned as a segment. The computational time of the hybrid method

is below the scanning period of the Lidar sensor. This enables the system to run in real time.

1 INTRODUCTION

An autonomous vehicle must perceive the obstacles

in its environment and track them for collision avoid-

ance. Autonomous perception systems are mostly

decomposed as a processing pipeline of point cloud

segmentation and object tracking. After the scene is

segmented into separate blobs for each object, these

blobs are tracked over consecutive time frames to esti-

mate their velocities and to predict their movements in

the future. The autonomous vehicle uses these predic-

tions to plan its own trajectory and to avoid collisions

with static and dynamic obstacles in the surroundings.

Many self-driving vehicle systems rely on simple

spatial relationships to segment the scene into objects.

3D point cloud points are grouped together using their

nearness in distance. For instance, points in the data

are assumed to belong to the same object if they are

adequately close to each other, or if points are far

away and disconnected they are assumed to be bound

up with different objects.

The segmentation part of perception systems re-

lies on spatial features with the assumption that

the individual trafﬁc participants are well-separated

from each other. However this assumption of well-

separated objects does not hold under the circum-

stances of many real-world cases. For example, in

the context of autonomous driving, pedestrians often

get very close with their neighboring objects. This re-

sults in an under-segmentation of the pedestrian with

its neighboring object, such as a building or a parked

car. If the intelligent vehicle can not recognize that

under-segmented pedestrian, the vehicle will have dif-

ﬁculty with the tracking of the pedestrian’s move-

ments. Such under-segmentation problems lead to in-

accurate or even wrong tracking results, mis-detection

of objects and, consequently, possible destructive col-

lisions. Improving the segmentation process is there-

fore an important step towards achieving a more ro-

bust object recognition and tracking process.

This paper presents a hybrid segmentation algo-

rithm which combines spatial and temporal informa-

tion in a simultaneous framework. Spatial and mo-

tion features proﬁt from each other to overcome the

under-segmentation issue of moving objects, i.e., as-

signing multiple objects to one segment. For example,

pedestrians often walk close to static objects so they

are spatially segmented together with their nearby ob-

jects. The proposed method determines if a spatially

extracted blob consists of one or several objects.

162

Tuncer, M. and Schulz, D.

A Hybrid Method Using Temporal and Spatial Information for 3D Lidar Data Segmentation.

DOI: 10.5220/0006471101620171

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 162-171

ISBN: Not Available

Combining the temporal and spatial cues allow us to

resolve such ambiguities. The 3D point cloud data

provides spatial features but the temporal information

needs to be acquired. For this purpose, a motion ﬁeld

of the environment is estimated for subsequent 3D Li-

dar scans based on an occupancy grid representation.

Grid cells are tracked using individual Kalman ﬁlters

and the estimated grid cell velocities are smoothed

for better motion consistency of neighboring dynamic

cells. Estimated velocities are transformed to one di-

mensional movement directions. Then we proposed

a hybrid approach using a mean-shift method (Fuku-

naga and Hostetler, 1975) and a distance dependent

Chinese Restaurant Process (ddCRP) (Blei and Fra-

zier, 2011). Instead of applying the computation-

ally expensive ddCRP method to each extracted blob

such as in (Tuncer and Schulz, 2015), the mean-shift

method roughly searches the number of possible ob-

jects in each blob. If the mean-shift method detects

an under-segmented blob, the ddCRP generates the ﬁ-

nal partition in this blob. Otherwise, the blob remains

the same and it is assigned as a segment, or an ob-

ject, in the scene. The hybrid method decreases the

computational time below the scanning period of the

Lidar sensor while providing even better error rates

than (Tuncer and Schulz, 2016b).

The layout of this paper is as follows. It starts with

a discussion of related work in Section 2. Section 3

explains the pre-processing of 3D point cloud data.

In Section 4, the proposed hybrid method is described

in detail. Section 5 evaluates the performance of the

presented framework on real trafﬁc data. Section 6

recapitulates the most important ﬁndings and gives an

outlook on future work.

2 RELATED WORK

Object segmentation and tracking has been studied

for years. 3D Lidar data is projected on a 2D rep-

resentation (Urmson et al., 2008; Montemerlo et al.,

2008). Given a known segmentation, tracking be-

comes a problem of state estimation and data as-

sociation (Moosmann et al., 2009; Douillard et al.,

2011). Many 3D Lidar based multi-target tracking

approaches (Klasing et al., 2008; Petrovskaya and

Thrun, 2009; Morton et al., 2011; Teichman et al.,

2011; Azim and Aycard, 2012; Choi et al., 2013) eas-

ily segment the scene and track objects independently

with the assumption that trafﬁc participants in urban

scenarios are well separated in the sensor data. These

methods use only the proximity of data points so they

are not able to resolve ambiguities when objects get

closer. Himmelsbach and Wuensche (Himmelsbach

and Wuensche, 2012) proposed a bottom-up approach

that considers the appearance and tracking history of

targets to discriminate static from moving objects. In

order to solve under- and over-segmentation prob-

lems, a probabilistic 3D segmentation method is pro-

posed in (Held et al., 2016). It combines spatial, tem-

poral, and semantic information to segment a scene.

For another solution of the under-segmentation

problem, Tuncer and Schulz (Tuncer and Schulz,

2015) applied the distance dependent Chinese Restau-

rant Process (ddCRP) (Blei and Frazier, 2011) to 3D

Lidar data. It estimates the motion ﬁeld of the scene

and then exploits spatial and motion features together

for 3D point cloud segmentation. However, it is a

computationally expensive method which can not run

in real time. For a faster approach, a sequential vari-

ant of ddCRP was proposed, called sequential-ddCRP

(s-ddCRP) (Tuncer and Schulz, 2016b). The sequen-

tial extension allows to overcome issues of under-

segmentation of the sensor data. The computational

cost of the approach is reduced by using a priori

coming sequentially from the previous time frames

and clustering grid cells agglomerative to super grid

cells. However, due to super grid cells, the algo-

rithm is prone to errors. In (Tuncer and Schulz,

2016a), the s-ddCRP segmentation approach is inte-

grated with a smoothed motion ﬁeld estimation and

an object tracking module. Smoothing the estimated

motion ﬁeld improves the segmentation performance

of the s-ddCRP. Our proposed hybrid approach, which

uses the mean-shift (Fukunaga and Hostetler, 1975;

Comaniciu and Meer, 2002) and ddCRP methods,

segments the environment based on spatial and tem-

poral information to avoid under-segmentation er-

rors. Incorporating the mean-shift and ddCRP algo-

rithms signiﬁcantly decreases the computational time

of the system compared to (Tuncer and Schulz, 2015;

Tuncer and Schulz, 2016b).

3 PRE-PROCESSING

We applied the pre-processing approach of (Tuncer

and Schulz, 2016a), which brieﬂy consists of occu-

pancy grid representation, ﬁltering and smoothing.

The 3D Lidar scanner used in our experiments pro-

vides huge amounts of data which poses a challenge

on the processing algorithms. To gain efﬁciency, the

data is sub-sampled by mapping individual point mea-

surements to an occupancy grid representation. The

grid cells store the center of mass of measurements,

averaged heights and the variance of the height of the

points falling into each grid cell. After the measure-

ments belonging to the ground are removed with a de-

A Hybrid Method Using Temporal and Spatial Information for 3D Lidar Data Segmentation

163

cision rule, a connected components algorithm (Bar-

Shalom, 1987) using 8 neighborhood on the grid is

applied to extract blobs spatially.

The temporal information of the scene is deter-

mined with a motion ﬁeld estimation approach. Grid

cells are treated as the basic elements of motion and

each cell is assigned to its own motion vector. Grid

cells of previous and current scans are associated

with a Gating and Nearest Neighbor (NN) ﬁlter. To

solve the estimation problem, individual Kalman ﬁl-

ters are applied to each non-ground grid cell. Then

a smoothing process is performed on the dynamic

grid cells to compensate the association errors as ex-

plained in (Tuncer and Schulz, 2016a). We ﬁnally ob-

tained the grid cell’s state vector x

= [x

, x

] in the

time frame t, where x

is the estimated motion direc-

tion of the grid cell and x

is the grid cell’s estimated

center of mass location in x and y directions.

4 THE HYBRID METHOD

This section explains our novel hybrid framework us-

ing the mean-shift algorithm and ddCRP for the seg-

mentation of 3D Lidar data by using temporal and

spatial information. Instead of applying the compu-

tationally expensive ddCRP method to each spatially

extracted blob such as in (Tuncer and Schulz, 2016a),

we ﬁrstly analyze the state space of each blob with

a fast mean-shift approach. After the pre-processing

step explained in Section 3, we spatially extract blobs.

For each blob in the scene, the mean-shift algorithm

seeks the number of modes in the state vector space.

If there is only one mode, then the blob remains the

same and it is taken as a correct segment. If the

mean-shift algorithm ﬁnds multiple modes, then the

ddCRP method estimates the ﬁnal partition and de-

termines the correct segmentation borders in the blob.

This procedure iteratively continues while searching

each blob in the scene at each time frame. After

the hybrid method has been applied to each blob in

a time frame, the algorithm outputs the segmented

scene. The cooperation of mean-shift and ddCRP

approaches signiﬁcantly decreases the computational

time compared to (Tuncer and Schulz, 2015; Tuncer

and Schulz, 2016b) as shown in Section 5.

4.1 Mean-shift

The mean-shift method is a non-parametric feature

space analysis algorithm for locating the maxima of

a density function given the discrete data. It is a pow-

erful tool for detecting the modes of the density in

the state space. The mean-shift method iteratively

seeks the modes. The modes represent different ob-

jects in an extracted blob. We randomly choose a

state vector x

as an initial estimate with a uniform

kernel function k(x

− x

t,n

). This function determines

the weight of nearby points for re-estimation of the

mean. n = 1, ...., N represents the number of grid cells

falling into the kernel’s region of interest with a radius

h. For the sake of brevity, we leave out the time index

t of the state vector x

t,n

from now on. For the given N

state vectors of grid cells in the d dimensional space

, the multivariate kernel density estimator can be

written as below.

f (x) =

∑

n=1



x − x



(1)

The ﬁrst step of state space analysis with the underly-

ing density is to ﬁnd the modes of this density. The

modes are among the zeros of the gradient ∇ f (x) = 0.

The mean-shift algorithm is a powerful approach to

ﬁnd these zeros without estimating the density. The

estimate of the density gradient can be deﬁned as the

gradient of the kernel density estimate as follows.

∇ f (x) ≡ ∇

f (x) =

∑

n=1

∇k



x − x



(2)

We set Equation (2) to zero, ∇

f (x) = 0, and we deﬁne

a function,

g(x) = − ∇k(x), (3)

assuming that the derivative of the kernel proﬁle k

exists for all x ∈ [0, ∞). Using the deﬁned g(x), we

have the mean shift vector, which iteratively shifts the

search window towards the modes, as below.

m(x) =

∑

n=1



x−x



∑

n=1



x−x



− x (4)

The mean shift vector computed with kernel g(x) is

proportional to the normalized density gradient esti-

mate obtained with the kernel k(x). The mean shift

algorithm seeks a mode or local maximum of density

of a given distribution.

Using the 3D Lidar data, the features x

and x

are

concatenated in the joint three dimensional spatial-

motion domain. Different natures of these features

have to be compensated by a proper normalization. A

multivariate kernel is therefore applied as the product

of two radially symmetric kernels as follows,

(x) =



(5)

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

164

(a)

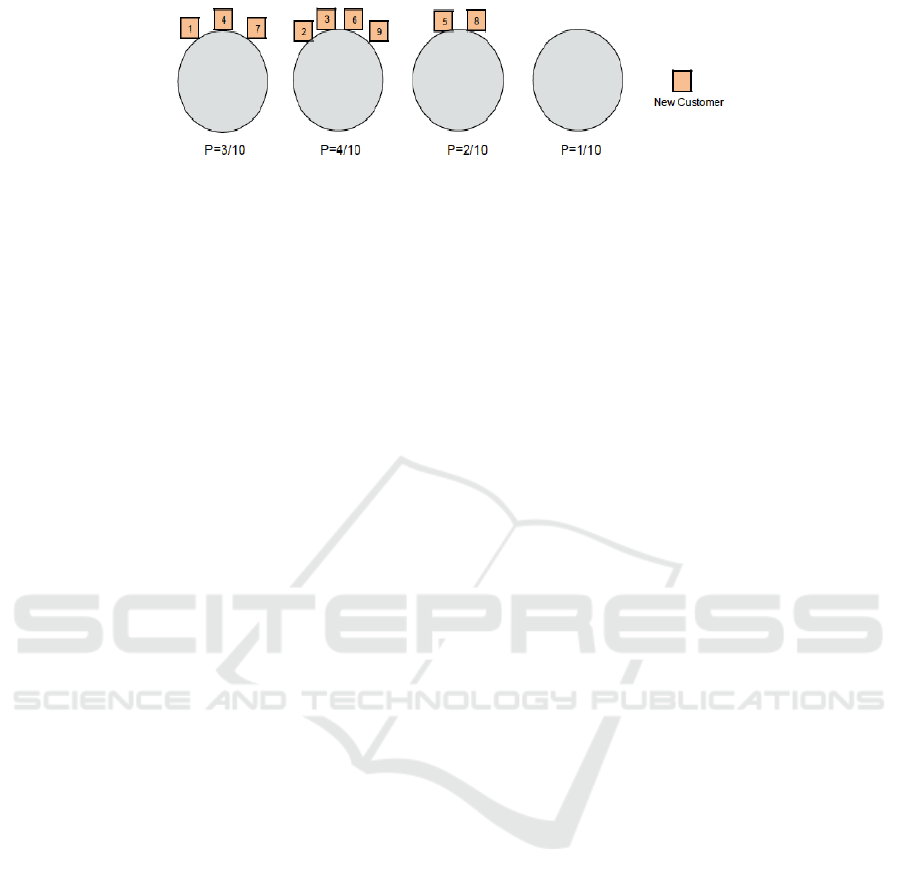
Figure 1: The Chinese Restaurant Process. Boxes represent the customers. Circles are the tables.

where C is the corresponding normalization constant.

represents the spatial resolution parameter which

affects the smoothing and connectivity. It is chosen

depending on the size of the object. h

is the resolu-

tion parameter of the motion feature which affects the

number of modes. It should be kept low if the vari-

ance of the state space is low. k(x) is the common

proﬁle used in both two domains with the employed

kernel bandwidths h

and h

. We have to set only the

bandwidth parameters h = (h

, h

). Controlling the

sizes of the kernels determines the resolution of the

mode detection. Because of the variant object sizes

in 3D point cloud data, the mean-shift method tends

to generate over- and under-segmentations. However,

it is still a powerful mode seeking algorithm which

successfully performs as the ﬁrst step of our proposed

hybrid method.

4.2 Chinese Restaurant Process

The ddCRP method presented in the following sub-

section is based on the Chinese Restaurant Process

(CRP) (Pitman et al., 2002), a hierarchical non-

parametric Bayesian clustering model originally pro-

posed for linguistic analysis and population genetics.

The CRP is typically introduced as a distribution over

partitions of data. For the generative process of a

CRP, a restaurant with a countably inﬁnite number of

circle tables is imagined. Costumers enter the restau-

rant one by one. Either a customer takes a seat at a

table with a probability proportional to the number of

people already seated at that table, i.e. he is more

likely to sit at a table with many customers than with

few, or the customer takes a seat at a new empty table

with a probability proportional to a scaling parameter

α. Figure (1) illustrates a simple example of how the

customers choose the tables in a random process. The

ﬁrst customer walks into the restaurant and sits at the

ﬁrst table. The tenth customer enters the restaurant

and sits at one of the three tables (which have previ-

ously been chosen by the other nine customers) with

a probability proportional to the number of people al-

ready sitting at that table (the probabilities are written

below the tables) or sits at the unoccupied new table

with a probability proportional to a scaling parame-

ter. After all customers have entered the restaurant

and have been seated at a table, the resulting seating

plan of costumers provides the clustering of data. Al-

though it is described sequentially, the CRP is an ex-

changeable model, which means that the order of ob-

served data (or customers coming into the restaurant)

does not affect the posterior distribution. This does

not hold for point cloud data because the coordinates

of grid cells need to be considered to obtain contigu-

ous object segments.

4.3 Distance Dependent Chinese

Restaurant Process

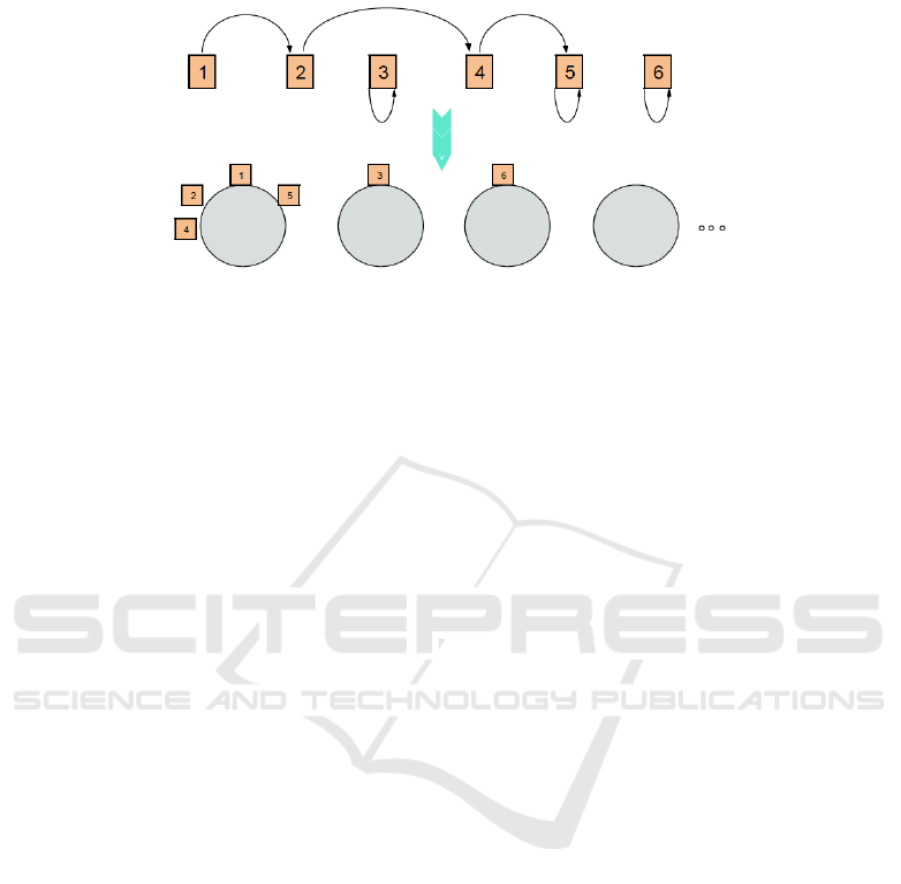
The distance dependent Chinese Restaurant Process

(ddCRP) was introduced to model random partitions

of non-exchangeable data. It deﬁnes a distribution

over partitions indirectly via distributions over links

between data points. This leads to a biased clustering,

which means that each observed data point is more

likely to be clustered with other data that is near in an

external sense. For a naive example, considering time

series data, points closer in time are more likely to be

grouped together. Speaking in CRP terms, customers

are linked to other customers instead of tables, which

is shown in Figure (2). The seating plan probability is

described in terms of the probability of a customer sit-

ting with each of the other customers. The allocation

of customers to tables is a by-product of this represen-

tation. If two customers are reachable by a sequence

of interim customer assignments, then they sit at the

same table.

For the task of 3D point cloud data segmentation,

a restaurant represents each spatially extracted blob

from the pre-processing step; tables denote the seg-

ments, or objects, in the blob on inquiry and cus-

tomers are grid cells belonging to the blob.

A grid cell gr

t,i

in the time frame t has a link vari-

able c

which links to another cell gr

t, j

or to itself ac-

cording to the distribution below,

A Hybrid Method Using Temporal and Spatial Information for 3D Lidar Data Segmentation

165

(a)

Figure 2: The distance dependent Chinese Restaurant Process. It links customers to other customers, instead of tables. For

3D Lidar data, tables denote the segments in the blob on inquiry and customers are grid cells belonging to the blob.

p(c

= j|A, α) ∝

(

i j

if i 6= j,

α if i = j.

(6)

where the afﬁnity A

i j

= f (d

i j

) depends on a spatial

distance d

i j

between the centers of mass of cells and

a decay function f (d). The decay function reﬂects

how the distances between grid cells affect the result-

ing distribution over partitions of the blob. We use a

window decay function f (d) = 1[d < a], which con-

siders grid cells that are at most a distance a away

from the center of mass of the current grid cell. The

spatial distance supports the discovery of connected

segments. Grid cells link together with a probability

proportional to A

i j

or cell gr

t,i

can stay alone and link

itself with a probability proportional to the scaling pa-

rameter α. It is shown in (Tuncer and Schulz, 2016b)

that larger α values favor partitions with more clus-

ters. Nearby cells are assigned to the same segment

if and only if they are in the same connected compo-

nent built by the grid cell links. The method enforces

the constitution of spatially connected segments. The

overall generative process can be summarized as fol-

lows:

1. For each grid cell gr

, sample its link assignment

v ddCRP(A, α)

2. Assign the customer links c

to the cluster assign-

ments z

. Then draw parameters θ

v G

for each

cluster.

3. For each grid cell, sample data x

v F(θ

) inde-

pendently. The s represents a segment in the blob.

The base distribution G

deﬁnes the mixture model

of the extracted clusters. It is selected as a con-

jugate prior of the data generating distribution with

Θ =



, σ



. The F(θ

) is a Gaussian distribution

with θ



, σ



. The state vector of a grid cell is

= [x

, x

], where x

is the one dimensional move-

ment direction of the grid cell and x

is its estimated

center of mass location in x and y directions. As the

nearby grid cells are probabilistically linked accord-

ing to x

by using Equation (6), the estimated motion

features x

are sampled according to the cell assign-

ments as the generative process described above.

4.4 Posterior Inference

Objects in spatially extracted blobs can be found by

a posterior inference. We explain how the ddCRP

framework determines the clusters, which represent

different objects, in a blob based on posterior infer-

ence. The key problem of inference is to compute

the posterior distribution of latent variables condi-

tioned on the spatial and temporal features. Due to

the huge combinatorial number of possible grid cell

layouts, it is intractable to evaluate the posterior prob-

ability directly. Therefore we make use of Gibbs sam-

pling (Geman and Geman, 1984) for the inference.

Gibbs sampling iteratively samples each latent vari-

able c

conditioned on the other latent variables c

−i

and the given state vector x as shown in the Equa-

tion (7) below,

p(c

−i

, x, Ω) ∝ p(c

|A, α) p (x|z (c) , Θ) (7)

where Ω =

{

A, α, Θ

}

. The A is the afﬁnity term, α

denotes the scaling factor, and Θ is the base distri-

bution. All these terms are explained in the previous

sub-section 4.3. The ﬁrst term of Equation (7) is the

s-ddCRP prior given in Equation (6). The second one

is the likelihood, which is factorized according to the

cluster index as follows,

p(x|z (c), Θ) =

∏

s=1



z(c)=s

|Θ



(8)

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

166

where x

z(c)=s

represents the state vectors of grid cells

assigned to the same segment s, and S denotes the

number of segments in a spatially extracted blob.

This factorization allows us to apply a block-wise

sampling because the algorithm does not need to re-

evaluate terms which are unaffected as the sampler

reassigns c

. Unless the cluster structure changes,

cached likelihood computations of previous iterations

can be used. Observations at each cluster are sam-

pled independently by using the parameters drawn

from the base distribution G

. The computation of

the marginal probability is given in Equation (9).



z(c)=s

|Θ



∏

i∈z(c)=s

p(x

|θ)

p(θ|Θ)dΘ

(9)

Here i denotes the indices assigned to the segment

s and the Θ is the parameters of the base distribu-

tion G

. Selecting the conjugate p(x

|θ) and G

en-

ables the marginalization of θ. Then Equation (9)

can be computed analytically (Gelman et al., 2003).

The sampling algorithm explores the space of possi-

ble clusters in each spatially extracted blob by reas-

signing links c

. If c

is the only link connecting two

clusters, they split after the reassignment. When there

are other alternative links connecting those clusters,

the partitions of data stay unchanged. Reassigning the

link c

might newly connect two clusters as well. The

sampler considers how the likelihood is affected by

removing and randomly reassigning the cell links. It

needs to consider the current link c

and all its con-

nected cells, because if a cell gr

connects to a differ-

ent cluster, then all cells which are linked to it also

move to that cluster.

The Gibbs sampler explores the space of possible

segmentations with these reassignments. It computes

all cases which change the partition layout. Assuming

the cluster indices a and l joined to cluster d in a spa-

tially extracted blob, then a Markov chain is speciﬁed

as below:

p(c

−i

, x, Ω) ∝

(

p(c

|A, α)Λ (x, z, Θ) if a ∪ l,

p(c

|A, α) otherwise,

(10)

where

Λ (x, z, Θ) =



z(c)=d

|Θ





z(c)=a

|Θ





z(c)=l

|Θ



(11)

The sampler generates different segmentation hy-

potheses and decides on the most probable ones by us-

ing temporal and spatial features together. The mean

value of the smoothed velocity vectors of grid cells

belonging to the same object can be assigned as a

motion feature of that object for tracking (Tuncer and

Schulz, 2016a).

5 EXPERIMENTAL RESULTS

The proposed method was evaluated on the real world

KITTI tracking data set (Geiger et al., 2012; Fritsch

et al., 2013; Geiger et al., 2013). That was recorded

using a Velodyne HDL-64D Lidar sensor and a high

precision GPS/IMU inertial navigation system. The

Lidar sensor has a frame rate of 10 Hz, a 360 degree

horizontal ﬁeld of view and it produces approximately

1.1 million point measurements per second. We tested

the methods with KITTI tracking data set which con-

sists of more than 42,000 3D bounding box labels on

roughly 7,000 frames across 21 sequences. One of

these sequences is used to select parameters and the

remaining 20 sequences are used for evaluation. Es-

timated grid cell velocities are transformed to one-

dimensional movement directions. We set the reso-

lution parameter of the motion feature as h

= 0.5.

For an 8-neighborhood, the spatial resolution param-

eter is chosen as h

= 1. For the ddCRP part of the

proposed method, larger α values bias the algorithm

towards more clusters so we set α = 10

−4

(Tuncer and

Schulz, 2016b). The ddCRP sampler is run with 20 it-

erations for each extracted blob.

Figure (3) shows how the proposed hybrid method

runs for the segmentation of 3D Lidar data. Within a

time frame t, the blobs are spatially extracted from

the scene as shown in Figure (3)(a). They are rep-

resented by 3D boxes and named as b1, b2, .., b8. In

Figure (3)(b), the blob b1 is on query. The mean-

shift method seeks for the number of modes in the

state space of blob b1. The mean-shift algorithm de-

termines whether the blob on query might consist of

one object or multiple objects. Since the mean-shift

algorithm ﬁnds one mode in the state space, the hy-

brid method does not jump to the ddCRP level. The

blob b1 therefore remains the same and it is assigned

as a segment s1 as illustrated in Figure (3)(c). The

next blob b2 is on query in the Figure (3)(d). The

mean-shift method seeks for the number of modes in

the state space of the blob b2. It ﬁnds multiple modes

in the feature space. This means that the blob b2 is

under-segmented. Then the ddCRP method performs

the ﬁnal partition on the blob b2 as illustrated in Fig-

ure (3)(e). The blob b2 is divided into three clusters,

which represent segments, or different objects. These

clusters are assigned as the segments s2, s3 and s4

as shown in Figure (3)(f). This procedure iteratively

continues while searching each blob in the scene at

A Hybrid Method Using Temporal and Spatial Information for 3D Lidar Data Segmentation

167

(a)

(b)

(c)

(d)

(e)

(f)

Figure 3: (a) Blobs are spatially extracted from the scene. The blobs are represented by 3D boxes and named such as

b1, b2, ...b8. (b) The mean-shift method seeks for the number of modes in the state space of blob b1. (c) Because the mean-

shift algorithm ﬁnds only one mode in the state space, the blob b1 remains the same and it is assigned as a segment s1. (d)

The next blob b2 is on query by the mean-shift method. (e) The mean-shift algorithm ﬁnds multiple modes in the feature

space of b2. Therefore the ddCRP method generates the ﬁnal partition on the under-segmented blob b2 and splits up the blob

into three clusters. (f) These clusters are assigned as the segments s2, s3 and s4.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

168

each time frame. After the hybrid method has been

applied to each blob in a time frame, the algorithm

outputs the segmented scene.

The KITTI dataset has been used to evaluate track-

ing and object detection in the literature rather than

evaluating segmentation performances. The proposed

segmentation method is therefore evaluated using a

similar procedure described in (Held et al., 2016). For

the evaluation, the best matching segment is assigned

to each ground-truth bounding box. For each ground

truth box gt, the set of non-ground points P

within

this box is identiﬁed. Then we assign the points P

to the segment s. The best matching segment to this

ground truth gt is found with Equation (12).

s = argmax

| P

∩ P

| (12)

After the best matching segment is assigned to the

ground truth gt, Equation (13) is used as an evalua-

tion metric.

E =

∑



∩ P

< τ



(13)

where 1 is an indicator function which is 1 if the input

is true and 0 otherwise. The τ

is a constant threshold.

Table 1: Segmentation accuracies.

Method % Errors

Spatial Only 13.8

Mean-shift 12.7

s-ddCRP (Tuncer and Schulz, 2016b) 9.4

Hybrid 9.1

ddCRP (Tuncer and Schulz, 2015) 8.9

Table (1) shows the segmentation accuracies for the

given methods. The proposed hybrid method pro-

vides better accuracy compared to the s-ddCRP seg-

mentation approach (Tuncer and Schulz, 2016b). The

s-ddCRP method uses a priori coming sequentially

from the previous time frames and clusters the grid

cells agglomerative into super grid cells. These super

grid cells make the s-ddCRP algorithm more prone

to segmentation errors. Because of stationary under-

segmented objects, which do not have temporal cues,

and the group of nearby pedestrians moving in the

same direction, the error rate stays around 9%. A clas-

siﬁcation module might improve these results, and,

thus, is part of our future work. In addition we

plan to provide detailed statistical analyses to demon-

strate the signiﬁcance of the improvement. Due to

the variant object sizes in 3D point cloud data, the

mean-shift method tends to generate over- and under-

segmentations, which results in a high error rate as

shown in Table (1). However, it is quite successful as

the ﬁrst step of our proposed hybrid method on deter-

mining whether the feature space of the blobs consists

one or more modes.

(a)

Figure 4: The averaged computation time comparisons of

the mean-shift, hybrid, s-ddCRP and ddCRP methods. Al-

gorithms are implemented in Matlab.

Figure (4) compares the averaged computation time

of the mean-shift, hybrid, s-ddCRP and ddCRP meth-

ods. According to the computational complexity

given in the Figure (4), the hybrid method’s averaged

computational time decreases below the scanning pe-

riod of the Lidar scanner, which is 100 ms, making

the algorithm able to run in real time.

6 CONCLUSION

We proposed a hybrid method for the segmentation of

3D point cloud data which uses the mean-shift and dd-

CRP approaches. The proposed framework beneﬁts

from the joint evaluation of geometrical and temporal

features to resolve ambiguities in complex dynamic

scenarios and to overcome the under-segmentation

problem of moving objects, i.e., assigning multiple

objects to one segment. For example, pedestrians of-

ten walk close to static objects so they are spatially

segmented together with their nearby objects. After

the motion ﬁeld of the environment is estimated in one

dimensional movement directions and the segmenta-

tion blobs are spatially extracted from the scene, the

mean-shift seeks the number of possible objects in the

state space of each blob. If the mean-shift algorithm

determines an under-segmented blob, the ddCRP per-

forms the ﬁnal partition in this blob. Otherwise, the

queried blob remains the same and it is assigned as

a segment. The proposed framework outputs a par-

titioning of the points in each time frame into dis-

joint segments, where each segment refers a single

object. Compared to the s-ddCRP and ddCRP seg-

mentation methods, incorporating the mean-shift and

ddCRP algorithms reduces the computational time re-

quirements of the system, which makes the algorithm

able to run in real time while having similar seg-

mentation accuracies. The autonomous vehicles’ sys-

tems segment the scene at the beginning of their per-

A Hybrid Method Using Temporal and Spatial Information for 3D Lidar Data Segmentation

169

ception pipeline so errors in segmentation propagates

throughout all the system. Better segmentation accu-

racy therefore improves other aspects of the system

such as tracking.

As future work, we plan to provide a detailed sta-

tistical analysis such as standard deviation to demon-

strate the signiﬁcance of the improvement on segmen-

tation. Also, showing the effect of segmentation accu-

racy on object tracking would be useful to reveal how

the under-segmentation problem effects the whole ob-

ject recognition system of an autonomous vehicle.

The presented method does not beneﬁt from the se-

quential nature of the problem. Adding a posterior

inference using prior knowledge from previous time

steps would speed up the overall system. The prior

knowledge obtained by the mean shift method could

also be used for this purpose.

Sub-sampling of 3D Lidar data by mapping indi-

vidual point measurements to an occupancy grid rep-

resentation and reduction of the motion estimation

into one dimension is sufﬁcient to successfully dis-

criminate moving objects from their neighbors such

as buildings or parked cars. However, because of

stationary under-segmented objects and the group of

pedestrians moving in the same direction, the er-

ror rate stays around 9%. Exploiting an appearance

model together with the features of the grid represen-

tation would help to detect stationary nearby objects

and to separate each pedestrian in a group moving to-

wards the same direction. Also, this error rate en-

courages us to integrate a classiﬁcation module as a

future work. Adding semantic cues would resolve the

under-segmentation problem of stationary nearby ob-

jects and, thus, improve the general segmentation ac-

curacy.

In addition, instead of estimating the motion of

the whole scene at each time step, the system might

decide to estimate only informative parts of the envi-

ronment by using semantic information. This could

further decrease the computational costs of the seg-

mentation and tracking components.

The detection of object classes would also be very

useful for the segmentation and tracking steps. To ob-

tain temporal information from the scene, applying

an iterative closest point approach would be interest-

ing instead of tracking each grid cell on an occupancy

grid. We intend to compare the performance of our

method with other novel algorithms proposed in the

literature.

ACKNOWLEDGEMENTS

We acknowledge the support by the EU’s Seventh

Framework Programme under grant agreement no.

607400 (TRAX, Training network on tRAcking in

compleX sensor systems) http://www.trax.utwente.nl/

REFERENCES

Azim, A. and Aycard, O. (2012). Detection, classiﬁcation

and tracking of moving objects in a 3d environment.

In Intelligent Vehicles Symposium (IV), 2012 IEEE,

pages 802–807. IEEE.

Bar-Shalom, Y. (1987). Tracking and data association.

Academic Press Professional, Inc.

Blei, D. M. and Frazier, P. I. (2011). Distance dependent

chinese restaurant processes. The Journal of Machine

Learning Research, 12:2461–2488.

Choi, J., Ulbrich, S., Lichte, B., and Maurer, M. (2013).

Multi-target tracking using a 3d-lidar sensor for au-

tonomous vehicles. In Intelligent Transportation

Systems-(ITSC), 2013 16th International IEEE Con-

ference on, pages 881–886. IEEE.

Comaniciu, D. and Meer, P. (2002). Mean shift: A robust

approach toward feature space analysis. IEEE Trans-

actions on pattern analysis and machine intelligence,

24(5):603–619.

Douillard, B., Underwood, J., Kuntz, N., Vlaskine, V.,

Quadros, A., Morton, P., and Frenkel, A. (2011).

On the segmentation of 3d lidar point clouds. In

Robotics and Automation (ICRA), 2011 IEEE Inter-

national Conference on, pages 2798–2805.

Fritsch, J., Kuhnl, T., and Geiger, A. (2013). A new per-

formance measure and evaluation benchmark for road

detection algorithms. In Intelligent Transportation

Systems-(ITSC), 2013 16th International IEEE Con-

ference on, pages 1693–1700. IEEE.

Fukunaga, K. and Hostetler, L. (1975). The estimation of

the gradient of a density function, with applications in

pattern recognition. IEEE Transactions on informa-

tion theory, 21(1):32–40.

Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).

Vision meets robotics: The kitti dataset. International

Journal of Robotics Research (IJRR).

Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we

ready for autonomous driving? the kitti vision bench-

mark suite. In Computer Vision and Pattern Recogni-

tion (CVPR), 2012 IEEE Conference on, pages 3354–

3361. IEEE.

Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B.

(2003). Bayesian data analysis. Chapman and

Hall/CRC Texts in Statistical Science.

Geman, S. and Geman, D. (1984). Stochastic relaxation,

gibbs distributions, and the bayesian restoration of im-

ages. IEEE Transactions on pattern analysis and ma-

chine intelligence, (6):721–741.

Held, D., Guillory, D., Rebsamen, B., Thrun, S., and

Savarese, S. (2016). A probabilistic framework for

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

170

real-time 3d segmentation using spatial, temporal, and

semantic cues. In Proceedings of Robotics: Science

and Systems.

Himmelsbach, M. and Wuensche, H.-J. (2012). Tracking

and classiﬁcation of arbitrary objects with bottom-

up/top-down detection. In Intelligent Vehicles Sym-

posium (IV), 2012 IEEE, pages 577–582. IEEE.

Klasing, K., Wollherr, D., and Buss, M. (2008). A clus-

tering method for efﬁcient segmentation of 3d laser

data. In Robotics and Automation, 2008. ICRA 2008.

IEEE International Conference on, pages 4043–4048.

IEEE.

Montemerlo, M., Becker, J., Bhat, S., Dahlkamp, H., Dol-

gov, D., Ettinger, S., Haehnel, D., Hilden, T., Hoff-

mann, G., Huhnke, B., et al. (2008). Junior: The

stanford entry in the urban challenge. Journal of ﬁeld

Robotics, 25(9):569–597.

Moosmann, F., Pink, O., and Stiller, C. (2009). Segmen-

tation of 3d lidar data in non-ﬂat urban environments

using a local convexity criterion. In Intelligent Vehi-

cles Symposium, 2009 IEEE, pages 215–220. IEEE.

Morton, P., Douillard, B., and Underwood, J. (2011). An

evaluation of dynamic object tracking with 3d lidar.

In Proc. of the Australasian Conference on Robotics

& Automation (ACRA).

Petrovskaya, A. and Thrun, S. (2009). Model based vehicle

detection and tracking for autonomous urban driving.

Autonomous Robots, 26(2-3):123–139.

Pitman, J. et al. (2002). Combinatorial stochastic processes.

Technical Report 621, Dept. Statistics, UC Berkeley,

2002. Lecture notes for St. Flour course.

Teichman, A., Levinson, J., and Thrun, S. (2011). Towards

3d object recognition via classiﬁcation of arbitrary ob-

ject tracks. In Robotics and Automation (ICRA), 2011

IEEE International Conference on, pages 4034–4041.

IEEE.

Tuncer, M. A. C¸ . and Schulz, D. (2015). Monte carlo based

distance dependent chinese restaurant process for seg-

mentation of 3d lidar data using motion and spatial

features. In Information Fusion (FUSION), 2015 18th

International Conference on, pages 112–118. IEEE.

Tuncer, M. A. C¸ . and Schulz, D. (2016a). Integrated object

segmentation and tracking for 3d lidar data. In Pro-

ceedings of the 13th International Conference on In-

formatics in Control, Automation and Robotics - Vol-

ume 2: ICINCO, pages 344–351.

Tuncer, M. A. C¸ . and Schulz, D. (2016b). Sequential dis-

tance dependent chinese restaurant processes for mo-

tion segmentation of 3d lidar data. In Information Fu-

sion (FUSION), 2016 19th International Conference

on, pages 758–765. IEEE.

Urmson, C., Anhalt, J., Bagnell, D., Baker, C., Bittner, R.,

Clark, M., Dolan, J., Duggins, D., Galatali, T., Geyer,

C., et al. (2008). Autonomous driving in urban envi-

ronments: Boss and the urban challenge. Journal of

Field Robotics, 25(8):425–466.

A Hybrid Method Using Temporal and Spatial Information for 3D Lidar Data Segmentation

171