
A Multi-objective Mathematical Model for Problems Optimization in
Multi-modal Transportation Network
Mouna Mnif
1
and Sadok Bouamamaa
1,2
1
ENSI, University of Manouba, COSMOS Laboratory, Tunisia
2
FCIT, University of Jeddah, K.S.A.
Keywords: Multimodal, Transportation Network, Optimization Problem, Mathematical Formulation, Multi-Objective
Optimization, Planning Problem.
Abstract: In order to reach a sustainable planning in a rather complicated transport system, it is of high interest to use
methods included in Operations Research areas. This study has been conducted to solve the transportation
network planning problems, in accordance with the optimization problem and multi-objective transport
network in multi-modal transportation. Firstly, we improve the implementation of the existing literature model
proposed in (Cai, Zhang, and Shao, 2010; Zhang and Peng, 2009) because after the conducted
experimentation, we show that there are two previously proposed constraints that make the solution
unrealizable for the transportation problem solving. Secondly, we develop the proposed multi-objective
programming model with linear constraints. Computational experiments are conducted to test the
effectiveness of the proposed model. The mathematical formulation is developed to contribute to success
solving the optimization problem, taking into account important aspects of the real system which were not
included in previous proposals in the literature, and review. Thus, it gives ample new research directions for
future studies.
1 INTRODUCTION
The multimodal transportation offers a full range of
transportation modes and routing options, allowing
them to coordinate supply, production, storage,
finance, and distribution functions to achieve the
most efficient relationships. The goal is to move from
the starting city to the destination city through other
intermediate cities, of which there are several routes
between two cities. In the multi-objective optimiza-
tion problem, the decision maker is charged by an
efficiency choice of existing routes in order to select
the best itinerary according to a compromise solution
between a set of objectives such as the minimization
of the transport cost and the duration of transport, the
maximization of service quality, etc.
The multimodal transportation network studies
were carried out by several problems such as
planning networks, shortest path, maritime or airline
with urban centers, freight transport, transmission
line, loading-unloading terminals, schedules, etc. The
focus of most widely research in the literature has
been based on planning network.
There are various measures to evaluate a multi-
modal path, for example, the travel cost, in-vehicle
time, waiting time, length, travel time, transfer time,
the number of transfers and so on. The optimization
and the operation research play an important role to
solve this problem. The main objective of this
problem is to determine the shortest and efficient way
of satisfying a set of objectives, and a set of
operational constraints according to customer
demands.
In general, the objective of a multimodal network
planning problem is to optimize reliable transport
chains for passenger or freight. The mathematical
formulation of the transit network design is usually
intractable by exact approaches. In (Wan and Lo,
2003) a MILP formulation that minimizes the
operating cost to a bus capacity constraint is
proposed. A characteristic of their formulation is that
it allows generating implicitly the structure of the
routes. However, this requires that a maximum
number of routes in the solution should be specified.
The objective minimizing the operating costs,
according to constraints within the system
considering the capacity and bounded exchange
action frequency.
The multimodal shortest path problem (M-SPP) is
concerned with finding a path from a specific origin
352
Mnif, M. and Bouamama, S.
A Multi-objective Mathematical Model for Problems Optimization in Multi-modal Transportation Network.
DOI: 10.5220/0006472603520358
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 352-358
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

to a particular destination in a given multimodal
network while minimizing total costs associated. The
complexity of finding multi-modal route is obviously
much higher than single modal one. The multi-criteria
multi-modal shortest path problem (MM-SPP) with
transfer delaying and arriving time-window
belongs to the set of problems, which are known as
NP-hard. In (Liu, Mu, and Yang, 2014; Liu, Yang,
Mu, Li, and Wu, 2013) the exact algorithms for
solving the MM-SPP to minimize the total travel time
have been suggested, in which the delaying time in
the transfer parking and the arriving at a time window
of destination are considered, as well as the total
travel cost.
Each case treated is defined by the specific
parameters at the problem type. Since, each variant
possesses its own characteristics, it requires a
different decision depending on the considered
context. These decisions are based on the
special characteristics of the transportation mode, and
on specific constraints of the treated problem. These
constraints are specified for each customer, vehicle,
mode, road or means of transport, as well as the type
of the problem.
Being based on the existing works of the literature
research, we have adopted a mathematical model,
while relying on the existent works with the
objectives, and constraints set to take into account the
recommendations made by experts according to the
hypotheses of our treated problem. This proposed
formulation will be cited and validated by tests, which
will be detailed in the rest of this paper.
The structure of our paper is organized as follows:
In section 2, we’ll present the construction model
with the proposed formulation in order to solve the
multi-objective and multimodal transportation
problem. Section 3 discusses our contribution and
motivation. Section 4 provides the proposed model by
some numerical experiments. Thereafter, in section 5
we will discuss a critical comment on our work by a
synthesis of the obtained results. Finally, section 6
concludes our work with a summary and proposes
some future research directions.
2 A MULTI-OBJECTIVE
MATHEMATICAL MODEL
The main objective of the multimodal network
problem is to determine a shortest and an optimal path
between a start point and an end point to according to
several criteria relating to the transportation mode or
the itinerary, etc., to satisfy a set of objectives that are
distinct to the treated case problem. In fact, a
multimodal problem requires the consideration of
multiple objectives and linked constraint of a
sequence of frequently used modes. For an optimal
choice of a transport mode or an itinerary by a
transport mode selected, the various criteria must be
taken into consideration, although these criteria are
conflicting.
The multi-objective optimization can be defined
as the problem that is finding a vector of decision
variables which satisfies all constraints and optimizes
a vector of objective functions. These functions from
a mathematical description of performance criteria
are usually in conflict with each other. In this paper,
we have treated a multi-objective optimization
problem. We consider the problem studied is to find
viable multimodal and multi-objective transport
processes, in order to minimize the total
transportation cost and the total time of the itinerary,
while respecting the arriving of goods at a customer
in the corresponding time window. First, we will
present and discuss the model of (Cai et al., 2010).
2.1 Model Assumptions and Code
Description
2.1.1 The Assumptions
Let us define the following assumptions as:
Only one mode of transport and a path can be
chosen between two nodes to carry the goods.
Transport costs are directly proportional to the
realization, namely, the choice of the quantity
and the unit transportation cost.
The limited capacity constraint of each mode is
respected.
If a vehicle arrives at the node before the start
date of his time window, he waits.
Transshipment of goods can only happen once
more at each node.
2.1.2 The Sets and Settings
N
: The set of all nodes;
K
: The set of transport mode;
Q : The total quantity of goods;
P : The maximum transfers duration;
p
i
: The delay period at node i if delay occurred;
f
i
: The overhead expenses per hour if delay occurred
at node i;
A Multi-objective Mathematical Model for Problems Optimization in Multi-modal Transportation Network
353

: The transport cost of a unit quantity from node i
to node j, by using k
th
transport mode;
: The fee for transport mode changed from k to l
at the node i;
: The transport time from node i to node j, with
k
th
transport mode selected;
: The largest time windows of cargos arriving
from node i to node j;
: The shortest time windows of cargos arriving
from node i to node j;
: The transfer time from transport mode k to the
transport mode l at the node i;
: The vehicle capacity from the k
th
transportation
mode.
: The number of vehicles used by the k
th
transportation mode in order to transport the
whole quantity of the freights. With,
upward, that returning the smallest
integral value that is not less than
2.1.3 The Decision Variables
The decision is related to the optimization process
which focuses on itinerary scheduling and the
decision of selecting each transportation mode of
corresponding transportation means. Thus, we need
to define the decision variables that explain the
variables associated with each considered parameter
of our treated problem. These decision variables are
used to express the constraints and optimization
criteria.
,
=
1 if the
transport mode is selected from to ,
0 otherwise
,
=
1 transport mode changed from to at ,
,
0 otherwise
=
1 if there is a delay at the node i
0 otherwise
2.1.4 The Formulation
The mathematical formulation is a determinant
step in the resolution step and the optimization step of
any problem. Indeed, it allows us to define and
characterize the sets, the parameters, the decision
variables, the optimization criteria and constraints
that will satisfy the specific decisions. The paper
presents an effective solution for determining the
shortest and efficient way of satisfying a certain set of
demands under several criteria and also a large set of
operational constraints. Our proposed formulation is
presented as follows:
Minimize
ii
Ni
i
lk
i
Ni Kk Kl
lk
i
k
ji
k
Ni Nj Kk
k
ji
pfuycxSC .....
,,
,,
(1)
(2)
0,...
0,...
,,
,,
,,
,,
i
Ni
i
lk
i
Ni Kk Kl
lk
i
k
ji
Ni Nj Kk
k
ji
Ni Nj
ij
Ni Nj
iji
Ni
i
lk
i
Ni Kk Kl
lk
i
k
ji
Ni Nj Kk
k
ji
puyaxttwMax
TWpuyaxtMax
(3)
Subject to
Njix
Kk
k
ji
,1
,
(4)
Njixx
k
ij
Kk
k
ji
,0
,,
(5)
Njiyxx
lk
i
l
ji
k
ij
,.2
,
,,
(6)
Niy
Kk Kl
lk
i
1
,
(7)
NiPay
lk
i
Ni Kk Kl
lk
i
,,
.
(8)
KlkNetjiyx
lk
i
k
ji
,,0,1,
,
,
(9)
The equations that describe this mathematical
formulation can be summarized as follows. Equation
(1) represents the first objective that seeks to
minimize the total cost of the multimodal network,
including the cost of the itinerary, transshipment cost
and overhead cost on delay. Equation (2) defines the
second objective, which seeks to minimize the total
duration of multimodal transportation, including the
period of the itinerary, changing period and delay
duration. Equation (3) expresses the third objective
that guaranteed the arriving at the destination in the
time window. Constraint (4) is specific to the
selection of transportation mode, that only one mode
of transport and one itinerary can be selected between
two nodes. If it is zero, it means that the i node is not
included in the transport. Equation (5) demonstrates
that in the itinerary the destination node is the start
node for the next itinerary. Constraint (6) shows that
i
Ni
i
lk
i
Ni Kk Kl
lk
i
k
ji
Ni Nj Kk
k
ji
puyaxt ...
,,
,,
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
354

the selection of the route should be ensured by a
continuous itinerary. Equations (7) and (8) are
relative to the transshipment constraints. Constraint
(7) indicates that one change of transport mode can
happen once at each node. Constraint (8) represents
the maximum time to be respected by the total
transshipment time. The decision-making variables
taking the integer binary value are described by the
equation (9).
3 CONTRIBUTION AND
MOTIVATION
In this paper, we have proposed a multi-objective
mathematical program inspired from (Cai et al., 2010)
and (Zhang and Peng, 2009). The authors have
addressed the multi-modal transport problem with
full loads at time limit. The problem is defined by the
search of a multimodal path in order to reach the
destination through several cities, knowing that there
are several transport modes possible between any two
cities. Each itinerary is characterized by a transport
duration, a cost, and a transportation capacity
between two cities. In fact, the authors proposed a
combination model for multi-modal transport of full
loads with time window constraint. The considered
assumptions are: firstly only one mode of transport
can be selected between two cities and secondly, the
transport cost is linear with distance. The same model
defined in (Zhang and Peng, 2009)is presented in (Cai
et al., 2010). The distinction parameters between our
mathematical formulation and the one presented by
(Cai et al., 2010; Zhang and Peng, 2009) are
presented as follows:
: The transport distance from i to j with the
transport mode selected, for j=i+1.
T: The time limit from start point to the end.
The distinction constraints that indicates:
The cargos to be arriving in limited time.
That a number of cargos cannot exceed the
capacity of conveyance.
The time-window between two nodes.
Although, we describe the main improvements
made to the literature model. The first objective is to
minimize the total cost of transport. This cost is
measured by the sum of three terms. At the
transportation cost term, we replaced the distance
parameter by a measured relative to the goods
transported (the number of used units of transport),
according to experts of the domain. In our case, we
will ignore the setting of the distance since there is
only one path between two nodes made by the same
transport mode k. We also note that it is useless to
consider the distance parameter when calculating the
transportation cost. On the other hand, we show the
importance of considering the goods quantity and the
number of transport units used in measuring the
transportation cost.
The third objective is provided by the
transformation of the time window constraint
, to an
objective, which assured to the goods arrive at a well-
determined interval of time. The main reason for this
transformation is on the one hand, in order to give
more chance to find a compromise solution, which
can be eliminated when it is a constraint. In fact, the
given solution of a problem must satisfy all the
constraints while minimizing (or maximizing) one or
more objectives. On the other hand, when it is an
objective we can easily play on their weight or
priority relative to the other objective. Moreover, that
we can find a solution that is preferred according to a
customer that will be eliminated by this constraint.
Indeed, the requirements of customers are different.
In some cases, the customer prefers that the arrival of
their goods, regardless of the time of this
merchandise’s arrival.
Pointing out the limitation of the previous
formulation is indicated as follows. Taking into
account the constraints (4) and (5) on the model of
(Cai et al., 2010), the model resolution remains non-
feasible. With regard to the definition of constraint (4)
that express that cargos will be arriving in limited
time, we consider that it is useless to introduce the
first part of the expression proposed by the authors.
So, we limit the constraint to its second part.
The constraint (5) makes it a non-feasible problem,
because if we consider the example of a product
fertilizer with a quantity Q = 122 tons, we can't
transport all this quantity in a single vehicle. One
railroad car can carry 61 tons of fertilizers. Therefore,
two railroad cars are needed if railway transport is
selected. Each car can carry 35 tons per vehicle, if the
road transport is chosen, the total of 3.5 cars,
therefore, four cars are needed to transport all the
quantity. Each boat can carry 10 tons, if water
transport is selected, a total of 12.2 vessels, is taken
A Multi-objective Mathematical Model for Problems Optimization in Multi-modal Transportation Network
355
as 13 boats. So, the equation (5) with these data are
expressed as the following: by railroad
mode, by road transport mode and
by maritime transport mode, which is an
impossible inequality. Consequently, this constraint
is missing a whole other decision variable. A new
parameter must be added a such as
that is the
number of vehicle used by the transport mode k.
Therefore, this constraint becomes,
. We consider the example test that is
provided by one compound fertilizer company
located in Linyi City.
The element of the first objective
depends only on to the parameter i,
so it must be replaced by
. In regards to
the element of the second objective
depends only on to the parameter i, so
it must be replaced by
. Therefore, the delay
in a city is compared to the desired arrival time.
When the index of the parameters are considered
according to i, j for j= i+ 1, then the passage is forced
by all the nodes according to an increasing order.
Therefore, the parameters should be defined by the
index i, j in order to guarantee that the choice of the
nodes and the order are provided by the model.
Based on the discussion of features, the
organization of multi-modal transportation modes,
and time-windows introduced, we defined a more
efficient model for multi-modal transport of full loads
with time-windows.
4 EXPERIMENTATION RESULTS
In this section, we present the obtained results that
show the capability of the proposed model for solving
a complex problem with multiple objectives (linear
and non-linear) simultaneously that proves their
efficiency in decision-making. This section is devoted
to presenting the computational experiments carried
out for assessing the performance of our
mathematical model. In fact, we implemented an
integer program for solving the multi-objective and
multimodal transportation networks planning models,
by using Concert Technology of CPLEX 12.4
Optimizers, with Microsoft Visual Studio 2010.
Computational experiments are conducted to test the
effectiveness of the proposed model.
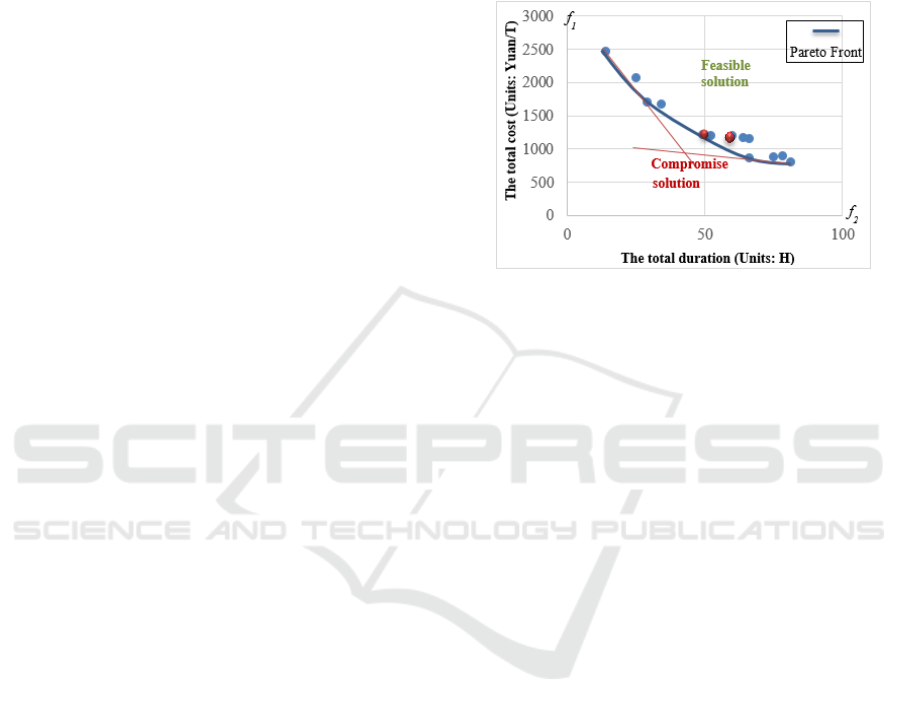
For a visual representation of the experimental
results, the reader is referred to Figure 1 as illustrated
below. The optimal solutions are represented by the
curve of the set of Pareto solution. The feasible
optimistic of the first objective vary between
max
Z
=
2475.200 Yuan and
min
Z
= 804.96 Yuan. The
optimistic solutions of the second objective vary
between
max
Z
= 81H and
min
Z
= 14 H. The optimistic
solutions of the third objective vary between
max
Z
=
81H and
min
Z
= 34 H. These solutions are obtained
by a set of tests sample generation.
Figure 1: Illustration of the Pareto optimality of a two
objectives minimization problem.
We observed that the third objective and the
second objective were synchronized objectives. But,
the two objectives are showing that they are clearly
contradictory with the first objective.
The overall measurement results are summarized
in Table 1 and 2 that are presented in the Appendix
section. The best solution that minimizes the first
objective gives a bad value for the second objective,
and vice versa. In this case, we must seek the solution
that satisfies the best compromise between these
objectives. This solution is presented in Figure 1 with
a red point, which is the closest value of the origin.
The Multiple Pareto optimal solutions based on five
distinct solutions found by the experimentations tests,
are represented by a blue curve in Figure 1. Hence, a
solution is called a Pareto optimal, if no feasible
vector exists which can decrease some criterion
without causing a simultaneous increase in at least
one criterion. In figure 1, a continuous line is used to
mark this boundary for a bi-objective minimization
problem in which, there is no single perfect solution
that minimizes both f
1
and f
2
. The aim is of
minimizing the compromise between the total cost
and the total duration for an itinerary of the
multimodal transportation network.
The set of all Pareto optimal solutions, called non-
dominated set or Pareto front, is located on the
boundary of the objective vector space (feasible
solution space) showing the tradeoff information
between the conflicting objectives. Instead, there are
compromises between optimal solutions such as the
solution presented by red. We can say that the
Compromise
solution
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
356

solutions presented in the Pareto front are more
optimistic than the dominated solutions.
The various solutions which belong to the front of
Pareto are optimistic solutions. However, the
decision-maker is provided by the search of the best
compromise solution between the goals, which is
included on the Pareto Front. The CPLEX tool uses
the dynamic mixed-integer programming (MIP) as a
search method, the balance optimality, and feasibility
MIP emphasis. Indeed, the relaxation solution
obtained by a Branch and Cut algorithm through a
deterministic parallel mode, uses up to 4 threads.
The definition of Pareto optimality is similar to
that of efficiency, and a Pareto optimal point in the
criterion space is often considered the same as a non-
dominated point. Therefore, a solution is considered
as Pareto optimal, in a multi-objective minimization
problem, if there exists no other feasible solution
which would decrease some criteria without causing
a simultaneous increase in at least one criterion. This
set also called Pareto front helps the decision maker
to identify the best compromise solution by an
elimination of inferior ones. Then, the retained
solution as elite is the one which has the best
compromise between all the objectives.
5 DISCUSSION AND COMMENTS
According to the tests achieved for our work, giving
the priority to the first objective by minimizing the
total cost is much better than giving the executing
priority of the total duration which perfectly complies
with the third objective that respects the arriving at a
time window. Therefore, we note that the first
objective significantly improves the results as shown
in the Appendix.
For real case problems, the mathematical
formulation is not always reliable for a user, since we
cannot consider fixed rules for all possible
alternatives and treated cases associated with each
customer. According to the experts of a transit
company, the choice of transportation mode is
depends on the several factors, such as customer
requirements, the nature, and characteristics of the
goods, that can be a major condition for the selection
of the mode's problem. There are several features of
the goods, such as the expensive, bulky or perishable
goods, also the goods category or type such as
dangerous, fragile, light, stackable or non-stackable
goods, etc.
On the basis of the promising findings presented in
this paper, further research will be needed to solve
more optimization constraints. Artificial intelligence
approaches to the issue are still required. (Bouamama,
2010) proposed a multi-agent approach based on a
dynamic, distributed Practical Swarm Optimization
algorithm, which is proven to be useful for hard
optimization problems. (Mathlouthi and Bouamama,
2015) proposed two new approaches, a centralized
and distributed honey-bee optimization, enhanced by
a new parameter called local optimum detector. These
two approaches are applied to solve the maximal
constraint satisfaction problems.
6 CONCLUSIONS AND FUTURE
WORKS
This paper presents a new mathematical model in
order to solve multi-modal transport problems that
satisfy multiple objectives according to several
criteria. The proposed multi-objective model is
defined by three objectives, the minimization of the
total cost, and the total duration of an itinerary while
respecting the arriving of goods to a customer at the
time window.
In fact, the following conclusions can be drawn
as: Firstly, an improvement over the literature model
was achieved in order to find feasible solutions.
Secondly, a validation of our proposed model by
implementation. Thirdly, we summarized our work
by computation's test and experimentation results in
order to prove the efficiency of our model.
This paper presents a decision method based on a
mathematical model which plays a significant role in
resolving the transportation problem. Although there
has been a fruitful development of models and
solution techniques to solve this problem by a
relevant decision in transport networks, many future
pieces of research prospects are still missing, such as
the following:
There are still opportunities for integrating
problems that can be solved separately, by using a
multi-criteria analysis approach.
The development of robust, or dynamic
approaches used to solve a planning problem.
The consideration of several types of
products, around on the corresponding product’s
cluster with the same characteristics, since the
choice of the transport mode depends on the
product volume and the value associated with
each product.
The activation or cancellation of a goal according
to customer wishes by adding weights to each
objective, according to the client's need.
A Multi-objective Mathematical Model for Problems Optimization in Multi-modal Transportation Network
357

REFERENCES
Bouamama, S. (2010). A New Distributed Particle Swarm
Optimization. Knowledge-Based and Intelligent
Information and Engineering Systems, 312–321.
Cai, Y., Zhang, L., and Shao, L. (2010). Optimal multi-modal
transport model for full loads with time windows. 2010
International Conference on Logistics Systems and
Intelligent Management, ICLSIM 2010, 1, 147–151.
Liu, L., Mu, H., and Yang, J. (2014). Toward algorithms for
multi-modal shortest path problem and their extension in
urban transit network. Journal of Intelligent
Manufacturing, Springer S.
Liu, L., Yang, J., Mu, H., Li, X., and Wu, F. (2013). Exact
algorithms for multi-criteria multi-modal shortest path
with transfer delaying and arriving time-window in urban
transit network. Applied Mathematical Modelling, 38(9–
10), 2613–2629.
Mathlouthi, I., and Bouamama, S. (2015). A family of honey-
bee optimization algorithms for Max-CSPs.
International Journal of Knowledge-Based and
Intelligent Engineering Systems, 19(4), 215–224.
Wan, Q. K., and Lo, H. K. (2003). A Mixed Integer
Formulation for Multiple-Route Transit Network Design.
Journal of Mathematical Modelling and Algorithms,
2(4), 299–308.
Zhang, L., and Peng, Z. (2009). Optimization model for
multi-modal transport of full loads with time windows.
Proceedings - International Conference on Mana-
gement and Service Science, MASS 2009.
APPENDIX
Table 1: The experimentations tests in order of priority: objective 2 then objective 1.
Objective
IInf
Best integer
Cuts/Best Bound
ItCnt
Gap
Solutions
S1
Z2*
25
1
--
2
integral
0
14
14
1
0.00%
Z1 if Z2*
2475.2
S2
Z1 if Z2<=29
2003.40
2
--
2
integral
0
1701.57
1701.57
2
0.00%
S4
Z1 if Z2<=64
2725.69
8
---
3
904.3059
6
2725.69
904.3059
8
66.82%
1244.74
904.3059
8
27.35%
1158.2820
2
1244.74
Cuts:7
11
6.95%
1169.49
1158.2820
11
0.96%
Cutoff
1169.49
11
0.00%
S5
Z1 if Z2<=75
1455.72
8
--
4
827.544
2
1455.72
827.544
8
43.15%
1168.19
827.544
8
29.16%
878.02
1
1168.19
Cuts:4
9
24.84%
884.62
878.02
9
0.75%
883.62
878.02
9
0.63%
Cutoff
883.62
883.62
9
0.00%
Table 2. The experimentations tests in order of priority: objective 1 then objective 2.
Objective
IInf
Best integer
Cuts/Best Bound
ItCnt
Gap
Solutions
S1
Z1*
1153.89
2
--
2
integral
0
804.96
804.96
2
0.00%
Z2 if Z1*
81
S2
Z2? if
Z1<=1170
75.0
5
--
3
51.6294
6
75.0
51.6294
5
31.16%
66.0
51.6294
5
21.77%
64.0
51.6294
5
19.33%
cutoff
64.0
5
0.00%
S3
Z2? if
Z1<=1500
75.0
7
---
3
37.4761
3
75.0
37.4761
7
50.03%
49.0
37.4761
7
23.52%
46.0
37.4761
7
18.53%
39.2491
9
46.0
Cuts:5
13
14.68%
Cutoff
46.0
46.0
13
0.00%
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
358
