Conformance Checking in Integration Testing of Time-constrained

Distributed Systems based on UML Sequence Diagrams

Bruno Lima and João Pascoal Faria

Faculty of Engineering, University of Porto, Porto, Portugal

INESC TEC, Porto, Portugal

Keywords:

Model-based Integration Testing, Conformance Checking, Distributed Systems, Time Constraints, UML.

Abstract:

The provisioning of a growing number of services depends on the proper interoperation of multiple products,

forming a new distributed system, often subject to timing requirements. To ensure the interoperability and

timely behavior of this new distributed system, it is important to conduct integration tests that verify the inter-

actions with the environment and between the system components. Integration test scenarios for that purpose

may be conveniently speciﬁed by means of UML sequence diagrams (SDs) enriched with time constraints.

The automation of such integration tests requires that test components are also distributed, with a local tester

deployed close to each system component, coordinated by a central tester. The distributed observation of exe-

cution events, combined with the impossibility to ensure clock synchronization in a distributed system, poses

special challenges for checking the conformance of the observed execution traces against the speciﬁcation,

possibly yielding inconclusive verdicts. Hence, in this paper we investigate decision procedures and criteria

to check the conformance of observed execution traces against a speciﬁcation set by a UML SD enriched with

time constraints. The procedures and criteria are speciﬁed in a formal language that allows executing and

validating the speciﬁcation. Examples are presented to illustrate the approach.

1 INTRODUCTION

In a growing number of domains, the provisioning of

end-to-end services to the users depends on the proper

interoperation of multiple products (devices, applica-

tions, etc.) from different vendors, forming a new dis-

tributed system, often subject to timing requirements.

Examples can range from sports monitoring applica-

tions (Taylor, 2015) to fall detection systems for se-

niors (Lima and Faria, 2016) or IoT systems.

To ensure interoperability and the timely behavior

of such distributed systems, it is important to conduct

integration tests that verify the interactions between

the system components and with the environment. In-

tegration test scenarios for that purpose may be con-

veniently speciﬁed by means of UML Sequence Di-

agrams (OMG, 2015) (SDs), because they are an in-

dustry standard well suited for describing and visual-

izing the interactions that occur between the compo-

nents and actors of a distributed system.

In previous work (Lima and Faria, 2016) we pro-

posed an overall approach to automate the integra-

tion testing in distributed and heterogeneous systems.

The only manual activity required is the description

of the participants and behavior of the services un-

der test with UML SDs. In the proposed approach,

a local tester is deployed close to each system com-

ponent, coordinated by a central tester. However, the

distributed observation of execution events by the lo-

cal testers, combined with the impossibility to ensure

clock synchronization in a distributed system, poses

special challenges for checking the conformance of

observed execution traces against the speciﬁcation.

The main contributions of this paper are novel

decision procedures and criteria to check the con-

formance of distributed execution traces against a

speciﬁcation set by a UML SD enriched with time

constraints. The procedures and criteria are speci-

ﬁed in the VDM formal language (Fitzgerald et al.,

2005)(Larsen et al., 2016), which allows executing

and validating the speciﬁcation. Examples are pre-

sented to illustrate the approach.

Section 2 presents background on our approach

for the integration testing of distributed systems; sec-

tion 3 presents the decision procedures and criteria for

conformance checking in the presence of time con-

straints; related work is presented in section 4; sec-

tion 5 concludes the paper.

Lima, B. and Faria, J.

Conformance Checking in Integration Testing of Time-constrained Distributed Systems based on UML Sequence Diagrams.

DOI: 10.5220/0006474004590466

In Proceedings of the 12th International Conference on Software Technologies (ICSOFT 2017), pages 459-466

ISBN: 978-989-758-262-2

459

2 BACKGROUND

In previous work (Lima and Faria, 2016) we proposed

a scenario-based approach for automating the integra-

tion testing of end-to-end services in distributed and

heterogeneous systems.

Test scenarios are speciﬁed using an accessible

front-end notation such as UML SDs, which are au-

tomatically translated to a back-end formal notation

suitable for efﬁcient test input generation and confor-

mance checking at runtime. At the end of test execu-

tion, test results (errors and coverage information) are

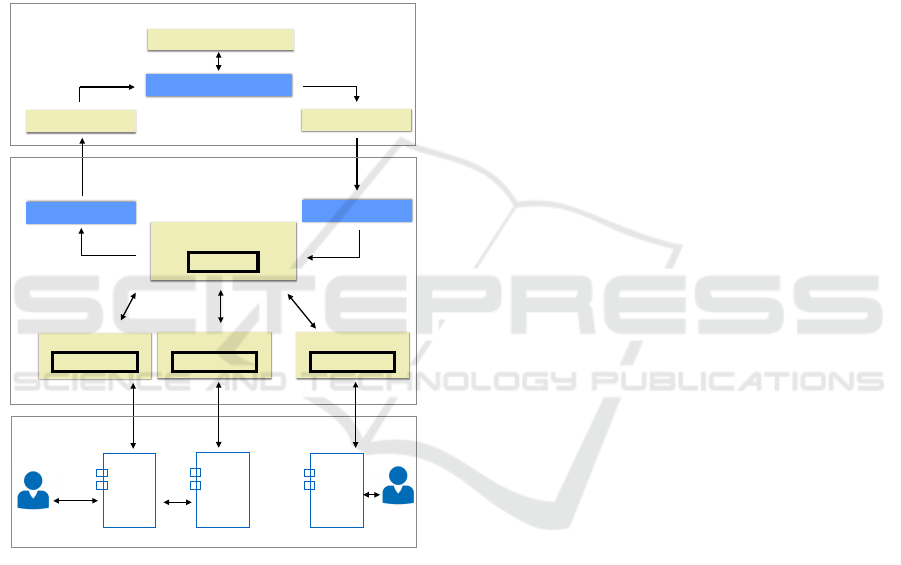
mapped back to the front-end notation (see Figure 1).

Visual Behavioral Model

Translation Tool

Modeling Tool

Mapping Tool

Formal Runtime Model

Test Results

…

Central Tester

System Under Test

Component

Under

Test

…

CUT

Distributed Test Generation and Execution Engine

Visual Modeling Environment

Global State

Local Tester 1

Local State 1

LT 2

Local State 2

LT N

Local State n

Figure 1: Architecture for model-based integration testing

of distributed systems (Lima and Faria, 2016).

We follow an online model-based testing (MBT)

strategy (or adaptive), to cope with non-determinism

common in distributed systems. In an online strategy,

test generation and execution are performed together,

allowing test inputs to be decided based on the outputs

observed so far (Utting and Legeard, 2007).

In order to be able to check not only the inter-

actions with the environment but also the interac-

tions between the components of the system under

test (SUT), we follow a hybrid test architecture, in

which a local tester is deployed close to each system

component, and a central tester coordinates the lo-

cal testers (see Figure 1). This is more effective than

a purely centralized approach or a purely distributed

approach, meaning that more conformance errors can

be detected (Hierons, 2014).

In the case of a component under test (CUT) that

interacts with actors (users or external applications)

in the environment (see Local Tester 1 in Figure 1),

the local tester is responsible for simulating the ac-

tors, injecting the inputs from the actors to the CUT

(acting as a test driver) and monitoring and checking

the outputs from the CUT to the actors (acting as a

test monitor). Besides that, it is also responsible for

monitoring all the messages exchanged between that

CUT and the rest of the SUT. In the case of a CUT

that does not interact with the environment (see Local

Tester 2 in Figure 1), the local tester is responsible for

monitoring and checking all the messages exchanged

between that CUT and the rest of the SUT, acting as a

test monitor.

In such a test architecture, it is important to mini-

mize the communication overhead during test execu-

tion, namely in the presence of time constraints. It is

equally important to detect errors as early as possible

and closely as possible to the offending component, to

provide more helpful test reports and facilitate fault

localization. To that end, besides the test monitor-

ing and control activities, model execution and con-

formance checking activities need also be distributed.

In more recent work (Lima and Faria, 2017) we

investigated distributed conformance checking but

without taking time observation and time constraints

into consideration.

3 CONFORMANCE CHECKING

WITH TIME CONSTRAINTS

As said before, conformance checking in the presence

of time constraints in a distributed system is specially

challenging. Hence, in this section, we investigate the

decision procedures and criteria to check the confor-

mance of observed execution traces against a speci-

ﬁcation set by a UML SD enriched with time con-

straints.

As in our previous work, the decision procedures

and criteria are speciﬁed with the VDM formal spec-

iﬁcation language (Fitzgerald et al., 2005)(Larsen

et al., 2016), to enable us to execute and validate the

speciﬁcation with a support tool, such as Overture

(http://overturetool.org/).

Before investigating the conformance procedures

and criteria, we need to formalize the structure and

semantics of time-constrained SDs.

ICSOFT 2017 - 12th International Conference on Software Technologies

460

3.1 Time-constrained SDs

UML SDs may be annotated with time con-

straints (OMG, 2015). Although the UML standard

allows the speciﬁcation of more complex constraints,

in this paper we restrict our attention to the types

of time constraints that are commonly addressed in

the literature of time-constrained distributed systems

(see Related Work) and are most relevant in practice:

constraints that specify the minimum and maximum

delays (time elapsed) between two events (message

sending or receiving) in the same lifeline, or between

the sending and receiving of a message between two

lifelines. We assume that the minimum and maximum

delays are constant values (or expressions that can be

evaluated before the scenario execution).

{0..2}

{0..5}

{0..2}

Figure 2: Example of a time-constrained SD.

Figure 2 presents a scenario with that type of

time constraints in UML. Each interval is denoted

{min..max}, where min or max can be omitted. De-

noting by ti the time instant of event ei, the only

valid execution trace deﬁned by this SD is the time-

constrained trace [(e1, t1), (e2, t2), (e3, e3), (e4, t4)]

with t2 ∈ [t1, t1 + 2], t3 ∈ [t2, t2 + 2], t4 ∈ [t3, t3 +

2] and t4 ∈ [t1, t1 + 5]. An example of a valid

timed trace (with the time instant of each event) is

[(e1, 1), (e2, 3), (e3, 4), (e4, 5)]. An example of an in-

valid timed trace is [(e1, 1), (e2, 3), (e3, 5), (e4, 7)].

To check if an observed trace is valid, besides ver-

ifying if the observed events occurred by a certain or-

der, it is also necessary to verify if their time instants

satisfy the time constraints deﬁned in the SD, as will

be formalized in the next two subsections. We start by

computing the valid time-constrained traces deﬁned

by a SD.

In UML, an SD is a variant of an Interaction

(OMG, 2015). Figure 3 presents an excerpt of the

formalization of the structure of Interactions in VDM,

highlighting the elements added to support time con-

straints as compared to our previous work (Lima and

Faria, 2017). For simplicity, we omit the deﬁnition

of combined fragments (which can be found in our

previous work), integrity constraints, and some ba-

sic types. An Interaction comprises a set of lifelines

(representing in our case CUTs or actors), messages

(restricted in our case to asynchronous messages, al-

though synchronous messages could easily be han-

dled), combined fragments and time constraints. For

each message, we deﬁne the locations of the send and

receive events (sendEvent and receiveEvent), and

the (optional) variables that represent the instants of

time of occurrence of those events (sendTimestamp

and rcvTimestamp).

A TimeConstraint imposes minimum and max-

imum values on the time that can elapse between two

events (identiﬁed by the timestamp variables). Either

the minimum or the maximum may be omitted.

3.2 Valid Traces deﬁned by a

Time-constrained SD

In general, the semantics of an Interaction is ex-

pressed in terms of two sets of valid and invalid traces

(OMG, 2015). In this paper, we don’t handle the

rarely used constructs for deﬁning invalid traces (such

as the neg operator), so only the valid traces are rele-

vant here. A trace is a sequence of event occurrences

(OMG, 2015), corresponding, in this context, to the

emission or reception of messages at lifelines. Fig-

ure 3 shows the structure of traces in VDM with tim-

ing information, by means of an optional timestamp

associated with each event. Depending on the context,

the timestamp may be a variable (as in (e1, t1)) or a

concrete value (as in (e1, 1)). In this paper we assume

a discrete time scale (in an appropriate unit, such

as seconds or microseconds), but a continuous scale

would equally work. Hence, time instants (Time) and

elapsed time (Duration) are represented by natural

numbers.

Since we are dealing with distributed systems, we

assume there is no global clock, so time instants are

measured with the local clocks. Although it is impos-

sible to ensure perfect clock synchronization between

lifelines, in practice we can assume, like other authors

did (see Related Work), that there is a maximum dif-

ference (or skew) between the readings of any two

clocks (MaxClockSkew). For example, the Network

Time Protocol (NTP) (Mills, 1991), designed to syn-

chronize the clocks of computers over a network to a

common timebase (usually UTC), achieves synchro-

nization accuracies of 10 ms over Internet, and 1 ms

on LAN.

For computing the set of valid traces deﬁned

by an Interaction with time constraints (see func-

tion validTraces in Figure 4), we ﬁrst com-

pute the valid traces ignoring time constraints

(validTracesUntimed), following a procedure pre-

sented in our previous work for SDs without time con-

straints (Lima and Faria, 2017), and subsequently ex-

clude the traces for which the deﬁned time constraints

Conformance Checking in Integration Testing of Time-constrained Distributed Systems based on UML Sequence Diagrams

461

types

Interaction ::

lifelines : Lifeline-set

messages : Message-set

combinedFragments: CombinedFragment-set

timeConstraints : TimeConstraint-set;

Message ::

id : MessageId -- unique

sendEvent : LifelineLocation -- unique

receiveEvent : LifelineLocation -- unique

signature : MessageSignature -- may not be unique

sendTimestamp: [Variable] -- unique

recvTimestamp: [Variable]; -- unique

LifelineLocation = Lifeline  Location;

TimeConstraint ::

firstEvent : Variable --identified by timestamp var.

secondEvent: Variable-- identified by timestamp var.

min : [Duration]

max : [Duration];

Variable :: name : String;

Trace = Event*; -- seq of 0 or more

Event ::

type : EventType

signature: MessageSignature

lifeline : Lifeline

timestamp: [Variable|Time];

EventType = <Send> | <Receive>;

Time = ℕ;

Duration = ℕ;

TimeInterval = [Time]  [Time]; -- (min, max) pair

values

MaxClockSkew : Duration = 10; -- configurable

Figure 3: Interactions and traces.

are not satisﬁable (function isSatisfiable). A set C

of time constraints is satisﬁable for a trace t if there is

an assignment of non-decreasing time instants to the

event occurrences in t that satisﬁes all the time con-

straints in C. Before explaining the procedure for de-

termining satisﬁability, we start by presenting a run-

ning example.

Figure 5 presents a SD that describes a real sce-

nario of a fall detection service. In this scenario, a

care receiver has a smartphone that has installed a fall

detection application. When this person falls, the ap-

plication detects the fall and provides the user a mes-

sage which indicates that it has detected a drop giving

the possibility for the user to conﬁrm whether he/she

needs help. If the user responds that he/she does not

need help, the application does not perform any ac-

tion; however, if the user conﬁrms that needs help or

does not respond within 10 seconds, the application

sends an alert to a web application called AAL4ALL

Portal. In addition to the time constraint of 10 seconds

between a reception of the conﬁrmation request and

the user response, other time restrictions are also rep-

resented, namely one second as the maximum deliv-

ery time of the messages and 13 seconds between the

sending of the notiﬁcation to the user and the sending

functions

-- Gives the set of valid traces defined by an

-- Interaction.

validTraces: Interaction Trace-set

validTraces(sd) ≜ {t | t  validTracesUntimed(sd) 

isSatisfiable(t, sd.timeConstraints)};

-- Checks if a set of time constraints (C), imposing

-- min/max delays between pairs of events, is

-- satisfiable for a trace t.

isSatisfiable: Trace  TimeConstraint-set 𝔹

isSatisfiable(t, C) ≜

let cp = getConstrainedPairs(t, C),

minGiven= {mk_(i,i+1)↦0 | i  {1,...,|t|-1}} ++

{mk_(i,j)↦c.min |

mk_(i,j,c)  cp  c.min  nil},

maxGiven= {mk_(i,j)↦c.max |

mk_(i,j,c)  cp  c.max  nil},

minDeriv= longestDistances(minGiven),

maxDeriv= shortestDistances(maxGiven)

in ∄ p  dom minDeriv  dom maxDeriv 

 minDeriv(p) > maxDeriv(p);

-- Given trace t and time constraints C, returns

-- tuples (i,j,c) of indices i and j of events in t

-- that are subject to a constraint c in C.

getConstrainedPairs: Trace  TimeConstraint-set

(ℕ ℕ TimeConstraint)-set

getConstrainedPairs(t, C) ≜

{mk_(i,j,c) | i  inds t, j  inds t, c  C 

i < j

 t

.timestamp = c.firstEvent

 t

.timestamp = c.secondEvent

 ∄ k  {i+1, ..., j-1} 

.timestamp c.firstEvent,c.secondEvent}};

Figure 4: Valid traces deﬁned by an Interaction with time

constraints.

of the alert message in case of no response.

In this example, if time constraints are ignored,

there are ﬁve valid traces (see Valid Traces Untimed

in Figure 5). The last two traces correspond to per-

mutations of the third trace in which event e4 occurs

after events e11 and/or e12. This happens because, if

time constraints are ignored, the presented SD doesn’t

impose any relative ordering between event e4 and

events e11 and e12. However, if time constraints are

considered, those traces are no longer valid. In fact, it

is easy to check that the deﬁned time constraints are

not satisﬁable for those traces: event e4 must occur

up to 1 time unit after e3, whilst event e11 must occur

at least 13 time units after e3, so e4 cannot occur after

e11.

Let’s return to the procedure for determining satis-

ﬁability of time constraints. For the type of time con-

straints we are considering in this paper, satisﬁability

can be determined in polynomial time, following the

steps depicted in Figure 4 (function isSatisfiable)

and explained next:

1. compute the pairs of event occurrences (identiﬁed

by their indexes in t) that are subject to a time con-

straint (variable cp); as illustrated in Figure 7, in

case of multiple occurrences of the same event in

an execution trace (caused by loops), we assume

ICSOFT 2017 - 12th International Conference on Software Technologies

462

confirm? {..1}

Fall Detection

APP

Care Receiver

alt

e1e1

e4e4

e2e2

e3e3

e5e5

e6e6

e7e7

e8e8

fall_signal

yes {..1}

notify_fall

AAL4ALL

Portal

no {..1}

e9e9

e10e10

e11e11

e12e12

notify_possible_fall

Valid Traces Timed:

[e1, e2, e3, e4, e5, e6, e7, e8],

[e1, e2, e3, e4, e9, e10],

[e1, e2, e3, e4, e11, e12]

Unintended Traces Timed:

{}

Unintended Traces Untimed:

[e1, e2, e3, e4, e5, e11,  ],

[e1, e2, e3, e4, e9, e11,  ],

[e1, e2, e3, e4, e11, e5,  ],

[e1, e2, e3, e4, e11, e9,  ],

[e1, e2, e3, e4, e11, e12, e5,  ],

[e1, e2, e3, e4, e11, e12, e9,  ],

[e1, e2, e3, e11,  ]

Uncheckable Locally Timed: {}

Valid traces involving inter-lifeline

constraints:

[e1, e2, e3, e4, e11, e12], 

Invalid traces that are locally valid, caused

by optional messages lost:

[e1, e2, e3, e4, e11], 

Invalid traces that are locally valid, caused

by inter-lifeline constraints not respected

(and possibly messages lost):

[e1, e2, e3, e11, e12, e4, e9]

Uncheckable Locally Untimed:

{..10}

{13..}

Valid Traces Untimed:

[e1, e2, e3, e4, e5, e6, e7, e8],

[e1, e2, e3, e4, e9, e10],

[e1, e2, e3, e4, e11, e12] ,

[e1, e2, e3, e11, e4, e12] ,

[e1, e2, e3, e11, e12, e4]

Figure 5: Example of a fall detection scenario with time

constraints.

that time constraints apply only to pairs of closest

occurrences;

2. create two weighted directed acyclic graphs (dag)

representing the minimum and maximum delays

between pairs of event occurrences, based on the

ordering of event occurrences in t and the result of

the ﬁrst step (variables minGiven and maxGiven);

3. derive weighted dags with the longest and shortest

distances between all pairs of connected vertexes

in graphs minGiven and maxGiven, respectively

(variables minDerived and maxDerived, repre-

senting derived minimum and maximum delays);

4. check that there aren’t pairs of event occurrences

(identiﬁed by their indexes in t) constrained by in-

compatible derived minimum and maximum de-

lays.

Figure 6 illustrates the application of this proce-

dure for trace [e1, e2, e3, e11, e4, e12] in Figure 5. We

conclude that the trace is invalid because of the con-

ﬂicting minimum and maximum delays required be-

tween events e3 and e4.

3.3 Conformance Checking based on

Distributed Observations

In general an observed global trace t conforms to the

speciﬁcation if it belongs to the set of valid traces

(computed as explained in the previous section) and

satisﬁes the time constraints.

However, in distributed testing, global traces are

not directly observed, but only the local traces ob-

served at each lifeline, which raises the need to infer

isSatisfiable([e1, e2, e3, e11, e4, e12])?

e12e4e11e3e2e1

0 0

2a. Min delays given:

2b. Max delays given:

e12e4e11e3e2e1

1. Constrained pairs of event occurrences:

{..1}

{13..}

e12e4e11e3e2e1

0 0

3a. Min delays derived (longestDistances(minGiven)):

e4e3

Max: 1

Min: 13

4. Conflicting min/max delays

…

… …

3b. Max delays derived (shortestDistances(maxGiven)):

e12e4e11e3e2e1

Figure 6: Example of satisﬁability checking.

e3e3

e4e4

e2e2

e1e1

loop

e5e5

e6e6

e7e7

e8e8

{0..10}

{0..5}

{0..12}

[e1, e2, e3, e4, e5, e6, e3, e4, e5, e6, e7, e8]

5 12

Figure 7: Example of computation of constrained pairs in

the presence of multiple occurrences of the same event.

global traces from the observed local traces, possibly

leading to inconclusive verdicts.

In distributed testing, conformance checking is

best performed in two phases: ﬁrst, local confor-

mance checking is performed at each lifeline in and

incremental way and, in case a local failure is de-

tected, the test fails globally; secondly, in case all lo-

cal checks pass, conformance checking is performed

globally. For some scenarios (called locally observ-

able), the second step is not needed, but the deter-

mination of conditions upon which such step is not

needed is outside the scope of this paper.

Conformance Checking in Integration Testing of Time-constrained Distributed Systems based on UML Sequence Diagrams

463

For performing incremental conformance check-

ing locally, we assume that each local tester receives

a speciﬁcation of the traces to be accepted locally

and the time constraints checkable locally at the begin

of test execution. For performing ﬁnal conformance

checking globally, we assume that the global tester

receives from the local testers the traces observed lo-

cally at the end of test execution.

We present in Figure 8 the primitives to perform a

ﬁnal conformance check globally by the central tester.

Our procedure for determining if the observed local

traces (including timestamp values) conform to the

speciﬁcation (SD), comprises the following steps (see

function finalConformanceCheck):

Step 1. Obtain the set V of valid traces (with

timestamp variables, but not timestamp values) de-

ﬁned by the given SD, as explained in the previous

section. This step is performed only once per SD.

Step 2. Compute the set J of all feasible joins of

the traces observed locally (with timestamp values).

By a feasible join we mean a global trace obeying

the following conditions: (i) the projections onto the

lifelines yield the local traces (ensured incrementally

by joinActualTraces); (ii) messages cannot be re-

ceived before being sent, although they can be lost

in the transmission channel (ensured incrementally by

isFeasibleAddition); (iii) event occurrences from

different lifelines must be ordered in a way consis-

tent with their time instants, considering the maxi-

mum clock skew deﬁned (ensured incrementally by

isFeasibleAddition). Since we assume that only

the message signature is guaranteed to be observable,

in the presence of multiple message occurrences with

the same signature, we can only make sure that, at any

given point in the trace under analysis, the number of

’send’ occurrences is greater or equal to the number

of ’receive’ occurrences (see isFeasibleAddition).

In practice, there is only one or a few possible joins.

Step 3. If all feasible joins match at least one valid

global trace, the test passes. A trace with timestamp

values (actual trace) matches a trace with timestamp

variables (formal trace) if they are identical when

timing information is removed (matchesUntimed),

and the former satisﬁes the time constraints asso-

ciated with the latter. Because of the clock skew

between lifelines, checking inter-lifeline constraints,

and hence matching, may yield an inconclusive result

(see checkConstraint in Figure 8 and Figure 9).

Step 4. If all the feasible joins fail to match all

valid global traces, the test fails. Otherwise, we get

an inconclusive result.

Examples of traces yielding different verdicts are

shown in Figure 10.

For the sake of completeness, we present in Figure

types

Verdict = <Pass> | <Inconclusive> | <Fail>;

-- dislayed from best to worse

functions

-- Global conformance checking, given the observed

-- local traces.

finalConformanceCheck: Interaction Lifeline

𝑚

→

Trace)  Verdict

finalConformanceCheck(sd, localTraces) ≜

let V = validTraces(sd), C = sd.timeConstraints,

J = joinActualTraces([], localTraces),

in if ∀jJ∀vVmatches(j,v,C)=<Fail>then<Fail>

elseif∀jJ∃vVmatches(j,v,C)=<Pass>then<Pass>

else<Inconclusive>;

-- Gives the feasible joins of traces from different

-- lifelines, respecting the order of events per trace

-- and message. The first argument is an accumulator

-- for already processed events (initially empty).

joinActualTraces: Trace(Lifeline

𝑚

→Trace)  Trace-set

joinActualTraces(t, m) ≜

if  l  dom m m(l) = [] then {t}

else⋃ {joinActualTraces(t↷[hd m(l)],m++{l↦ tl m(l)})

| l dom m  m(l)  [] 

isFeasibleAddition(t, hd m(l))};

-- Checks if an event occurrence is a feasible

-- addition to a trace, i.e., respects the fact that

-- messages can only be received after being sent, and

-- respects timestamp ordering.

isFeasibleAddition: Trace Event  𝔹

isFeasibleAddition(t, e) ≜

(e.type = <Receive> 

#{i | i inds t t

.type = <Send> 

 t

.signature = e.signature} >

#{i | i inds t  t

.type = <Receive> 

 t

.signature = e.signature})

(∀ f t  e.timestamp ≥ f.timestamp -

(iff.lifeline=e.lifeline then0elseMaxClockSkew));

-- Checks if an actual trace (a) matches a formal

-- trace (f), given a set of time constraints (C).

matches: Trace  Trace  TimeConstraint-set  Verdict

matches(a, f, C) ≜

if  matchesUntimed(a, f) then <Fail>

else worseVerdict({checkConstraint(a

,c) |

mk_(i,j,c) getConstrainedPairs(f,C)});

-- Checks if an actual trace (a) matches a formal

-- trace (f), ignoring time constraints.

matchesUntimed: Trace  Trace  𝔹

matchesUntimed(a, f) ≜

|a| |f|   i inds a 

 mu(a

, timestamp ↦ nil) mu(f

, timestamp ↦ nil);

-- Checks a time constraint (c) between two events (e1

-- before e2).

checkConstraint:EventEventTimeConstraintVerdict

checkConstraint(e1, e2, c) ≜

let d = e2.timestamp – e1.timestamp,

s = (if e1.lifeline e2.lifeline then 0

else MaxClockSkew),

ds = mk_(max(d-s, 0), d+s)

incasesintersect({mk_(c.min, c.max), ds}):

(ds)  <Pass>,

nil  <Fail>,

others  <Inconclusive>

end;

Figure 8: Global conformance checking in the presence of

time constraints.

11 the primitive needed to perform incremental con-

formance checking locally in each lifeline by each lo-

cal tester. Because only intra-lifeline time constraints

are checked locally, matching is never inconclusive.

ICSOFT 2017 - 12th International Conference on Software Technologies

464

min

max

[ ]

[ | ]

d-s d d+s

[ | ]

d-s d d+s

[ | ]

d-s d d+s

[ | ]

d-s d d+s

[ | ]

d-s d d+s

Pass FailFail Inconclusive Inconclusive

Figure 9: Checking imprecise duration observations (d±s)

against a required interval (function checkConstraint).

# Observed local traces

(locally valid)

Possible Joins *

(with first

problematic event

underlined)

Verdict

Care

Receiver

Fall

Detection

App

AAL4ALL

Portal

[(e1, 0),

(e4, 4.2),

(e5, 14.2)]

[(e2, 2),

(e3, 4),

(e6, 14.5),

(e7, 14.6)]

[(e8,16)] [(e1, 0), (e2, 2),

(e3, 4), (e4, 4.2),

(e5,14.2), (e6,14.5),

(e7,14.6), (e8,16)]

Pass

[(e1, 0),

(e4, 4.2),

(e5, 14.2)]

[(e2, 2),

(e3, 4),

(e6, 15.2),

(e7, 15.6)]

[(e8,16)] [(e1, 0), (e2, 2),

(e3, 4), (e4, 4.2),

(e5,14.2), (e6,15.2),

(e7,15.6), (e8,16)]

Inconclu

sive (a)

[(e1, 0),

(e4, 4.2),

(e5, 14.2)]

[(e2, 2),

(e3, 4),

(e6, 18),

(e7, 18.6)]

[(e8,19)] [(e1, 0), (e2, 2),

(e3, 4), (e4, 4.2),

(e5, 14.2),

(e6, 18)

(e7,18.6), (e8,19)]

Fail (b)

[(e1, 0),

(e4, 16.8)]

[(e2, 2),

(e3, 4),

(e11, 17)]

[(e12,18)] [(e1, 0), (e2, 2),

(e3, 4), (e4,16.8),

(e11,17), (e12,18)]

[(e1, 0), (e2, 2),

(e3, 4), (e11, 17),

(e4,16.8), (e12,18)]

Fail (c)

* Assuming MaxClockSkew = 0.5s

(a) Time constraint between e5 and e6 (1s) possibly not respected.

(b) Time constraint between e5 and e6 (1s) not respected.

Figure 10: Examples of traces with different conformance

checking verdicts in the fall detection scenario.

functions

-- Checks if the next observed event occurrence (e) in

-- a lifeline is valid, given a valid sequence of

-- previously observed event occurrences in the

-- lifeline (p), the set of valid local traces (V) and

-- the set of local time constraints (C).

checkNextEvent: Trace Event  Trace-set 

TimeConstraint-set  𝔹

checkNextEvent(p, e, V, C) ≜

∃ t  V 

|t| > |p|  matches(p ↷ [e], t

1, …, |p|+1

, C) = <Pass>;

Figure 11: Incremental conformance checking in the pres-

ence of time constraints.

4 RELATED WORK

Several works in the literature use temporal con-

straints in scenario-based speciﬁcations similar to the

ones considered in our work, although with different

objectives. One of them is the work from Zheng et

al. (Zheng et al., 2002), in which the authors use an

alternative representation of timed traces that incorpo-

rate time events between normal events. They derive

the valid traces for Timed Message Sequence Charts

(T-MSCs), which have many similarities with UML

SDs, but do not address the problem of conformance

checking based on distributed observations.

Another work is presented by Gaston et al. (Gas-

ton et al., 2013). As in our work, they assume a dis-

tributed test architecture and no global clock. They

provide a composition result, which allows checking

conformance in two phases: in the ﬁrst phase, each

local tester checks local conformance according to

the tioco conformance relation; in the second phase,

the traces observed locally are brought together and it

is analyzed if events are exchanged following some

communication rules. In our case, conformance

checking is also performed in two phases. However,

different assumptions are considered in both works:

they use timed input output transition systems whilst

we use UML SDs; they assume that internal commu-

nication is multicast, whilst we assume unicast com-

munication according to the UML standard (OMG,

2015); they assume that messages are never lost, con-

trarily to our assumption.

Akshay et al. (Akshay et al., 2007) presented a

timed model of communicating ﬁnite-state machines,

which communicate by exchanging messages through

channels and use event clocks to generate collections

of T-MSCs. Compared to our work, we use simi-

lar time constraints to MSCs with timing constraints

(TC-MSCs) where they associate lower and upper

bounds on the time interval between certain pairs of

events. However they do not address the problem of

conformance checking.

In a more recent work (Akshay et al., 2015),

the authors address model checking message-passing

systems with real-time requirements. As behavioral

speciﬁcations, they use TC-MSCs. As system model,

they use a network of communicating ﬁnite state ma-

chines with local clocks, whose global behavior can

be regarded as a timed automaton. Their goal is to

verify (by model checking) that all timed behaviors

exhibited by the system model conform to the timing

constraints imposed by the speciﬁcation, whilst in our

work we want to check the conformance of traces ex-

hibited by the actual system implementation and not

the system model.

Regarding timed traces, in (Hierons et al., 2012),

the authors take advantage of time information to re-

ﬁne the conformance relation, assuming that there is

a local clock at each port (point of interaction with

the environment) and that events at port p are times-

tamped with the current time of the local clock at port

p. They assume that the local clocks differ by at most

a know value α. In our work we have something sim-

ilar, but further distinguish inconclusive traces and

also check time constraints.

Conformance Checking in Integration Testing of Time-constrained Distributed Systems based on UML Sequence Diagrams

465

5 CONCLUSIONS

We presented decision procedures and criteria to

check the conformance of observed execution traces

against a test speciﬁcation set by a UML SD, in the

context of integration testing of time-constrained dis-

tributed system. As a consequence of the distributed

nature of the system, the test verdict reached may be

inconclusive in some cases.

As future work, we will investigate conditions

for local observability and local controllability of

distributed integration test scenarios with time con-

straints. We will also investigate procedures to over-

come the lack of local observability and/or local con-

trollability.

ACKNOWLEDGEMENTS

This work was performed in scope of project

“NanoSTIMA: Macro-to-Nano Human Sensing: To-

wards Integrated Multimodal Health Monitoring

and Analytics/NORTE-01-0145-FEDER-000016”, ﬁ-

nanced by the North Portugal Regional Operational

Programme (NORTE 2020), under the PORTUGAL

2020 Partnership Agreement, and through the Euro-

pean Regional Development Fund (ERDF). This work

was also ﬁnanced by the Portuguese Foundation for

Science and Technology (FCT), under research grant

SFRH/BD/115358/2016.

REFERENCES

Akshay, S., Bollig, B., and Gastin, P. (2007). Automata

and logics for timed message sequence charts. In

International Conference on Foundations of Software

Technology and Theoretical Computer Science, pages

290–302. Springer.

Akshay, S., Gastin, P., Mukund, M., and Kumar, K. N.

(2015). Checking conformance for time-constrained

scenario-based speciﬁcations. Theoretical Computer

Science, 594:24–43.

Fitzgerald, J., Larsen, P. G., Mukherjee, P., Plat, N., and

Verhoef, M. (2005). Validated Designs For Object-

oriented Systems. Springer-Verlag TELOS, Santa

Clara, CA, USA.

Gaston, C., Hierons, R. M., and Le Gall, P. (2013). An

implementation relation and test framework for timed

distributed systems. In IFIP International Confer-

ence on Testing Software and Systems, pages 82–97.

Springer.

Hierons, R. M. (2014). Combining Centralised and Dis-

tributed Testing. ACM Trans. Softw. Eng. Methodol.,

24(1):5:1–5:29.

Hierons, R. M., Merayo, M. G., and Núnez, M. (2012). Us-

ing time to add order to distributed testing. In Inter-

national Symposium on Formal Methods, pages 232–

246. Springer.

Larsen, P. G., Lausdahl, K., Battle, N., Fitzgeral, J., Wolff,

S., Sahra, S., Verhoef, M., Tran-Jørgensen, P., Oda, T.,

and Chisholm, P. (2016). VDM-10 Language Manual.

Technical report.

Lima, B. and Faria, J. P. (2016). Software Technologies:

10th International Joint Conference, ICSOFT 2015,

Colmar, France, July 20-22, 2015, Revised Selected

Papers, chapter Automated Testing of Distributed and

Heterogeneous Systems Based on UML Sequence Di-

agrams, pages 380–396. Springer International Pub-

lishing, Cham.

Lima, B. and Faria, J. P. (2017). Towards decentralized

conformance checking in model-based testing of dis-

tributed systems. In Software Testing, Veriﬁcation and

Validation Workshops (ICSTW), 2017 IEEE Ninth In-

ternational Conference on, pages 356–365. IEEE.

Mills, D. L. (1991). Internet time synchronization: the net-

work time protocol. IEEE Transactions on communi-

cations, 39(10):1482–1493.

OMG (2015). OMG Uniﬁed Modeling Language TM

(OMG UML) Version 2.5. Technical report, Object

Management Group.

Taylor, A. G. (2015). Keeping active with the activity app.

In Get Fit with Apple Watch, pages 63–69. Springer.

Utting, M. and Legeard, B. (2007). Practical Model-Based

Testing: A Tools Approach. Morgan Kaufmann Pub-

lishers Inc., San Francisco, CA, USA.

Zheng, T., Khendek, F., and Hélouët, L. (2002). A seman-

tics for timed msc. Electronic Notes in Theoretical

Computer Science, 65(7):85–99.

ICSOFT 2017 - 12th International Conference on Software Technologies

466