Real-Time Setup with PD and Backstepping Control for a

Pelican Quadrotor

Jos

e Alejandro Dena Ruiz and Nabil Aouf

Centre of Electronic Warfare, Defence Academy of the United Kingdom,

Cranﬁeld University, Shrivenham, SN6 8LA, U.K.

Keywords:

PD Control, Backstepping Control, Kalman Filter, Optitrack, ROS.

Abstract:

In this paper, a real-time setup and an implementation of a Proportional Derivative (PD) controller for ori-

entation and comparison between PD and BackStepping (BS) controllers for linear positioning are presented

using a Pelican quadrotor from Ascending Technologies (AscTec). An onboard Inertial Measurement Unit

(IMU) was used for orientation control and Optitrack Vision Tracking System for linear positioning control.

A linear Kalman ﬁlter was implemented for linear velocity estimation. The software and hardware integration

was achieved with the help of the Robot Operating System (ROS). Simulations and experiments with this

drone platform are achieved in order to implement different controller algorithms and analyse them in order

to achieve better aircraft performance.

1 INTRODUCTION

The studies in quadrotor control designing have been

increasing rapidly in recent years. Linear controllers

design for quadrotors have been achieved in sev-

eral work, like the Linear Quadratic Regulator(LQR)

and a Proportional Integral Derivative (PID) (Khatoon

et al., 2014) (Reyes-Valeria et al., 2013). Nonlinear

control design has also been achieved with different

techniques, like Backstepping (Das et al., 2009), Slid-

ing Mode (Runcharoon and Srichatrapimuk, 2013)

and Feedback Linearisation (Saif, 2009). (Castillo

et al., 2005) compared the performance of a nonlin-

ear control algorithm with a LQR control law. Results

show the unstable response of a linear controller ap-

plied to a nonlinear system, while the nonlinear con-

troller shows stable response. (Gomes et al., 2016)

used an AR.Drone quadrotor and a Vicon motion cap-

ture system to track a moving target with a Propor-

tional Derivative (PD) controller for linear position-

ing. (Mashood et al., 2016) showed experimental re-

sults of two AR.Drone following a squared path us-

ing VICON system and MATLAB/SIMULINK for

feedback and control implementation. This was

possible with AR Drone Simulink Development Kit

(ARDSDK). (Campbell et al., 2012) showed the de-

sign and implementation of a quadrotor aircraft au-

topilot, allowing the UAV to take off, transit from

one location to another and land at a desired loca-

tion. The position data is obtained from an Opti-

track system and a PID control technique was used

to achieve the desired response for (X,Y,φ, θ) and PD

controller for (Z,ψ), the integration of the motion

system and the controllers were developed on MAT-

LAB/SIMULINK.

An improved PID controller was implemented by

(Zheng et al., 2016) showing the comparison against

the traditional PID and Backstepping (BS). Simula-

tion and experimental results show stability and track-

ing performance, using a motion capture system and

MATLAB/SIMULINK as the feedback measurement

and the platform for control implementation respec-

tively.

(Corona-Sanchez and Rodriguez-Cortes, 2013)

presented outdoor and indoor experimental validation

of a nonlinear controller for a quadrotor vehicle. Also

showed a real-time programming strategy, parameter

identiﬁcation technique and a nonlinear gain tuning

procedure.

A lot of related work has been done so far. Nev-

ertheless the novelty of this paper is to show the use

of our particular drone platform along with the Robot

Operating System (ROS) and the Optitrack system for

real time experimental scenarios. The result of these

powerful components is to obtain an stabilised drone,

in one hand running an orientation PD controller at

1000 Hz in the embedded processor and in the other

hand for position control, a linear PD or a nonlinear

676

Ruiz, J. and Aouf, N.

Real-Time Setup with PD and Backstepping Control for a Pelican Quadrotor.

DOI: 10.5220/0006474306760681

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 676-681

ISBN: 978-989-758-263-9

Backsepping controllers are presented to demonstrate

the efﬁciency of ROS and optitrack at 120 Hz. This

way the setup remains open for the development and

implementation of a new control techniques.

2 THE QUADROTOR DYNAMIC

MODEL

The model is derived based on some assumptions, in

order to simplify the dynamics of the complex sys-

tem to be suitable for simulation and control design,

Figure 1. A symmetric and rigid structure, rigid pro-

pellers and ground effect has been ignored. The full

Model derivation can be found on (Bouabdallah and

Siegwart, 2005).

Figure 1: Quadrotor AscTec Pelican and inertial frame on

Gazebo Simulator.

Using Newton’s laws of Mechanics and Euler’s Dy-

namics equation, the model consists of six equations

for the system dynamics and four equations describ-

ing the inputs of the system:

X = (cos φ sinθcosψ + sin φsinψ)

(1)

Y = (cos φ sinθsinψ − sinφcosψ)

(2)

Z = (cos φcosθ)

− g (3)

φ =

ψ(

− I

) −

θΩ +

(4)

θ =

ψ(

− I

) +

φΩ +

(5)

ψ =

θ(

− I

) +

(6)

where equation 1, 2 and 3 describe the linear ac-

celeration of the vehicle in the direction of O

, O

and

axes using the North, East, Down (N, E, D) con-

vention respectively, while equations 4, 5 and 6 rep-

resent the angular accelerations of the vehicle about

the same axes respectively. l corresponds to the arm

length holding the propeller, φ, θ and ψ, represent the

Euler angles about the body axes B

, B

and B

re-

spectively. I

, I

and I

, are the inertial components

about the x-axis, y-axis and z-axis respectively. ˙x, ˙y

and ˙z are the translational velocity components along

the main axes. U

≡ 1, 2, 3, 4 represents the system

inputs.

∑

= b(Ω

+ Ω

) (7)

= (−T

+ T

) = bl(−Ω

+ Ω

) (8)

= (T

− T

) = bl(Ω

− Ω

) (9)

= (−1)

∑

= d(−Ω

+ Ω

− Ω

+ Ω

)

(10)

Ω = Ω

+ Ω

− Ω

(11)

where equation 7 represents the total thrust, 8 the

pitch moment, 9 the roll moment and 10 perform the

yaw moment. b is the thrust factor in hover and d

is the drag factor in hover. Increasing or decreasing

of the speed of the four propellers together will be

responsible for the altitude (z-axis) change in posi-

tion and velocity while varying the speed of one pair

of propellers (Ω

and Ω

) will cause the aircraft to

tilt about the y-axis which is denoted as pitch angle

θ. Similarly varying the speed of the propellers pair

(Ω

and Ω

) will cause the aircraft to tilt about x-axis

which is denoted as roll angle φ. Finally the vector

summation of the reaction moment produced by the

rotation of the pair (Ω

and Ω

) and the reaction mo-

ment produced by the rotation of the pair (Ω

and Ω

)

will cause the quadrotor to spin about its axis (z-axis),

which is denoted as yaw angle ψ.

3 QUADROTOR CONTROLLERS

In this section, a PD and Backstepping controller were

implemented for linear positioning, while only PD

controllers for orientation.

A set of PD controllers have been chosen for the

UAV attitude based on the good response in simula-

tions and experiments, fast response and less than ﬁve

percentage error in steady state. The Euler angles are

used as feedback signals to the proposed controller in

order to achieve the desired orientation. Traditional

implementation can be deﬁned as:

U = K

e(t) +K

(12)

Where K

is the proportional gain, K

the deriva-

tive gain, e(t) is the difference between the current

Real-Time Setup with PD and Backstepping Control for a Pelican Quadrotor

677

controlled value and the desired value. In our case,

three PD individual controllers are implemented:

= K

pφ

− φ) + K

dφ

−

φ) (13)

= K

pθ

− θ) + K

dθ

−

θ) (14)

= K

pψ

− ψ) + K

dψ

−

ψ) (15)

Where 13, 14 and 15 represent the torques for each

axis due to the rotor’s thrust, τ

, τ

and τ

respec-

tively. K

pφ

, K

pθ

and K

pψ

are the proportional gains

for each controller and K

dφ

, K

dθ

and K

dψ

the deriva-

tive ones. d

, d

and d

are the desired pitch, roll and

yaw, φ, θ and ψ correspond to the current attitude and

position values.

Considering that desired position d

, d

are

known and x, y, z can be measured, the equations 1, 2

and 3 can be solved in order to determine the control

variables:

cosφcos θ

+ g (16)

= arcsin(

sinψ − r

cosψ)) (17)

= arcsin(

cosψ + r

sinψ)) (18)

Where 16 is the force to control the vertical dis-

placement z, 17 and 18 are the desired angles to posi-

tion the drone at the desired x and y on the cartesian

plane respectively. r

and r

represent the output con-

trol signal of the desired control technique that will

be mapped to the desired angles, g is the acceleration

due to the gravity force and m is the aircraft mass.

Equations 19-21 represent the PD controllers for

the linear position of the UAV.

= K

− x) + K

˙x

− ˙x) (19)

= K

− y) + K

˙y

− ˙y) (20)

= K

− z) + K

˙z

− ˙z) (21)

Using the Backstepping approach, one can synthe-

sise the control law forcing the system to follow the

desired trajectory. Writing the model equations for

linear position in space-state:

= x (22)

= ˙x

= ˙x (23)

= y (24)

= ˙x

= ˙y (25)

= z (26)

= ˙x

= ˙z (27)

First, we consider the tracking-error for x

posi-

tion:

= x

− x

(28)

then, by considering the lyapunov function z

pos-

itive deﬁnite and it’s time derivative negative semi-

deﬁnite:

V (z

) =

(29)

V (z

) = z

( ˙x

− ˙x

) (30)

The stabilisation of z

can be obtained by intro-

ducing the virtual control input x

= ˙x

+ α

(31)

with : α

> 0 (32)

∴

V (z

) = −α

(33)

Now, we have to make x

= ˙x

+ α

creating

the variable z

= x

− ˙x

− α

(34)

For the second step, we consider the augmented

Lyapunov function:

V (z

, z

) =

+ z

) (35)

(36)

and it’s time derivative is:

V (z

) = z

− z

(

− α

+ α

)) − z

− α

(37)

Extracting r

and making

d = 0 is satisﬁed that

V (z

) < 0, now adding the term α

with α

> 0 to

stabilise z

and we apply the same procedure for the y

and z axis:

= z

− α

+ α

) − α

(38)

= z

− α

+ α

) − α

(39)

= z

− α

+ α

) − α

(40)

with:

= x

− x

(41)

= x

− ˙x

− α

(42)

= x

− x

(43)

= x

− ˙x

− α

(44)

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

678

4 THE PELICAN PLATFORM

The Pelican quadrotor from AscTec was chosen as the

prototype to develop the experiments, it’s physical ar-

chitecture made of carbon ﬁbre and well distributed

sensors and components make it a reliable platform

for research purposes. This Quadrotor offers plenty

of space and various interfaces for individual compo-

nents and payloads. The total quadrotor weight in-

cluding sensors and battery is 1.63 Kg. Figure 2.

Figure 2: Quadrotor AscTec Pelican with Autopilot and

Mastermind.

The basic electronic components are the AscTec Au-

topilot, Motor controllers and a single board com-

puter, the Mastermind. The AscTec Autopilot also

known as Flight-Control-Unit (FCU) contains the

High Level Processor and the Low Level Processor

(HLP and LLP) running at 1 Khz which are in charge

of the aircraft control. The overall architecture is pre-

sented on Figure 3, the LLP handles sensor data pro-

cessing, data fusion as well as an stable attitude con-

trol algorithm. The HLP is open for user purposes, to

implement control algorithms, sensor fusion, etc.

Figure 3: Autopilot electronic architecture.

The AscTec Mastermind is an onboard processor

board, which can be carried by the AscTec Pelican,

it can be used like a ground PC, but it is mounted

on the ﬂight system. In comparison to its weight and

size, it offers an extremely high processing power,

high data rates and a great variety of standard PC in-

terfaces to connect several kind of hardware devices.

Features like a Dual Core Atom, a Core 2 Duo, or a

Core i7, Firewire, WIFI and hardware serial ports are

supported.

5 THE QUADROTOR CONTROL

SYSTEM

The complete Quadrotor control system is presented

on ﬁgure 4. The full system is composed by the Pel-

ican from AscTec, which is the platform to control.

The PD orientation controllers obtained on equations

13, 14 and 15 were implemented in the HLP on Peli-

can, these controllers are using the angles provided by

the LLP as the feedback measurements. In the AscTec

Mastermind, a ROS application is interacting with the

HLP through the serial port, this application is send-

ing the new desired angles and receiving the current

states of the control variables and gives the user the

possibility of a real-time gain tuning. Figure 4 shows

the full control system overview.

Once the orientation controller is working, a sec-

ond ROS application is running parallel on the As-

cTec Mastermind, this application is performing the

linear position control algorithms for the Drone, al-

lowing the user to choose between the PD or BS con-

trollers obtained in section 3, create trajectories and

test new different control techniques. An Optitrack

Motion Capture System was used to retrieve the ac-

tual Drone position with a precision up to 2 mm. A

setup of 6 cameras connected to a 12-port POE switch

along with a host computer, Optitrack Motive appli-

cation runs and streams the current position of a rigid

body at 120 Hz to the AscTec Mastermind through a

wiﬁ router. This second application also allows the

user to select between a PD or Backstepping con-

troller for linear position as well as real-time gain tun-

ing.

Figure 4: Quadrotor Control System overview.

6 EXPERIMENTAL RESULTS

The real experiments were done using the AscTec Pel-

ican as a UAV, for orientation control angles and an-

Real-Time Setup with PD and Backstepping Control for a Pelican Quadrotor

679

gular velocities were obtained from the onboard au-

topilot IMU, whereas to retrieve the X, Y and Z posi-

tion the optitrack system was used. A ROS package

was used to publish into ROS network the position of

the rigid body and the use of a linear Kalman ﬁlter for

velocity estimation. A two metres squared trajectory

was chosen as the drone trajectory and altitude of one

metre.

Velocity estimation was achieved using the linear

Kalman ﬁlter based on (Kim, 2010). Optitrack system

provides a high accuracy on ground truth at 120 Hz

(dt=0.0083), taking this parameters into account and

the time-varying for the process noise matrix Q, the

values of the matrices resulted as follow:

A =







1 0 0 dt 0 0

0 1 0 0 dt 0

0 0 1 0 0 dt

0 0 0 1 0 0

0 0 0 0 1 0

0 0 0 0 0 1







(45)

H =





1 0 0 0 0 0

0 1 0 0 0 0

0 0 1 0 0 0





(46)

R =





4X10

−6

0 0

0 4X10

−6

0 0 4X10

−6





(47)

Q =







0 0 0 0 0 0

0 0 0 dt

0 0

0 0 0 0 dt

0 0 0 0 0 dt







(48)

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

0.2

0.4

0.6

0.8

1.2

Altitude in metres

Altitude PD controller

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-1

-0.5

0.5

Y position in metres

Y trajectory PD controller

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-2.5

-2

-1.5

-1

-0.5

0.5

X position in metres

X trajectory PD controller

Figure 5: Real XYZ displacement with a PD controllers.

Figures 5-7 show the results in real-time using the PD

controllers and Figures 8-10 show the results for the

BS controllers.

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-0.06

-0.04

-0.02

0.02

0.04

0.06

YAW( ) angle in radians

YAW( ) PD controller

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-0.015

-0.01

-0.005

0.005

0.01

YAW Torque control

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-0.4

-0.2

0.2

0.4

ROLL( ) angle in radians

ROLL( ) PD controller

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-0.06

-0.04

-0.02

0.02

0.04

0.06

ROLL Torque control

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-0.3

-0.2

-0.1

0.1

0.2

0.3

PITCH( ) angle in radians

PITCH( ) PD controller

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

time in (ms)

-0.06

-0.04

-0.02

0.02

0.04

0.06

PITCH Torque control

Figure 6: Real Torques and desired angles ROLL, PITCH

and YAW with a PD controllers.

-2.5

0.2

0.5

0.4

-2

X-Y-Z trajectory PD controller

0.6

Z position in metres

-1.5

0.8

Y position in metres

X position in metres

-1

-0.5

1.2

-0.5

-1

-1.5

0.5

Desired Trajectory

Trajectory

Figure 7: Real 3D trajectories using a PD controllers.

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

0.2

0.4

0.6

0.8

1.2

Altitude in metres

Altitude BS controller

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-1

-0.5

0.5

Y position in metres

Y trajectory BS controller

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-2.5

-2

-1.5

-1

-0.5

0.5

X position in metres

X trajectory BS controller

Figure 8: Real XYZ displacement with a BS controllers.

7 CONCLUSIONS

This paper presents the development of a quadrotor

control system for orientation and position control,

using the onboard IMU and Optitrack system to feed-

back current signals. On one hand the implementation

of the algorithms for orientation control was possible

using the HLP from the autopilot, the program was

developed on C and the execution rate was 1 kHz. On

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

680

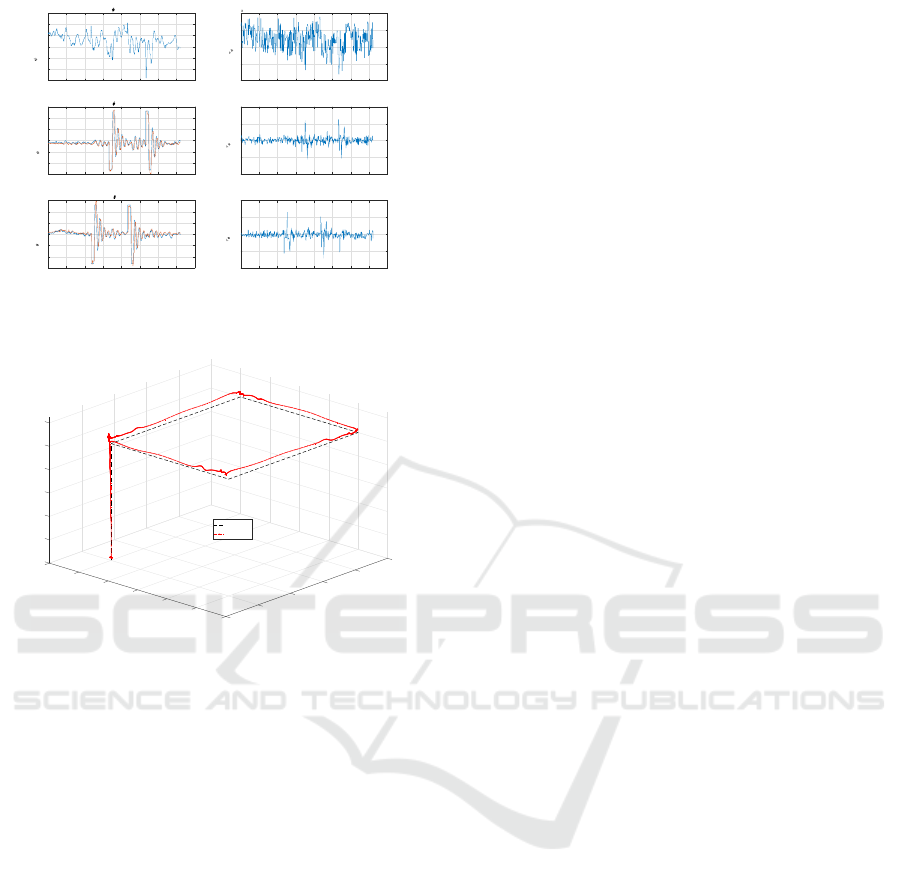
0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-0.02

0.02

0.04

0.06

0.08

0.1

YAW( ) angle in radians

YAW( ) PD controller

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-15

-10

-5

-3

YAW Torque control

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-0.3

-0.2

-0.1

0.1

0.2

0.3

ROLL( ) angle in radians

ROLL( ) PD controller

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-0.1

-0.05

0.05

0.1

ROLL Torque control

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-0.3

-0.2

-0.1

0.1

0.2

0.3

PITCH( ) angle in radians

PITCH( ) PD controller

0 500 1000 1500 2000 2500 3000 3500 4000

time in (ms)

-0.1

-0.05

0.05

0.1

PITCH Torque control

Figure 9: Real Torques and desired angles ROLL, PITCH

and YAW with a BS controllers.

-2.5

0.2

0.5

-2

0.4

0.6

X-Y-Z trajectory BS controller

-1.5

Z position in metres

Y position in metres

0.8

X position in metres

-1

-0.5

1.2

-1

-1.5

0.5

Desired Trajectory

Trajectory

Figure 10: Real 3D trajectories using a BS controllers.

the other hand for positioning control the control al-

gorithms were developed under C++ and ROS, which

allow us to create a network where the ground sta-

tion, robots and sensors can exchange information at

120 Hz. The Drone performance was tested using

an square trajectory with 2 metres side, which was

enough to move the desired roll and pitch angles and

see their control response with the PD controller. The

desired angles was reached within a short period of

time, for instance 0.25 rad in 100 ms on the experi-

mental results for roll angle as ﬁgure 6 shows. Re-

garding positioning control, a linear PD controller and

a non linear Backstepping controller were tested, get-

ting a better response for X and Y position with the

Backstepping controller in ﬁgure 8 than the PD in ﬁg-

ure 5, whereas for the altitude Z the PD controller had

a quicker response compared with BS as shown in ﬁg-

ures 7 and 10.

REFERENCES

Bouabdallah, S. and Siegwart, R. (2005). Backstepping and

sliding-mode techniques applied to an indoor micro

quadrotor. Proceedings - IEEE International Confer-

ence on Robotics and Automation, 2005(April):2247–

2252.

Campbell, J., Hamilton, J., Iskandarani, M., and Givigi, S.

(2012). A systems approach for the development of a

quadrotor aircraft. In SysCon 2012 - 2012 IEEE In-

ternational Systems Conference, Proceedings, pages

110–116.

Castillo, P., Lozano, R., and Dzul, A. (2005). Stabilization

of a mini rotorcraft with four rotors: Experimental

implementation of linear and nonlinear control laws.

IEEE Control Systems Magazine, 25(6):45–55.

Corona-Sanchez, J. J. and Rodriguez-Cortes, H. (2013). Ex-

perimental real-time validation of an attitude nonlin-

ear controller for the quadrotor vehicle. In 2013 Inter-

national Conference on Unmanned Aircraft Systems,

ICUAS 2013 - Conference Proceedings, pages 453–

460.

Das, A., Lewis, F., and Subbarao, K. (2009). Backstepping

approach for controlling a quadrotor using lagrange

form dynamics. Journal of Intelligent and Robotic

Systems: Theory and Applications, 56(1-2):127–151.

Gomes, L. L., Leal, L., and Oliveira (2016). Unmanned

quadcopter control using a motion capture system.

IEEE Latin America Transactions, 14(8):3606–3613.

Khatoon, S., Gupta, D., and Das, L. K. (2014). Pid &

lqr control for a quadrotor: Modeling and simulation.

Proceedings of the 2014 International Conference on

Advances in Computing, Communications and Infor-

matics, ICACCI 2014, pages 796–802.

Kim, P. (2010). Kalman Filter for Beginners with MATLAB

Examples. A-JIN, Republic of Korea, 1 edition.

Mashood, A., Mohammed, M., Abdulwahab, M., Abdul-

wahab, S., and Noura, H. (2016). A hardware setup

for formation ﬂight of uavs using motion tracking sys-

tem. In ISMA 2015 - 10th International Symposium on

Mechatronics and its Applications.

Reyes-Valeria, E., Enriquez-Caldera, R., Camacho-Lara, S.,

and Guichard, J. (2013). Lqr control for a quadrotor

using unit quaternions: Modeling and simulation bt -

electronics, communications and computing (coniele-

comp), 2013 international conference on. pages 172–

178.

Runcharoon, K. and Srichatrapimuk, V. (2013). Slid-

ing mode control of quadrotor. 2013 International

Conference on Technological Advances in Electrical,

Electronics and Computer Engineering (TAEECE),

(1):552–557.

Saif, A. A. H. (2009). Quadrotor control using feedback

linearization with dynamic extension. 2009 6th Inter-

national Symposium on Mechatronics and its Applica-

tions, ISMA 2009, (1):25–27.

Zheng, H., Zeng, Q., Chen, W., Zhu, H., and Chen, C.

(2016). Improved pid control algorithm for quadrotor

based on mcs. In Proceedings of 2016 IEEE Chinese

Guidance, Navigation and Control Conference, num-

ber 1, pages 1780–1783, Nanjin, China.

Real-Time Setup with PD and Backstepping Control for a Pelican Quadrotor

681