Relating Aircraft Altitude with Pilot’s Physiological Variables:

Towards Increasing Safety in Light-sport Aviation

Susana M. Vieira

, Alexandra Moutinho

, Margarida Solas

, Jos

e F. Loureiro

, Maria B. Silva

Sara Zorro

2, 3

, Lu

ıs Patr

, Joaquim Gabriel

and Jorge Silva

2, 5

IDMEC, LAETA, Instituto Superior T

ecnico, Universidade de Lisboa, Portugal

CERIS, CESUR, Instituto Superior T

ecnico, Universidade de Lisboa, Portugal

Faculdade de Ci

encias da Sa

ude, Universidade da Beira Interior, Portugal

INEGI, LAETA, Faculdade de Engenharia, Universidade do Porto, Portugal

Faculdade de Engenharia, Universidade da Beira Interior, Portugal

Keywords:

Light-sport Aviation, Classiﬁcation, Prediction, Neural Networks Model, Decision Support System.

Abstract:

Several applications require humans to be in high-altitude environments, whether for recreational purposes,

like mountaineering or light sport aviation, or for labour, as miners. Although in these conditions the monitor-

ing of physiological variables is, per se, of interest, the direct correlation of these variables with altitude itself

is not usually explored towards the development of decision-support systems and/or critical event alarms. This

paper proposes two neural networks approaches to assess and explore this correlation. One, based on dynamic

SISO models, estimates physiological variables using the aircraft pressure altitude as input. A second approach

uses static MISO networks to classify the ﬂight stage (and therefore the altitude variation) from physiological

variables. Both models were developed and validated using real data acquired in hypobaric chamber tests

simulating a real ﬂight. The good results obtained indicate the viability of the approach.

1 INTRODUCTION

The inﬂuence of altitude to human physiology is a

known issue, whether the scenario is underwater, on

the ground or in the air. Different monitoring systems

that allow to acquire relevant data to study this inﬂu-

ence are being developed for different applications.

In (Aqueveque et al., 2016), a wearable device is de-

signed to acquire and monitor physiological (elec-

trocardiogram, respiratory activity and body temper-

ature) and environmental (ambient temperature and

relative humidity) variables of miners working at high

altitude. Wagner (2011) proposes an ambulatory

biosensor (heat and respiratory rate, skin and core

temperature) system to be used during high altitude

mountaineering. Marques (2012) proposes a portable,

ergonomic system for the acquisition of ﬂight (posi-

tion, attitude, altitude, speed, g-load, heading, abso-

lute pressure and temperature inside the cabin) and

physiological (cerebral oximetry, electroencephalo-

gram and electrocardiogram) data, to be used in avia-

tion applications.

In light sport aviation, where aircraft may go as

high as 10,000 to 15,000 ft, cabins are not pressur-

ized. This means there is no conditioned air being

pumped into the aircraft cabin in order to guarantee a

stabilized pressure within proper limits for the human

body. The low pressure may lead to several physi-

ological problems like hypoxia, altitude and decom-

pression sickness, and barotrauma (Harding, 2002).

Of the different effects of low pressure exposure, hy-

poxia is known to impair mental functions and induce

sensory deﬁcits. Petrassi et al. (2012) indicate learn-

ing, reaction time, decision making and certain types

of memory, as examples of cognitive and psychomo-

tor deﬁcits resulting from hypoxia at moderate alti-

tudes (8,000 to 15,000 ft). Together with unforseen

climatic conditions, psychophysiological factors of

the pilot him/herself may affect the ﬂight safety. In

this scenario, the psychophysiologic factors play a

key role, as the heterogeneity of reactions of differ-

ent pilots attests (Patrao et al., 2013; Petrassi et al.,

2012).

To prevent adverse outcomes, either in aviation or

Vieira, S., Moutinho, A., Solas, M., Loureiro, J., Silva, M., Zorro, S., Patrão, L., Gabriel, J. and Silva, J.

Relating Aircraft Altitude with Pilot’s Physiological Variables: Towards Increasing Safety in Light-sport Aviation.

DOI: 10.5220/0006476903590364

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 359-364

ISBN: 978-989-758-263-9

359

in other applications, research has been conducted to

monitor a person (pilot) suffering from hypoxia. Gur-

jar et al. (2010) propose a hypoxia monitor capable of

detecting various physiological parameters (heart and

respiratory rates, blood velocity and blood oxygen

saturation levels) that change in response to reduced

oxygen availability. The onset of hypoxia is identiﬁed

based on the changes in their cross-correlation sig-

nals. Acharya et al. (2016) present a M-ary decision

fuzzy architecture capable of classifying the degree

of induced hypoxia as a function of the duration of

exposure to different altitude proﬁles. The proposed

monitoring system takes blood oxygen saturation lev-

els and altitude readings as inputs and estimates of the

level of hypoxia as outputs.

Although there is a growing interest in new acqui-

sition systems, there are not so many studies using the

correlation of the acquired data, namely the relation

between altitude and physiological variables, towards

the development of decision-support systems and/or

critical event alarms. This paper presents preliminary

results in this direction, with the purpose of estimat-

ing the occurrence of critical events during light sport

ﬂights using both physiological and ﬂight data. It pro-

poses two neural networks approaches to assess and

explore the correlation between altitude and physio-

logical variables. One, based on dynamic SISO mod-

els, estimates physiological variables using the air-

craft pressure altitude as input. A second approach

uses static MISO networks to classify the ﬂight stage

(and therefore the altitude variation) from physiolog-

ical variables. Results obtained using real data from

hypobaric tests validate the hypothesis.

2 DATA ACQUISITION AND

PREPROCESSING

The following sections present the data considered in

this work and the preprocessing methods applied prior

to the models development.

2.1 Data acquisition

In order to estimate critical events during light-sports

ﬂights, a monitoring system was used that measures

the pilot’s cerebral (rSO2) and peripheral (SpO2)

oximetry and heart rate (HR), and the aircraft alti-

tude (h). Data was acquired in the hypobaric cham-

ber (ﬁg. 1) of the Center of Aeronautic Medicine of

the Portuguese Air Force, at the Lumiar military base,

Lisbon, Portugal. This work considers data collected

during three tests performed by the same pilot at the

hypobaric chamber. The respective data is shown in

Figure 1: Data acquisition at hypobaric chamber.

ﬁg. 2. Observing the data from the three tests, it is

possible to observe a correlation between the periph-

eral oximetry and altitude curves. In fact, when the

altitude increases, the peripheral oximetry decreases,

and vice-versa. From the data from tests 2 and 3

(ﬁgs. 2(b)-2(c)), it also seems possible to correlate the

heart rate with the altitude, but this correlation is not

clear for test 1 (ﬁg. 2(a)).

2.2 Data Preprocessing

Observing the data in ﬁg. 2, it is noticeable that the

variables were not acquired during the same period of

time, and that they do not have the same sampling.

This is due to the fact that they were acquired with

different equipments. In order to use the data for

modeling purposes, it is required that these issues be

solved. A ﬁrst preprocessing step was then to truncate

(eliminate) the excessive data at the beginning and/or

end of the data set in order to have data sets where

all variables are present. Regarding the harmoniza-

tion of the variables sampling, two approaches were

considered. The ﬁrst approach considers the variable

with higher sampling period (altitude), and expands

the other variables (cerebral and peripheral oximetry

and heart rate) data in order for them to have the same

number of data points. This is accomplished using

the ZOH (zero-order hold) method, which holds the

previous value until a new one is available. The sec-

ond method takes the opposite direction, forcing the

lower sampling rate of variables heart rate and cere-

bral oximetry to the variables with higher sampling

(altitude and peripheral oximetry). The median was

used to obtain the most representative value in each

time interval. Although the average is a more intu-

itive measure, the median is less sensitive to possible

outliers, making this process analogous to a ﬁltering

step.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

360

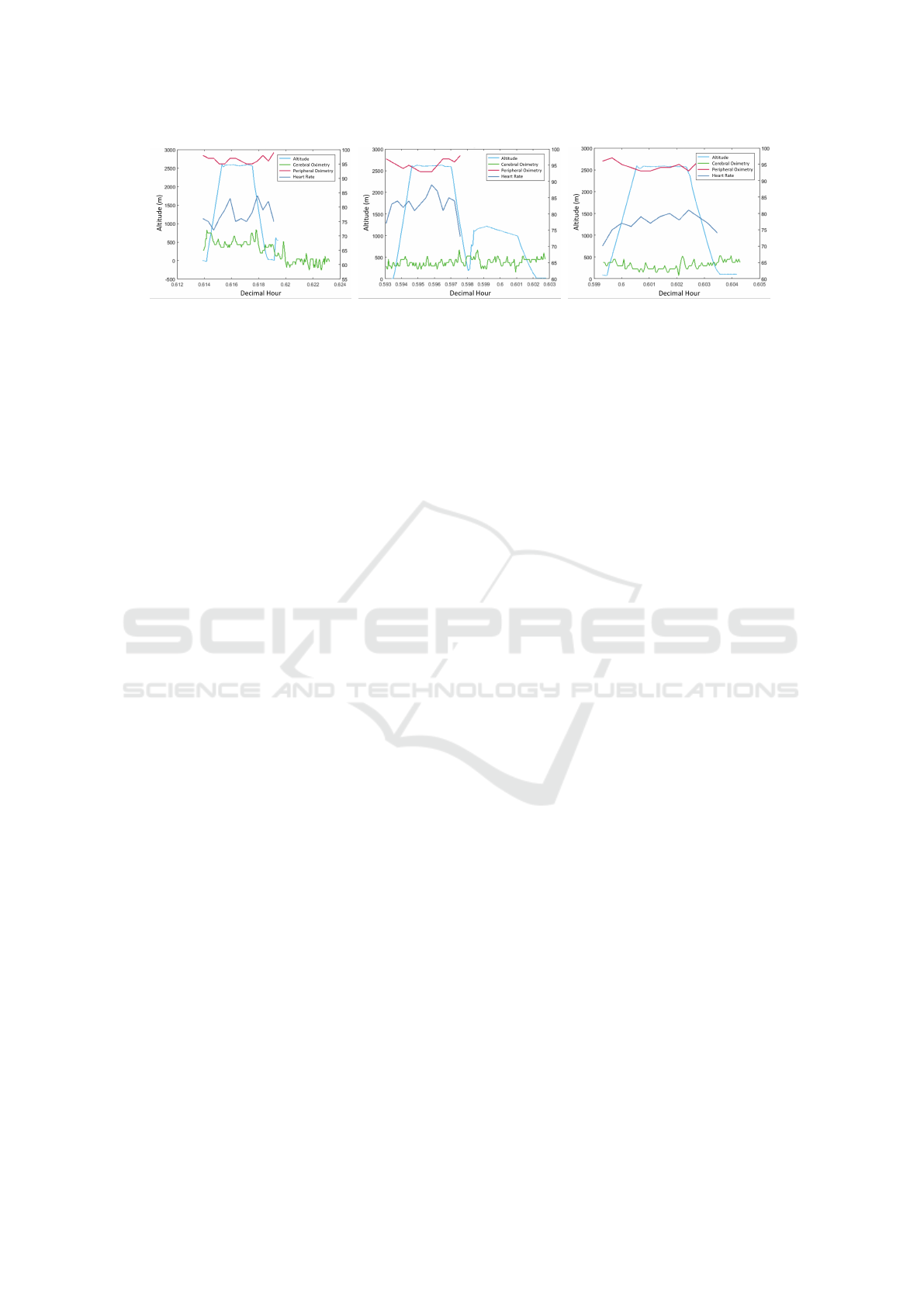
(a) Test 1 data (b) Test 2 data (c) Test 3 data

Figure 2: Original data obtained in three tests performed by the same pilot at the hypobaric chamber.

2.3 Data Analysis

After data preprocessing, it is now possible to eval-

uate the correlation between the physiological vari-

ables and the altitude. For each pair of variables, the

data were centered subtracting the mean value prior

to computing the covariance matrix:

Covariance [rSO2; h] =



1 −0.136

−0.136 1



Covariance [SpO2; h] =



1 −0.603

−0.603 1



Covariance [HR; h] =



1 0.3307

0.3307 1



The covariance matrix is a symmetric matrix that al-

lows to explore the linear relation between variables.

This matrix may be used to predict how one vari-

able varies relative to another. Analysing the values

of the cross-diagonals, it is possible to observe that:

(i) the relations between cerebral oximetry/heart rate

and altitude are weak, with the ﬁrst being the weakest

(lower value of correlation, -0.136); (ii) the periph-

eral oximetry shows a moderate negative correlation

(-0.603) with the altitude, indicating that when the al-

titude increases the peripheral oximetry will decrease

and vice-versa (as was already observed in ﬁg. 2).

3 NEURAL NETWORK MODEL

Artiﬁcial neural networks (ANN) are mathematical

models developed to mimic the functioning of the bi-

ological neural networks (Haykin, 1999). In the scope

of this work, artiﬁcial neural networks are used to

perform supervised learning from a training data set

where the values of the output variable are known.

The target output variable is a continuous real valued

variable and the problem is dealt as a regression prob-

lem.

3.1 Neural Network Parameters

Deﬁning the network structure is not a trivial task.

Besides the number of inputs and outputs, the number

of hidden layers of the network and the type of activa-

tion functions have to be deﬁned. The backpropaga-

tion algorithm was used to train the network to learn

the adequate weights and bias.

Network Type and Dimensions. Two approaches

were considered to assess the relation of the barom-

eter altitude with each physiological variable mea-

sured. The ﬁrst concerns the prediction of each phys-

iological variable using the altitude as network in-

put. The second considers the opposite direction and

aims to see if it is possible to identify the ﬂight stage

(take-off, cruise ﬂight, or landing), based on the cur-

rent values of the physiological variables. For that,

two types of neural networks are developed. One

corresponds to a static multiple-input, single-output

(MISO) network for ﬂight stage classiﬁcation (clas-

siﬁer neural network), and the other is a dynamic

single-input, single-output (SISO) network for pre-

dicting physiological variables based on the altitude

(dynamic neural network). For the classiﬁer neural

network (CNN), all samples are considered as inde-

pendent. For this type of model, the three available

ﬂight data sets can be concatenated and the data may

be randomly divided into the train, test and validation

data sets, as long as the class proportion is maintained

throughout all the data sets. The dynamic neural net-

work (DNN), or predictor, considers the information

on the present time sample as well as the historical

temporal sequence of the inputs and outputs. This

type of neural network present a very good perfor-

mance for the modeling of nonlinear systems.

Training, Test and Validation Data. The data was

divided into three different sets: train, test and vali-

dation. The bigger data set was used for training the

network, deﬁning the parameters (weights and bias)

that minimize the cost function (1). The validation set

is used during the training process to avoid the net-

work overﬁtting. The test set is used for the model val-

Relating Aircraft Altitude with Pilot’s Physiological Variables: Towards Increasing Safety in Light-sport Aviation

361

idation and is used after the training process of the

neural network is done. For the two types of neural

(a) Classiﬁer data parti-

tion.

(b) Predictor data parti-

tion.

Figure 3: Data set division in train validation and test.

networks used, the data were divided in two different

ways. For the classiﬁer the considered ﬂight data were

concatenated and the complete data set was then di-

vided randomly as the samples/observations are con-

sidered as being independent. The distribution of the

data was done according to ﬁgure 3(a). For the dy-

namic neural network, the data were not divided ran-

domly. The integrity of a complete data set corre-

sponding to a given ﬂight was maintained, so three

different ﬂights were considered and used as train,

validation and test according to ﬁgure 3(b). Please

note that in this case the size of the different sets is

very similar due to the similarity between ﬂights.

Cost Function. In a neural network, the cost function

is computed in the optimization algorithm used for the

network learning process. The cost function is used

to measure the current network performance, and is

also used to update the weights of the network during

the backpropagation method. In this work, the most

common cost function for regression problems was

used, the mean squared error (MSE):

C =

∑

i=1

− y

)

(1)

where t

is the i-th sample target output value, y

is the

respective estimated output value and K corresponds

to the number of samples. The cost function (1) is

only valid for neural networks with a single output,

where the learning process uses the complete set of

available samples at each iteration.

Training Algorithm. The performance of the ob-

tained neural network model strongly depends on the

training algorithm used. The Levenberg-Marquardt

algorithm was used as it is fast for simple networks

and in this work the expected neural network struc-

tures are small for both presented approaches.

Number of Hidden Layers. To identify the most ad-

equate number for the hidden layers, several networks

with different number of hidden layers were devel-

oped. In order to accommodate the inevitable varia-

(a) Classiﬁer (b) Predictor

Figure 4: Number of hidden layers.

tion on the network performance, for each number of

hidden layers tested, ﬁve experiments were run and

the median of the ﬁve was considered for the analy-

sis. From ﬁgures 4(a) and 4(b), it is possible to con-

clude that, as expected, the quality of the regression

increases with the number of hidden layers.

4 RESULTS

4.1 Flight Stage Classiﬁer

This section presents the designed ﬂight stage clas-

siﬁer, a neural network model that classiﬁes patterns

into categories. It receives the different physiological

variables (heart rate, cerebral oximetry and periph-

eral oximetry) as inputs and outputs the ﬂight stage

classiﬁcation. The ﬂight was divided into three ﬂight

stages, depending on the altitude rate: (C1) ascent, in-

cluding take-off (positive rate); (C2) cruise ﬂight (null

rate); and (C3) descent, including landing (negative

rate). The block diagram of the classiﬁer is repre-

sented in ﬁgure 5. The generated model is capable

Figure 5: Block diagram of ﬂight stage classiﬁer

(a) Cost function (b) Flight stage classiﬁca-

tion

Figure 6: Flight stage CNN model performance.

of identifying correctly 96.4% of the patterns of the

test data set. Table 1 presents the results obtained for

this data set, namely through the confusion matrix (ta-

ble 1(a)) and the performance measures (table 1(b)).

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

362

Figure 6(a) shows the evolution of the error for the

training data set, and ﬁg. 6(b) the comparison between

the classiﬁer output and the target (true output). These

results show the general good assessment of the clas-

siﬁer.

Table 1: Results of ﬂight stage classiﬁer for the test data set.

(a) Confusion matrix

Classiﬁer output

C1 C2 C3 Total

C1 851 18 869 869

Real C2 65 1503 18 1586

Flight Stage C3 0 11 965 976

Total 916 1532 983

(b) Performance measures

Classiﬁer

C1 C2 C3

Accuracy 0.9758 0.9674 0.9915

Sensitivity 0.9793 0.9477 0.9887

Precision 0.9290 0.9811 0.9817

Speciﬁcity 0.9646 0.9843 0.9927

4.2 Physiological Variables Predictor

This section presents the three single input, single

output (SISO) dynamic neural networks capable of

individually estimating the three physiological vari-

ables (cerebral oximetry, peripheral oximetry and

heart rate) from the barometric altitude. The respec-

tive block diagrams are depicted in ﬁg. 7. Table 2

Figure 7: Block diagrams of the SISO dynamic models.

shows the regression and mean squared error values

obtained for the best model of each type. The periph-

eral oximetry model has the best overall ﬁtting, given

that it has the lowest mean squared error (MSE) and

a regression value very close to the best value of the

heart rate model.

Table 2: Performance of the different dynamic SISO mod-

els.

Input Output Regression value MSE

Cerebral oximetry 0.9676 0.0132

Altitude Peripheral oximetry 0.9961 0.0033

Heart rate 0.9979 0.0226

Figure 8 depicts the results obtained for the cere-

bral oximetry predictor. With a linear regression ﬁt-

ting coefﬁcient of 0.9676, the model output shows a

nearly perfect ﬁt against the target values. The re-

sults obtained for the peripheral oximetry predictor

are depicted in ﬁgure 9. With a linear regression ﬁt-

ting coefﬁcient of 0.9961 and a MSE of 0.0033, the

model output is nearly perfect. In terms of the heart

rate predictor, the results obtained are depicted in ﬁg-

ure 10, showing a linear regression ﬁtting coefﬁcient

of 0.9979 and a MSE of 0.0226.

5 CONCLUSIONS

This paper assesses the use of neural network models

to relate physiological variables (heart rate, peripheral

oximetry and cerebral oximetry) with barometric alti-

tude. This assessment is twofold. First it considers

using the available physiological variables to classify

the altitude rate (ﬂight stage). Second, it considers dy-

namic models to predict each physiological variable

from the barometric altitude. Both approaches used

real data obtained from three hypobaric chamber tests

performed by the same pilot. The good results ob-

tained validate the proposed models. Moreover, they

may serve as the basis for the development of an alert

system of abnormal situations. For example, compar-

ing the altitude rate obtained from the barometric al-

titude with the ﬂight stage classiﬁed using the physi-

ological variables it may be possible to detect a mal-

function of the barometric sensor. Or comparing the

physiological variables prediction using the baromet-

ric altitude with the respective measured variables, it

may be possible to detect an unexpected physiolog-

ical behavior of the pilot, eventually caused by hy-

poxia or other conditioning factors. Following steps

also include analysing the sensitivity of the models to

different pilots data.

ACKNOWLEDGEMENTS

This work was supported by FCT, through IDMEC,

under projects LAETA (UID/EMS/50022/ 2013) and

iDecision4Care (IF/00833/2014/CP1238/ CT0002).

S. M. Vieira acknowledges the support by Program

Investigador FCT (IF/00833/ 2014) from FCT, co-

funded by the European Social Fund (ESF) through

the Operational Program Human Potential (POPH).

Relating Aircraft Altitude with Pilot’s Physiological Variables: Towards Increasing Safety in Light-sport Aviation

363

(a) Mean squared error (b) Regression (c) Target versus model output

Figure 8: Cerebral oximetry DNN model performance.

(a) Mean squared error (b) Regression (c) Target versus model output

Figure 9: Peripheral oximetry DNN model performance.

(a) Mean squared error (b) Regression (c) Target versus model output

Figure 10: Heart rate DNN model performance.

REFERENCES

Acharya, S., Rajasekar, A., Shender, B., Hrebien, L., and

Kam, M. (2016). Real time hypoxia prediction us-

ing decision fusion. IEEE Journal of Biomedical and

Health Informatics, PP(99).

Aqueveque, P., Gutierrez, C., Saavedra, F., and et al. (2016).

Monitoring physiological variables of mining workers

at high altitude. In Industry Applications Society An-

nual Meeting, pages 1–6. IEEE.

Gurjar, R., Seetamraju, M., Wolf, D. E., and Hastings, J.

(2010). High reliability, miniature personal hypoxia

monitoring system. In SPIE 7674, Smart Biomedi-

cal and Physiological Sensor Technologies VII, page

76740H76740H. International Society for Optics and

Photonics.

Harding, R. (2002). Medical Aspects of Harsh Environ-

ments, volume 2, chapter 32 - Pressure Changes and

Hypoxia in Aviation, pages 984–1013. Ofﬁce of The

Surgeon General, Dep.of the Army, United States of

America.

Haykin, S. (1999). Neural Networks: A Comprehensive

Foundation. Prentice-Hall.

Marques, A. (2012). Unpressurized light aviation aircrafts

ﬂight and physiological data acquisition system. Mas-

ter’s thesis, Universidade da Beira Interior, Covilh

Portugal.

Patrao, L., Zorro, S., Silva, J., Castelo-Branco, M., and

Ribeiro, J. (2013). Flight physiology training expe-

riences and perspectives: Survey of 117 pilots. Avia-

tion, Space, and Environmental Medicine, 84(6):620–

624.

Petrassi, F., Hodkinson, P., Walters, P., and Gaydos, S.

(2012). Hypoxic hypoxia at moderate altitudes: re-

view of the state of the science. Aviation, Space, and

Environmental Medicine, 83(10):975–984.

Wagner, D. (2011). Ambulatory recording of physiological

variables during an ascent of Mt Aconcagua. Wilder-

ness & Environmental Medicine, 22(1):58–61.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

364