
An Optimal Control Problem Formulation for a State Dependent
Resource Allocation Strategy
Paolo Di Giamberardino and Daniela Iacoviello
Department of Computer Control and Management Engineering ”A. Ruberti”, Sapienza University of Rome,
Via Ariosto 25, 00185, Rome, Italy
Keywords:
Optimal Control, State-based Cost Function, Switching Control, Epidemic Models, HIV Model.
Abstract:
In this paper, the problem of optimal resource allocation depending on the system evolution is faced. A
preliminary analysis defines the global effort required in any subset of the system state space according to
needed or desired goals. Then, in the definition of the cost function, the control action is weighted by a
piecewise constant function of the state, whose different constant values are defined for each subset previously
defined. The aim is to weight the control according to the distinct conditions, so getting different solutions
in each state space region so to optimize the planned resources according to the global goal. A constructive
algorithm to compute iteratively the final control law is outlined. The effectiveness of the proposed approach
is tested on a typical model of human immunodeficiency virus (HIV) present in literature.
1 INTRODUCTION
In a control problem formulation, the main attention
is given on the global performances of the system ac-
cording to the desired state or output behavior. There
are several cases in which the effort for the control
goal achievements must be taken into consideration
for a suitable, realistic and physically acceptable re-
sult, especially when optimality is also desired for
the time length of the control action. In fact, in such
cases, the containment of the control strength and the
problem of the resource limitations can be considered
together in the same way; this is usually performed
both by introducing constraints in the control and in
the ad hoc choice of the cost index in which the cost of
the control is suitable defined. This is a classical prob-
lem that can be easily solved by means of the Pon-
tryagin minimum principle; in the obtained solution
the optimal control can present discontinuities (Hartl
et al., 1995) at unknown instants, due to the presence
of the constraints on the input amplitude.
Applications of optimal control techniques range
from economics to biology, mechanics, telecommu-
nications and so on (Jun, 2004), (C.Liu et al., 2008),
(Nguyen and Sorenson, 2009). For the minimum time
problems with linear steady state system, the opti-
mal solution is bang-bang type with a limited number
of switching points (M.Athans and Falb, 1996). In
(Pasamontes et al., 2011) it is proposed to control
a solar collector making use of a switching control
strategy, showing that also changes in the dynamics
can be handled in the contest of optimal control. Im-
pulsive switching systems are another class of hybrid
dynamical systems in which global optimal control
strategies are proposed (R.Gao et al., 2010); they are
characterized by abrupt changes at the switching in-
stants.
The problem of optimal resources allocation
may arise when dealing with competing alterna-
tive projects which share common resources; this is
the so-called multi-armed bandit problem that has
received much attention especially in economics,
(Asawa and Teneketzis, 1996). In this case, the prob-
lem relies in determining the best strategy, among a
set of possible ones, knowing the state of each phase.
The decision is made on the basis of a payoff, i.e. a
cost, associated to the action.
In general, when dealing with the optimal control
of switched systems, like for examplethe optimal tim-
ing control problem, switching cost index can be in-
troduced to take into account the changes in the con-
trolled dynamics. One of the characteristic of these
problems is that the systems involved present continu-
ous dynamics subject to external discontinuous input
actuated by a switching signal generator. Different
schemes can be proposed and the optimal control the-
ory applied to hybrid systems allows to determine the
control input that optimizes a chosen performance
186
Giamberardino, P. and Iacoviello, D.
An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy.
DOI: 10.5220/0006477801860195
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 186-195
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

index defined on the state trajectory of the system.
This leads to two possible sub-problems, the time op-
timization problem and the optimal mode-scheduling
problem (Ding, 2009). The former relies in finding
the optimal placements of switching times assuming
a fixed switching sequence; the latter is the problem
of determining the optimal switching sequence of a
switched system.
The presence of (white) noise perturbations can be
also considered, as in (Liu et al., 2005); an interesting
aspect is that the control weights are indefinite and the
switching regime is described via a continuous-time
Markov chain. It is proposed a near-optimal control
strategy aiming at a reduction of complexity.
Numerical problems arising when dealing with
optimal switching control are considered in (Luus and
Chen, 2004) where a direct search optimization pro-
cedure is discussed.
In this paper the problem of optimal resource al-
location is related to the real time system behavior
considering the total amount of resources, i.e. the in-
put constraint, fixed, and acting on the cost function,
in particular on the weight of the input, in order to
change the total cost according to the operative con-
ditions. The idea is to replicate a planning scheme in
which the designer fixes the relevance of the control
action according to the conditions and, consequently,
changes the politics of intervention making the con-
trol effort more or less relevant. For example, in a
economic contest, within a prefixed total amount of
resources (input constraint), the investment of more
or less budget for the solution of some problem can
be driven by some social indicator indexes, like un-
employment below or over a prefixed critical percent-
ages, or the national PIL lower or higher a prefixed
threshold which guarantees economic grown, or the
level taxation, and so on.
Then, a cost index in which the control action is
weighted by a spatial piecewise constant function of
the state is introduced, so that its value changes de-
pending on the current state. The effect is to get dif-
ferent cost functions, defined over each state space re-
gion, which weight the control differently depending
on the region in which the system operates, in order to
implement, in the contextof the classical optimal con-
trol formulation, a state dependent strategy. Changing
the weight for the control for each distinct state space
region corresponds to give a different relevance to the
control amplitude action with respect to the other con-
tributions, mainly errors, in the cost function. The re-
sult is that planning the different constant weights for
the control reflects in allowing the control to use dif-
ferent amplitudes, clearly higher in correspondence to
lower costs and lower for higher costs.
While the system evolves remaining in the same
state space region, the solution of the optimal control
problem gives an optimal solution for the control ac-
tion. When, during the state evolution, the trajectory
crosses from one region to another, a switch of the
cost function occurs at the time instant in which the
state reaches the regions separation boundary. From
that time on, a different optimal control problem is
formulated, equal to the previous one except for the
input weight in the cost function.
This procedure is iterated until the final state con-
ditions are reached. The overall control results to be
a switching one, whose switching time instants are
not known in advance but are part of the solution of
the optimal control problem, depending on the op-
timal state evolution within each region. This kind
of approach is different from the others previously
recalled; here, the discontinuous switching solution
does not arise either for the presence of switching dy-
namics, or for control saturation, but comes from the
particular choice of the cost index. The control strat-
egy changes since in the cost index it is assumed that
the control needs to be weighted differently bringing
to different strategies depending on the actual state
value. It can be referred as a real time state dependent
weight.
A first use of a switching formulation for an op-
timal control problem is proposed in (Di Giamber-
ardino and Iacoviello, 2017), applied to a classical
SIR epidemic diffusion. The effectiveness of the pro-
posed approach is then here shown making use of a
biomedical example, the control of an epidemic dis-
ease, the immunodeficiency virus (HIV). The HIV
model proposed in (Wodarz, 2001) and modified in
(Chang and Astolfi, 2009) is adopted. The choice of
this example comes from the consideration that usu-
ally the medical and social interest for the presence
of an epidemic spread depends on the level of diffu-
sion of the infection, being considered in some sense
natural if it is lower than a physiologic level and be-
coming more and more relevant as the intensity of the
infection increases. Then, according to the present ap-
proach, a state dependent coefficient that weights dif-
ferently the control depending on the number of the
infected cells is introduced, taking as state space re-
gion division the sets that correspond to a physiolog-
ical level, a high but not serious level and a very high
risk level. This corresponds to change the interven-
tion strategy depending on the varied conditions; as
already noted, the possible switching instants are not
known in advance but are determined on the basis of
the dynamic variables evolution and on the optimiza-
tion process.
In general, the introduction of a continuous state
An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy
187

function as a weight in the cost index can be found
in (Behncke, 2000) for the case of SIR dynamics.
There, the feasibility of different control actions is in-
vestigated along with the possibility of introducing a
weight of the vaccination control depending on the
number of susceptible subjects; it is assumed the hy-
pothesis that vaccination at higher densities may be
less expensive and logistically easier. The continuous
weight tate space function brings to some additional
conditions, more than the usual ones of an optimal
control problem formulation, to be fulfilled.
The introduction of a spatial piecewise constant
function instead of a generic one as weight function
for the control brings back the problem formulation,
and then the problem solution, to a classical formu-
lation, except for the fact that the whole solution is
obtained composing the different local solutions com-
puted in each region in which the state trajectory
evolves.
The paper is organized as follows: Section 2 is
devoted to the description of the proposed approach,
based on an iterative optimal control computation
driven by the state values. In Section 3 some re-
calls on the HIV model and the control described in
(Chang and Astolfi, 2009) are given. Then, in Section
4 the proposed control strategy with the state depen-
dent cost index is applied to the HIV model. In Sec-
tion 5 the numerical results obtained for the case study
here considered are presented and discussed. Conclu-
sions and future work are outlined in Section 6.
2 PROBLEM FORMULATION
Starting from some brief recalls on the classical op-
timal control formulation, the proposed approach is
introuced and described.
2.1 Recalls on Optimal Control
Problem Formulation
In the optimal control theory, the following classical
minimum time problem is considered.
Given a generic dynamical system
˙x(t) = f (x(t), u(t)) (1)
with x ∈ ℜ
n
, u ∈ ℜ
m
, x(t
0
) = x
0
, where f ∈ C
2
with re-
spect to its arguments, and the q-dimensional inequal-
ity constraints on the control action
q(u(t)) ≤ 0 (2)
and assumed the cost index
J(u(t), T) =
Z
T
t
0
L(x(t), u(t))dt (3)
in which the Lagrangian L(x(t), u(t)) : ℜ
n+m
→ ℜ
depends on the state as well as on the control, find
the optimal values for the control (u
0
(t)) and the fi-
nal time (T
0
), under the state constraint (1) and the
inequality constraint on the input (2), satisfying the
final condition
χ(x(T), T) = x(T)− x
f
= 0 (4)
for a given x
f
∈ ℜ
n
, with χ ∈ C
1
, such that dim(χ) =
σ, 1 ≤ σ ≤ n+ 1.
As well known, once the constraints are given, the
obtained solution is optimal for the specific choice of
the cost function J(u(t), T). Changing such a func-
tion, also the solution changes. This means that the
choice of the function J(u(t), T) or, equivalently, of
the Lagrangian function L(x(t), u(t)) represents a cru-
cial aspect of the whole design procedure. In addi-
tion, their structure strongly affects not only the re-
sult but also the design procedure. In fact, usually,
a linear combination of linear or quadratic terms is
adopted for L, with constant coefficients representing
the weight of each term in the sum, i.e. how much it
is important in the evaluation of the optimality of the
solution.
Such a structure is justified by the simplicity in
the problem formulation and in the computation of
the solution as well.
There are authors proposing richer formulations,
in which some of the weights for the input variables
can be taken as nonlinear functions of the state vari-
ables, in order to assign different relevance to the
control action depending on the operative conditions,
(Behncke, 2000). Clearly, this kind of formulation
introduces some additional conditions to be fulfilled
and the complexity in the computation of the optimal
control grows significantly, requiring additional spe-
cific hypothesis on the system behavior.
The idea developed in the present work, and il-
lustrated in the next Subsection 2.2, is to maintain the
richness of the nonlinear state dependent weights and,
at the same time, to preserve the simplicity coming
from the use of linear/quadratic terms in the problem
formulation and solution.
2.2 The Proposed Approach
A generic quadratic function of u(t) in L(x(t), u(t))
depending on the state, can be written as u
T
P(x)u,
where P(x) represents the different weight of the input
as a function of the state and then of the operative
conditions.
In the proposed approach, which aims at simpli-
fying the optimal control formulation preserving the
richness of a state space dependent weight, the state
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
188

space is divided into N subsets I
i
, such that ∪
N
i=1
I
i
=
ℜ
n
, each of them corresponding to different strategies
to be adopted. Therefore, the function P(x) is defined
as
P(x) = Π
i
when x ∈ I
i
(5)
with Π
i
∈ ℜ
m×m
positive defined m × m matrix, i =
1, . . . , N, where the entries of Π
i
are designed in order
to manage the input cost as the state changes.
Then, while x ∈ I
i
, the term u
T
Π
i
u is used in the
Lagrangian L(x(t), u(t)) which can be rewritten as
L
Π
i
(x(t), u(t) to put in evidence such dependency.
Once that in the optimal control problem formula-
tion no state dependent weight is esplicitely present,
the solution can be found according to the well known
approach which makes use of the Hamiltonian
H
Π
i
(x, λ, u) = L
Π
i
(x, u) + λ
T
f (x, u) (6)
where λ : ℜ → ℜ
n
, λ(t) ∈ C
1
almost everywhere, is
the n–dimensional multiplier function for the differ-
ential constraint given by the dynamics. Clearly, such
a formulation holds only when x ∈ I
i
.
Under the constraints (2) and (4), the optimal solu-
tion can be obtained solving the necessary conditions
given by
˙
λ = −
∂H
Π
i
(x, λ, u)
∂x
T
(7)
0 =
∂H
Π
i
(x, λ, u)
∂u
T
+
∂q(u)
∂u
T
η (8)
η
T
q(u) = 0 (9)
η ≥ 0 (10)
0 = H (x(T), λ(T), u(T)) (11)
λ(T) = −
∂χ(x(T), T)
∂x(T)
T
ζ (12)
where η(t) ∈ ℜ
p
, η ∈ C
0
almost everywhere, ζ ∈ ℜ
σ
,
and along with conditions (1), (2) and (4). The solu-
tion obtained holds until x(t) ∈ I
i
and it is optimal in
such a region. If the solution is such that the com-
puted trajectory goes outside the region I
i
entering
a contiguous region I
j
, then a new problem has to
be formulated with initial condition for the state as
the value on the boundary between the regions I
i
and
I
j
reached by the previously computed control, and
making use of the Lagrangian L
Π
j
(x, u) and, then, of
H
Π
j
(x, λ, u) in the necessary conditions.
The final solution is obtained by concatenating all
the partial solutions computed.
Clearly, such a solution cannot be defined as op-
timal since in this formulation it is not computed ac-
cording to a unique cost index, but it is optimal if re-
stricted to each state space region.
In order to better illustrate the proposed approach,
an example in the epidemiological field is provided;
in this kind of problems, the classical medical ap-
proach makes use of thresholds to classify the severity
of the infection and then this can be used to modulate
the control weight in the cost index.
In next Section 3 the mathematical model of one
case study, the HIV infection, is briefly introduced,
and the proposed procedure is used in Section 4.
3 THE MATHEMATICAL MODEL
OF THE SAMPLE SYSTEM
Many different models have been proposed to de-
scribe the HIV (human immunodeficiency virus); the
virus infects the CD4 T-cells in the blood of an HIV-
positive subject; when the number of these cells is
below 200 in each mm
3
the HIV patient has AIDS.
Models of the HIV generally consider the unin-
fected CD4 T-cells, the infected CD4 T-cells, the in-
fectious virus, the noninfectious virus and the im-
mune effectors, (Banks et al., 2006). In (Chang and
Astolfi, 2009) also the effects of cytotoxic T lym-
phocyte (CTL) are taken into account aiming at de-
termining a control that drives the patients into the
long-term non progression (LTNP) status, instead to
progress to the AIDS one. A simplified system is pre-
sented in (Joshi, 2002) where only the concentration
of CD4 T-cells and the concentration of the HIV parti-
cles are analyzed; in this case two different treatments
strategies are introduced in the differential equations.
Among all the proposed strategies, the policy using
two drug controls appears to be the best one, since it
reduces the number of virus particles, beyond the rise
of the number of uninfected CD4 T-cells, (Zhou et al.,
2014). The problem of the fast mutation of the HIV is
faced in (E.A.H. Vargas, 2014); this could cause resis-
tance to specific drug therapies; the model predictive
control shows the best performance among the ones
based on a switched linear system to a nonlinear mu-
tation model. In (Ding et al., 2012) it is suggested the
use of the fractional-order HIV model as a descrip-
tion more realistic than traditional ones, thus obtain-
ing very low levels dosage of anti-HIV drugs.
In this paper, the HIV model proposed in (Wodarz,
2001) and modified in (Chang and Astolfi, 2009) is
used. It will be shortly recalled hereafter. In the com-
plete model the state variables to be considered are:
• the uninfected CD4 T-cells, denoted by x
1
(t);
• the infected CD4 T-cells, denoted by x
2
(t);
• the helper–independent CTL, denoted by z
1
(t);
An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy
189

• the CTL precursor, denoted by w(t): it provides
long term memory for the antigen HIV;
• the helper-dependent CTL, denoted by z
2
(t): it
destroys the infected cells x
2
(t).
The equations describing the relations among
these variables are
˙x
1
(t) = γ− dx
1
(t) − β(1− u(t))x
1
(t)x
2
(t) (13)
˙x
2
(t) = β(1− u(t))x
1
(t)x
2
(t) − αx
2
(t) +
−(p
1
z
1
(t) + p
2
z
2
(t))x
2
(t) (14)
˙z
1
(t) = c
1
z
1
(t)x
2
(t) − b
1
z
1
(t) (15)
˙w(t) = c
2
x
1
(t)x
2
(t)w(t) − c
2
qx
2
(t)w(t) +
−b
2
w(t) (16)
˙z
2
(t) = c
2
qx
2
(t)w(t) − hz
1
(t) (17)
where γ, d, β, α, p
1
, p
2
, c
1
, c
2
, b
1
, b
2
and h are the
models parameters whose numerical values are dis-
cussed in (Wodarz, 2001) and the control u(t) is as-
sumed bounded.
In (Chang and Astolfi, 2009) the Authors aim to
determine a control making use of equations (13)
and (14) only, through a simplified representation
in which the contribution of (15), (16) and (17) to
the (13)–(14) dynamics is reduced to an approxi-
mated near-equilibrium polynomial term. The pro-
posed modified model is
˙x
1
(t) = γ− dx
1
(t) − β(1− u(t))x
1
(t)x
2
(t) (18)
˙x
2
(t) = −βx
1
(t)x
2
(t)ut + π(x
2
(t)) (19)
with
π(x
2
(t)) = a+ Bx
2
(t) + Cx
2
2
(t) + Dx
3
2
(t) (20)
For sake of simplicity, in the sequel the model
(18)–(19) with position (20) will be assumed, with
the initial conditions denoted by x
1
(t
0
) = x
1,0
and
x
2
(t
0
) = x
2,0
.
As well known, in optimal control the central as-
pect is the definition of the cost index, that is what is
required to be minimized; in this case, the control ef-
fort and the number of infected subjects seem to be a
good choice.
Another aspect to be considered is the problem of
resources allocation especially when they are partic-
ularly limited. For example, in (Yuan et al., 2015)
this problem is faced when a limited quantity of vac-
cine has to be distributed between two non-interactive
populations; in that case, a stochastic epidemic model
is assumed.
Hereafter, the resource limitation is introduced by
a constraint as (2).
4 IMPLEMENTATION OF THE
PROPOSED APPROACH
The example introduced in previous Section 3 can be
effectively used to describe the proposed approach.
In fact, it is possible to define different strategies in
terms of control effort to be applied according to the
severity of the infection, measured by the number
x
2
(t) of infected cells. In other words, for sake of sim-
plicity, it is possible to find three levels of necessity
of intervention; if x
2
(t) is below a certain threshold,
say ξ
1
, no actual infection is diagnosed and then no
intervention is required; then, defined ξ
2
as the level
of infected cells over which the infection presents se-
vere effects, it is possible to choose two different ef-
fort in case of x
2
(t) ≥ ξ
1
is greater or lower than ξ
2
:
in the first case a stronger action is required than the
one in the second case, and this requirement can be
introduced in the control design setting a lower cost,
i.e. weight, to the control if x
2
(t) ≥ ξ
2
and a higher
weight when ξ
1
≤ x
2
(t) < ξ
2
.
So, according to the procedure described in Sub-
section 2.2, the state space x = (x
1
x
2
)
T
is divided into
three regions:
I
1
=
x ∈ ℜ
2
: x
2
< ξ
1
I
2
=
x ∈ ℜ
2
: ξ
1
≤ x
2
< ξ
2
(21)
I
3
=
x ∈ ℜ
2
: x
2
≥ ξ
2
I
1
is the region in which no control action is needed;
I
2
is the region corresponding to the presence of the
infection while I
3
corresponds to a severe stadium of
infection.
Choosing the cost function
J(u(t), T) =
Z
T
t
0
[K
1
+ K
2
x
1
(t)x
2
(t)u(t) + K
3
x
2
(t)+
+P(x(t))u
2
(t)
dt (22)
with K
i
> 0, i = 1, 2, 3, the state function P(x(t)) can
be set as
P(x(t)) = Π
1
, x ∈ I
1
P(x(t)) = Π
2
, x ∈ I
2
(23)
P(x(t)) = Π
3
, x ∈ I
3
with Π
3
< Π
2
, so that the control can assume higher
values when the infection is severe (x ∈ I
3
), being
cheaper than in the case of x ∈ I
2
. As far as Π
1
is
concerned, its value is not relevant since when x ∈ I
1
no control action is required and then no control prob-
lem has to be formulated.
Assuming the nontrivialinitial conditions x
1,0
∈ ℜ
and x
2,0
≥ ξ
1
, x
0
∈ I
i
for a certain i > 1, the constraint
(4) can be rewritten as
χ(x(T), T) = x
2
(T) − ξ
1
= 0 (24)
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
190

while the resources limitation, i.e. the control con-
straint (2), can be explicitly written as
q(u(t)) =
q
1
(t)
q
2
(t)
=
−u(t)
u(t) −U
≤ 0 (25)
U > 0, where the first component represents the non
negativity condition while the second one is the upper
bound limitation.
To solve the problem the classical optimal control
theory is applied; the Hamiltonian in each region I
i
is
defined as
H
Π
i
(x
1
(t), x
2
(t), λ
1
(t), λ
2
(t), u(t)) =
= K
1
+ K
2
x
1
(t)x
2
(t)u(t) + K
3
x
2
(t) + Π
i
u
2
(t) +
+λ
1
(t)(γ − dx
1
(t) − β(1− u(t))x
1
(t)x
2
(t)) +
λ
2
(t)(−βx
1
(t)x
2
(t)ut + π(x
2
(t))) (26)
and then the necessary optimal conditions given in
Subection 2.2 assume the explicit expressions
˙
λ
1
(t) = −
∂H
Π
i
∂x
1
= −K
2
x
2
(t)u(t) + dλ
1
(t) +
+β(1− u(t))x
2
(t)λ
1
(t) +
+βx
2
(t)λ
2
(t)u(t)
˙
λ
2
(t) = −
∂H
Π
i
∂x
2
= −K
2
x
1
(t)u(t) − K
3
+
+β(1− u(t))x
1
(t)λ
1
(t) +
+βx
1
(t)λ
2
(t)u(t) +
−λ
2
(t)
B+ 2Cx
2
(t) + 3Dx
2
2
(t)
0 =
∂H
Π
i
∂u
+
∂q
1
∂u
η
1
+
∂q
2
∂u
η
2
= 2Π
i
u(t)
+K
2
x
1
(t)x
2
(t) + βx
1
(t)x
2
(t)λ
1
(t) +
−βx
1
(t)x
2
(t)λ
2
(t) − η
1
(t) + η
2
(t)
0 = η
1
(t)q
1
(u(t))
0 = η
2
(t)q
2
(u(t))
η
1
(t) ≥ 0
η
2
(t) ≥ 0
0 = H
Π
i
(x(T), λ(T), u(T))
λ
1
(T) = 0
λ
2
(T) = −ζ
2
ζ
2
∈ ℜ
with condition (24) too.
After some computations, defining the function
W(t) as
W(t) = x
1
(t)x
2
(t)(−K
2
− βλ
1
+ βλ
2
) (27)
the optimal control satisfying the necessary condi-
tions previously introduced can be expressed as
u
1
(t) =
0 if W(t) < 0
W(t)
2Π
i
0 <
W(t)
2Π
i
< U
U if
W(t)
2Π
i
> U
(28)
By integration, denoting with
T
1
, x
1
1
(t), x
1
2
(t), u
1
(t)
the solution obtained over the
time interval
t
0
, T
1
, it is also the optimal solution as
long as x(t) ∈ I
i
.
If x
0
∈ I
i
and x(t) ∈ I
i
∀t ∈
t
0
, T
1
, one
has that the solution is the whole optimal solu-
tion, which can be indicated with the superscript
0
:
T
0
, x
0
1
(t), x
0
2
(t), u
0
(t)
=
T
1
, x
1
1
(t), x
1
2
(t), u
1
(t)
, and
x
2
T
0
= ξ
1
. Otherwise, there exists a time instant
t = t
1
such that x(t
−
1
) ∈ I
i
and x(t
+
1
) ∈ I
j
, i 6= j. Then,
a new optimal control problem must be solved, with
the same conditions as the previous ones after the sub-
stitutions t
0
= t
1
, x(t
0
) = x(t
1
), and the index j instead
of i.
In the present case, being two the effective re-
gions, the optimal solution obtained in the first of the
previous case necessarily means that i = 2. Other-
wise, the switching condition does hold for i = 2 and
j = 3 or vice versa.
The control computation ends at step k ≥ 1 when,
after a a priori unknownnumber k−1 ≥ 0 of switches,
the solution
T
k
, x
k
1
(t), x
k
2
(t), u
k
(t)
is such that x(t) ∈
I
2
∀t ∈
t
k−1
, T
k
and condition (24) is satisfied.
For k > 1, the whole solution is then given by con-
catenating the k partial ones, so getting a switching
solution with switching times t
i
, i = 1, 2, . . . , k−1 and
optimal time T
0
= t
k
.
It is important to stress that in the proposed ap-
proach the presence of switching instants depends on
the evolution of the state: no information can be avail-
able, even on their existence. The state dependent
switching conditions makes possible a different in-
terpretation; the control law computed following this
procedure can be regarded as a continuous time op-
timal control over a discrete time feedback update
of the control parameters. The optimal control can
be computed and applied until the state belongs to
the given region I
i
; crossing the regions boundary is
equivalent to an event driven discrete state feedback
which updates all the parameters, mainly the Π
i
, and
recompute a new optimal control over the new state
space region I
j
.
5 SIMULATION RESULTS
In this Section the results of some numerical simula-
tions are presented, showing the behavior of the pro-
posed control design approach making use of the HIV
model presented in Section 3. In all the simulations
performed, the parameters reported in Table 1, taken
from (Chang and Astolfi, 2009), have been used for
the model (18)–(19), along with the initial conditions
An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy
191
x
1,0
= 0.2 and x
2,0
= 3.
Table 1: Numerical values used for the HIV system param-
eters.
γ 1 B -3.1540
d 0.1 C 2.9402
β 1 D -0.6
α 0.0668
The choice of the HIV case study is quite meaning-
ful, since a switching control form takes the form
of a classical therapy strategy, being usually a piece-
wise constant control with the aforethought switching
times: it consists of a full drug dose for a limited time
and then a switch to zero, (Wodarz, 2001), sometimes
putting in evidence the daily therapy, (Chang and As-
tolfi, 2009).
An optimal control approach demands to the cost
function the ability to modulate the control accord-
ing to all the variables involved, possibly increasing
the performances of the control action. For a choice
of the cost index as in (22), the solution depends on
the values given to the weights assigned to each term.
In fact, in a classical minimum time optimal control
formulation, for the numerical choice of the constant
weights K
1
= 10, K
2
= 1 and K
3
= 20, taking for ex-
ample a constant weight P(x(t)) = P = 1 ∀x ∈ ℜ
2
, for
U = 0.9 as in (Chang and Astolfi, 2009) and ξ
1
= 0.03
in (4), the optimal control solution u
0
(t) obtained is
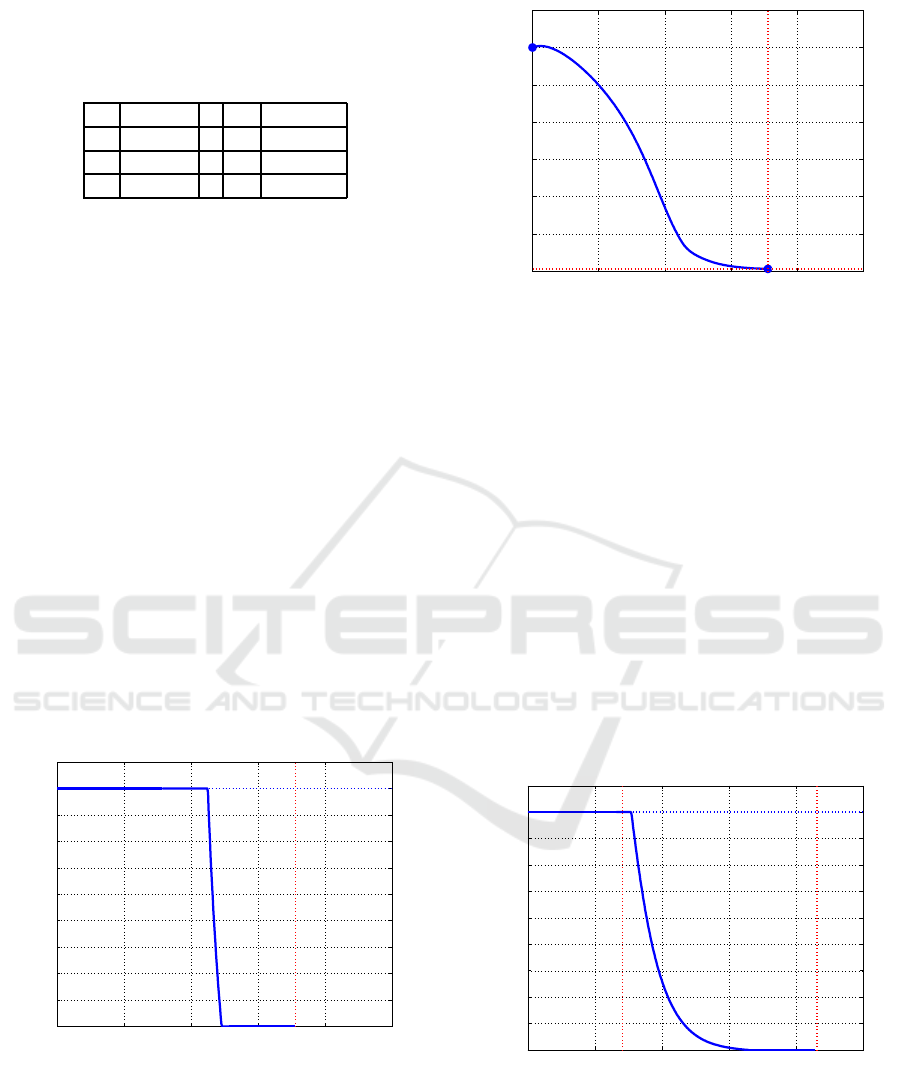
depicted in Figure 1, while Figure 2 reports the opti-
mal time evolution of the infected cells x
0
2
(t).
0 1 2 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Time t
Optimal control u
o
(t): drug dose
Upper bound
T
o
Figure 1: Optimal control for constant input weight P = 1.
As expected, the choice of the weight for the input
u(t) in the cost index lower or equal to the ones as-
signed to the terms containing the infected cells pro-
duces an optimal control behavior equal to the upper
bound value from t
0
= 0 until the number of infected
cells is reduced at a level in which a high control ac-
tion is too expensive with respect to such a number,
0 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
Time t
Infected cells x
2
o
(t)
ξ
1
T
o
Figure 2: Infected cells evolution under optimal control.
and then it goes to zero as the x
2
(t) component de-
creases, so assuming a so called bang–bang behavior
between the upper and the lower bounds.
If the approach proposed in this paper is adopted,
the regions I
1
, I
2
and I
3
as in (21) must be introduced,
with their meaning discussed in Section 4, and with
the correspondingweights Π
i
as in (23) for the control
in the cost function (22).
The numerical values chosen are ξ
2
= 2, so that
the initial condition lies in the dangerous regionI
3
and
the solution must cross the normal region I
2
, Π
2
=
100 and Π
3
= 1, while Π
1
in this is not used due to the
no action region I
1
. The values for Π
2
and Π
3
with
Π
2
≫ Π
3
have been chosen in order to significantly
put in evidence the difference between a low cost, and
then a higher margin for the control effort and a high
cost, which should act against a high control effort.
0 1 2 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Time t
Optimal control u
o
(t): drug dose
Upper bound
t
1
T
o
=T
2
Figure 3: Full control for switched value of P(x(t)).
The solution obtained, depicted in Figure 3, is, con-
firming what planned, the concatenation of two seg-
ments; a first optimal segment over the region I
3
in
the time interval 0 = t
0
≤ t < t
1
= 1.41, computed
with P(x(t)) = Π
3
, and then, at t = t
1
, the switch of
P(x(t)) from Π
3
to Π
2
produces the second segment
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
192
which brings to the final condition x
2
(T
0
) = ξ
1
= 0.03
at time t = T
0
= 4.31.
This composition of the whole control in the form
of a switching solution can be well put in evidence
plotting the solution obtained in the first step of the
procedure, under the hypothesis that the state is con-
tained in the set I
3
, and marking the time instant t = t
1
in which the state trajectory reaches the boundary of
I
3
. This is done in Figure 4.
0 1 2 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Time t
u
1
(t)
Upper bound
t
1
T
1
Figure 4: Optimal control obtained in the first step of the
procedure, with the effective part from 0 to t
1
evidenced.
0 1 2 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Time t
u
2
(t)
Upper bound
t
1
T
2
Figure 5: Optimal control obtained in the second step of the
procedure, with the effective part from t
1
to T
2
evidenced.
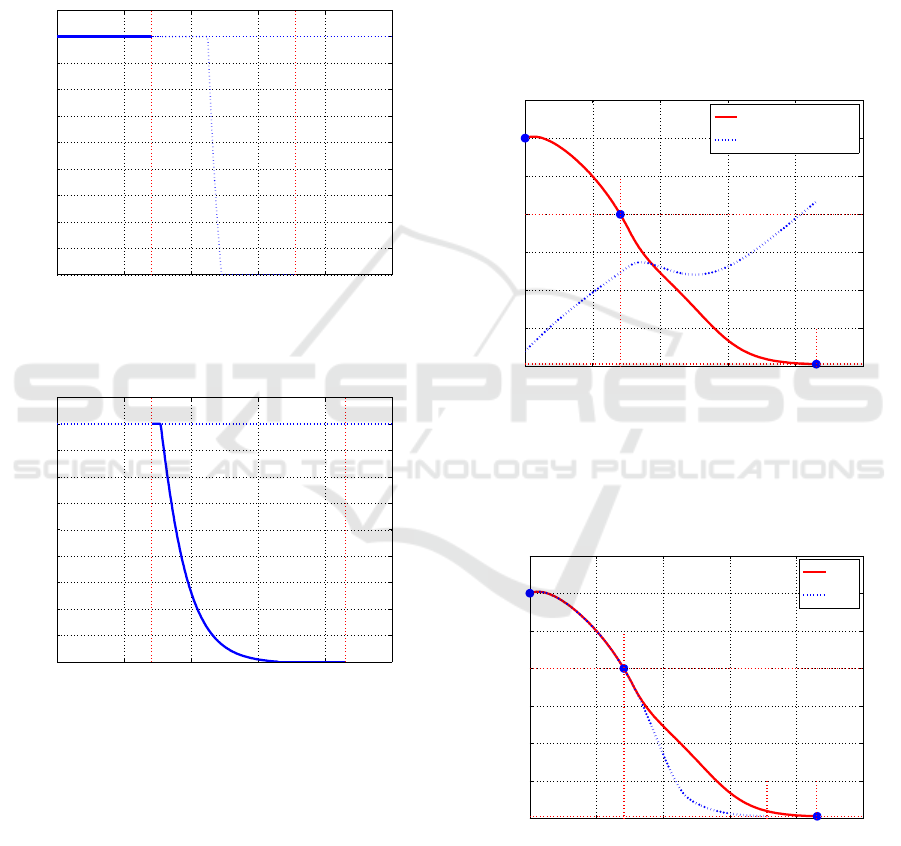
Then, in Figure 5 the solution of the optimal con-
trol problem defined over I
2
starting from the initial
condition on its boundary corresponding to the value
reached in the previous phase is plotted. Comparing
the two Figures 4 and 5, it is possible to understand
the effect of the different weights of the input vari-
able on the control law obtained; in the first case,
with a lower cost, the upper bound, i.e. the maximum
value, of the control is kept longer than in the second
case, being cheaper. In the second case, the cost of
the control forces the solution to reduce it as much as
possible to guarantee that the state reaches the final
condition balancing the cost of the error with the one
of the control. The change of the control weight in
the cost function at the boundary between I
2
and I
3
produces a new behavior, characterized by a shorted
saturated action and a smoother decreasing shape, as-
suring, however, the convergence to the final state.
The concatenation of the effective part in Figure 4
with the one in Figure 5 yelds Figure 3. Note that the
time instant in which the solution depicted in Figure
3 starts to decrease from the upper limit does not co-
incides with the switching instant t
1
: after the switch,
the control remains at its maximum but for less time
than in the non switching case.
0 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
Time t
Optimal state evolution
ξ
1
ξ
2
t
1
T
o
=T
2
Infected cells x
2
tot
(t)
Uninfected cells x
1
tot
(t)
Figure 6: State evolution given by the full switched control.
The time history of the uninfected (x
1
(t)) and in-
fected (x
2
(t)) cells is depicted in Figure 6 where the
switching conditions and the corresponding time in-
stants are evidenced.
0 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
Time t
Infected cells x
2
(t)
ξ
1
ξ
2
t
1
T
1
T
o
=T
2
x
2
tot
(t)
x
2
1
(t)
Figure 7: Time evolution of the infected cells in switched
and non switched case: a comparison.
A comparison between the evolution of the infected
cells obtained with the switching formulation and the
classical one coming from the use of a unique con-
stant value for the input weight is reported in Figure
7. Note that the non switching solution corresponds to
An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy
193

keep P(x(t)) = Π
3
for all the state values, i.e. consid-
ering I
2
and I
3
as a unique region with a low cost for
the input, like in a standard optimal control problem
formulation. It can be noted that in the time interval
corresponding to the evolution in the I
2
region, the
solution, obtained using a low control weight only,
makes the state reach the final condition faster and
keeps the number of the infected cells lower than in
the other case. Obviously, this is due to the fact that
the higher cost for the control brings the optimal con-
trol formulation to save the control effort, still bring-
ing to an effective solution as well.
Nevertheless, this apparent drawback is fully com-
pensated by the fact that the control, over the whole
time interval during which the drug is provided, re-
quires a lower contribution. This can be shown com-
puting and plotting the function
R
t
0
u(τ)dτ which give
a measurement of the total drug to be used in the ther-
apy.
Figure 8 is then obtained, showing that until both
solutions require the full control action (t = t
1
), up
to its bound, the functions are obviously coincident;
then, the decrement of the control in the switching
case, starting when the classical one is still at max-
imum, produces a reduction of the total amount of
input quantity, and then a reduced impact on the in-
fected patient and, at the same time, on the cost re-
lated to the therapy, despite its longer time of applica-
tion.
0 1 2 3 4 5
0
0.5
1
1.5
2
2.5
3
3.5
Time t
Time integral of the control u(t)
t
1
T
1
T
2
Switching solution
Classical non switching solution
Figure 8: Integral cost of the control action for the switching
solution and for the classical case: a comparison.
6 CONCLUSIONS
In this work a suitable non-linear cost index is as-
sumed in a minimum time optimal control problem
formulation, weighting the control by a state depen-
dent locally constant function. This approach can
deal with changes in the external conditions since it
is based on the state evolutions; it can tackle practi-
cal applications in telecommunications, biology, me-
chanics, economics, just to mention a few. The ef-
fectiveness of the proposed approach is verified con-
sidering a model of human immunodeficiency virus
(HIV) and proposing a cost index in which the con-
trol effort is weighted taking into account the number
of infected cells, giving higher attention when they
are dangerously over a fixed critical value and con-
sidering the infection not much severe below. Obvi-
ously the result can be easily generalized to the case
of more than one critical value. The results obtained
show that this approach provides an efficient resource
allocation, so being more effective, for example from
an economical point of view, than the classical theory
with the constant weight choice.
REFERENCES
Asawa, M. and Teneketzis, D. (1996). Multi-armed bandits
with switching penalties. IEEE Trans. On Automatic
Control, 41(3):328–348.
Banks, H., Kwon, H., Toivanen, J., and Tran, H. (2006). A
state-dependent riccati equation-based estimator ap-
proach for hiv feedback control. Optimal control ap-
plications and methods, 27.
Behncke, H. (2000). Optimal control of deterministic epi-
demics. Optimal control applications and methods,
21.
Chang, H. and Astolfi, A. (2009). Control of hiv infection
dynamics. IEEE Control Systems.
C.Liu, Gong, Z., Feng, E., and Yin, H. (2008). Opti-
mal switching control for microbial fed-batch culture.
Nonlinear analysis: Hybrid systems, 2.
Di Giamberardino, P. and Iacoviello, D. (2017). Optimal
control of sir epidemic model with state dependent
switching cost index. Biomedical Signal Processing
and Control, 31.
Ding, X. (2009). Real-time optimal control of autonomous
switched systems. PhD thesis, Georgia Institute of
Technology.
Ding, Y., Wang, Z., and Ye, H. (2012). Optimal control
of a fractional-order hiv- immune system with mem-
ory. IEEE Trans. On Control System Technology,
30(3):763–769.
E.A.H. Vargas, P. Colaneri, R. M. (2014). Switching strate-
gies to mitigate hiv mutation. IEEE Trans. On Control
System Technology, 22(4):1623–1628.
Hartl, R., S.P.Sethi, and Vickson, R. (1995). A survey of
the maximum principles for optimal control problems
with state constraints. Society for Industrial and Ap-
plied Mathematics, 37:181–218.
Joshi, H. (2002). Optimal control of an hiv immunology
model. Optimal control applications and methods, 23.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
194

Jun, T. (2004). A survey on the bandit problem with switch-
ing cost. The Economist, 152(4):513–541.
Liu, Y., Yin, G., and Zhou, X. (2005). Near optimal con-
trols of random-switching lq problems with indefinite
control weight costs. Automatica.
Luus, R. and Chen, Y. (2004). Optimal switching control
via direct search optimization. Asian Journal of Con-
trol, 6(2):302–306.
M.Athans and Falb, P. (1996). Optimal Control. McGraw-
Hill, Inc., New York.
Nguyen, D. and Sorenson, A. (2009). Switching control for
thruster-assisted position mooring. Control Engineer-
ing Practice, 17.
Pasamontes, M., J.D.Alvarez, J.L.Guzman, Lemos, J., and
Berenguel, M. (2011). A switching control strategy
applied to a solar collector field. Control Engineering
Practice, 19(2):135–145.
R.Gao, Liu, X., and Yang, J. (2010). On optimal control
problems of a class of impulsive switching systems
with terminal states constraints. Nonlinear Analysis,
73.
Wodarz, D. (2001). Helper-dependent vs. helper-
independent ctl responses in hiv infection: Implica-
tions for drug therapy and resistance. Journal theor.
Biol., 213.
Yuan, E., Alderson, D., Stromberg, S., and Carlson, J.
(2015). Optimal vaccination in a stochastic epidemic
model of two non-interacting populations. PLOS
ONE.
Zhou, Y., Yang, K., Zhou, K., and Wang, C. (2014). Optimal
treatment strategies for hiv with antibody response.
Journal of applied mathematics.
An Optimal Control Problem Formulation for a State Dependent Resource Allocation Strategy
195
