An Improved Secure Image Transmission Technique via Mosaic Images

by Nearly Reversible Color Transformations

Freddy Acosta Buena˜no

1,2

, Gonzalo Olmedo Cifuentes

, Inmaculada Mora-Jim´enez

and

Jos´e Luis Rojo

Alvarez

Departamento de El´ectrica y Electr´onica, Universidad de las Fuerzas Armadas ESPE, Av. General Rumi˜nahui s/n,

Sangolqu´ı, 171-5-231B, Ecuador

Department of Signal Theory and Communications, Telematics and Computing, Universidad Rey Juan Carlos,

Madrid, 28943, Spain

Keywords:

Image Transmission, Mosaic Image, Color Transformation, Statistical Simpliﬁcation.

Abstract:

Current multimedia communication systems seek to transmit images supporting contents by the data stream,

which requires speciﬁc effort for their bandwidth optimization. In this scenario, security of data and informa-

tion that is being transmitted is highly relevant. A new concept has been recently used in the ﬁeld of secure

image transmission, known as secret-fragment-visible mosaic image. In this case, a mosaic image is created

and used as a camouﬂage for a secret image. The mosaic image is similar to a target image freely chosen. We

propose here a technique based on a statistical simpliﬁcation approach to reduce the number of required bits

for recovering the secret image from the mosaic image. We benchmarked the performance of the method and

the quality of the recovered image. Experimental results showed that the number of bits with the proposed

method was dramatically reduced (close to 3 to 1), and quality metrics were about Root Mean Squared Er-

ror of 32 and Mean Structural Similarity of 0.7 for the created mosaic image. Our proposal paves the way

towards improved procedures that are suitable for multimedia systems like digital terrestrial television and

similar applications.

1 INTRODUCTION

Nowadays, images are transmitted through most of

the communication systems for countless applica-

tions, and new technologies are creating a plethora

of platforms for content exchange. Many methods

have been proposed for securing image transmis-

sion. Two usual approaches are image encryption

and data hiding. Image encryption techniques pro-

vide a noisy image, which may arouse attacker’s at-

tention during transmission (Fridrich, 1998; Chen

et al., 2004; Zhang et al., 2013; Kwok and Tang,

2007; Behnia et al., 2008; Xiao et al., 2009; Pati-

dar et al., 2011; Suresh and Ajai, 2016; Senthil Ku-

mar and Anandhi, 2016; Sarwate and Dakhore, 2015).

Data hiding methods mainly use Least Signiﬁcant

Bit (LSB) substitution (Chan and Cheng, 2004), his-

togram shifting (Ni et al., 2006), difference expan-

sion (Tian, 2003; Hu et al., 2008), prediction-errorex-

pansion (Sachnev et al., 2009; Li et al., 2011), recur-

sive histogram modiﬁcation (Zhang et al., 2013), or

discrete cosine or wavelet transformations (Fridrich

et al., 2001; Chang et al., 2007; Lee et al., 2007;

Lin et al., 2008; Jitha and Sivadasan, 2015). A main

drawback of methods for hiding data is the difﬁculty

in handling a large amount of data into a single im-

age. Speciﬁcally, to hide a secret image into a camou-

ﬂage image of the same size, the secret image must be

highly compressed in advance. (Lee and Tsai, 2014).

In this paper, a statistical approach is proposed for

getting the standard deviation values of the secret im-

age and the statistical and structural parameters of the

target image. The process is controlled by secret im-

ages statistical parameters and a secret key, and with

knowledge of these parameters and the key anyone

can recover the secret image with an acceptable loss.

It decreases the amount of required data remarkably,

with the subsequent bandwidth reduction.

The proposed method is inspired by the one de-

veloped by (Lee and Tsai, 2014), where an image

transmission technique by Nearly Reversible Color

Transformation (NRCT) was proposed to automati-

cally transform a secret image into a so-called secret-

fragment-visible mosaic image. The mosaic image

has the same size of the secret image and looks simi-

Buenaño, F., Cifuentes, G., Mora-Jiménez, I. and Álvarez, J.

An Improved Secure Image Transmission Technique via Mosaic Images by Nearly Reversible Color Transformations.

DOI: 10.5220/0006477900870092

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 5: SIGMAP, pages 87-92

ISBN: 978-989-758-260-8

lar to a target image freely chosen. It is also used as a

camouﬂage for the secret image by dividing the secret

image into blocks and transforming their color char-

acteristics to be similar to those of the corresponding

target image. Limitations of this approach come from

the number of required bits for recovering secret im-

ages embedded to a disguising mosaic image with no

compression.

Since it is highly desirable to optimize the bits for

recovering secret images, our goal is to propose an

algorithm to reduce as much as possible the informa-

tion embedded into the mosaic image. Secret image

data related with block position indices, mean values,

and rotation angles, are generated as in (Lee and Tsai,

2014). The required target image data are not inte-

grated in the bit stream, but instead they will be esti-

mated in reception. The exponential probability den-

sity function (pdf) is used to estimate the standard de-

viation of secret image blocks, therefore reducing the

number of transmitted bits. In this case, the receiver

has to be efﬁcient enough to reconstruct the whole se-

cret image all by itself.

Regarding the organization of this paper, ideas

of the proposed method and procedural aspects are

described in Section 2. Algorithm for creating the

stream of statistical data is detailed in Section 3. In

Section 4, experimental results and performance eval-

uation are presented to show the feasibility of the pro-

posed method, followed by conclusions in Section 5.

2 METHODOLOGY

The ﬂow diagram of our approach is in Fig. 1. It in-

cludes two main phases, mosaic image creation with

data stream assembling, and secret image recovery.

In the ﬁrst phase, a mosaic image is yielded to

serve as a container to include the data stream to be

!"#$"%&

'()*"&

+,+&-'%&!"#$"%&

'()*"&./0#12&

'3%0&4)$*"%&

'()*"&./0#12&

+,5&6")$/7&$"8"$2'./"&

#0/0$&%$)3290$():03&

)3;&./0#12&$0%):03&

+,<&=)$)("%"$'>):03&

09&2%)3;)$;&;"8'):03&

8)/?"2&09&!"#$"%&

'()*"&./0#12&

+,@&A)%)&

2%$")(&

)22"(./'3*&

5,+&B/0#1&$0%):03&)3;&

"2:():03&09&&

C)$)("%"$'>";&2%;&

8)/?"2&)3;&4)$*"%&

'()*"&'390$():03&

5,5&6")$/7&$"8"$2'./"&&

#0/0$&%$)3290$():03&

&.)#1&

5,<&D"#08"$7&09&%E"&&

!"#$"%&'()*"&

4)$*"%&'()*"F&

9$""/7&2"/"#%";&&

G02)'#&

'()*"&

Figure 1: Flow diagram of the proposal.

recovered in reception. The mosaic image consists of

blocks of an input secret image with NRCT applica-

tion and embedded data stream. This phase consists

of four stages: (1) matching blocks of the secret im-

age into those of the target image; (2) rotating each

secret image block to get the minimum Root Mean

Squared Error (RMSE) with respect to its correspond-

ing target block, and transforming the color character-

istic of each block in the secret image by NRCT; (3)

simplifying the content related to the standard devia-

tion in the secret image blocks through the parameters

of the underlying exponential pdf; and (4) preparing

the data stream for the recovery of the secret image in

reception.

In the second phase, the data stream is used to re-

cover a fairly good version of the secret image. This

phase includes three stages: (1) estimating blocks po-

sition indices, mean and standard deviation values,

and target image by assuming an exponential pdf and

using mosaic image information and blocks rotation;

(2) reverse NRCT processing; and (3) recovering the

secret image through estimated values.

2.1 NRCT Principles

Previously (Reinhard et al., 2001) proposed a color

transfer scheme converting the image statistics asso-

ciated with each color component to those of another

image by considering the lαβ color space. In (Lee

and Tsai, 2014), the same idea was adopted but using

the RGB color space.

More speciﬁcally, let secret blocks (T) and target

blocks (B) be described as two pixel sets p

, p

,..., p

and p

′

, p

′

,..., p

′

, respectively. Let the color of p

denoted by (r

) and that of p

′

by (r

′

). At

ﬁrst, we compute the mean and standard deviation

values of blocks in T and B for each color channel,

denoting c

and c

′

with c = r, g, or b as components of

pixels p

and p

′

, respectively. Next, we compute new

values (r

′′

) for each p

in T by

′′

= q

− µ

) + µ

′

, (1)

where q

= σ

′

/σ

is the standard deviation quotient

and µ

′

are the mean values of the correspond-

ing block components in the secret and target images,

respectively.

Authors in (Lee and Tsai, 2014) expressed a bit

stream M as

M = t

...t

...m

...q

...d

, (2)

where bit segments t

...t

, r

, m

...m

...q

, and d

...d

codify the indices of target

blocks B, the rotation angle of T, the mean values

of T and B, the standard deviation quotients, and the

SIGMAP 2017 - 14th International Conference on Signal Processing and Multimedia Applications

overﬂow/underﬂow residuals, respectively. Stream M

varies in size for each block, since segment d

de-

pends on the number of residuals (Huffman encoding

for residuals). The number of required bits for M is

discussed next with more detail: (1) the index of B

needs m bits to codify it, with m computed as

m =



log





, (3)

where N

is the size of the image block, and W

and

are the width and height of secret image S, respec-

tively; (2) 2 bits are required to code the rotation angle

(4 possible orientations); (3) 48 bits are necessary to

represent the average value of every block (secret and

target, 8 bits per component); (4) 21 bits are used to

represent the standard deviation quotients in the three

color channels, with 7 bits per channel; and (5) k bits

for representing the residuals, depending on the num-

ber of overﬂows and underﬂows.

3 PROPOSED METHOD

We propose an algorithm to reduce the required num-

ber of bits for recovering the secret image. This goal

is achieved by estimating the underlying distribution

of standard deviation values in blocks of the secret

image, which can be modelled by an exponential pdf.

Then, the information required to recover a block T

can be coded by a bit stream with three segments of

the form

= t

...t

...m

, (4)

where bit segments t

...t

, r

, and m

...m

code indices of one secret blocks T, the rotation an-

gle of T, and the mean values of blocks in T, respec-

tively. Then, bit streams of all blocks are ordered and

concatenated into a single bit stream M

for the en-

tire secret image. M

, together with the mean parame-

ter of the exponential pdf that represents the standard

deviation values of secret image blocks (S

shown in

Section 3.1), make the total bit stream M

of the form

= M

(5)

The number of bits to code M

is next discussed.

For the three segments in M

we use the method

in (Lee and Tsai, 2014): (1) m bits to code block in-

dices of secret image; (2) 2 bits to represent the rota-

tion angle; and (3) 24 bits for the average of secret im-

age blocks (8 bits per color channel). The bit stream

associated to the standard deviation values of the se-

cret image blocks needs 8 bits to represent the mean

parameter of the exponential pdf.

0 20 40 60 80

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

(a)

0 20 40 60 80 100

0.01

0.02

0.03

0.04

0.05

0.06

0.07

Mosaic image data

Target image data

(b)

Target image

Mosaic image

1000

2000

3000

(c)

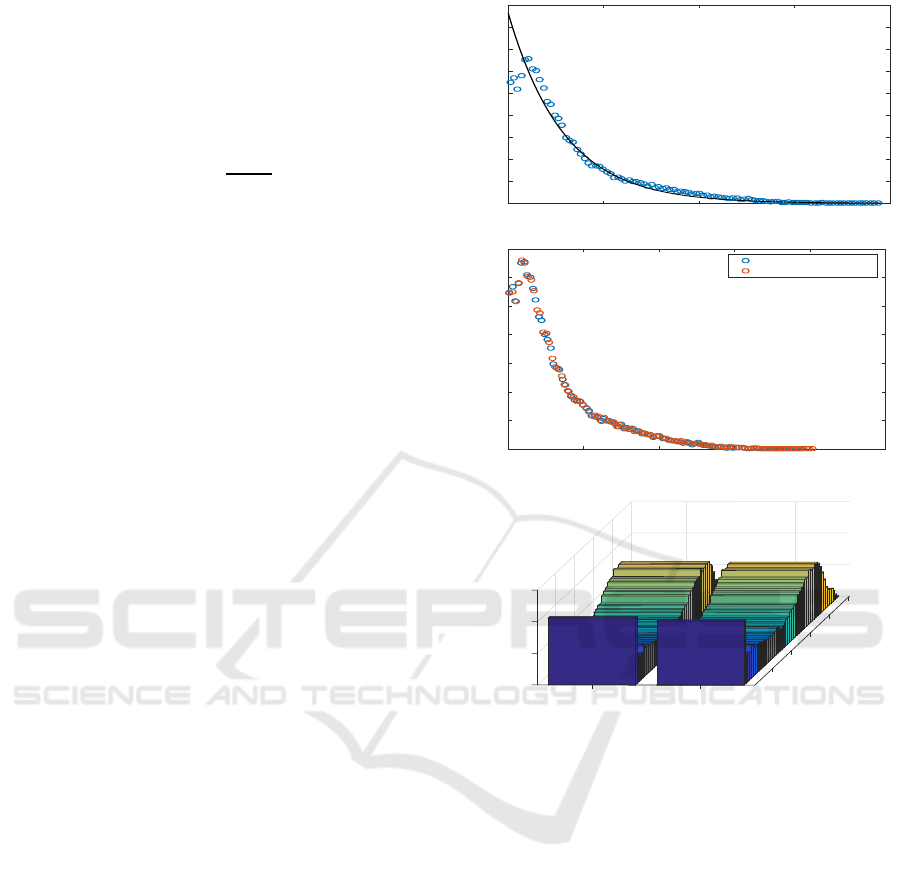
Figure 2: Adjustment between exponential pdf of standard

deviation values and experimental distribution.

3.1 Exponential Estimation Coding

Experiments were carried out with other pdfs, being

the log normal the best suited to the experimental dis-

tribution. Since values close to zero do not signiﬁ-

cantly inﬂuence, the exponential pdf was considered

instead of the log normal one, mainly to reduce the

mathematical complexity of the method.

We use the average of the standard deviation in

the secret image blocks as the value to be sent, repre-

sented by S

= s

...s

. The reason for this approach

is shown in Fig. 2(a). Note that the standard deviation

distribution can be modelled by an exponential pdf,

hence avoiding the need to transmit the standard de-

viation value of each block in the secret image and

transmit just a single value that can be represented

with eight bits. Note in Fig. 2(a) that the empirical

distribution moves away from the exponential pdf in

values very close to zero. Nevertheless, they have lit-

An Improved Secure Image Transmission Technique via Mosaic Images by Nearly Reversible Color Transformations

tle inﬂuence on the obtained results, so it was obvi-

ated.

3.2 Mosaic Image Information Coding

With respect to the target image information (standard

deviations, means, and position indices), it was esti-

mated in reception by using the mosaic image statis-

tical parameters. Means and standard deviations of

target and mosaic images are represented in Fig. 2(b)

and (c), respectively, clearly showing that an estima-

tion of these parameters can be considered in the re-

ceiver without need to transmit target image retrieval

information.

4 EXPERIMENTAL RESULTS

Using a set of images with size W

x H

pixels, a se-

ries of experiments were conducted to test the pro-

posed algorithm. Fig. 3 shows the number of re-

quired bits for recovering the secret image with dif-

ferent block size (namely, 8 x 8, 16 x 16, and 32 x 32)

when our approach and that by (Lee and Tsai, 2014)

are compared. Note that the number of bits increases

as the block size is reduced.

Performance measures were considered to evalu-

ate differences between the recoveredand the original

secret images, and also between the mosaic and the

target images. On the one hand, the RMSE was ob-

tained. On the other hand, the Mean Structural Sim-

ilarity Index (MSSIM) was provided to evaluate the

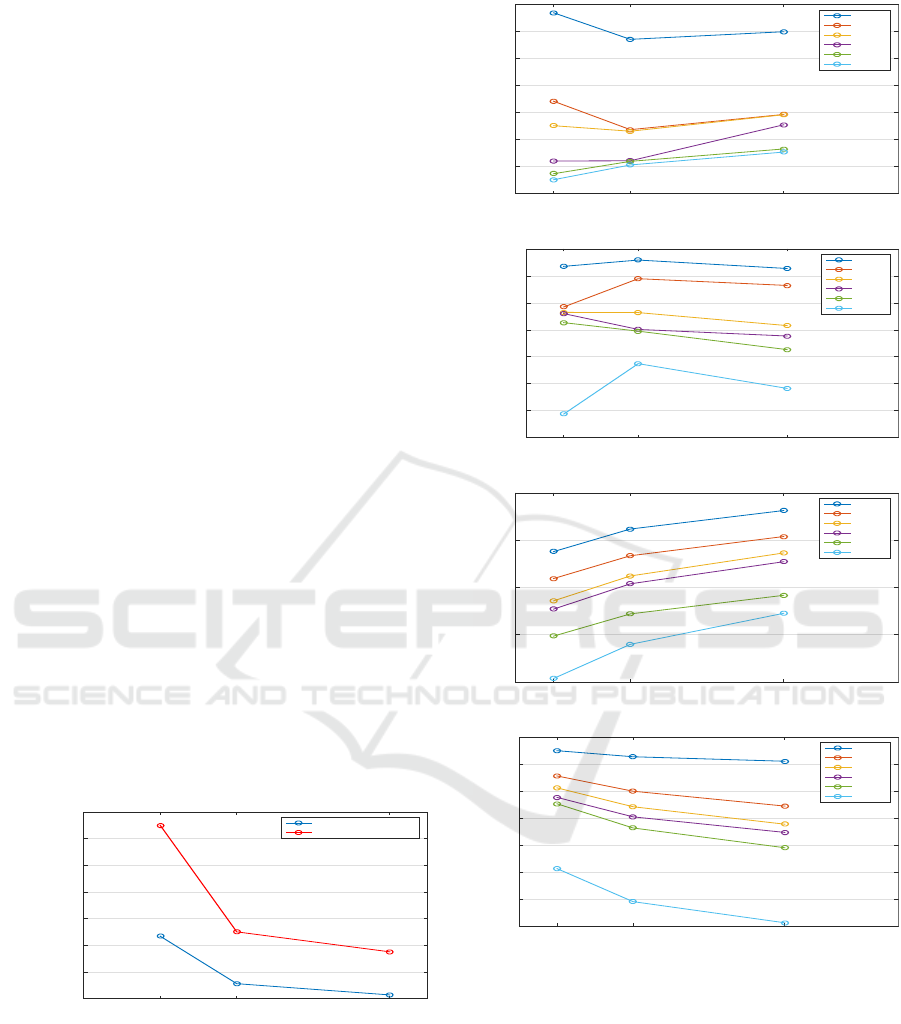
overall image quality. Fig. 4 shows the performance

evaluation results.

Block size

8x8 16x16 32x32

Required bits

200000

400000

600000

800000

1000000

1200000

1400000

Proposed method

Lee and Tsai

Figure 3: Number of required bits for recovering the secret

image.

We can see from Fig. 4(d) that the MSSIM value

of the created mosaic image with respect to the tar-

get image has an average value close to 0.8, showing

that the similarity of the details of the created mosaic

image to those of the target image is good enough for

the estimation consideration in Section 3.2.

Block size

8x8 16x16 32x32

RMSE

I-311

I-71

Mean

I-75

I-42

I-419

(a)

Block size

8x8 16x16 32x32

MSSIM

0.92

0.93

0.94

0.95

0.96

0.97

0.98

0.99

I-75

I-71

I-419

I-42

Mean

I-311

(b)

Block size

8x8 16x16 32x32

RMSE

I-419

I-42

I-71

Mean

I-311

I-75

(c)

Block size

8x8 16x16 32x32

MSSIM

0.3

0.4

0.5

0.6

0.7

0.8

0.9

I-419

I-42

I-71

Mean

I-311

I-75

(d)

Figure 4: RMSE and MSSIM versus block sizes (8×8,

16×16, 32×32) with secret and target images coming from

a large dataset: (a) RMSE between the recovered secret im-

ages and the original ones; (b) MSSIM between the recov-

ered secret images and the original ones; (c) RMSE between

the mosaic and the target images; (d) MSSIM between the

mosaic and the target images.

A comparison of the results yielded by the pro-

posed method with those by (Lee and Tsai, 2014) is

shown in Fig. 5. Here, panel (a) refers to the secret

image, panel (b) is the target image, panel (c) shows

SIGMAP 2017 - 14th International Conference on Signal Processing and Multimedia Applications

(a) (b)

(e) (f)

Figure 5: Comparison of results of (Lee and Tsai, 2014)

and proposed method; (a) Secret image; (b) Target image;

Tsai, 2014); (d) Mosaic image, created from (a) and (b) by

proposed method; (e) and (f) Recovered secret images by

(Lee and Tsai, 2014) and proposed method.

the mosaic image created by (Lee and Tsai, 2014)

with MSSIM=0.76, panel (d) is that created by the

proposed method with MSSIM=0.95, panels (e) and

(f) shows recovered secret images by (Lee and Tsai,

2014) and proposed method with MSSIM=0.96 and

MSSIM=0.98 respectively.

In order to show the ﬂexibility of the proposed

method to choose any target image, we selected the

secret image in Fig. 6 (a), and the two target images

shown in panels (b) and (c) of Fig. 6. The resulting

mosaic images are in panels (d) and (e). Note that

the recovered secret images look similar to the respec-

tive secret images (panels (f) and (g)) even though the

target images look quite different from the secret im-

ages. Images presented in this paper can be accessed

on the internet

For guidance, the processing time in our program-

ming simulator using MATLAB in a computer with 8

GB RAM, i5 2.5 GHz processor and 500 GB SATA

hard disk, for a process with block size N = 8, was in

the transmitter t

= 95s, and in the receiver t

= 54s.

We can see in Fig. 7 that the processing time decreas

es with increasing block size N.

Images are available at https://www.pexels.com/ and

http://gratisography.com/

(a) (b) (c)

(d) (e)

(f) (g)

Figure 6: Mosaic and recovered images with the same se-

cret image; (a) Secret image; (b) Target image One; (c) Tar-

get image Two; (d) and (f) Mosaic images, and (e) and (g)

Recovered secret images from (a) and (b), and (a) and (c),

respectively.

Block size

8x8 16x16 32x32

Processing time in seconds

100

Transmitter

Receiver

Figure 7: Processing time required by the method in trans-

mitter and receiver with different block size N, in a com-

puter with 8 GB RAM, i5 2.5 GHz processor and 500 GB

SATA hard disk.

5 CONCLUSIONS

An algorithm has been proposed to reduce the amount

of bits required to retrieve the secret image, based on

the method proposed in (Lee and Tsai, 2014). This

algorithm allows us to get better bandwidth perfor-

mance for transmission, by the use of an exponential

pdf to model the standard deviation of the secret im-

age, as well as an estimation by statistical parameters

of mosaic image to model target image parameters.

An Improved Secure Image Transmission Technique via Mosaic Images by Nearly Reversible Color Transformations

The number of required bits was dramatically reduced

(close to 3 to 1). Also, the original secret images can

be recovered nearly losslessly from the created mo-

saic images. Good experimental results have shown

the feasibility of the proposed method. Future studies

may be directed to apply further statistical simpliﬁca-

tions to the position indices and means, among other

low-complexity options.

REFERENCES

Behnia, S., Akhshani, A., Mahmodi, H., and Akhavan, A.

(2008). A novel algorithm for image encryption based

on mixture of chaotic maps. In Chaos Solit. Fract.,

vol. 35, pp. 408 - 419.

Chan, C. K. and Cheng, L. M. (2004). Hiding data in images

by simple lsb substitution. In Pattern Recognition, vol.

37, pp. 469 - 474.

Chang, C. C., Lin, C. C., Tseng, C. S., and Tai, W. L.

(2007). Reversible hiding in dct-based compressed

images. In Inf. Sci., vol. 177,pp. 2768 - 2786.

Chen, G., Mao, Y., and Chui, C. K. (2004). A symmet-

ric image encryption scheme based on 3d chaotic cat

maps. In Chaos Solit. Fract., vol. 21, pp. 749 - 761.

Fridrich, J. (1998). Symmetric ciphers based on two-

dimensional chaotic maps. In Int. J. Bifurcat. Chaos,

vol. 8, pp. 1259 - 1284.

Fridrich, J., Goljan, M., and Du, R. (2001). Invertible au-

thentication. In Proc.SPIE, vol. 3971, pp. 197 - 208.

Hu, Y., Lee, H. K., Chen, K., and Li, J. (2008). Difference

expansion based reversible data hiding using two em-

bedding directions. In IEEE Trans.Multimedia, vol.

10, pp. 1500 - 1512.

Jitha, R. and Sivadasan, E. T. (2015). A survey paper on

various reversible data hiding techniques in encrypted

images. In IEEE International Advance Computing

Conference (IACC), pp. 1139 - 1143.

Kwok, H. S. and Tang, W. K. S. (2007). A fast image en-

cryption system based on chaotic maps with ﬁnite pre-

cision representation. In Chaos Solit. Fract.,vol. 32,

pp. 1518 - 1529.

Lee, S., Yoo, C. D., and Kalker, T. (2007). Reversible im-

age watermarking based on integer-to-integer wavelet

transform. In IEEE Trans. Inf. Forens. Secur.,vol. 2,

pp. 321 - 330.

Lee, Y. and Tsai, W.-H. (2014). A new secure image trans-

mission technique via secret-fragment-visible mosaic

images by nearly reversible color transformations. In

IEEE Transactions on circuits and systems for video

technology, VOL. 24.

Li, X., Yang, B., and Zeng, T. (2011). Efﬁcient reversible

watermarking based on adaptive prediction-error ex-

pansion and pixel selection. In IEEE Trans.Image

Process., vol. 20, pp. 3524 - 3533.

Lin, W. H., Horng, S. J., Kao, T. W., Fan, P., Lee, C. L.,

and Pan, Y. (2008). An efﬁcient watermarking method

based on signiﬁcant difference of wavelet coefﬁcient

quantization. In IEEE Trans. Multimedia, vol. 10, pp.

746 - 757.

Ni, Z., Shi, Y. Q., Ansari, N., and Su, W. (2006). Reversible

data hiding. In IEEE Trans. Circuits Syst. Video Tech-

nol., vol. 16, pp. 354 - 362.

Patidar, V., Pareek, N. K., Purohit, G., and Sud, K. K.

(2011). A robust and secure chaotic standard

map based pseudorandom permutation- substitution

scheme for image encryption. In Opt. Commun., vol.

284, pp. 4331 - 4339.

Reinhard, E., Ashikhmin, M., Gooch, B., and Shirley, P.

(2001). Color transfer between images. In IEEE Com-

put. Graph. Appl., vol. 21, pp. 34 - 41.

Sachnev, V., Kim, H. J., Nam, J., Suresh, S., and Shi,

Y. Q. (2009). Reversible watermarking algorithm us-

ing sorting and prediction. In IEEE Trans.Circuits

Syst. Video Technol., vol. 19, pp. 989 - 999.

Sarwate, S. and Dakhore, H. (2015). An approach to color

transformation for image encryption and data hiding.

In Global Conference on Communication Technolo-

gies, pp. 792 - 796.

Senthil Kumar, A. and Anandhi, T. (2016). Multi image

integration and encryption algorithm for security ap-

plications. In Industrial Electronics Society - 42nd

Annual Conference of the IEEE, pp. 986 - 991.

Suresh, A. and Ajai, R. (2016). Vlsi implementation of text

to image encryption algorithm based on private key

encryption. In International Conference on Electrical,

Electronics, and Optimization Techniques, pp. 4879 -

4881.

Tian, J. (2003). Reversible data embedding using a differ-

ence expansion. In IEEE Trans. Circuits Syst. Video

Technol., vol. 13, pp. 890 - 896.

Xiao, D., Liao, X., and Wei, P. (2009). Analysis and im-

provement of a chaos- based image encryption algo-

rithm. In Chaos Solit. Fract., vol. 40,pp. 2191 - 2199.

Zhang, W., Hu, X., Li, X., and Yu, N. (2013). Recursive his-

togram modi- ﬁcation: Establishing equivalency be-

tween reversible data hiding and lossless data com-

pression. In IEEE Trans. Image Process., vol. 22,pp.

2775 - 2785.

SIGMAP 2017 - 14th International Conference on Signal Processing and Multimedia Applications