
Design of a Sensor-based Controller Performing U-turn to Navigate
in Orchards
A. Durand-Petiteville
1
, E. Le Flecher
2,3
, V. Cadenat
2,3
, T. Sentenac
2
and S. Vougioukas
1
1
Department of Biological and Agricultural Engineering, University of California, Davis, CA, 95616, U.S.A.
2
CNRS, LAAS, 7 avenue du colonel Roche, F-31400 Toulouse, France
3
Univ. de Toulouse, UPS, LAAS, F-31400, Toulouse, France
Keywords:
Mobile Robots, Sensor-based Control, Orchard Navigation, Spiral Following.
Abstract:
In this work, the problem of designing sensor-based controllers allowing to navigate in orchards is considered.
The navigation techniques classically used in the literature rely on path following using metric maps and met-
ric localization obtained from onboard sensors. However, it appears promising to use sensor-based approaches
together with topological maps for two main reasons: first, the environment nature is rather changing and
second, only high-level information are sufficient to describe it. One of the key maneuver when navigating
through an orchard is the u-turn which must be performed at the end of each row to reach the next one. This
maneuver is generally performed using only dead reckoning because of the lack of dedicated sensory data. In
this paper, we propose two sensor-based control laws allowing to perform u-turns, improving the performance
quality. They allow following particular spirals which are defined from laser rangefinder data and adapted to
realize the desired maneuver. Their stability is studied and their performances are thoroughly examined. Fi-
nally, they are embedded in a complete navigation strategy to show their efficiency in our agricultural context.
1 INTRODUCTION
To meet the demands of nine billion people in 2050,
scientists predict that the agricultural production has
to double (Foley et al., 2011). Robotics has been iden-
tified as one of the solutions with the highest poten-
tial to achieve this goal (Reid, 2011). Indeed, robots
can improve the efficiency of each process of the
crops production: field preparation, seeding/breeding,
transplanting, planting, growing, maintenance, har-
vesting, sorting and packing. To successfully perform
most of those tasks, the navigation is one of the key
challenges. Indeed the robot has to safely drive up
along one row, turn at the end of the row and enter the
next one (Siciliano and Khatib, 2016). For open field
crops, e.g. wheat or lettuce, the navigation strategies
mostly rely on path following using GPS-based lo-
calization, such as the works presented in (Bak and
Jakobsen, 2004), (Fang et al., 2006), (Eaton et al.,
2009) and (Johnson et al., 2009). However, these
approaches are no more suitable for orchards crops,
e.g. apples or pears, because of poor satellite recep-
tion under thick canopies. It is then required to local-
ize and/or control robots thanks to embedded sensors
such as inertial units, cameras, lidars, radars, etc. The
work presented in (Barawid et al., 2007) focused
solely on straight line recognition of the tree rows us-
ing a laser scanner as a navigation sensor. A Hough
transform is applied to the points cloud to recognize
the tree row, which is then used to autonomously drive
the robot in the orchard. In (Hansen et al., 2011), a
metric localization is performed thanks to a 2D laser
scanner, an odometer and a gyroscope. The collected
data are then processed in three derivative free filters
in order to localize the robot. In (Zhang et al., 2014),
a mapping method takes as input readings from the
lidar and encoders as the vehicle is manually driven
around the orchard for at least two full rounds. Then,
the collected data are processed off-line to generate a
metric map, which is then permanently stored on the
vehicles on-board computer in order to navigate. In
(Bayar et al., 2015), the navigation is performed by
following metric paths. To do so, the localization and
control are based on a laser range-finder and wheels
and steering encoders. All the mentioned approaches
rely on a path following using a metric localization.
This latter has to deal with slopped and slippery ter-
rains, branches sticking out of the canopy, tall grass,
and missing trees. Moreover, the u-turns are usually
partially performed using dead-reckoning because of
172
Durand-Petiteville, A., Flecher, E., Cadenat, V., Sentenac, T. and Vougioukas, S.
Design of a Sensor-based Controller Performing U-turn to Navigate in Orchards.
DOI: 10.5220/0006478601720181
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 172-181
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the absence of trees in the field of view of the sensors
while following outside-the-row trajectories.
To overcome these limitations, we propose, based
on the work presented in (Durand-Petiteville et al.,
2015), to design an approach relying on non-metric
maps and sensor-based controllers in order to navi-
gate in an orchard. First, having an up to date met-
ric map of the orchards seems challenging because of
the changing nature of the environment. Indeed, over
the years, the trees grow and are pruned; over the sea-
sons, the leaves grow and disappear; over the days, the
fruits grow, bend the branches and finally fall. More-
over, to identify when the robot has to drive through
the row or switch from one row to the next one, only
high level localization data are required. Topologi-
cal maps being barely sensitive to local environment
modifications (i.e. size of the trees, presence or not
of leaves, position of the branches, ...) and providing
high level localization, they seem relevant to model
the orchard. Then, when navigating in an orchard, the
robot main goal is not to reach a destination, but to
locally behave appropriately. Indeed, it has to drive
through a row while staying at a defined distance with
respect to the trees when picking fruits, or to follow a
local path when switching from one row to the other.
For this reason, it looks appropriate to use sensor-
based controllers
1
.
In this paper, we focus on the sensor-based controllers
required to navigate in an orchard. First, driving
through the row consists in following the line in the
middle of the trees. It exists a large collection of
controllers performing such a task, e.g. simple PID
controllers. To complete the navigation system, the
challenge consists in designing a sensor-based con-
troller allowing to perform a u-turn to switch from
one row to the next one. In this paper, we propose
to address this issue by designing two sensor-based
controllers following spirals around a point of inter-
est. The first one allows to follow a spiral whose dis-
tance to the center is not known whereas the second
one follows a spiral at a known distance from it. The
design of the controllers relies on the work presented
in (Boyadzhiev, 1999) which describes how insects
fly around a point of interest by performing a spiral.
In other words, it shows how to follow a path, a spi-
ral in this particular case, by simply knowing the co-
ordinates of a point of interest in the moving object
frame. This work has already been used on a UAV
(Mcfadyen et al., 2014) and a ground robot (Futter-
lieb et al., 2014) to design sensor-based controllers
avoiding obstacles. The relative position of the obsta-
1
Sensor-based controllers only use the data regarding the
surrounding environment and provided by the embedded
sensors.
cle with respect to the robot is used to push the robot
away from danger. Thus, the robots modify their be-
havior without following a path/spiral. The work pre-
sented in this paper aims at designing controllers fol-
lowing spirals. Thus, by tracking a point of interest, a
tree in our case, it will become possible for the robot
to actually follow a path ending in the next row.
The work is presented as follows. In the next sec-
tion the spiral model is briefly summarized. Then two
controllers allowing to perform a spiral following are
designed in section 3. Next, some simulations results
showing the efficiency of our approach are presented.
In a last section, an example of sensor-based naviga-
tion architecture is first presented, then simulations of
a navigation in an orchard are provided.
2 SPIRAL
Spirals have been studied in (Boyadzhiev, 1999),
where the author presents a large variety of equations
to model them. The present work focuses on some
ideas extracted from (Boyadzhiev, 1999) and more es-
pecially on the one claiming that a spiral can be seen
as the path described by a point O
p
moving on a plane
with respect to a fixed point O
s
. From now on this
point will be considered as the center of the spiral.
~
v
∗
is the velocity vector applied to O
p
and its norm is de-
noted v
∗
(t). Moreover
~
d
∗
is the vector connecting O
s
to O
p
whose norm is d
∗
(t). Finally α
∗
(t) is defined as
the oriented angle between
~
v
∗
and
~
d
∗
.
α
∗
α
∗
α
∗
α
∗
−→
v
∗
−→
d
∗
−→
d
∗
−→
d
∗
−→
d
∗
−→
v
∗
−→
v
∗
−→
v
∗
O
S
O
P
O
P
O
P
O
P
Figure 1: Spiral model.
In (Boyadzhiev, 1999) it is shown that if both v
∗
(t)
and α
∗
(t) are constant then O
p
describes a spiral
whose center is O
s
. For this reason they are respec-
tively denoted v
∗
and α
∗
from now on. Moreover
the author provides an important equation regarding
d
∗
(t):
˙
d
∗
(t) = −v
∗
cos(α
∗
) (1)
As it can be seen in this equation, the type of spiral
performed depends on the sole parameter α
∗
. First
if 0 < α
∗
< π, O
p
turns counter-clockwise with re-
Design of a Sensor-based Controller Performing U-turn to Navigate in Orchards
173

-5 0 5
X(m)
-4
-2
0
2
4
6
Y(m)
(a) Inward spiral - α
∗
=
15π
32
-5 0 5
X(m)
-6
-4
-2
0
2
4
6
Y(m)
(b) Outward spiral - α
∗
=
17π
32
Figure 2: Example of spirals - Black cross: center of the
spiral - Green cross: initial position - Red cross: final posi-
tion.
spect to O
s
otherwise if −π < α
∗
< 0 it turns clock-
wise. Then if 0 ≤ α
∗
< π/2 or −π/2 ≤ α
∗
< 0,
d
∗
(t) decreases with time (see figure 2(a)). In other
words, O
p
is describing an inward spiral around O
s
.
If π/2 < α
∗
≤ π or −π ≤ α
∗
< −π/2 then d
∗
(t) in-
creases with time (see figure 2(b)) which means O
p
is describing an outward spiral around O
s
. Finally,
if α
∗
= π/2 or α
∗
= −π/2, d
∗
(t) = d
∗
(0). O
p
then
describes a circle of radius d
∗
(0) around O
s
.
Equation (1) and its analysis highlight our interest in
spirals. Indeed, by adapting the spiral model to a
robot and then making converging α, angle between
its linear velocity vector and the point of interest O
s
,
towards α
∗
, it is possible to make the vehicle follow a
spiral defined by α
∗
. Thus the sensor space is used to
control the robot path.
3 CONTROLLER DESIGN
In the previous section, it has been explained how to
choose a value for α
∗
in order to define a spiral. In
this section, controllers allowing a robot to perform
such a spiral are presented. To do so, we first present
the model of the robot and how to adapt the spiral
approach to it. Then a first controller following a spi-
ral only defined by its α
B
value is designed and its
performance is analyzed. Finally a more advanced
controller allowing to follow a specific spiral, i.e. de-
fined by its α
∗
value and the initial distance to O
S
, is
introduced.
3.1 Robot Modeling
In this work we consider the differential robot pre-
sented in figure 3. Let F
w
= (O
w
,~x
w
,~y
w
,~z
w
) and
F
r
= (O
r
,~x
r
,~y
r
,~z
r
) the frames respectively attached to
the world and the robot. The robot state vector is de-
fined as χ(t) = [x(t),y(t),θ(t)]
T
, where x(t) and y(t)
are the coordinates of O
r
in F
w
, whereas θ(t) is the an-
gle between ~x
w
and ~x
r
. Finally the robot is controlled
using the input vector
˙
χ(t) = [v(t), ω(t)]
T
where v(t)
is the linear velocity along ~x
r
, and ω(t) the angular
velocity around~z
r
.
!x
w
!y
w
!x
r
!y
r
α(t)
−→
d
O
r
O
w
O
s
β(t)
θ( t)
x(t)
y(t)
Figure 3: Robot model.
As previously mentioned, this work focuses on fol-
lowing a spiral whose center is denoted O
s
. It then
requires to adapt the spiral model to the robot. The
vector connecting O
s
to O
r
is named
~
d and α(t) is the
angle between ~x
r
and
~
d. It should be noticed that:
α(t) = π − θ(t) + β(t) (2)
˙
α(t) = −
˙
θ(t) +
˙
β(t) = −ω(t) +
v(t)
d(t)
sin(α(t)) (3)
Finally d(t) represents the distance between O
s
and O
r
, and it can be shown (see (Boyadzhiev, 1999))
that:
˙
d(t) = −v(t) cos(α(t)) (4)
3.2 First Approach
A first solution to follow a spiral consists in designing
a controller which makes α(t) converge to a desired
angle named α
B
= α
∗
. α
B
determines if the spiral is
an inward one, an outward one or a circle. Once the
robot has converged towards the spiral, it either in-
creases, decreases or keeps constant d(t). In order to
design such a controller, we impose a constant linear
velocity such as v(t) = v
∗
. Then we define an error
e
B
(t) and compute ˙e
B
(t):
e
B
(t) = α(t) − α
B
(5)
˙e
B
(t) =
˙
α(t) = −ω(t) +
v
d(t)
sin(α(t)) (6)
As it can be seen in (6), ˙e
B
(t) depends on both v and
ω(t). As it has been decided to fix a constant linear
velocity, it is then required to compensate its effect
while controlling the robot using solely ω(t). More-
over, to make the error e
B
(t) vanish, we propose to
define a controller proportional to it. Thus it follows
that:
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
174

ω(t) = λ
B
e
B
(t) +
v(t)
d(t)
sin(α(t)) (7)
where λ
B
is a positive scalar. The controller obtained
in equation (7) can be used to force the robot to follow
a spiral defined by α
B
. Thus it is possible to control
if the robot increases, decreases or keeps constant the
distance d(t). However it does not allow to follow a
specific spiral. In order to analyze the stability of the
designed controller, we propose to define the follow-
ing Lyapunov function:
V
B
(x
B
(t)) =
x
B
(t)
2
2
(8)
with x
B
(t) = e
B
(t). The equilibrium state x
BE
=
x
B
(t) = 0 corresponds to the robot following the spiral
defined by α
B
. Moreover V
B
(x
B
(t)) > 0 for x
B
(t) 6=
x
BE
and V
B
(x
B
(t)) = 0 when x
B
(t) = x
BE
. To study
the evolution of V
B
(x
B
(t)), its derivative with respect
to time is computed:
˙
V
B
(x
B
(t)) = ˙x
B
(t)x
B
(t)
=
˙
α(t)[α(t) − α
B
]
= [−ω(t) +
v
d(t)
sin(α(t))][α(t) − α
B
]
= −λ
B
e
B
(t)
2
(9)
Thanks to equation (9), it can be seen that
˙
V
B
(x
B
(t)) <
0 for x
B
(t) 6= x
BE
and
˙
V
B
(x
B
(t)) = 0 when x
B
(t) = x
BE
as λ
B
> 0. Thus we can conclude that the designed
controller has a global exponential stability.
3.3 Second Approach
The controller in equation (7) allows to control the
robot behavior, i.e. to increase, decrease or keep con-
stant the distance d(t). Nevertheless it does not allow
to follow a specific spiral. Indeed it exists an infin-
ity of spirals defined by α
B
and in order to define a
specific spiral it is mandatory to select both the an-
gle α
B
and the initial distance d
∗
(0). When using the
controller in equation (7), d
∗
(0) is not chosen and it
corresponds to d(t
c
), where t
c
is the time when α(t)
has converged to α
B
. Thus, in order to follow a spe-
cific spiral, we once again impose a constant linear
velocity such as v(t) = v
∗
. Then we propose to define
the following error:
e
S
(t) = α(t) − α
S
(t) = α(t) − α
B
− α
D
ε(t) (10)
In order to make the new error e
S
(t) vanish, the
constant reference α
B
has been replaced by a non-
constant one, α
S
(t) = α
B
+ α
D
ε(t). The vanishing
error in equation (10) should lead to two successive
robot behaviors. First while d
∗
(t) 6= d(t), the robot
has to navigate towards the spiral in order to make
d
∗
(t) = d(t). To do so the new angle of reference
α
S
(t) is equal to α
B
modified by the amount α
D
∗ε(t).
α
D
is the maximal value that can be added/subtracted
to α
B
in order to make the robot converge towards the
spiral without changing its sense of rotation with re-
spect to the center of the spiral (clockwise or counter-
clockwise). Then ε(t) should have its norm equal to
1 when ||d(t) − d
∗
(t)|| ≥ ||d(0) − d
∗
(0)||, and equal
to 0 when d(t) = d
∗
(t). Thus, when the robot is
far from the spiral, it converges towards it using the
greater angle possible, i.e. α
S
(t) = 0 or α
S
(t) = ±π
depending on the initial conditions. Moreover, when
d(t) = d
∗
(t), then α
S
(t) = α
B
. Thus the robot follows
the spiral while keeping the desired distance. This
last part corresponds to the second behavior expected
when controlling the robot by vanishing e
S
(t). In or-
der to obtain the previously explained behaviors, we
propose to define ε(t) and α
D
as:
ε(t) = sign(d
∗
(t) − d(t)) min
||
d
∗
(t) − d(t)
|d
∗
(0) − d(0)|
||,1
(11)
and
α
D
=
sign(α
B
) ∗ π − α
B
if d
∗
(0) > d(0)
α
B
if d
∗
(0) < d(0)
(12)
ε(t) is the normalized error between d
∗
(t) and d(t).
It has been saturated to ±1. Thus its value belongs
to the domain [0, 1] if d
∗
(0) > d(0) or [−1,0] if
d
∗
(0) < d(0). Thus, α
S
6= α
B
when d
∗
(t) 6= d(t),
whereas α
S
= α
B
when d
∗
(t) = d(t). Regarding
equation (12), when α
B
∈ [0,π] then it is mandatory
that α
S
∈ [0, π]. Otherwise when α
B
∈ [0, −π] then
α
S
∈ [0,−π]. Equations (11) and (12) guarantee that
the robot rotation direction is not modified by α
D
ε(t),
while allowing the robot to converge towards d
∗
(t).
Now that the new error has been defined, we propose
to compute its derivative with respect to time in order
to identify the terms involved in its dynamics.
˙e
S
(t) =
˙
α(t) − α
D
˙
ε(t)
= −ω(t) +
v(t)
d(t)
sin(α(t)) − α
D
˙
ε(t)
(13)
In order to make e
s
(t) vanish, we propose to design
a controller proportional to it which also compensate
the other terms involved in (13). It leads to:
ω(t) = λ
S
e
S
(t) +
v(t)
d(t)
sin(α(t)) − α
D
∗
˙
ε(t) (14)
where λ
S
is a positive scalar. The controller (14)
makes possible for the robot to converge towards any
specific spiral. In order to analyze the stability of
the controller, we propose to define the following
Lyaponuv function:
V
S
(x
S
(t)) =
x
S1
(t)
2
+ x
S2
(t)
2
2
(15)
Design of a Sensor-based Controller Performing U-turn to Navigate in Orchards
175

with
x
S
(t) =
x
S1
(t)
x
S2
(t)
=
α(t) − α
B
− α
D
∗ ε(t)
d(t) − d
∗
(t)
The equilibrium state x
SE
= [x
S1
(t),x
S2
(t)]
T
= [0,0]
T
corresponds to the robot following the spiral defined
by α
B
while being at the distance d
∗
(t), i.e. when
α(t) = α
B
and d(t) = d
∗
(t). Moreover, V
S
(x
S
(t)) > 0
for x
S
(t) 6= x
SE
and V
S
(x
S
(t)) = 0 when x
S
(t) = x
SE
. In
order to study the evolution of V
S
(x
S
(t)), its derivative
with respect to time is computed:
˙
V
S
(x
S
(t))
= ˙x
S1
(t)x
S1
(t) + ˙x
S2
(t)x
S2
(t)
= −λ
S
e
S
(t)
2
+ [
˙
d(t) −
˙
d
∗
(t)][d(t) − d
∗
(t)]
= −λ
S
e
S
(t)
2
−v[cos(α(t)) − cos(α
B
)][d(t) − d
∗
(t)]
(16)
In equation (16), it can be seen that
˙
V
S
(x
S
(t)) = 0
for x
S
(t) = x
SE
. However, it can not be proved
that
˙
V
S
(x
S
(t)) < 0 for x
S
(t) 6= x
SE
. Indeed even
if −λ
S
e
S
(t)
2
< 0 for x
B
(t) 6= x
SE
, the second term
v[cos(α(t)) − cos(α
B
)][d(t) − d
∗
(t)] is not always
positive. For certain initial configurations the sign
of cos(α(t)) − cos(α
B
) is different from the one of
d(t) − d
∗
(t). Moreover, the initial robot orientation
may not allow it to reduce ||d(t) − d
∗
(t)|| when it
starts to move. This is due to the fact that only one
control input, ω(t), is used to control the two de-
grees of freedom α(t) and d(t) of a non-holonomic
robot. Thus it might be first required to orientate
the robot. During this orientation step the distance
||d(t) − d
∗
(t)|| increases. Thus we can conclude that
the controller is not globally asymptotically stable.
However it is straightforward to show that:
If d(t) > d
∗
(t):
cos(α(t)) − cos(α
B
) > 0 if α(t) > α
B
If d(t) < d
∗
(t):
cos(α(t)) − cos(α
B
) < 0 if α(t) < α
B
(17)
As it can be seen in equation (17), it is guaranteed that
the controller is locally asymptotically stable once the
α(t) overpasses α
B
. Thus the obtained results do not
completely fulfill our expectations, but are sufficient
for our needs. A more accurate value of α(t) allowing
a local stability could be found. It would depend on
v(t), λ
S
and the initial conditions. Finally, as it will
be shown in the simulation section, it is possible to
sequence these two controllers to bring the robot in an
initial state where the stability of the second control
law is guaranteed.
In this section two controllers have been designed.
The first one allows to follow a spiral having an un-
known distance d
∗
(t). It can be used when control-
ling the robot behavior, i.e. increasing, decreasing
or keeping constant d(t) This controller is sufficient
when the distance is not available, eg. when the data
are provided by a single camera. The second con-
troller allows to follow a spiral while controlling d(t).
It is then required to provide d(t), using for example
a stereo camera, a Lidar, etc.
3.4 Validation
In this section we present simulations of a robot fol-
lowing a spiral using the two previously designed
controllers. The results aim to illustrate the efficiency
of our approach and also highlight its performances
and limitations. Moreover we will propose ideas to
investigate in order to overcome some issues and/or
adapt the presented approach to another application.
For all the simulations the sampling time is T
s
= 0.1
second. Moreover the coordinates of the spiral cen-
ter are [0, 0] and the linear velocity is v
∗
= v(t) = 0.2
m/s. The first set of simulations, the results of which
can be seen in figure 4, are performed using the first
controller from equation (7) and λ
B
= 1. The first test
aims to follow an inward spiral by using α
B
=
15π
32
when the robot initial state is χ(0) = [5,0,π]
T
(see
figure 4(a)). The second one follows an outward spi-
ral with α
B
=
17π
32
and an initial state χ(0) = [5, 0, 0]
T
(see figure 4(c)). In both figures 4(a) and 4(c), the dot-
ted red line is the path of reference whereas the solid
blue one is the path performed by the robot while us-
ing the controller from equation (7). Moreover, some
robot states, and especially the first one, are repre-
sented. The green and red lines represent ~x
r
(t) and
~y
r
(t), respectively. In both cases, the robot first ori-
entates itself in order to make α(t) converge towards
α
B
, then it follows a spiral by keeping α(t) = α
B
. This
behavior is shown in figures 4(b) and 4(d) where the
evolution of the Lyapunov function V
B
(x
B
(t)) is pre-
sented. Indeed x
B
(t)
2
= (α(t) − α
B
)
2
first decreases
down to zero, and then stays at the constant null value.
This result matches with the proposed analysis pre-
sented in section 3.2. However it should be noticed
that the robot does not follow a predefined spiral, but
the one met once V
B
x
B
(t) = 0. Thus we can conclude
that the controller from equation (7) can be used in or-
der to control the behavior of a robot with respect to
a point, i.e. it increases, decreases or keeps constant
d(t), but it does not allow to follow a specific spiral,
i.e. control the distance d(t).
The second set of simulations uses the spiral follow-
ing controller presented in equation (14). For the first
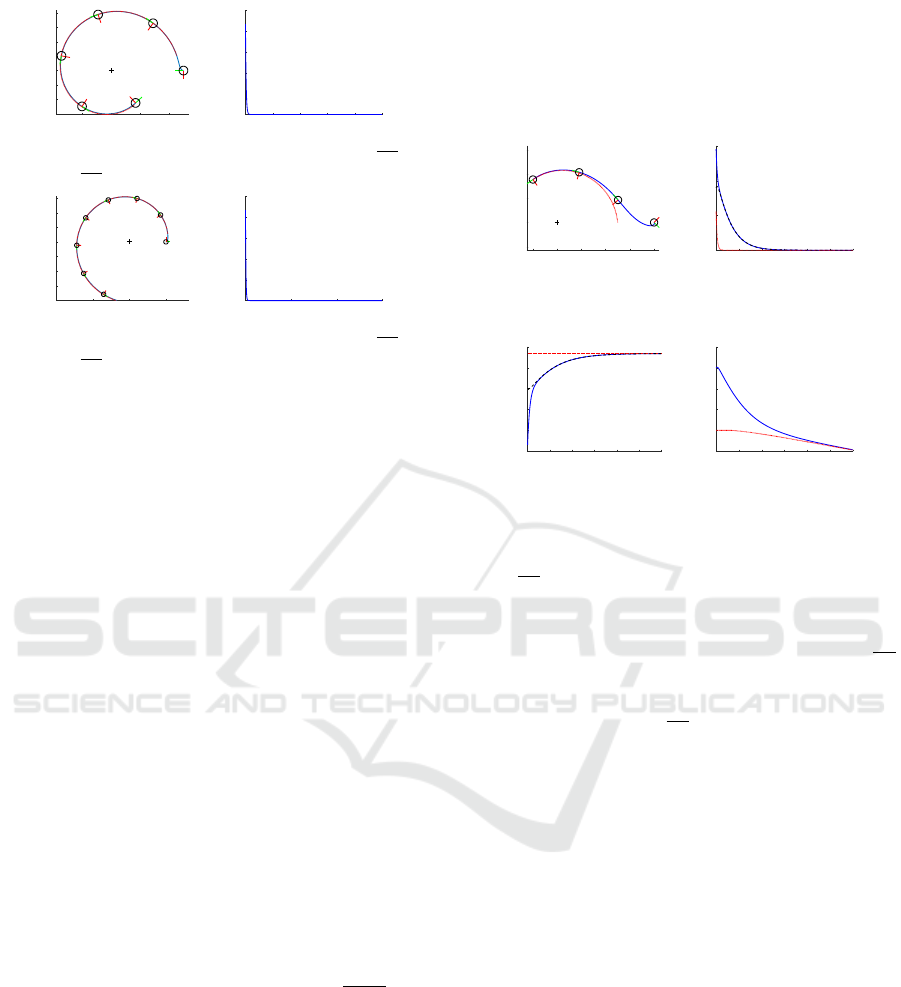
test (see figure 5), λ
S
= 1, α
B
=
15π
32
and d
∗
(0) = 5 m.
Moreover the robot initial state is χ(0) = [8,0,−
π
4
]
T
.
In this simulation the robot has to follow the specific
spiral defined by α
B
=
15π
32
and passing by the point
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
176
-2 0 2 4
X(m)
-3
-2
-1
0
1
2
3
4
Y(m)
(a) Robot trajectory
| α
B
=
15π
32
0 20 40 60 80 100
Time(s)
0
0.5
1
1.5
2
2.5
V
B
(x
B
(t))
(b) V
B
(x
B
(t)) | α
B
=
15π
32
-5 0 5
X(m)
-8
-6
-4
-2
0
2
4
6
Y(m)
(c) Robot trajectory
| α
B
=
17π
32
0 50 100 150
Time(s)
0
0.5
1
1.5
2
2.5
V
B
(x
B
(t))
(d) V
B
(x
B
(t)) | α
B
=
17π
32
Figure 4: Spiral following using the first controller - Black
cross: center of the spiral - Solid line: robot trajectory -
Doted line: spiral of reference.
whose coordinates are [5,0]. In figure 5(a), it can be
seen that the robot successfully manages to follow
the predefined spiral by simultaneously orienting it-
self toward the spiral (see figure 5(c)) and making the
distance d(t) converge towards d
∗
(t) (see figure 5(d)).
Figure 5(b) presents the evolution of V
S
(x
S
(t)), x
S1
(t)
and x
S2
(t). It can be seen that x
S1
(t) = e
S
(t) is perma-
nently decreasing and converges towards zero. Then
it should be noticed that x
S2
(t) = d(t) − d
∗
(t) slightly
increases before decreasing down to zero. Moreover
it vanishes after x
S1
(t). This behavior is due to the fact
that the non-holonomic robot is initially not well ori-
ented. Thus, while orienting itself, x
S2
(t) increases.
Once the robot is correctly oriented towards the spiral,
vanishing e
S
(t) allows the robot to converge towards
the specific spiral and then to follow it. It can be
also seen that V
S
(x
S
(t)) is constantly decreasing and
is then equal to zero when the robot is on the spiral.
In this test the increase of x
S2
(t) due to the orientation
step is not large enough with respect to the reduction
of x
S1
(t) to not allow V
S
(x
S
(t)) to be constantly de-
creasing. Those results match the stability analysis
proposed in section 3.3. First, V
S
(x
S
(t)) =
x
S1
(t)
2
2
can-
not be used as a Lyapunov function to guarantee that
the robot follow a spiral. Indeed, x
S1
(t) = 0 before the
robot is on the spiral. Then, only an appropriate ori-
entation of the robot guarantees the decrease of x
S2
(t)
and then V
S
(x
S
(t)). However, despite of not being ini-
tially well oriented, the robot manages to perform its
task successfully. Finally it should be noticed that in
our case, the robot is always moving forward. A so-
lution to obtain an monotonically decreasing x
S2
(t)
could be to allow the robot to move backward in or-
der to perform a maneuver. This solution has not been
selected in this work because the designed controllers
have to be used to perform obstacles avoidance or u-
turn while navigating. Moving backward would be an
inappropriate motion with respect to such a naviga-
tion task.
-2 0 2 4 6 8
X(m)
-2
0
2
4
6
Y(m)
(a) Solid line: Robot tra-
jectory - Dotted line: ref-
erence spiral
0 10 20 30 40 50 60
Time(s)
0
5
10
15
V
B
(x
B
(t)) | x
S1
(t) | x
S2
(t)
(b) Solid line: V
B
- Dot-
ted line: x
S1
- Dashed line:
x
S2
0 10 20 30 40 50 60
Time(s)
-150
-100
-50
0
50
100
α(t) vs α
B
(deg)
(c) Solid line: α(t) - Dot-
ted line: α
B
- Dashed line:
α
S
(t)
0 10 20 30 40 50 60
Time(s)
4
5
6
7
8
9
d(t) vs d
*
(t) (m)
(d) Solid line: d(t) - Dot-
ted line: d
∗
(t)
Figure 5: Spiral following using the second controller with
α
B
=
15π
32
.
For the second simulation using the controller given
by equation (14) (see figure 6), λ
S
= 0.2, α
B
=
17π
32
and d
∗
(0) = 5 m. Moreover, the robot initial state is
χ(0) = [3,0,π]. The robot has to follow the specific
spiral defined by α
B
=
17π
32
and passing by the point
whose coordinates are [5,0]. As previously the robot
successfully follows the predefined spiral even if the
time to converge towards it is much greater than be-
fore (see figure 6(a)). Similarly to the previous sim-
ulation the initial robot state requires an orientation
step leading to an increase of x
S2
(t) (see figures 6(d)
and 6(b)). Moreover, in order to make x
S2
(t) vanish,
α(t) has to overshoot α
B
(see figure 6(c)). This is due
to the term α
D
∗ε(t) in equation (10). However it does
not lead to any increase of x
S1
(t) over the spiral fol-
lowing (see figure 6(b)). In this particular simulation,
having λ
B
= 0.2 introduces an increase of V
S
(x
S
(t))
at the beginning of the simulation. Indeed, the varia-
tions of x
S2
(t) due to the orientation step are no more
compensated by the strong decrease of x
S1
(t). One
more time the reduction of V
S
(x
S
(t)) is only guaran-
teed once the robot is correctly oriented with respect
to the spiral. Despite this issue in term of stability
analysis, the robot manages to converge towards the
spiral and then to follow it.
In a last simulation (see figure 7), we propose to use
successively both controllers. The spiral to follow, the
robot initial state and the parameter values are identi-
Design of a Sensor-based Controller Performing U-turn to Navigate in Orchards
177
-5 0 5
X(m)
-6
-4
-2
0
2
4
6
8
Y(m)
(a) Solid line: Robot trajec-
tory - Dotted line: reference
spiral
0 50 100 150 200
Time(s)
0
2
4
6
8
10
12
14
V
B
(x
B
(t)) | x
S1
(t) | x
S2
(t)
(b) Solid line: V
B
- Dotted
line: x
S1
- Dashed line: x
S2
0 50 100 150 200
Time(s)
0
50
100
150
200
α(t) vs α
B
(deg)
(c) Solid line: α(t) - Dot-
ted line: α
B
- Dashed line:
α
S
(t)
0 50 100 150 200
Time(s)
0
2
4
6
8
10
d(t) vs d
*
(t) (m)
(d) Solid line: d(t) - Dotted
line: d
∗
(t)
Figure 6: Spiral following using the second controller with
α
B
=
17π
32
.
cal to the previous simulation. Initially the robot is
controlled using the first controller and thus it fol-
lows a non-specific spiral having α
B
=
17π
32
. Once
α(t) = α
B
, the robot then switches to the second con-
troller to follow the spiral having α(t) = α
B
and pass-
ing by the point with coordinates [5, 0]. This approach
allows to obtain the robot to reach an initial state
that guarantees the convergence of the second con-
troller. Indeed, in figure 7(b), it can be seen that both
V
B
(x
B
(t)) and V
S
(x
S
(t)) are decreasing. Other than
the Lyapunov functions, the path and the evolution of
α(t) and d(t) are almost the same as in the previous
simulation (figures 7(a) 7(c) and 7(d)). This approach
allows to guarantee the convergence of the robot to-
wards a specific spiral despite its initial state, but it
does not drastically change its performances.
4 NAVIGATION STRATEGY
In this section we propose to present how the sensor-
based spiral controller can be used into a navigation
architecture to allow a robot to drive through an or-
chard. First, a possible navigation is described: robot,
sensors, map, controllers and supervision. Then, we
present results obtained in simulation to highlight the
efficiency of the sensor-based approach.
-10 -5 0 5
X(m)
-6
-4
-2
0
2
4
6
Y(m)
(a) Solid line: Robot trajec-
tory - Dotted line: reference
spiral
0 50 100 150 200 250
Time(s)
0
2
4
6
8
10
12
14
V
B
(x
B
(t))
(b) Solid line: V
B
- Dotted
line: V
S
0 50 100 150 200 250
Time(s)
0
50
100
150
200
α(t) vs α
B
(deg)
(c) Solid line: α(t) - Dot-
ted line: α
B
- Dashed line:
α
S
(t)
0 50 100 150 200 250
Time(s)
0
2
4
6
8
10
d(t) vs d
*
(t) (m)
(d) Solid line: d(t) - Dotted
line: d
∗
(t)
Figure 7: Spiral following using successively both con-
trollers. The switch occurs at t = 26.2 s.
4.1 Robot and Sensory Data
To navigate through the orchard, we consider the
Toro workman MDE vehicle, which is a car-like
robot equipped with three laser rangefinders (see
figures 8 and 9). The state vector is χ
c
(t) =
[x(t),y(t), θ(t), γ(t)]
T
, with γ(t) the steering angle,
and the input vector is u
c
(t) = [v(t),γ(t)]
T
. It should
be noticed that the second term of the control input
vector, which used to be an angular velocity for the
differential model, is now an angular position. It is
then required to convert the angular velocity ω(t) to
an angular position γ(t) allowing the robot to rotate
by the same amount. To do so, we use the following
equation:
γ(t) = tan
−1
(
L ω(t)
v(t)
) (18)
where L is the distance between the front axle and the
rear axle.
!x
w
!y
w
!x
r
!y
r
α(t)
−→
d
O
r
O
w
O
s
β(t)
θ( t)
x(t)
y(t)
γ(t)
L
Figure 8: Car-like model.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
178

The first laser rangefinder mounted in front of the
robot and facing towards, aims at detecting the trees
in order to drive trough the rows. The acquired data
are processed in order to identify the trees in the field
of view of the laser rangefinder (the circled trees in
figure 9). Next the trees are separate into two clus-
ters: left row (red circles) and right row (green cir-
cles). Next, the best fitting lines ∆
L
and ∆
R
are calcu-
lated for the left and right cluster respectively. Then,
∆
M
, the line median to ∆
L
and ∆
R
is computed. Fi-
nally, the orientation error ε
θ
and the lateral position
error ε
Y
are calculated in the front rangefinder frame
F
f
= (O
f
,~x
f
,~y
f
,~z
f
)
2
(see figure 9). These last two
values are used to drive through the row.
Figure 9: Data acquisition during a row following.
Two laser rangefinders are mounted at the back of the
robot and face the right and left sides respectively (see
figure 9). They are used to detect the trees when per-
forming a u-turn. The data acquired in the rangefinder
frame are first projected in the robot frame. Next,
they are processed to detect the closest tree. Then,
the angle α(t) and the distance d(t) are computed in
the robot frame (see figure 10). These values are used
to control the robot while performing a u-turn.
4.2 Environment Modeling
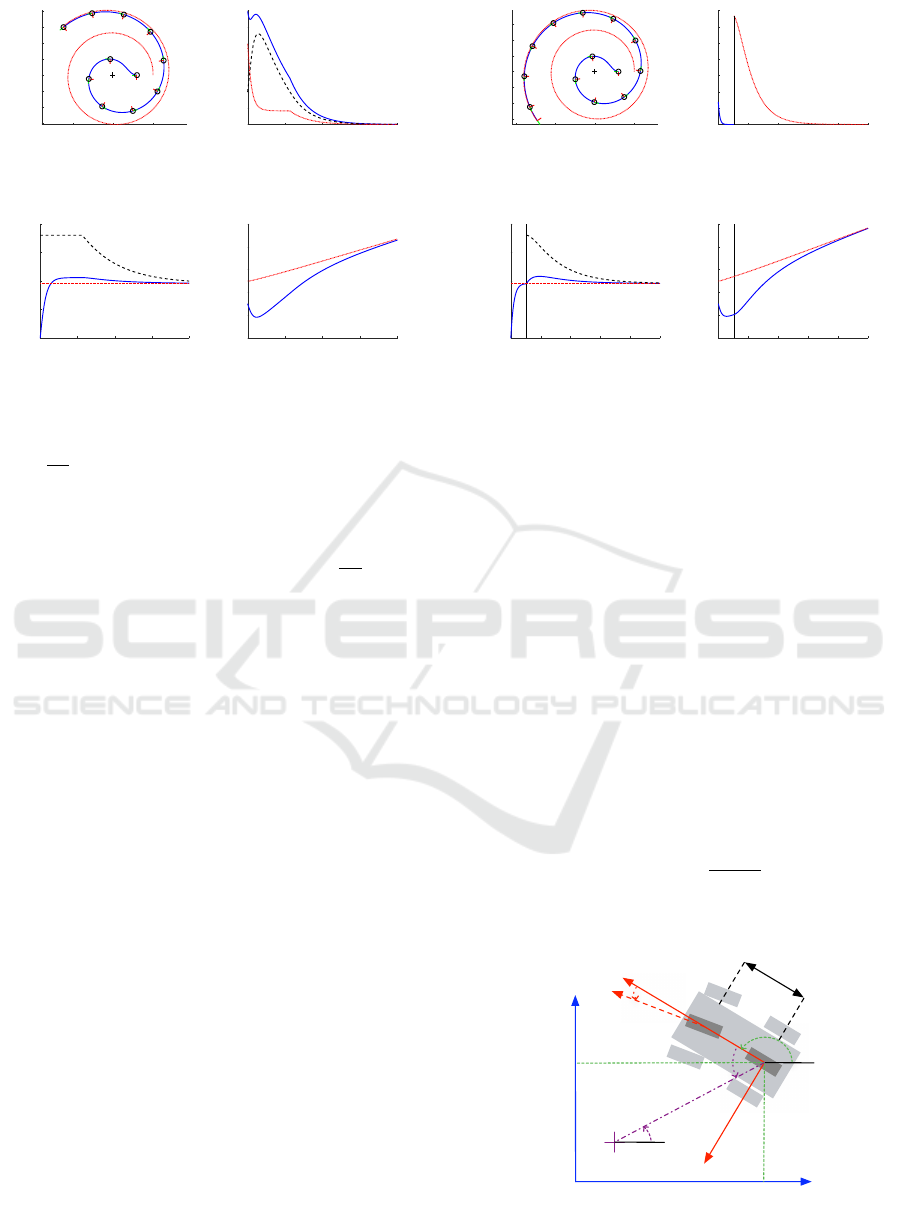
In this simulation, we consider an orchard composed
of 4 rows made of 8 trees (see figure 11). It forms tree
rows for the robot to navigate through.The rows width
is 8 meters whereas the trees are spaced by 3 meters.
To model the orchard, we have chosen to use the topo-
logical map presented in figure 12 which consists in
an oriented graph. Here, the nodes (U
1
,D
1
), (U
2
,D
2
)
and (U
3
,D
3
) represent the first, second and third row
respectively. U
x
is used when the robot drives upward
2
These parameters have to expressed in the robot frame.
However, their values are the same in F
r
and F
f
.
Figure 10: Data acquisition during a u-turn.
in row x, whereas D
x
is used when it drives down-
ward. The nodes R
yz
and L
yz
represent the right and
left turns from row y towards row z. At the begin-
ning of the navigation, the user provides initial and
final nodes. Thanks to these informations, a path is
computed. For example from U
3
to U
1
the path is
P = {U
3
,L
32
,D
2
,R
21
,U
1
}.
Figure 11: Simulated orchard.
Figure 12: Topological map.
Design of a Sensor-based Controller Performing U-turn to Navigate in Orchards
179
4.3 Control Strategy
Over the navigation, the robot is controlled using two
controllers. The first one allows the robot to drive
through the rows while staying in the middle of it. It
is defined as:
ω = λ
θ
ε
θ
+ λ
Y
ε
Y
(19)
where λ
θ
and λ
Y
are two positive scalar gains. Next,
the controller to perform a u-turn, is one of the two
ones previously presented, i.e. either controller (7) or
(14). Finally, it has to be determined when the robot
has to switch from one controller to the other based on
the data provided by the on-board sensors. First, it is
required to switch from the row following controller
to the u-turn one when i) the front laser range finder
does not perceive a tree anymore, ii) α
l,r
< |π/2 + ε
s
|,
where α
l,r
are the α(t) values provided by the left and
right camera and ε
s
is a very small angle. In other
words, the robot has to be at the end of the row, with
the two side laser rangefinders at the level of the last
two trees. Finally, the robot switches from the u-turn
mode to the row following one, when the side sensor
which is not used to perform the u-turn perceives two
trees. It should be noted that the linear velocity is
defined by the user when both following the rows and
performing a u-turn.
4.4 Validation
The presented navigation strategy has been imple-
mented in ROS and coupled with Gazebo in order
to provide a simulation environment. The following
gains have been selected: λ
θ
= 1, λ
Y
= 1, λ
B
= 5 and
λ
S
= 5. Moreover the linear speed is v(t) = 2 m/s
when the robot is in the rows, whereas v(t) = 1 m/s
when it performs a u-turn. Finally α
B
= ±π/2, forc-
ing the robot to follow a circle when switching rows.
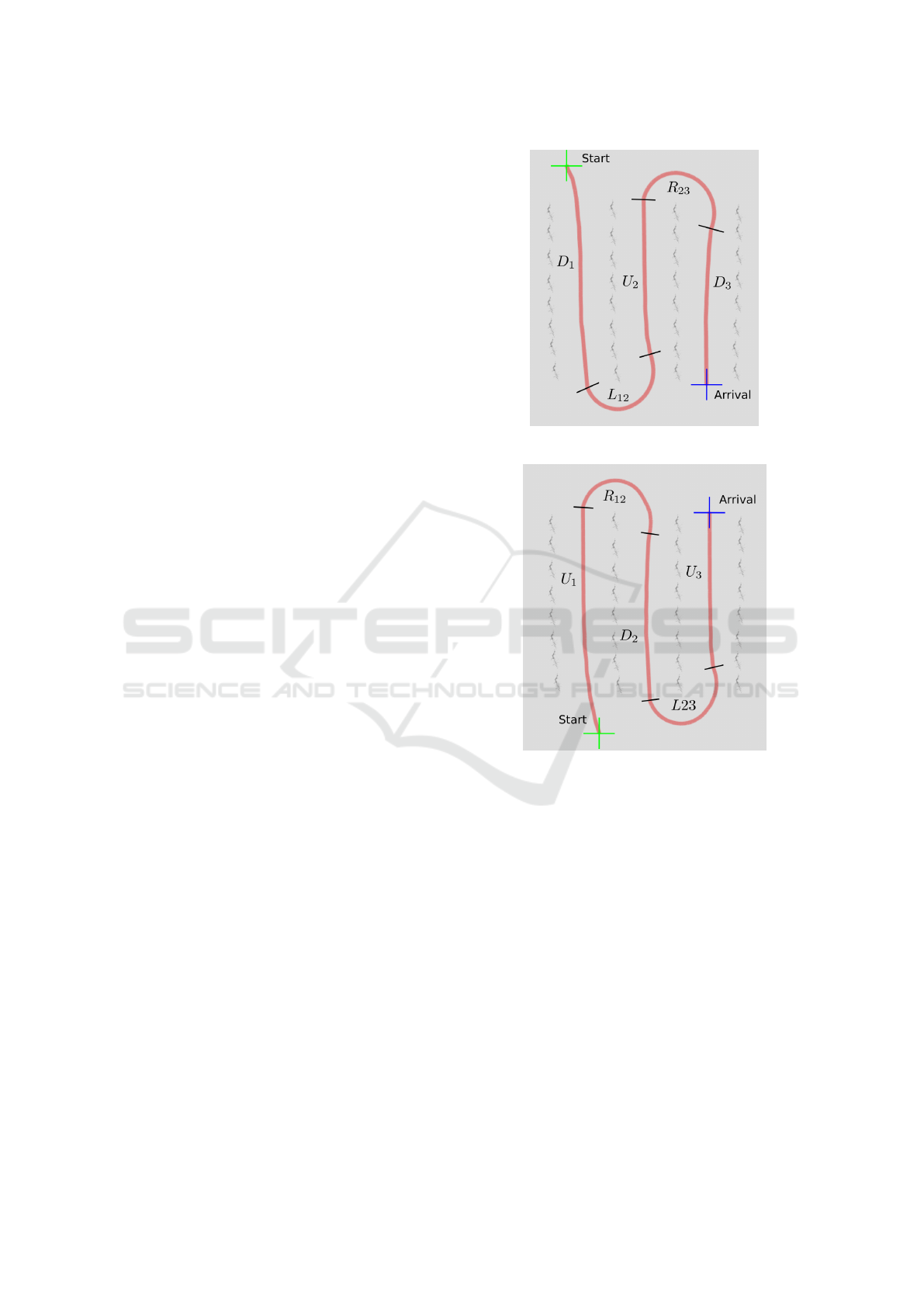
During the first simulation, the robot starts at D
1
and
follows the path P = {D
1
,L
12
,U
2
,R
23
,D
3
}. In order
to switch rows, controller (7) is used. As it can be
seen in figure 13, the robot successfully switch from
one controller to the other in order to navigate through
the orchard and reach its destination. During L
12
and
R
23
, the distance to the trees is not controlled. How-
ever, because it is initially located at the center of the
row, the robot manages to switch rows.
In a second simulation the controller (14) is used to
switch rows. The robot starts in U
1
and has to fol-
low the path P = {U
1
,R
12
,D
2
,L
23
,U
3
}. Once again,
it manages to use both controllers to drive through the
orchard and reach the goal. In R
12
and L
23
, the dis-
tance to the trees is controlled and fixed to 4 m. It
allows to guarantee that the robot will enter the n the
middle of the following row.
Figure 13: Orchard navigation #1.
Figure 14: Orchard navigation #2.
5 CONCLUSION
We have considered the problem of designing sensor-
based controllers allowing to navigate in orchards.
More particularly, we have focused on the realiza-
tion of u-turns which are traditionnally realized using
deadreckoning only. To improve the quality of the
maneuver, we have developed two sensor-based con-
trollers. They allow to follow particular spirals which
are defined from laser data and adapted to realize the
desired maneuvre. It is important to note that the per-
formances are different for both controllers. The first
one allows to follow a spiral, but the distance to its
center is not controlled. The second controller is more
advanced and allows to follow a specific given spiral,
i.e. angle α(t) and distance d(t) are controlled. In this
approach data from the sensor space are sufficient to
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
180

control the robot path. No localization are required
with the proposed method. In addition a stability anal-
ysis of those controllers and simulations highlighting
the efficiency of our approach have been provided. In
a second step, we have embedded them in a complete
navigation strategy allowing to navigate through an
orchard. We have explained how the different data
necessary for the control are derived, how the environ-
ment is modeled and how the robot is controlled using
the appropriate controllers. Finally a complete simu-
lation using ROS and Gazebo shows the efficiency of
the chosen approach in our agricultural context. The
next step of our work is to implement the controllers
on the Toro workman MDE robot. Finally, we also
plan to develop this sensor-based approach and take
advantage of its reactivity in order to navigate in a
dynamic environment.
REFERENCES
Bak, T. and Jakobsen, H. (2004). Agricultural robotic plat-
form with four wheel steering for weed detection.
Biosystems Engineering, 87(2):125–136.
Barawid, O. C., Mizushima, A., Ishii, K., and Noguchi,
N. (2007). Development of an autonomous naviga-
tion system using a two-dimensional laser scanner
in an orchard application. Biosystems Engineering,
96(2):139–149.
Bayar, G., Bergerman, M., Koku, A. B., and ilhan Konuk-
seven, E. (2015). Localization and control of an au-
tonomous orchard vehicle. Computers and Electron-
ics in Agriculture, 115:118–128.
Boyadzhiev, K. N. (1999). Spirals and conchospirals in the
flight of insects. The College Mathematics Journal,
30(1):21–31.
Durand-Petiteville, A., Cadenat, V., and Ouadah, N. (2015).
A complete sensor-based system to navigate through
a cluttered environment. In Informatics in Control,
Automation and Robotics (ICINCO), 2015 12th Inter-
national Conference on, volume 2, pages 166–173.
IEEE.
Eaton, R., Katupitiya, J., Siew, K. W., and Howarth, B.
(2009). Autonomous farming: Modelling and control
of agricultural machinery in a unified framework. In-
ternational journal of intelligent systems technologies
and applications, 8(1-4):444–457.
Fang, H., Fan, R., Thuilot, B., and Martinet, P. (2006).
Trajectory tracking control of farm vehicles in pres-
ence of sliding. Robotics and Autonomous Systems,
54(10):828–839.
Foley, J. A., Ramankutty, N., Brauman, K. A., Cassidy,
E. S., Gerber, J. S., Johnston, M., Mueller, N. D.,
O’Connell, C., Ray, D. K., West, P. C., Balzer, C.,
Bennett, E. M., Carpenter, S. R., Hill, J., Monfreda,
C., Polasky, S., Rockstr
¨
om, J., Sheehan, J., Siebert,
S., Tilman, D., and Zaks, D. P. M. (2011). Solutions
for a cultivated planet. Nature, 478:337–342.
Futterlieb, M., Cadenat, V., and Sentenac, T. (2014). A Nav-
igational Framework Combining Visual Servoing and
Spiral Obstacle Avoidance Techniques. In Interna-
tional Conference on Informatics in Control, Automa-
tion and Robotics ( ICINCO ) , pages 57–64, Vienna,
Austria. INSTICC.
Hansen, S., Bayramoglu, E., Andersen, J. C., Ravn, O., An-
dersen, N., and Poulsen, N. K. (2011). Orchard navi-
gation using derivative free kalman filtering. In Amer-
ican Control Conference (ACC), 2011, pages 4679–
4684. IEEE.
Johnson, D. A., Naffin, D. J., Puhalla, J. S., Sanchez, J., and
Wellington, C. K. (2009). Development and imple-
mentation of a team of robotic tractors for autonomous
peat moss harvesting. Journal of Field Robotics, 26(6-
7):549–571.
Mcfadyen, A., Durand-Petiteville, A., and Mejias, L.
(2014). Decision strategies for automated visual col-
lision avoidance. In Unmanned Aircraft Systems
(ICUAS), 2014 International Conference on, pages
715–725.
Reid, J. (2011). The impact of mechanization on agricul-
ture. Nat. Acad. Eng. Bridge, Issue Agric. Inf. Tech-
nol., 41(3):22–29.
Siciliano, B. and Khatib, O. (2016). Springer handbook of
robotics. Springer.
Zhang, J., Maeta, S., Bergerman, M., and Singh, S. (2014).
Mapping orchards for autonomous navigation. In
Proc. American Society of Agricultural and Biologi-
cal Engineers Annu. Int. Meeting.
Design of a Sensor-based Controller Performing U-turn to Navigate in Orchards
181
