
Modeling Inhibitory and Excitatory Synapse Learning in the Memristive
Neuron Model
Max Talanov
1
, Evgeniy Zykov
1
, Victor Erokhin
2
, Evgeni Magid
1
, Salvatore Distefano
1
,
Yuriy Gerasimov
1
and Jordi Vallverd
´
u
3
1
Higher School of Information Technology and Information Systems, Kazan Federal University,
Kremlyovskaya str. 35, Kazan, Russian Federation
2
Institute of Materials for Electronics and Magnetism, Italian National Council of Research, Parma, Italy
3
Philosophy Department, Universitat Aut
`
onoma de Barcelona, Barcelona, Catalonia, Spain
Keywords:
Cognitive Architecture, Memristive Elements, Circuits, Artificial Neuron, Affects, Biologically Inspired
Robotic System.
Abstract:
In this paper we present the results of simulation of exitatory Hebbian and inhibitory “sombrero” learning
of a hardware architecture based on organic memristive elements and operational amplifiers implementing
an artificial neuron we recently proposed. This is a first step towards the deployment on robots of a bio-
plausible simulation, currently developed in the neuro-biologically inspired cognitive architecture (NeuCogAr)
implementing basic emotional states or affects in a computational system, in the context of our “Robot dream”
project. The long term goal is to re-implement dopamine, serotonin and noradrenaline pathways of NeuCogAr
in a memristive hardware.
1 INTRODUCTION
In this paper we propose a new hardware architec-
ture to implement an artificial neuron based on or-
ganic memristive elements (Hern
´
andez-Mej
´
ıa et al.,
2017) and operational amplifiers (Ibrayev et al., 2014;
Samsonovich and Robertson, 2014), towards a possi-
ble integration and embodiment of a (cluster based)
bio-realistic simulation of a mammalian brain into a
robotic system acting as an evolutionary information
processing system (Rodriguez and Granger, 2016).
This work originated by the neuro-biologically
inspired cognitive architecture (NeuCogAr) project,
which aims at implementing basic emotional states
or affects in a computational system (Talanov et al.,
2016; Talanov et al., 2017), according to a three-
dimensional neuromodulatory “cube of emotions”
model (L
¨
ovheim, 2012). In this model, axes corre-
spond to the levels of serotonin, dopamine and nora-
drenaline neuromodulators that, properly combined,
can identify eight basic emotions on this 3D cube. For
example, “fear” corresponds to high dopamine, low
serotonin and noradrenaline, while “interest” corre-
sponds to high noradrenaline, high serotonin and
dopamine (Balkenius and G
¨
ardenfors, 2016). How-
ever, the relationships between these neurotransmit-
ters and the psychological emotion space is mostly
unexplored and currently under investigation, there-
fore there is room for further development since pre-
liminary results are promising. The L
¨
ovheim model
is an interesting attempt in this direction, establish-
ing a, so far qualitative, connection between brain
mechanisms and emotions through neurotransmitters.
These emotional values are not only directly related
to emotional or affective moods and states, but also
have great importance in the regulation of the subtle
mechanisms of cognitive processes (Damasio, 1999;
Fellous and Arbib, 2005; Minsky, 2007).
On this premise, we propose to integrate
dopamine, serotonin and noradrenaline pathways pre-
viously developed in NeuCogAr (Talanov et al., 2016;
Talanov et al., 2017) into embodiment hardware
memristors schemes suitable for the implementation
of basic emotional states or affects on a “thinking”
machine, and specifically on a bio-inspired, cognitive
robotic system (Khusainov et al., 2015; Magid et al.,
2011).
From the high-level perspective the focus of this
work is the idea and implementation of inhibitory
514
Talanov, M., Zykov, E., Erokhin, V., Magid, E., Distefano, S., Gerasimov, Y. and Vallverdú, J.
Modeling Inhibitory and Excitatory Synapse Learning in the Memristive Neuron Model.
DOI: 10.5220/0006478805140521
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 514-521
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

memristive neuron schematic. Currently among
works dedicated to memristive biomimetic imple-
mentation of STDP we could not find the implp-
mentation of an inhibitory processes and learning
(Prezioso et al., 2016; Strukov et al., 2008; Serb
et al., 2016; Egorov et al., 2015; Matveyev et al.,
2015). According to current understanding of emo-
tional and neuromodulatory processes the inhibition
plays important role in balancing a mammalian brain
in dopamine, serotonin, noradrenaline pathways (Vo-
gels et al., 2013). This way we have to start from most
basic and important mechanism of a mammalian neu-
ron the inhibition including inhibitory learning and
excitatory/inhibitory sub-threshold balancing.
This lays at the intersection between bio-inspired
and cognitive robotics, implementing a new way of
controlling and acting on robots driven by emotions,
sort of affective robotics.
2 PROBLEM RATIONALE
2.1 Robot Dream
As starting point for our work we identified the
embodiment problem for bio-plausible simulation
(Tchitchigin et al., 2016b; Tchitchigin et al., 2016a),
approached by using the neuro-simulator NEST (Pot-
jans W., 2010) on the Hodkin-Huxley and Izhike-
vich models of neurons (Izhikevich, 2006) to simu-
late dopamine, serotonin and noradrenaline pathways
in the NeuCogAr project (Talanov et al., 2016; Ta-
lanov et al., 2017). The simulation of one second of
dopamine neuromodulation took 1 hour of comput-
ing, not compatible with real-time requirements and
operations. Since the robotic system that we want to
use for embodiment must operate in (quasi) real-time,
we have proposed the “Robot dream” two phases ap-
proach represented in the Figure 1. The real-time cog-
nitive robotic system should provide proper perfor-
mance and should be able to act independently, pe-
riodically synchronizing with simulated brain struc-
tures.
In the current paper we are focused on the robotics
embodiment system. A possible alternative to this
two step solution could be to adopt a hardware ap-
proach, e.g. based on memristors. This way mem-
ristors should be used as the electronic analogue for
synapse and paly important role in training/learning
an electronic neuron. The first block, the elementary
and main functional unit of this cognitive robotic em-
bodiment system with a “robotic brain” is the artifi-
cial/electronic neuron. Based on artificial/electronic
memristive neurons, in a longer term we will build
Figure 1: The “Robot dream” two phase architecture: dur-
ing the wake phase robotic embodiment system operates
real-time and stores inbound information and actuators ac-
tivation in form of pseudo-neuronal activity; during the
“dream” phase stored experience is “played back” through
direct translation via simulated neuronal structures of the
“dreaming brain” and after several cycles is transferred
back to the robotic system via synchronization of synaptic
weights of the memristive schema.
the robot brain as a bio-mimetic neural network struc-
ture similar to a rat brain This way, we will be able to
recreate the emotional subsystems and behaviors of
a rat through dopamine, serotonin and noradrenaline
pathways. as described in (Talanov et al., 2016; Ta-
lanov et al., 2017).
The overall schema of a memristive neuron could
be described as follows:
1) approximately 10
4
input channels are con-
nected to other excitatory and inhibitory memristors;
2) the threshold adder and generator plays the role
of axon hillock accumulating inbound excitatory and
inhibitory signals and triggering outbound signal or
“spike”;
3) two integrators and the inverting adder imple-
ments the inhibitory learning feedback by taking in
account ∆t variations of inbound and outbound sig-
nals to generate the “sombrero”-shaped learning sig-
nal to inhibitory memristors;
4) the inverting adder via monostable multivibra-
tor, relay and slave inverter transforms the outbound
signal flipping the left part of “sombrero” along Y axis
to produce similar to
1
x
graph and then forwards it to
excitatory memristors.
The aim of the present work is to study the feasi-
bility of the implementation of complex systems, in-
cluding a large number of memristive devices, allow-
ing mimicking a mammalian brain learning, in par-
ticular, Hebbian learning (reinforcement of outbound
signals) and “sombrero” learning (inhibition of out-
bound signals).
Modeling Inhibitory and Excitatory Synapse Learning in the Memristive Neuron Model
515

2.2 Memristive Approach to a “Robot
Brain”
After the first work on the physical implementation
of memristors (Strukov et al., 2008), hypothetical
devices, varying the resistance as a function of the
passed charge (Chua, 1971), the activity in the field
was explosively increased due to possible applica-
tions in new types of non-volatile memory arrays.
Currently, these elements are widely considered also
for neuromorphic applications. Organic memristive
device (Erokhin et al., 2005; Erokhin and Fontana,
2011) was developed exactly for mimicking some
synaptic properties in electronic circuits. As a bench-
mark, mnemotrix was taken the other hypothetical
element, used by Valentino Britenberg in his men-
tal experiment, explaining learning process (Braiten-
berg, 1984). Thus, these elements were supposed to
be used as electronic analogs of nervous system el-
ements, as shown by direct comparison of essential
features (Erokhin et al., 2010)
The synapse mimicking properties of the polyani-
line organic memristive device were demonstrated by
the electronic circuit with architecture and properties
similar to the part of the nervous system of pond snail,
responsible for learning of the animal during feeding
(Erokhin et al., 2011). Recently, these elements were
used for the hardware realization of artificial neural
networks (elementary (Demin et al., 2015) and double
layer (Emelyanov et al., 2016) perceptrons). These
works have directly demonstrated the capability of
memristive devices to be used as elements, varying
their weight functions during learning essential char-
acteristics for neuromorphic networks organization.
3 MEMRISTIVE NEURON
MODEL
We have described the electronic system that provides
two types of learning: excitatory and inhibitory, and
it has been developed through memristors. The Fig-
ure 2 represents the wiring diagram, where excitatory
and inhibitory impulses are transmitted to memristive
elements X j, with j = 1..n + m where n is the num-
ber of excitatory synapses or memristors and m is the
number of inhibitory memristors. When the accu-
mulated voltage on the memristive elements exceeds
the threshold, the one-shot multivibrator on the oper-
ational amplifier OA1 provides a single short pulse,
with the duration that is determined by
T 1 = C2 · R2 · ln(1 + R3/R4) (1)
Signals from “Out” and OA1 output are then transmit-
ted to integrators on op-amps OA2 and OA3, which
set the impulse descending edge of the learning func-
tion.
The pulse-rise time constant of the integrating cir-
cuit is
t = R5 ·C3 = R7 ·C4 (2)
Output signals from integrators are transmitted to the
inverting adder on op-amp OA4. The output signal
(the turned upside down “sombrero”) is applied to in-
hibitory “Inh” memristive elements. The monostable
multivibrator on the op-amp OA4 is triggered by a
positive pulse of the signal Out. The pulse duration is
determined by the circuit elements via:
T 2 = C6 · R13 · ln(1 + R14/R15) (3)
and equals T1. Output positive pulse is applied to the
MOSFET key M1, that controls a state of not invert-
ing input of the controlled inverter of op-amp OA6.
When the non-inverting input of the operational am-
plifier on op-amp OA6 is shorted to the ground, the
operational amplifier works as an inverter; otherwise,
it acts as a normal amplifier of the signal from invert-
ing adder op-amp OA4. From the output of op-amp
OA6 the signal is transmitted to excitatory memristive
elements “Ex” i, where i = 1..n.
4 RESULTS
Simulation methods were used to calculate needed
nominal values of the electronic components and to
validate the quality of the proposed model. We’ve
used integrated schematic editor and mixed ana-
log/digital simulator Micro-Cap. Temporal and am-
plitude characteristics of impulses have been simu-
lated. Impulses have been investigated in the time
range from 1 to 800 milliseconds. The excitatory and
inhibitory impulses replicate the Hebbian and “som-
brero” learning functions according to the theoreti-
cally predicated forms.
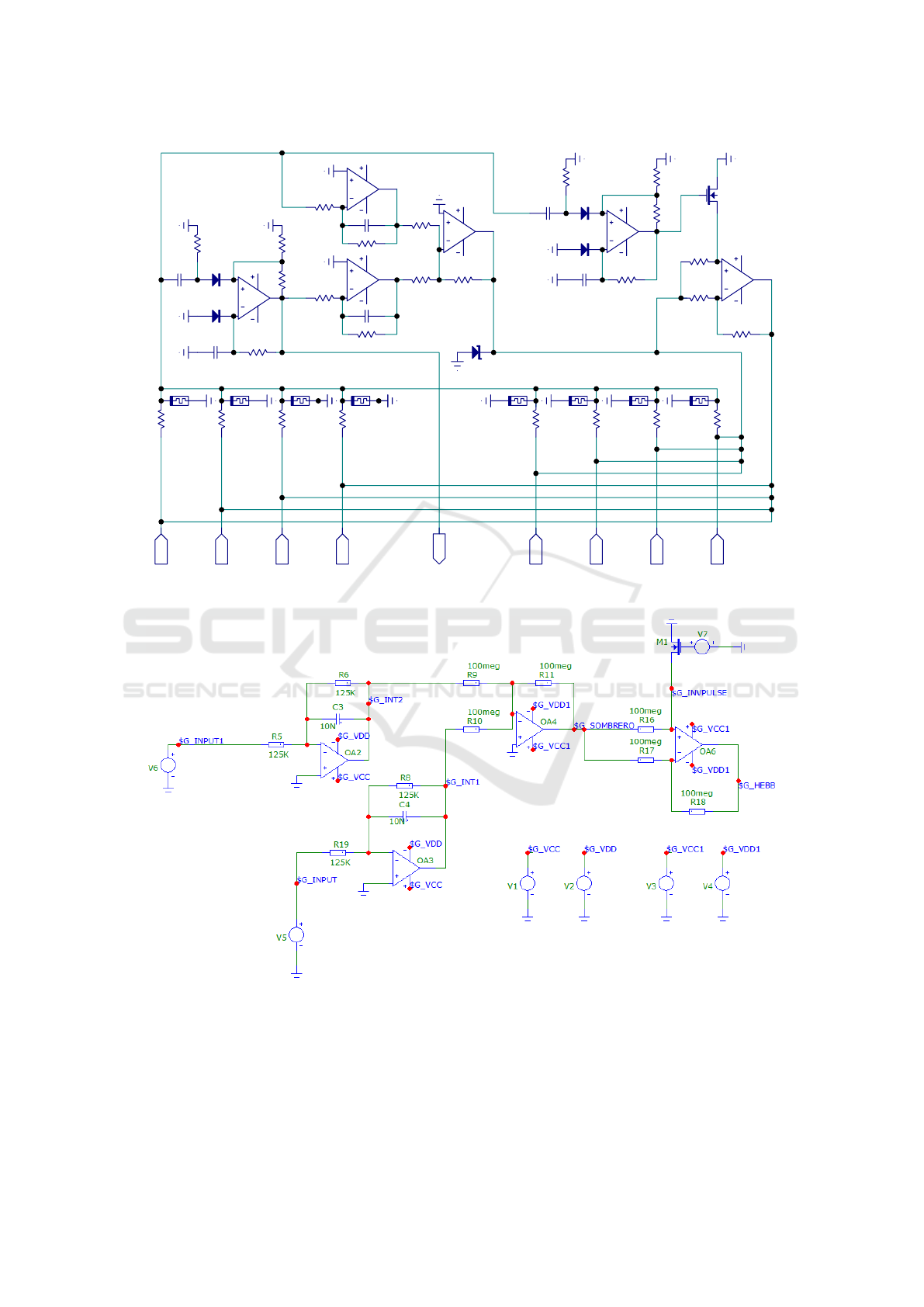
We have created the schema represented in the
Figure 3 for the simulation and validation of our idea
wiring schematic represented in the Figure 2. The
goal of the validation is to indicate the correlation
of the inhibitory and excitatory learning impulses to
∆t in form of “sombrero” and flipped along Y axcis
“sombrero” similar to
1
x
. Where the inhibitory out
is $G SOMBRERO and excitatory is $G HEBB. The
input signals, are generated by voltage sources V5 and
V6, their graphs are displayed in the Figure 4, and
tagged: $G INPUT and $G INPUT1. The vertical
axis represent voltage, relative to ground, while time
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
516
OA1
R2
VD1
VD2
R4
R3
C2
R1
C1
OA6
R17
R18
OA3
C4
R7
OA2
C3
R5
OA4
R9
R10 R11
OA5
R13
VD4
VD5
R15
R14
C6
R12
C5
R16
X3
Ex3
X2
Ex2
X1
Ex1
X(n+1)
Inh1 Inh2 Inh3 Inh(m)
X(n)
Ex(n)
REx1 REx2 REx3 REx(n)
RInh1 RInh2 RInh3
RInh(m)
X(n+2)
X(n+3) X(n+m)
VD3
Out
R8
R6
M1
Figure 2: The wiring schematic of memristive artificial neuron.
Figure 3: Experimental schematic for the inhibitory and excitatory simulation.
(seconds) is reported in the horizontal axis. Two dif-
ferent sources generate signals with different phase to
gain the effect of viable ∆t where Deltat is time differ-
ence between inbound signal and outbound signal of
the memristive neuron in similar way to pre-synaptic
and post-synaptic spikes. The V5 source output signal
is same as the monostable multivibrator signal, built
on operational amplifier OA1 at Fig.2. Period of input
signal was set to 5 ms. The voltage source V6 output
signal imitating input signal with different period to
Modeling Inhibitory and Excitatory Synapse Learning in the Memristive Neuron Model
517

Figure 4: Service signals, used for controlling and debugging the system.
Figure 5: Experimental results of the inhibitory learning feedback.
create phase shift. Period of V6 output signal was set
to 5.1 ms.
Nominal values of passive elements for two inte-
grating circuits OA2 and OA3, are selected in the way,
that rising and falling times of impulses in $G INT1
and $G INT2 are close to 2 ms and are indicated in the
Figure 4 in lines 2 and 3 and labeled as $G INT1 and
$G INT2. Results of these integrating circuits with
corresponding input signals are indicated in the Fig-
ure 4, labeled: $G INT1 and $G INT2. These two
signals are then provided to inverting adder OA4. All
passive components values selected in the way that
there no amplification of any signal. The learning
pulses are represented by $G SOMBRERO graph in
the Figure 5.
To generate Hebbian learning signal, we have in-
verted the left half of “sombrero” signals. We have
used the inverter circuit built on OA6. In order to in-
vert only half of the signal, we have used the addi-
tional voltage source V7, simulating monostable mul-
tivibrator, based on OA5 in the Fig.2. The learning
pulses are represented as $G
HEBB in the Figure 5.
The Figure 6 represents the correlation of the am-
plitude of the learning pulse $G SOMBRERO to ∆t:
the phase shift of output pulse ($G PULSE Figure 4)
to the phase shift of the input pulse ($G INPUT1 Fig-
ure 4). The graph has the shape of “sombrero”, with
maximum of this function at the point, when phase
shift or ∆t has minimal value. The excitatory learing
function is represented in the Figure 7 we have used
“sombrero” as base function and flipped along the Y
axis to replicate the basic form of the
1
x
function.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
518
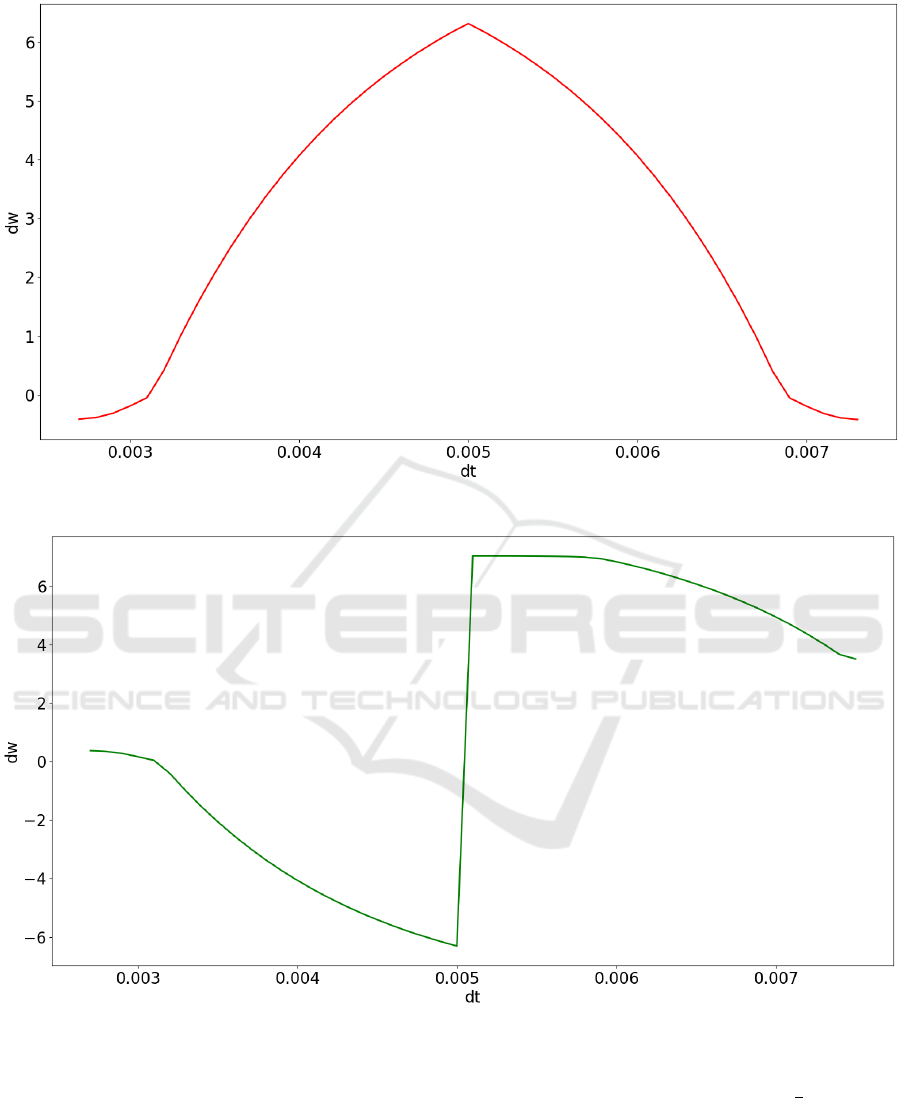
Figure 6: The inhibitory “sombrero” learning function or amplitude of learning pulse ∆w to ∆t.
Figure 7: The excitatory learning function or amplitude of learning pulse ∆w to ∆t.
5 CONCLUSIONS
In this paper we have discussed on our implementa-
tion of the excitatory or Hebbian and inhibitory or
“sombrero” learning mechanisms for the memristive
architecture of electronic-artificial neurons. The cor-
responding architecture contains two feedback loops
for two learning functions: similar to
1
x
and “som-
brero” where the learning impulse amplitude depends
from ∆t, i.e. the correlation of inbound and out-
bound impulses or “spikes”. We have successfully
demonstrated that the amplitude of the learning im-
pulse matches the learning functions depending from
the ∆t parameter. To the best of our knowledge, this
Modeling Inhibitory and Excitatory Synapse Learning in the Memristive Neuron Model
519

is the first attempt on implemementing the inhibitory
“sombrero” learning for the memristive architecture
of neurons to represent the natural inhibitory synapse
learning (Vogels et al., 2013).
This way, preliminary results obtained from sim-
ulations have demonstrated the feasibility of the idea
enabling the implementation of complex determinis-
tic networks, based on organic memristive devices,
with two types of learning: Hebbian (excitatory) and
“sombrero” (inhibitory) ones. This finding opens new
perspectives for the better understanding of processes
in nervous system and for the implementation of a
“Robot brain”, allowing learning and decision mak-
ing on thinking machines and robots as well.
ACKNOWLEDGEMENTS
The work is performed according to the Russian Gov-
ernment Program of Competitive Growth of Kazan
Federal University. The work was partially supported
by the MaDEleNA project financed by the Provincia
Autonoma di Trento, call Grandi Progetti 2012.
REFERENCES
Balkenius, C. and G
¨
ardenfors, P. (2016). Spaces in the
brain: From neurons to meanings. Frontiers in Psy-
chology, 7.
Braitenberg, V. (1984). Vehicles. experiments in synthetic
psychology. MIT press.
Chua, L. (1971). Memristorthe missing circuit element. ieee
transactions on circuit theory. 18:507–519.
Damasio, A. (1999). The feeling of what happens : body
and emotion in the making of consciousness. New
York.
Demin, V., Erokhin, V., Emelyanov, A., Battistoni, S.,
Baldi, G., Iannotta, S., Kashkarov, P., and Kovalchuk,
M. (2015). Hardware elementary perceptron based on
polyaniline memristive devices. Organic Electronics,
25:16–20.
Egorov, K. V., Kirtaev, R. V., Lebedinskii, Y. Y., Markeev,
A. M., Matveyev, Y. A., Orlov, O. M., Zablotskiy,
A. V., and Zenkevich, A. V. (2015). Complementary
and bipolar regimes of resistive switching in TiN/HfO
2
/TiN stacks grown by atomic-layer deposition: Com-
plementary and bipolar regimes of resistive switching
in TiN/HfO
2
/TiN stacks. physica status solidi (a),
212(4):809–816.
Emelyanov, A., Lapkin, D., Demin, V., Erokhin, V., Battis-
toni, S., Baldi, G., Dimonte, A., Korovin, A., Iannotta,
S., Kashkarov, P., and Kovalchuk, M. (2016). First
step towards the realization of a double layer percep-
tron based on organic memristive devices. AIP Adv,
6:111301.
Erokhin, V., Berzina, T., Camorani, P., Smerieri, A.,
Vavoulis, D., Feng, J., and Fontana, M. (2011). Ma-
terial memristive device circuits with synaptic plastic-
ity: Learning and memory. BioNanoScience, 1:24–30.
Erokhin, V., Berzina, T., and Fontana, M. (2005).
Hybrid electronic device based on polyaniline-
polyethylenoxide junction. J. Appl. Phys., 97:064501.
Erokhin, V. and Fontana, M. (2011). Thin film electrochem-
ical memristive systems for bio-inspired computation.
J. Computational Theor. Nanosci., 8:313–330.
Erokhin, V., Sch
¨
uz, A., and Fontana, M. (2010). Organic
memristor and bio-inspired information processing.
Int. J. Unconventional Computing, 6:15–32.
Fellous, J.-M. and Arbib, M. A. (2005). Who needs emo-
tions?: The brain meets the robot. Oxford University
Press.
Hern
´
andez-Mej
´
ıa, C., Sarmiento-Reyes, A., and V
´
azquez-
Leal, H. (2017). A novel modeling methodology
for memristive systems using homotopy perturbation
methods. CSSP, 36(3):947–968.
Ibrayev, T., Fedorova, I., Maan, A. K., and James, A. P.
(2014). Memristive operational amplifiers. In 5th
Annual International Conference on Biologically In-
spired Cognitive Architectures, BICA 2014, Cam-
bridge, MA, USA, November 7-9, 2014, pages 114–
119.
Izhikevich, E. M. (2006). Polychronization: Computation
with spikes. Neural Computation.
Khusainov, R., Shimchik, I., Afanasyev, I., and Magid, E.
(2015). Toward a human-like locomotion: Modelling
dynamically stable locomotion of an anthropomorphic
robot in simulink environment. In Int. Conf. on In-
formatics in Control, Automation and Robotics, vol-
ume 2, pages 141–148.
L
¨
ovheim, H. (2012). A new three-dimensional model for
emotions and monoamine neurotransmitters. Medical
hypotheses, 78(2):341–8.
Magid, E., Tsubouchi, T., Koyanagi, E., and Yoshida, T.
(2011). Building a search tree for a pilot system of a
rescue search robotin a discretized random step envi-
ronment. 23(1):567–581.
Matveyev, Y., Egorov, K., Markeev, A., and Zenkevich, A.
(2015). Resistive switching and synaptic properties of
fully atomic layer deposition grown TiN/HfO
2
/TiN
devices. Journal of Applied Physics, 117(4):044901.
Minsky, M. (2007). The Emotion Machine: Commonsense
Thinking, Artificial Intelligence, and the Future of the
Human Mind. Simon & Schuster.
Potjans W., Morrison A., D. M. (2010). Enabling functional
neural circuit simulations with distributed computing
of neuromodulated plasticity. Frontiers in Computa-
tional Neuroscience, 4:1–17.
Prezioso, M., Merrikh Bayat, F., Hoskins, B., Likharev, K.,
and Strukov, D. (2016). Self-Adaptive Spike-Time-
Dependent Plasticity of Metal-Oxide Memristors. Sci-
entific Reports, 6:21–31.
Rodriguez, A. and Granger, R. (2016). The grammar
of mammalian brain capacity. Theor. Comput. Sci.,
633:100–111.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
520

Samsonovich, A. V. and Robertson, P., editors (2014).
5th Annual International Conference on Biologically
Inspired Cognitive Architectures, BICA 2014, Cam-
bridge, MA, USA, November 7-9, 2014, volume 41 of
Procedia Computer Science. Elsevier.
Serb, A., Bill, J., Khiat, A., Berdan, R., Legenstein, R.,
and Prodromakis, T. (2016). Unsupervised learning in
probabilistic neural networks with multi-state metal-
oxide memristive synapses. Nature Communications,
7:12611.
Strukov, D., Snider, G., Stewart, D., and Williams, R.
(2008). The missing memristor found. Nature,
453:80–83.
Talanov, M., Vallverd
´
u, J., Hu, B., Moore, P., Toschev,
A., Shatunova, D., Maganova, A., Sedlenko, D., and
Leukhin, A. (2016). Emotional simulations and de-
pression diagnostics. Biologically Inspired Cognitive
Architectures, 18:41–50.
Talanov, M., Zagulova, M., Distefano, S., Pinus, B.,
Leukhin, A., , and Vallverdu, J. (2017). The Imple-
mentation of Noradrenaline in the NeuCogAr Cog-
nitive Architecture. In Proceedings of the Ninth In-
ternational Conference on Advanced Cognitive Tech-
nologies and Applications, pages 10–15. IARIA XPS
Press.
Tchitchigin, A., Talanov, M., and Safina, L. (2016a). Neu-
romorphic robot dream. BioNanoScience, pages 1–2.
Tchitchigin, A., Talanov, M., Safina, L., and Mazzara, M.
(2016b). Robot Dream, pages 291–298. Springer In-
ternational Publishing, Cham.
Vogels, T. P., Froemke, R. C., Doyon, N., Gilson, M.,
Haas, J. S., Liu, R., Maffei, A., Miller, P., Wierenga,
C., Woodin, M. A., Zenke, F., and Sprekeler, H.
(2013). Inhibitory synaptic plasticity: spike timing-
dependence and putative network function. Frontiers
in Neural Circuits, 7:119.
Modeling Inhibitory and Excitatory Synapse Learning in the Memristive Neuron Model
521
