
Metaheuristic Solutions for Solving Controller Placement Problem in
SDN-based WAN Architecture
Kshira Sagar Sahoo
1
, Anamay Sarkar
1
, Sambit Kumar Mishra
1
, Bibhudatta Sahoo
1
, Deepak Puthal
2,†
,
Mohammad S. Obaidat
3,4,†,‡
and Balqies Sadun
5
1
National Institute of Technology, Rourkela, India
2
University of Technology Sydney, Australia
3
Fordham University, U.S.A.
4
University of Jordan, Jordan
5
Al-Balqa Applied University, Jordan
Keywords:
SDN, Controller, CPP, FireFly, PSO.
Abstract:
Software Defined Networks (SDN) is a popular paradigm in the modern networking systems that decouples
the control logic from the underlying hardware devices. The control logic has implemented as a software com-
ponent and residing in a server called controller. To increase the performance, deploying multiple controllers
in a large- scale network is one of the key challenges of SDN. To solve this, authors have considered con-
troller placement problem (CPP) as a multi-objective combinatorial optimization problem and used different
heuristics. Such heuristics can be executed within a specific time-frame for small and medium sized topology,
but out of scope for large scale instances like Wide Area Network (WAN). In order to obtain better results,
we propose Particle Swarm Optimization (PSO) and Firefly two population-based meta-heuristic algorithms
for optimal placement of the controllers, which take a particular set of objective functions and return the best
possible position out of them. The problem has been defined, taking into consideration both controllers to
switch and inter-controller latency as the objective functions. The performance of the algorithms evaluated
on a set of publicly available network topologies in terms execution time. The results show that the FireFly
algorithm performs better than PSO and random approach under various conditions.
1 INTRODUCTION
In recent years, the use of Software Defined Net-
working (SDN) has become an emerging technology
that provides many advantages to the cloud data cen-
ters and network service providers. Both SDN and
Network Function Virtualization (NFV) technology
creates the new era of network innovation through
the virtualization of network resources (Jarraya et al.,
2014),(Jammal et al., 2014). The underlying principle
of SDN is the abstraction of the control plane from
the data plane. It introduces the logically centralized
control plane also referred to as Network Operating
System (NOS), that hides the network complexities to
the application developer by introducing well known
southbound APIs. The network intelligence moved
†
Fellow of IEEE & Fellow of SCS
‡
Corresponding author
onto one or more external servers from the hardware
devices, called controllers, which has a global view of
the entire network(Sahoo et al., 2016).
Although placing a single controller is economi-
cally advantageous, it suffers single point of failure.
Hence, deploying multiple controllers in the network
is an alternate solution. However, random placing of
controllers affects the performance of the system and
degrades end to end QoS. So, it requires a proper plan-
ning to find the optimal location of the controller to
get satisfactory performance and a reliable SDN. The
CPP is an optimization problem is similar to facility
location problem; which has considered as a NP-hard
problem. Authors in (Heller et al., 2012), shows the
performance of the network by varying the position of
the controller in the network. So, it is a big challenge
to find the location as well as number of controllers to
be deployed in the network. Dynamically changing
Sahoo, K., Sarkar, A., Mishra, S., Sahoo, B., Puthal, D., Obaidat, M. and Sadun, B.
Metaheuristic Solutions for Solving Controller Placement Problem in SDN-based WAN Architecture.
DOI: 10.5220/0006483200150023
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 1: DCNET, pages 15-23
ISBN: 978-989-758-256-1
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

the network architecture especially for WAN is a chal-
lenging task for the network operator. To adapt to this
dynamics; the optimized location needs to be calcu-
lated. The POCO (Hock et al., 2014) framework has
capable of handling small and medium size topology
which provide the solution within seconds.However,
for the large-scale network, it requires a lot of time for
exhaustive evaluation for finding the location which
may not cope with the dynamics of the network. The
summary of our contributions are as follows:
• The main objective of this work is to minimize
controller to node and inter-controller latency in
the average and worst case scenario.
• To best of our knowledge, we are the first to
propose the population-based meta-heuristic tech-
niques to solve CPP on a set of real topologies
considering the above as the objective function.
The rest of this paper has organized as follows. The
Section II introduced the related work; the mathemat-
ical formulation described in Section III. The con-
sidered meta-heuristics algorithms have discussed in
Section IV. Then Section V exhibits the performance
analysis during the experiment followed by conclu-
sion in Section VI.
2 RELATED WORK
In a given network which comprises of certain
nodes(node may be switch, router, firewall etc.) , how
to place the controllers is an open question. At first,
Heller et al.(Heller et al., 2012) examined both aver-
age and worst case latency between the switch and
controller in the Internet2 topology. The latency and
traffic load between switch and controller have em-
phasized by Yao (Yao et al., 2014). In another work,
Bari (Bari et al., 2013), proposed a dynamical provi-
sioning of controllers aims to reduce flow set-up time
and reassignment time of a switch to another con-
troller in case of an overloaded situation. The POCO
framework has been formulated with different met-
rics. The trade-off between the different metrics with
all possible placements is examined in POCO. Al-
though the inter-controller latency has considered it
has not discussed in-depth in their work. In his work
Lange et la.(Lange et al., 2015) extends the POCO
framework and deploy K controller in the dynamic
topologies. In their work, they have used Pareto Sim-
ulated Annealing (PSA) a meta-heuristic to solve the
CPP. Hu et la. (Hu et al., 2013) worked on the re-
liability of the controller. They have used a met-
ric to quantify the reliability called expected percent-
age of control path loss but ignores inter-controller
latency. The paper(Sallahi and St-Hilaire, 2015),
solve the CPP with various multi-objective functions.
To the best of our knowledge, the authors have not
used any population-based meta-heuristic technique
in their work.
3 PROBLEM FORMULATION
In this work, we represent the network as a graph
G(V,E), where V and E represent as the node set
and edge set. The node set consists of the switch,
router, and controllers. In SDN, the switches and con-
trollers are the forwarding elements. Here, we as-
sumed that the controller locations are some of the
forwarding nodes. Let d(v,c) is the shortest path dis-
tance from a forwarding node v ∈ V to one of the con-
troller c ∈ C. For a particular placement the number
of controllers is fixed to k, i.e. |C
i
| = k. The all pos-
sible controller placement set can be represented as
C = {C
1
,C
2
,...,C
m
}. For finding out a location for
the controller c
i
∈ C
j
; can be set as an optimization
problem where the evaluation metrics are optimized.
In our work, we have used latency as the evaluation
metric. Latency refers to the time taken to reach a
packet from source node to the destination node. But
in case of SDN, the propagation latency between node
and controller is proportional to the distance between
a node to controller.
3.1 Controller to Switch Latency
It is the most common metric used in CPP. It is the
longest distance between a node (v
i
) and a controller
(c
j
) i.e. max d(v
i
,c
j
). This is considered as the worst-
case switch to controller latency. The objective of this
worst case latency is to minimize the longest distance.
π
worstlat
(C) = min
v∈V
max
c∈C
i
d(v,c) (1)
For the average latency case, the average distance be-
tween the placed controllers and remaining nodes as-
signed to them is calculated. In order tocompute it,
the following equation has used.
π
avglat
(C) =
1
|V |
∑
v∈V
min
c∈C
i
d(v,c) (2)
3.2 Inter-controller Latency
The latency between the individual controllers has a
major significance because communications between
these controllers are required to achieve proper syn-
chronization of the network state. In order to mini-
mize the controller to controller communication cost,
DCNET 2017 - 8th International Conference on Data Communication Networking
16

they should deploy near to each other. To compute
this metric, the d
0
must be calculated. The new
d
0
(c
i
,c
j
) is produced from d(i, j) that signifies the
shortest distance between controller c
i
to controller
c
j
. The matrix d
0
removes the node that does not hold
as a controller. The following equation is used to cal-
culate the above metric.
π
avgiclat
(C) =
1
|k|
∑
c
i
,c
j
∈C
min d(c
i
,c
j
) (3)
For worst-case inter-controller latency the maxi-
mum distance that separates controllers is computed.
The considered metric can be formulated as:
π
worsticlat
(C) = max
c
i
,c
j
∈C
d(c
i
,c
j
) (4)
4 META-HEURISTIC
TECHNIQUES FOR CPP
PROBLEM
With a given the number of controllers k to be de-
ployed in the network, the goal of our work is to find
a placement C
i
from the set C, such that the consid-
ered metrics must be minimized.
The single state meta-heuristic techniques like
simulated annealing (SA) has a single candidate so-
lution. This solution is used to compare with possible
new solutions. Population-based algorithms like Fire-
fly, PSO store many candidate solutions and the solu-
tion set compare them against each other. For explor-
ing large and continuous space regions, single state
algorithms are not suitable for large search space be-
cause of the possibility of stuck in local optima and
lack of comparisons between candidate solutions.
4.1 PSO Algorithm for CPP
Particle Swarm Optimization (PSO) is a population-
based stochastic technique. This algorithm searches
the optimum solution from a population called the
swarm. Based on two types of learning i.e. cogni-
tive and social learning; it finds the best solution out
of many. At the initial phase cognitive factor required
for determining the best position. After searching the
local best, social factor helps to find the global best
position.
Let there are n particles, that represent the poten-
tial solutions and each particle represented as a d-
dimension vector. Let, the current position of the
particle is χ
i
= [x
i1
,x
i2
,...,x
id
], where i ∈ 1...n. The
current velocity is V
i
= v
i1
,v
i2
,...,v
id
. The best posi-
tion of the particle P
i
is p
i1
, p
i2
,..., p
id
. The P
gb
is the
global best position vector.
At the time t +1, it updates the position (χ
t+1
id
) and
velocity (V
t+1
id
) of the individual particle is defined as
follows:
V
t+1
id
= ωV
t
id
+ c1
0
r1(P
id
− χ
t
id
) + c2
0
r2(P
gbd
− χ
t
id
)
(5)
χ
t+1
id
= χ
t
id
+V
id
+t (6)
Where ω represents initial weight,r1 and r2 denotes
the random sequence: r1,r2 ∈ {0, 1}. The positive
constant c1
0
and c2
0
adjusts the cognitive part and so-
cial part respectively. The value of ω is used for im-
proving the performance of the algorithm. The adap-
tive adjustment of ω helps to improve the local as well
as global search ability, which can be represented as:
ω = ω
max
−
ω
max
− ω
min
I
max
× I (7)
In the Equation 7, I
max
represents the maximum num-
ber of iteration it can hold and I represents the current
iteration. The ω
max
and ω
min
represents the maximum
weight and minimum weight respectively.
4.2 Algorithm for CPP PSO
The CPP PSO Algorithm takes the co-ordinates
of the nodes (latlng), required number of
controllers(nCont), and the matrix containing
the shortest path from each node to all other nodes
(srtPathMtrx)as the inputs.The algorithm produces
the semi-optimized value (bstCst) of the cost function
and the final location of the Controllers ( f nlPosPSO).
The algorithm begins by setting the number of
Nodes (numNod), x and y-co-ordinates of latlng
as latlngX and latlngY , initializing the number
of maximum iterations (maxIt), the population of
the swarm (nPop), inertia coefficient (ω), damping
ratio for inertia coefficient (ωdamp), individual
(c1) and social (c2) acceleration coefficients and
sets Global Best Cost (glBest.Cst) to infinity. It
initializes each particle’s position (par(i).Pos) as
a random permutation of nCont out of numNode.
Each particle’s velocity in x (par(i).Vel.x) and y
(par(i).Vel.y) components set to zeros. Also it
initializes each particle’s cost (par(i).Cst) using the
objective function. It also initializes best position of
each particle (par(i).Bst.Pos) as the current position
and best cost(par(i).Bst.Cst) as the current cost and
sets Global Best Cost(glBest.Cst) as the optimum
value among all the particles and Global Best Position
( f nl pos PSO) as the position of the particle giving
the optimal value. For each iteration and for the each
particle the Algorithm 2 updates the particle’s x and
y component of velocity and the position. With the
current position of the particle, x and y component of
velocity and latlng are given as input and updates the
Metaheuristic Solutions for Solving Controller Placement Problem in SDN-based WAN Architecture
17

Algorithm 1 CPP PSO
Input: latlng, nCont,srtPathMtrx
Output: optimized cost (bstCst), Final position of controllers ( f nlPosPSO)
Initialization :
1: numNod ← Size of latlng
2: latlngX , latlngY ← x- and y- co-ordinates of latlng
3: maxIt ← maximum number of iterations
4: nPop ← Swarm Size
5: w ← inertia coefficient
6: wdamp ← damping ratio
7: c1 ← personal acceleration coefficient
8: c2 ←social acceleration coefficient
9: glBest.Cst ←Set Global Best Cost to ∞
10: for i = 1 to nPop do
11: par(i).Pos ←Randomly select nCont positions from numNodes
12: par(i).Vel.x ←Initialize x-component of velocity with 0
13: par(i).Vel.y ←Initialize y-component of velocity with 0
14: par(i).Cst ← Pass par(i).Pos,latlngX , srtPathMtrx to CST NC
15: par(i).Bst.Pos ← par(i).Pos
16: par(i).Bst.Cst ← par(i).Cst
17: if (par(i).Bst.Cst < glBest.Cst) then
18: glBest.Cst ← par(i).Bst.Cst
19: f nl pos PSO ← par(i).Pos
20: end if
21: end for
22: BstCost ←Initialize the Best Cost with 0
Optimization Loop
23: for it = 1 to maxIt do
24: for i = 1 to nPop do
25: par(i).Vel.x ←Update x component using Equation 5
26: par(i).Vel.y ← Update y component of velocity similar to x
component of velocity
27: par(i).Pos ← Pass
par(i).Pos, par(i).Vel.x, par(i).Vel.y,latlngX , latlngY to
updPos PSO
28: par(i).Cst ← Pass par(i).Pos,latlngX , srtPathMtrx to CST NC
29: if (par(i).Cst < par(i).Bst.Cst) then
30: par(i).Bst.Pos ← par(i).Pos
31: par(i).Bst.Cst ← par(i).Cst
32: if (par(i).Bst.Cst < glBest.Cst) then
33: glBest.Cst ← par(i).Bst.Cst
34: f nlPosPSO ← par(i).Pos
35: end if
36: end if
37: end for
38: BstCost(it) ← glBest.Cst
39: w ← w × wdamp
40: end for
41: z ← BstCost from last iteration
42: return z, f nlPosPSO
cost of the particle using the considered objective
function. If the new cost is better than the previous
cost of the particle, update the particle’s current po-
sition and cost. If the updated cost is better than the
previous one then, the global best cost and global best
positions are updated to the particle’s cost and posi-
tion respectively.
The updPos CPP PSO Algorithm takes the cur-
rent position of the particle (x), x-component of veloc-
ity (vx), y-component of velocity (vy) , x-coordinates
of all nodes (latlngX) and y-coordinates of all nodes
(latlngY ) as input and produces the updated posi-
tion (z). In order to obtains the x-component of
particle’s i
th
controller position (xPos(i)), this al-
gorithm get the sum of x-coordinate of i
th
con-
troller (latlngX(x(i))) and x-component of velocity
of i
th
particle (vx(i)). This process is similar for
the y-component of particle’s i
th
controller position
(yPos(i)). For each controller location, it initializes
minimum distance between final position and any ac-
tual node co-ordinate (mini) to infinity and initializes
the index (mini index) of such a node to 0. Then,
for each controller location, it checks all other nodes
and updates mini index as the index of the node which
gives minimum distance.
Algorithm 2 updPos CPP PSO
Input: x,vx, vy,latlngX,latlngY
Output: updated position (z)
Initialization :
1: sze ←size of x
2: numNode ← size of latlngX
3: xPos ←Initialize the x component of position with zero
4: yPos ←Initialize the y component of position with zero
5: dist←Initialize the final location with 0s
Main Body
6: for i = 1 to sze do
7: xPos(i) ← latlngX (x(i)) + vx(i)
8: yPos(i) ← latlngY(x(i)) + vy(i)
9: end for
10: for i = 1 to sze do
11: mini ← ∞
12: mini index ← 0
13: for j = 1 to numNode do
14: if (Distance between i
th
position and j
th
node is less than mini)
then
15: mini← Distance between i
th
position and j
th
node
16: mini index ← j
17: end if
18: end for
19: dist for i
th
iteration ← mini index
20: end for
21: z← dist
22: return z
4.3 Firefly Algorithm (FFA)
This Algorithm 3 is based on the flashing characteris-
tics of the fireflies. The biochemical process of illu-
minating light from firefly is called bio-luminescence
has a significance role. The basic objective of this al-
gorithm is to attract the opponent through rhythmic
flashes. The inverse squared law inferred that the in-
tensity of the light(I) decreases as the distance r in-
creases. So, in a simple form the FFA based on the
equation 8.
I ∝
1
r
(8)
DCNET 2017 - 8th International Conference on Data Communication Networking
18

The light intensity (I)is having a fixed absorption co-
efficient γ, which has given in the equation 9.
I = I
0
e
−rγ
(9)
Where, I
0
is the initial light intensity. For simplicity
and to avoid singularity at r = 0, we can combine both
the equations.
I = I
0
e
−r
2
γ
(10)
The attractiveness (β) is directly proportional to the
intensity of the light, that are coming from nearby
fireflies, which has given in the below equation.
β = β
0
e
−r
2
γ
(11)
In the Equation 11 β
0
is the attractiveness at r = 0.
For faster calculation we normalize the equation as a
monotonically decreasing function.
β = β
0
e
−r
m
γ
;(m ≥ 1) (12)
The movement of one butterfly(i) to another butterfly
( j) is determined by the given equation 13
x
i
= x
i
+ β
0
e
r
2
i j
γ
(x
j
− x
i
) + αε
i
(13)
The third term is used for randomization where, α is
the randomized parameter and ε
i
is the vector of ran-
dom numbers.
4.4 Algorithm for CPP FFA
The Algorithm 3 takes the co-ordinates of the nodes,
number of controllers and the matrix containing the
shortest path from each node to all other nodes as in-
put. Similar to CPP PSO it produces the optimized
value of the cost function and the final location of the
controllers.
The Algorithm 4 takes all the fireflies (par), light
intensity of the firefly (Lightn), randomness coeffi-
cient (α), absorption coefficient (γ) , x co-ordinates
of nodes (latlngX) and y co-ordinates of the nodes
(latlngY) as inputs. It returns the updated position of
all the fireflies (par). The algorithm begins by ini-
tializing the number of nodes (numNode), number
of particles (numPar) and the number of controllers
(numCon) as the size of any particle. For each con-
troller (numCon) the following steps are performed.
It sets the x-coordinate (xo) and y-coordinate (yo) of
all fireflies for all controllers to zeros. Then the x-
coordinate (xo(i)) and y-coordinate of each particle
(yo(i)) are updated. For each particle, set r as the dis-
tance between i
th
particle and j
th
particle. If the light
intensity of i
th
particle (Lightn(i)) is greater than the
light intensity of j
th
particle (Lighto( j)), then set β as
the negative exponent of product of γ and r. The pa-
rameter xn(i) set as in per the equation 13. Finally the
algorithm sets dist as the updated position of the fire-
flies, in terms of the indices of the corresponding
Algorithm 3: CPP FFA.
Input: latlng, nCont,avlPathMtrx, srtPathMtrx
Output: bstCst, f nlPosFire
Initialization :
1: numNode ← size o f latlng
2: latlngX ← x co − ordinates o f latlng
3: latlngY ← y co − ordinates o f latlng
4: nPop ←Initialize number of fireflies
5: maxGen ←Initialize number of iterations
6: α ←Set the randomness coefficient
7: γ ←Set the absorption coefficient
8: δ ←Set the randomness reduction coefficient
9: minCst ←Initialize the minimum cost of objective function to infinity
10: Lightn ←Initialize the light intensity of all the fireflies to zeros
11: for i = 1 to nPop do
12: par(i).Pos ←Randomly select nCont from numNode
13: end for
Optimization Loop
14: for i = 1 to maxGen do
15: zn ←Initialize the cost for all the fireflies with zeros
16: for j = 1 to nPop do
17: zn( j) ←Pass par( j).Pos,latlngX,srtPathMtrx to Objective
function
18: end for
19: [Lightn] ← Return sorted zn in Lightn
20: Lighto ← Make a copy of Lightn
21: par ← Pass par,Lightn, Lighto,α, γ,latlngX,latlngY to
updPos Fire()
22: α ← α∗ δ
23: if (minCst > Lighto(1)) then
24: mincost ← Lighto(1)
25: f nlPosFire ←Set f nlPosFire as the position of firefly that gave
the minimum Cost
26: end if
27: end for
28: bstCst ← minCst;
29: return bstCst, f nlPosFire
controller location and then it sets each firefly’s cor-
responding controller location (par(g).Pos(k)).
4.5 Algorithm for the Cost Functions
In the main body of the algorithm, the average con-
troller latency is added with average inter-controller
latency. Average node latency and average controller
latency are added to obtain the objective function (z),
which is returned by the Algorithm 6.
5 EXPERIMENT
To evaluate of this work, we have taken various
topologies from the TopologyZoo website. As per
our knowledge since, no one has used any population-
based meta-heuristic technique to solve CPP problem.
In this work, we have used two metrics, which have
been already discussed in the previous section.
Metaheuristic Solutions for Solving Controller Placement Problem in SDN-based WAN Architecture
19

Algorithm 4: updPos FireFly.
Input: par, Lightn,Lighto, α,γ, latlngX,latlngY
Output: par
Initialization :
1: numNode ← size o f latlng
2: numPar ← size o f par
3: numCon ←Set number of controllers as size of any particle
Main Body
4: for k = 1 to numCon do
5: xo ←Initialize x-coordinates of the fireflies by zeros
6: yo ←Initialize y-coordinates of the fireflies by zeros
7: for i = 1 to numPar do
8: xo(i) ←Set the x-coordinate of ith particle’s kth controller loca-
tion from latlngX
9: yo(i) ←Set the y-coordinate of ith particle’s kth controller loca-
tion from latlngY
10: end for
11: xn ← xo
12: yn ← yo
13: for i = 1 to numPar do
14: for j = 1 to numPar do
15: r ←Distance between ith and jth particle
16: if (Lightn(i) > Lighto( j)) then
17: β ←Set as the negative exponent of product of γ and r
18: xn(i) ←Set as the sum of (product of previous xn(i) and
1 − β) and (product of previous xo( j) and β) and (product
of α and a random number)
19: yn(i) ←Set as the sum of (product of previous yn(i) and
1 − β) and (product of previous yo(j) and beta) and (prod-
uct of α and a random number)
20: end if
21: end for
22: end for
23: dist ←Initialize the final location of k
th
controller of all fireflies with
0s
24: for i = 1 to numPar do
25: mini ← Initialize with in f inity
26: mini index ← Initialize with 0s
27: for j = 1 to numNode do
28: if (Distance between i
th
particle’s k
th
controller location and
j
th
node is less than mini) then
29: mini ← Distance between i
th
particle’s k
th
controller lo-
cation and j
th
node
30: mini index ← j
31: end if
32: end for
33: dist f or i
th
iteration ← mini index
34: end for
35: for g = 1 to numPar do
36: par(g).Pos(k) ← Set the g
th
particle’s k
th
controller location as
g
th
entry of dist
37: end for
38: end for
39: return par
All the algorithms are written in Matlab version
R2014a and runs on a system having Intel Core i5
with 4-Core processors and 8 GB RAM with Ubuntu
13.10 of 64-bit Operating System. The results are
obtained by running the algorithms 30 times on the
graph. Among 261 networks in the Topology-Zoo,
Algorithm 5: CST NC.
Input: x,latlngX,srtPathMtrx
Output: z
Initialization :
1: sze ←Set number of Controllers as the size of x
2: numNode ←Set number of Nodes as the size of latlngX
3: contLat ←Initialize average controller latency with 0
4: nodeLat ← Initialize average node latency with 0
Main Body
5: for i = 1 to sze do
6: for j = 1 to sze do
7: contLat ← contLat + srtPathMtrx(x(i), x( j))
8: end for
9: end for
10: contLat ← contLat/(sze ∗ sze)
11: for i = 1 to numNode do
12: mini ← ∞
13: for j = 1 to sze do
14: mini ← min(mini,srtPathMtrx(i,x( j)))
15: end for
16: nodeLat ← nodeLat + mini
17: end for
18: z ← nodeLat + contLat
19: return z
Algorithm 6: CST NC.
Input: x,latlngX,srtPathMtrx
Output: z
Initialization :
1: sze ←Set number of Controllers as the size of x
2: numNode ←Set number of Nodes as the size of latlngX
3: contLat ←Initialize average controller latency with 0
4: nodeLat ← Initialize average node latency with 0
Main Body
5: for i = 1 to sze do
6: for j = 1 to sze do
7: contLat ← contLat + srtPathMtrx(x(i), x( j))
8: end for
9: end for
10: contLat ← contLat/(sze ∗ sze)
11: for i = 1 to numNode do
12: mini ← ∞
13: for j = 1 to sze do
14: mini ← min(mini,srtPathMtrx(i,x( j)))
15: end for
16: nodeLat ← nodeLat + mini
17: end for
18: z ← nodeLat + contLat
19: return z
we have considered 20 topologies for our work. The
network sizes range from 50 to 150 nodes and among
them the total number of controllers considered are
between 5 to 20. The TataNld topology has been cho-
sen as an example, which contains 144 nodes and 141
edges. When more than one metric are optimized, it
is usually difficult to find an exact solution that satis-
fies all at the same time. So, there is a trade-off that is
required between these two or more metrics. Thus to
justify the necessity, the Pareto frontier is used.
DCNET 2017 - 8th International Conference on Data Communication Networking
20
5.1 How Worthwhile to Optimize the
Controller Position?
The Fig.1 and 2 shows the ratio of random deploy-
ment of the controller to our proposed algorithms on
the same topology. It has clearly observed that the av-
erage latency of the proposed algorithms is about 1.7
times greater than random deployment. For the larger
value of K(18), the cost of the random placement is
almost 70% higher than that of other placements. For
the worst case latency, this cost is even larger for
both the algorithms. The ratio starts from 1.5 for a
single controller, but for the higher value of K, the
CPP FFA increases to 2.1x, whereas CPP PSO in-
creases to 1.9x. Hence, it is important to optimize the
placement of controllers in a given topology.
0 2 4 6 8 10 12 14 16 18
1.5
1.55
1.6
1.65
1.7
1.75
Number of Controllers
ratio
CPP_FIREFLY
CPP_PSO
Figure 1: Ratio of random deployment to CPP PSO and
CPP FFA (Average-case).
0 2 4 6 8 10 12 14 16 18
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
Number of Controllers
ratio
CPP_FIREFLY
CPP_PSO
Figure 2: Ratio of random deployment to CPP PSO and
CPP FFA (Worst-case).
5.2 Performance of the Algorithms
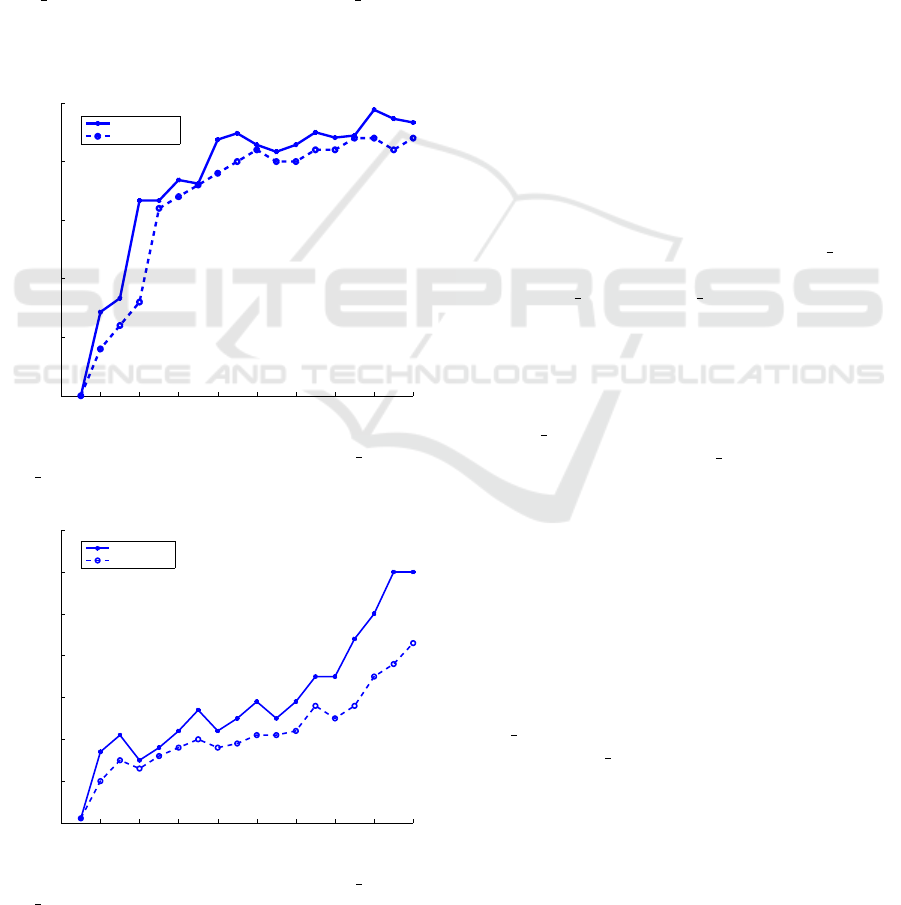
The Fig. 3 and Fig. 5 analyzes the impact of average
and maximum latency on increasing the number of the
controller, k ranges from 1 to 20, under the same net-
work topology. The experimental result shows that by
increasing the number of controllers for each place-
ment, the both the latencies (cost) is decreased as ex-
pected. The average latency is calculated using both
Equation 2 and Equation 3. From the plot it can be
observed that, when k > 15 both average and worst
case latency are almost linear,so we restrict the num-
ber of controllers to 15 for the topology. Similar to
average case the worst case inter-controller latency is
computed using Equations 1 and 4. The average de-
lay of both meta-heuristic algorithms is usually rela-
tively more stable than random algorithm. When K
=16, the cost within an acceptable range for both the
algorithms,
5.3 Computational Time of the
Proposed Algorithms
With the increasing number of controller it can be
seen from the Fig. 4 and Fig. 6 that CPP FFA al-
gorithm takes the shortest time. The processing time
of both CPP FFA and CPP PSO is much faster than
random algorithm. Due to the randomness and non-
uniformity nature, the random algorithm behaves like
it. But, the execution time taken by the two meta-
heuristic techniques is almost close to each other in
both the cases. For the larger network like TataNld,
the CPP FFA algorithm converges to the optimal so-
lution slightly faster than CPP PSO.
5.4 Optimal Positions of the Controllers
Now, we compare the geographic locations of the
controllers with respect to the different objective
functions. The Fig. 7 and Fig. 8 shows the final out-
come of the simulation with 15 controllers on TataNld
topology. The black circle represents the controller
position and the white circle represents the other than
controller. The Fig. 7 depicts the locations of the
controller that minimizes the average latency using
CPP FireFly algorithm, and the Fig. 8 represents the
same using CPP PSO algorithm.
6 CONCLUSIONS
In this paper, we discuss the controller placement
problem for SDN-based WAN architecture. The
greedy and brute force methods are well suited for
Metaheuristic Solutions for Solving Controller Placement Problem in SDN-based WAN Architecture
21

Figure 3: Impact of average case latency on deploying con-
trollers.
Figure 4: In average case the computational time of the al-
gorithms.
Figure 5: Impact of worst-case latency on deploying con-
trollers.
Figure 6: In worst case the computational time of the algo-
rithms.
small and medium-sized problem instances, but for
large scale problem instances a heuristic mecha-
nism is a wise choice. Hence, we propose two
meta-heuristic algorithms named as CPP PSO and
72 74 76 78 80 82 84 86 88 90
5
10
15
20
25
30
35
Longitude
Latitude
Other nodes
Controller Locations
Figure 7: Optimal placement using CPP FFA in the TataNld
(Average-case latency).
72 74 76 78 80 82 84 86 88 90
5
10
15
20
25
30
35
Longitude
Latitude
Other nodes
Controller Locations
Figure 8: Optimal placement using CPP PSO in the
TataNld (Average-case latency).
CPP FFA for evaluating CPP. In particular, such al-
gorithms optimize a set of objectives that find the
optimal number and location of the controller. The
objective of this work is to minimize the latency
between controllers as well as from switch to con-
trollers. Experimental results show that for average
case and worst case latency, the CPP FFA has better
performance than CPP PSO. The time taken by both
CPP PSO and CPP FFA are in almost close level.
When network size is larger, CPP FFA converges
to the optimal solution slightly faster than CPP PSO
as it is the inherent property of these Meta-heuristic
techniques. Finally, the scope of this paper is not lim-
ited to only this two objectives. As future work, we
plan to incorporate other objective functions like load
balancing and multi-path connectivity.
REFERENCES
Bari, M. F., Roy, A. R., Chowdhury, S. R., Zhang, Q.,
Zhani, M. F., Ahmed, R., and Boutaba, R. (2013). Dy-
namic controller provisioning in software defined net-
works. In Network and Service Management (CNSM),
2013 9th International Conference on, pages 18–25.
IEEE.
Heller, B., Sherwood, R., and McKeown, N. (2012). The
controller placement problem. In Proceedings of the
DCNET 2017 - 8th International Conference on Data Communication Networking
22

first workshop on Hot topics in software defined net-
works, pages 7–12. ACM.
Hock, D., Gebert, S., Hartmann, M., Zinner, T., and Tran-
Gia, P. (2014). Poco-framework for pareto-optimal
resilient controller placement in sdn-based core net-
works. In Network Operations and Management Sym-
posium (NOMS), 2014 IEEE, pages 1–2. IEEE.
Hu, Y., Wendong, W., Gong, X., Que, X., and Shiduan,
C. (2013). Reliability-aware controller placement for
software-defined networks. In Integrated Network
Management (IM 2013), 2013 IFIP/IEEE Interna-
tional Symposium on, pages 672–675. IEEE.
Jammal, M., Singh, T., Shami, A., Asal, R., and Li, Y.
(2014). Software defined networking: State of the art
and research challenges. Computer Networks, 72:74–
98.
Jarraya, Y., Madi, T., and Debbabi, M. (2014). A sur-
vey and a layered taxonomy of software-defined net-
working. IEEE Communications Surveys & Tutorials,
16(4):1955–1980.
Lange, S., Gebert, S., Zinner, T., Tran-Gia, P., Hock, D.,
Jarschel, M., and Hoffmann, M. (2015). Heuristic ap-
proaches to the controller placement problem in large
scale sdn networks. IEEE Transactions on Network
and Service Management, 12(1):4–17.
Sahoo, K. S., Mohanty, S., Tiwary, M., Mishra, B. K., and
Sahoo, B. (2016). A comprehensive tutorial on soft-
ware defined network: The driving force for the fu-
ture internet technology. In Proceedings of the In-
ternational Conference on Advances in Information
Communication Technology & Computing, page 114.
ACM.
Sallahi, A. and St-Hilaire, M. (2015). Optimal model for
the controller placement problem in software defined
networks. IEEE Communications Letters, 19(1):30–
33.
Yao, G., Bi, J., Li, Y., and Guo, L. (2014). On the ca-
pacitated controller placement problem in software
defined networks. IEEE Communications Letters,
18(8):1339–1342.
Metaheuristic Solutions for Solving Controller Placement Problem in SDN-based WAN Architecture
23
