Neural Network Inverse Model for Quality Monitoring

Application to a High Quality Lackering Process

Philippe Thomas

1,2

, Marie-Christine Suhner

1,2

, Emmanuel Zimmermann

1,2,3

, Hind Bril El Haouzi

1,2

André Thomas

1,2

and Mélanie Noyel

Université de Lorraine, CRAN, UMR 7039, Campus Sciences, BP 70239, 54506 Vandœuvre-lès-Nancy cedex, France

CNRS, CRAN, UMR7039, France

Acta-Mobilier, parc d’activité Macherin Auxerre Nord 89270 Moneteau, France

Keywords: Neural Network, Product Quality, Inverse Model, Quality Monitoring.

Abstract: The quality requirement is an important issue for modern companies. Many tools and philosophies have

been proposed to monitor quality, including the seven basic tools or the experimental design. However, high

quality requirement may lead companies to work near their technological limit capabilities. In this case,

classical approaches to monitor quality may be insufficient. That is why on line quality monitoring based on

the neural network prediction model has been proposed. Within this philosophy, the dataset is used in order

to determine the optimal setting considering the operating point and the product routing. An inverse model

approach is proposed here in order to determine directly the optimal setting in order to avoid defects

production. A comparison between the use of a classical multi-inputs multi-outputs NN model and a

sequence of different multi-inputs single-output NN models is performed. The proposed approach is tested

on a real application case.

1 INTRODUCTION

Product quality control is became a major issue in

the mass customization context. Different policies,

such as Total Quality Management (TQM) or Just in

Time (JiT), have been developed in order to control

quality. These two policies are related to the Lean

Manufacturing (LM) concept (Vollmann et al.,

1984).

These policies require the use of different tools,

such as the seven basic quality tools (Ishikawa chart,

check sheet, control charts, histogram, Pareto chart,

scatter diagram, stratification) which allow to

control quality a posteriori. This approach leads to

reject or to downgrade a large part of the production

(Thomas et al., 2013).

A first improvement was given by Taguchi

(1989) which proposed to set up the parameters

control in order to avoid the defects production. The

aim of the Optimal Experimental Design (ODE)

proposed by Taguchi is to provide a setting of the

parameters robust to changing conditions. However,

robust setting is generally non optimal when the

actual conditions are considered. Well, for high

quality production, the process works often near the

limits of its capabilities. In this case, non optimal

setting are insufficient to limit the defects production

(Noyel et al., 2013a).

Noyel et al., (2013b) have proposed to exploit

the production data, collected and stored with

traceability goal, in order to perform on-line quality

monitoring. This approach exploits prediction

models able to predict the defect occurrence risk as a

function of the actual operating range and the

product routing.

In order to improve this approach, another

philosophy can be exploited. In the domain of

automatic control, adaptive inverse control is based

on inverse processes identification where the output

of the process becomes the input of the model

(figure 1) (Widrow and Bilello, 1993).

The design of the inverse model is often

performed by using the neural network approach and

this type of control has been applied with success to

the control of many non linear process such as,

synchronous motor (Liu et al., 2013), Maglev

system (Hajimani et al., 2014) and robotic (Yildirim,

2004).

The main idea developed here, is to propose an

on line quality monitoring approach based on

Thomas P., Suhner M., Zimmermann E., Bril El Haouzi H., Thomas A. and Noyel M.

Neural Network Inverse Model for Quality Monitoring - Application to a High Quality Lackering Process.

DOI: 10.5220/0006485901860191

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 186-191

ISBN: 978-989-758-274-5

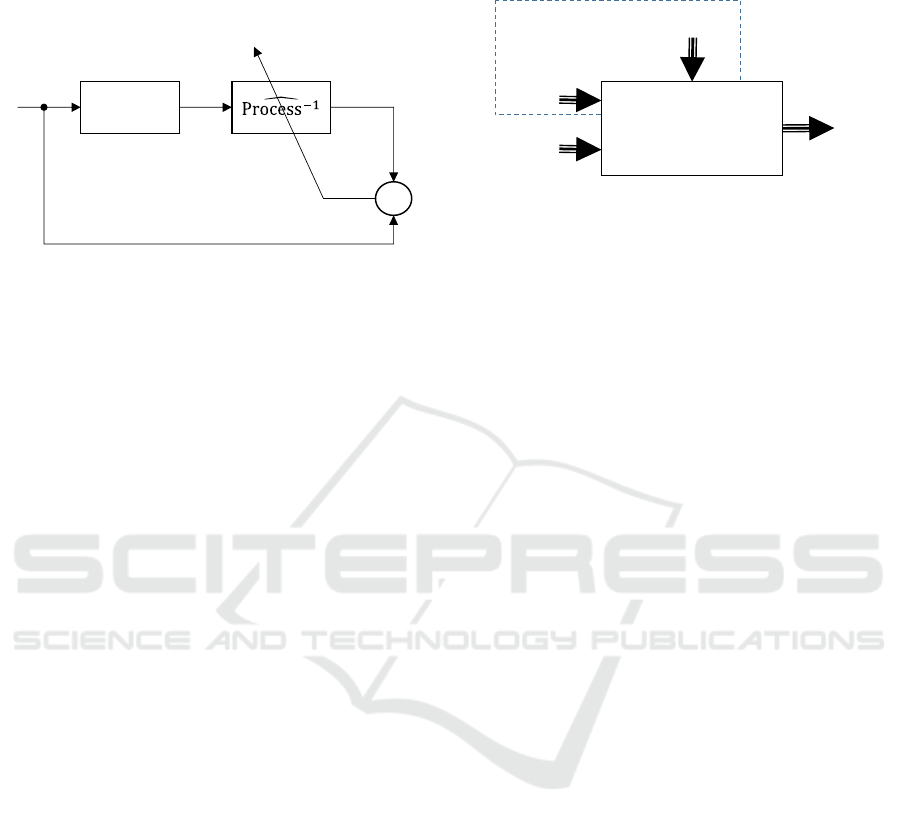
inverse neural model. The goal is to design a model

able to determine the optimal setting from the

tunable parameters, considering the operating point,

the product routing and the defects occurrence risks.

Process



error

input

Figure 1: Inverse identification (Widrow and Bilello,

1993).

The main goal of such approach is to obtain

directly a setting able to avoid defects. Moreover, if

a pruning procedure is performed on the neural

model, some inputs may be removed of the model. If

one or more of these inputs correspond to defect

types, this implies that a subsidiary benefit is to

determine if a tunable parameter has an impact or

not on some defect types occurrence.

First we will recall succinctly the quality

monitoring problem. In a second step, the proposed

procedure will be describe. Two approaches will be

discussed:

 Using of one multi inputs multi outputs (MIMO)

model;

 Using of several multi inputs single output

(MISO) models;

The structure of the neural network and the tools

used will be also presented. After, the industrial

application case and the results obtained will be

presented before to conclude.

2 QUALITY MONITORING

Quality monitoring needs to understand which

factors have an impact on the defects production.

Ishikawa (1986) has proposed the 6M method which

classes these factors into 6 categories: Machine

(technology), Method (process), Material, Man

Power, Measurement (inspection), Milieu

(environment). In the context of on line quality

monitoring which needs to design a prediction

model of the defect, it is more useful to classify

these factors into controllable and non-controllable

factors (Noyel et al., 2013b). The controllable

factors group together the setup parameters when the

non-controllable factors include the operating point

(environmental factors, process constraints…) and

the routing product factors.

Setup

parameters

Environmental

factors

Routing

product

Defects

types

Uncontrollable factors

process

Figure 2: Data collection.

So, in this context, three main types of data must

be collected and stored: controllable and

uncontrollable factors upstream of the process, and

the defects types downstream of the process (figure

2).

Two ways may be used to search the “zero defect”

goal:

 By optimizing the settings of various factors;

 By drifts monitoring and prevention;

The on line quality monitoring philosophy refers to

the first way. The goal is to determine the best

setting of the controllable factors, for each product

or batch (taking into account its routing constraints),

considering the existing conditions (current

operating point) (Thomas et al., 2013).

3 ON LINE QUALITY

MONITORING

The proposed approach is based on the design of a

neural model able to determine the optimal setting of

controllable factors. The neural network used here is

a multilayer perceptron which seems to be perfectly

adapted to our needs because it is an universal

approximator (Cybenko, 1989, Funahashi, 1989).

3.1 Multilayers Perceptron

The classical multilayer perceptron (MLP) is a

feedforward neural network including only one

hidden layer using a sigmoidal activation function

and on output layer using an activation function

which can be linear for regression problem or

sigmoidal for classification problem. Its structure is

given by (for the output k):

2101

1...

kkiihhik

zg wg wxb b

with k n















(1)

where,

are the

outputs and

are the n

inputs

of the neural network,

w are the weights

connecting the input layer to the hidden layer,

are

the biases of the hidden neurons,

(.) is the

activation function of the hidden neurons (here, the

hyperbolic tangent),

are the weights connecting

the hidden neurons to the output

b is the bias of

the output neuron

k, g

(.) is the activation function of

the output neuron. Because of the problem is to

obtain the optimal setting of controllable parameters,

we are faced to a regression problem, so

(.) being

chosen linear.

No normalisation is performed on the dataset.

This fact implies to use an initialisation algorithm

able to take into account the different value ranges

between the inputs (Nguyen and Widrow, 1990).

The dataset is a real industrial dataset polluted

with outliers. So the learning algorithm used must be

robust to these outliers (Thomas et al., 1999). In

order to evaluate the generalization capabilities of

the model, the dataset must be divided into learning

and validation datasets. The learning dataset is used

in order to adapt the parameters of the MLP when

the validation one is used to estimate the

performance of the model.

The accuracy of the neural model depends on the

structure (number of hidden neurons, inputs and

parameters). Too few parameters or hidden neurons,

and the learning can’t find accurate parameters. Too

much parameters, and the learning can lead to the

well-known overfitting problem. To avoid this

problem, the learning is performed on a largely

oversized structure with too much hidden neurons

and a pruning procedure is used to reduce this

structure (Thomas and Suhner, 2015). This

procedure presents the advantage to be able to

discard some spurious inputs.

3.2 Tuning of Controllable Parameters

The main idea is to determine the optimal setting of

the controllable parameters by using MLP model.

This model is designed by using the dataset

constituted by the controllable and uncontrollable

factors collected upstream of the process, and the

defects types collected downstream of the process.

This model is designed under the inverse concept

where the outputs of the model are constituted by

some inputs of the process, when the inputs of the

models includes some inputs of the process and its

outputs (figure 3).

Setup

parameters

Environmental

factors

Routing

product

Defects

types

Uncontrollable factors

NN model

Figure 3: Inverse model design.

To do that, the classical and simplest approach is

to design a multi-inputs multi-outputs (MIMO)

neural network. However, in this case, the pruning

phase don’t allow to determine if a defect type

(input) is related to a particular setup parameter

(output).

To outperform this drawback, another structure

is used, where different multi-inputs single-output

(MISO) neural networks are designed sequentially.

The figure 4 presents an example of such structure,

where 3 setup parameters are considered.

Setup

Parameter 1

Environmental

factors

Routing

product

Defects

types

Uncontrollable factors

NN MISO

model 1

NN MISO

model 2

Setup

Parameter 2

NN MISO

model 3

Setup

Parameter 3

Figure 4: Sequential MISO NN models (case of 3 setup parameters).

Considering this structure, four advantages can

be listed:

 Each NN model includes less parameters (only

one output, possibly less hidden neurons,

possibly more inputs pruned). This fact improves

the learning and using speeds and limits the

overfitting risk.

 The learning of each NN model is independent.

This fact implies that the learning of these

different model may be performed in parallel.

 The pruning step allows to pruned inputs in each

NN model. This fact implies that a causal link

may be discarded between some defect types

(pruned inputs) and the considered setup

parameter.

 Each NN model may use, as inputs, the outputs

(setup parameters) of the upstream NN models in

the sequential structure. This fact allows to

improve the global accuracy of the structure.

The sequence of the different MISO NN models

selected is the one which optimize the accuracy of

the complete structure on the validation dataset.

In the sequel, the performances of the proposed

structure will be tested and compared with those

obtained with a single MIMO model on a real

industrial case.

4 INDUSTRIAL APPLICATION

4.1 Presentation of the Process

The considered problem is a quality monitoring

problem in a company which produces high quality

lacquered panels made in MDF (Medium Density

Fibreboard) for kitchen, bathroom, offices, hotel

furniture, stands, shops... This study focuses on its

main process which is a robotic lacquering

workstation. This workstation is free of human

factors, but defects rates are important and very

fluctuant, and could expand from 10% to 45% from

one day to another. This fact is mainly due to the

high quality requirements, which implies that this

workstation works at its limit capabilities. So,

despite the design of an ODE in order to tune this

robotic workstation, the company fails to reduce the

defects rates.

That’s why an on line quality monitoring

approach is performed. Expert knowledge has

allowed to list parameters able to have impact on the

defects generations. These parameters can be

classified into:

 Three environmental factors (temperature,

humidity, pressure).

 Five product routing parameters (number of

passes, time per table, litre per table, number of

layers, drying time)

 Three setup parameters (load factor, basis

weight, number of products).

These different factors and parameters are able to

have an impact on thirty different defects types.

Considering the inverse model structure, the

dataset is constituted by three outputs (setup

parameters) and thirty eight inputs (environmental

factors, product routing parameters, and types of

defects). The dataset includes 2167 data and is split

into two datasets for identification (1088 data) and

validation (1079).

In order to limit the risk of local optimum

trapping, the learning of all the NN models is

performed with twenty initial parameters sets and

the best one is retained.

The selection criterion used is the classical Root

Mean Square Error (RMSE) calculated on the

learning and validation datasets:



() ()

RMSE z n y n







(2)

where

z(n) is the output given by the network for the

data n and y(n) is the corresponding target.

The first NN model designed is the MIMO one.

The initial number of hidden neuron is set to twenty.

Table 1 presents the RMSE values obtained with the

best MIMO model for the three different outputs.

These values highlight the difference between the

variation ranges and amplitudes of the outputs. This

fact may have an impact on the learning accuracy.

During the learning, the criterion to minimize is the

errors sum squared performed on the three outputs.

In this case, the risk is that the learning algorithm

favours one output over the others.

Table 1: RMSE values for the MIMO NN model.

learning validation

load factor 0.4057 0.4406

basis weight 191.8222 238.2346

products number 307.3382 381.0269

The results obtained with the MIMO model must

be compared to those obtained with the sequence of

MISO models.

To design the sequence of MISO models, it is

necessary to determine in which order the setup

parameters must be considered. The selected order is

the one which maximize the sequence accuracy.

Table 2: RMSE values for the different MISO NN models.

MISO model

load facto

asis wei

roducts number

asis wei

ht load facto

load facto

products number products number basis weight

learnin

0.3698 0.3509 0.2339 0.2381

validation 0.4336 0.4466 0.2856 0.2805

learning 177.3311 185.1477 182.785 178.9352

validation 230.4716 226.6402 224.0547 228.0947

learning 297.5479 223.1687 365.6229 218.7272

validation 361.2214 264.4579 369.2758 256.713

MISO model

supplementary

uts

Load factor

basis weight

products number

MISO model

Different MISO NN models must be designed

with different structures. For all these models the

initial number of hidden nodes is setup to twenty.

The inputs number depends of the order of the

sequence. The first MISO model must determine its

output by using the same thirty eight inputs of the

MIMO model. The second one shall have one

additional input (the output of the first MISO

model). The third one shall have two additional

inputs (the outputs of the two preceding MISO

models).

The table 2 presents the RMSE values obtained

for the learning and the validation datasets for the

different MISO NN models designed. The first line

indicates if the considered model is the first, the

second or the third of the sequence. The second line

indicates which the supplementary inputs if

available are.

First, it can be noticed that the use of one or two

supplementary inputs improve the accuracy for the

three outputs. As example, the RMSE value for the

validation dataset for load factor is reduced with a

reduction from 0.4336 to 0.2856 (34%

improvement) when product number is used as

supplementary input. The same observation may be

performed for the two other outputs.

So it is necessary to determine the optimal

sequence of MISO models. To do that, the decrease

in terms of percent of RMSE (compared with the

results obtained with the MIMO model) is studied

and the sequence which minimizes the sum of the

three “RMSE decreased in terms of percent” values

for the three outputs (on the validation dataset) is

selected. With this criterion, two sequences gives

very similar results:

 First: products number (5%); second: basis

weight (6%); third: load factor (36%).

 First: products number (5%); second: load factor

(35%); third: basis weight (4%).

For the sequel, we choose arbitrarily the first

sequence and the results obtained for the three

MISO models of the sequence are highlighted in

table 2. This is these results which must be

compared to those obtained with the MIMO models

presented table 1. These results show a slight

improvement for two outputs (5% for products

number and 6% for basis weight) which is not very

significant. However, the improvement obtained for

the third output (load factor) is relevant and reaches

36%.

It can be noticed that the choice of the sequence

is important to obtain the best results, but all

sequences allows to improve substantially the results

compared to those obtained with the MIMO model.

In our case, the worst sequence is:

 First: load factor (2%);

 Second: products number (4%);

 Third: basis weight (31%).

The choice of the sequence may also be performed

by using expert knowledge.

The three selected MISO models have been

pruned in order to find the optimal structure of the

model and to limit the overfitting risk. A second

advantage is, that it allows to determine if a causal

link occurs between the considered setup parameter

(output) and the defects types (some of the inputs).

For the setup parameter “products number” the

pruning algorithm has preserved only one defect

type: “grain on face”. This fact implies that the

optimal tuning of this parameter has no impact on

the twenty nine other defects types.

For the second setup parameter: “basis weight”,

only three defects types are discarded: “grain on

back”, “scratch” and “sanding defect”. So, the

optimal setting of this parameter may have an

impact on the twenty seven other defects types.

For the third setup parameter: “load factor”,

seven defects types are discarded: “grain on back”,

“stain under the paint”; “scratch”, “paint refusal”;

“priming defect”, “sanding defect”, “silicone mark”.

It can be noticed that some types of defects are

impacted by none of the setup parameters: “grain on

back”, “scratch” and “sanding defect”. This is due to

the fact that these types of defects don’t find their

origin in the considered workstation. Scratch defects

are mainly caused by handling problem. Sanding

defect are certainly produced during the preceding

sanding step. Grain on back are performed during a

preceding step of lacquering.

It can be noticed that some defects types which

probably don’t find their origin in the considered

workstation are not pruned in the second MISO

model: “priming defect” or “silicone mark”. This

fact is probably due to the pruning algorithm

accuracy.

5 CONCLUSIONS

An on line quality monitoring approach based on

neural network models is proposed here. The main

goal of this proposed approach is to determine

quickly and simply the optimal tuning of setup

parameters considering the actual operating point

and the product routing. This quality monitoring is

based on inverse approach NN models which try to

determine the tuning of setup parameters by using

both, non controllable parameters collected upstream

of the workstation, and quality defects occurrence

collected downstream of the workstation.

Two approaches may be used to perform the

design of the inverse model. The simplest is to use a

multi-inputs multi-outputs model able to set up all

the controllable parameters simultaneously. The

second one is to use a sequence of different multi-

inputs single-output models able each to set up only

one parameter. These two approaches are tested and

compared. The results have shown that the second

approach allows to improve the accuracy of the

complete system.

Moreover, the using of a pruning algorithm next

the learning allows to determine if a causal link

occurs between some defects types and the

considered setup parameter.

In some extreme environmental conditions, it is

possible that none setup is able to avoid defects

production for certain product routing. In this case,

one drawback of the proposed approach is that our

system will give a setup, possibly the best one, but

which will be insufficient. Our future works will

focus on the detection of these particular conditions

in order to be able to propose to the operator to delay

the machining of the considered products.

REFERENCES

Cybenko, G., 1989. Approximation by superposition of a

sigmoïdal function. Math. Control Systems Signals, 2,

4, 303-314.

Hajimani, M., Dashti, Z.A.S., Gholami, M., Jafari, M.,

Shoorehdeli, M.A., 2014. Neural adaptive controller

for magnetic levitation system, Iranian Conf. on

Intelligent Systems ICIS’14, Bam, Iran.

Ishikawa, K., 1986. Guide to quality control. Asian

Productivity Organization.

Liu, G.,Chen, L., Zhao, W., Jiang, Y., Qu, L., 2013.

Internal Model control of permanent Magnet

synchronous motor using support vector machine

generalized inverse, IEEE Trans. on Industrial

Informatics, 9, 2, 890-898.

Nguyen, D., Widrow, B., 1990. Improving the learning

speed of 2-layer neural networks by choosing initial

values of the adaptative weights. Proc. of the Int. Joint

Conference on Neural Networks IJCNN'90, 3, 21-26.

Noyel, M., Thomas, P., Charpentier, P., Thomas, A.,

Brault, T., 2013a. Implantation of an on-line quality

process monitoring. 5

Int. Conf. on Industrial

Engineering and Systems Management IESM'13a,

Rabat, Maroc.

Noyel, M., Thomas, P., Charpentier, P., Thomas, A.,

Beauprêtre, B., 2013b. Improving production process

performance thanks to neuronal analysis. 11

IFAC

Workshop on Intelligent Manufacturing Systems

IMS'13, Sao Paulo, Brazil.

Taguchi, G., 1989. Quality enginnering in production

systems, NY, MacGraw-Hill.

Thomas, P., Bloch, G., Sirou, F., Eustache, V., 1999.

Neural modeling of an induction furnace using robust

learning criteria. J. of Integrated Computer Aided

Engineering, 6, 1, 5-23.

Thomas, P., Noyel, M., Suhner, M.C., Charpentier, P. and

Thomas, A., 2013. Neural Networks ensemble for

quality monitoring, 5

Int. Joint Conf. on

Computational Intelligence IJCCI'13, Vilamoura,

Portugal, 515-522.

Thomas, P., Suhner, M.C., 2015. A new multilayer

perceptron pruning algorithm for classification and

regression applications. Neural Processing Letters, 42,

2, 437-458

Vollmann, T.E., Berry, W.L. and Whybark, C.D., 1984.

Manufacturing Planning and Control Systems, Dow

Jones-Irwin.

Widrow, B., Bilello, M., 1993. Adaptive inverse control,

Proc. of the Int. Symp. on Intelligent Control, Chicago,

Illinois, USA.

Yildirim, S., 2004. Adaptive robust neural controller for

robots. Robotics and Autonomous Systems, 46, 3, 175-

184.