A Novel Influence Diffusion Model based on User Generated Content
in Online Social Networks
Flora Amato, Antonio Bosco, Vincenzo Moscato, Antonio Picariello and Giancarlo Sperl
´
ı
University of Naples “Federico II”, Via Claudio 21, 80125 Naples, Italy
CINI - ITEM National Lab, Complesso Universitario Monte Santangelo, 80125, Naples, Italy
Keywords:
Multimedia Social Network, Influence Analysis, Big Data.
Abstract:
Social Network Analysis has been introduced to study the properties of Online Social Networks for a wide
range of real life applications. In this paper, we propose a novel methodology for solving the Influence Maxi-
mization problem, i.e. the problem of finding a small subset of actors in a social network that could maximize
the spread of influence. In particular, we define a novel influence diffusion model that, learning recurrent user
behaviours from past logs, estimates the probability that a given user can influence the other ones, basically
exploiting user to content actions. A greedy maximization algorithm is then adopted to determine the final set
of influentials in the network. Preliminary experimental results shows the goodness of the proposed approach,
especially in terms of efficiency, and encourage future research in such direction.
1 INTRODUCTION
The growing popularity of Online Social Networks
(OSN), and in particular, their huge amount of data
lay the foundations for analyzing several sociological
phenomena useful for a large number of applications.
From a technological point of view, OSNs are en-
abled as Internet applications that provide a set of
common functionalities, such as: i) information shar-
ing capabilities, ii) user generated content manage-
ment and iii) support by means of several tools to
different ways of communication and collaboration
among users. Thus, OSN can be seen as a digital plat-
form that “lives” on the Web and which content and
services are delivered to final users through a variety
of technological devices.
From a sociological perspective, OSNs are social
structures constituted by a set actors (individuals or
organizations), sets of dyadic ties, and other social in-
teractions, often instantiated through the shared infor-
mation, among actors themselves. In this case, math-
ematical models can be adopted to study the social
network structure, the related generated content and
its temporal evolution.
The most natural and simple way to model an
OSN is to use a directed graph composed by a set of
nodes/vertices – representing the individual actors of
a social community – and a set of edges – represent-
ing the different kinds of relationships among actors,
in many cases instantiated through the user generated
content.
Social Network Analysis (SNA) (Scott, 2012) has
been introduced to study the properties of OSNs with
the aim of supporting a wide range of applications: in-
formation retrieval, influence analysis, recommenda-
tion, viral marketing, event recognition, expert find-
ing, community detection, user profiling, security and
social data privacy and so on.
Many OSNs are extremely rich in information,
and they typically contain a tremendous amount of
content and linkage data which can be jointly ex-
ploited for analysis. The linkage data is essentially the
graph structure of the social network and the commu-
nications between entities; whereas the content data
contains the text, images and other type of content in
the network
The majority of SNA techniques mainly exploit
“user to user” interactions, leveraging the graph the-
ory as powerful tool to support the different kinds of
analytics.
More recently, in according to a data-centric view
of OSN, also “user to content”’ relationships have
been considered together with content features to pro-
vide more advanced forms of analysis.
Generally, the SNA techniques can be inspired by
two different approaches (Aggarwal, 2011):
• Linkage-based and Structural Analysis: an analy-
314
Amato, F., Bosco, A., Moscato, V., Picariello, A. and Sperlí, G.
A Novel Influence Diffusion Model based on User Generated Content in Online Social Networks.
DOI: 10.5220/0006486703140320
In Proceedings of the 6th International Conference on Data Science, Technology and Applications (DATA 2017), pages 314-320
ISBN: 978-989-758-255-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sis of the linkage behavior of the network is per-
formed in order to determine important nodes,
communities, links, and evolving regions of the
network.
• Content-based Analysis: Many social networks,
such as Flick and Youtube, contain a tremendous
amount of content (multimedia and tags) which
can be leveraged to improve the analysis.
In this paper, we propose an hybrid SNA method-
ology to determine the most influential actors (influ-
entials) wihin an OSN. In particular, we define a novel
influence diffusion model that learns recurrent user
behaviours from past logs to estimate probability that
a given user can influence the other ones, basically ex-
ploiting user to content actions. Then, a greedy max-
imization algorithm is adopted to determine the final
set of influentials.
The paper is organized as in the following. Sec-
tion 2 introduces the theoretical background for our
work. Section 3 presents a novel influence diffusion
model for OSNs and some properties related to it,
useful for defining the influence graph. Section 4 de-
scribes the adopted greedy algorithm for the influence
maximization based on the influence graph. Finally
several experiments are discussed in Section 5, while
related works and conclusion are reported in Sections
6 and 7 respectively.
2 THEORETICAL BACKGROUND
As prevously described, in a social network links
among nodes usually represent a variety of relation-
ships, from intimate friendships to common inter-
ests for a multimedia object (e.g., tweet, post, video,
photo, etc.): they determine a “flow” of information
and hence indicate a user’s influence on the others,
a concept that is crucial in sociology and viral mar-
keting. As well known, studying influence patterns
can help us better understand why certain trends or in-
novations are adopted faster than others and how we
could help advertisers and marketers design more ef-
fective campaigns.
Traditional communication theories state that a
minority of users, called influentials, excel in per-
suading others; a more modern view, in contrast, de-
emphasizes the role of influential and posits that the
key factors determining influence are the different
kinds of relationship among ordinary users and the
readiness of a society to adopt an innovation (Watts
and Dodds, 2007).
Moving from theory into practice, an influence
analysis problem can be faced using two steps.
In the first one, a diffusion model is defined with
the aim of describing the influence spread in the
network; this phenomenon is usually modeled by a
stochastic process where the activation of each node
is based on its neighbours state. In the second step,
a maximization algorithm is exploited to identify the
set of nodes such that their activations maximize the
diffusion or the propagation of influence.
The selection of the most influence nodes is an op-
timization problem that has been proven by Kempe et
al.(Kempe et al., 2003) to be NP-Hard. In particular,
chosen S as the initial active seed-set, Kempe et al.
defined its influence σ(S) as the total number of acti-
vated nodes in the network at the end of the diffusion
process.
The influence function σ(S) maps subsets of ele-
ments of a finite set to a non-negative number. The
final goal is to find a k-element seed set S that maxi-
mizes σ(S), which is a NP-Hard problem. To address
this complexity, several greedy strategies exploiting
a non-negative, submodular and monotone influence
function have been proposed to obtain a solution that
is no worse than (1 −1/e) of the optimal one.
In this paper, we model influence and the related
spread in a novel way, as depicted in the following.
Let Giank and Boscus be two users of a OSN. Evi-
dence suggests that user Giank influences Boscus if an
action of Giank at time t causes one or more actions of
Boscus at time t
0
> t. As an example considering user
to content actions, if Giank publishes a certain photo
at t his influence on Boscus can be proved by the fact
that at time t
1
> t, Boscus puts a “like” on the picture,
and that at time t
2
> t
1
> t he publishes an audio that
is semantically similar to the Giank’s photo. In addi-
tion, the more the two multimedia objects are similar,
the more user Giank has influenced user Boscus.
Assuming the same hypothesis of Kempe, we will
define a maximization algorithm based on this novel
influence model.
3 THE INFLUENCE MODEL
The basic assumption in our model is the existence of
a finite set of Actions (A) representing all the possible
“interactions” among the set of Users (U) and the set
of Objects (O) in one ore more online social networks,
which can be properly captured during user browsing
sessions exploiting log information (Sang et al., 2015;
Guo et al., 2016).
In particular, we denote with A
u
(t) the set of ac-
tions performed by a given user u ∈ U in a specific in-
stance of time t. Similarly, we indicate with A
u
(t,∆t)
the set of actions of u within the interval ]t,..., ∆t].
A Novel Influence Diffusion Model based on User Generated Content in Online Social Networks
315

In such a context, we can consider different ex-
amples of actions: users’ reactions or comments to
user generated content (e.g., post, pictures and so on),
post visualization or rating, for giving few examples.
Table 1 summarizes the available user-to-content re-
lationships in the most diffused social networks.
In the following, we will describe the foundamen-
tal aspects of the proposed influence model.
Definition 3.1 (Log tuple). A log tuple can be de-
fined by the information l = (a,u,o, λ
1
,·· · ,λ
k
), where
a ∈ A, u ∈ U, o ∈ O and λ
1
,·· · ,λ
k
, are particular
attributes (e.g., timestamp, type of reaction, text and
tags of a comment, etc.) used to describe an action.
Definition 3.2 (Log). A Log (L) is a finite sequence
of log tuples.
Intuitively, a log tuple corresponds to an observa-
tion of l.a performed by the user l.u on a given object
l.o along with the associated attributes of the obser-
vation λ
1
,·· · ,λ
k
. By convention, if action a
2
occurs
after a
1
in a log, then the action a
2
occurred tempo-
rally after a
1
.
Using information on past logs, we can introduce
a reaction operator between two actions .
Definition 3.3 (Reaction Operator). The Reaction
Operator reac
∆t
(a
1
,a
2
) between two actions a
1
of
user u
i
and a
2
of user u
j
– and both the actions are
performed on the same object o (or on similar ob-
jects
1
) – returns the probability that a
2
occurs after
a
1
within the interval ∆t.
It is simple to observe that the following property
stands for the reaction operator:
reac
∆t
(a
1
,a
2
) ≥ τ
1
∧ reac
∆t
(a
2
,a
3
) ≥ τ
2
→ reac
∆t
(a
1
,a
3
) ≥ τ
3
τ
3
= f (τ
1
,τ
2
)
f being a function whose value is less then
min(τ
1
,τ
2
).
Example 3.1 (Log and reaction operator). Consider
a log, obtained from Flickr, whose associated se-
quence of actions is:
h publishing, vinni, photo1,10/05/2017 13:30, ‘sunset’ i,
h like, flora, photo1,10/05/2017 13:31 i,
h comment, flora, photo1,10/05/2017 13:32, ‘wonderful’ i,
h publishing, picus, photo2,10/05/2017 13:38, ‘sunset’ i,
h like, giank, photo2,10/05/2017 13:40 i,
h like, boscus, photo2,10/05/2017 13:42, i,
h comment, vinni, photo2,10/05/2017 13:45,‘’you too..’ i
h like, boscus, photo1,10/05/2017 13:47 i
1
The evaluation of such condition needs the defiinition
of a similarity function between two objects.
It is simple to observe that considering ∆t =2 minutes
the reaction operator returns a probability value of
1 for the couple of actions (publishing,like). In turn,
the probability value is 0.5 for the couple of actions
(publishing,comment) and 0.33 for (like,like). If we
consider a more wide temporal interval and assume
the images published by picus and vinni very similar,
the reaction operator will return a probaility value of
0.5 for the couple of actions (publishing,publshing) .
Definition 3.4 (Influence Operator). Let u
1
,u
2
∈ U be
respectively two users, we say that u
1
→
τ
u
2
, if each
action a
u
1
∈ A
u
1
(t) of user u
1
at time t determines
an action a
u
2
∈ A
u
2
(t, ∆t) of user u
2
in the interval
]t, ..., ∆t] within a log L:
u
1
→
τ
u
2
⇐⇒ ∀t
i
∈ T ∃a
1
∈ A
u
1
(t
i
),a
2
∈ A
u
2
(t
i
,∆t) ∈
L : reac
∆t
(a
1
,a
2
) ≥ τ
T = {t
1
,t
2
,.. .,t
m
} being a sequence of temporal in-
stants such that t
1
< t
2
< . ..t
m
and τ ∈ [0,1] a proba-
bility value.
The influence operator estimates the influence
that user u
1
exerts on u
2
within the time t + ∆t.
Example 3.2 (Log and influence operator). Consid-
ering the log of Example 3.1 as past log (it can be
used for the learning of reaction operator) and as
current log the following sequence of actions:
h publishing, vinni, photo1,11/05/2017 19:30, ‘california’ i,
h like, flora, photo1,10/05/2017 19:31 i,
h like, boscus, photo1,10/05/2017 19:32 i
h comment, flora, photo1,10/05/2017 19:32, ‘wow!!!!!!l’ i,
h publishing, picus, photo2,10/05/2017 19:58, ‘hollywood’ i,
h like, giank, photo2,10/05/2017 19:59 i,
h like, boscus, photo2,10/05/2017 19:59 i
It is simple to observe that considering ∆t =2
minutes we say that user vinni certainly influences
flora and bosco and user picus certainly influences
giank and boscus.
3.1 Properties and Theorem
We assume that the following properties stand for the
influence operator:
Property 3.1 (Not Self Reflexivity). u
1
9
τ
u
1
Property 3.2 (Not Commutativity). u
1
→
τ
u
2
; u
2
→
τ
u
1
Property 3.3 (Not Transitivity). u
1
→
τ
u
2
∧ u
2
→
τ
u
3
; u
1
→
τ
u
3
KomIS 2017 - Special Session on Knowledge Discovery meets Information Systems: Applications of Big Data Analytics and BI -
methodologies, techniques and tools
316

Table 1: User-to-Content relationships in Online Social Networks.
Twitter Facebook Instagram Google+ Last.FM Flickr
Publishing X X X X X X
Tagging X X X X X X
Comment X X X X X X
Like X X X X X
Resharing X X X
Favorites X X X
Visualization X X X X
Theorem 3.1 (Influence Diffusion). Let u
1
,u
2
and u
3
three users and L a given log,



u
1
→
τ
1
u
2
u
2
→
τ
2
u
3
⇒ u
1
→
τ
3
u
3
(1)
τ
3
≤ min(τ
1
,τ
2
).
Proof. Let us consider the definition of influence op-
erator and the property of reaction operator; we ob-
serve that, for the theorem hypothesis, there will al-
ways exist the two actions a
u
1
∈ A
u
1
(t) and a
u
3
∈
A
u
3
(t : ∆t
‘
) and the reaction operator will always
return for the couple (a
1
,a
3
) a probability τ
3
≤
min(τ
1
,τ
2
).
3.2 Influence Graph
Definition 3.5 (Influence Graph). An Influence Graph
is a labeled graph G = (V,E,τ) where:
• V is the set of nodes such that each v ∈ V corre-
sponds to a user u ∈ U ;
• E ⊆ V ×V is the set of edge (with no self-loops);
• τ : V ×V → [0,1] is a function that assigns to each
edge e = (v
i
,v
j
) a label, representing the proba-
bility that user u
i
can influece user u
j
.
Example 3.3 (Example of Influence Graph). In the
Figure 1, we show how from the log of Example 3.2 it
is possible to derive an influence graph on the base of
defined influence and reaction operators.
Figure 1: Influence Graph.
Definition 3.6 (Direct Influence). Let G = (V,E, τ)
and u
i
,u
j
be respectively an influence graph and two
users, we say that user u
i
directly influences u
j
if there
exists an edge that connects u
i
to u
j
.
Definition 3.7 (Indirect Influence). Let G = (V,E,τ)
and u
i
,u
j
be respectively an influence graph and
two users, we say that user u
i
indirectly influ-
ences u
j
if there exists a path p = (e
1
,.. .,e
n
), with
e
1
,e
2
,.. .,e
n
∈ E that connects u
i
to u
j
.
4 τ-greedy ALGORITHM
In this section we describe the proposed approach for
influence maximization problem exploiting the influ-
ence graph.
To better explain our idea, we firstly analyze the
chosen model to design the spread of influence over
the network. We assume that each node of the graph
could be either an active node or inactive node. Then,
we choose a Linear Threshold (LT) model (Kempe
et al., 2003) for describing the influence spread be-
cause of it represents in very effective way the typical
behavior of a user that is led to adopt a new idea or
technology as more of his friends become active.
For this reason, we define a reactive threshold for
each node describing the weighted percentage of its
neighbors needed to led a specific user to adopt a
given idea. This value corresponds to a lower bound
for activating each node and is computed consider-
ing her/his behavior respect to the action performed
by the community of users. More in details, given a
specific interval of analysis ]t, ...,∆t], we compute for
each user u the reactive threshold θ(u, ∆t) on the ba-
sis of the ratio between the average number of actions
of u in any interval
ˆ
A
u
(t, ∆t) and the maximum num-
ber of actions that it is possible to observe in the log
within the same interval:
θ(u,∆t) = 1 −
ˆ
A
u
(t, ∆t)
max
t
(A(t,∆t))
(2)
Our idea is to leverage the greedy strategy pro-
posed by Kempe et al.(Kempe et al., 2003), taking
into account the τ value in the influence function to-
gether with the reactive threshold, that corresponds to
the probability that a user is activated based on a spe-
cific weighted amount of its neighbor.
Thus, we provide the following definition of influ-
ence function.
A Novel Influence Diffusion Model based on User Generated Content in Online Social Networks
317

Definition 4.1 (Influence function). Let G = (V,E)
be an influence graph, S a set of seed nodes and δ(v)
a function that returns true if node v is actived, we
define influence function:
σ
τ
(S) =
∑
v∈(V −S)
∑
u∈S
τ
uv
∗ δ(v)
Our approach, called τ - Greedy (see Algorithm
1), provides in addition an a-priori pruning strategy
based on τ values to reduce the space and time com-
plexity of the problem. In particular, given a user de-
fined threshold, we analyze the spread of influence
through direct or indirect paths that allows to obtain
an overall influence values greater than τ
s
.
Algorithm 1: τ - Greedy Algorithm.
1: procedure τ - GREEDY ALGORITHM(G,τ
s
)
2: S ← 0
3: for i ← 1,k do
4: j ← argmax
v∈V
(σ
τ
(S ∪ v) − σ
τ
(S))
5: S ← S ∪ { j}
6: return S
5 EXPERIMENTS
The experiments were performed using Databricks
2
,
a cloud-based big data processing environment based
on Spark, using 5 computing nodes each one com-
posed by 4 core and 30 GB Memory, on which are
installed Spark 2.1.0 and Hadoop 2.7.3. Experiments
for efficiency evaluation have been carried on the
Yahoo Flickr Creative Commons 100 Million Data
(YFCC100M)
3
dataset. Using the Flickr API
4
we ex-
tract the main social information and the different ac-
tions that compose a log. Table 2 provides the char-
acterization of the dataset.
Table 2: Dataset characterization.
Log Influence Graph
Social elements Nodes Edges
17.493 1.264 4.686
Then, we performed a comparison of the execu-
tion times using the proposed Influence Graph, with
respect to other influence diffusion models.
In particular, we computed the running times of
τ-greedy algorithm on our proposed Influence Graph
and compared them with the same approach based on
another graph. We built the second graph by instan-
tiating a direct edge between two node u
i
and u
j
if
2
https://www.databricks.com/
3
https://webscope.sandbox.yahoo.com
4
https://www.flickr.com/services/api
(a) Running Times varying seed set
(b) Running Times varying τ
s
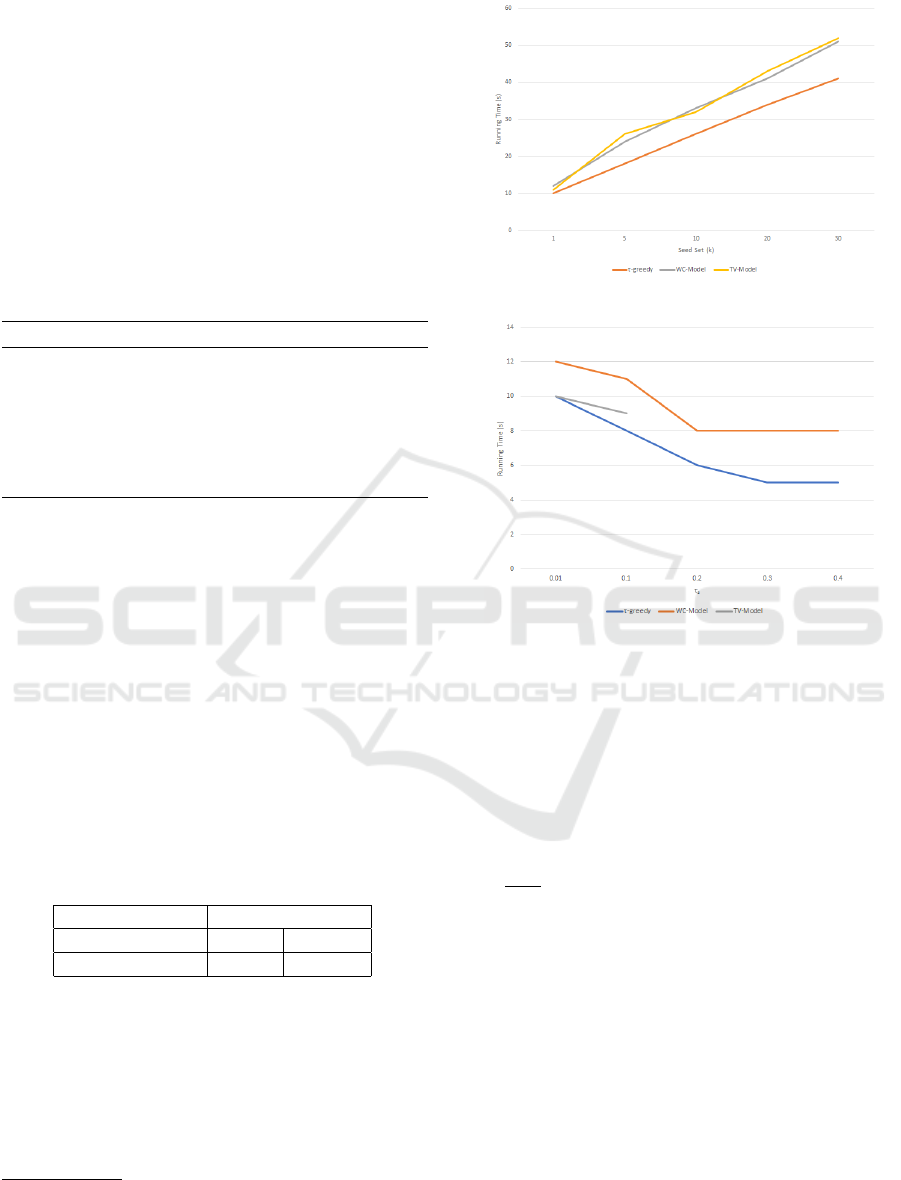
Figure 2: Efficiency of the τ-greedy algorithm using differ-
ent influence diffusion models.
there is an action in the log from the first user to the
second one (both performed on the same object within
a given temporal interval), and we assign a weight to
it using the two following methods:
• Weighted Cascade Model: in which the probabil-
ity of in-coming edges for a vertex v is equal to
1
d
in
(v)
, d
in
(v) being the in-degree of v.
• Trivalency Model: in which each edge weight is a
random probability chosen from the three values:
0.1, 0.01, 0.001.
In Figure 2, we show the running times varying
the number of seed set elements and using different
values of τ
s
. Note that in Figure 2(b) the TV-Model
results are limited to the interval [0.01,0.1] due to the
considered influence probability.
6 RELATED WORK
In the last decade, the huge amount of heterogeneous
data that can be extracted from social networks (such
KomIS 2017 - Special Session on Knowledge Discovery meets Information Systems: Applications of Big Data Analytics and BI -
methodologies, techniques and tools
318

as Facebook, Twitter, Flickr and so on) led to a con-
tinuous growth of interest in the use of such networks
for a large variety of applications.
Deciding whether to adopt an innovation (such
as a political idea or product), individuals are fre-
quently influenced, explicitly or implicitly, by their
social contacts. Indeed, the way in which new prac-
tices spread through a population depends mainly on
the fact that people influence each others behaviour. It
is essential for companies to target “opinion leaders”,
as influencing them will lead to a large cascade of fur-
ther recommendations. This is the goal of each viral
marketing and social advertisement campaigns, and
corresponds in solving an influence analysis problem.
The influence analysis is composed by the follow-
ing two aspects:
• Influence Spread/Diffusion: it consists of the anal-
ysis of the influence spread throughout the social
network nodes;
• Influence Maximization: this means finding the
seed set of users that maximize the total number
of influenced users over the network.
6.1 Diffusion Models
A social network can be considered as a directed
graph G = (V,E), where V is the set of vertices/nodes
and E is the set of edges. To design an influence al-
gorithm we have to define a diffusion model that de-
scribes how the influence is propagated across the net-
work nodes.
The diffusion models can be classified into differ-
ent categories:
• Stochastic diffusion models: they exploit a ran-
domized process for computing the influence
spread. The most used models are the Indepen-
dent Cascade (IC) and the Linear Threshold (LT)
(Kempe et al., 2003) models. In the IC model, at
each step an active node makes an attempt to ac-
tivate its neighbours in according to a Bernoulli
trial. The problem of this model is that a node can
be influenced only by another one. The LT model
is proposed to overcome this problem where each
node could be activated if the sum of the influence
weights of its active neighbours is greater than its
activation threshold.
• Epidemic diffusion models: these approaches con-
sider the influence diffusion as the spread of a
disease among biological individuals of a popu-
lation (Wallinga and Teunis, 2004; Rodriguez and
Sch
¨
olkopf, 2012). A node can be: susceptible (the
node does not have the disease but upon a contact
it will be infected), infected (when it has been in-
fected and thus influenced) or recovered, (when it
was infected in the past and now it cannot be in-
fected). In particular, several models have been
proposed, and they differ for the chance that a
node has to return susceptible or not, after an in-
fection.
• Percolation theory: the influence diffusion prob-
lem can be studied as a bond percolation from the
nodes that belong to the seed-set (Li et al., 2015).
This model does not stand for finding the expect-
ing number of active nodes given a seed-set or de-
termining the best k size seed-set that maximizes
influence spread.
6.2 Influence Maximization
The Influence maximization problem try to identify
the top-k nodes that allow to maximize the spread
of influence in an OSN. Kempe et al.(Kempe et al.,
2003) proved the NP-Hardness of this problem. The
proposed approaches can be classified in four groups:
• Stochastic approaches: they leverage a random-
ized process for generating the active set of nodes
S for each instance of time, from the initial
seed sets. To address the complexity of prob-
lem, greedy algorithms can be used to find an
approximation of the optimal solution with re-
spect to the stochastic diffusion model. Kempe
et al.(Kempe et al., 2003) developed a greedy al-
gorithm that provides an approximation guarantee
of σ(S) ≥ (1 − 1/e) · σ(S
∗
), assuming that the in-
fluence function σ is a monotone and sub-modular
function, where S
∗
is the seed-set that maximizes
the value of σ and S is the initial seed set. The ba-
sic algorithms in this category are the Kempe et al.
approach based on Monte-Carlo approximation,
TIM/T IM
+
(Tang et al., 2015) and IMM (Tang
et al., 2015). These algorithms use a martingale
approach and are based on RIS algorithm (Borgs
et al., 2014). The fastest one is IMM that outper-
forms TIM/T IM
+
and Kempe et al.’s approaches.
• Biological Inspired approaches: in this category
there are the algorithms inspired by some bio-
logical phenomena. Two of main approaches are
those inspired by the bee waggle-dance when they
search food (Karaboga and Basturk, 2007), and by
ant colony optimization (Yang et al., 2012; Yang
et al., 2016).
• Game Theory approaches: they consider the in-
fluence maximization problem as model where
each individual can make a selfish choice in terms
of payoff in using a new product. One of the
A Novel Influence Diffusion Model based on User Generated Content in Online Social Networks
319

main approach of this category is the Multi-Armed
Bandit (MAB) theory (?): it leverages a classical
probability model where a player has to choose
one of a set of arms at each round. Each arm gives
a reward to the player, based on some stochastic
functions. The player has to choose the best set of
arms to maximize the total reward.
• Genetic algorithms based approaches: It is pos-
sible to find a solution to influence maximization
problem in feasible time using genetic algorithm.
Promising approaches are the evolutionary algo-
rithms (Bucur and Iacca, 2016). Here, individuals
evolve during time and can be in several states: se-
lection,reproduction,mutation and recombination.
This is inspired by the natural selection of the
species and can overcome the drawback of the
searching for a local maximum of the greedy ap-
proach. Such approach is non deterministic but it
has results even better compared to deterministic
algorithms like greedy ones.
Differently from the other works, in this paper we
have provided novel stochastic diffusion model and
we have exploited a simple greedy algorithm to max-
imize the influence spread in the network.
7 DISCUSSION AND
CONCLUSIONS
In this paper, we defined a novel influence diffusion
model that learns recurrent user behaviours from past
logs to estimate probability that a given user can influ-
ence the other ones, basically exploiting user to con-
tent actions. Then, a greedy maximization algorithm
is adopted to determine the final set of influentials.
We reported some preliminary experimental results
that show the goodness of the proposed approach.
Future work will be devoted to improve the diffu-
sion models defining other properties that can allow to
optimize the calculus of the influentials. In addition,
we are planning to extend the proposed experimen-
tation considering other influence analysis algorithms
and big data coming from heterogeneous networks.
REFERENCES
Aggarwal, C. C. (2011). An introduction to social network
data analytics. Social network data analytics, pages
1–15.
Borgs, C., Brautbar, M., Chayes, J., and Lucier, B. (2014).
Maximizing social influence in nearly optimal time. In
Proceedings of the Twenty-Fifth Annual ACM-SIAM
Symposium on Discrete Algorithms, pages 946–957.
SIAM.
Bucur, D. and Iacca, G. (2016). Influence maximization in
social networks with genetic algorithms. In European
Conference on the Applications of Evolutionary Com-
putation, pages 379–392. Springer.
Guo, G., Zhang, J., and Yorke-Smith, N. (2016). A novel
recommendation model regularized with user trust
and item ratings. IEEE Transactions on Knowledge
and Data Engineering, 28(7):1607–1620.
Karaboga, D. and Basturk, B. (2007). Artificial bee colony
(abc) optimization algorithm for solving constrained
optimization problems. In International Fuzzy Sys-
tems Association World Congress, pages 789–798.
Springer.
Kempe, D., Kleinberg, J., and Tardos,
´
E. (2003). Maximiz-
ing the spread of influence through a social network.
In Proceedings of the ninth ACM SIGKDD interna-
tional conference on Knowledge discovery and data
mining, pages 137–146. ACM.
Li, D., Zhang, Q., Zio, E., Havlin, S., and Kang, R.
(2015). Network reliability analysis based on percola-
tion theory. Reliability Engineering & System Safety,
142:556–562.
Rodriguez, M. G. and Sch
¨
olkopf, B. (2012). Influence
maximization in continuous time diffusion networks.
arXiv preprint arXiv:1205.1682.
Sang, J., Deng, Z., Lu, D., and Xu, C. (2015). Cross-osn
user modeling by homogeneous behavior quantifica-
tion and local social regularization. IEEE Transac-
tions on Multimedia, 17(12):2259–2270.
Scott, J. (2012). Social network analysis. Sage.
Tang, Y., Shi, Y., and Xiao, X. (2015). Influence maximiza-
tion in near-linear time: A martingale approach. In
Proceedings of the 2015 ACM SIGMOD International
Conference on Management of Data, SIGMOD ’15,
pages 1539–1554, New York, NY, USA. ACM.
Wallinga, J. and Teunis, P. (2004). Different epidemic
curves for severe acute respiratory syndrome reveal
similar impacts of control measures. American Jour-
nal of epidemiology, 160(6):509–516.
Watts, D. J. and Dodds, P. S. (2007). Influentials, networks,
and public opinion formation. Journal of consumer
research, 34(4):441–458.
Yang, Q., Chen, W.-N., Yu, Z., Gu, T., Li, Y., Zhang, H.,
and Zhang, J. (2016). Adaptive multimodal continu-
ous ant colony optimization. IEEE Transactions on
Evolutionary Computation.
Yang, W.-S., Weng, S.-X., Guestrin, C., Faloutsos, C.,
VanBriesen, J., and Glance, N. (2012). Applica-
tion of the ant colony optimization algorithm to the
influence-maximization problem. International Jour-
nal of Swarm Intelligence and Evolutionary Compu-
tation, 1(1).
KomIS 2017 - Special Session on Knowledge Discovery meets Information Systems: Applications of Big Data Analytics and BI -
methodologies, techniques and tools
320