
Parallelization of Real-time Control Algorithms on Multi-core
Architectures using Ant Colony Optimization
Oliver Gerlach, Florian Frick, Armin Lechler and Alexander Verl
Institute for Control Engineering of Machine Tools and Manufacturing Units (ISW), University of Stuttgart,
Seidenstr. 36, 70174 Stuttgart, Germany
Keywords:
Ant Colony Optimization, Parallelization, Industrial Control System, Real-time System, Multi-core.
Abstract:
The emerging digitalization of production is accelerating the transformation of Industrial Control Systems
(ICSs) from simple logic controllers to sophisticated systems utilizing complex algorithms which are running
under strict real-time conditions. The required performance has now reached the limitations of single-core pro-
cessors, making a transition to multi-core systems necessary. The parallelization of the currently monolithic
and sequentially designed control algorithms is a complex problem that is further complicated by inherent
hardware dependencies and real-time requirements. A fine-grained distribution of the algorithms on multi-
ple cores while maintaining deterministic behavior is required but cannot be achieved with state of the art
parallelization and scheduling algorithms. This paper presents a new parallelization approach for mapping
and scheduling of model-based designs of control algorithms onto ICSs. Since the mapping and scheduling
problem is N P -complete, an ACO algorithm is utilized and the solution is validated by experimental results.
1 INTRODUCTION
Industrial Control Systems (ICSs) used to be robust,
though rather simple devices regarding their compu-
tational complexity and algorithms. On the one hand,
open systems like Programmable Logic Controllers
(PLCs) enable users to implement logic operations or
control sequences easily. On the other hand, there are
highly specialized systems for specific tasks like con-
trollers for motion applications. In both cases, the
control algorithm itself is executed cyclically with a
fixed frequency. Since ICSs are coupled with real
machines and processes, the computation of the con-
trol algorithm must be completed within the given
time. Violating these hard real-time requirements
could have severe consequences, such as degradation
of the products, damage to machines or even safety
issues for humans.
In the past, specialized embedded systems, includ-
ing custom processors, were used as hardware plat-
forms for ICSs. Advances in communication tech-
nologies and decreasing cost for standard IT hard-
ware led to the development of PC-based control sys-
tems that are performing the computation on a PC
while using inputs and outputs connected through a
field bus to interact with the environment. The afore-
mentioned transition is a key driver of the dominant
trend in the field of industrial control: the digitaliza-
tion of production. Various approaches are currently
being researched to add value to the production pro-
cess through digitalization, including big data, trace-
ability, machine learning and human machine interac-
tion. These approaches can be classified as either add-
ons or integral modifications of the control algorithm.
Add-ons have no direct feedback in the real-time loop
of the control systems. In contrast, integral modifica-
tions have a direct feedback in the control algorithms
and therefore have to fulfill strict requirements regard-
ing the deterministic real-time behavior.
One example of such an integral modification is an
innovative approach that is currently being researched
by our institute (Abel et al., 2014). This new method
for collision avoidance is motivated by the current
trend towards custom manufacturing, i.e. producing
batches down to lot size one. Hereby, a key cost factor
is the changeover time since the first run of a program
after a modification usually needs to be performed
slowly and with human supervision in order to avoid
collisions. In order to make these test runs obsolete,
a new method for online collision avoidance using
a multi-domain real-time simulation was developed.
It uses a parallel simulation of material removal and
collision detection, allowing not only a detection of
collisions between machine parts, but also collisions
with the material. All potential collision items are
protected by boundary boxes allowing for detection
Gerlach O., Frick F., Lechler A. and Verl A.
Parallelization of Real-time Control Algorithms on Multi-core Architectures using Ant Colony Optimization.
DOI: 10.5220/0006489701920199
In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 192-199
ISBN: 978-989-758-274-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

CNC
Production Process
Control System
Field Bus
Kinematic
Simulation
Material
Removal
Simulation
Collistion
Detection
Emergency
Stop
Real-Time
Simulation
Figure 1: Concept of the real-time collision avoidance.
before a collision occurs. The simulation is tightly
coupled to a standard Computer Numerical Control
(CNC) which is responsible for the generation of the
motion. If an upcoming collision is detected in the
simulation, the real system is stopped to avoid dam-
age to the workpiece or the machine. To guarantee
this functionality, strict real-time requirements have
to be fulfilled during execution. Figure 1 depicts the
new approach.
The new collision avoidance method, as well as
many other advanced control algorithms, have sig-
nificantly higher performance requirements than clas-
sic control systems, easily exceeding the performance
provided by a single-core CPU. Previously, this is-
sue was addressed by constantly increasing the clock
frequency. Since this is no longer possible, the per-
formance of standard IT applications is now being
improved by the integration of multiple processing
core into CPUs. Modern software systems usually
consist of a large number of independent tasks that
can be executed independently on multiple process-
ing resources and thereby benefit from multiple cores.
The algorithms executed on ICSs are different re-
garding their structure. Usually they are rather se-
quential and data-dependent, making parallelization
more complex. As shown in (Graf, 2014), a straight-
forward parallelization strategy can easily result in a
degradation of the overall system performance rather
than an improvement. A further challenge is to main-
tain the determinism on a multi-core system.
2 SYSTEM ENVIRONMENT
ICSs differ from other system types in various as-
pects. An efficient parallelization of the control al-
gorithms must consider the specific properties of the
algorithms as well as those of the ICSs. ICSs consist
a
+
+
In1
In2
R
R
+
+
R
c
Out1
Out2
Out3
b
Figure 2: Model-based description of a simple algorithm.
of a hardware platform and a software system.
Industrial Control Systems (ICSs) appear to be
rather heterogeneous; however, they all share a simi-
lar internal structure. They are connected to the phys-
ical environment, for example a machine, through in-
puts and outputs (IO). All types of ICSs run a control
software, which cyclically performs three main steps:
input sampling, computation of the control algorithm
and updating of the outputs. The frequency in which
this loop is executed depends on the system and usu-
ally ranges in between 100 Hz and 100 kHz.
2.1 Control Algorithm Design
There are different methodologies for the design of
control algorithms. Quite common and increasingly
popular are model-based design approaches in which
the function is defined by a composition of building
blocks. New algorithms are composed of existing
building blocks.
This design approach is widespread for ICSs and
available for various applications. The types of blocks
and their capabilities can be very different. They
are often organized hierarchically so that the complex
blocks are composed of simpler ones. Models con-
sisting of many blocks with simpler functions are of-
ten referred to as fine-grained models, while those de-
fined by fewer but more powerful blocks are known as
coarse-grained. Analyzing typical control algorithms
reveals that many models are locally parallelizable but
globally rather sequential. Therefore, an efficient par-
allelization method must be fine-grained. An example
for a fine-grained model is given in Figure 2.
There are two approaches to execute the model-
based algorithms on the target ICSs. They are either
compiled or executed in a run-time system. Com-
pilation might potentially have a better performance,
though it has significant drawbacks regarding usabil-
ity and real-time behavior. Worst Case Execution
Time (WCET) guarantees for compiled algorithms
are challenging to provide. A run-time system is con-
figured by instantiating existing blocks. The blocks
are tested and their individual WCET is known so that
a WCET for the entire algorithm can be guaranteed.
Core 1
L1 Cache
L2 Cache
Shared L3 Cache
Memory Controller
IO Controller
Core 2
Core 3
Core 4
L1 Cache
L2 Cache
L1 Cache
L2 Cache
L1 Cache
L2 Cache
Core 2
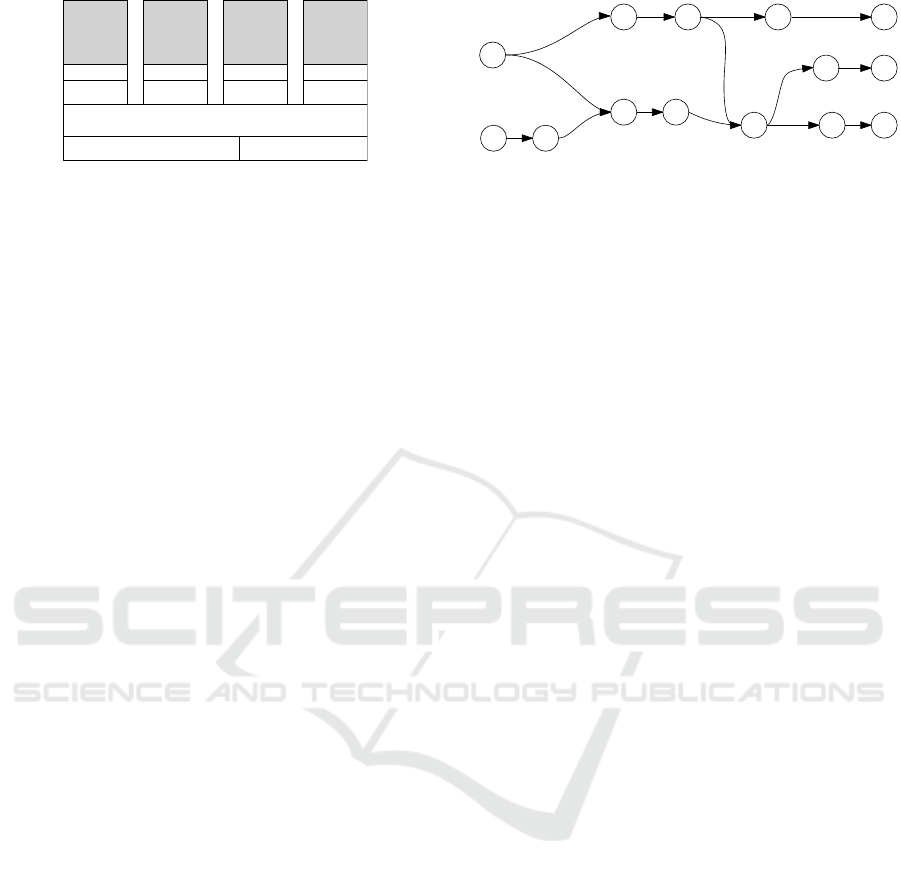
Figure 3: State-of-the-art CPU architecture.
2.2 Hardware
When using a coarse-grained parallelization ap-
proach, the CPUs of a multi-core system can be con-
sidered as independent units. Fine-grained paral-
lelization is more complex, particularly because the
hardware platform has a significant impact.
A processor’s performance is limited by its data
access rate. Since quickly accessible memory is ex-
pensive and limited, current CPUs are equipped with
a multi-level cache architecture. Small but fast mem-
ories are located close to the processor (registers +
L1-Cache). Increasingly larger and slower caches (L2
and L3) are used before accessing the main memory
by the memory controller. The access times decrease
by magnitudes on each level. On multi-core architec-
tures, the link between the cores is usually the L3-
cache. A typical architecture is shown in Figure 3.
As depicted, there is no direct path to switch from
one to another processor. In consequence, paralleliza-
tion can suffer significantly from delays introduced by
switching to another core. The effect is more signif-
icant when the ratio of switching to sequential com-
putation is higher, as it is the case for fine-grained
algorithms.
3 APPROACH FOR MODELING
AND PARALLELIZATION
The parallelization approach described in this paper
is designed for algorithms using a model-based de-
scription. Parallelization of an algorithm for a target
platform is an optimization problem. The optimiza-
tion goal is to map and schedule all function blocks
of the algorithm model to resources of the target plat-
form so that the WCET does not exceed the maximum
allowed processing time whilst taking dependencies
between function blocks of the model into account.
This requirement can be solved by optimizing for the
lowest processing time and checking if the resulting
WCET is below the allowed maximum.
o
1
o
2
o
3
o
7
o
4
o
6
o
8
o
9
o
10
o
14
o
12
o
13
o
11
o
15
Multiply
Input
Input
Gain
Sum
Gain
Integrator
Integrator
Sum
Integrator
Out
Out
Out
Gain
t
2
t
1
t
4
t
3
t
5
t
7
t
6
t
8
t
9
t
10
t
11
t
13
t
12
t
14
Figure 4: Graph representing the algorithm of Figure 2.
3.1 Model Description
In an algorithmic perspective, the model-based de-
scription of the control algorithm can be seen as a
graph which, in general, is a directed cyclic graph
(DCG). For parallelization, it is required to transform
this graph into a directed acyclic graph (DAG). The
approach taken in this paper is to ensure that each
loop contains at least one delay. This delay is rep-
resented as an output and an delayed input in the re-
sulting DAG. Requiring delays in cyclic graphs is a
constraint generally accepted by practitioners (Ben-
veniste et al., 2003).
This DAG is the basis for our model of the algo-
rithm and is referred to as G. This type of graph is a
common subject of optimization (Kwok and Ahmad,
1998; Bautista and Pereira, 2007). The vertices of G
are called operations o
i
with O = {o
i
|1 ≤ i ≤ |O|}. A
function block is represented by one or more opera-
tions. Operations are selected from the set of all pos-
sible operations Ω. The edges of the DAG are called
transitions t
i
with T = {t
i
|1 ≤ i ≤ |T|}. Therefore, the
graph is described by G = (O, T). G represents the
algorithm to be scheduled. A graph for the algorithm
shown in Figure 2 is shown in Figure 4.
The target system for the algorithm has to be mod-
eled as well. It is called platform P and consists of
resources r
i
and channels c
i
. P is fully described by
P = (R, C) with R = {r
i
|1 ≤ i ≤ |R|} and C = {c
i
|1 ≤
i ≤ |C|}. Resources are processor cores or other de-
vices that can process operations. A resource can ei-
ther be able to process all possible operations or only a
subset ω
r
i
⊆ Ω. Resources can process one operation
at a time. After completion, resources are available
for other operations, i.e. they are renewable. Multi-
Core-Processors are homogenous. Every task can run
on every real-time core at equal costs. However, it
is quite common for ICSs to feature dedicated hard-
ware for certain tasks. This specialized hardware can
process a subset ω
r
i
only. An optimization model suit-
able for industrial control applications must be able to
handle such heterogeneous operation environments.
Therefore, a relation γ : R × Ω → N is defined, spec-
ifying the execution time for each operation on this
resource, which is called cost in our model. If an op-

Local Mem
Local Mem
I/O Controller
CPU1
Local Mem
CPU0
System Bus
R1
R2
R3
C1
C2
C4
C3
Operation
Cost
add
multiply
integral
gain
10
20
35
18
Operation
Cost
input
output
25
20
(a)
(b)
Cost = 5
Cost = 5
Cost = 5
Cost = 15
Operation
Cost
add
multiply
integral
gain
10
20
35
18
Figure 5: Example of a basic platform and its modeling.
eration cannot be processed by a resource, the cost is
∞.
Resources are connected by communication chan-
nels, which have to be modeled as well. Channels
can be bus systems, shared memory regions or a lo-
cal cache. Modeling local cache as a channel allows
the optimizer to assign every transition to a channel.
In our model, a channel is specified by the connected
resources and the costs for using this channel. Simi-
lar to a resource, a channel is renewable. Since it is
common for a run-time system to connect many re-
sources to a single channel, channels are a bottleneck
for optimization.
A model of a basic platform is depicted in Fig-
ure 5. It consists of two generic processor cores and
a specialized IO controller. While the cores can pro-
cess all except IO operations, the IO controller can
only host IO operations. All resources in the example
are connected via a bus system which is modeled as a
channel, as is the local memory of each resource.
3.2 Related Approaches
There are similar approaches in literature that also fo-
cus on optimizing a DAG. The Assembly Line Bal-
ancing Problem (ALBP) in particular has much in
common with the problem described above (Boysen
et al., 2008). A given set of tasks has to be performed
on a pool of workstations. Workstations are similar to
resources in our model described above. In ALBP, the
tasks have to be processed in a specific order given by
a precedence graph, which is a DAG (Boysen et al.,
2008). If there are parallel processing routes, an as-
sembly task will unite these routes, resulting in a DAG
with a single root. This is different from the problem
described in this paper, which can contain multiple in-
puts as well as multiple outputs. The most common
optimization criterion for ALBP is not the processing
time, but rather the production rate and the amount of
workstations used. Unlike the problem described in
this paper, the workstations in ALB can be reused for
the next product to be manufactured while the previ-
ous product is at another workstation. In our model,
resources will be reused for different operations of the
same algorithm. Other problems with similar prop-
erties like the ALBP exists, like Job Shop Schedul-
ing (Cheng et al., 1996).
An approach much closer to the problem de-
scribed in this paper was proposed by Ferrandi et
al (Ferrandi et al., 2010; Ferrandi et al., 2013). Their
work also deals with the problem of assigning op-
erations (or tasks) of a DAG to different compo-
nents of a heterogeneous embedded system. Unlike
the definition above, they consider processing ele-
ments to be different from resources. For them, re-
sources are memory regions or Field-Programmable
Gate Array (FPGA) logic units which are assigned to
the operation to be executed on the associated pro-
cessing element. As such, they might be renewable
or non-renewable. The system described in chap-
ter 2 combined with a model-based approach elim-
inates the requirement to consider this type of re-
source as each processing element already has a non-
changeable memory region assigned to it. The ap-
proach proposed by Ferrandi et al. assumes that the
amount of data transferred between tasks varies lead-
ing to task- and channel-dependent costs for channels.
The run-time model that is the target of our optimiza-
tion has a fixed data package to be transferred be-
tween operations, thereby making channel costs ide-
pendent from tasks. Ferrandi et al. consider the im-
plementation of an application on a generic system,
while our problem targets a run-time system with pre-
existing elements for processing operations and tran-
sitions.
Although this work focuses on multi-core archi-
tectures which can be considered homogenous with
regard to the operations they can process, the em-
bedded nature of control systems requires a heteroge-
neous approach. If cores are distributed over multiple
processors, certain IOs might be restricted to certain
cores. Therefore, resources have constraints on which
tasks or operations can be performed. An advantage
of the optimization model described in this paper is
that its operations are directly derived from the func-
tion block diagram of the algorithm. Unlike in other
algorithms, tasks do not have to be identified by the
user or a solver. This advantage stems directly from
the model-based approach.

4 PARALLELIZATION
ALGORITHM
As noted by others, scheduling and mapping a DAG
to parallel processing units is an N P -complete prob-
lem (Bernstein et al., 1989). Thus, exact solutions
cannot be determined within a reasonable amount of
time. For problems with large graphs, bio-inspired
meta-heuristics like Simulated Annealing (SA), Ant
Colony Optimization (ACO), Particle Swarm Opti-
mization (PSO) and Genetic Algorithm (GA) have
been used successfully (Scholl and Becker, 2006;
Wang et al., 1997; Zheng et al., 2006; Clerc, 2004).
GA has been used to solve mapping and scheduling
problems for heterogeneous systems with consider-
able success (Wang et al., 1997). However, ACO
has been found superior to other approaches with re-
spect to computation time and quality of the solu-
tion (Ferrandi et al., 2010). Because of its superior
performance in solving similar problems, ACO is the
chosen algorithm to solve the optimization problem
of mapping and scheduling graph G to platform P,
namely the ACO variant Ant System (AS) (Dorigo
et al., 1996).
4.1 Ant System Description
AS is an optimization algorithm based on a set of
independent agents (called ants) cooperating through
indirect communication. Given m agents, each agent
k traverses the solution graph S to the given prob-
lem and generates a solution, which is called path ξ
k
.
A path is an ordered list of the vertices s
i
of S with
S = {s
i
, s
i, j
|1 ≤ i ≤ |S|, 1 ≤ j ≤ |S|} and s
i, j
being the
edges of S. The performance of ξ
k
is evaluated and is
used to modify the so called pheromone values which
are assigned to each edge of S. The update function
for the pheromone values is given by
τ
i, j
← (1 − ρ)τ
i, j
+
m
∑
k=1
∆τ
k
i, j
(1)
with
∆τ
k
i, j
=
(
Q
L
k
if ant k moved from s
i
to s
j
0, otherwise
(2)
Here τ
i, j
is the pheromone value on edge s
i, j
, ρ
is the pheromone decay value, ∆τ
k
i, j
the amount of
pheromone added by ant k, L
k
is the performance of
ξ
k
and Q is a weighting factor for L
k
(Dorigo et al.,
1996).
The pheromone value τ
i, j
is the communication
mechanism for the agents. Each agent evaluates
o
1
r
1
o
2
o
4
r
2
r
1
r
3
Figure 6: Beginning of the solution graph for Figure 4.
the pheromone values when building its solution ξ
k
.
Starting from a vertex s
i
of S, it selects any of the ver-
tices of S that are connected with s
i
via an edge s
i, j
using
p
k
i, j
=
τ
α
i, j
·η
β
i, j
∑
s
a
∈N
Rk
τ
α
i,a
·η
β
i,a
, if s
j
∈ N
Rk
0, otherwise
(3)
with
η
i, j
=
1
d
i, j
(4)
p
k
i, j
is the probability for agent k to choose s
i, j
for the next step, η
i, j
is the heuristic value for s
i, j
, α
and β are weighting factors for the pheromone value
and the heuristic value respectively, N
Rk
is the set of
valid edges to choose from, and d
i, j
is the cost value
for edge s
i, j
(Dorigo et al., 1996). Valid edges are
all edges connected with the current vertex excluding
those that lead to vertices visited before. The last con-
dition is fulfilled for all edges when S is a DAG.
4.2 Creation of the Solution Graph
To apply ACO to our problem, a solution graph S has
to be constructed from G and P that can be traversed
by the ants. To find a solution to the problem given in
chapter 3, traversing S must provide a valid schedul-
ing of G as well as a mapping of all elements of G to P
while preserving the precedence of G. It also assigns
each element of O to an element of R and each ele-
ment of T to an element of C. One possible solution
graph starts with an element o
i
of O without prede-
cessors and adds it to S as s
1
. It then adds vertices
for each element of R that o
i
can be assigned to and
creates edges s
1, j
for each connection between each
of the resource vertices and s
1
. Another element of O
is then selected from a list of operations without un-
processed predecessors and the process repeats until
all elements of O are added as vertices into S and fol-
lowed by at least one vertex representing an element
of R. An example is given in Figure 6.
So far, transitions have not been considered when
building S. Transitions can be represented similarly
in S to the operations. While this approach allows for
a very simple and straightforward construction of S,
it also increases the risk of creating an invalid solu-
tion: An agent might select a channel for a transition
that could lead to the selection of a task for which
no resource is reachable from the selected channel.
While this can be detected, it results in many unsuc-
cessful iterations to create a solution. Additionally,
this approach further increases the solution space. To
avoid these problems, neither C nor T is represented
in S. Instead, for every t
i
, the fastest channel and the
time for the data transfer is used to calculate the per-
formance of ξ
k
. As a result, no pheromone value is
assigned to the selection of channels. They influence
the pheromone values of s
i, j
by their impact on the
performance of the solution.
To simplify the creation as well as the traversing
of S, two additional operations are added to O, which
are called Nest and Food. Transitions from the Nest
are added to T for all operations o
i
of O that do not
have a predecessor. Similarly, transitions are added to
T for all operations o
i
of O without a successor (Chi-
ang et al., 2006). To build S, an additional resource
r
i
is defined that can process these new operations.
The resulting DAG now has a single start vertex and
a single end vertex.
The heuristic values η
i, j
of all edges of S have not
yet been considered. For problems like the Traveling
Salesman Problem (TSP), these values are constant
and do not change when building a solution (Dorigo
et al., 1996). However, for the problem described in
this paper, the heuristic values for each s
i, j
of S largely
depend on the path ξ. Since the heuristic values are
the costs for traversing a specific edge s
i, j
, they di-
rectly correlate with the time between the end of pro-
cessing s
i
and the beginning of processing s
j
. Ideally,
s
j
is processed one execution step after s
i
has been
processed. However, the channel execution time has
to be considered as well, if the s
j
is an operation and
one or more transitions are required for s
j
to be pro-
cessable. In this case, the heuristic values not only de-
pend on the static channel cost, but also on the avail-
ability of the resource used for s
j
and the availabil-
ity of the channel used. Both might be occupied by
parallel running operations or transitions, impacting
the overall performance of the solution. As a result,
edge s
i, j
, which led to a good performance for a previ-
ously found solution, might worsen another solution,
depending on ξ. This requires a reasonable balance
between the heuristic value and the pheromone value.
Model-Based
Algorithm
Parallelization Tool
Conf.
Conf.
Conf.
Conf.
Algorithm Design
Hardware
Software
Platform Description
Industrial Control Platform
Importer
Exporter
ACO
Visualization
Windows + TwinCAT
Run-Time System
RT
Task
RT
Task
RT
Task
RT
Task
Exporter
Description
Figure 7: Overview of the sample implementation.
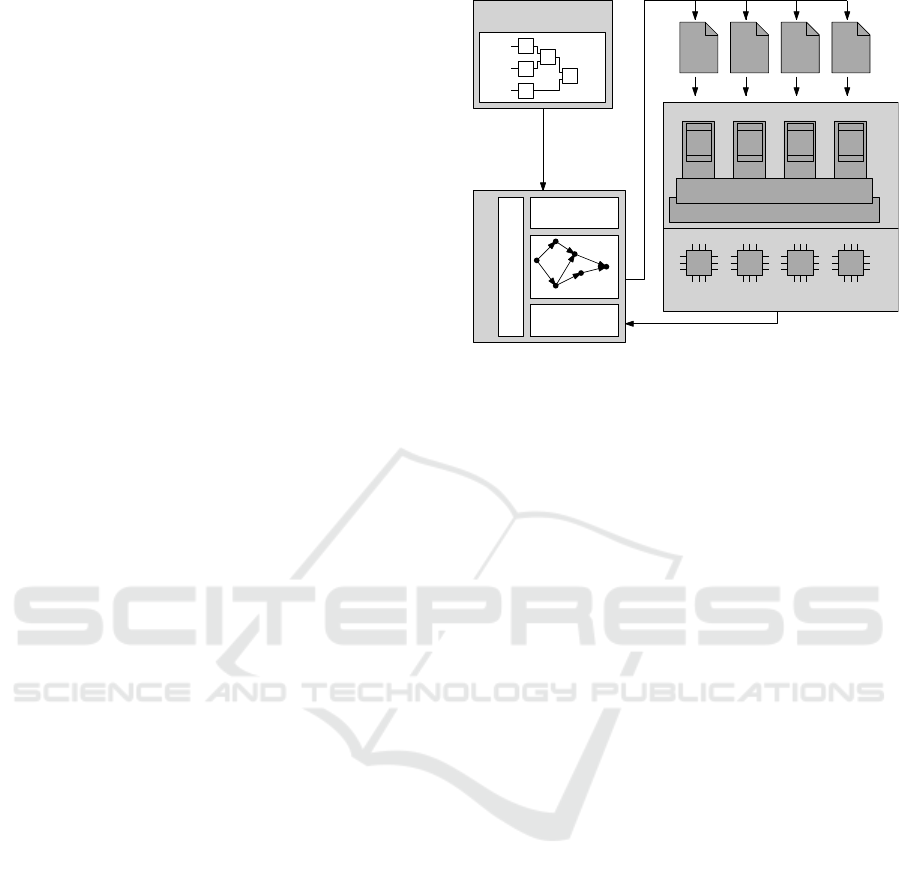
5 EXPERIMENTAL
IMPLEMENTATION
Testing and benchmarking the developed paralleliza-
tion algorithm under real conditions requires addi-
tional functions besides the implementation of the al-
gorithm itself. The overall structure is depicted in Fig-
ure 7.
A model-based description of the algorithm cre-
ated in Matlab Simulink and a description of the tar-
get platform is the input for the parallelization algo-
rithm. A dedicated parallelization tool translates the
imported model to a DAG as described in chapter 3
and then performs the optimization according to chap-
ter 4. It generates a configuration for the run-time
system. The run-time system is located on a control
platform and executes the algorithm in real-time.
5.1 ICS Platform
The selected target platform for the test setup is an
IPC equipped with an Intel i5 quad-core processor.
Inputs and outputs are connected through a field bus
interface. For the experimental setup, Windows and
the real-time control system TwinCAT are used. The
run-time system is implemented as a module of the
RTOS used and performs the actual computation of
the control algorithm. It is composed of run-time
tasks, one per core. Each run-time task must be con-
figured, defining which operation is executed in which
order. In addition, there are channels between all of
the tasks, allowing for communication between the
cores. Ports are available to the RTOS to couple the
run-time system with the existing IOs and other mod-
ules, like PLCs or CNCs.

Table 1: Performance Gains for Example Algorithm in Figure 2.
Platform Costs [%] Coefficient of variation [%]
β = 0.8 β = 1.1 β = 1.2 β = 1.6 β = 1.2 β = 0.8 β = 1.1 β = 1.6
Single-Core 100.0 100.0 100.0 100.0 0.0 0.0 0.0 0.0
Dual-Core 80.6 72.1 70.6 68.6 4.6 5.3 4.5 4.6
Quad-Core 60.4 60.8 58.2 59.2 6.7 5.3 5.9 6.2
Table 2: Performance Evaluation for Collision Avoidance Algorithm in Figure 8.
Platform Costs [%] CPU Time [us] CPU Time [%] Max f [Hz]
Core 1 Core 2 Core 3 Core 4 Total
Single-Core 100 3100 - - - 3100 100 322
Dual-Core 51.7 1650 1600 - - 3250 55 606
Quad-Core 27.6 850 870 790 930 3440 31 1075
&
Collision Detection
Kinematic
Model
Material Removal Simulation
Figure 8: Description of the collision avoidance algorithm.
5.2 Reference Algorithms
Various control algorithms were implemented and
parallelized. The algorithm shown in Figure 2 was
used as a simple test case for an highly parallelizable
algorithm. Additionally, small example systems were
used to test the optimizer. Finally, the collision avoid-
ance method described in the introduction was paral-
lelized. The model-based description of the algorithm
is depicted in Figure 8.
There are three sub-models included in the algo-
rithm. A kinematic model is used to trace the position
of all machine parts. Based on the actual position of
the tool and initial information about the work piece, a
material removal simulation is performed. The infor-
mation about the machine parts as well as the actual
shape of the work piece are used as inputs to the col-
lision detection algorithm. The algorithm consists of
multiple steps: First, possible collision pairs are iden-
tified. These pairs are then distributed over multiple
collision detection tasks. Finally, information about
potential collisions is collected.
5.3 Experimental Results
First, the quality of the parallelization of the algorithm
in Figure 2 was evaluated. The pheromone value scal-
ing factor α was set to 1.0 while the heuristic value
scaling factor β was varied. The algorithm was paral-
lelized to run on 1, 2 or 4 cores. For each solution the
highest costs of all cores were taken as the WCET.
Since the costs for single core execution are constant,
they are taken as reference and each other solution is
given in comparison to the single core solution.
The algorithm is dividable in two parallel paths
and therefore an improvement of approximately 45 %
can theoretically be achieved using two cores. How-
ever, adding additional cores should not further im-
prove the performance due to the algorithms structure
(theoretic value for 4 cores: 47 %). Table 1 shows the
resulting relative costs for the algorithm in Figure 2,
also including the coefficient of variation based on a
representative number of test runs. Depending on the
value of β, performance improvements for two cores
vary between 19 % and 31 %. While not optimal, a
significant performance gain can be achieved by au-
tomatic parallelization. Solutions for four cores are
much closer to the theoretical optimum, because the
larger solution space makes it more likely to not con-
verge into a local minimum. The necessity of avoid-
ing local minima also influenced the final choice of β.
While higher values of β produce better results for the
example algorithm, they put a higher weight on the
heuristic value, making it more likely for the ants to
choose a locally optimal path, which might not lead to
a globally optimal path. Choosing β = 1.2 proved to
be a reasonable compromise for the algorithm evalu-
ated in Table 1 as well as other algorithms. This value
was therefore chosen for the parallelization of the col-
lision avoidance algorithm given in Figure 8.
Again, the algorithm was parallelized for 1, 2 or 4
cores. The run-time system was configured to run the

same number of task. Thereby, the system is behav-
ing as if single, dual or quad-core systems were used.
The remaining cores were not used by the run-time
system. The execution time on every core was mea-
sured. The results are shown in Table 2. The overall
performance defined by the maximum possible con-
trol frequency increases with every additional core.
Looking at the total execution time reveals that a cer-
tain overhead is generated by the parallelization. This
was expected due to the necessary communication be-
tween the cores. Comparing the highest CPU Time
of all cores with the estimated costs reveals that the
cost estimate is only slightly optimistic. Most impor-
tantly, the generated solution allows real-time execu-
tion of the collision avoidance algorithm for complex
production processes.
6 CONCLUSION
In this paper, an approach for fine-grain paralleliza-
tion of control algorithms using ACO-based optimiza-
tion is presented. The goal of this parallelization is to
enable ICSs to benefit from increasing hardware per-
formance to be used for new algorithms. A collision-
avoidance-algorithm was used as a test case for par-
allelization of machine tooling algorithms. It was
shown that the approach successfully parallelizes the
algorithm and enables ICSs to benefit from multi-core
CPUs.
While the presented research focuses on proving
the applicability of ACO for the parallelization prob-
lem, optimizing ACO for the specific problem will be
the focus in the future. Furthermore, the approach
will be extended for systems utilizing dedicated hard-
ware accelerators based on FPGAs. It is intended
to implement the parallelized collision avoidance al-
gorithm into an industrial real-time hardware-in-the-
loop simulation environment for ICSs development.
REFERENCES
Abel, M., Eger, U., Frick, F., Hoher, S., and Lechler, A.
(2014). Systemkonzept f
¨
ur eine echtzeitf
¨
ahige Kol-
lisions
¨
uberwachung von Werkzeugmaschinen unter
Nutzung von Multicore-Architekturen. In Proceed-
ings of SPS IPC Drives 2014, pages S. 441–445–. Ap-
primus Verlag.
Bautista, J. and Pereira, J. (2007). Ant algorithms for a
time and space constrained assembly line balancing
problem. European Journal of Operational Research,
177(3):2016–2032.
Benveniste, A., Caspi, P., Edwards, S. A., Halbwachs, N.,
Le Guernic, P., and de Simone, R. (2003). The syn-
chronous languages 12 years later. Proceedings of the
IEEE, 91(1):64–83.
Bernstein, D., Rodeh, M., and Gertner, I. (1989). On
the complexity of scheduling problems for paral-
lel/pipelined machines. IEEE Transactions on Com-
puters, 38(9):1308–1313.
Boysen, N., Fliedner, M., and Scholl, A. (2008). Assembly
line balancing: Which model to use when? Interna-
tional Journal of Production Economics, 111(2):509–
528.
Cheng, R., Gen, M., and Tsujimura, Y. (1996). A tutorial
survey of job-shop scheduling problems using genetic
algorithms – I. representation. Computers & indus-
trial engineering, 30(4):983–997.
Chiang, C.-W., Lee, Y.-C., Lee, C.-N., and Chou, T.-Y.
(2006). Ant colony optimisation for task matching and
scheduling. IEE Proceedings - Computers and Digital
Techniques, 153(6):373.
Clerc, M. (2004). Discrete particle swarm optimization, il-
lustrated by the traveling salesman problem. In New
optimization techniques in engineering, pages 219–
239. Springer.
Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant sys-
tem: optimization by a colony of cooperating agents.
IEEE Transactions on Systems, Man, and Cybernet-
ics, Part B (Cybernetics), 26(1):29–41.
Ferrandi, F., Lanzi, P. L., Pilato, C., Sciuto, D., and Tumeo,
A. (2010). Ant colony heuristic for mapping and
scheduling tasks and communications on heteroge-
neous embedded systems. IEEE Transactions on
Computer-Aided Design of Integrated Circuits and
Systems, 29(6):911–924.
Ferrandi, F., Lanzi, P. L., Pilato, C., Sciuto, D., and Tumeo,
A. (2013). Ant colony optimization for mapping,
scheduling and placing in reconfigurable systems. In
2013 NASA/ESA Conference on Adaptive Hardware
and Systems (AHS-2013), pages 47–54. IEEE.
Graf, R. (2014). Chancen und Risiken der neuen Prozessor-
Architekturen. Computer-Automation.
Kwok, Y.-K. and Ahmad, I. (1998). Benchmarking the task
graph scheduling algorithms. In Proceedings of the
First Merged International Parallel Processing Sym-
posium and Symposium on Parallel and Distributed
Processing, pages 531–537. IEEE Comput. Soc.
Scholl, A. and Becker, C. (2006). State-of-the-art exact
and heuristic solution procedures for simple assem-
bly line balancing. European Journal of Operational
Research, 168(3):666–693.
Wang, L., Siegel, H. J., Roychowdhury, V. P., and Ma-
ciejewski, A. A. (1997). Task matching and schedul-
ing in heterogeneous computing environments using a
genetic-algorithm-based approach. Journal of parallel
and distributed computing, 47(1):8–22.
Zheng, S., Shu, W., and Gao, L. (2006). Task scheduling
using parallel genetic simulated annealing algorithm.
In Service Operations and Logistics, and Informat-
ics, 2006. SOLI’06. IEEE International Conference
on, pages 46–50. IEEE.
