A Comparative Study for Cost-Utility Analysis Methods: An

Application to a Case Study on Multicomponent Vaccine against

Meningococcal B Disease

Paolo Landa

, Elena Tànfani

and Angela Testi

Medical School, University of Exeter, Heavitree road, EX1 2LU, Exeter, U.K.

Department of Economics and Business Studies, University of Genoa, 16126 Genoa, Italy

Keywords: Discrete Event Simulation, Decision Tree, Markov Model, Cost-Utility Analysis, Health Technology

Assessment, Health Economics.

Abstract: The aim of this study is to explore and compare the results of application of three different modelling

techniques used to perform Cost-utility Analysis in Health Economics and Health Technology Assessment

(HTA). The three modelling techniques described are Decision Tree, Markov model and Discrete Event

Simulation. For each of these modelling techniques was evaluated the introduction of a multicomponent

serogroup B meningococcal vaccine. The preliminary cost-utility analysis herein developed considers societal

perspective, and evaluates the impact of vaccination on Italian infants less than one year of age. The models

validation and the Incremental Cost-Effectiveness Ratio (ICER) resulting from each technique are reported,

in preliminary results each modelling technique gives different ICER, depending on the modelling technique.

1 INTRODUCTION

In Health Economics and Health Technology

Assessment (HTA) the use of modelling techniques is

strongly recommended for the introduction of a new

device, drug, clinical pathway, vaccine or other

instruments that can have an impact on patients’

health and on National Health Service (NHS)

budgets. For the decision-maker, usually represented

by NHS, it is important to know the incremental cost-

effectiveness of the technology that represents the

change in cost and effectiveness achieved by the new

technology compared with current practice. In

international literature the main modelling techniques

applied to evaluate the introduction of new

technologies are: Decision Tree, Markov Model and

Discrete Event Simulation. Each technique has its

strength and weak characteristics that enable the

method to be the best to fit the analysis.

While in the literature the use of Decision Tree

and Markov models are the main techniques applied

for Cost Effectiveness Analysis (Muennig and

Bounthavong, 2016), the adoption of DES is recent.

Decision trees are simple and directed graph

without recursion and they represent a formal way to

describe decisions, embodying the paradigm of

decision analysis. Each decision can be divided into

three components: the decision node (the

representation of the moment when the decision

maker has to do a choice between competing

strategies), the decision strategy (represented by the

set of actions or events consequent to a certain

decision) and the outcome nodes (which represent the

outcome in cost and effectiveness).

Even if it is the simplest method of analysis, the

use of decision trees (Aleem et al., 2009) presents

some limitations from the perspective of performance

and outcome analysis. Firstly simplification errors

may occur when measuring the final outcome of

treatment decisions with values such as quality-

adjusted life years (Van der Velde, 2005; Naglie et

al., 1997). It is also difficult to perform adequately an

analysis considering the variation of some parameters

during a long time horizon in a clinical environment

(Aleem et al., 2009) and various factors (including

expenses and patient preferences for medical

services) are involved in the decision-making

process, and these cannot be accurately reflected in a

decision tree (Burch et al., 2012; Bhandari et al.,

2003).

Markov models are cyclic directed graphs used

when a decision problem has the exposure to some

Landa, P., Tànfani, E. and Testi, A.

A Comparative Study for Cost-Utility Analysis Methods: An Application to a Case Study on Multicomponent Vaccine against Meningococcal B Disease.

DOI: 10.5220/0006490201630170

In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 163-170

ISBN: 978-989-758-265-3

163

risks or events is variable or changes during a certain

time horizon. Most of Markov models used in

healthcare are semi-Markov state transition models,

where state transitions can vary during the time

horizon (Stahl, 2008).

DES is a very flexible modelling method in which

entities may interact or compete with each other for

resources in a system. Every interaction between

entities (with each other or with the resources in the

system) is an event. Every interaction changes the

state of the entity involved and of the system as a

whole (Stahl, 2008).

The time between each event can be handled

probabilistically, using fixed time increments, or

both, depending on the nature of the system being

modelled. DES are composed by entities, attributes,

queues and resources. In a simulation model entities

are objects characterised by attributes, usually entities

are represented by patients or element of a chain, such

as products, that can interact with the other entities

inside the system. Entities are the main element of the

simulation and are generated in the beginning of the

model or during the execution.

Attributes are specific characteristics of each

entity, represent the information of the entity such as

the chronic disease of a patient, the health status if we

consider patients as entities. Attributes can vary

during the simulation and they are very important in

the simulation when the entity interact with other

entities inside the system or when some events

occurs.

Events are actions or things that can occur inside

the simulation environment or to an entity (e.g. an

infection or a virus that change the health status of a

patient). Resources are represented by service

providers for entities inside the model. Most of the

resources are limited (e.g. the nurses of a Cardiology

Unit or the MRI machines inside a Radiology

department). When resources are used by entities,

other entities have to wait, creating a queue. Queues

are managed following several rules, depending also

on the modeller choice (e.g. priority queues, First In -

First out, Last In – First out). All the elements above

described work and interact and compete in a specific

frame of time, usually it is the period time to represent

the system. (Karnon et al., 2002)

The disadvantage of cost-effectiveness analysis

limitations and inaccuracies of Markov models are

easily avoided with the use of DES. In literature

several studies describe the principles and the

methodologies of decision-analytical modelling for

Health Technology Assessment (Sun and Faunce,

2007).

In this study three modelling techniques were

applied to verify the cost utility of the introduction of

a new multicomponent vaccine for the Neisseria

meningitidis serogroup B (NmB) in the Italian NHS

context.

The Neisseria meningitidis (Nm) is a gram

negative bacterium that cause meningitis or other

forms of meningococcal diseases. Even if the

incidence of this disease in Italy has low values, the

diseases caused by Nm represent a public health

problem that produce a sensible economic impact on

the society (Anonychuk et al., 2013; Davis et al.,

2011). The incidence of disease is variable within the

geographical areas (Harrison et al., 2009), since after

the introduction of meningococcal serogroup C

vaccination, the serogroup B has become the main

agent of meningococcal disease. The disease most

affects children under one year of age are mainly

affected. In Italy, about 60% of typed cases of

meningococcal disease are now caused by NmB

(European Centre for Disease Prevention and

Control, 2010; Istituto Superiore di Sanità, 2014).

2 MODEL DESCRIPTION

In order to perform the technique comparison on

Cost-utility evaluation three models with three

techniques were developed: Decision tree, Markov

and DES models. The three techniques were

developed using respectively TreeAge® Pro 2015,

Microsoft Excel® 2013 and Lanner Witness® 2016.

2.1 Decision Tree Model

The decision tree herein presented (Figure 1) belongs

to a previous study developed for economic

evaluation of Bexsero® vaccine in Italy (Gasparini et

al., 2016).

Figure 1: Decision tree model.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

164

The tree is composed firstly by the choice node

where begin the two branches representing the

strategies: “Vaccinate infant Italian population” and

“Not vaccinate infant Italian population”. Vaccinated

infants can be immunised or not immunised against

NmB, immunisation depends on the effectiveness of

the vaccine. If infants are immunised then they can

have adverse events or not, usually represented by

allergic reactions or flue. Infant not immunised for the

missed effectiveness of the vaccine can have adverse

event or not, but they have the same conditions and

risks of infants that do not participate to vaccination

program.

Infants that are not immunised can live their entire

life without contracting the disease. If an infant has

the NmB disease, there can be three different health

status: Death, Survive with sequelae (the

consequence of the disease represented by chronic

diseases or disabilities) and Survive without sequelae.

The list of possible sequelae are: Amputation with

substantial disability, Anxiety, Arthritis, Depression,

Motor Deficits, Blindness, Epilepsy or Seizure,

Severe Neurological Disability, Mental retardation

(cognitive problems), Hearing loss with cochlear

implantation, Moderate/Severe bilateral Hearing loss,

Moderate/Severe unilateral Hearing loss, Renal

Failure, Chronic migraine, Skin necrosis, Scars and

Severe Speech or communication problem.

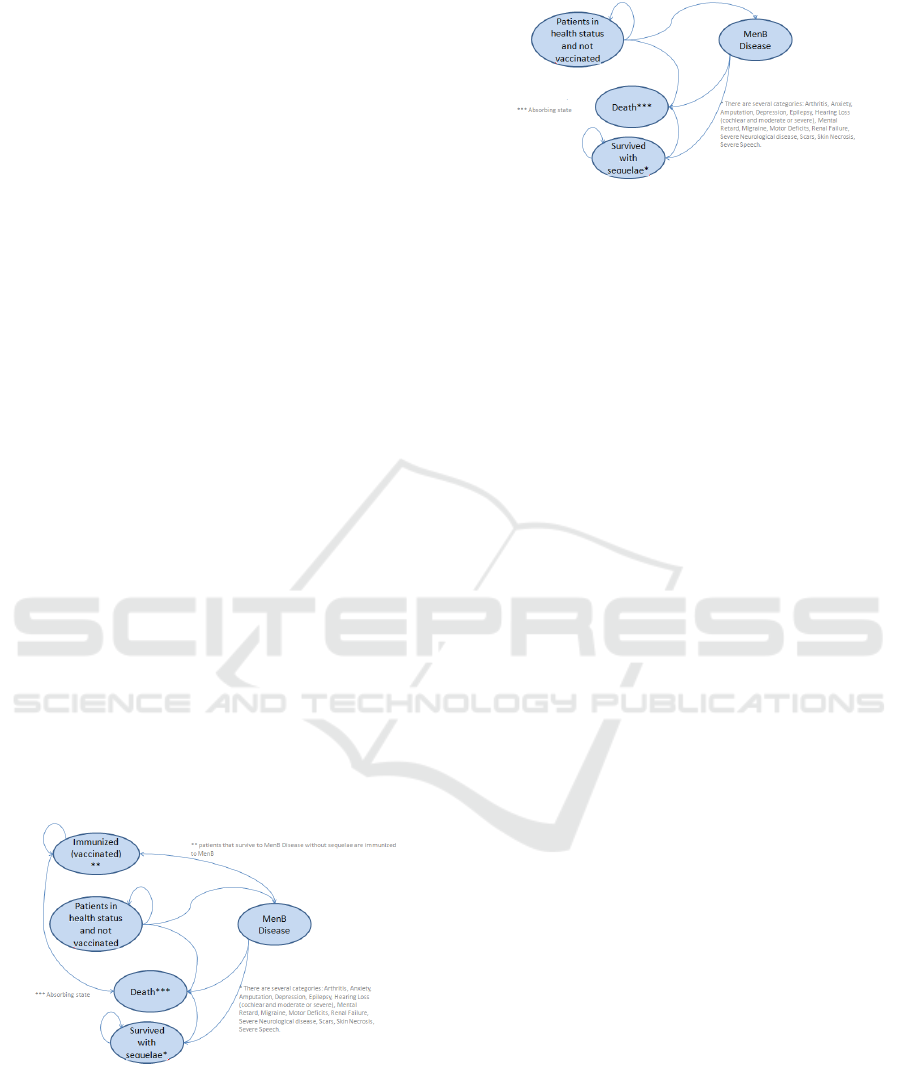
2.2 Markov Model

Markov models are widely adopted into Cost-

Effectiveness Analysis. The model herein developed

is split into two sub-models: Vaccination program

(Figure 2) and No Vaccination program (Figure 3).

Figure 2: Markov model for vaccination program.

The first model is composed by five status:

Patients in health status and not vaccinated,

Immunized (vaccinated), MenB disease, Death and

Survived with sequelae. Firstly all infants are in a

good health status and are not vaccinated. If the infant

Figure 3: Markov model for no vaccination program.

population is vaccinated then there can be two status:

infant that are immunized change the status into

“Immunized”, while not immunized infants are still

in the previous status. Infants that will have NmB

disease pass through the transitional status “MenB

Disease” and consequently transferred into one the

following health status: “Death” if infant dies,

“Survived with sequelae” if infant survives with

sequelae and “Patients in health status and not

vaccinated” if infant survives without sequelae. The

No Vaccination program model has the same

configuration but it is not considered the

“Immunized” health status for the missing

vaccination program. The absorbing state for each

model is “Death”.

2.3 Discrete Event Simulation Model

Simulation enables to develop models built to

determine the response of a system to changes in its

internal structure and inputs. It can reproduce a

simplified representation of a dynamic process that is

too complex for a direct analysis, considering that it

is a cheaper and simple tool for analysts.

Two DES sub-models were developed: the first

sub-model shown in Figure 4, represents and

describes the clinical pathway that infants have to

follow when they are vaccinated (vaccination model).

The second sub-model, shown in Figure 5, describes

the actual scenario where all the infants are not

vaccinated against NmB (the so-called

“comparator”).

2.3.1 Vaccination Model

Infants when are vaccinated can be immunized or not,

considering the effectiveness of the vaccine. If the

vaccine is effective then the infant is immunized and

protected for lifetime. If vaccine is effective then

there can be adverse or not adverse events (high body

temperature or allergic reaction). Infants not

immunized can acquire the NmB during their life of

survive without contracting the disease. If infants

acquire the NmB disease can die, survive without

A Comparative Study for Cost-Utility Analysis Methods: An Application to a Case Study on Multicomponent Vaccine against

Meningococcal B Disease

165

sequelae or survive without sequelae. The description

of the pathway for vaccinated infants is shown in

Figure 4.

Figure 4: Flow chart for Vaccination model.

2.3.2 No Vaccination Model

The second DES model (Figure 5) describes the

actual scenario where infants are not vaccinated and

consequently not immunized against NmB. If the

National Health Service does not include vaccination,

infants can live their whole life without contracting

the disease. If during their life they acquire the

disease, then infants can have two possible outcomes:

death or Survive. Survivors are divided into two

different categories: without or with sequelae.

Figure 5: Flow chart for No Vaccination model.

2.3.3 Elements of DES Model

Infants are entities in the model and correspond to the

number of infants born in a year.

Once infants are generated by the simulator, then

they are sent to the “Vaccination” queue, where the

“Vaccination” resource distribute infants into

“Adverse Events”, “No Adverse Events” and “No

Vaccination” queues. These queues contain

respectively infants that had adverse events after the

vaccination cycle, that had not any adverse event and

that were not immunized by the vaccine

(unprotected).

This last resource named “No Vaccinated Flow”

collects patients that are not vaccinated or

unprotected and submit them to the “Incidence”

resource, that distribute entities into “Disease” and

“No Disease” queues. Infants that have the disease are

hospitalized and the resource “Effect of Disease”

distribute them into “Deaths”, “Survival with No

Sequelae”, “Sequelae” (with the different sequelae

reported previously) queues. The distribution of

elements inside the model follows the probability

distributions described in Gasparini et al. (2016).

3 CASE STUDY

3.1 General Characteristics

The three modelling techniques were applied to the

Italian epidemiological scenario of 2012. Data used

in this study refer to a previous study (Gasparini et al.,

2016) where a Cost-Utility Analysis was performed

using a decision tree model.

3.2 Model Parameters, Costs and

Utilities

A detailed specification of data, incidence of disease,

model assumptions, cost and outcome values and

distribution is herein reported.

The main parameters and assumption respect the

criteria given by Italian guidelines for economic

evaluation in healthcare (AIES, 2009; Capri et al.,

2001). The adoption of discount rate for both costs

and utilities is needed to evaluate the relative values

during the long time horizon. The probability of

disease is provided by the Italian Institute of

Healthcare (Istituto Superiore di Sanità) and it is

related to NmB cases occurred annually in Italy from

2007 to 2012. The vaccine herein evaluated is

supposed to give a full lifetime protection. In Table 1

general model parameters are reported.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

166

Table 1: General model parameters.

Parameter

Value

Probability of disease

0.0000023

Vaccine compliance

0.9

Discount rate for costs and utility

0.03

Probability of death

0.0673

Probability of Amputation with

substantial disability

0.01

Probability of Anxiety

0.068

Probability of Arthritis

0.025

Probability of Depression

0.05

Probability of Motor deficits

0.019

Probability of Blindness

0.004

Probability of Epilepsy or Seizure

0.02

Probability of Severe Neurological

disability

0.021

Probability of Mental retardation

(cognitive problems)

0.254

Probability of Hearing loss requiring

cochlear implantation

0.02

Probability of Moderate/severe bilateral

hearing loss

0.05

Probability of Moderate unilateral

hearing loss

0.05

Probability of Skin necrosis

0.015

Probability of Scars

0.03

Probability of Severe speech or

communication problems

0.037

Probability of Renal failure

0.019

Probability of Chronic migraine

0.10

Probability of Survive without sequelae

0.402

Outcomes were measured using Quality Adjusted

Life Years (QALYs), one of the main measures of the

value of health outcomes. The classification system

assumed for QALY was EuroQoL EQ-5D. In Table 2

are reported annual health outcomes for all the health

status related to the NmB sequelae, death and

survival.

Costs reported in the model are annual costs in

Euro (€) currency at January 2013 values, previous

years costs were adjusted to January 2013 levels. Four

categories were defined for costs: Direct costs related

to meningococcal sequelae, Indirect costs related to

meningococcal sequelae, Costs related to acute phase

of disease and Costs associated to vaccination (Table

3).

The first category represents all the direct cost

associated to sequelae (e.g. the direct cost of

seizures), while the second category includes social

costs that indirectly affect patients with the sequelae

(e.g. the special education needed in school for

children with cognitive problems, or the lost income

of a parent that had to quit the job to follow the child

with severe neurological disability).

Table 2: Health outcomes.

Health status

QALY

Death

Survive

Amputation with substantial disability

0.613

Anxiety

0.687

Arthritis

0.690

Depression

0.729

Motor deficits

0.830

Blindness

0.260

Epilepsy or Seizure

0.830

Severe Neurological disability

0.060

Mental retardation (cognitive problems)

0.541

Hearing loss requiring cochlear

implantation

0.810

Moderate/severe bilateral hearing loss

0.910

Moderate unilateral hearing loss

0.910

Skin necrosis

0.900

Scars

1.000

Severe speech or communication problems

0.390

Renal failure

0.820

Chronic migraine

0.814

Table 3: Costs for economic evaluation.

Cost

Euro(€)

Amputation with substantial disability

7,339

Anxiety

1,146

Arthritis

1,184

Depression

3,192

Motor deficits

7,682

Blindness

4,076

Epilepsy or Seizure

2,272

Severe Neurological disability

94,880

Mental retardation (cognitive problems)

7,507

Hearing loss requiring cochlear

implantation

6,327

Moderate/severe bilateral hearing loss

3,163

Moderate unilateral hearing loss

3,163

Skin necrosis

1,066

Scars

533

Severe speech or communication problems

9,796

Renal failure

56,126

Chronic migraine

892

Medical care: cost of hospitalization per

case

7,900

Public Health Response

3,223

Acute phase lost productivity of parent or

relatives

870

Acute phase lost productivity of patient

1,426

Special case education

14,556

Lost productivity of parent

24,500

Lost productivity of patient

24,500

Primary cycle of vaccination (4 doses)

200

Vaccine administration per dose

5.80

Hospitalization for 1 anaphylactic reaction

1175

Mild or moderate adverse event

3.40

A Comparative Study for Cost-Utility Analysis Methods: An Application to a Case Study on Multicomponent Vaccine against

Meningococcal B Disease

167

The costs of acute phase of disease is the third

category and it represents the costs bore by the

national healthcare system and the society during

both the hospitalisation and the treatment of the

individuals that might be at risk of NmB (e.g. the

DRG of hospitalisation and the chemoprophylaxis

treatment). Also were considered indirect costs of

parents and patient during the acute phase of the

disease, represented by the missing income of parents

and patient during the hospitalisation. The fourth and

final category is the costs associated to vaccination,

where are included the cost of the vaccine, the cost of

administration of the vaccine, the costs of

anaphylaxis reaction and the mild or moderate

adverse event, usually managed with one box of

paracetamol.

4 PRELIMINARY RESULTS

4.1 Model Validation

In order to perform a validation it is necessary to

compare the model predictions with data used to in

the simulation model (Eddy, 1985).

There is not a simple and universally applicable

procedure to apply for model validation. Each case

can be considered by itself, but to simplify it can be

achieved identifying the desirable characteristics in

the reporting of cost-effectiveness models (Mc Cabe

and Dixon, 2000).

The first validation was done for the Decision tree

model, where using the strategy of “No Vaccination”

was checked if the results were corresponding in

terms of incidence, deaths, survival with and without

sequelae and number of patients with the sequelae.

This first validation gave the same results as the

actual epidemiological scenario without the

vaccination program.

Model validation was performed using the

following values for “No vaccination” and

“Vaccination” sub-models of Decision Tree, Markov

and DES models. For model validation the following

values were selected: the total number of infant in the

model, the number of deaths for NmB disease, the

number of sequelae, the number of infants without

sequelae. In Table 4 the validation show a slight

variation within the models. This small variation is

given by the characteristics of each techniques, where

events can happen at the end of a cycle or in a

particular point in time.

Table 4: Model validation.

Value

Decision

tree

Markov

DES

Infant population

at the end of the

simulation/cohort

531,372

No of deaths

(Vaccine Model)

No of infants with

sequelae (Vaccine

Model)

# Survived

without sequelae

(Vaccine model)

# deaths (No

Vaccine Model)

# infants with

sequelae (No

Vaccine Model)

# Survived

without sequelae

(No Vaccine

model)

4.2 ICERs Comparison

Incremental Cost Effectiveness Ratio (ICER) is used

in economic evaluation in health economics to

evaluate a new technology (e.g. drugs, vaccines,

therapeutics) and compare it with other technologies.

The evaluation requires different results in order to

confirm or not the introduction of a new technology,

one of these results is the incremental cost-

effectiveness ratio (ICER), which is the ratio of the

change in costs of a new technology (compared to the

alternative, such as doing nothing or using the best

available alternative treatment) to the change in

effects. For the three techniques the corresponding

ICER were reported in Table 5.

Table 5: ICER values for DT, MM and DES techniques.

Modelling technique

Value (€)

Decision Tree

109,762

Markov Model

117,713

Discrete-Event Simulation

115,675

Considering a threshold value defined by the

National Health Technology Assessment guidelines

(Capri et al., 2001) of € 40,000.00, the introduction of

vaccine is not advisable for the Italian

epidemiological scenario.

The ICER values given by each technique are

different and each variation in the result can be

explained by the characteristics of model adopted for

cost-utility evaluation. Decision tree is not able to

represent the future events that depends on previous

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

168

events in the time (e.g. herd immunity). It is possible

to achieve it with data approximation of these events,

by modelling data with a detailed analysis, usually

with the joint use of commercial spreadsheets and

dedicated software, but these approximations can

affect the final result.

The Markov Model can better represent the

decision problem involving risk that is continuous

over time, considering the timing of events and the

possibility that events may happen more than once

(Sonnenberg and Beck, 1993). As the ability of

Markov models consists in representing repetitive

events, time dependence of both probabilities and

utilities that allow a more accurate representation of

clinical reality for the model (Briggs and Schulper,

1998), the weakness is in the total missing of

memory. The behaviour of the process subsequent to

any cycle inside Markov models depends only on its

description in that cycle. This means that the process

has no memory for earlier cycles (Sonnenberg and

Beck, 1993). Finally DES provides a flexible

approach to represent complex systems (Law, 2007)

and, its ability enable this technique to be one of the

better techniques to perform Cost-Effectiveness

analysis (Karnon et al., 2012, Caro et al., 2010).

Events can happen in any moment in the time (not in

the beginning of the end of the cycle as Markov

models), being able to better represent reality.

5 CONCLUSIONS

The choice of modelling technique is very important

in Health Technology Assessment for the economic

evaluation and the study of impact of the introduction

of a new technology in a National Healthcare System.

In this study each of these techniques were applied to

evaluate the introduction of a new vaccine against

Neisseria meningitidis serogroup B. For each model

developed was described the characteristics and the

composition in detail. The three techniques were

validated and it was computed the Incremental Cost

Effectiveness Ratio (ICER) and compared to the

Willingness to pay value of € 40,000.00.

The preliminary results show that the introduction

of the vaccine is not advisable in Italy. The

comparison between the three modelling techniques

shows that ICERs resulting have some differences.

The limitation of this study is represented by the

adoption of the same assumptions for each of the

technique. A further study aims at analysing the

techniques with different model assumptions, and to

evidence the main differences in terms of

performance indicators.

ACKNOWLEDGEMENTS

The authors acknowledge support from the Italian

Ministry of Education, University and Research

(MIUR), under the grand FIRB n. RBFR081KSB.

Data was provided by a previous collaboration with

the Department of Health Science (Prof. Roberto

Gasparini, Prof. Donatella Panatto and Dr. Daniela

Amicizia) and the Department of Economics and

Business studies of the University of Genoa (Italy).

REFERENCES

AIES, 2009 Proposta di line guida per la valutazione

economica degli interventi sanitari in Italia

PharmacoEconomics – Italian Research Articles;

11(2):83-93.

Aleem, I. S., Jalal, H., Aleem I. S., Sheikh, A. A., Bhandari,

M., 2009 Clinical decision analysis: incorporating the

evidence with patient preferences. Patient Prefer

Adherence, 3:21-24.

Anonychuk, A., Woo, G., Vyse, A., Demarteau, N., Tricco,

A. C., 2013 The cost and public health burden of

invasive meningococcal disease outbreaks: a

systematic review. Pharmacoeconomics.31(7) 563-76.

Bhandari, M., Devereaux, P. J., Swiontkowski, M. F.,

Tornetta, P., Obremskey, W., Koval, K. J., et al., 2003.

Internal fixation compared with arthroplasty for

displaced fractures of the femoral neck. A meta-

analysis. J Bone Joint Surg Am. 85-A:1673-1681.

Briggs, A., Sculpher, M., 1998. An introduction to Markov

modelling for economic evaluation.

Pharmacoeconomics. 13(4):397-409.

Burch, J., Hinde, S., Palmer S., Beyer F., Minton J., Marson

A., et al. The clinical effectiveness and cost-

effectiveness of technologies used to visualize the

seizure focus in people with refractory epilepsy being

considered for surgery: a systematic review and

decision-analytical model. Health Technology

Assessment 2012; 16:1-157.

Capri, S., Ceci, A., Terranova, L., Merlo, F., Mantovani, L.

2001 Guidelines for economic evaluations in Italy:

Recommendations from the Italian Group of

Pharmacoeconomic Studies. Drug Information Journal.

35:189-201.

Caro, J. J., Möller, J., Getsios, D., 2010. Discrete Event

Simulation: The Preferred Technique for Health

Economic Evaluations? Value in Health 13(8) 1056-

1060

Davis, K. L., Misurski, D., Miller, J., Karve, S., 2011 Cost

impact of complications in meningococcal disease:

evidence from a United States managed care

population. Human Vaccine. 27(4) 458-465.

Eddy, D., Technology assessment: the role of mathematical

modelling. In: Mosteller F., editor. Assessing medical

technologies. Washington, DC: National Academy

Press, 1985: 144-60

A Comparative Study for Cost-Utility Analysis Methods: An Application to a Case Study on Multicomponent Vaccine against

Meningococcal B Disease

169

European Centre for Disease Prevention and Control:

Surveillance of invasive bacterial diseases in Europe

2008/2009. http://www.ecdc.europa.eu. Accessed 2013

Gasparini, R., Landa, P., Amicizia, D., Icardi, G., Ricciardi,

W., de Waure, C., Tànfani,E., Bonanni, P., Lucioni, C.,

Testi, A., Panatto, D., 2016 Vaccinating Italian infants

with a new multicomponent vaccine (Bexsero®) against

meningococcal B disease: A cost-effectiveness analysis.

Human Vaccine and Immunotherapeutiscs 12(8) 111-

222. DOI: 10.1080/21645515.2016.1160177

Harrison, L.H., Trotter, C.L., Ramsay, M.E., 2009 Global

epidemiology of meningococcal disease. Vaccine 27

Suppl 2:B51-63.

Istituto Superiore di Sanità (ISS): Dati di sorveglianza delle

malattie batteriche invasive aggiornati al 10/04/2013.

http://www.simi.iss.it/dati.htm. Accessed May 2014.

Karnon, J., Stahl, J., Brennan, A., Caro, J. J., Mar, J., MD,

Moeller, J., 2012. Modeling Using Discrete Event

Simulation: A Report of the ISPOR-SMDM Modeling

Good Research Practices Task Force–4. Med Decis

Making 32(5):701–711. doi: 10.1177/

0272989X12455462

Law M. A., 2007. Simulation Modeling & Analysis.

McGraw-Hill, 4th ed.

Muennig, P. and Bounthavong M., 2016. Cost-

Effectiveness Analysis in Health: A Practical

Approach. Jossey-Bass, 3

ed.

Naglie, G., Krahn, M. D., Naimark, D., Redelmeier, D. A.,

Detsky, A. S., 1997. Primer on medical decision

analysis: part 3--Estimating probabilities and utilities.

Med Decis Making.17:136-141

Oostenbrink, R., Moll, H. A., Essink-Bot, ML. 2002 The

EQ-5D and the Health Utilities Index for permanent

sequelae after meningitis: a head-to-head comparison.

J Clin Epidemiol; 55:791-99; PMID:12384194;

http://dx.doi.org/10.1016/S0895-4356(02)00448-1

Sonnenberg, F. A., Beck J. R., 1993. Markov Models in

Medical Decision Making. A Practical Guide. Med

Decis Making. 13 (4) 322-338. doi: 10.1177/

0272989X9301300409

Stahl, J. E., 2008. Modelling Methods for

Pharmacoeconomics and Health Technology

Assessment. An Overview and Guide

Pharmacoeconomics 2008; 26 (2): 131-148

Sun, X., Faunce, T., 2007. Decision-analytical modelling in

health-care economic evaluations. The European

Journal of Health Economics 9 (4), 313-323. DOI

10.1007/s10198-007-0078-x

Van der Velde G. 2005. Clinical decision analysis: an

alternate, rigorous approach to making clinical

decisions and developing treatment recommendations.

J Can Chiropr Assoc 2005; 49: 258-263

Witness (2015). User guide. Lanner Group, London, UK

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

170