
Towards Real-Time Fleet-Event-Handling for the Dynamic Vehicle
Routing Problem
Simon Anderer
1
, Max Halbich
1
, Bernd Scheuermann
1
and Sanaz Mostaghim
2
1
Faculty of Management Science and Engineering, Hochschule Karlsruhe, Moltkestrasse 30, Karlsruhe, Germany
2
Institute for Intelligent Cooperating Systems, Otto-von-Guericke Universit
¨
at, Magdeburg, Germany
Keywords:
Dynamic Vehicle Routing Problem, Evolutionary Algorithm, Event Processing.
Abstract:
This paper proposes an approach to real-time fleet event handling for the Dynamic Vehicle Routing Problem
based on evolutionary computation. For this purpose, a communication protocol between a fleet of vehicles
and an optimization back-end is presented and the related changes to the evolutionary algorithm are illustrated.
This allows for information exchange and event-handling in real-time. Furthermore, this paper describes the
adaption of benchmark files for the static Vehicle Routing Problem to a dynamic real-time scenario including
time-dependent travel times, as well as dynamic travel and service times. The adapted benchmark files are
then used for the evaluation of the proposed system.
1 INTRODUCTION
Transportation costs are one of the major cost drivers
enterprises have to consider in their daily operations.
The increasing complexity and multilateral dependen-
cies of entire industrial ecosystems create challeng-
ing requirements for the supply chain and distribu-
tion management. Huge amounts of goods need to
be planned and distributed within short time periods.
Customers expect on-schedule deliveries in the B2B
as well as in the B2C market. It is crucial to be able
to react towards unforeseen events like traffic jams or
service delays and to track the progress of delivery
execution.
This paper presents a system for the Dynamic Ve-
hicle Routing Problem (DVRP) and ensures an imme-
diate reactivity towards events, by using an adapted
evolutionary algorithm. The system includes a sim-
ulator, which is able to model entire delivery periods
with lengths of up to one day. To validate the system,
different realistic scenarios have been created, con-
sisting of a static and a subsequent dynamic optimiza-
tion process. By receiving the customer requests a
day in advance, the static optimization process is run-
ning over night, providing a proper solution. With the
start of the actual delivery period, dynamic optimiza-
tion is initiated in order to be able to react to changing
traffic conditions or fluctuating service times. As the
system is running in real-time, it provides real-world
feedback to the optimization process.
The steering process is based on a newly devel-
oped two way communication protocol, which trig-
gers information updates in an event-based fashion.
Due to the implemented information protocol the sim-
ulator can be substituted by mobile devices, providing
the same event-based information updates. The proto-
col is designed bilaterally. Status updates of the indi-
vidual vehicles are sent to the optimization back-end,
which in return provides routing updates to the vehi-
cles. The information flow is steered by the so-called
decision maker, which represents an information in-
terface. Direct event processing enables an immediate
reactivity towards dynamic travel and service times.
The system aims at practical application.
The remainder of the paper is structured as fol-
lows: In Section 2, a literature-review is presented.
Section 3 illustrates the general framework of the op-
timization scenario. In chapter 4, the architecture of
the proposed DVRP-system is described while Sec-
tion 5 explains the corresponding algorithmic aspects.
In Section 6, the proposed system is evaluated. Fi-
nally, Section 7 and 8 conclude the paper and present
future research possibilities.
2 RELATED WORK
As the Vehicle Routing Problem (VRP) is one of the
most studied combinatorial optimization problems,
Anderer S., Halbich M., Scheuermann B. and Mostaghim S.
Towards Real-Time Fleet-Event-Handling for the Dynamic Vehicle Routing Problem.
DOI: 10.5220/0006491300350044
In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 35-44
ISBN: 978-989-758-274-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

numerous papers were published in the last decades.
A good overview of recent publications in the field of
DVRP is given in the work of (Psaraftis et al., 2016).
In this work, the authors deploy a taxonomy, consist-
ing of eleven criteria, and classify 117 publications.
The review published by Ritzinger et al. focuses on
dynamic and stochastic VRPs (Ritzinger et al., 2015).
For further surveys on the general DVRP, please refer
to (Bektas et al., 2014) and (Pillac et al., 2013).
Out of the 117 reviewed papers of Psaraftis et al.
eleven approaches can be classified as genetic or evo-
lutionary algorithms. Whilst nine of the mentioned
approaches exclusively address the processing of dy-
namic customer orders, only two refer to the process-
ing of dynamic travel times or the processing of both
dynamic elements. A major part of the mentioned ap-
proaches is based on the temporal segmentation of the
optimization period into smaller sub-segments, which
are processed with static solution approaches.
In (Barkaoui and Gendreau, 2013), a two-level ge-
netic algorithm is used to handle problems with dy-
namic customer orders. (Cr
´
eput et al., 2012), as well
as (Elhassania et al., 2014) are based on static so-
lution methods to process temporal sub-segments of
the actual problem instance. In contrast to the work
of Elhassania et al., which uses an ordinary GA, the
paper of Cr
´
eput et al. combines a GA with a self-
organizing map approach. Furthermore, the two pub-
lications of Ghannadpour et al., are also based on the
consecutive static processing of several temporal seg-
ments. Whereas the first paper can be used to process
dynamic customer orders and dynamic travel times
(Ghannadpour et al., 2013), the second one focuses
on dynamic customer orders exclusively (Ghannad-
pour et al., 2014). A related approach, which is also
based on the iterative processing of multiple time seg-
ments for dynamic customer orders can be found in
(Hanshar and Ombuki-Berman, 2007). A differing
concept is presented in (Taniguchi and Shimamoto,
2004) where the GA is applied to a newly developed
road network and focuses on dynamic travel times.
(Haghani and Jung, 2005) address dynamic optimiza-
tion of customer orders, including time dependent
travel times. A combined rolling horizon strategy in
combination with an annealing GA is presented in the
publication of (Gan et al., 2013).
(Branke et al., 2005) implemented various vehi-
cle waiting strategies for the purpose of anticipating
future customer orders. The goal is to maximize the
success rate of including additional customer orders
without violating any constraint. Another concept
was published by (AbdAllah et al., 2017). Again,
the dynamic VRP instance is modeled as a sequence
of static VRP instances. By enhancing the underling
GA, the authors try to increase the population diver-
sity and the capability to escape from local optimas.
The paper at hand progresses beyond the state of
the art as the proposed system provides an immediate
reactivity towards incoming information. Instead of
the partitioning into temporal segments, the optimiza-
tion period can be processed in a continuous, holistic
way. While other papers consider only few different
event types, the communication protocol proposed in
this work results in various event types. These are are
considered in a dynamic real-time delivery scenario
with changing traffic conditions and stochastic service
times to model different real-world scenarios. Fur-
thermore, delivery plans are evaluated economically
by a cost-based fitness function, since this is the basis
of decision making for transportation companies.
3 SCENARIO DESCRIPTION
3.1 Problem Description
In the static VRP optimization, delivery plans are cal-
culated regardless of any real-time information like
status updates on fleet events, even though this in-
formation is easily available nowadays. Hence, the
proposed delivery plan is likely to become obsolete
rather instantly. This is due to changes in traffic flows
or other unexpected changes of the environment.
One first step to overcome this issue is to mon-
itor the whole delivery period. Therefore, we have
established a communication protocol between the
individual vehicles and the optimization back-end.
Each vehicle is represented by a state machine (Figure
1), submitting status updates in terms of event data,
whenever the corresponding event occurs. One im-
portant assumption (A), that can directly be derived
from the definition of the state machine, is that for
each vehicle en route the next customer is fixed and
cannot be altered. This is due to the fact that the op-
timization back-end receives the next status update at
the arrival at the next customer location.
The defined model can simulate an arbitrary
amount of vehicles, using predefined mathematical
distributions for the generation of dynamic travel and
service times.
Unlike other work on the dynamic VRP, the pro-
posed communication protocol leads to the integra-
tion of various event types (Ready for Departure,
Started, Arrived, Unloaded, Departed) into the VRP,
which result from simulation in this work, but could
easily be obtained from mobile devices in real-world
applications. These events trigger different algorith-
mic actions which also include changes and correla-
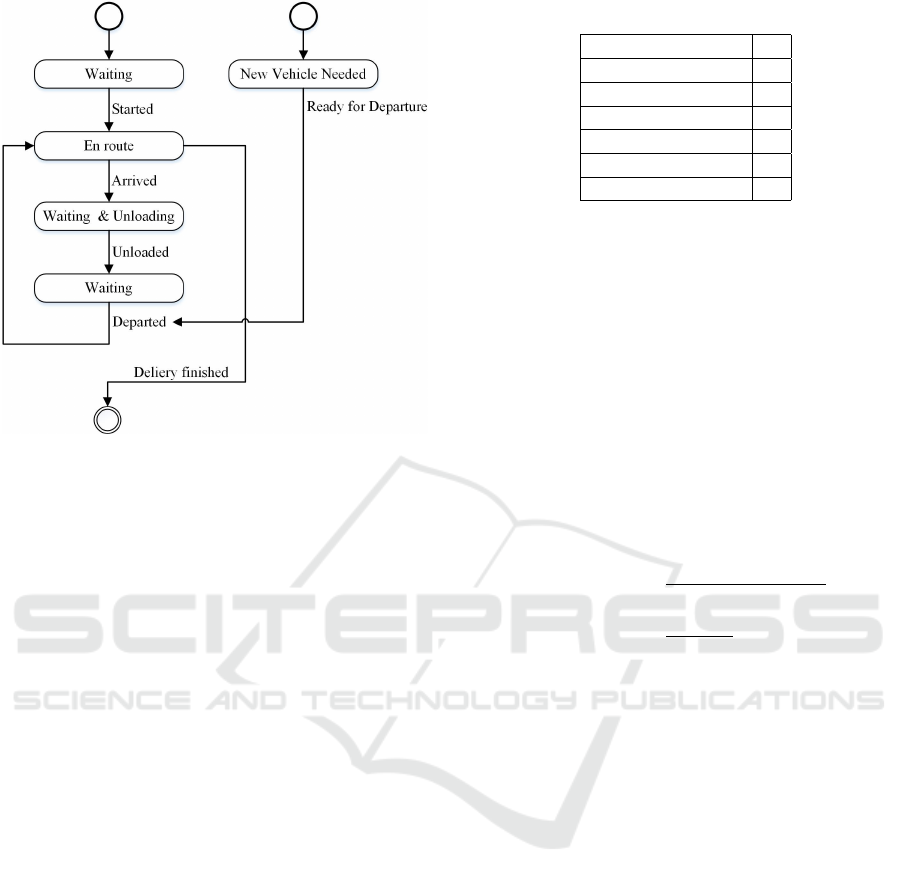
Figure 1: State machine model for individual vehicle.
tions to solution representations. The interaction of
event data and optimization process is explained in
detail in Section 5.
3.2 General Setting and Simulation
Unfortunately, exploring dynamic VRPs in real-
time lacks the availability of compatible benchmarks,
whereas benchmarks for static VRPs are very com-
mon. Hence, one solution to generate an appro-
priate setting for the real-time dynamic VRP is to
adapt static benchmark files to suit a real-time im-
plementation. Foundations to our work are the well-
known Gehring & Homberger benchmarks for the
static capacitated VRP with time windows (Gehring
and Homberger, 1999).
3.2.1 Description of the Benchmark Files
Besides the maximum number of vehicles K and a
uniform maximum capacity q of each vehicle, the
Gehring & Homberger benchmark files consist of a
list of N customers. Note, that the first customer c
0
is
the depot. Each customer can be considered a 7-ary-
tuple containing the values listed in Table 1.
Distances between customers are calculated as
Euclidean distances. Commonly, these benchmarks
suppose that one time unit equals one distance unit.
As this assumption is contradictory to realistic use-
cases, our approach differentiates between time and
distance by using average speed values to calculate
travel times from the given distances.
Table 1: Definition of customer c
i
.
Customer Number i
x-Coordinate x
i
y-Coordinate y
i
Demand d
i
Ready Time e
i
Due Date l
i
Service Time f
i
3.2.2 Introduction of Real-Time
To further enhance the benchmark towards real-time
scenarios, three additional parameters are introduced:
the start time of the delivery period is denoted as t
start
,
its planned duration is denoted as l
period
and the aver-
age velocity of a vehicle is represented by v. Due to
the fact, that the presented approach runs in system
time, all relevant time parameters must be converted
into milliseconds. Based on these parameters and the
due date of the depot l
0
, which marks the end of the
delivery period in the static benchmark, two basic co-
efficients can be derived:
f
time
:=
l
period
· 60 ·60 · 1000
l
0
(1)
f
distance
:=
v · l
period
l
0
(2)
Using these coefficients, time and location data of
the benchmark files can be adapted to create a real-
time environment. The time and location data of ev-
ery customer c
i
is adapted as shown below.
x
i,new
:= x
i
· f
distance
(3)
e
i,new
:= e
i
· f
time
+t
start
(4)
All other relevant parameters are adapted accord-
ingly.
3.2.3 Time-Dependent Travel Times
Time-dependent travel times are crucial as they em-
body changing traffic conditions. Based on the con-
cept of (Ichoua et al., 2003), the calculation period is
divided into discrete, equidistant time intervals with
predefined speed factors. The total travel distance re-
sults as sum of the iteratively calculated partial dis-
tances in each time interval. The travel time can then
be calculated based on the total distance. One advan-
tage of this method is the straightforward implemen-
tation of the FIFO principle, which guarantees, that a
later departure at a specified destination cannot lead
to a sooner arrival at another.

3.2.4 Dynamic Travel and Service Times
In real-world applications, traffic conditions underlie
dynamic changes due to accidents, construction sites,
congestion and more. To represent this adequately,
we apply a gamma distribution on the time-dependent
speed factors of the model. Specific parametrizations
then allow the simulation of different traffic scenarios
(Chiang and O. Roberts, 1980).
Additionally, staffing problems and occupied
loading zones e.g. by delay of preceding unloading
processes are only exemplary reasons that cause de-
layed service times in real-world scenarios. For this,
queuing theory proposes the gamma distribution to
generate dynamic service times (Liebermann et al.,
1997). More details on the specific parametrizations
are provided in Section 6.
3.2.5 Time Windows and Penalty Function
In the Gehring & Homberger benchmarks, each cus-
tomer c
i
is associated with a time window (e
i
, l
i
), in
which the delivery should be started. Time window
violations are taken into account by a penalty func-
tion, which assigns a penalty cost value p
i
to each
customer. Depending on the end of the time window
l
i
and the arrival time s
i
at customer c
i
, this is calcu-
lated as follows:
p
i
=
(
c
penalty
+ c f
penalty
· (s
i
− l
i
) if s
i
> l
i
,
0 else.
(5)
In this context, c f
penalty
is a cost factor rating the time
of delay and c
penalty
is the fixed cost part in case of
time window violation.
3.2.6 External Vehicles
For each of the Gehring & Homberger benchmark
files, a maximum number of vehicles K is specified.
However, real-time reaction to dynamic events may
require the use of additional vehicles in order to serve
all customer requests, preferably in the given time
windows. Hence, it is possible that K needs to be ex-
ceeded. In this case, our model assumes the possibil-
ity to hire different transportation companies by rent-
ing external vehicles (and drivers) which then carry
out some of the customer requests. Certainly, this im-
plies additional costs. These are assumed to be 20%
higher than the costs in case all customers could be
served by vehicles of the own fleet.
4 ARCHITECTURE
The proposed DVRP-system consists of three main
components, which are reflected in Figure 2. The op-
timizer represents the core component of the system
and is responsible for the actual optimization process.
The simulator executes delivery plans in real-time and
produces event data of the simulated fleet. Events for
each vehicle are raised according to the state machine
introduced in Figure 1. The decision maker handles
those events in real-time by updating the information-
base of the optimizer. A further responsibility of the
decision maker is to decide whether it is economically
viable to realize new delivery plans in case a new plan
is proposed by the optimizer.
Figure 2: Architecture of the DVRP-system.
4.1 Optimizer
An evolutionary algorithm is proposed, which en-
hances the hybrid multi-objective evolutionary algo-
rithm (HMOEA) by (Tan et al., 2006). Major parts of
the HMOEA have been adapted, enlarged or substi-
tuted to comply with the requirements of the environ-
mental model. The genotype is encoded as visualized
in Figure 3. According to the representation, a de-
livery plan consists of various tours, which represent
all customers dedicated to a specific vehicle. A tour
starts and ends at the depot c
0
. Besides all customers
c
i
are represented as integer values.
Figure 3: Encoding of a delivery plan.
The formerly used Pareto fitness ranking of the
HMOEA was replaced by the restricted tournament
selection (RTS) of Harik (Harik, 1995) and com-
bined with a selection method as well as a sim-
ple elitism method. To enable the evaluation of
the distance of different individuals as required in
the RTS, the optimizer uses the Jaccard-Coefficient
in combination with the 2-Gram method (Naumann
and Herschel, 2010). Furthermore, we adopted
the route-exchange-crossover, the three optional mu-
tation methods (split-route-mutation, merge-route-

mutation, partial-swap-mutation), as well as all lo-
cal search heuristics (intra-route-heuristic, lambda-
interchange-heuristic, shortest-path-heuristic) of the
original HMOEA, but adapted them to fit the require-
ments of the real-time model.
4.1.1 Cost Function
To evaluate the fitness of a solution, a newly devel-
oped cost function C
total
was implemented. As costs
are crucial for enterprises and their practical applica-
tion of the VRP, the cost function aggregates three
major cost drivers: distance-dependent costs C
distance
,
time-dependent costs C
time
and penalty costs C
penalty
.
For that, the tour time of a vehicle (from start to end
of its delivery) t
j
is weighted with a time cost factor
c f
time
. Analogously, the tour distance of each vehicle
d
j
is weighted by c f
distance
. The total time and dis-
tance costs are then both calculated as sum of the cost
values of all K vehicles. The overall penalty costs
C
penalty
result from the individual penalty costs p
i
of
all N customers.
C
total
= C
distance
+C
time
+C
penalty
(6)
C
distance
=
K
∑
j=0
(c f
distance
· d
j
· δ
j
) (7)
C
time
=
K
∑
j=0
(c f
time
·t
j
· δ
j
) (8)
C
penalty
=
N
∑
i=0
p
i
(9)
To reflect the possibility of hiring external vehi-
cles and the associated extra costs, δ
j
is introduced
and defined as follows:
δ
j
:=
(
1.0 if vehicle j is part of fleet,
1.2 if vehicle j is not part of fleet.
(10)
4.2 Simulator
The simulator is responsible for the generation of the
events, which includes the simulation of the dynamic
travel and service times. Aligned to the approach of
(Ichoua et al., 2003), the simulator generates individ-
ual speed factors for each road segment and each time
interval. Based on the simulated speed factors the ac-
tual travel time can be calculated. The dynamic ser-
vice times are simulated by applying the integrated
gamma distribution directly to the updated service
time values of the benchmark file. The flexible im-
plementation of the simulator facilitates the modular
exchange of different traffic/queuing models, as well
as the integration of real traffic data. Furthermore,
it is possible to substitute the simulator for mobile
devices or vehicle-based on-board devices, using the
same event-based communication protocol.
4.3 Decision Maker
The decision maker represents the interface between
the simulator and the optimizer. It is responsible for
plan updates and the information flow towards the
individual vehicles. For this purpose, the decision
maker continuously compares the current best plan of
the optimizer with the plan currently executed and de-
cides whether a change should be realized. Thereby
an real-time reactivity towards new information, as
well as the alignment of the delivery plan towards the
currently best solution is ensured throughout the en-
tire optimization period.
As all information emerging from the simulator
passes the decision maker, the decision maker is also
responsible for the event handling process. This com-
prises the update of the information base, as well as
the execution of repair routines. These are necessary
in case the individuals of the HMOEA-population
need to be adapted throughout the dynamic optimiza-
tion process.
5 ALGORITHMIC ASPECTS
The communication protocol between the vehicles
and the optimization back-end requires a thorough
definition of the submitted event data and their
algorithmic consequences. For this purpose, the
decision maker is implemented as interface between
the simulator and the optimizer to handle incoming
events. The tasks of the decision maker can be
divided as follows:
Update of Information-Base
To properly use the incoming information, it has to be
embedded into the information base of the optimizer.
This includes the real-time update of actual and
expected travel/service times as well as the update of
the customer base.
Adaption of Population
Some events also require an update on the population
of the HMOEA to guarantee a consistent set of fea-
sible individuals for the further execution of the opti-
mization process. The importance of this will be ex-
plained subsequently.

5.1 Event Handling
Referring to Figure 1, this section describes all types
of events and their inherent changes to the optimiza-
tion process.
The Arrived-event marks the arrival of a vehicle at
a customer and is handled with a simple routine. The
decision maker processes the received information by
replacing the expected arrival time at the correspond-
ing customer (which was used by the optimizer for
plan calculations until then) by the actual arrival time.
The same procedure is valid for the Unloaded-
event which marks the end of the service period of a
vehicle at a customer. In this case, the decision maker
replaces the expected service time by the actual ser-
vice time.
The Departed-event however requires more so-
phisticated routines. On the one hand the expected
departure time has to be replaced by the actual depar-
ture time. On the other hand the served customer c
old
,
which the vehicle has departed from, has to be deleted
from the representation. Due to (A) we obtain a fixed
customer c
next
as a next target for the considered vehi-
cle. This causes the necessity to update the population
of the HMOEA as c
old
has to be deleted from each in-
dividual of the population. Each individual shall now
contain one vehicle heading to c
new
(which means one
tour with c
new
at first position).
The same adaptions have to be conducted for the
Started-event, where c
old
is considered as a substitute
for the depot. Additionally, this event marks the be-
ginning of the delivery period and therefore the shift
from static to dynamic optimization.
In case the decision maker proposes the utiliza-
tion of an additional vehicle, the Ready for Depar-
ture-event is triggered and a new vehicle departs at
the depot c
old
heading to a customer c
new
. As a con-
sequence, all individuals of the population have to be
expanded by one vehicle also heading to c
new
(A).
5.2 Repair Routines
To guarantee the individuals of the HMOEA-
population to be feasible at all times, the events
Started and Departed trigger repair mechanisms for
the entire HMOEA-population. Each individual has
to be adapted such that the new customer c
new
is di-
rectly targeted by a vehicle, whereas the served cus-
tomer c
old
is deleted from all individuals. In some
cases, it may be required to relocate several unserved
customers within the individual. Therefore these
customers are transferred to a so-called reloctaion-
list (RL) and later reinserted by a special insertion
method.
5.2.1 Repair Routine for the Departed-Event
In case c
old
and c
new
are scheduled to be served by
the same vehicle, the corresponding tour will be cut
before c
new
, thus making sure that this vehicle serves
c
new
as next customer. Furthermore, the customers
between c
old
and c
new
are put on the RL (Figure 4).
Figure 4: Repair routine for the Departed-event (case 1).
If c
new
is contained in a different tour than c
old
, all
customers of the tour that contains c
old
will be trans-
ferred to the RL. The customers of the tour containing
c
new
will be divided as visualized in Figure 5. This en-
sures that the considered vehicle keeps on heading to
the customer that it is targeting (customer 6 in the ex-
ample) while the vehicle, whose tour contained c
old
,
is now targeting c
new
.
Figure 5: Repair routine for the Departed-event (case 2).
Repair Routine in Pseudo-Code:
Find tour containing c_old;
Delete c_old;
if(c_new is contained in same vehicle)
Put customers before c_new on RL;
Delete customers before c_new;
else
Delete last customer (depot);
Put remaining customers on RL;
Find tour containing c_new;
Divide tour at c_new;
Replace vehicle that contained c_old;
5.2.2 Repair Routine for the Started-Event
In the case of the Started-event all scheduled vehicles
leave the depot at the beginning of the delivery pe-
riod. Thereby, each vehicle gets assigned a fixed first
customer (c
new
). In the following, the set containing
these customers is denoted S. To update the individu-
als of the HMOEA-population, in a first step the depot
at first position of each vehicle’s tour is deleted. Sub-
sequently, for each tour it is checked whether its first
customer is contained in S. If so, this tour remains un-
changed and the corresponding customer gets deleted
from S. In the other case, the vehicle is put to a recom-
bination list. In a third step, the remaining customers

Figure 6: Repair routine for the Started-event.
in S are deleted from the tour. Finally the customers
in S are recombined with the remaining tours in a cost
efficient way to create a new individual that is fea-
sible. For a short example on this repair routine see
Figure 6.
In case no feasible way of recombination is found,
customers of the remaining vehicle representations
are transferred step by step to the relocation list
until a feasible recombination is obtained. After this
procedure, the customers of the RL are reinserted
using the insertion method.
Repair Routine in Pseudo-Code:
Delete first customer of each individual;
for (each tour)
if (first customer of tour is in S)
Delete customer from tour;
Delete customer from S;
else
Put tour on recombination list;
end
Delete customers in S from tours;
Recombine customers in S with remaining tours
of recombination list;
while (no feasible combination found)
Put random customer (not contained in S)
to relocation list;
Recombine customers in S with remaining
tours of recombination list;
end
5.2.3 Insertion Method
The insertion method is in charge of the reinsertion of
the customers that were transferred to the relocation
list by the repair routines. To minimize the loss of
optimization knowledge, it is aspired to maintain
the major parts of the customer-sequence. There-
fore, this method randomly inserts (and instantly
deletes) the first customer of the RL at a predefined
number of positions in the genotype and calculates
the corresponding cost value. Subsequently, the
customer is inserted at the position, that causes
minimal additional costs. If no feasible insertion
position is found, a new vehicle is required to serve
this customer. Thereafter, all following customers
are inserted and deleted from the RL as long as there
is no violation to the capacity limitation. In case of
violation this procedure starts anew.
Insertion Method in Pseudo-Code:
while(customers contained in RL)
for (counter < number of attempts)
Insert first customer of RL at random
position in genotype;
if (feasible)
Evaluate cost function;
Delete first customer from genotype;
Counter++;
end
if (feasible position found)

Insert first customer at best position;
else
Insert customer in new vehicle;
while (no violation to capacity)
Insert following customers from RL;
end
end
6 EVALUATION
The aim of this chapter is a holistic evaluation of
the repair routines. As a first step, this paper vali-
dates their general functionality and impact towards
different dynamic problem instances. Future research
should focus on a detailed analysis and the further en-
hancement of the approach. In order to evaluate the
performance of the dynamic optimization, the evalu-
ation concept is based on the comparison of the ini-
tial delivery plan and the actual plan. The actual plan
P
actual
results from the initial delivery plan P
initial,static
by constant changes through the continuous reactions
of the optimization back-end to the dynamic environ-
ment, whereas the initial plan is the result of the static
optimization at the beginning of the delivery period.
Assuming this delivery plan is exposed to the dy-
namic events without online re-optimization, Figure
7 shows the respective cost as P
initial,simulated
. To en-
sure the comparability of P
initial,simulated
with P
actual
,
it is crucial to use the same underlying traffic condi-
tions and service times. Figure 7 shows the typical
progression of the cost functions of the three consid-
ered plans.
Figure 7: Typical progression of the cost functions.
6.1 Test Setup
The real-time test setup employs the C101 instances
of the Gehring & Homberger benchmarks for 200,
400, 600, 800 and 1000 customers. Each of these
instances was simulated using three different shifted
gamma distributions. Every combination of the test
instances and the gamma distributions was repeated
ten times with different random seeds, which resulted
in 150 test runs. All instances model an entire real-
time distribution period starting the static optimiza-
tion at 8.00 pm the day before the actual delivery took
place. Dynamic optimization starts with the begin-
ning of the distribution period at 8.00 am and contin-
ues until 4.00 pm. All relevant parameters used in the
test setup are shown in Table 2. For a detailed defi-
nition of the genetic parameters, please refer to (Tan
et al., 2006).
Table 2: Test parameters.
Crossover-rate 0.7
Mutation-rate 1.0
Elastic-rate 0.5
Squeeze-rate 0.7
Population-size 20
Elitism-quantity 3
c f
distance
1e/km
c f
time
60e/h
c f
penalty
50e/h
c
base
100e
t
start
8:00 am
l 8h
v 70km/h
The focus is set on evaluating different traffic con-
ditions and their impact on the optimization process.
Hence, one single parameter setting was used for the
simulation of the dynamic service times. The service
time is reflected by the gamma distribution (1, 0.25)
which is shifted by 0.75. The three gamma distribu-
tions, which were used for the simulation of the dy-
namic service times are shown in Table 3 .
Table 3: Parameter for the gamma distribution.
Distribution 1: Γ(1, 0.25), Shift: 0.75
Distribution 2: Γ(1, 0.50), Shift: 0.5
Distribution 3: Γ(1, 0.75), Shift: 0.25
The distribution parameters have been chosen fol-
lowing the approach of (Russell and Urban, 2008)
where the gamma distribution was applied to model
dynamic travel times. The expected value equals 1 in
all cases.
6.2 Test Evaluation
The final average results of all 150 test instances
grouped by the number of customers are shown in Ta-
ble 4. The results indicate the percentage, as well as
the total deviation of P
actual
from P
initial,simulated
. In
total, an average saving of 6.58% in the overall costs

Table 4: Test results on different instances of the adapted Gehring & Homberger C101 benchmark files.
could be achieved. The overall saving is primarily
caused by a significant reduction of the penalty costs
and usually results in an increase of the distance and
time values. As shown in the table, the increase in the
distance and time values seems to correlate with the
number of processed customers. The instances with
less customers generally indicate a higher increase
in the corresponding values, than the instances with
more customers. The number of additional vehicles
is also increasing by 0.92% to 3.92% which means
up to three additional vehicles in average. However,
there was no test instance in which the number of
vehicles exceeded the maximum fleet size K of the
C101 Gehring & Homberger benchmarks. This im-
plies that no external vehicle was needed in all test
instances. The percentual reduction of time window
violations is decreasing with the number of processed
customers, whereas the total number reaches its peak
at the test instances with 600 customers. As the num-
ber of time window violations is directly affecting the
penalty costs, similar characteristics are reflected in
these results. The achieved results indicate a reli-
able performance of the implemented repair routines
in various test settings, by achieving overall average
savings between 4.98% and 7.66%.
7 CONCLUSION
This paper proposed an approach to real-time fleet
event handling for the DVRP based on evolutionary
computation. In contrast to other approaches, the sys-
tem allows for rapid responses to dynamic events and
processes dynamic travel times as well as dynamic
service times. The system is able to simulate real-time
delivery periods lasting up to one day and is designed
for further expansion like the inclusion of GPS-data
or real event data. With the two newly developed
repair routines, new innovative methods were imple-
mented to ensure a continuous creation of feasible de-
livery plans. The system runs a time-dependent travel
time model and optimizes the total costs of the deliv-
ery plan including penalty costs for delayed delivery.
In empirical studies the system and its repair routines
could be validated in different test scenarios. Further-
more, the DVRP-system led to cost savings between
4.98% and 7.66% in all test scenarios.
8 FUTURE WORK
The flexible and modular system implementation, al-
lows for easy extension and adaption. Even the sub-
stitution of essential parts such as the simulator is pos-
sible with little effort. This is enabled by a smart and
lightweight system architecture with a clearly struc-
tured message exchange protocol between the system
components.Therefore, the system could be extended
by additional dynamic aspects such as dynamic cus-
tomer orders. In order to test the system in a real-
life scenario, the simulator is projected to be substi-
tuted and replaced by mobile devices and/or be con-
nected to on-board vehicle-based systems. Such alter-
nate edge devices would then be responsible for the
information (event) transfer towards the optimization
back-end. The adaption of the current system would
require very little effort only. As a long-term goal, it
is aspired to include GPS-data. Besides these struc-
tural adaptions of the system, it is crucial for further
development to enlarge the test evaluation towards ad-
ditional benchmark tests. Especially, more restrictive
settings considering the fleet size would be preferable
to evaluate the concept of external vehicles and the
influence of the associated extra costs δ
j
. Further re-
search focuses on a detailed analysis of repair routines
and their impact on the optimization process. Ad-
ditionally, existing optimization algorithms like Ant
Colony Optimization or Particle Swarm Optimization

and other solution strategies for the DVRP (Psaraftis
et al., 2016) need to be adapted to the proposed dy-
namic real-time VRP-environment to ensure compa-
rability. The gathered insights can then be used to
gain optimization performance.
REFERENCES
AbdAllah, A. M. F., Essam, D. L., and Sarker, R. A. (2017).
On solving periodic re-optimization dynamic vehicle
routing problems. Applied Soft Computing, 55:1–12.
Barkaoui, M. and Gendreau, M. (2013). An adaptive
evolutionary approach for real-time vehicle routing
and dispatching. Computers & Operations Research,
40(7):1766–1776.
Bektas, T., Repoussis, P., and Tarantilis, C. (2014). Dy-
namic vehicle routing problems. In Toth, P. and Vigo,
D., editors, Vehicle routing, MOS-SIAM series on op-
timization, pages 299–347. Society for Industrial and
Applied Mathematics and Mathematical Optimization
Society, Philadelphia.
Branke, J., Middendorf, M., Noeth, G., and Dessouky, M.
(2005). Waiting strategies for dynamic vehicle rout-
ing. Transportation Science, 39(3):298–312.
Chiang, Y.-S. and O. Roberts, P. (1980). A note on transit
time and reliability for regular-route trucking. Trans-
portation Research Part B: Methodological, 14(1-
2):59–65.
Cr
´
eput, J.-C., Hajjam, A., Koukam, A., and Kuhn, O.
(2012). Self-organizing maps in population based
metaheuristic to the dynamic vehicle routing problem.
Journal of Combinatorial Optimization, 24(4):437–
458.
Elhassania, M., Jaouad, B., and Ahmed, E. A. (2014). Solv-
ing the dynamic vehicle routing problem using ge-
netic algorithms. In 2014 International Conference on
Logistics and Operations Management (GOL), pages
62–69.
Gan, Z., Tao, L., and Ying, Q. (2013). Automated guide ve-
hicles dynamic scheduling based on annealing genetic
algorithm. Indonesian Journal of Electrical Engineer-
ing and Computer Science, 11(5):2508–2515.
Gehring, H. and Homberger, J. (1999). A parallel hy-
brid evolutionary metaheuristic for the vehicle rout-
ing problem with time windows: Jyv
¨
askyl
¨
a, finnland.
In Miettinen, K., M
¨
akel
¨
a, M., and Toivanen, J., ed-
itors, Proceedings of EU-ROGEN99, pages 57–64,
Jyv
¨
askyl
¨
a, Finnland.
Ghannadpour, S. F., Noori, S., and Tavakkoli-Moghaddam,
R. (2013). Multiobjective dynamic vehicle routing
problem with fuzzy travel times and customers’ sat-
isfaction in supply chain management. IEEE Trans-
actions on Engineering Management, 60(4):777–790.
Ghannadpour, S. F., Noori, S., Tavakkoli-Moghaddam, R.,
and Ghoseiri, K. (2014). A multi-objective dynamic
vehicle routing problem with fuzzy time windows:
Model, solution and application. Applied Soft Com-
puting, 14:504–527.
Haghani, A. and Jung, S. (2005). A dynamic vehicle routing
problem with time-dependent travel times. Computers
& Operations Research, 32(11):2959–2986.
Hanshar, F. T. and Ombuki-Berman, B. M. (2007). Dy-
namic vehicle routing using genetic algorithms. Ap-
plied Intelligence, 27(1):89–99.
Harik, G. (1995). Finding multimodal solutions using re-
stricted tournament selection. In Eshelman, L. J., edi-
tor, Proceedings of the Sixth International Conference
on Genetic Algorithms, pages 24–31. M. Kaufman,
San Francisco, Calif.
Ichoua, S., Gendreau, M., and Potvin, J.-Y. (2003). Vehicle
dispatching with time-dependent travel times. Euro-
pean Journal of Operational Research, 144(2):379–
396.
Liebermann, G. J., Hillier, F. S., Fackler, M., Bauer,
G., Honold, G., Michels, K.-N., Rehklau, U.,
and Weigert, M. (1997). Operations Research:
Einf
¨
uhrung. Internationale Standardlehrb
¨
ucher der
Wirtschafts- und Sozialwissenschaften. De Gruyter
Oldenbourg, M
¨
unchen, 5. aufl. edition.
Naumann, F. and Herschel, M. (2010). An introduction to
duplicate detection, volume #3 of Synthesis lectures
on data management. Morgan & Claypool Publishers,
San Rafael, Calif.
Pillac, V., Gendreau, M., Gu
´
eret, C., and Medaglia, A. L.
(2013). A review of dynamic vehicle routing prob-
lems. European Journal of Operational Research,
225(1):1–11.
Psaraftis, H. N., Wen, M., and Kontovas, C. A. (2016). Dy-
namic vehicle routing problems: Three decades and
counting. Networks, 67(1):3–31.
Ritzinger, U., Puchinger, J., and Hartl, R. F. (2015). A sur-
vey on dynamic and stochastic vehicle routing prob-
lems. International Journal of Production Research,
54(1):215–231.
Russell, R. A. and Urban, T. L. (2008). Vehicle routing with
soft time windows and erlang travel times. Journal of
the Operational Research Society, 59(9):1220–1228.
Tan, K. C., Chew, Y. H., and Lee, L. H. (2006). A hybrid
multiobjective evolutionary algorithm for solving ve-
hicle routing problem with time windows. Computa-
tional Optimization and Applications, 34(1):115–151.
Taniguchi, E. and Shimamoto, H. (2004). Intelligent trans-
portation system based dynamic vehicle routing and
scheduling with variable travel times. Transporta-
tion Research Part C: Emerging Technologies, 12(3-
4):235–250.
