Comparing Small Population Genetic Algorithms over Changing

Landscapes

Michael Curley and Seamus Hill

College of Engineering and Informatics, National University of Ireland Galway, Ireland

Keywords:

Genetic Algorithms, Changing Landscapes, Population Size, Adaptability.

Abstract:

This paper examines the performance and adaptability of a number of small population Genetic Algorithms

(GAs) over a selection of dynamic landscapes. Much of the research in this area tends to focus on GA

with relatively large populations for problem optimisation. However there is research, which suggests that

GAs with smaller populations can also be effective over changing landscapes. This research compares the

performance and adaptability of a number of these small population GA over changing landscapes. With small

population GAs, convergence can occur quickly, which in turn affects the adaptability of a GA over dynamic

landscapes. In this paper ﬁve GA variants using small population sizes are run over well-known unimodal and

multimodal problems, which were tailored to produce dynamic landscapes. Adaptability within the population

is considered a desirable feature for a GA to optimise a changing landscape and different methods are used

to maintain a level of diversity within a population to avoid the problem of premature convergence, thereby

allowing the GA population adapt to the dynamic nature of the search space. Initial results indicate that small

population GAs can perform well in searching changing landscapes, with GAs which possess the ability to

maintain diversity within the population, outperforming those that do not.

1 INTRODUCTION

Genetic Algorithms (GAs) (Holland, 1992) (Gold-

berg, 1989) are search algorithms based on Darwinian

principals of survival of the ﬁttest. GAs are popula-

tion based optimisers and as population evolve from

generation to generation they tend to become homo-

geneous as the population converges. GAs are widely

used for various optimisation problems, however op-

timisation over changing landscapes, can prove more

difﬁcult compared to that of static landscapes as the

populations needs to be able to adapt and escape local

optima as the landscape changes. Therefore, if popu-

lations tend to converge on a particular solution, a GA

needs to be able to evolve its population to respond to

changes over a changing landscape. Because of this,

the ability for the GA population to adapt to changes

in the search space is critical in optimising changing

landscapes. Adaptability (Mori and Kita, 2000)(Kr-

ishnakumar, 1990)(Mumford, 2004) is considered to

play an important role in how GA searches through a

changing landscapes. Associated with adaptability is

the maintenance of diversity within the population.

With this in mind, a decision needs to be taken

whether it is better to use a standard GA and restart

the population when the landscape alters or to use a

GA which maintains an element of diversity within

the population. Research such as (Cobb and Grefen-

stette, 1993; Krishnakumar, 1990; Grefenstette et al.,

1992; Goldberg and Smith, 1987) looked at station-

ary and non-stationary landscapes and found that GAs

were able to optimise functions over both landscapes,

with the maintenance of population diversity being a

critical feature. Population size is also an important

consideration in the optimisation of a changing land-

scape. Researchers such as (Ahn and Ramakrishna,

2002) (Grefenstette, 1986) (Whitely, 1989) (Krish-

nakumar, 1990) found small populations to be just

as effective in optimizing certain landscapes, thereby

avoiding the additional overhead associated with a

larger population.

This paper examines and compares the perfor-

mance and adaptability over changing landscapes, of

a number of GA implementations using small pop-

ulations. The motivation is to compare the perfor-

mance and adaptability of a number of small popu-

lation GAs over changing landscapes in order to ex-

amine the impact of diversity maintenance and deter-

mine whether restarting a standard GA or the inclu-

sion of a diversitymaintenance technique is most ben-

Curley M. and Hill S.

Comparing Small Population Genetic Algorithms over Changing Landscapes.

DOI: 10.5220/0006497802390246

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 239-246

ISBN: 978-989-758-274-5

eﬁcial over the given landscapes. The contribution is

to develop an insight into the ability of various small

population GAs to adapt and optimise changing land-

scapes by comparing their performance over speciﬁ-

cally designed landscapes. Initial results indicate that

the use of particular diversity maintenance techniques

in small population GAs, proves beneﬁcial over the

chosen landscapes. The paper is laid out as follows:

Section 2 examines the background literature. Sec-

tion 3 outlines the GAs and the test suite used in the

experiments. Section 4 describes the ﬁndings, Section

5 concludes and Section 6 outlines future work.

2 BACKGROUND

In relation to population diversity and convergence,

De Jong (DeJong, 1975) set a threshold value of

95% similarity between loci alleles to indicate con-

vergence. By examining ﬂuctuations in online per-

formance we can get a indication of the level of con-

vergence within the population. Work carried out by

Mahfoud (Mahfoud, 1995) deﬁned convergence as

occurring when the average population ﬁtness value

for the previous 4 generations is greater than the av-

erage ﬁtness value for the present generation. Allen

et al. (Allen and Karjalainen, 1999) used a simple ap-

proach to measure convergence and deﬁned that if no

progress has been made after 25 generations then the

GA has converged. The approach used is this research

is Allen’s method because of its simplicity; further-

more this method give the GA a better opportunity of

avoiding getting caught in local optima in the land-

scapes used in this research.

GA theory would suggest that larger GA popula-

tions should maintain an element of diversity within

the population for a longer period when compared

to small population GAs (Leung et al., 1997) (Gold-

berg and Deb, 1991). If diversity can be maintained,

the additional genetic material or building blocks

should assist in the adaptability of the GA. How-

ever, this comes at a cost of time and complexity as

the larger population takes longer to search through

(Ahn and Ramakrishna, 2002) there exists a trade

off between the advantages of having a large popu-

lation in terms of searching a search space and the

associated additional overhead. Research by Gref-

fenstette (Grefenstette, 1986) and also by Whitley

(Whitely, 1989), found that smaller population sizes

with slightly higher crossover and mutation rates to be

just as affective when searching a landscape. The mu-

tation operator plays a role in introducing diversity by

allowing a population which has converged on a par-

ticular solution, to open up the landscape to further

exploration. However, there is a limit to it’s ability to

introduce diversity, before it becomes a random walk.

3 EXPERIMENTAL SET UP

In this paper we compare the performance and adapt-

ability of GAs using small populations over changing

landscapes. We contrast the results of a simple GA

(SGA) (Holland, 1992) to four GA variations: GA

with Elitism (GAE), Immigration GA (GAI), Micro

GA (MGA) and Diploid GA (DGA). The GA with

elitism (GAE) (Goldberg, 1989) retains the ﬁttest

chromosomesfrom generation to generation. As there

is no guarantee of a chromosome surviving selec-

tion, with a standard GA, elitism guarantees that the

ﬁttest individual will be maintained in the population.

The immigration GA (GAI), implemented as outlined

by (Yang, 2008), results in the best solution being

maintained in the population, while the worst indi-

vidual is replaced by a random immigrant. The Mi-

cro GA (MGA) (Krishnakumar and Bailey, 1990) re-

tains the best individual from generation to genera-

tion and once convergence is detected, the remainder

of the population is randomly initialised. Finally, the

Diploid GA (DGA) used in this research is as outlined

in (Goldberg and Smith, 1987).

3.1 Test Suite

De Jong(DeJong, 1975) used the Sphere function and

Shekel’s function in his paper and these functions

were used to test a number of parameters at differ-

ent values. Population size, crossover and mutation

rates were examined at different levels and the results

produced from these experiments lay the foundation

parameters which are still in use today on these func-

tions. The Sphere function is used to test the general

efﬁciency of a GA and Shekel’s function is used to

test the GAs ability to avoid getting caught in the 25

local optima or foxholes that are present in that land-

scape. DeJong found that the GA was able to optimise

both landscapes and the that the values of mutation

population and crossover values play an important in

how efﬁciently a GA optimises a landscape. Other re-

searchers such as Digalakis et al. (Digalakis and Mar-

garitis, 2002) carried out these experiments and were

able to optimise the Sphere and Shekel’s function by

using DeJong parameter values.

3.1.1 Sphere Function

According to DeJong (DeJong, 1975) the sphere func-

tion is a unimodallow-dimensionalquadratic function

with a minimum of zero, in other words it contains no

local optima. The Sphere Model (DeJong, 1975) is

relatively easy to optimise as it is continuous, con-

vex and unimodal. This function is normally used to

measure the efﬁciency of a particular algorithm. The

Sphere function is represented as follows:

f(x) =

∑

i=1

where: min( fx) = fx(0, .. . , 0) = 0 and d is the num-

ber of dimensions, −5.12 ≤ x

≤ 5.12 and for all

i = 1, . . . , d. The changing environment experiments

allow the GAs to search the landscape deﬁned by the

Sphere model, with the function being inverted after

100 generations. By changing the ﬁtness function in

this manner, what was the global optimum becomes

the furthest point from the new global optimum.

3.1.2 Shekel’s Function

Shekel’s function is a continuous non-convex, non

quadratic two-dimensional multimodal function with

25 local minima based at the points. This 2-

dimensional function contains 25 different foxholes,

each varying in depth, surrounded by relatively ﬂat

surfaces. Shekel’s Foxhole function has the following

deﬁnition:

f(x) =

500

∑

j=1

j +

∑

i=1

− a

)

−1

where:

−65.536 ≤ x

≤ 65.536



−32 −16 0 16 32 −32 .. . 0 16 32

−32 −32 −32 −32 −32 −16 . . . 32 32 32



Shekel’s Foxhole is a minimising problem, where

f(x) = f(0, . . . , 0) = f(−32, −32) ≈ 1. At generation

500 the objective function is inverted, meaning that

the old global optimum is now the furthest point from

the new global optimum.

3.2 Parameter Settings

Parameter setting in GA is a key component in get-

ting the algorithm to operate in an efﬁcient and effec-

tive manner. Researchers have come up with slightly

different parameters over time but are problem de-

pended. The values used in this research are taken

from Grefenstette (Grefenstette, 1986) and found

that smaller population sizes with slightly higher

crossover and mutation rates to be just as positive to

converge on a solution and with quicker results time

due to less processing time.

Table 1: Parameter Settings.

Parameter settings Changing Sphere Changing Shekels

population size 30 30

crossover 0.7 0.7

mutation 0.01 0.01

generations 200 1000

runs 20 20

4 FINDINGS

This section outlines the results for each of the

GAs over the changing Sphere function and chang-

ing Shekel’s function. With graphs plotting the On-

line (average) and Ofﬂine (best) results. As these are

minimising problems the results tend to zero on the

graph as the GA evolves. The dynamic Sphere func-

tion experiments were run over 200 generations, with

the objective function altering at generation 100. The

dynamic Shekel’s function experiments ran for 1000

generations, with the ﬁtness function changing at gen-

eration 500. A two sided paired Wilcoxon test was

carried out on the ofﬂine results for each of the exper-

iments to access whether the population means dif-

fer for the variant GA when compared to the SGA.

Results were considered to be statistically signiﬁcant

with a Pvalue < 0.005.

4.1 SGA (SGA) Changing Sphere

Function Results

The SGA results indicate that the algorithm had lit-

tle difﬁculty in solving the problem, both before and

after the landscape change. Figure 1 illustrates both

the online and ofﬂine performance. As shown in Ta-

ble 2, the SGA located the global optimum value of

0, both before and after the change. The results also

indicate that the population converges quite quickly,

shown by the closeness of the online and ofﬂine re-

sults. However, as the population had converged on

chromosomes representing the original global opti-

mum, once the objective function altered, this turns

what were good chromosomes with high ﬁtness val-

ues, into very poor solutions. This change in the land-

scape is designed to examine the GAs ability to adapt

and locate the new global optimum. Optimisation

takes longer at this point, as the population is made

up of solutions that are much further away from the

solution than the initialised population at the start.

The SGA adapting to the change in the objective

function and searching for the new global optimum

is shown by the slight increase in distance between

the online and ofﬂine results, as the population be-

gins to move away from the area of the search space

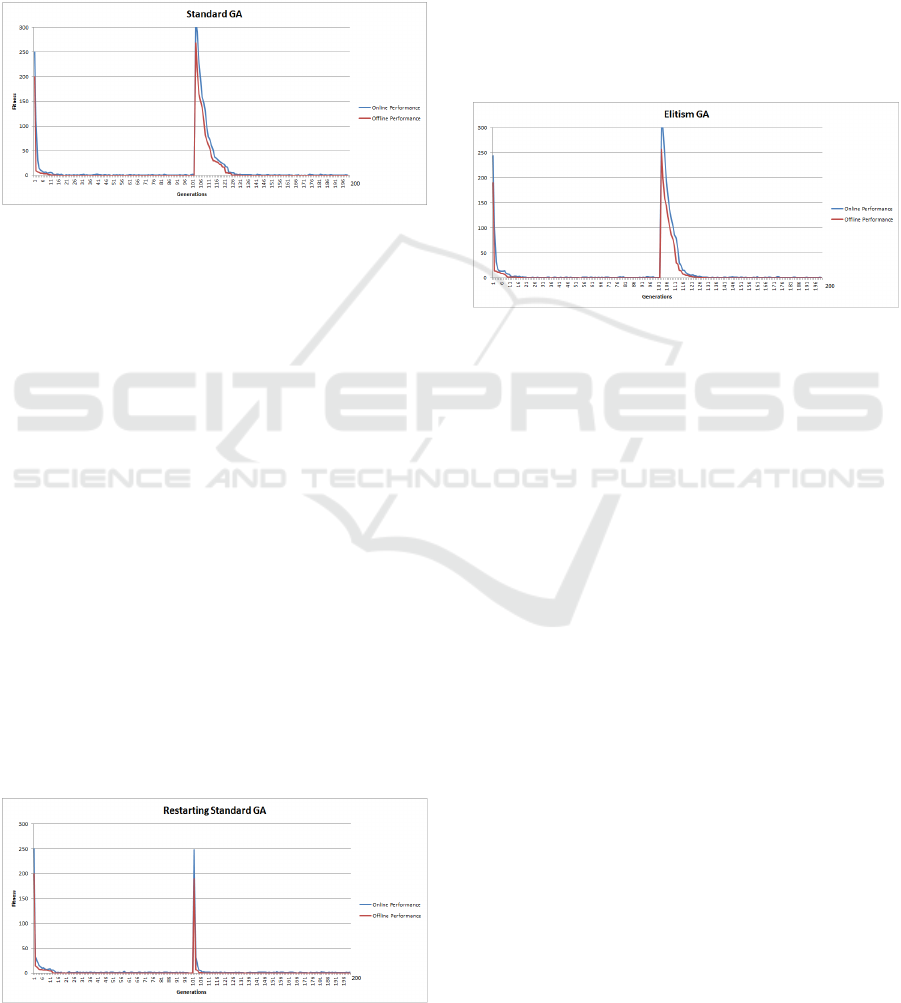
where is had converged. Following the change in

the ﬁtness function, the SGA eventually locates the

global optimum (see Table 2) and begins to converge

as the distance between the ofﬂine and online results

decreases. Overall the SGA, using a small popula-

tion, had little difﬁculty in optimising the landscape

both before and after the ﬁtness solution representa-

tions were changed, this is largely due to the nature of

the Sphere function.

Figure 1: SGA Changing Sphere Function.

4.2 SGA Restart (SGAR) Changing

Sphere Function Results

Figure 2 outlines the online and ofﬂine performance

of restarting or reinitialising the population of the

SGA when the landscape alters. The results indicate

that in the initial phase of the search, the performance

of the SGAR is similar to that of the SGA. However,

once the landscape changes, the early online and of-

ﬂine results of the SGAR are better than those of the

SGA. This appears to indicate that the SGAR, through

random initialisation, appears ﬁnd it easier to locate

the new global optimum. One reason for this is that in

the random initialisation of the population, conducted

after the change in the objective function, leaves the

population, on average, closer to the new global op-

timum, rather than converged around the old global

optimum as is the case for the SGA. Table 2 indi-

cates that in terms of locating the global optimum

the performance of the SGAR is comparable with that

of the SGA, but marginally better after the landscape

change. Comparing the ofﬂine results of the SGAR to

Figure 2: SGA Changing Sphere Function.

those of the SGA, the results were shown to be statis-

tically highly signiﬁcant (p − value < 2.2e

4.3 GA with Elitism (GAE) Changing

Sphere Function Results

Figure 3 contains the ofﬂine and online results for

the GAE. Overall, the GAE’s online and ofﬂine per-

formances appear marginally better than that of the

SGA, due to the introduction of elitism (see Table 2).

The ofﬂine results of the SGA compared to GAE were

shown, using to be statistically highly signiﬁcant with

a p − value of 2.817e

−08

Figure 3: GA with Elitism (GAE) Dynamic Sphere Func-

tion.

4.4 Immigration GA (GAI) Changing

Sphere Function Results

The GAI results (see Figure 4), the global optimum

value of 0 was located on average, at generation 4.

Once the landscape altered, the ofﬂine global opti-

mum of 0 was located at generation 138. The GAI

used in this paper, removes the worst solution in each

generation and replaces it with the best solution from

the previous generation. This allows the GAI to insert

and remove solutions based on the ﬁtness function for

the particular landscape. The results, illustrated in Ta-

ble 2, indicate that over the changing Sphere function,

the Immigration GA outperforms the SGA, SGAR

and GAE, before and after the landscape change. Al-

though the ofﬂine results compare favourably, it is in-

teresting to note that the online results shown in Fig-

ure 4, after the landscape change, illustrate the GAI’s

ability to adapt through the introduction of diversity

into the population. This is shown in the graph by

the increase in distance between the online and ofﬂine

lines. The ofﬂine results of the SGA and GAI for the

Dynamic Sphere experiment were statistically highly

signiﬁcant (p − value < 2.2e

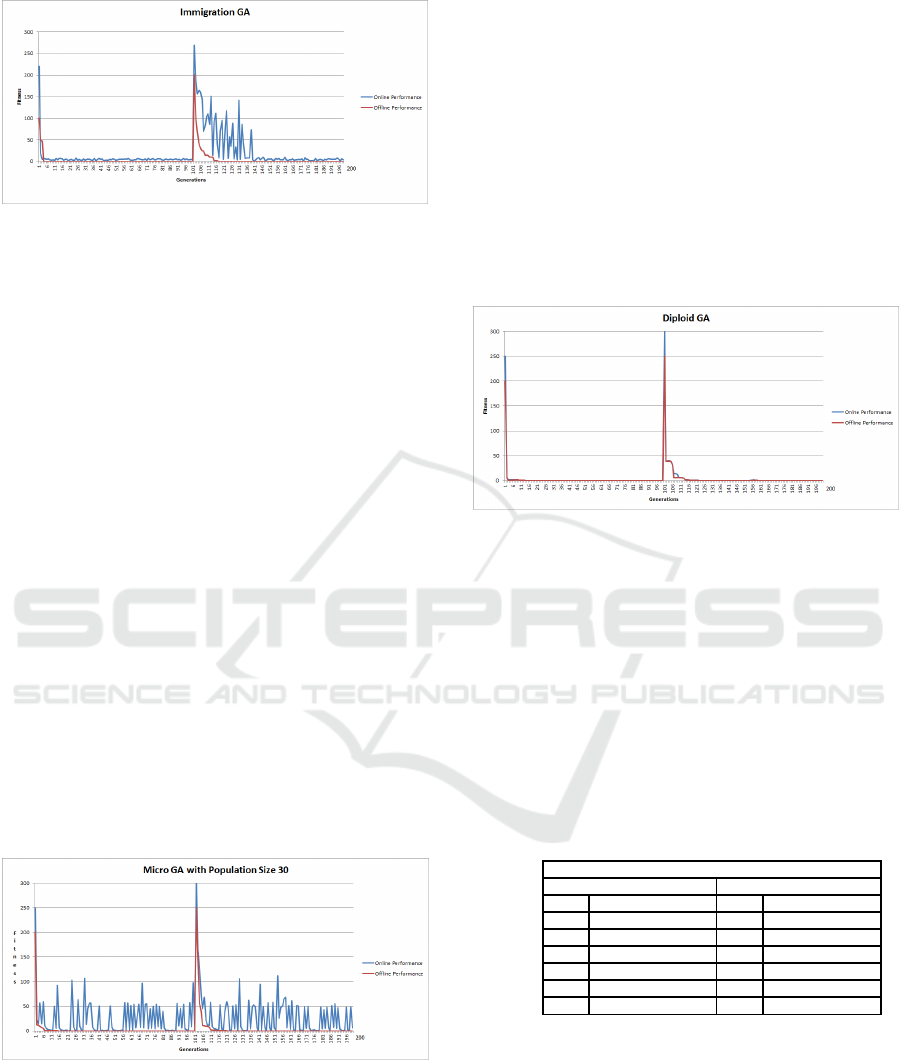
Figure 4: Immigration GA (GAI) Changing Sphere Func-

tion.

4.5 Micro GA (MGA) Changing Sphere

Function Results

The results of the MGA are shown in Figure 5. The

results of the MGA, in locating the global optimum,

indicate an improvement over the SGA, SGAR and

GAE algorithms, both before and after the objective

function changes (see Table 2). The restarting mech-

anism and elitism of the MGA appears to allowed

the algorithm adapt much quicker to the altered land-

scape, thus optimization the changing Sphere prob-

lem in the least amount of generations. The of-

ﬂine MGA result, were statistically highly signiﬁcant

when compared to the ofﬂine SGA results, with a

p − value = 0.0009585. The other interesting fea-

ture of the MGA relates to the online performance,

both before and after the landscape alters, the MGA’s

online performance suggests a signiﬁcant degree of

diversity is maintained in the population. This dif-

fers dramatically from the SGA’s online performance,

which suggests a large degree of convergence. This

suggests that the ability to maintain diversity within

the population, as implemented by the MGA, assists

in adapting to the landscape change.

Figure 5: Micro GA (MGA) Changing Sphere Function.

4.6 Diploid GA (DGA) Changing

Sphere Function Results

The DGA results, seen in Figure 6, shows the ofﬂine

value of 0 was found at generation 5. At generation

100 the landscape alters, with the ofﬂine value of 0

located at generation 141. The results indicate that

over the dynamic Sphere landscape the DGA outper-

formed the SGA and the ofﬂine results, when com-

pared were statistically signiﬁcant with a p−value =

0.03033. When looking at the results of the DGA,

it appears that the maintenance of diversity associ-

ated with the diploid structure, assists in adapting to a

changing landscape. There is however, an additional

overhead associated with the diploid structure com-

pared to haploid GA. Further, in terms of the ﬁtness

of each of the diploid solutions, there is a large degree

of convergence as indicated by the online results.

Figure 6: Diploid GA (DGA) Changing Sphere Function.

Table 2 outlines the results of the changing Sphere

Function experiments, identifying whether the global

optimum was located both before and after the land-

scape changed. The results indicate that the most

adaptable small population GAs were the GAI, MGA

and DGA. However, in terms of adaptability over the

dynamic Sphere function landscape, all of the GAs

succeeded in locating the global optimum. One rea-

son for this is the relative ease of the Sphere function,

however using the Sphere function indicates the efﬁ-

ciencies of each GA variant.

Table 2: Changing Sphere Optimisation

Changing Sphere Function Experiments

Before Landscape Change After Landscape Change

Gen. Optimum Gen. Optimum

SGA 85 Yes 170 Yes

SGAR 90 Yes 165 Yes

GAE 58 Yes 161 Yes

GAI 4 Yes 138 Yes

MGA 34 Yes 136 Yes

DGA 5 Yes 141 Yes

4.7 SGA Changing Shekel’s Function

Results

The SGA results (Figure 7) evolved for a pre-

determined number of generations and the problem

was optimised in generation 470. The results indi-

cate that Shekel’s function proved more difﬁcult for

the SGA compared to the Sphere function. At gen-

eration 500 the objective function inverted causing

the landscape to change. At this point the population

has evolved around the old global optimum which is

much further away from the solution than the initial-

ized population, thereby making the adaptation more

difﬁcult. The SGA however, managed to locate the

new global optimum at generation 990. The SGA lo-

cated the global optimum both before and after the

landscape change (see Table 3). The online results

are interesting as, they illustrate the increase in difﬁ-

culty of Shekel’s function in comparison to the Sphere

function, with slightly less convergence within the

population.

Figure 7: SGA Dynamic Shekel’s Function.

4.8 SGA Restart (SGAR) Dynamic

Shekel’s Function Results

Figure 8 illustrates the results of restarting the SGA

when the landscape alters. The global optimum was

located before and after the change in the objective

function, as shown in Table 3. The performance was

in line with that of the SGA, with a minor improve-

ment. The ofﬂine results, compared to those of the

SGA were statistically highly signiﬁcant.

Figure 8: SGA Dynamic Sphere Function.

4.9 GA with Elitism (GAE) Dynamic

Shekel’s Function Results

The GAE results (see Figure 9) shows the global op-

timum being discovered before and after the land-

scape changed. The performance was largely similar

to that of the SGA and SGAR, this is shown in Table

3. The ofﬂine performance results of the GAE and

SGA were shown to be statistically highly signiﬁcant

(p − value < 2.2e

−16

Figure 9: GA with Elitism - Dynamic Shekel’s Function.

4.10 Immigration GA (GAI) Dynamic

Shekel’s Function Results

The online and ofﬂine results of the GAI experiments

are illustrated in Figure 10. The results indicate that

there is a higher degree of diversity maintained within

the population in comparison to the SGA, SGAR and

GAE (illustrated by the online performance). The of-

ﬂine performance showsthe global optimum being lo-

cated in both phases of the search, see Table 3. The

performance of the GAI showed an improvement over

that of the SGA beforethe objectivefunction changes.

After the change, however the results indicate that the

GAI adapted quicker in locating the new global opti-

mum. This is due to the ability of the GAI to main-

tain diversity into the population. The ofﬂine per-

formances of both algorithms was statistically highly

signiﬁcant with a probability value < 2.2e

Figure 10: Immigration GA (GAI) Dynamic Shekel’s Func-

tion.

4.11 Micro GA (MGA) Dynamic

Shekel’s Function Results

Figure 11 shows the ofﬂine and online results for

MGA. The ofﬂine performance illustrates the success

in locating the global both before and after the land-

scape changes. The online performances shows the

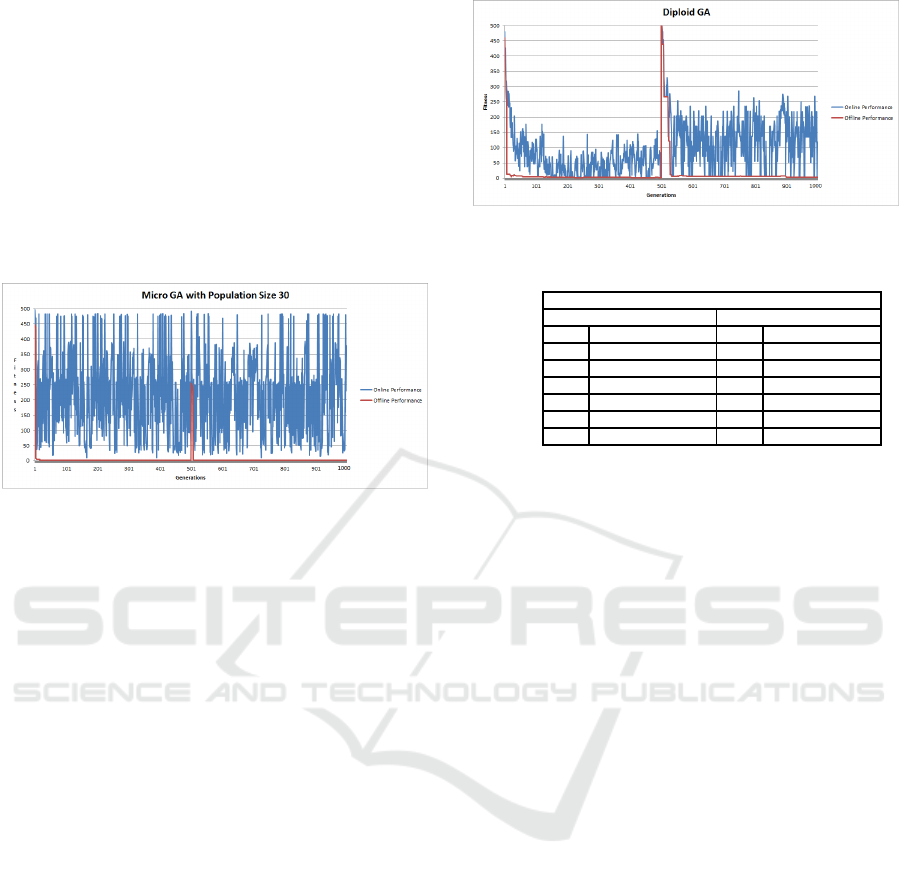
large amount of diversity being introduced into the

population as the average ﬁtness values vary errati-

cally. However, Table 3 indicates that the MGA ex-

hibited the ability to succeed in the search, locating

the global optimum before and after the alteration, in

the fewest number of generations, compared to the

other GA variations. The ability to continuously in-

troduce new individuals into the population, appears

to beneﬁcial over the given landscape. Statistically,

the ofﬂine performance of the MGA compared to that

of the SGA was shown to be highly signiﬁcant with a

p− value < 2.2e

Figure 11: Micro GA Dynamic Shekel’s Function.

4.12 DGA Dynamic Shekel’s Function

Results

For the DGA, the ofﬂine global optimum was found

at generation 450. At generation 500, when the land-

scape was altered, the new global optimum was lo-

cated during generation 900 (see Table 3). When ex-

amining Figure 12, the ofﬂine performance is simi-

lar to that of the SGA, SGAR and GAE. The Diploid

GA maintained a high level of diversity within the

population due to the double chromosome structure.

This can be seen through the ﬂuctuating ofﬂine per-

formance associated with the DGA, particularly after

the landscape changes as it attempts to adapt to the

changing objective function. However, in terms of

adapting to the more difﬁcult Shekel’s function, the

DGA did not perform as well as the other diversity

maintenance GA variations, the MGA and GAI. One

reason for this may be due to the diploid structure,

which through its dominance scheme, struggles with

the landscape in question. Again, when comparing

the results of the ofﬂine performance of the SGA to

those of the DGA, the results were found to be statis-

tically highly signiﬁcant with a p − value < 2.2e

A summary of the Dynamic Shekel’s function ex-

periments is shown in Table 3. The results indicate

that although all of the GAs managed to locate the

global optimum, before and after the landscape al-

tered, the GAI and MGA were the most successful.

Figure 12: Diploid GA - Dynamic Shekel’s Function.

Table 3: Dynamic Shekle’s Optimisation.

Dynamic Shekel’s Function

Before Landscape Change After Landscape Change

Gen. Optimum Gen. Optimum

SGA 470 Yes 990 Yes

SGAR 460 Yes 950 Yes

GAE 450 Yes 938 Yes

GAI 437 Yes 622 Yes

MGA 23 Yes 614 Yes

DGA 450 Yes 900 Yes

5 CONCLUSION

The results presented indicate that the small pop-

ulation GAs variations were capable of optimising

both the dynamic Sphere landscape and the dynamic

Shekel’s landscape. The research suggests, as ex-

pected, that GAs which maintained diversity into the

population, were quicker to adapt when a changing

environment was presented. However, what was in-

teresting is that each of the GAs had a relatively

small population to work with, in comparison to pre-

vious research. The ﬁndings of the DGA experiments

tended to concur with previous research where Gold-

berg (Goldberg and Smith, 1987) suggested not much

improvement over the SGA in terms of number of

generations required to optimize the landscapes. The

greater level of diversity in the population produced

disappointing results in the changing landscape given

the additional overhead required.

The dynamic Sphere results indicate that the GAs

associated with diversity maintenance,that is the GAI,

MGA and DGA all possess an ability to adapt to a

changing landscape and outperform the SGA, SGAR

and GAE. The changing Shekel’s function results

show some evidence that the GAE had more difﬁ-

culty in getting out ofthe local optima when compare

to the GAI and MGA. The algorithm would continu-

ously keep adding the best chromosome to the pop-

ulation and so may end up getting caught in some of

the foxholes of the changing Shekel’s landscape while

the algorithm optimized the solution it required more

generations to work through the landscape.

Overall the MGA exhibited the greatest ability to

adapt over the more difﬁcult dynamic Shekel’s land-

scape, in comparison to the other GAs. The MGA

also proved a useful GA variation over the dynamic

Sphere landscape, producing, along with the GAI,

the lowest number of generations required in order

to adapt to the change in objective function. The re-

sults seem to imply that over changing landscapes, the

combination of small populations and diversity main-

tenance can prove successful. This may suggest that

diversity maintenance techniques coupled with small

populations, can reduce the computational overhead

and assist GAs over changing landscapes, particularly

as the level of difﬁculty increases.

6 FUTURE WORK

Future work includes further examination into the

coupling of small population GA and diversity main-

tenance techniques over more difﬁcult and varied dy-

namic landscapes to see if the maintenance of diver-

sity within a small population GA continues to offer

an advantage.

REFERENCES

Ahn, C. W. and Ramakrishna, R. S. (2002). A genetic al-

gorithm for shortest path routing problem and the siz-

ing of populations. IEEE transactions on evolutionary

computation, 6(6):566–579.

Allen, F. and Karjalainen, R. (1999). Using genetic algo-

rithms to ﬁnd technical trading rules. Journal of ﬁ-

nancial Economics, 51(2):245–271.

Cobb, H. G. and Grefenstette, J. J. (1993). Genetic algo-

rithms for tracking changing environments. Technical

report, DTIC Document.

DeJong, K. A. (1975). An Analysis of the Behavior Of A

Class Of Genetic Adaptive System. PhD thesis, Uni-

versity of Mitchigan.

Digalakis, J. G. and Margaritis, K. G. (2002). An exper-

imental study of benchmarking functions for genetic

algorithms. International Journal of Computer Math-

ematics, 79(4):403–416.

Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-

timization, and Machine Learning. Addison-Wesley

Pulishing Company, INC,, Reading, Massachusetts,

US.

Goldberg, D. E. and Deb, K. (1991). A comparative anal-

ysis of selection schemes used in genetic algorithms.

Foundations of genetic algorithms, 1:69–93.

Goldberg, D. E. and Smith, R. E. (1987). Nonstationary

function optimization using genetic algorithms with

dominance and diploidy. In ICGA, pages 59–68.

Grefenstette, J. J. (1986). Optimization of control param-

eters for genetic algorithms. IEEE Transactions on

systems, man, and cybernetics, 16(1):122–128.

Grefenstette, J. J. et al. (1992). Genetic algorithms for

changing environments. In PPSN, volume 2, pages

137–144.

Holland, J. H. (1992). Adaptation in Natural and Artiﬁcial

Systems: An Introductory Analysis with Applications

to Biology, Control and Artiﬁcial Intelligence. MIT

Press, Cambridge, MA, USA.

Krishnakumar, K. (1990). Micro-genetic algorithms for sta-

tionary and non-stationary function optimization. In

1989 Advances in Intelligent Robotics Systems Con-

ference, pages 289–296. International Society for Op-

tics and Photonics.

Krishnakumar, K. and Bailey, J. (1990). Inertial energy dis-

tribution error control for optimal wind-shear penetra-

tion. Journal of Guidance, Control, and Dynamics,

13(6):944–951.

Leung, Y., Gao, Y., and Xu, Z.-B. (1997). Degree of popula-

tion diversity-a perspective on premature convergence

in genetic algorithms and its markov chain analysis.

IEEE Transactions on Neural Networks, 8(5):1165–

1176.

Mahfoud, S. W. (1995). Niching methods for genetic algo-

rithms. Urbana, 51(95001):62–94.

Mori, N. and Kita, H. (2000). Genetic algorithms for adap-

tation to dynamic environments-a survey. In Industrial

Electronics Society, 2000. IECON 2000. 26th Annual

Confjerence of the IEEE, volume 4, pages 2947–2952.

IEEE.

Mumford, C. L. (2004). Simple population replacement

strategies for a steady-state multi-objective evolution-

ary algorithm. In Genetic and Evolutionary Computa-

tion Conference, pages 1389–1400. Springer.

Whitely, D. (1989). Optimizing neural networks using

faster, more accurate genetic search. Proc. of ICGA-

89.

Yang, S. (2008). Genetic algorithms with memory-and

elitism-based immigrants in dynamic environments.

Evolutionary Computation, 16(3):385–416.