The Behavior of Deep Statistical Comparison Approach for Different

Criteria of Comparing Distributions

Tome Eftimov

1,2

, Peter Koro

sec

1,3

and Barbara Korou

c Seljak

Computer Systems Department, Jo

zef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia

zef Stefan International Postgraduate School, Jamova cesta 39, 1000 Ljubljana, Slovenia

Faculty of Mathematics, Natural Sciences and Information Technologies, Glagolja

ska ulica 8, 6000 Koper, Slovenia

Keywords:

Statistical Comparison, Single Objective Functions, Deep Statistics, Stochastic Optimization Algorithms.

Abstract:

Deep Statistical Comparison (DSC) is a recently proposed approach for the statistical comparison of meta-

heuristic stochastic algorithms for single-objective optimization. The main contribution of the DSC is a rank-

ing scheme, which is based on the whole distribution, instead of using only one statistic, such as average

or median, which are commonly used. Contrary to common approach, the DSC gives more robust statis-

tical results, which are not affected by outliers or misleading ranking scheme. The DSC ranking scheme

uses a statistical test for comparing distributions in order to rank the algorithms. DSC was tested using the

two-sample Kolmogorov-Smirnov (KS) test. However, distributions can be compared using different criteria,

statistical tests. In this paper, we analyze the behavior of the DSC using two different criteria, the two-sample

Kolmogorov-Smirnov (KS) test and the Anderson-Darling (AD) test. Experimental results from benchmark

tests consisting of single-objective problems, show that both criteria behave similarly. However, when algo-

rithms are compared on a single problem, it is better to use the AD test because it is more powerful and can

better detect differences than the KS test when the distributions vary in shift only, in scale only, in symmetry

only, or have the same mean and standard deviation but differ on the tail ends only. This inﬂuence is not

emphasized when the approach is used for multiple-problem analysis.

1 INTRODUCTION

Over recent years, many meta-heuristic stochastic op-

timization algorithms have been developed. Perfor-

mance analysis of a new algorithm compared with the

state-of-the-art is a crucial task and one of the most

common ways to compare their performance is to use

statistical tests based on hypothesis testing (Lehmann

et al., 1986). Making, such statistical comparisons,

however, requires sufﬁcient knowledge from the user,

which includes knowing which conditions must be

fulﬁlled so that the relevant and proper statistical test

(e.g., parametric or nonparametric) can be applied

(Garc

ıa et al., 2009).

The nature of stochastic optimization algorithms

means that a set of independent runs must be executed

on a single instance of a problem in order to get a rel-

evant data set over which either average or median

are typically calculated. Further, because the required

conditions (normality and homoscedasticity) for the

safe use of the parametric statistical tests are usually

not satisﬁed when working with stochastic optimiza-

tion algorithms an appropriate nonparametric statis-

tical test is required. Nonparametric statistical tests

are based on a ranking scheme that is used to trans-

form the data prior to analysis. The standard rank-

ing scheme used by many of the nonparametric sta-

tistical tests ranks the algorithms for each problem

(function) separately with the best performing being

ranked number 1, the second best ranked number 2,

and so on. In case of ties, average rankings are as-

signed. Unfortunately, using either the average or the

median can negatively affect the outcome of the re-

sults of a statistical test (Eftimov et al., 2016). For ex-

ample, averaging is sensitive to outliers, which should

be handled appropriately since stochastic optimiza-

tion algorithms can produce poor runs. For instance,

let us suppose that two algorithms, A

and A

, are

used to optimize the parabola problem, y = x

, and

the results after 10 runs are 0, 0,0,0,0, 0,0, 0,0, 10,

and 0, 1,0, 1,0, 1,0, 1,0, 1, for each algorithm, respec-

tively. We see that the average of A

is 1, while the av-

erage of A

is 0.5. The standard ranking scheme will

rank, A

and A

as 2 and 1, respectively. From this,

Eftimov T., KoroÅ ˛aec P. and KorouÅ ˛aiÄ

G Seljak B.

The Behavior of Deep Statistical Comparison Approach for Different Criteria of Comparing Distributions.

DOI: 10.5220/0006499900730082

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 73-82

ISBN: 978-989-758-274-5

it follows that A

is better, but we can see that the al-

gorithm A

has only one poor run (outlier), which af-

fects the average. In the case when poor runs are not

present, the average can be in some ε-neighborhood,

which is deﬁned as the set of all numbers whose

distance from a number is less than some speciﬁed

number ε, and the algorithms will obtain different

rankings. In order to overcome this problem, medi-

ans are sometimes used because they are more ro-

bust to outliers. However, medians can be in some

ε-neighborhood, and based on these the algorithms

will obtain different rankings. The question is, there-

fore, how to deﬁne the ε-neighborhood for different

test problems that have different ranges of obtained

data e.g. 10

−9

, 10

−2

, 10

, etc. Let us suppose that

two algorithms, A

and A

, are new algorithms used

to optimize a given problem, and the results from 100

runs of both algorithms are distributed according to

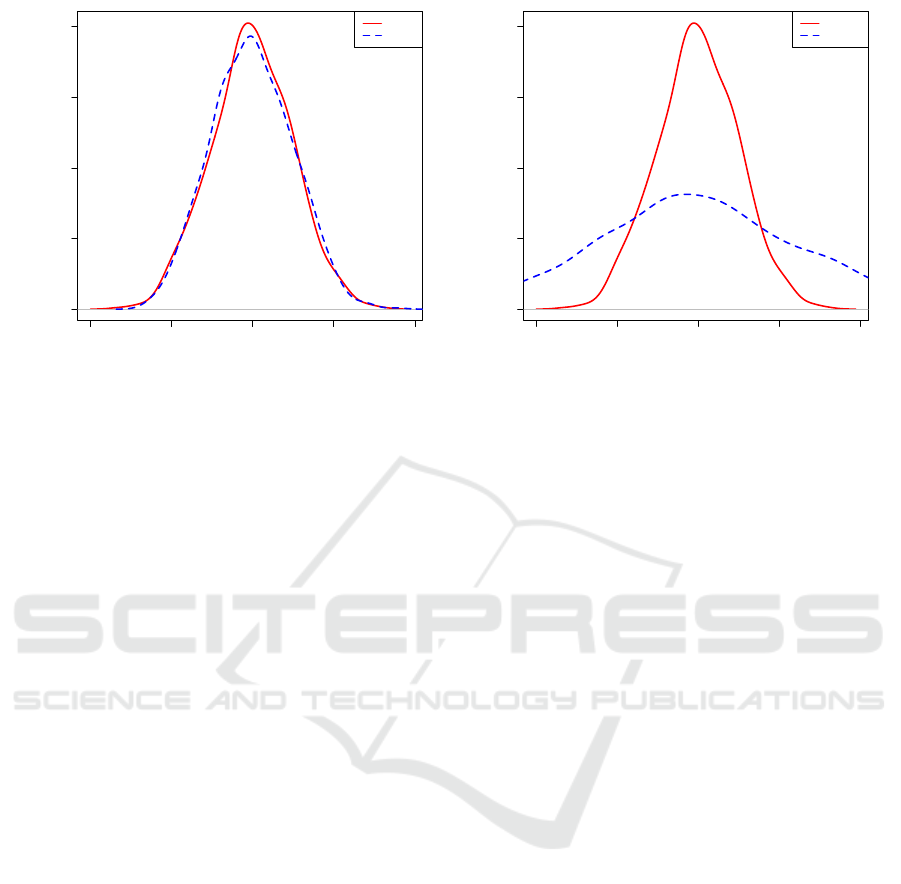
N(0;1). Figure 1(a), shows the probability density

function of the two algorithms. In this case, the distri-

butions are the same, the median values are in some

ε-neighborhood, and because of this the algorithms

should obtain the same ranking. Now let us sup-

pose that two new algorithms, A

and A

, are used for

the optimization of a given problem, and the results

from 100 runs are distributed according to N(0; 1) and

N(0;2.5), respectively. Figure 1(b), shows the proba-

bility density function of the two algorithms. In this

case, the distributions are not the same and the me-

dian values are in some ε-neighborhood, and because

of this the algorithms should obtain different rank-

ings. If this is a case, then the algorithms rankings

are obtained either by the averages or the medians,

so the algorithm which has smaller value for aver-

age or median is the better one. For these reasons,

a novel approach was proposed, called Deep Statisti-

cal Comparison (DSC) (Eftimov et al., 2017), which

removes the sensitivity of the simple statistics to the

data and enables calculation of more robust statistics

without fear of outliers inﬂuence or some errors inside

ε-neighborhood.

The reminder of the paper is organized as fol-

lows. Section II gives an overview of the related

work, while Section III reintroduces the DSC rank-

ing scheme used to compose a sample of results for

each algorithm for multiple-problem analysis. Sec-

tion IV presents statistical comparisons of stochastic

optimization algorithms over multiple problems. This

is then followed by a discussion of the results. In Sec-

tion V, power analysis of DSC is presented when dif-

ferent statistical tests for comparing distributions are

used in the ranking scheme. The conclusions of the

paper are presented in Section VI.

2 RELATED WORK

Statisticians (Gill, 1999) have shown that researchers

have difﬁculties performing empirical studies and this

could lead them into misinterpreting their results.

Leven et al. (Levine et al., 2008) also state that the hy-

pothesis testing is also frequently misunderstood and

abused. To select an appropriate statistical test and

to choose between a parametric and a nonparametric

test (Garc

ıa et al., 2009), the ﬁrst step is to check the

assumptions of the parametric tests, in other words,

the required conditions for the safe use of parametric

tests.

Dem

sar (Dem

sar, 2006) theoretically and empir-

ically examined several suitable statistical tests that

can be used for comparing machine learning algo-

rithms. Following a statistical tutorial on machine

learning algorithms, Garcia et al. (Garc

ıa et al.,

2009) presented a study on the use of nonparametric

tests for analyzing the behaviour of evolutionary al-

gorithms for optimization problems. They conducted

their study in two ways: single-problem analysis and

multiple-problem analysis. Single-problem analysis

is a scenario when the data derives from multiple runs

of the stochastic optimization algorithms on one prob-

lem. This scenario is common in stochastic optimiza-

tion algorithms, since they are stochastic in nature,

meaning we do not have any guaranty that the re-

sult will be the same for every run. Even the path

leading to the ﬁnal solution is often different. To

test the quality of an algorithm, it is not sufﬁcient

to performed just a single run, but many runs are

needed to draw a conclusion. The second scenario,

the multiple-problem analysis, is the scenario when

several stochastic optimization algorithms are com-

pared over multiple problems. In this case, as in most

published papers on this topic, the authors use the av-

erage of the results for each problem in order to pro-

duce results for each algorithm. We call this approach

the “common approach” because it is the one most of-

ten used for making a statistical comparison of meta-

heuristic stochastic optimization algorithms.

Recently, a novel approach for statistical compar-

ison of stochastic optimization algorithms for mul-

tiple single-objective problems was proposed. The

approach is known as Deep Statistical Comparison

(DSC) (Eftimov et al., 2017). The term Deep statis-

tics comes from the ranking scheme that is based on

the whole distribution of multiple runs obtained on a

single problem instead of using some simple statis-

tics such as averages or medians. For this propose,

the DSC was tested using one criteria for comparing

distributions, the two-sample KS test. The approach

consists of two steps, the ﬁrst step uses a newly pro-

-4 -2 0 2 4

0.0 0.1 0.2 0.3 0.4

-4 -2 0 2 4

Value

Probability density function

N(0,1)

(a) Same distributions

-4 -2 0 2 4

0.0 0.1 0.2 0.3 0.4

Value

Probability density function

N(0,1)

N(0,2.5)

(b) Different distributions

Figure 1: Probability density functions.

posed ranking scheme to obtain the data that will be

used to make a statistical comparison. The second

step is a standard omnibus statistical test that can be

a parametric or a nonparametric one. DSC approach

also allows users to calculate more robust statistics,

while avoiding wrong conclusions due to either the

presence of outliers or a ranking scheme that is used

in some standard statistical tests.

3 DEEP STATISTICAL

COMPARISON

In this paper, we analyze the behavior of DSC taking

into account different criteria for comparing distribu-

tions used in the DSC ranking scheme. We did this

to see if different criteria for comparing distributions

inﬂuence the results from the DSC. The two most

commonly used statistical tests for comparing distri-

butions were selected, the two-sample Kolmogorov-

Smirnov (KS) test and the two-sample Anderson-

Darling (AD) test (Engmann and Cousineau, 2011),

as different criteria for comparing distributions. To

explain this, we start by reintroducing the DSC.

3.1 DSC Ranking Scheme

Let m and k be the number of algorithms and the num-

ber of problems that are used for statistical compari-

son, respectively, and n be the number of runs per-

formed by each algorithm on the same problem.

Let X

be a n × m matrix, where i = 1,.. ., k. The

rows of this matrix correspond to the results obtained

by multiple runs on the i-th problem, and the columns

correspond to the different algorithms that are used.

The matrix element X

[ j,l], where j = 1,. .. ,n, and

l = 1 .. ., m, corresponds to the result obtained by the

j-th run on the i-th problem of the l-th algorithm.

The ranking scheme is based on the whole distri-

bution, instead of ranking according to the averages

or medians. The ﬁrst step is to compare the probabil-

ity distributions of multiple runs of each algorithm on

each problem. For this purpose, a statistical test for

comparing distributions should be used. Two most

commonly used tests are the two-sample KS test and

the two-sample AD test.

The two-sample KS test is a nonparametric test

of the equality of continuous, one-dimensional prob-

ability distributions that can be used to compare two

samples. The two-sample KS test is one of the most

useful and general non-parametric methods for com-

paring two samples, as it is sensitive to differences

in both location and shape of the empirical cumula-

tive distribution functions of the two samples (e.g., a

difference with respect to location/central tendency,

dispersion/variability, skewness, and kurtosis) (Sen-

ger and C¸ elik, 2013).

The two-sample AD test has the same advantages

mentioned for the KS test, sensibility to shape and

scale of a distribution and its applicability to small

samples. In addition, it has two extra advantages over

the KS test. First, it is especially sensitive towards

differences at the tails of distributions, and second it

is better capable of detecting very small differences,

even between large sample sizes. More about compar-

ison of the two tests when shift, scale, and symme-

try of distributions are varied independently for dif-

ferent sample sizes can be found in (Engmann and

Cousineau, 2011).

Let α

be the signiﬁcance level used by the statis-

tical test that is selected for comparing distributions.

By using a statistical test for comparing distributions,

m · (m − 1)/2 pairwise comparisons between the al-

gorithms are performed, and the results are organized

into a m × m matrix, M

as follows:

[p,q] =

(

value

, p 6= q

1, p = q

, (1)

where p and q are different algorithms and p,q =

1,. .. ,m.

Because multiple pairwise comparisons are made,

this could lead to the family-wise error rate (FWER)

(van der Laan et al., 2004), which is the probability

of making one or more false discoveries, or type I er-

rors, among all hypotheses when performing multiple

hypotheses tests. In the cases when a few algorithms

are compared the inﬂuence of multiple comparison in

the FWER may not be very large, but as the num-

ber of compared algorithms increases, the FWER can

increase dramatically. In order to counteract the prob-

lem of multiple comparisons, the Bonferroni correc-

tion (Garc

ıa et al., 2010) is used to correct the ob-

tained p-values. The Bonferroni correction is based

on the idea of testing u different hypotheses. One

way of reducing the FWER is to test each individ-

ual hypothesis at a statistical signiﬁcance level of

times the desired maximum signiﬁcance level. In our

case the number of multiple pairwise comparisons,

or the number of different hypotheses, is given as





m·(m−1)

The matrix M

is reﬂexive. Also, it is symmetric

because M

= M

, but the key point for the ranking

scheme is to check the transitivity, since the ranking

is made according to it. For this purpose, the matrix

is introduced using the following equation:

[p,q] =

(

1, M

[p,q] ≥ α

0, M

[p,q] < α

. (2)

The elements of the matrix, M

, are deﬁned accord-

ing to the p-values obtained by the statistical test used

for comparing distributions corrected by the Bonfer-

roni correction. For example if the element M

[p,q] is

1 that means that the null hypothesis used in the sta-

tistical test for comparing distributions, which is the

hypothesis that the two data samples obtained by the

p-th and the q-th algorithm come from the same dis-

tribution, is not rejected. If the element M

[p,q] is 0

that means that the null hypothesis is rejected, so the

two data samples come from different distributions.

Before the ranking is performed, the matrix M

calculated to check the transitivity. If the M

has a 1

in each position for which M

has non-zero element,

the transitivity is satisﬁed, otherwise it is not.

If the transitivity is satisﬁed, the ﬁrst step is to

split the set of algorithms into w disjoint sets of algo-

rithms Φ

, f = 1,...,w, such as each algorithm be-

longs only in one of these sets. Each of these sets

contains the indices of the algorithms that are used in

the comparison for which the transitivity is satisﬁed.

The cardinality of the union of these sets needs to be

∑

f =1

|Φ

| = m. The next step is to deﬁne a w × 2

matrix, W

. The elements of this matrix are deﬁned

with the following equation

[ f ,x] =

(

mean(Φ

{

}

), x = 1

|Φ

|, x = 2

, (3)

where h is the number that is ceiled to the nearest inte-

ger of a number obtained by the uniform distribution

of a random variable Y ∼ U (1, |Φ

|). The algorithm

from each set, whose average value will be used, can

be chosen randomly because the data samples for all

the algorithms that belong to the same set come from

the same distribution. Then the rows of the matrix are

reordered according to the ﬁrst column sorted in as-

cending order. Let Mean

and C be a w × 1 vectors

that correspond to the ﬁrst and the second column of

the matrix W

, respectively. Finally, the rankings to

the sets, Φ

, need to be assigned and organized into

a w × 1 vector Rank

. For the set with lowest average

value, Mean

[1], the ranking is deﬁned as

Rank

[1] =

C[1]

∑

r=1

r/C[1]. (4)

For remaining sets, the ranking is deﬁned as

Rank

[ f ] =

C[ f −1]+C[ f ]

∑

r=C[ f −1]+1

r/C[ f ]. (5)

After obtaining the rankings of the sets, each algo-

rithm obtains its ranking according to the set to which

it belongs by using the following equation:

Rank[i, l] = Rank

[ f ], l ∈ Φ

. (6)

If the transitivity is not satisﬁed, the ﬁrst step is

to deﬁne two 1× m vectors, Index

and Mean

, whose

elements are the indices of the algorithms and the av-

erage values of the multiple runs for each algorithm.

The both vectors are sorted in ascending order accord-

ing to the average values. Then, the rankings of the

sorted algorithms are organized into a 1 × m vector,

Rank

, whose elements are deﬁned with the following

equation.

Rank

[l] =







l, ∃! Mean

[l] ∈ Mean

∑

r=l−c+1

r/c, otherwise

(7)

where c is the number of elements from Mean

that

have value Mean

[l]. Finally, the algorithms obtain

their rankings according to the rankings assigned to

their average values by using the following equation:

Rank[i, Index

[l]] = Rank

[l]. (8)

By using the ranking scheme for the algorithms on

each problem, a k × m matrix, Rank, is deﬁned. The

i-th row of this matrix corresponds to the rankings of

the algorithms obtained by the ranking scheme using

the data samples from the i-th problem. Further, this

matrix is used as input data for statistical comparison

for multiple-problem analysis.

3.2 Selection of a Standard Omnibus

Statistical Test

After ranking the algorithms, the next step is to

choose an appropriate statistical test. The guidelines

on which test to choose are given in (Garc

ıa et al.,

2009). Using the new ranking scheme we transformed

only the data that is available for further analysis,

while everything else remain the same.

4 RESULTS AND DISCUSSION

4.1 Black-Box Benchmarking 2015 Test

Functions

To evaluate the behavior of the DSC taking into ac-

count different statistical tests for comparing distribu-

tions, the results from the Black-Box Benchmarking

2015 (BBOB 2015) (Black Box Optimization Com-

petition, ) are used. BBOB 2015 is a competition that

provides single-objective functions for benchmark-

ing. From the competition 15 algorithms are used.

The algorithms used are: BSif (Po

ık and Baudi

2015), BSifeg (Po

ık and Baudi

s, 2015), BSqi (Po

ık

and Baudi

s, 2015), BSrr (Po

ık and Baudi

s, 2015),

CMA-CSA (Atamna, 2015), CMA-MSR (Atamna,

2015), CMA-TPA (Atamna, 2015), GP1-CMAES

(Bajer et al., 2015), GP5-CMAES (Bajer et al.,

2015), RAND-2xDefault (Brockhoff et al., 2015),

RF1-CMAES (Bajer et al., 2015), RF5-CMAES (Ba-

jer et al., 2015), Sif (Po

ık and Baudi

s, 2015), Sifeg

(Po

ık and Baudi

s, 2015), and Srr (Po

ık and Baudi

2015). For each of them results for 22 different noise-

less test problems in 5 dimensionality (2, 3, 5, 10, and

20) are selected. More details about test problems can

be found in (Hansen et al., 2010). Each algorithm pro-

vided data for 15 runs.

4.2 Experiments

Let Ψ be the set of the selected 15 stochastic opti-

mization algorithms. For the experiments, the dimen-

sion is ﬁxed to 10. A 100 random combinations of

3 distinct algorithms were generated (combinations

without repetition) and used for statistical compar-

isons.

For each combination, the DSC ranking scheme

is used to rank the algorithms for each problem sep-

arately. To compare the results using different cri-

teria for comparing distributions, the DSC ranking

scheme is used with the two-sample KS test and the

two-sample AD test. Then, the results are also com-

pared with the common approach, for which a sample

of results for each algorithm is composed by averag-

ing the data from multiple runs for each problem.

After obtaining the data for statistical comparison

over multiple problems, the next step is to select an

appropriate statistical test. In the case of the DSC

the signiﬁcance level for the ranking scheme is set to

= 0.05, and the signiﬁcance level for the statistical

test is set to α = 0.05.

Table 1 presents the p-values obtained for 6 com-

binations out of 100 generated, using the two versions

of DSC approach, by using the KS test and the AD

test, and the common approach with averages. The

value

corresponds to the p-values obtained by the

Friedman test, which in our case is one of the appro-

priate omnibus statistical tests. From this table, we

can see that the results for the ﬁrst 2 combinations (1-

2) differ. By using the common approach with aver-

ages, the null hypothesis is rejected, so there is signif-

icant statistical difference between the performance

of the algorithms, while with both versions of DSC

approach, the null hypothesis is not rejected, so we

can assume that there is no signiﬁcant statistical dif-

ference between the performance of the algorithms.

The number of such combinations in our experiment

is 5 out of 100. For the next 2 combinations (3-4), the

common approach and both DSC versions give the

same results, the p-values obtained are greater than

0.05, so the null hypothesis is not rejected, and we can

assume that there is no signiﬁcant statistical differ-

ence between the performance of the algorithms. The

number of such combinations in our experiment is 9

out of 100, from which 2 randomly selected are pre-

sented in the table. For the last 2 combinations from

this table (5-6), the results obtained are the same, the

p-values are smaller than the signiﬁcance level used,

so the null hypothesis is rejected, and we can assume

that there is a signiﬁcant statistical difference between

the performance of the algorithms. The number of

such combinations in our experiment is 86 out of 100,

from which 2 are randomly selected and presented in

the table.

In order to explain the difference that appears us-

ing the common approach and the two versions of the

DSC, one example where the result from the common

approach and both versions of the DSC differs is ran-

domly selected and presented in detail. The ﬁrst com-

bination from the Table 1 is selected, which is a com-

parison between the algorithms GP5-CMAES, Sifeg,

and BSif. For the analysis, the Friedman test was se-

lected. In the case of the common approach, the null

hypothesis is rejected, while when the DSC approach

is used, the null hypothesis is not rejected. The rank-

ings obtained by the Friedman test using the common

approach with averages and both versions of the DSC

ranking scheme are presented in Table 2. Comparing

the rankings obtained by the common approach and

the DSC ranking scheme, the difference between the

rankings that appears by using them can be clearly ob-

served. To explain the difference, separate problems

are discussed in detail.

In Figure 2 the cumulative distributions (the step

functions) and the average values (the horizontal

lines) obtained from the multiple runs for different

functions of the three algorithms are presented. In

this ﬁgure details about the function, f

, are pre-

sented. The rankings obtained using the common ap-

proach with averages are 1.00, 2.00, and 3.00, and

they are different because all of them have different

averages. The rankings obtained using the two ver-

sions of DSC ranking scheme, by using KS test and

AD test, are 1.00, 2.50, and 2.50. The DSC ranking

scheme used the cumulative distributions in order to

assign the rankings of the algorithms. From the ﬁg-

ure, one may assume that there is no signiﬁcant dif-

ference between the cumulative distributions of Sifeg

and BSif, but they differ from the cumulative distribu-

tion of GP5-CMAES. This result is also obtained by

using the two-sample KS and AD test. The p-values

obtained for the pairs of algorithms are 0.00 (GP5-

CMAES, Sifeg), 0.00 (GP5-CMAES, BSif), and 0.07

(Sifeg, BSif), by using the KS test, while the p-values

obtained for the same pairs of algorithms by using the

AD test are 0.00 (GP5-CMAES, Sifeg), 0.00 (GP5-

CMAES, BSif), and 0.02 (Sifeg, BSif). Because mul-

tiple pairwise comparisons are made, these p-values

are further corrected by using the Bonfferoni correc-

tion. In this case, the transitivity of the matrix M

satisﬁed, so the set of all algorithms is split into two

disjoint sets {GP5-CMAES}, and {Sifeg, BSif}, and

the rankings are deﬁned using Equations 4 and 5.

In Figure 2(c) the results for the function, f

are presented. The rankings obtained using the com-

mon approach with averages are 1.00, 2.00, and 3.00,

and they are different because all of them have differ-

ent average. The rankings obtained using the DSC

ranking scheme by using the KS test and AD test

are 2.00, 2.00, and 2.00. From the ﬁgure, it is not

clear if there is a signiﬁcant difference between the

cumulative distributions of GP5-CMAES, Sifeg, and

BSif. To check this, the two-sample KS test and

AD test are used. The p-values obtained for the

pairs of algorithms are 0.38 (GP5-CMAES, Sifeg),

0.07 (GP5-CMAES, BSif), and 0.38 (Sifeg, BSif),

and 0.41 (GP5-CMAES, Sifeg), 0.02 (GP5-CMAES,

BSif), and 0.29 (Sifeg, BSif), respectively. Because

multiple pairwise comparisons are made, these p-

values are further corrected using the Bonfferoni cor-

rection. In this case, the transitivity of the matrix M

is satisﬁed, but the set of all algorithms is not split into

disjoint sets because all algorithms belong to one set,

{GP5-CMAES, Sifeg, BSif}.

In Figure 2(b), the results for the function, f

, are

presented. This example is interesting because both

versions of the DSC ranking scheme that use differ-

ent criteria for comparing distributions, the KS test

and AD test, give different results. For the function

, the rankings obtained by the common approach

are 1.00, 2.00, and 3.00. The rankings obtained by

the DSC ranking scheme with KS test are 1.00, 2.50,

and 2.50, while the AD test are 1.00, 2.00, and 3.00.

So the two different criteria used by the DSC rank-

ing scheme give different results. The p-values ob-

tained by using the KS test for the pairs of algorithms

are 0.00 (GP5-CMAES, Sifeg), 0.00 (GP5-CMAES,

BSif), and 0.03 (Sifeg, BSif). Because multiple pair-

wise comparisons are made, these p-values are further

corrected by using the Bonfferoni correction. In this

case, the transitivity of the matrix M

is satisﬁed, so

the set of all algorithms is split into two disjoint sets

{GP5-CMAES}, and {Sifeg, BSif}. The p-values ob-

tained by using the AD test for the pairs of algorithms

are 0.00 (GP5-CMAES, Sifeg), 0.00 (GP5-CMAES,

BSif), and 0.01 (Sifeg, BSif). Because multiple pair-

wise comparisons are made, these p-values are further

corrected using Bonfferoni correction. In this case,

the transitivity of the matrix M

is not satisﬁed, so

the algorithms obtain their rankings according to their

averages. So, the two different criteria give different

results. This result is important when we compare al-

gorithms on one problem (function), while it does not

inﬂuence the result when we are performing multiple-

problem analysis. Even more, when we are compar-

ing algorithms on one problem, it is better to use AD

test because it is more powerful and it can better de-

tect differences than the KS test when the distributions

vary in shift only, in scale only, in symmetry only, or

that have the same mean and standard deviation but

Table 1: Statistical comparisons of 3 algorithms.

Algorithms

Common approach DSC approach (KS) DSC approach (AD)

value

1 GP5-CMAES, Sifeg, BSif

(.02) (.42) (.44)

2 BSif, RF1.CMAES, Sifeg

(.00) (.28) (.33)

3 BSifeg, RF1-CMAES, BSrr (.16) (.28) (.48)

4 Sif, Bsrr, GP1-CMAES (.35) (.77) (.83)

5 BSifeg, GP1-CMAES, CMA-CSA

∗

(.00)

∗

(.00)

∗

(.00)

6 BSrr, RAND-2xDefault, Srr

∗

(.00)

∗

(.00)

∗

(.00)

indicates that the null hypothesis is rejected, using α = 0.05

value

corresponds to the p-value obtained by the Friedman test

Table 2: Rankings for the algorithms A

=GP5-CMAES, A

=Sifeg, and A

=BSif.

Common approach

(Friedman test)

DSC ranking

scheme (KS test)

DSC ranking

scheme (AD test)

3.00 2.00 1.00 3.00 2.00 1.00 3.00 2.00 1.00

13.00 2.00 1.00 3.00 2.00 1.00 3.00 2.00 1.00

3.00 1.00 2.00 3.00 1.00 2.00 3.00 1.00 2.00

3.00 1.50 1.50 2.00 2.00 2.00 2.00 2.00 2.00

3.00 1.00 2.00 3.00 1.00 2.00 2.50 1.00 2.50

1.00 2.00 3.00 1.00 2.50 2.50 1.00 2.50 2.50

3.00 1.00 2.00 3.00 1.50 1.50 3.00 1.00 2.00

3.00 1.00 2.00 3.00 1.50 1.50 3.00 1.50 1.50

1.00 2.00 3.00 1.00 2.50 2.50 1.00 2.50 2.50

3.00 2.00 1.00 3.00 1.50 1.50 3.00 1.50 1.50

2.00 1.00 3.00 1.50 1.50 3.00 1.50 1.50 3.00

3.00 1.00 2.00 2.50 2.50 1.00 2.50 2.50 1.00

2.00 1.00 3.00 2.00 2.00 2.00 2.00 2.00 2.00

2.00 1.00 3.00 2.00 2.00 2.00 2.00 1.00 3.00

1.00 2.00 3.00 1.00 2.50 2.50 1.00 2.50 2.50

1.00 2.00 3.00 1.00 2.50 2.50 1.00 2.00 3.00

3.00 1.00 2.00 3.00 1.50 1.50 3.00 1.50 1.50

1.00 2.00 3.00 2.00 2.00 2.00 2.00 2.00 2.00

differ on the tail ends only (Engmann and Cousineau,

2011). Also, it requires less data than the KS test to

reach sufﬁcient statistical power. To see this differ-

ence, in Figure 3 the probability density functions for

the data of each algorithm obtained on the function

are presented. From it, we can see that the KS test

can not detect the small differences that exist between

the probability distributions of the algorithms Sifeg

and BSif, but the AD test can detect them.

If the null hypothesis is rejected by an omnibus

statistical test, an appropriate post-hoc test should be

used (Dem

sar, 2006; Garc

ıa et al., 2009). Post-hoc

tests are not a subject in this paper because we ana-

lyze the behavior of a ranking scheme that can be used

for omnibus statistical tests. However, one of them is

used to show differences that exist in the case of the

common approach and the DSC approach. Since we

are interested to compare all algorithms to each other,

we decided to use the Nemenyi test (Nemenyi, 1963),

which is an appropriate post-hoc test for the Friedman

0 20 40 60 80 100

0.0 0.2 0.4 0.6 0.8 1.0

Value

Cumulative distirbution

0 10 20 30 40

Mean

GP5-CMAES

Sifeg

BSif

DSC

mean

(a) f

0 20 40 60 80 100

0.0 0.2 0.4 0.6 0.8 1.0

Value

Cumulative distirbution

0 10 20 30 40

Mean

GP5-CMAES

Sifeg

BSif

DSC

mean

(b) f

0 5 10 15 20 25

0.0 0.2 0.4 0.6 0.8 1.0

Value

Cumulative distirbution

0 10 20 30 40

Mean

GP5-CMAES

Sifeg

BSif

DSC

mean

Figure 2: Cumulative distributions (the step functions) and

mean values (the horizontal lines) for different functions of

GP5-CMAES, Sifeg, and BSif.

0 10 20 30 40 50

0.00 0.05 0.10 0.15 0.20

Value

Probability density function

GP5-CMAES

Sifeg

BSif

Figure 3: Probability density functions for f

for the algo-

rithms GP5-CMAES, Sifeg, and BSif.

test. In Figure 4, the results obtained by the Nemenyi

test are presented for the common approach with av-

erages and both versions of DSC approach. When

comparing all the algorithms against each other, the

groups of algorithms that are not signiﬁcantly differ-

ent are connected together.

CD=0.71

1.0

GP5-CMAES

Sifeg

BSif

1.5 2.0 2.5 3

(a) Comparison of all algorithms against each other with the

Nemenyi test (common approach using averages).

CD=0.71

1.0

Sifeg

BSif GP5-CMAES

1.5 2.0 2.5 3

(b) Comparison of all algorithms against each other with the

Nemenyi test (DSC approach with KS test).

CD=0.71

1.0

GP5-CMAES

BSif

Sifeg

1.5 2.0 2.5 3

Nemenyi test (DSC approach with AD test).

Figure 4: Visualization of post-hoc tests used for the algo-

rithms GP5-CMAES, Sifeg, and BSif.

5 POWER ANALYSIS

The power of a statistical test is deﬁned as the proba-

bility that the test will (correctly) reject the false null

hypothesis. The comparison of the statistical power

of the two-sample KS test and the two-sample AD test

is presented in (Engmann and Cousineau, 2011). The

comparison of the statistical power between the DSC

and the common approach is presented in (Eftimov

et al., 2017). Here we focus on power analysis be-

tween the two versions of the DSC approach that use

different criteria for comparing distributions. For this

purpose the power analysis is presented through an

experimental analysis introduced in (Dem

sar, 2006).

The experimental analysis of the power is made by

a Monte-Carlo simulation. When we are comparing

algorithms, samples of ten problems (functions) were

randomly selected so that the probability for the prob-

lem i being chosen was proportional to

1+e

−kd

, where

is the difference between the rankings of the algo-

rithms that are randomly chosen on that problem and

k is the bias through which we can regulate the dif-

ferences between the algorithms. Figure 5(a) repre-

sents the number of hypotheses rejected between the

three algorithms considered with a signiﬁcance level

of 0.05 and Figure 5(b) represents their associated av-

erage p-values. From them, we can conclude that both

versions of DSC approach behave similarly. The two-

sample AD test has better power than the two-sample

KS test (Engmann and Cousineau, 2011), but this in-

ﬂuence is not emphasized in the case of the DSC ap-

proach.

6 CONCLUSION

We analyze the behavior of the deep statistical com-

parison (DSC) approach taking into account differ-

ent criteria for comparing distributions. The approach

consists of two steps. In the ﬁrst step, a new ranking

scheme is used to obtained data for mulitple-problem

analysis. The ranking scheme is based on comparing

distributions, instead of using simple statistics such

as averages or medians. The second step is a stan-

dard omnibus statistical test, which uses the data ob-

tained by the DSC ranking scheme as input data. By

using the DSC, the wrong conclusions caused by the

presence of outliers or ranking scheme used by some

standard statistical tests can be avoided.

In this paper, different criteria for comparing dis-

tributions were used in the DSC ranking scheme, to

see if there is a difference between the obtained re-

sults. We used two criteria for comparing distri-

butions, the two-sample Kolmogorov-Smirnov (KS)

0 5 10 15 20

0 100 200 300 400

Number of hypotheses rejected

DSC approach (KS test)

DSC approach (AD test)

(a) Number of hypotheses rejected

0 5 10 15 20

0.2 0.4 0.6 0.8

Average p-value

DSC approach (KS test)

DSC approach (AD test)

(b) Average p-value

Figure 5: Power analysis for the combination CMA-MSR,

Sifeg, and BSifeg.

test and the two-sample Anderson-Darling (AD) test.

From the experimental results obtained over the al-

gorithms presented in the BBOB 2015, we can con-

clude that both versions of DSC approach behave sim-

ilarly. However, when we are comparing algorithms

on one problem, it is better to use AD test because it

is more powerful and it can better detect differences

than the KS test when the distributions vary in shift

only, in scale only, in symmetry only, or have the

same mean and standard deviation but differ on the

tail ends only (Engmann and Cousineau, 2011). Also,

it requires less data than the KS test to reach sufﬁcient

statistical power. The two-sample AD test has better

power than the two-sample KS test, but this inﬂuence

is not emphasized when the DSC approach is used for

multiple-problem analysis.

ACKNOWLEDGEMENTS

This work was supported by the project ISO-FOOD,

which received funding from the European Union’s

Seventh Framework Programme for research, techno-

logical development and demonstration under grant

agreement no 621329 (2014-2019) and the project

that has received funding from the Slovenian Re-

search Agency (research core funding No. L3-7538).

REFERENCES

Atamna, A. (2015). Benchmarking ipop-cma-es-tpa and

ipop-cma-es-msr on the bbob noiseless testbed. In

Proceedings of the Companion Publication of the

2015 on Genetic and Evolutionary Computation Con-

ference, pages 1135–1142. ACM.

Bajer, L., Pitra, Z., and Hole

na, M. (2015). Benchmark-

ing gaussian processes and random forests surrogate

models on the bbob noiseless testbed. In Proceed-

ings of the Companion Publication of the 2015 on

Genetic and Evolutionary Computation Conference,

pages 1143–1150. ACM.

Black Box Optimization Competition, B. Black-

box benchmarking 2015. http://coco.gforge.inria.fr/

doku.php?id=bbob-2015. Accessed: 2016-02-01.

Brockhoff, D., Bischl, B., and Wagner, T. (2015). The

impact of initial designs on the performance of mat-

sumoto on the noiseless bbob-2015 testbed: A prelim-

inary study. In Proceedings of the Companion Publi-

cation of the 2015 on Genetic and Evolutionary Com-

putation Conference, pages 1159–1166. ACM.

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. The Journal of Machine

Learning Research, 7:1–30.

Eftimov, T., Koro

sec, P., and Korou

c Seljak, B. (2016).

Disadvantages of statistical comparison of stochastic

optimization algorithms. In Proceedings of the Bioin-

spired Optimizaiton Methods and their Applications,

BIOMA 2016, pages 105–118. JSI.

Eftimov, T., Koro

sec, P., and Seljak, B. K. (2017). A novel

approach to statistical comparison of meta-heuristic

stochastic optimization algorithms using deep statis-

tics. Information Sciences, 417:186–215.

Engmann, S. and Cousineau, D. (2011). Comparing dis-

tributions: the two-sample anderson-darling test as an

alternative to the kolmogorov-smirnoff test. Journal

of Applied Quantitative Methods, 6(3):1–17.

Garc

ıa, S., Fern

andez, A., Luengo, J., and Herrera, F.

(2010). Advanced nonparametric tests for multi-

ple comparisons in the design of experiments in

computational intelligence and data mining: Exper-

imental analysis of power. Information Sciences,

180(10):2044–2064.

Garc

ıa, S., Molina, D., Lozano, M., and Herrera, F. (2009).

A study on the use of non-parametric tests for ana-

lyzing the evolutionary algorithms behaviour: a case

study on the cec2005 special session on real parameter

optimization. Journal of Heuristics, 15(6):617–644.

Gill, J. (1999). The insigniﬁcance of null hypothesis

signiﬁcance testing. Political Research Quarterly,

52(3):647–674.

Hansen, N., Auger, A., Finck, S., and Ros, R. (2010).

Real-parameter black-box optimization benchmark-

ing 2010: Experimental setup.

Lehmann, E. L., Romano, J. P., and Casella, G. (1986). Test-

ing statistical hypotheses, volume 150. Wiley New

York et al.

Levine, T. R., Weber, R., Hullett, C., Park, H. S., and Lind-

sey, L. L. M. (2008). A critical assessment of null

hypothesis signiﬁcance testing in quantitative commu-

nication research. Human Communication Research,

34(2):171–187.

Nemenyi, P. (1963). Distribution-free multiple compar-

isons. In PhD Thesis. Princeton University.

ık, P. and Baudi

s, P. (2015). Dimension selection in

axis-parallel brent-step method for black-box opti-

mization of separable continuous functions. In Pro-

ceedings of the Companion Publication of the 2015 on

Genetic and Evolutionary Computation Conference,

pages 1151–1158. ACM.

Senger,

O. and C¸ elik, A. K. (2013). A monte carlo

simulation study for kolmogorov-smirnov two-sample

test under the precondition of heterogeneity: upon

the changes on the probabilities of statistical power

and type i error rates with respect to skewness mea-

sure. Journal of Statistical and Econometric Methods,

2(4):1–16.

van der Laan, M. J., Dudoit, S., and Pollard, K. S. (2004).

Multiple testing. part ii. step-down procedures for

control of the family-wise error rate. Statistical appli-

cations in genetics and molecular biology, 3(1):1–33.