A Framework for Automatic Generation of Fuzzy Evaluation Systems for
Embedded Applications
Daniele De Martini
1
, Gianluca Roveda
1
, Alessandro Bertini
1
, Agnese Marchini
2
and Tullio Facchinetti
1
1
Department of Electrical, Computer and Biomedical Engineering, Universit
`
a degli Studi di Pavia, Pavia, Italy
2
Department of Earth and Environmental Sciences, Universit
`
a degli Studi di Pavia, Pavia, Italy
Keywords:
Fuzzy System, Fuzzy Logic, Fuzzy Indices, F-IND, Automatic Rule Generation.
Abstract:
Fuzzy logic is a powerful modelling approach to build control applications and to generate knowledge-based
evaluation indices. In both cases, however, the applicability to complex systems is limited by the effort re-
quired to formulate the rules, whose number grows rapidly with the number of input variables and membership
functions. This work presents a framework that implements the F-IND fuzzy model to simplify the formula-
tion of fuzzy indices, where the rules are automatically generated on the basis of the specification of best and
worst cases on the membership functions of each input variable. The paper discusses the method and presents
the organization of the framework that allows automatic code generation, targeting the efficient execution of
the calculations on an embedded system. The framework has been tested and validated on real hardware.
1 INTRODUCTION
Fuzzy logic is widely used to represent systems char-
acterized by high complexity and uncertainty such as
those encountered in biology, sociology or economy.
Applications of fuzzy logic have been proposed in
several scientific domains, from ecology (Zhu et al.,
1996; Pouw and Kwiatkowska, 2013) to engineer-
ing (Feng, 2006), medicine (Mahfouf et al., 2001) and
economics and management (Wong and Lai, 2011).
The advantage of using fuzzy logic over other tech-
niques stands in its capability to apply meaning to im-
precise concepts and using uncertainty as additional
source of information. In particular, fuzzy logic is
suitable for developing knowledge-based indices, as
it allows for incorporating expert judgement in the in-
dex design process, while providing the tools to han-
dle subjectivity with mathematical rigour.
It must be pointed out that a “general” fuzzy
model does not exist because the three stages of
fuzzy modelling (fuzzification, inference, defuzzifi-
cation) include a series of decisional steps: selection
of relevant variables and their properties (number and
shape of membership functions), structure of rule-
base, mathematical interpretation of the logical con-
nectives IF...THEN, AND, OR, defuzzification strat-
egy, which can be implemented in several different
ways. For example, the published fuzzy models of
environmental conditions offer a wide variety of so-
lutions (see (Marchini, 2009) for a review). While
guaranteeing high modelling flexibility, the variety
of choices that exist at each stage may be seen as
an impediment due to the high degree of subjectiv-
ity (Silvert, 1997). Determining or tuning good mem-
bership functions and fuzzy rules is not always an
easy task (Adriaenssens et al., 2004), since optimal
parametrization of membership functions, weights,
rules, etc., is only possible when a large amount of
experimental data is available, which in some dis-
ciplines is difficult to achieve. This is especially
problematic when many variables and many mem-
bership functions are involved in a model: because
of the exponentially increasing number of inference
rules, the fuzzy rule base has been considered both
non-transparent and challenging to apply (Cornelis-
sen et al., 2001).
An approach to overcome these difficulties was
proposed by (Marchini et al., 2008), who devel-
oped F-IND, a framework to develop fuzzy indices
of ecological conditions (quality, vulnerability, etc.)
that uses an algorithm for automatic assessment and
weighting of inference rules. The requirements to
develop a fuzzy expert system with F-IND are: (i)
the identification of relevant variables and the cate-
De Martini D., Roveda G., Bertini A., Marchini A. and Facchinetti T.
A Framework for Automatic Generation of Fuzzy Evaluation Systems for Embedded Applications.
DOI: 10.5220/0006501802810288
In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 281-288
ISBN: 978-989-758-274-5
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

gories that express attributes of the variables (e.g.,
low, medium, high), designed in the form of fuzzy
membership functions; (ii) the identification of the
‘best-case’ and ‘worst-case’ categories, (iii) the as-
sessment of variable weights (optional) and (iv) the
definition of output categories. F-IND generates a
graphical user interface for a rapid and easy process-
ing of input data, to produce a risk value (model out-
put) between 0 and 100. The main advantage of F-
IND is that it does not require the manual definition
of fuzzy rules, since such rules are automatically de-
rived from the distances calculated between member-
ship functions. The automatic calculation requires the
association of a ‘worst’ and a ‘best’ membership func-
tion to each variable. Best and worst functions repre-
sent the references to calculate the weights that are
used for the automatic derivation of the rules.
This work describes a framework for the efficient
implementation of the F-IND method. The paper
firstly recalls the mathematical details of the method
introduced in (Marchini et al., 2008). The main con-
tribution consists in the description of the software
framework that implements the method. A dedicated
configuration format based on the TOML language
is used to define the model, i.e., the parameters of
variables and membership functions. The descrip-
tion of the model feeds a program that generates the
source code implementing the model. The generator
program is written in Python language, which allows
a straightforward and flexible implementation, while
the generated code is standard C language, which fa-
vors the portability on any computing platform – with
specific attention to resource constrained embedded
systems – and efficiency of the execution. The per-
formance of the generated code is evaluated on real
hardware (Arduino embedded board).
The automatic generation of rules in fuzzy infer-
ence systems is a topic that was tackled from differ-
ent perspectives. (Angelov and Buswell, 2003) adopts
genetic algorithms to derive fuzzy rules from data,
providing the benefit of neural networks with the ex-
pressiveness of fuzzy systems. Template-based code
generation methods are already available (Hasan,
1994). However, on one hand, the existing frame-
works do not address the automatic generation of
rules provided by F-IND. In (McCarty et al., 2013),
a framework for automatic generation of a fuzzy con-
troller is proposed. The focus is on visual tools to
configure, model and run the controller. Indications
on automatic rule generation are given also in (Byte
Craft, 2008) for traditional models.
2 SYSTEM MODEL
The proposed framework implements the F-IND
method, i.e., an approach that simplifies the defini-
tion of the rules in a fuzzy inference system. The F-
IND method is based on the Mamdani model, since it
puts into relationship input and output fuzzy sets; the
output sets can be defuzzified to determine the crisp
value of the index.
The method is designed to simplify the definition
of fuzzy indices. The main advantage of F-IND is
the possibility to express the inference rules between
inputs and outputs by defining a reduced number of
parameters. Indeed, the method uses such parame-
ters associated to input variables to calculate a set of
weights, thus allowing for an automatic definition of
the rules; the designer is thus exempted by the manual
definition of the rules.
We consider a fuzzy model with N
in
input vari-
ables V
i
, i ∈ [1, N
in
], valid in the interval [V
min
i
, V
max
i
].
Each variable V
i
is defined as a set of M
i
member-
ship functions, denoted as f
i
j
(·), j ∈ [1, M
i
] (e.g., vari-
able V
i
has M
i
= 3, and f
i
1
≡ “low”, f
i
2
≡ “medium”,
f
i
3
≡ “high”).
With this notation, in standard fuzzy models the
number of rules to define is:
N =
N
in
∏
i=1
M
i
The F-IND method reduces the number of parameters
to tune to
N = 2 N
in
This is an important feature, since rule definition can
be both a time consuming and challenging process.
Notice that these parameters only refer to those
necessary to define the fuzzy rules. In particular, the
parameters that define the membership functions are
not accounted, since we assume that the same effort is
required in the traditional model as in F-IND to define
the membership functions.
There are some requirements to be satisfied to
guarantee the correctness of the calculations:
• Membership grades are in the [0, 1] interval;
• For every input variable V
i
it must hold:
∀x ∈

V
min
i
, V
max
i

,
M
i
∑
j=1
f
i
j
(x) = 1 (1)
• For every variable V
i
, there are at most two non
null membership grades for any given point x, i.e.:
∀x ∃ j :





f
i
j
(x) 6= 0, j ≤ M
i
f
i
j+1
(x) = 1 − f
i
j
(x), j < M
i
f
i
k
(x) = 0, k 6= j, j + 1
(2)

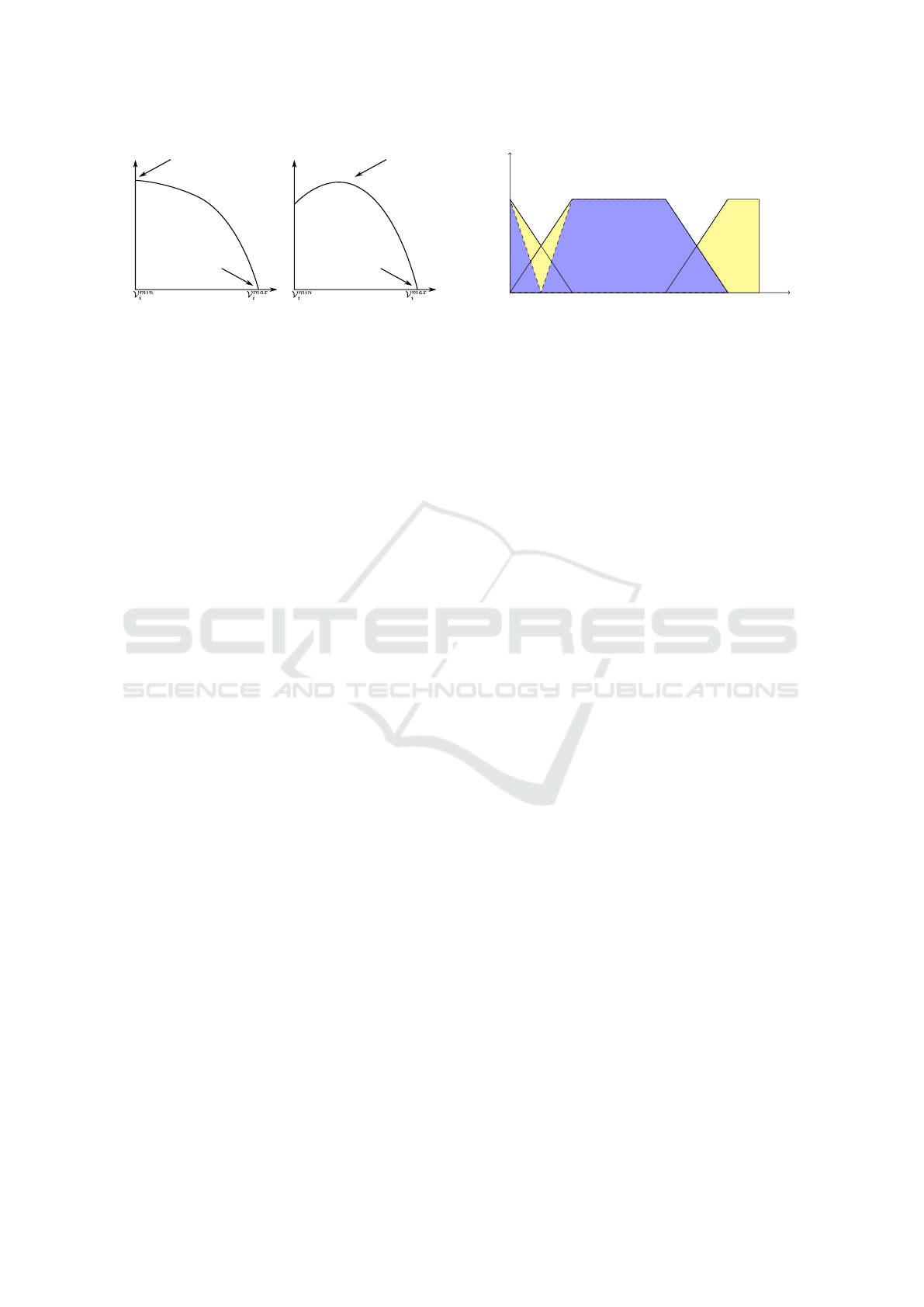
best
case
worst
case
desired index behaviour
(a)
best
case
worst
case
desired index behaviour
(b)
Figure 1: Examples of desired behaviours of the index for a
particular input variable V
i
: on the left the case of best and
worst cases on the boundaries and on the right the case of
best case within the valid range of the variable V
i
.
When a variable V
i
is evaluated for a given input
value x, we say that such variable is full degree if
∃ f
i
j
: f
i
j
(x) = 1.
This section will describe the methodology behind
the F-IND framework, from the definition of inputs
to the process of weights assignment and the actual
calculation of the index.
2.1 Inputs and Outputs
The definition of a fuzzy variable under the F-IND
method requires the association of best and worst
cases to each variable. The best and worst member-
ship functions define, respectively, the most and the
less favourable cases w.r.t. the corresponding variable.
The calculation of the weights that define the fuzzy
rules is based on the distances between membership
functions of a variable. Figure 1 shows the best and
worst values of a variable in the range [V
min
i
, V
max
i
].
As mentioned before, the number of model pa-
rameters required by this method is reduced to N =
2 N
in
, i.e. the definition of best and worst cases for
each input variable.
2.2 Weights
The F-IND method overcomes the problem of man-
ual rule definition by means of an automatic rules-
assessment procedure. This is based on the qualita-
tive concept of best and worst membership functions
described in section 2.1. Indeed, the meaning of these
concepts is that the maximum value of the fuzzy in-
dex is obtained when the membership grade of the
best membership functions is 1 for all the variables.
Similarly, the minimum value of the index (i.e., equal
to zero) is obtained when the membership grade of the
worst membership functions is 1 for all the variables.
The weights used in the F-IND model are essen-
tially the distances of the membership functions rep-
x
f
0
1
25 50 100
A
(Best)
B C
(Worst)
Figure 2: Internal difference between A and B.
resenting the properties of a variable from the worst
function of the same variable. Such a distance de-
pends on the shape of the membership function and
their “proximity” along the horizontal axis.
For each variable, the best and worst membership
functions must be distinct. Moreover, any of the avail-
able functions can be selected as best and worst cases.
The procedure to calculate the distances between the
membership functions ensures that such distance has
always the highest possible value between best and
worst functions. This is achieved using the concepts
of internal distance and external distance. The ac-
tual distance of the considered membership function
is either equal to the internal or the external distance
depending on the position of the function w.r.t. the
worst and best functions.
Since most of the systems are affected by best and
worst cases placed on the boundaries of the input in-
terval, only the concept of internal distance is relevant
and will be discussed in this section, while both are
implemented in the code.
The internal distance is defined as the sum of two
values: the internal difference and the internal gap.
The former value is defined as the integral of the ab-
solute value of the difference between the two adja-
cent membership functions. This value is calculated
by eq. (3).
id
i
j, j+1
=
Z
V
max
i
V
min
i
k f
i
j
(x) − f
i
j+1
(x)k dx (3)
Figure 2 shows the calculation of id for f
i
j
= A and
f
i
j+1
= B.
The internal gap ih
i
j, j+1
is instead defined as the
integral of the “hole” between the two adjacent mem-
bership functions, as shown in fig. 3, as calculated in
eq. (4).
ih
i
j, j+1
=
Z
V
max
i
V
min
i
h
i
j, j+1
(x) dx (4)
The term h
i
j, j+1
in eq. (4) is defined in eq. (5), where
¯x ∈ [V
min
i
, V
max
i
] is the value such as f
i
j
( ¯x) = f
i
j+1
( ¯x).

x
f
0
1
25 50 100
A
(Best)
B C
(Worst)
Figure 3: Internal gap between A and B.
h
i
j, j+1
(x) =
(
1 − f
i
j
(x), if x < ¯x
1 − f
i
j+1
(x), if x ≥ ¯x
(5)
The internal distance between two adiacent mem-
bership function belonging to the i-th variable is de-
rived as in eq. (6).
ID
i
j, j+1
= id
i
j, j+1
+ ih
i
j, j+1
(6)
This way, all the distances between consecutive mem-
ber functions can be calculated.
Once the distance between adjacent functions is
known, it is possible to calculate the distance of any
function from the worst function. The distance be-
tween the j-th and the ( j + n)-th functions is the sum
of the distances between consecutive functions f
i
k
and
f
i
k+1
for all k ∈ [i, j + n − 1] (see eq. (7)).
ID
i
j, j+n
=
j+n−1
∑
k= j
ID
i
k,k+1
(7)
The calculation of the weight associated to the j-th
membership function f
i
j
assumes that ID
i
j,w
is the dis-
tance between f
i
j
and the worst function, while ID
i
b,w
is the distance between the best and worst functions.
The weight W
i
j
associated to f
i
j
is calculated as in
eq. (8).
W
i
j
=
ID
i
j,w
(V
max
i
− V
min
i
)
∑
N
in
i=1
ID
i
b,w
(8)
This normalization process is performed in order to
have weights independent from the variable range.
2.3 Index Calculation
Once the weights have been calculated, the F-IND ap-
proach can be applied to the input values. Given an in-
put, only the membership functions that obtain a non-
zero membership grade are considered to define the
active rules. For evaluating each rule the and operator
is used, implemented as the multiplication operator.
Since for each input the maximum number of
membership functions with non null degree is two,
as in eq. (2), the maximum number of active rules is
N = 2
N
in
, with N
in
being the number of input vari-
ables.
Denoting with V
k
the product of all the member-
ship functions in the active rule R
k
, as:
V
k
=
∏
{i∈[1,N
in
], f
i
j
∈R
k
}
f
i
j
(x) (9)
and W
k
the sum of the weigths of the same member-
ship functions, as:
W
k
=
∑
{i∈[1,N
in
], f
i
j
∈R
k
}
W
i
j
(x) (10)
where f
x
i
is the i-th membership function, present in
the k-th active rule.
We define the weight of the l-th membership func-
tion of the output as:
W
l
=
∑
k
V
k
f
l
(W
k
) (11)
Finally, the output index is calculated us-
ing eq. (12).
I = 100· div ·
∑
l
l ·W
l
(12)
where l is the index of the membership function and
div is defined as: div = (N
out
− 1)
−1
with N
O
being
the number of membership functions in the output
variable.
3 SOFTWARE
IMPLEMENTATION
This section describes the implementation of the F-
IND model and the organization of the implemented
modules. The software framework is made by three
main parts: two libraries of procedures that imple-
ment fuzzy systems, written in C and Python lan-
guages, and a template engine that automatically gen-
erates the source code from configuration and tem-
plate files
1
.
3.1 Operational Workflow
The software implementation of the F-IND model is
based on a configuration file that allows to define the
components of the model (input and output variables,
membership functions, etc.). Afterwards, the C li-
brary is created from the template engine and can be
built into an executable program. Finally, the user can
1
The project is available for download at
https://github.com/lab-robotics-unipv/pyFUZZYgenerator

run it either as a standalone C program or in a Python
environment, both on a computer or on top of an em-
bedded platform.
The whole process can be used to create and run
either a standard Mamdani fuzzy system or a F-IND
model. The latter is presented in details in this paper.
3.2 The Python Library
Since the use of the C language to define the model
from scratch could be a relatively time consuming op-
eration, a dedicated library has been implemented us-
ing the Python language. Due to its simple syntax,
powerful and modern features, and the availability of
a huge set of libraries, the Python language repre-
sents an ideal solution for software prototyping, and
to act as abstraction layer on top of more efficient (but
less flexible) languages. Since the F-IND Python li-
brary generates pure C code, no native Python code
is required to be executed for the calculation of in-
dex, which eliminates the well known overhead due
Python code execution. This is obtained by means
of a configuration process and a template engine that
will be discussed below.
3.2.1 Configuration of a Fuzzy Model
To simplify the design and the implementation of a
fuzzy model, the model can be configured by editing
a dedicated configuration text file. In particular, the
configuration file uses the TOML
2
syntax. TOML is
a minimal text file format that is clear and readable,
but still implements flexible data structures such as
arrays and dictionaries.
The configuration facility can define either stan-
dard or F-IND fuzzy models, depending on the type
field in the file. The two cases differ in terms of the in-
formation required to define a model: while standard
fuzzy systems need the explicit definition of rules be-
side input and output details, F-IND models require
the specification of best and worst functions for each
input variable, while the rules are automatically de-
rived as described in section 2.
The syntax used in the configuration file has been
inspired by the Fuzzy Control Language (FCL) (IEC
61131-7, 2000). In the FCL the various components,
such as variables and rules, are encoded in blocks. A
custom configuration file format based on the TOML
language was used instead of the standard FCL for-
mat for one main reason: the FCL format, despite
being standardized, is not really widespread in com-
puter science applications dealing with fuzzy systems.
2
Tom’s Own Minimal Language: https://github.com/toml-
lang/toml.
[[model]]
name = "Example model"
description = "Example model"
version = "1.0alpha"
type = "f-ind"
[[model.input_var]]
name = "I"
description = "An input variable"
best = "A"
worst = "B"
[[model.input_var.mf]]
name = "A"
type = "trapezoid"
parameters = [0.0, 0.0, 0.7, 0.9]
[[model.input_var.mf]]
name = "B"
type = "triangle"
parameters = [0.7, 0.9, 1.05]
[[model.output_var]]
name = "O"
description = "The index value"
best = "A"
worst = "B"
[[model.output_var.mf]]
name = "A"
type = "triangle"
parameters = [0.0, 0.0, 1.0]
[[model.output_var.mf]]
name = "B"
type = "triangle"
parameters = [0.0, 1.0, 1.0]
Figure 4: An excerpt of the configuration format proposed
in the framework.
This is due to its complicate format, which is diffi-
cult to parse. For this reason, only few libraries are
available to parse FCL files. On the other hand, the
proper encoding of fuzzy concepts using the TOML
format allows a trivial parsing of the configuration file
(this is done with one single instruction in Python),
while libraries for parsing TOML files are available
for dozens of programming languages, making this
file format easily adoptable in other software projects
that require the implementation of fuzzy models.
An excerpt of the configuration file format, con-
taining the configuration of a single input F-IND sys-
tem, is reported in fig. 4. The human readability and
the straightforward syntax are evident in the exam-
ple. The framework allows the use of commonly
shaped membership functions, including trapezoids,
triangles, crisps, sigmoids and gaussians. It is notice-
able that the [[model]] syntax defines an array. This

means that in a single configuration file the user can
define more than a single fuzzy model, allowing for
the definition and the simultaneous generation of mul-
tiple, complex models.
3.2.2 Automatic Code Generation
The generation of the C code is done by means of tem-
plates that are filled with the proper parameter values
to obtain a program that can be successfully built us-
ing standard ANSI C compilers.
In this project, the Jinja
3
text-based template en-
gine was used. Thanks to its syntax, it is highly inte-
grated with the Python programming language. Dif-
ferently from basic template engines, where specific
parts of the templates are filled with the right text,
Jinja offers more flexible and powerful options in-
cluding the embedding of pure Python objects and
programming statements directly in the template it-
self, and template inheritance. These features allow
a modular implementation of the framework, a clear
and concise definition of the templates, which trans-
late to a clear and readable C library.
The code generation follows a hierarchy of three
different levels: the models are stored in separate
files, one for each model, while the included logic
to process each type of fuzzy model (e.g. F-IND or
standard model) is included as a library only when
there is at least one model requiring it. Finally, com-
mon files shared among all models are created and
included, such as a main.c file containing the main
function. This latter provides to the user an exam-
ple on how each defined index can be initialized and
executed. Descriptions for each model are generated
from the TOML and provided as comments both in
each model file and in the sample main.c.
The automatic code generation handles all but
index calculation, which depends on the input and
therefore must be calculated online. In particular, the
automatic code generation uses eqs. (3) and (4) to cal-
culate the distance between membership functions as
in eq. (7) and evalutes the relative weights (eq. (8)).
Model and variable names defined in the configu-
ration file are used as identifiers in the code, to achieve
the desired level of readability of the generated code.
Some variable types are also automatically inferred
by the model properties.
3.3 The C Library
The goal of the proposed framework is to generate an
executable program that suitably runs a fuzzy infer-
ence system on resource constrained embedded hard-
3
Jinja template engine: http://jinja.pocoo.org/.
ware. Therefore, C programming language has been
chosen for its resource efficiency. The generated C
code is structured in several libraries containing the
procedures to compute the supported fuzzy indexes.
The source code of each index is written within a ded-
icated .c, along with the necessary parameter values
to implement the index. These values include the ref-
erences to input and output membership functions and
the normalized weights. All these values are statically
allocated in memory to optimize the memory usage
in the constrained environment that characterizes typ-
ical embedded applications. Dynamic allocation (the
family of malloc functions) is not used in the library
since several platforms do not support it. Most of the
required memory is used to store models parameters;
the index calculation only makes use of a few local
variables. As a side benefit, this approach allows to
estimate the required memory beforehand. Moreover,
thanks to eq. (2), we know that only up to two adja-
cent membership functions have non-null value, and
their values are related, since they sum up to 1. There-
fore, once the first “active” membership is identified,
there is no need to calculate nor to store the next mem-
bership values. As a result, exactly one value per in-
put variable is stored, and possible time consuming
calculations are eliminated; this is especially relevant
when complex functions need to be evaluated.
Valgrind analysis shown that around 90% of the
computation time is spent in detecting and evaluating
the membership functions having non-null value, and
to calculate the automatically generated rules. There-
fore, the optimization of the code focused on the eval-
uation of the rules (see eqs. (9) and (10)). An efficient
method to evaluate such equations is to store the in-
dexes of the first active membership function for each
variable – and their values – into one-dimensional ar-
rays, which are indexed using a properly encoded bit-
mask. In particular, the indexes of the first active MF
and their values for each variable are stored and in-
dexed using a properly encoded bit-mask. The advan-
tage is that the update of the bit-mask is done effi-
ciently.
Furthermore, when a variable is detected to be full
degree, half of the remaining rules, i.e., those includ-
ing the adjacent membership function (which has de-
gree equal to 0) can be skipped. An empirical evalua-
tion of this behaviour is reported in section 4.2.
As consequence, the worst case computation time
(WCET) corresponds to the evaluation of all the rules.

4 EXPERIMENTAL RESULTS
This section evaluates the performance of the F-IND
library on the real hardware of an embedded platform.
The goal is to assess the computational performance
of the generated C code running on top of an em-
bedded micro-controller. For this reason, the exper-
iments define a simple index based on the measure-
ments from an accelerometer interfaced to the micro-
controller. The F-IND index runs on the embedded
board and is required to produce an indication of the
planarity of the board in the 2D space. The index shall
be equal to 100% when the inclination of the board is
null; the index value decreases when the two angles
increase. The angles along the two orthogonal axes
are denoted with α and β. They can assume values in
the interval [0
◦
, 60
◦
]. The index is designed such that
it is less sensitive to changes in the low range of the β
angle, while being equally sensible to both angles for
high values of the angles. These specifications trans-
late to the membership function depicted in figs. 5(a)
and 5(b), respectively for α and β.
Figure 5(c), instead, shows the same relationships
in a surface plot.
4.1 Hardware Setup
The assessment of the computational performance of
the F-IND index was carried out on the Arduino Pro
Mini 3.3 V board, which is a low-end development
board with rather constrained memory and processing
power. It features an ATmega micro-controller with-
out floating point operations unit (FPU)
4
. The board
is connected to the computer by an FTDI to USB con-
nector that is used both for programming and for se-
rial communication between the two devices.
The microcontroller samples acceleration mea-
surements from a ADXL335B accelerometer
5
. An
analogue signal is sampled for each of the three axes.
These values are fed into the C function that calcu-
lates the index, and both the index and timing infor-
mation are sent to the computer for logging.
4.2 Results
The full program occupies 555 B of memory, around
27% of the total memory available to the Arduino
Pro Mini. Since the serial library alone takes 198 B
of memory, it turns out that the fuzzy library alone
4
The complete specifications can be found at
https://www.arduino.cc/en/Main/ArduinoBoardProMini.
5
The complete datasheet can be found at
https://www.sparkfun.com/datasheets/Components/SMD/
adxl335.pdf.
requires about 357 B of memory using the defined
model. The time required for the index calculation
ranges from 500 µs to 2 500 µs, depending on input
values (as explained in Section 3.3).
The performance of the generated C code was
tested on more complex models to evaluate the scal-
ability of the solution as a function of the number of
model parameters (i.e., the number of variables). The
test was performed on the same Arduino Pro Mini
platform, where increasingly larger indexes were run
and fed with random input values. Figure 6 shows the
memory usage as a function of the number of input
variables, either in case of 3 and 5 membership func-
tions per variable. The memory usage changes almost
linearly with the number of input variables, while
it increases with the number of membership func-
tions. The memory occupation mem can be approx-
imated using the following linear regression: mem =
29.5·M + 98.98 B. The R
2
value is 0.99.
As mentioned in section 3.3, the time required to
compute the index greatly depends on the number of
inputs, while it does not significantly change with the
number of membership functions used to define the
input variables. Figure 7 shows the time required to
calculate the index using two different models, hav-
ing 4 and 5 input variables respectively; each vari-
able has 5 membership functions in both cases. The
models are fed with random input values. As can be
seen in the figures, the computation time required by
the index calculation is distributed in a number of dis-
crete clusters, depending on the number of full degree
variables, which in turn depends on the input values.
Defining N
f ull
as the number of full degree variables,
and C the time required to evaluate one single rule, it
holds that the time required to evaluate the index is
around Time = 2
N
in
−N
f ull
·C, with small approxima-
tions due to execution overheads, which lead to small
variability within each cluster. As a consequence, the
WCET is obtained when N
f ull
= 0, i.e. when the num-
ber of active rules is maximum (2
N
in
).
5 CONCLUSIONS
This paper presented a framework for the generation
of software programs that implement fuzzy indices
with automatic generation of inference rules. The
latter feature leverages the F-IND model, which was
proposed with the aim of simplifying the specification
of models to define fuzzy indices.
One relevant contribution was the introduction of
a file format to describe fuzzy models that is based
on a standard text format, making it straightforward
to parse the new format for both read and write opera-

f
1
0 20 30 40 50 60
L
(Best)
LM M MH H
(Worst)
(a)
1
0 40 50 60
L
(Best)
M H
(Worst)
f
(b)
α [rad]
β [rad]
0
20
40
Index
60
80
100
0.8
1
0.6
0.4
0.2
0
1
0.8
0.6
0.4
0.2
0
F-IND curve
(c)
Figure 5: Membership functions for the α and β input variable, and resulting 3D surface.
1 2 3 4 5 6
Number of input variables
Memory usage (B)
3 membership functions
5 membership functions
200
600
1000
Figure 6: Memory usage on the Arduino Pro Mini versus
the number of input variables.
0 5 10 15 20 25
Time (ms)
0.0
0.5
1.0
1.5
2.0
Executions (%)
(a) 4 inputs and 5 membership functions per input
0 5 10 15 20 25
Time (ms)
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
Executions (%)
(b) 5 inputs and 5 membership functions per input
Figure 7: Distribution of execution times with random-
sampled inputs for different sized models.
tions. The proposed framework was demonstrated on
real hardware.
REFERENCES
Adriaenssens, V., Baets, B. D., Goethals, P. L., and Pauw,
N. D. (2004). Fuzzy rule-based models for decision
support in ecosystem management. Science of The To-
tal Environment, 319(1-3):1–12.
Angelov, P. and Buswell, R. (2003). Automatic generation
of fuzzy rule-based models from data by genetic algo-
rithms. Information Sciences, 150(1-2):17–31. Recent
Advances in Soft Computing.
Byte Craft (2008). Fuzzy logic in embedded microcomput-
ers and control systems. Byte Craft Limited.
Cornelissen, A., van den Berg, J., Koops, W., Grossman,
M., and Udo, H. (2001). Assessment of the contri-
bution of sustainability indicators to sustainable de-
velopment: A novel approach using fuzzy set theory.
Agriculture, Ecosystems and Environment, 86(2):173–
185.
Feng, G. (2006). A survey on analysis and design of model-
based fuzzy control systems. IEEE Tran. on Fuzzy
Systems, 14(5):676–697.
Hasan, S. (1994). A Template-based Fuzzy Logic Code Gen-
erator for Microcontrollers. University of Florida.
IEC 61131-7 (2000). Programmable controllers - fuzzy
control programming.
Mahfouf, M., Abbod, M., and Linkens, D. (2001). A sur-
vey of fuzzy logic monitoring and control utilisation
in medicine. Artificial Intelligence in Medicine, 21(1-
3):27–42.
Marchini, A. (2009). Fuzzy indices of ecological condi-
tions: review of techniques and applications. In Var-
gas R.E, editor, Fuzzy Logic: Theory, Programming
and Applications, pages 115–172. Novascience Pub-
lishers, New York.
Marchini, A., Facchinetti, T., and Mistri, M. (2008). F-ind:
a framework to design fuzzy indices of environmental
conditions. Ecological Indicators.
McCarty, K., Manic, M., and Gagnon, A. (2013). A fuzzy
framework with modeling language for type 1 and
type 2 application development. In 2013 6th Inter-
national Conf. on Human System Interactions (HSI),
pages 334–341.
Pouw, F. A. and Kwiatkowska, M. (2013). An overview
of fuzzy-logic based approaches to ecology: Address-
ing uncertainty. In Joint IFSA World Congress and
NAFIPS Annual Meeting, pages 540–545.
Silvert, W. (1997). Ecological impact classification with
fuzzy sets. Ecological Modelling, 96(1):1 – 10.
Wong, B. and Lai, V. (2011). A survey of the application
of fuzzy set theory in production and operations man-
agement: 1998-2009. International Journal of Pro-
duction Economics, 129(1):157–168.
Zhu, A.-X., Band, L., Dutton, B., and Nimlos, T. (1996).
Automated soil inference under fuzzy logic. Ecologi-
cal Modelling, 90(2):123–145.