
Evolving Illumination Design Following Genetic Strategies
Alice Plebe, Vincenzo Cutello and Mario Pavone
Department of Mathematics and Computer Science, University of Catania,
V.le A. Doria 6, I-95125 Catania, Italy
Keywords:
Lighting Design, Multi-objective Optimization, Genetic Algorithm, Blender, NSGA-II.
Abstract:
Interior lighting design is a challenging task where are involved multiple constraints that need to be optimized
for producing an accurate illumination avoiding possible glare. This paper, then, takes up the issue of provid-
ing a computational tool able to produce a proper lighting plan in interior spaces for a comfortable and optimal
vision in all environments, taking also into account the energy consumption as little as possible. For finding
acceptable solutions we have used the metaphor of the genetic evolution in a multi-objective model, where in-
dividuals are lists of possible light sources, their positions and lighting levels. For finding acceptable solutions
we have used the metaphor of the genetic evolution in a multi-objective model, where every individual is a list
of light sources; their positions; and lighting levels. Further, for properly evaluating each individual, we have
developed two conflicting objective functions, one for optimizing the level of brightness, and the second one
for maximising the energy saving, satisfying, obviously, the additional constraints to respect the architectural
structure to be lighted. From the randomly initial population of individuals generations are constructed using
crossover and mutation operators, whilst the fittest offspring is preserved via an elitist Pareto-dominance se-
lection approach. In addition to the multi-objective genetic algorithm, the 3D graphic software Blender has
been used in order to reproduce the architectural space to be lighted, with the aim to evaluate then, the accu-
racy and uniformity of the produced lighting through a physical simulation of its brightness. The main goal of
the developed tool is to provide to the designer (i.e. the decision maker) a set of interiors illumination design
options, for the given environment to be lit, ensuring (i) uniform illumination distribution; (ii) accuracy of the
illumination produced; (iii) avoiding harsh brightness, and glare; and (iv) low energy consumptions. Two case
studies have been considered in our evaluation experiments, and for each of these the algorithm was performed
on two different instances and with different types of complexity respectively.
1 INTRODUCTION
Forms of artificial lighting have been introduced since
antiquity to make visual perception possible when,
and where sunlight is lacking (Wunderlich, 2003).
In most of the contemporary world a considerable
amount of time is spent indoor, and often with insuf-
ficient daylight illumination. The human vision sys-
tem, like in most primates and several mammals, is
able to adapt itself to very low light levels so that we
may properly move inside interior environments, ori-
ent ourselves, and carry out actions. Unfortunately,
this adaptation occurs through the rod photoreceptor-
based scotopic vision, deprived from color and de-
tailed local feature analysis. The vision with full color
perception, and object recognition based on local fea-
tures, is produced via cone photoreceptor-based pho-
topic vision, that becomes active with adequate light
levels only (Palmer, 1999). In view of this, the light-
ing equipment selection and its placement becomes
crucial, in order to offer comfortable living environ-
ments, and improve the quality of life. Thus, integrat-
ing luminaries into the buildings aims to assign a vi-
sual perception to a sufficient level for reliable recog-
nition, and cope with the environment, and, some-
times, elevate the vision to higher levels of appreci-
ation, as for instance in interior spaces hosting art-
works (Cuttle, 2015). However, providing comfort-
able and pleasant visual experiences is not an easy
task, because to determine the proper lighting equip-
ment selection, and their correct placements require
the designer to satisfy several constraints, such as the
type of occupants and the type of activities in the
given space, or the interior surface finishes, and fur-
nishings (Gordon, 2014; Livingston, 2015). Quite of-
ten, the aim to provide enough indoor light for a com-
fortable photopic vision, must take into account also
the demand in terms of energy to be spent for lighting
Plebe A., Cutello V. and Pavone M.
Evolving Illumination Design Following Genetic Strategies.
DOI: 10.5220/0006501902890296
In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 289-296
ISBN: 978-989-758-274-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Sansoni et al., 2015). In U.S. the energy consumed
for lighting accounts for about 30% of the total en-
ergy consumed by commercial buildings, whilst in the
European Union the yearly consumption is over 170
TWh (Bertoldi et al., 2012).
The problem of the interior lighting design is then
a challenging task due to its complex and hard proper-
ties, and the many constraints to be satisfied. Indeed,
to perform a proper and accurate illumination, the de-
signer must not only take care about a right combina-
tion between daylight and artificial illumination, but
primarily must take into account: (1) the light reflec-
tion (specular, diffuse, or directional-diffuse), which
strongly depend on the materials composition used;
(2) degree of reflection; (3) shading; (4) uniform dis-
tribution of luminaries; (5) energy consumption, with
the purpose to avoid harsh brightness, and glare. The
disadvantage of using the traditional methodologies is
that the designer must specify the location, and power
of the luminaries; run a computational tool for achiev-
ing an illuminance proposal, and check if it is satis-
factory. If however it isn’t the required one, then the
computational tool must be run again.
It is clear that the interior lighting design involves
multiple factors, often conflicting, proving, thus, the
multi–objective properties of the problem. This pa-
per proposes a method for searching lighting solu-
tions for interior environment, based on the use of a
multi-objective genetic algorithm optimization tech-
nique, and followed by a clustering of the solutions
on the Pareto front. Typically multi-objective op-
timization methods generates too many solutions in
the final Pareto set, and selecting a single one that
best reflects the preferences of the architect requires
a drastic reduction of the search space of solutions,
here implemented with clustering. The computation
of the direct illumination, necessary to compute the
fitness of the population of solutions during the ge-
netic algorithm, is performed using the 3D graphic
software Blender, which allows to physically evaluat-
ing the lighting produced. Finally, results on a variety
of interior environments, with different architectural
complexities, will be shown in order to evaluate the
accuracy and efficiency of the presented method.
The paper is structured as follow: in Sect. 2 we
describe the evolutionary multi-objective approach,
focusing on the description and details of the algo-
rithm developed; in Sect. 3 we introduce the 3D
graphic software Blender, used as simulation environ-
ment, whilst in Sect. 4 is described the clustering of
the solutions approach, which was designed for re-
strict search space of solutions, facilitating, then, the
decision maker in choosing of the best illumination
option produced; Sect. 5 contains the experimental
results performed; and, finally, Sect. 6 contains the
concluding remarks.
2 THE NSGA-II FOR INTERIOR
ILLUMINATION DESIGN
Solve the interior illumination design problem means
satisfying multiple constraints involved but often in
conflict, showing a natural multi-objective approach.
Multi-objective optimization problems are character-
ized by having two or more objective functions to be
optimized; therefore, in contrast to single-objective
ones, the goal becomes to determine the set of best
tradeoffs between all the conflicting criteria, whose
set is called Pareto optimal set.
In this work, for solving the described problem,
we propose the well-known NSGA-II algorithm, in
which we developed a novel chromosomal represen-
tation of solutions, specifically tailored for lighting
design optimization. Each individual represents a
possible illumination configuration, and it is coded
as a vector of variable length, containing a set of
lamp specifications, that is the set of features describ-
ing the luminaries in the 3D environment, including
position and orientation, intensity, color temperature
of light, and model of light fixture (wall or ceiling
mount). Special operators of crossover and mutation
have been designed to handle this peculiar chromo-
somal representation. The design of such operators
is, however, facilitated by the transparency of the rep-
resentation itself. Therefore, our approach is intro-
duced especially to deal with representation of com-
plex structured individuals, and it ensures more flexi-
bility with respect to previous proposals.
The Non-dominated Sorting Genetic Algorithm
II (NSGA-II) (Deb et al., 2000), is an elitist multi-
objective genetic algorithm that performs well with
real world problems, producing Pareto-optimal so-
lutions to the optimization problem. The elitist ap-
proach favours the best solutions of a population by
giving them an opportunity to be directly carried over
to the next generation. This strategy makes sure that
the best fitness values do not deteriorate during the
evolution, and it enhances the probability of creating
better offspring. The elitism is integrated in the al-
gorithm by selecting the next-generation population
of size N among the best individuals from the off-
spring and the parent population combined together
(size 2N). This selection strategy, named crowded
tournament selection, takes into account two criteria:
the non-domination and the crowding distance of the
individuals. The first is the non-domination rank of
the solution in the population, and it is used to classify

the entire 2N population into non-dominated fronts.
The second criterion is a measure of the search space
around the solution, which is not occupied by any
other solution in the population. Giving preference to
solutions that are less crowded (with larger crowding
distances) ensures a better spread among the solutions
during the evolution. These conditions make sure that
non-dominated individuals belonging to a high-rank
front and residing in a less crowded area, are selected
to reproduce more than others. The result of the al-
gorithm is the set of non-dominated solutions of the
whole final population, namely the Pareto front.
In the implementation of the NSGA-II algorithm
proposed in this paper, at each step t of evolu-
tion, there is a population P
(t)
=
{
I
i
}
, which el-
ements are individuals, coding a lighting solution:
I =
h
L
1
, L
2
, ··· , L
L
i
, and L =
h
d,
{
C,W
}
, p, l, w, k
i
.
The genetic code of an individual I is a ordered set of
lamp descriptions L, in which d is a code identifying
the type of commercial lamp, the second parameter
specifies the type of placement: C for ceiling or W
for wall. The vector p specifies the 3D coordinates
of the lamp placement, l is the intensity of the lamp
in lumen, w its electrical consumption in watt, and
k the color temperature in Kelvin degrees. Note that
the number of lamp description L in a single individ-
ual is not fixed, but constrained: L
MIN
≤ L ≤ L
MAX
.
The initial population P
(0)
is generated randomly, us-
ing a set of predefined real lamps, each with a set of
feasible combinations of intensity l and color temper-
ature k. The type of lamp d specifies if the lamp can
be mounted on the ceiling or on walls. The variation
of the population is based on two fundamental opera-
tions: crossover and mutation. Given two individuals,
I
1
=
D
L
(1)
1
, ··· , L
(1)
L
(1)
E
, and I
2
=
D
L
(2)
1
, ··· , L
(2)
L
(2)
E
,
we define as two-points crossover the following func-
tion:
χ(
h
I
1
, I
2
i
) =
D
L
(1)
1
, ··· , L
(1)
i
, L
(2)
i+1
, ··· , L
(2)
j
, ··· , L
(1)
j+1
, ··· , L
(1)
L
(1)
E
,
D
L
(2)
1
, ··· , L
(2)
i
, L
(1)
i+1
, ··· , L
(1)
j
, ··· , L
(2)
j+1
, ··· , L
(2)
L
(2)
E
(1)
where i and j are two random integers such that
1 < i < j < min{L
(1)
, L
(2)
}. Note that χ(·) takes two
individuals as input and returns two modified individ-
uals. The mutation function ω(·) operates on a single
individual, and it is the composition of two different
levels of mutation. The upper level is that of the or-
dered set of lamp descriptions, and it is mutated as
following:
ω
U
(I ) =
(
I \ L
i
if r < 0.5
I
S
{
L
L+1
}
if r > 0.5
(2)
where r, here and in all the following equations, is a
random number in range 0 ···1, i is a random integer
in range 1···L. The lamp description L
L+1
is a new
lamp taken randomly from the set of possible lamps.
Mutation at the lower level, that of single lamp de-
scription, is given by:
ω
L
(L) =
h
d
0
,
{
C,W
}
, p, l, w, k
i
if r > π
d
h
d,
{
C,W
}
, p + ∆p, l, w, k
i
if r > π
p
h
d,
{
C,W
}
, p, l
0
, w, k
i
if r > π
l
h
d,
{
C,W
}
, p, l, w, k
0
i
if r > π
k
(3)
where d
0
is a new lamp code, extracted randomly from
the set of available types of lamps, l
0
is a new level of
illumination, selected randomly from the set of possi-
ble light intensities for the lamp of type d, similarly
for k
0
. The displacement ∆p of lamp positioning is
computed in a random direction from the center p,
and with random offset within a neighbourhood, de-
creased in the course of the evolution. The param-
eters π
{d,p,l,k}
are the mutation probabilities for, re-
spectively, lamp code, lamp position, lighting level,
and color temperature.
During the evolution the entire population is re-
placed, P
(t+1)
← P
(t)
, using the crowded tournament
selection strategy described above. The size of the
population remains constant during evolution. In this
last equation the tournament dominance criterion is
based on two contrasting objectives: the quality of
the light, and the saving of energy. In turn, the light
quality is computed as the combination of two objec-
tives: achieving an illuminance level closest as possi-
ble to the given target, an obtaining light distribution
uniform enough in the given space. The evaluation
of light quality is preformed on samples S, surfaces
distributed in the interior space, that can be placed
in ways convenient to ensure best lighting quality in
key portions of the space. Compliance with the target
level of light, and degree of uniformity, are combined
in a single fitness f
1
of the individual I, with the fol-
lowing computations:
t (I) =
1
M
M
∑
i=0
|
S
i
− T
k
(4)
u(I) =
s
1
M
M
∑
i=0
S
i
− S
2
(5)
f
1
(I) = wt(I) + (1 − w)u(I) (6)
where S
i
is the illumination measured on the sample
S
i
produced by the lighting configuration of individual

I, and M is the number of samplers S. Note that treat-
ing t(I) and u(i) as separate fitness in multi-objective
optimization would be incorrect, because are not con-
flicting. It can be easily verified in the limit case of
an individual
ˆ
I that illuminates all samplers exactly at
target level T , from equations (4) and (5) we obtain
t(
ˆ
I) = u(
ˆ
I) = 0. The weight w control the balance be-
tween the desired compliance with the target level of
light and uniformity, the default value used in all re-
ported results is 0.5. Energy consumption represents
the second fitness and it is quantified as the overall
power consumption of the lamps (measured in Watt)
divided by the volume of the room:
f
2
(I) =
1
V
N
∑
i=0
C
i
(7)
where C
i
is the amount of Watts consumed by the i-th
lamp of the individual I, V the volume of the interior
environment in m
3
, and N the number of lamps com-
posing the solution.
In the presented problem of lighting optimization
there are some conditions on the design process to be
satisfied, therefore a constraint handling method has
to be considered as well. The constrains in question
concern positioning the lamps inside the interior en-
vironment, where a lamp should be mounted on the
walls or on the ceiling in accordance with its model of
light fixture and in contact with the room surface, and
two lamps cannot be placed in the same location. Fur-
thermore, depending on the room design, there might
be some areas where the lamp placement is not al-
lowed, for example in presence of windows, pillars,
or supporting beams. The constraint specifications
are provided to the system within the 3D model of the
environment itself. The walls and ceiling are struc-
tured as a discrete grid of vertices, each representing
a feasible position for a lamp. With this approach,
the set of constraints can be effortlessly reformulated
for different experiments, ensuring absolute flexibil-
ity in the design process. Since the satisfaction of the
above constraints is mandatory for the problem, they
can be referred as hard constraints. To handle them,
we adopted a strategy based on preserving feasibility
of solutions, where crossover and mutation operations
are specifically designed to always produce feasible
offspring from feasible solutions.
3 BLENDER AS SIMULATION
ENVIRONMENT
For the purpose of evaluating a lighting configuration,
a virtual environment able to accurately reproduce
the architectural space and its spectral reflectometric
properties is needed. Moreover, a physical simula-
tion platform must be considered as well for correct
illumination calculation in sample points of the archi-
tectural space.
This paper investigates the adoption of the 3D
graphic software Blender as a unified solution to the
two requirements stated above. Firstly, Blender is
the most comprehensive open-source 3D computer
graphic tool available. It is particularly suitable for
modeling architectural interiors, with the possibility
of importing components from CAD files. Secondly,
Blender provides a physically based rendering engine,
named Cycles, able to exhaustively evaluate lighting
configurations needed for solving the inverse lighting
problem. Moreover, Blender embeds a Python inter-
preter, which can run scripts supplied by the user, in
order to extend its functionalities. Thanks to its intrin-
sic versatility, Blender has already been applied to a
number of different problems, from the medical field
(Daenzer et al., 2007) to industrial applications (Plebe
and Grasso, 2016).
The algorithm here presented has been imple-
mented in the form of a Blender script, composed
of 9 main Python modules. The first group of mod-
ules, which rely on Blenders modeling features, per-
forms the simulation environment set-up. The archi-
tectural interior scene of interest is represented inside
the computer graphics software by means of geomet-
ric meshes and material shaders. The room structure
(walls, floors, ceiling) and its furnishings are defined
by the meshes, while colors, textures and reflectiv-
ity properties of the objects are specified through the
shaders. When evaluating the fitness of a solution,
the 3D scene is enriched with further supporting ele-
ments: the proposed lamps illuminating the environ-
ment, and basic 3D structures employed to perform
individual lighting measurements at locations of inter-
est. Using a sophisticated ray-tracing render engine,
Blender executes an accurate simulation of illumina-
tion, taking into account a variety of environmental
factors. The second group of python modules to ex-
tract light intensity values and their distribution across
the interior space processes the obtained rendered im-
ages.
These outputs are used, in the third group of mod-
ules, by the genetic algorithm to compute the actual
fitness values of a solution. After evaluating the en-
tire current population and selecting the mating pool,
the genetic operators of crossover and mutation are
applied to generate the offspring. The operators are
specifically implemented for the presented case prob-
lem, as mentioned in in the previous sections, with the
support of an evolutionary computation python
Quality
Consumption
Quality
Consumption
Quality
Consumption
Quality
Consumption
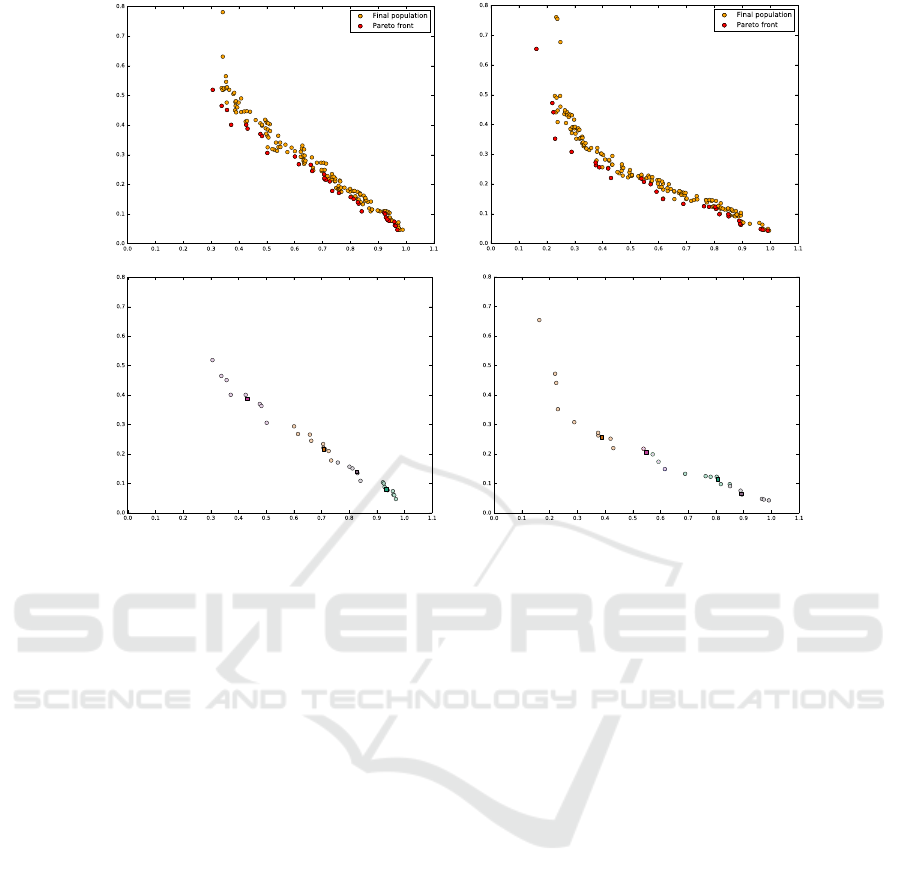
Figure 1: Final populations of the optimization in the two case studies: the coffee shop on the left, and the shopping mall on
the right. The plots in the upper row are the complete populations at the end of the optimization, and the Pareto fronts, in
the lower row there are the results of the clustering, solutions with the star mark are the representative solutions of the four
clusters.
framework named DEAP (Fortin et al., 2012), which
allows to freely customize any component of the ge-
netic algorithm workflow. At the end of the execu-
tion of the algorithm, the obtained result is the Pareto
front of the final population, namely the set of non-
dominated solutions, each one of them representing
an optimal lighting configuration for the given inte-
rior environment. Optionally, a photorealistic render-
ing of the illuminated scene can be generated.
4 CLUSTERING THE FINAL
POPULATION
As in most multi-objective optimization problems,
our lighting design system typically generates too
many solutions in the final Pareto set, and selecting a
single one that best reflects the preferences of the ar-
chitect can be a daunting task. A considerable amount
of research effort has been devoted to alleviate this in-
convenience in the general multi-objective case, with
several proposed methods that reduce the Pareto op-
timal set to a set of solutions that is attractive to the
decision maker. A large part of the proposed methods
assumes that the preferences of the decision maker are
well known in advance, and can be expressed in math-
ematical terms and incorporated in the optimization
algorithm (Jaimes and Coello, 2013; Bechikh et al.,
2015). The situation of the architectural lighting de-
sign is different. Although the objectives defined in
our optimization problem capture important require-
ments of the design process, there are aesthetic and
stylistic components of the design process that elude
mathematical formulations. The great advantage of a
tool like the one here proposed is for the architect to
drastically restrict the search space of solutions, and
to concentrate his or her creativity on a small number
of simulated solutions. It is difficult to prescribe in
advance any preferred part of the Pareto front, in prin-
ciple the entire front can offer attractive solutions to
the lighting designers, the choice is up to their exper-
tise and aesthetic disposition. For this reason we fo-
cused on methods commonly classified as a posteriori
(Zio and Bazzo, 2010), where the selection of a small
subset of solutions is made on the entire final approx-
imate Pareto front, computed without the incorpora-
tion of preferences from the the decision maker.
First, we partitioned the set of solutions into a
predefined number of clusters N
c
, using the subtrac-
tive clustering algorithm (Chiu, 1994; Zio and Bazzo,
2012). Let us define O the set of vectors in the fitness

space of the final solutions F : O = {f (S )|S ∈ F }.
The vectors are normalized with all dimensions in
range [0, 1], we call
¯
O the set of normalized vectors.
For each solution a “potential” function ψ is intro-
duced, that captures the neighborhood size of the so-
lutions: ψ
(0)
(o
i
) =
∑
o∈
¯
O
e
4
r
I
2
k
o
i
−o
k
, o
i
∈
¯
O. The su-
perscript (0) is meant because the previous equation
provides the initial values of the potentials, which are
updated recursively, each time identifying as a cluster
center the solution with the largest potential:
c
k
= argmax
o∈
¯
O
n
ψ
(k)
(o)
o
, (8)
∆ψ
(k)
(o
i
) = e
4
r
O
2
β
k
o
i
−c
k
k
ψ
(k)
(c
k
), o
i
∈
¯
O, (9)
ψ
(k+1)
(o
i
) = ψ
(k)
(o
i
) − ∆ψ
(k)
(o
i
), o
i
∈
¯
O.(10)
Equation (8) computes the center of the k-th cluster,
the recursive loop is terminated when k = N
c
, the pre-
defined number of clusters. The parameters r
I
and r
O
act effectively as radii, influencing, respectively, the
range of neighborhood of a solution and the close-
ness of distinct cluster. Their values are computed
as a function of the number of desired clusters N
c
:
r
I
=
2
N
c
, r
O
=
2.5
N
c
.
All solutions S in F are partitioned in the clus-
ters according to the distance of the vectors in fitness
space to the cluster centers. Calling
¯
S
(k)
the solution
in F that is center of cluster k, corresponding to the
normalized vector c
k
, the partitioning is done as fol-
lowing:
Q =
S : arg max
k∈[1..N
c
]
n
f(S) − f(
¯
S
(k)
)
o
= 1
,
··· ,
S : arg max
k∈[1..N
c
]
n
f(S) − f(
¯
S
(k)
)
o
= N
c
.
(11)
The solutions offered to the architect for her subjec-
tive evaluation and final decision are the centers of the
clusters.
5 RESULTS
We evaluated empirically our lighting optimization al-
gorithm on two case studies. As discussed in the In-
troduction, a satisfactory lighting quality is highly de-
pendent on the visual tasks that are to be performed
in the interior space, and on specific requirements
of visual interest within the space. These specifica-
tions are passed to the model with the placement of
the samplers and fixing the target illumination level.
All genetic parameters of the model have been tuned
in a preliminary phase on simpler and smaller rooms,
and these settings did not required further tweaking in
the two case studies. The chosen case environments
are both complex architectural interiors, with irreg-
ular and non-convex planimetries, demonstrating that
there are no limitations in the flexibility of application
of the presented system. The first case study environ-
ment is the interior of a coffee shop. The architec-
ture of this room has size of 14 × 10 × 2.8 meter, and
it is characterized by a long and narrow dining area
leading to a wider space with a lounge room and a
bar counter. A total of 13 samplers have been used
to evaluate illumination levels, placed in key areas
where light should create visual interest. The genetic
algorithm has been run with a population of 200 indi-
viduals, the final population is shown in Fig. 1, where
it is possible to appreciate how the solutions smoothly
span a large Pareto front of the two fitness. The final
solutions are clustered in order to provide a small and
manageable subset of solutions, we used four clus-
ters in both the cases here experimented. It is then a
designer choice to pick a desired solution among the
four proposed, as a tradeoff between lighting quality
and energy consumption. The Fig. 2 shows photo-
realistic renderings of two solutions belonging to the
Pareto front. The second case study is the hall of a
shopping mall, of size 12 × 11 × 4.0 meter. It is com-
posed of a central area connected to secondary small
shop. The main space contains a column with display
stands and an area serving as lounge room, while the
secondary area for the small shop has a lower ceiling
level and contains several product racks and a counter
with the cash register. A total of 14 samples have been
used, with a genetic population of 200 individuals.
The Fig. 3 shows two optimal solutions of lighting
configurations. As in the previous case study, there
is a wide and smooth coverage of the Pareto front.
However, as can be seen in Fig. 1, the Pareto front of
this case study reached even better levels of consump-
tion fitness than the previous one. This result can be
explained by the brighter shading of walls and floors
in the mall environment (pale yellow and white) re-
flecting more light than the deep red and beige color
tones of the coffee shop, which requires more intense
light sources in order to reach the same perceived il-
lumination level. Nonetheless, the visual results are
rather satisfying in both case studies, demonstrating
how the presented algorithm can be a suitable tool to
effectively design light configuration for a variety of
different environments, with minimum effort from the
user.

Figure 2: Two interior views of two different optimal lighting configurations in the coffee shop environment.
Figure 3: Two interior views of two different optimal lighting configurations in the shopping mall case study.
6 CONCLUSIONS
Most part of life in industrial contemporary society
is spent indoor, with activities going on even when
daylight is over. Therefore there is a demand for
artificial lighting, which is often a critical compro-
mise between the achievement of light level allowing
full photopic vision everywhere in the interior space,
and energy consumption. The strategy here proposed
takes as input an arbitrary layout of interior space, in-
cluding realistic furniture and materials, and a list of
possible realistic light sources, generating as output

solutions, optimal under the compliance with the tar-
get illumination level, and the consumption of elec-
tric power. However, for designing an accurate in-
terior illumination and able to not be glare nor inad-
equate, it is needed to optimize multiple constraints,
often conflicting, which make hard the use of classical
computational methods. Thus, a multi-objective ge-
netic algorithm has been developed for interior light-
ing design, with the main aim to (1) optimize the level
of luminous intensity, and (2) maximizing the energy
saving. Moreover, a clustering of solutions approach
has been also developed, in order to reduce the search
space and the Pareto front, helping, then, the deci-
sion maker in the choice and selection of the more
appropriate illumination. In combination to NSGA-
II, the proposed computational tool is based also on
a 3D graphic software, that is Blender, for providing
a rendering engine for direct illumination and repro-
duce the architectural space to be lighted. Two dif-
ferent case studies have been considered in order to
evaluate the accuracy, and efficiency of the illumina-
tion produced, based on different complex shapes of
the architectural interiors (irregular and non-convex),
which make harder the design of an uniform illumina-
tion distribution. Finally, from the analysis of the sev-
eral experiments performed, the presented algorithm
has showed to be a suitable and effective tool for in-
terior lighting design in a variety of different environ-
ments.
REFERENCES
Bechikh, S., Kessentini, M., Said, L. B., and Gh
´
edira, K.
(2015). Preference incorporation in evolutionary mul-
tiobjective optimization: A survey of the state-of-the-
art. Advances in Computers, 98:141–207.
Bertoldi, P., Hirl, B., and Labanca, N. (2012). Energy effi-
ciency status report. Technical report, European Com-
mission – Institute for Energy and Transport.
Caldas, L. (2016). Painting with light: An interactive evo-
lutionary system for daylighting design. Building and
Environment. doi: 10.1016/j.buildenv.2016.07.023.
Chiu, S. L. (1994). Fuzzy model identification based on
cluster estimation. Journal of Intelligent & fuzzy sys-
tems, 2:267–278.
Cuttle, C. (2015). Lighting design: a perception-based ap-
proach. Routledge, New York.
Daenzer, S., Montgomery, K., Dillmann, R., and Un-
terhinninghofen, R. (2007). Real-time smoke and
bleeding simulation in virtual surgery. In Westwood,
J. D., Haluck, R. S., Hoffman, H. M., Mogel, G. T.,
Phillips, R., Robb, R. A., and Vosburgh, K. G., ed-
itors, Medicine Meets Virtual Reality, pages 94–99.
IOS Press, Amsterdam.
Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. (2000).
A fast elitist non-dominated sorting genetic algorithm
for multi-objective optimization: NSGA-II. In In-
ternational Conference on Parallel Problem Solving
From Nature, pages 849–858.
Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A., Parizeau,
M., and Gagn
´
e, C. (2012). DEAP: Evolutionary algo-
rithms made easy. Journal of Machine Learning Re-
search, 13:2171–2175.
Gordon, G. (2014). Interior lighting for designers. John
Wiley, New York.
Jaimes, A. L. and Coello, C. A. C. (2013). Interactive ap-
proaches applied to multiobjective evolutionary algo-
rithms. In Doumpos, M. and Grigoroudis, E., editors,
Multicriteria decision aid and artificial intelligence:
Theory and applications, pages 191–207. John Wiley,
New York.
Livingston, J. (2015). Designing with light: the art, science,
and practice of architectural lighting design. John Wi-
ley, New York.
Palmer, S. (1999). Vision Science – Photons to Phe-
nomenology. MIT Press, Cambridge (MA).
Plebe, A. and Grasso, G. (2016). Simulating fire outbreaks
in industrial plants. In Blender Conference, Amster-
dam.
Sansoni, P., Farini, A., and Mercatelli, L., editors (2015).
Sustainable Indoor Lighting. Springer-Verlag, Berlin.
Wunderlich, C.-H. (2003). Light and economy: an essay
about the economy of prehistoric and ancient lamps.
In Chranovski, L., editor, Lychnological news, pages
251–264. LychnoServices, Hauterive (Suisse).
Zio, E. and Bazzo, R. (2010). Multiobjective optimization
of the inspection intervals of a nuclear safety system:
A clustering-based framework for reducing the pareto
front. Annals of Nuclear Energy, 37:798–812.
Zio, E. and Bazzo, R. (2012). A comparison of methods
for selecting preferred solutions in multiobjective de-
cision making. In Kahraman, C., editor, Computa-
tional Intelligence Systems in Industrial Engineering
With Recent Theory and Applications, pages 23–43.
Atlantis Press, Paris.
